当下是金融经济的飞速发展时代, 个人信用评估数据普遍表现为高维度、高复杂度等特点, 无关、冗余的评价因子会直接影响信用评估模型的准确性, 而评价因子的优劣取决于特征选择方法的选择是否合理、全面. 目前常用的特征选择方法包括过滤法(filter)、包裹法(wrapper)、嵌入法(embedded)^[1]. Filter方法利用统计学方法评估变量与预测变量间的关系, 该方法优势在于计算简单、速度快; wrapper方法通过对生成的子特征组合与其他组合进行比较, 依赖于学习算法的准确度; embedded方法是通过在训练模型的过程中根据准确度学习并选择出最优的特征组合. 本文选用的信息量模型(information value)与XGBoost (extreme gradient boosting)分别是Filter和Embedded方法的实现. 结合两种不同的特征选择方法不仅能够提高输入变量的有效性同时增强了整个模型的可解释性.

近二十年来, 信用风险评估方法主要分为两部分: 统计学方法和机器学习方法. Fernandes等^[2]利用逻辑回归算法建立了信用评估模型, 并通过实验证实了logistic算法在信贷评估业务的可行性, 成为了主流的统计学方法之一. 郭畅^[3]将IV与Lasso-Logistic结合, 通过IV排除风险识别能力、稳定性较差的变量, 整体提升了信用预测模型的效果. 然而随着信息技术的迅猛发展, 传统的统计学评分模型暴露出3个主要问题: 一是模型单一; 二是处理数据维度较小; 三是主要以专家评价法为主, 预测结果缺乏客观性^[4]; 为了解决这些问题, 学者们尝试将机器学习建模技术应用在个人信用评估业务中, 其中主要包括决策树^[5]、BP神经网络^[6]、支持向量机(SVM)^[7]等模型, 但单一机器学习模型处理的数据维度和预测精度有限, 为决定该问题, 集成算法逐渐应用在个人信用评估领域中. Twala^[8]、Zhu等^[9]使用5类信用数据证实了集成算法在信用评估领域表现出更优的预测效果并且多个分类器组合显著提高了整个模型的学习能力; 萧超武等^[10]基于组合分类模型随机森林(RF), 发现RF模型分类准确率、稳定性更高, 并且噪声容忍度高, 训练过程中能够效避免过拟合现象. 周永圣等^[11]首次将XGBoost和随机森林模型两种不同的集成算法融入到信用评估中, 证实了XGBoost算法基于特征重要性能有效剔除信用数据冗余变量, 但该实验缺少对比实验且变量选取较随意、可靠性较低. 李欣等^[12] 提出一种基于改进网格搜索优化的XGBoost模型, 实验结果显示F-score和G-mean均优于其他机器学习模型, 进一步表明集成算法的优越性.

鉴于个人信用数据维度高、变量冗余度高的特点, 本文采用IV-XGBoost组合特征选择方法对随机森林模型进行优化, 不仅避免了传统特征选择方法的单一性同时能够更好解决数据维度过高的问题; IV值剔除冗余、无预测能力的变量, XGBoost利用变量打分机制筛选变量, 采样逐步排除法输出最优特征集, 相比根据特征重要性排名随意选取的方法, 该组合特征选择模型更加合理并且可信度高; 此外超参数组合会直接影响RF模型的预测效果, 利用网格-5折对RF中的重要参数进行参数寻优. 最后实验结果表明基于新型的组合特征选择方法的随机森林相比其他单一的机器学习方法以及原始的集成算法有着更高的稳定性和预测准确率.

1 特征选择理论与方法 1.1 证据权重(WOE)与信息价值(IV)

WOE (weight of evidence)即为证据权重, 通过编码的方式将自变量表示成其对目标变量的区分程度的形式. 根据WOE值大小反映某属性对目标的影响, 若同一属性的不同划分标准计算出的WOE值越大, 则表明该属性对目标属性的区分度越大, 其计算公式:

$ WOE({{x}}) = \ln \left( {\frac{{p{y_{_i}}}}{{p{n_T}}}} \right) = \ln \left({{\frac{{{y_i}}}{{{y_T}}}} \mathord{\left/ {\vphantom {{\frac{{{y_i}}}{{{y_T}}}} {\frac{{{n_i}}}{{{n_T}}}}}} \right. } {\frac{{{n_i}}}{{{n_T}}}}}\right) $

(1)

其中, WOE(x)是变量进行分箱处理后第i组的WOE值, 其中py_i是该组未响应样本(‘未违约客户’)占比; pn_i是响应样本(‘违约客户’)占比; y_i是某变量第i个属性对应的未响应样本数, y_T是所有未响应样本数; n_i是某变量第i个属性对应的响应样本数, n_T是是所有响应样本数.

信息量(IV)是基于WOE算法改进的衡量指标, 其计算本质是某变量所有属性的WOE值加权求和, 其值大小反映了变量对目标变量的预测能力. IV通常应用在风控模型中评价因子的选择, 其计算公式:

$ \begin{split} I{V_{}} &= \sum\limits_i {\left( {\frac{{{y_i}}}{{{y_T}}} - \frac{{{n_i}}}{{{n_T}}}} \right)} \times \ln \left[ {{{\frac{{{y_i}}}{{{y_T}}}} \mathord{\left/ {\vphantom {{\frac{{{y_i}}}{{{y_T}}}} {\frac{{{n_i}}}{{{n_T}}}}}} \right. } {\frac{{{n_i}}}{{{n_T}}}}}} \right] \hfill \\ \hfill \\ & = \sum\limits_i {\left( {\frac{{{y_i}}}{{{y_T}}} - \frac{{{n_i}}}{{{n_T}}}} \right)} \times WO{E_i} \end{split}$

(2)

其中, $WO{E_i}$ 是某变量进行离散化处理后第i组的WOE值; 其中 ${y_i}$ 是某变量第i个属性对应的未响应样本数; T是所有未响应样本数; ${n_i}$ 是某变量第i个属性对应的响应样本数; ${n_T}$ 所有响应样本数.

1.2 XGBoost特征选择 1.2.1 算法原理

XGBoost^[13]是基于梯度提升算法GBDT改进的新型集成学习算法, 其主要算法思想是将多个分类精度较低的子树模型进行迭代组合从而构建出准确度、稳定性更强的模型. XGBoost在 GBDT的原目标函数上加入了正则项, 因此加快了收敛效率的同时降低过拟合风险. 其变换后的公式如下:

$ {H^{\left( i \right)}} = \sum\limits_{i = 1}^n {\left( {l\left( {{y_{i, }}{{\hat y}_i}} \right) + \Omega \left( {{f_i}} \right)} \right)} $

(3)

$ \Omega (f) = \gamma N + \frac{1}{2}\lambda ||O|{|^2} $

(4)

式(3)中 $ l\left( {{y_{i, }}{{\hat y}_i}} \right) $ 是预测值 $ {\hat y_i} $ 与 ${y_i}$ 之间的平方差损失函数.

式(4)计算所有子树的复杂度总和, 其中 $ \Omega (f) $ 是正则化项; N代表子树中叶子节点个数; $ \lambda $ 代表了叶子节点权重O的惩罚系统值; $ \gamma $ 是衡量树的分割难度大小, 用于控制树生长.

XGBoost与GBDT的不同之处在于前者是以泰勒公式二阶导展开, 从而加快了函数收敛速度且提高了模型预测准确度, 其变换后目标函数为:

$ {H^i} = - \frac{1}{2}\sum\limits_{j = 1}^N {\frac{{{{\left( {\displaystyle\sum\limits_{i \in {I_j}} {{g_i}} } \right)^2}}}}{{\displaystyle\sum\limits_{i \in {I_j}} {{h_i} + \lambda } }}} + \gamma N $

(5)

其中, $ {I_j} \in \left\{ {q\left( {{X_i}} \right) = j} \right\} $ , $ {h_i} $ 为 $ [l(\alpha )]'' $ , ${g_i}$ 为 $ [l(\alpha )]' $ .

1.2.2 XGBoost特征选择原理

机器学习中特征选择是建模工作中至关重要的环节, XGBoost采用梯度提升的原理对样本进行分类, 该模型是根据计算各个变量的重要性来进行特征选择, 其主要原理是子树节点在分裂的同时计算其信息增益量, 并选择差值最大的指标作为下一次的分裂属性, 直到完成全部计算. 本文根据XGBoost计算后输出的特征重要性排名, 由低到高逐个加入到特征集并计算RF模型准确度, 选取准确度最高的特征集作为最终特征选择的结果.

2 改进的随机森林个人信用评估模型 2.1 随机森林算法

随机森林是Breiman^[14]提出的基于树的集成学习算法, 根据特征数对每个样本选取分裂指标进而构建单棵子树. 随机森林旨在集成多个弱分类器来构建一个强分类器, 各个基分类器之间相互互补, 降低了方差以及过拟合的风险, 从而提高模型的性能.

RF是在Bagging集成学习和随机子空间的基础上进一步优化的集成学习算法, 由服从独立同分步随机向量 ${\theta _i}$ 生成的i棵树 $\left\{ {{W_i}\left( {x, {\theta _i}} \right), i = 1, 2, 3,\cdots} \right\}$ , i棵子树最终形成集成树模型. RF模型的最终结果采用基分类器中平均票数最多的结果作为输出. 随机森林模型算法流程如下:

(1)采用Bootstrap方法有放回的从总量为W的训练集中随机抽取形成N个子训练集 $\left\{ {{N_{\text{i}}}} \right\}$ , $i \in \{1, 2, 3, 4, $ $ 5, \cdots, k\}$ 每个训练子样本对应一棵CART树.

(2)随机森林由i棵分类树构成, 每棵分类树的子节点在进行分裂时随机选择分裂指标数n $\left( {n \le M} \right)$ , 其中M为总样本的指标个数, 根据衡量指标大小选择最优分割指标进行划分.

(3)不断重复步骤(2), 直至森林中所有的子树构建完成.

(4)由i棵子树形成最终随机森林, 将待测试样本引入构建好的随机森林, 最终结果采用投票选举的方式产生. 其最终的决策函数 $ {{P} _{rf}}(X) $ 由式(6)得出:

$ {{{P}} _{rf}}(X) = \arg \mathop {\max }\limits_Y \sum\limits_{i = 1}^k {I\left( {w\left( {X, {\theta _i}} \right) = Y} \right)l\left( \cdot \right)} {Y_c} $

(6)

其中, $ w\left( {X, {\theta _i}} \right) $ 为单个分类决策树; $ l\left( \cdot \right) $ 为指标函数表示满足式子的样本总数; k为待建子树棵数; Y为目标变量, 解释为是否违约; $ {\theta _i} $ 是随机变量.

随机森林的决策结果取决于每一棵子树的训练结果, 分裂指标的选取决定了分裂标准, 随机森林一般采用基尼指数(Gini), 其大小衡量了各节点混乱程度, 其计算如下:

$\begin{split} Gini\left( c \right) &= \sum\limits_{y = 1}^u {\sum\limits_{y' \ne y}^{} {{p_y}\left( {y|c} \right){p_{y'}}\left( {y'|c} \right)} } \\ &= 1 - \sum\limits_{y = 1}^u {p{{\left( {y|c} \right)}^2}^{}}\end{split} $

(7)

其中, $ p\left( {y|c} \right) $ 为客户类别y在子树c节点的条件概率; 一般来说基尼指数越大, 表明在该节点处的数据越趋向均匀分布, 样本越纯; 当Gini指数为0时, 表明该节点所有样本均为一个类.

2.2 改进的RF模型流程

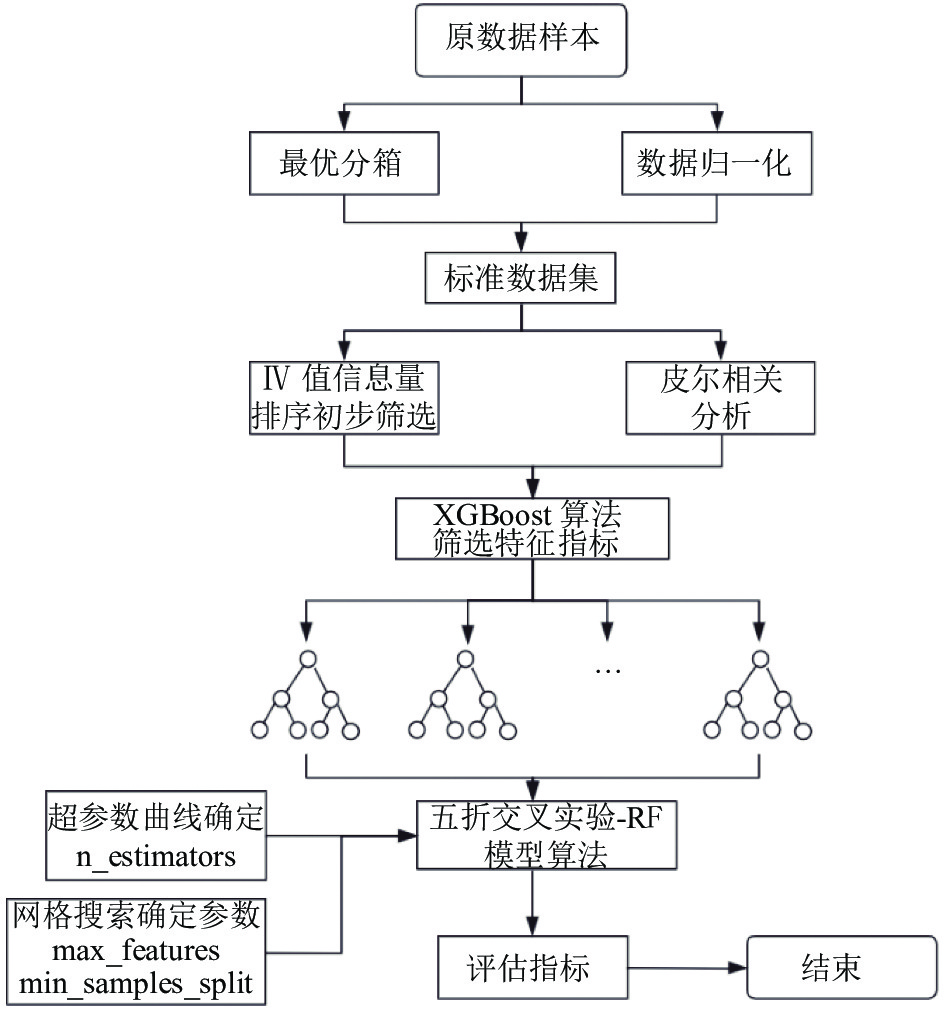
基于IV-XGBoostRF的个人信用评估算法模型流程图(如图1), 其运行步骤如下:

步骤(1)剔除异常值、重复值、缺失值, 对数据中的连续型变量采用最优决策树分箱进行离散化、归一化.

步骤(2)采用皮尔逊相关分析排除变量间的强相关变量进而排除变量间共线性可能; 同时进行WOE编码以及计算分箱后各变量属性的IV值, 并通过IV值筛选产生初步的特征集; 根据XGBoost输出该特征集的重要性完成组合特征选择.

步骤(3)利用超参数曲线确定森林大小参数n_estimators、网格搜索确定其他重要参数; 为了减少训练集、测试集划分的随机性, 实验过程采用五折交叉验证, 将数据集A随机分为5份训练样本, A₁, A₂, …, A₅, 每一个样本A_i都逐次作为训练数据, 其余为测试数据.

步骤(4)模型评估.

3 实证分析 3.1 实验数据

实验数据集来自UCI德国某银行信用数据, 利用该数据集验证改进的随机森林模型的可行性, 数据集主要从个人基本信息、账户信息、贷款信息3个方面对客户进行描述, 样本大小为1 000个样本, 其中正例700例, 反例300, 不平衡率为2.3, 具体的指标信息如表1所示.

3.2 数据预处理与分析

(1)变量分箱

选用最优决策树分箱, 通过比较Gini系数大小决定分箱点, 对数据集中R2 (贷款期限)、R5 (贷款金额)、R13 (年龄) 3个连续型变量进行决策树分箱同时计算IV、WOE值, 结果如表2所示.

(2)皮尔逊相关分析

根据计算得到各变量间相关性系数范围为0.01–0.4, 各指标间关联性均呈弱相关, 因此排除变量间共线性可能. 同时结果显示支票账户情况、贷款期限、信用记录特征与是否违约相关度较高.

3.3 特征选择

基于IV-XGBoost进行特征筛选, 具体步骤如下:

(1)根据信息价值计算公式分别计算20个指标对应IV值(如表3), 剔除信息量小于0.02的特征, 即R17、R19、R11、R18, 剩余16个待筛选特征.

(2)根据图2中XGBoost对16个特征的重要性排名结果, 采用逐步减小变量个数(如表4), 以准确度作为衡量标准最终选择XGBoost重要性排名前14的特征(加粗为准确度最高).

3.4 模型性能评估

经过信息值IV以及XGBoost特征选择后保留了14个信用评估特征, 使用超参数学习曲线结合网格搜索确定RF模型重要参数n_estimators=104、max_features=4、min_samples_split=3, 该参数组合下的RF评估性能最优. 为了进一步验证改进后的随机森林模型的性能, 实验分别与其他五种机器学习模型相比较; 实验过程采用五折交叉验证减小随机性对结果的影响, 据此作以下分析:

(1)根据表5实验结果, 改进后的随机森林的准确度分别高于默认参数下的随机森林、逻辑回归、支持向量机、BP神经网络模型0.90%、3.80%、2.70%、1.30%.

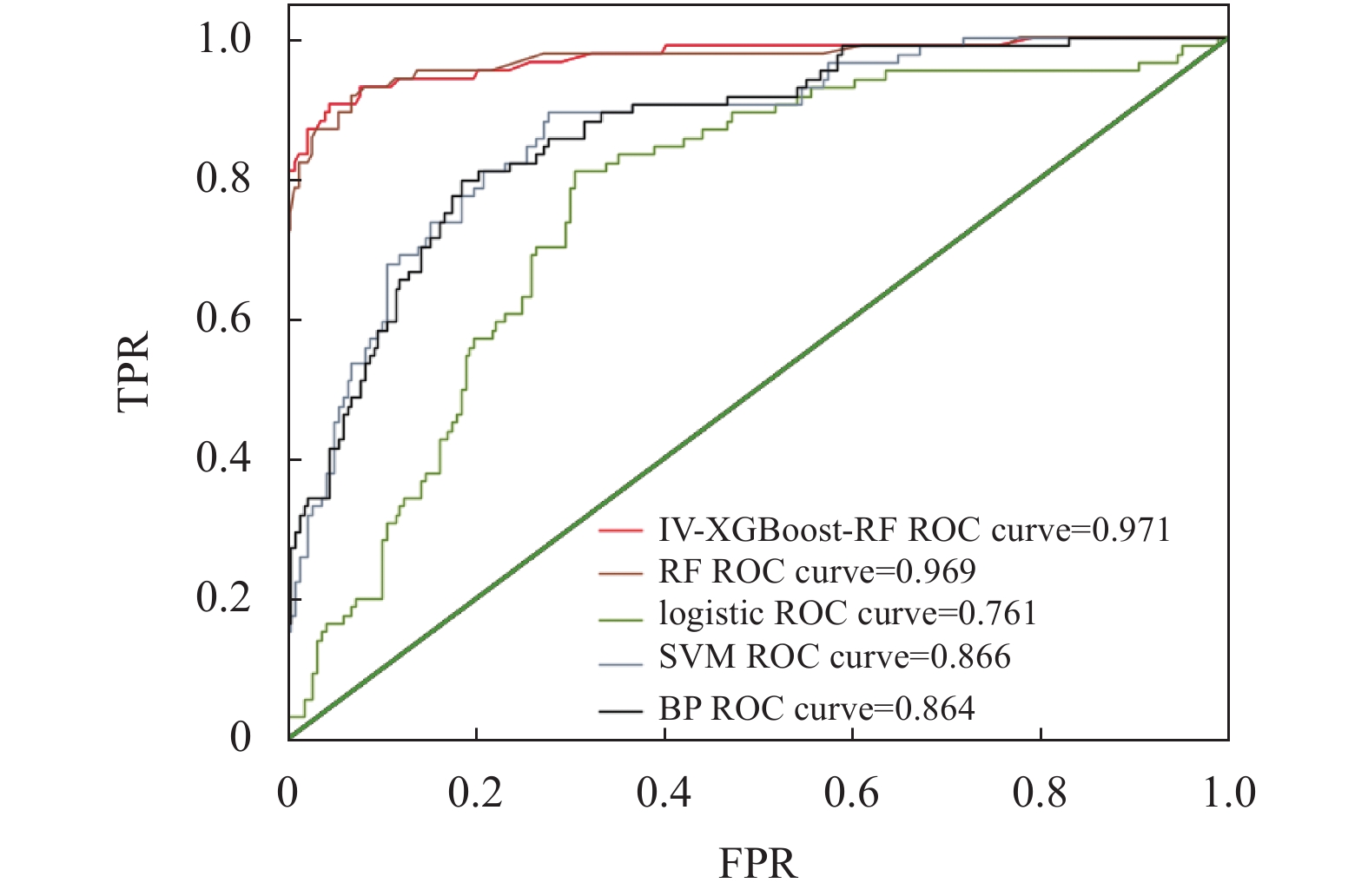
(2) ROC曲线用来衡量模型分类性能优劣的一种图像, ROC曲线越靠近左上方模型分类效果越好; 其ROC曲线下方于X、Y轴围成的面积为AUC值, 其范围在0–1之间, AUC值越高表明模型性能越优. 图3显示改进的随机森林模型AUC值高于其他模型, 其AUC值为到0.971, ROC曲线更靠近左上方.

(3)未改进的随机森林模型F-score为0.874 2, 改进后随机森林F-score为0.895 7, 有明显的提升.

4 结论与展望

本文提出了组合特征选择的方法, 首次将传统的风控指标-信息价值(IV)和新型集成学习方法XGBoost相结合, 以随机森林作为信用评估器. 现针对提出的改进方法作以下几点总结:

(1)根据组合特征选择结果总结出银行系统应该更关注贷款与账户相关信息, 如支票账户状态、信用记录、贷款期限、贷款目的、储蓄账户情况、固定资产等银行账户等因素; 个人基本信息中更关注就业情况、婚姻状况因素. 符合常理.

(2)基于IV-XGBoost的组合特征选择方法相比直接通过分类算法的特征重要性排序剔除特征更加合理且符合业务逻辑; 同时 IV计算量小且简单, 当数据维度较大时, 可以有效地减少模型训练时间从而进一步提高算法整体性能.

(3)与未改进的随机森林模型比较, 改进的随机森林模型Accuracy平均值提高0.90%, F-score提高了2.15%, AUC提高了0.20%, 证实本文提出的IV-XGBoost组合特征选择方法的有效性和可行性.

不足以及未来展望: 1)本文的实验还有一些不足, 由于条件有限实验数据集较小, 仅能证实特征选择方法和集成模型有效性和可行性, 在大数据集上该组合特征选择的效率高低并未得到证实; 2)面对大数据集的个人信用数据, 能否将大数据技术与集成学习算法相结合也是未来研究的主要方向.