2. 福建省应用数学中心(福建师范大学), 福州 350117;
3. 福建师范大学 数字福建环境监测物联网实验室, 福州 350117;
4. 福建师范大学 福建省网络安全与密码技术重点实验室, 福州 350007
2. Fujian Provincial Center for Applied Mathematics (Fujian Normal University), Fuzhou 350117, China;
3. Digital Fujian Environment Monitoring IoT Laboratory, Fujian Normal University, Fuzhou 350117, China;
4. Fujian Provincial Key Lab of Network Security and Cryptology, Fujian Normal University, Fuzhou 350007, China
5G技术的发展促使工业物联网得到全面提升, 使全球加速进入第4次工业革命时代[1]. 工业物联网在提升生产效率的同时, 会产生海量、超高维、复杂异构的实时流数据, 业界称之为工业数据流[2–4]. 这些流数据不能再做静态数据假设, 数据量大实时性强, 又必须在有限内存内处理[5,6], 从而工业物联网所产生的海量实时数据给数据流聚类分析带来了巨大的挑战.
近年来, 数据流聚类已经成为了工业物联网数据挖掘分析的关键性研究领域, 其目的是为了识别无界且无序观测流中的模式[5,7,8]. 数据流聚类技术通常是采用在线和离线两个阶段. 在线阶段主要通过优化数量和更新簇的位置, 以便更好地表示底层数据; 在离线阶段提取相关信息, 而不对数据进行存储并且重新评估所有的结果. 数据流聚类技术发展至今, 主要可以分为这3类: 基于距离的流聚类方法、基于网格的流聚类方法、基于预测的流聚类方法.
第1类: 基于距离的流聚类方法. 该类方法是最流行的方法, 它通过简单的插入规则来构建簇, 基于概要数据结构来总结与簇相关的观测值, 而不存储每个单独的数据点. 最具有代表性的是: CluStream[9], DBSTREAM[10]以及BOCEDS[11]等. 2003年, Aggarwal等人提出了CluStream算法[9]. 其算法核心思想主要是通过在线阶段利用微族的概要存储结构存储数据流的汇总结果, 并按金字塔式时间结构将中间结果进行保存; 而其离线部分则根据用户指定的观察阶段及聚类数量, 快速生成聚类结果. 在2016年, Baer等人提出了DBSTREAM算法[10]. 该算法采用了微簇之间密度共享机制来确定所属宏族, 该机制利用保持微族的共享密度来作为它们之间的半径, 并且在离线阶段具有高共享密度的微簇归属于同一个宏族. 在2019年Islam等人提出了BOCEDS算法[11], 它仍然采用了概要技术存储微簇信息, 该算法主要增加了一个缓存机制来处理数据流演化以及漂移问题.
第2类: 基于网格的流聚类方法. 该类方法通过网格将数据空间沿各维度进行分隔, 以创建多个网格结构. 通过将数据点映射到单元格, 可以保持密度估计[8]. 最具有影响力的代表性算法如: 2007年Chen等人提出的D-Stream流聚类方法[12], 它将新的数据点映射到所属单元格中, 并通过将所有密集单元格分配给单个簇进行初始化, 并经相邻网格扩展; 还有2014年Amini等人所提出的HDCStream[13]以及其在2016年提出的Mudi-Stream[14]等. 基于网格的流聚类方法可以识别任意形状的簇, 这也是该方法所具备的重要特征.
第3类: 基于预测的流聚类方法. 该类方法是一种高维数据流的流聚类方法. 该类方法可以在数据流维度十分大的空间中识别簇, 从而为高维数据流提供了一个利基. 该类方法最具有代表性的是: HPStream[15]、HDDStream[16]等. 2004年Aggarwal等人提出了HPStream算法[15], 它基于CluStream算法[9]在高维上进行了扩展. 通过定期采样当前簇的标准差, 调整现有的聚类, 使每个维度标准化, 通过更新簇分配每个簇的关联维度. 在每个簇中暂定添加一个新的观测点, 以更新维度. 如果聚类数据点不超过阈值则不增加聚类半径, 且将其添加到最近的聚类中.
以上方法各有优点: 基于距离的流聚类算法通常计算负荷低、基于网格的流聚类算法可以识别任意形状的簇; 基于预测的流聚类算法能有效应对维度灾难. 但是也存在如下的缺陷: 基于距离的流聚类算法往往依赖于参数的设定, 基于网格的聚类算法却由于网格是动态确定的而增加了计算负荷, 而基于预测的流聚类算法增加了宏族选择子空间的复杂性.
面对着内存受限、高维度灾难、低聚类质量以及低处理速度数据流特性来说, 目前数据流聚类研究主要存在着以下3个方面的困难:
(1)对于持续、快速、以及高维数据流来说, 数据源源不断地流入, 导致微簇数量的持续性增加, 聚类方法中隐含高负荷剪枝操作.
(2) 聚类簇数的确定一直是流聚类方法中的困难问题, 同时聚类簇数也对聚类质量有非常大的影响.
(3) 生产环境是开放的, 所产生的数据流会不断演化, 许多数据流聚类方法未能将一些离核心微簇较远、信息量较少的微簇进行异常检测.
针对工业物联网实时数据流的上述挑战问题, 在我们小组已有的基础性工作[17]的基础之上, 本文提出了一种新的工业物联网数据流自适应聚类算法(简称MCStream). 本文的方法与现有的方法完全不同, 第一, 在处理海量高维数据的聚类上, 目前基于密度的流聚类算法对于参数值的变化很敏感, 往往由于参数的细微变化在很大程度上影响了聚类质量; 第二, 在动态数据聚类过程中, 存在着大量数据的插入以及移除操作, 进一步地引起大规模的交叉微簇连接操作, 目前基于密度的流聚类算法未能有效的解决这样复杂计算问题. 本文算法引入一种新的引力能量函数的方法对参数进行递归的更新操作, 很好地解决了参数敏感性问题, 并且通过高斯核函数计算微簇密度峰值方式代替了大规模交叉微簇连接操作, 进一步地加快了数据流聚类映射速度. 因此本文的主要贡献如下:
(1) 提出了一种新的微簇构建方法. 该方法采用引力能量更新函数, 对微集群进行递归在线更新; 同时取消交叉微簇连接操作, 从而达到微簇构建与数据映射实时响应.
(2) 提出了一种新的自适应计算聚类簇数的方法. 该方法以微簇作为参与宏簇聚类的样本数据, 利用各微簇的局部密度以及距离值, 计算微簇的密度峰值, 并通过这两个变量值来自适应求出聚类簇数, 从而更好地处理大规模数据.
(3) 构建了一种新的检测异常微簇的判定方法. 该方法采用一个局部密度上界来标识宏簇, 以区分密集簇和离群簇, 使异常族检测更加精确.
1 运动目标检测工业物联网聚类框架及基本概念 1.1 工业物联网聚类框架工业物联网数据流的自适应聚类方法是工业物联网时代信息处理要解决的基本问题. 本文构建了工业物联网数据流挖掘总体框架. 它主要分为: 数据收集层, 数据挖掘层以及数据应用层, 如图1所示. 由于工业物联网数据量巨大、协议标准众多、安全性考虑不足等缺陷, 数据收集层大多采用传统传感器技术来获取数据, 如GPS、Network Flow以及海量信息化数据等[4,18,19]. 数据挖掘层接收来自数据收集层中的数据, 以流的形式传入处理器中; 在数据挖掘层中采用的是先利用本文提出的工业物联网自适应聚类技术进行聚类分析, 再将聚类结果集通过数据传输存储到总服务器中. 在数据应用层中, 数据存储总服务器通过类别分别传入到对应的应用上, 从而达到分布式管理. 对数据达到针对性应用. 在对工业物联网自适应聚类算法详细介绍之前, 我们先对工业物联网数据流及其相关概念进行介绍.
1.2 基本概念定义1 (工业数据流).设D是一个工业数据流:
定义2 (概念漂移). 设
定义3 (微簇结构). 设
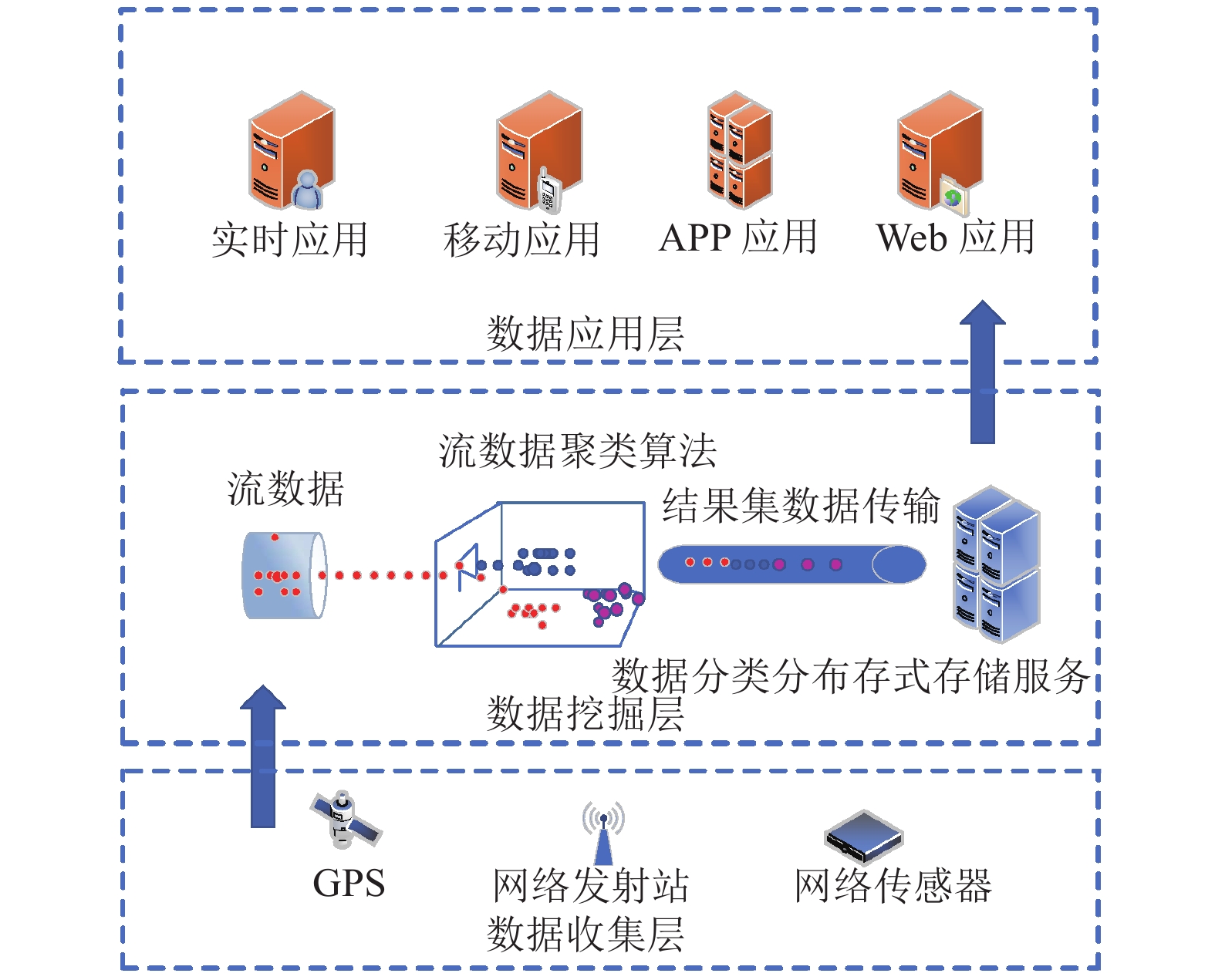
|
图 1 工业物联网聚类框架 |
(1)
(2)
| $ {N_{t + 1}} = {N_t} + 1 $ | (1) |
(3)
| $ S{N_t} = {N_t} - C{N_t} $ | (2) |
(4) C为微簇中心, 表示微簇在空间中的位置.
| $ C_{t + 1}^k = \frac{{(S{N_t} - 1) \times C_t^k + X_{t + 1}^k}}{{S{N_{t + 1}}}} $ | (3) |
(5) 微簇的衰减因子我们使用
(6)
| $ {W_{t + 1}} = {W_t} - \left\{ \frac{{r - dis({x_{t + 1}}, {C_t})}}{r}\right\} \times \frac{1}{\theta } $ | (4) |
定义4 (核心簇). 核心簇用CoreClusters表示, 在t时刻的核心簇中, 簇总数据点数
定义5 (潜在核心簇). 潜在核心簇用pCoreCluster表示, 在t时刻的潜在核心簇中, 簇总数据点数
定义6 (离线缓冲簇). 离线缓冲簇用OBufferCluster表示, 在t时刻的离线缓冲簇中, 簇总数据点数
定义7 (微簇局部密度). 微簇局部密度
| $ {P_{mi}} = \sum\nolimits_{j \in CoreCluster\backslash {{\{ i}}\} } {{{\rm{e}}^{ - {{\left(\frac{{{d_{ij}}}}{{{d_{\min }}}}\right)}^2}}}} $ | (5) |
定义8 (微簇距离). 基于定义7, 对微族局部密度进行排序, 当微族
| ${\delta _{qi}} = \left\{ {\begin{array}{*{20}{l}} {\min \{ {d_{qi}},{d_{qj}}\} ,\;j < i,\;i \geqslant 2}\\ {\max \{ {\delta _{qj}}\} ,\;j \geqslant 2,\;i = 1} \end{array}} \right. $ | (6) |
在上述定义当中, 微簇中心是通过计算壳区域数据点的平均值, 而不是通过计算整个簇数据点的平均值, 这是因为他们通过限制微簇的移动来阻止微簇无休止地跟随数据流的漂移[20], 在聚类过程中, 只有核心簇参与到簇聚类, 对于离群簇则会进行移除操作, 当微簇CoreCluster具有最大局部密度时,
本文算法主要分为6个阶段, 分别为: 初始化微族, 微族映射, 更新微族, 移除离群族, 构建微族决策树, 更新族图.
2.1 初始化微簇在数据流D中第一个数据点到来时候, 它不属于任何簇结构, 因此将创建一个微簇来存储信息. 这一步与之后的新的微簇创建同时发生. 微簇的创建首先要初始化特征向量. 新簇的簇中心C和半径r定义了微簇在数据空间中位置以及覆盖范围; 簇中心C初始设置为
在任意t时刻, 数据流
| $ dis({x_i}, clusters) \leqslant r $ | (7) |
第1种就是参与集群聚类的核心簇(CoreClusters), 第2种就是潜在核心簇(pCoreCluster), 第3种就是存储在缓冲器当中的离线缓冲簇(OBufferCluster). 为了找到目标微簇, 该算法首先计算核心簇与数据点
在图像预对于集群当中任何微簇结构. 任何一个微簇集群只要接收到了新数据, 那么该微簇结构的概要信息都会进行更新. 如果在t时刻数据点属于核心簇CoreCluster, 那么将会使用式(1)更新微簇数据点的数量; 如果它是映射到核心簇壳区域, 那么会使用式(3)更新映射微簇中心. 这种簇中心更新机制是为了防止微簇集群由于数据点的增加而出现数据漂移, 并且会使用式(2)更新壳区数据点的数量. 使用式(4)更新微簇权重.
| $ 0 \leqslant dis \leqslant r/2 $ | (8) |
如果数据点
伴随着流数据的不断流入, 在数据点不断地映射到微簇群之后; 该算法会对所有簇群中的微簇进行权重更新. 在核心簇、潜在核心簇、离线缓冲簇中, 由于有些微簇持续性没有新的数据映射进来; 其微簇权重都会不断地降低, 这也体现着数据流演化特性. 对于核心簇群来说, 每个核心微簇如果权重小于0, 那么该微簇将会从核心簇当中移入缓冲簇中; 并且会对其能量设置为原有初始能量的一半. 而在对潜在核心簇以及离线缓冲簇来说; 如果长时间的没有新的数据对其微簇进行更新, 那么说明这些微簇跟数据流内容长期无关并且是正在消亡的微簇. 对于流式算法来说低内存是其中一个不可或缺的评价标准; 因此这些正在消亡的微簇就需要从内存中永久性的移除.
2.5 构建微簇决策树当核心簇以及其他两个簇群发生改变时, 该算法会进行维护聚类图操作. 而对于聚类我们都需要保证聚类中心的密度最大, 以及各个微簇聚类中心的距离相对较远. 只有这样才能让各簇之间区分明显, 并且自适应的确定宏簇聚类簇数.
在微簇进行更新之后. 为了获取根据核心簇的数据特性而自适应的求出微簇所需要聚类簇数; 我们首先需要计算核心微簇群当中所有微簇之间相互的欧式距离值. 通过计算这个距离值可以构建一个核心微簇的距离矩阵. 在获取到距离矩阵后我们通过对这个距离进行排序以此来获取一个截断距离dmin; 其中等于比dmin更接近核心簇i的数据点数. 由于这个值的选择跟核心簇中不同的微簇距离相关, 因此dmin的选择是鲁棒性的. 通过式(5)可知, 与微簇i之间的距离小于dc的越多, 那么与微簇i的局部密度就越大. 当微簇i为核心簇局部密度最大的点时, 我们通过计算与微簇i距离最大的点的距离; 而对于其他局部密度的微簇, 则通过计算比它局部密度更大的点中距离最小的微簇之间的距离; 通过这两个值, 我们可以直观的反应聚类中心的特性. 局部密度大以及各聚类中心之间相差很远.
2.6 更新簇图在簇图更新中, 我们在式(5)得到了微簇局部密度以及距离. 我们将每一个参与聚类的微簇作为一个数据点. 首先将每个微簇的局部密度以及距离进行归一化处理; 然后将他们的乘积λ作为以微簇为聚类点的聚类中心的评判标准. 如果微簇C[i]是聚类中心, 并且属于第k簇, 那么将其宏簇属性设定为k; 如果不是微簇, 那么将其属性赋值为−1. 在所有聚类中心确定之后, 我们需要对非聚类中心微簇进行归类操作. 这里是按照密度值从大到小的顺序进行的遍历; 这样做可以逐层的扩充每一个微簇. 微簇通过这两步操作, 即完成了聚类中心及微簇的归类操作. 我们进一步将每个宏簇分为cluster core 以及cluster halo两类; 这里是通过属性来进行标识. 对于cluster core, 是指那些局部密度较大者; 而对于cluster halo是指那些局部密度较小的, 我们通过了为每一个宏簇设定一个局部密度平均上界来确定cluster core 以及cluster halo. 这样能将离聚类中心以及信息量较少的微簇进行标识.
3 相关理论分析 3.1 时间复杂度算法时间的消耗主要来源于数据点的映射以及簇图的聚类过程, 假设在
该算法内存消耗主要来源于微簇的存储以及簇图的存储, 维度为M的数据流产生了
进行对于任何聚类算法来说, 空间复杂度以及时间复杂度两个值都决定着聚类的优劣. 而对于流聚类算法来说, 微簇数量的边界决定着算法运行速度以及空间存储需求, 因此我们针对本文算法分析了在每一个周期内微簇数量M的边界值.
对于每一个时间周期内, 微簇数量M的产生总是满足:
| $ M \leqslant \frac{{3\theta }}{{2 minPts}} $ |
证明: 在任意的一个时间周期上, 衰减因子
| $ 0 \leqslant C\_of\_c \leqslant \frac{\theta }{{2 minPts}} $ |
因此, 对于一个时间周期内, 该算法所产生的微簇数量
| $ M \leqslant \frac{{3\theta }}{{2 minPts}} $ |
假设
证明: 设
| $ {C_t} - {T_s} \leqslant {W_t} + {\beta ^{\delta - 1}} \lt 2 \cdot {W_t} $ |
为验证本文所提出流聚类方法的先进性, 下面将与当前已发表的同类前沿方法进行对比试验, 针对各项性能进行评测. 所设定的实验PC硬件环境为: RAM 12 GB, 主频2.4 GHz; 操作系统Windows 10专业版, 语言平台: Python 3.6. 我们使用了多个数据集来仿真工业物联网中海量传感器数据. 在快速处理、有限内存的约束下, 流聚类技术的高聚类质量是我们的追求目标, 而聚类纯度、聚类精度是评价聚类质量的重要指标, 因此我们拟采用与目前基于密度的聚类算法分别从数据点处理速度, 聚类纯度以及算法内存消耗3个方面进行对比, 并设计了3组实验.
根据以上3个方面, 所进行的3组实验如下.
实验1. 测试不同数据流长度对各类密度聚类算法处理能力进行对比.
实验2. 比较不同聚类算法的平均聚类纯度.
实验3. 设置不同衰减因子, 测试CMStream算法从低维到高维数据流处理的响应时间.
工业物联网所产生的数据数量庞大, 超高维度, 因此为了更好验证CMStream算法在工业物联网环境的性能, 我们使用了3个海量、高维的数据集, 为了让数据集仿真真实环境, 本文通过时间窗口的形式将静态数据集进行动态化模拟测试.
(1) KDDCUP’99: 数据集包含4898431个实例, 每个实例包含着41维向量, 它产生于现代工业的网络流量记录.
(2) Bag of Words: 数据集包含着8000000条实例, 每个实例包含着100000维向量, 它从收集于文本数据集.
(3) EPM: 数据流包含着230318条数据集, 每个数据集13维向量, 它是一个学习分析数据集.
4.1 对比算法(1) CEDAS[20]: 2016年Hyde等人提出了CEDAS算法. 该算法是一种基于完全在线的算法将演化数据流聚成任意形状的簇, 它主要分为两个阶段, 一个是微簇维护阶段, 一个是宏簇聚类阶段.
(2) DBCLPG[21]: 2019年Halim等人提出了DBCLPG算法. 该算法是基于密度的大概率图聚类, 与其他算法不同的是, 它在聚类过程是利用节点度以及邻域信息为引导, 通过图的密度对大概率图进行聚类.
(3) BOCEDS[11]: 2018年Islam等人提出了BOCEDS算法. 该算法是一种基于缓冲区的演化数据流在线聚类方法, 在CEDAS[20]的基础上提出了一个缓存机制来存储无关微簇以及从这个缓冲区提取暂时无关微簇的在线剪枝聚类算法.
(4) microTEDAclus[22]: 2019年Maia等人提出了microTEDAclus算法. 该算法是基于典型性混合的进化聚类算法, 基于TEDA框架所提出来的, 将聚类问题划分为两个子问题, 一个是微簇构建, 一个是微簇进化成宏簇.
4.2 聚类处理速度对比为了探究在随着数据集中数据点不断流入的情况下MCStream算法聚类处理速度, 以及对于在同样数据集长度下不同维度数据集的聚类处理速度, 在实验过程中, 我们分别与当前最前沿的多个方法如: CEDAS[20]方法DBCLPG[21]方法microTEDAclus[22]方法以及BOCEDS[11]方法在不同维度的数据集上进行了对比. 我们在数据集EPM以及KDDCUP’99分别设置不同长度来测试这些聚类算法的处理速度 (如图2、图3所示), 其中每1 000个数据点设置为一个时间窗口长度, 图3显示了MCStream以及其他算法在不同维度数据集上响应时间.
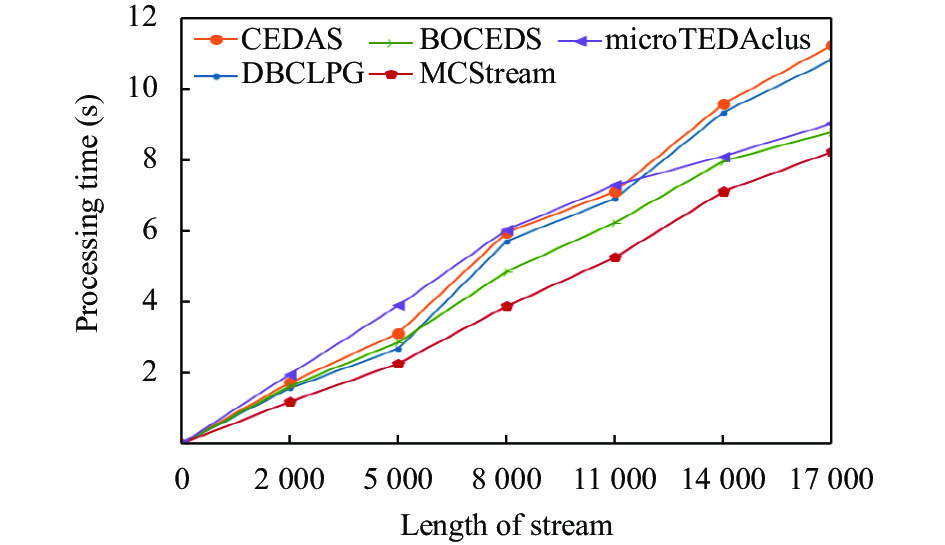
|
图 2 在EPM数据集上测试对MCStream算法进行测试 |
从图2、图3中可以看出, MCStream聚类算法随着数据点的不断增大在聚类处理时间上明显低于其他聚类算法. 而且在图2的结果数据中可以看出, 面对着数据量更大以及维度更高的EPM数据流来说, 各类聚类算法处理时间长度都显著增加. 这是由于维度大小与时间复杂度存在着线性关系. 对于CEDAS[20]以及BOCEDS[11]来说, 随着数据量不断增加, 微簇数量也呈线性增加; 而创建新的微簇来维护簇群以及更新微簇的边缘, 这是一个十分巨大的耗时任务. MCStream算法都是明显优于其他聚类算法, 这说明MCStream算法聚类算法可以在较低的处理时间和延迟代价来扩展到更高维的数据空间中.
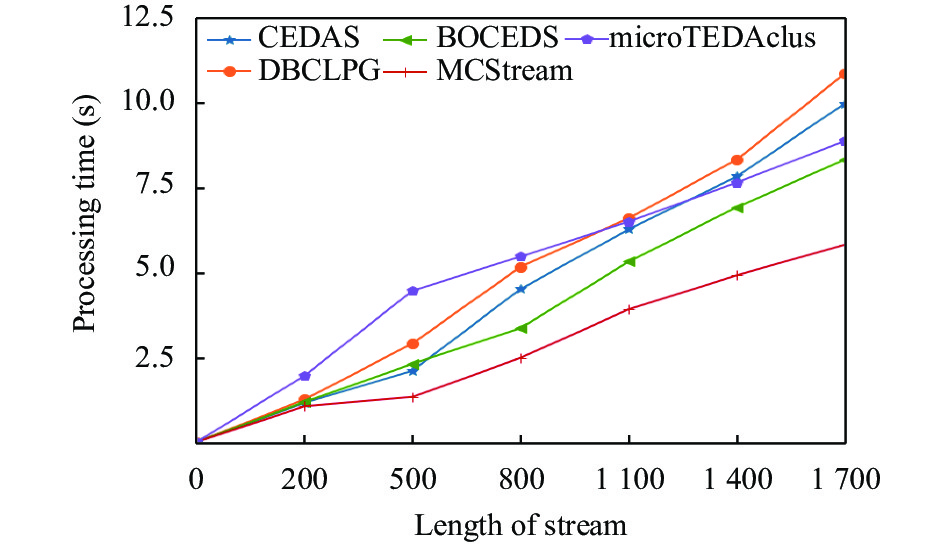
|
图 3 在KDDCUP’99数据集上测试对MCStream算法进行测试 |
4.3 聚类纯度对比
本组实验的目的是为了研究MCStream算法在数据流中聚类的纯度从而反映其聚类性能. 在评价聚类的指标中聚类纯度是其中比较流行的一种评价方法, 在式(9)给出了纯度的详细定义.
| $ purity = \frac{1}{K}\sum\limits_{i = 1}^K {\frac{{{m_i}}}{m}} \mathop {\max }\limits_j \left(\frac{{{m_{ij}}}}{{{m_i}}}\right) $ | (9) |
其中, K是所有宏簇数, m是所有参与聚类的数据点数,
目前在据流聚类时比较受欢迎一类流聚类数据集是KDDCUP’99数据集, 它可以测试不断演化的数据流聚类算法. 我们通过以500个数据点为一个长度分别设置不同长度来测试CEDAS[20]、DCLPG[21]、microTEDAclus[22]、BOCEDS[11]以及本文提出的MCSTream在该数据集中聚类纯度, 实验结果在图4柱状图中显示.

|
图 4 测试不同算法的聚类纯度 |
从图4数据中可以看出, 在不同的时期聚类纯度都有所不同, 在后期所有聚类纯度都有所降低. 这是因为随着数据流长度的不断增长, 微簇数量也在不断增加, 数据点错分的概率也随着线性增加, 从而降低聚类纯度. 尽管这样, MCStream聚类算法仍然保持了一个平稳的较高聚类纯度. 这是由于在宏簇聚类中MCStream移除了信息量较少且离簇中心较远却又参与到宏簇聚类的异常簇, 从而保证了高质量聚类, 这表明MCStream算法在大规模数据集上有着良好的稳定性.
4.4 参数影响以及聚类精度定义在本文所规划的实验中, 需要设定相关参数以研究权重衰减因子对聚类响应速度, 以及对于聚类精度的影响.
聚类精度的定义在式(10)中给出, 该公式中变量与式(9)中的变量定义是一样的. 在本实验中, 我们在高维数据流Bag of Words 以及KDDCUP’99中分别测试了不同衰减因子在不同维度对于MCStream聚类反应时间, 以及不同衰减因子对于聚类精度的影响. 为了模拟数据流的大规模性, 本文采取了以1 000个数据点为一个数据窗口长度, 设置不同数据流长度的方式对MCStream算法进行测试. 图3的实验结果显示了不同衰减因子在不同维度下算法MCStream对于每个数据点的平均处理速度. 在图4的柱状图中显示了对于不同的衰减因子对于聚类精度的影响.
| $ accuracy = \frac{{\displaystyle\sum\nolimits_{i = 1}^n {|c_i^d|} }}{{\displaystyle\sum\nolimits_{i = 1}^n {|{c_i}|} }} \times 100{\text{%}} $ | (10) |
从图5可以看出, 各类算法在不同维度下无论设置什么衰减因子其处理速度都在显著的增加. 这是因为数据维度是和时间复杂度呈线性相关, 维度的升高, 数据映射时间也会显著性增加. 而对于衰减因子来说, 衰减因子是和微簇数量呈正相关. 衰减因子增加会导致权重衰减得越慢, 从而微簇数量势必会增加, 这对于新数据点所归属簇群的映射计算量也会显著性增强. 从簇群方面来说, 微簇的量增加, 那么对于维护簇群压力也会增大. 因此, 衰减因子越大, 数据点平均处理延迟也会越大.
从图6可以看出, 随着衰减因子不断增加, 各类聚类算法的聚类精度也会随之下降, 这是因为上述所说的衰减因子与微簇数量呈正相关. 微簇数量的增加, 将会导致异常微簇数量增加, 从而导致整体聚类精确度降低. 对CEDAS[20]以及BOCEDS[11]来说, 微簇数量的增加, 会把更多的异常簇加入到聚类宏簇当中; 而对于MCStream来说, 由于在宏簇聚类过程中有一个平均局部密度上界来区分一些边缘微簇, 从而大大提升了聚类的精度.
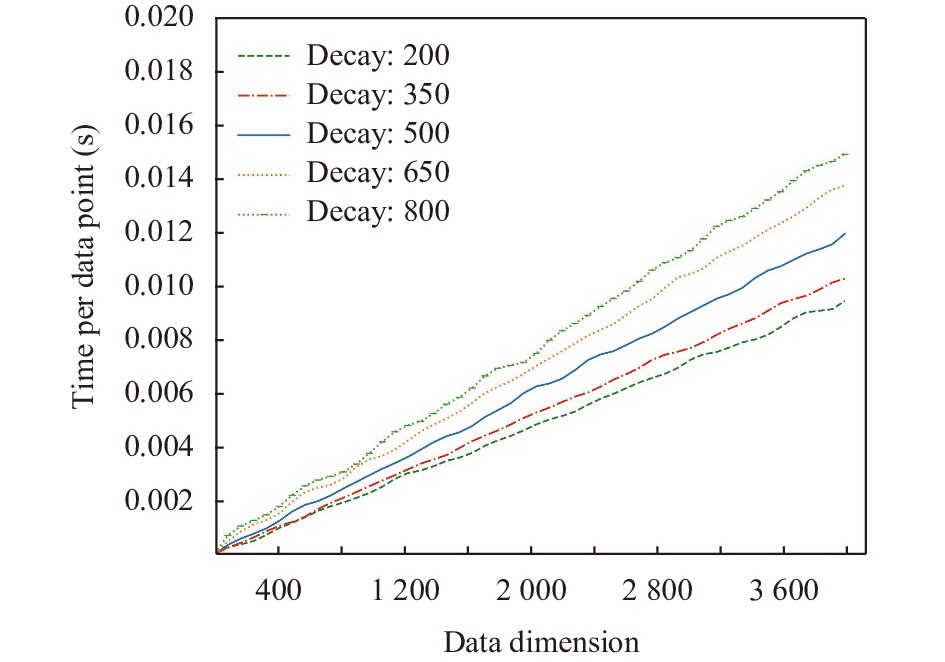
|
图 5 不同衰减因子在不同维度上对数据点处理速度 |

|
图 6 不同衰减因子参数下对聚类精度的影响 |
在本部分我们通过使用了3个数据集在处理时间、聚类纯度、精确度以及衰减参数上分别验证了基于微簇结构的流聚类算法的有效性. 实验结果表明MCStream具有较高的聚类能力, 然而对于高维数据仍然对聚类处理时间有着较大的影响. 在与流数据聚类算法进行对比的过程中, 我们不仅得出了高速聚类的重要性, 也验证了MCStream的有效性和高效性.
5 结束语工业物联网产生的工业数据流具有无限、高维、无序的特点, 因此构建高质量自适应流式聚类算法处理工业数据流具有十分重要的意义. 本文提出了一种工业物联网数据流自适应聚类算法, 根据微簇的高密度性, 将每一个微簇作为一个参与聚类的数据样本点, 计算每个微簇的局部密度以及微簇之间的距离, 通过微簇的局部密度以及微簇距离来构建宏簇聚类决策树从而确定聚类中心以及自适应确定宏簇聚类数. 并且通过引入了引力能量函数来不断地更新微簇权重, 从而来移除老化的微簇以防止概念演化以及数据漂移问题. 此外, 本文方法去除了微簇构建过程中相交微簇之间的计算, 维护了宏观簇所需的最小计算量. 通过在3个仿真的大规模数据流中对算法从多个方面进行了评测, 并且与当前前沿的聚类算法进行了充分的比较, 证明了该算法具有显著性优势. 由于该算法面向的是稠密数据集, 面对着稀疏数据集时由于会产生大量单个稀疏微簇, 聚类质量会显著性降低.
目前, 工业物联网正发展迅猛, 其数据结构越来越复杂, 其规模也越来越大. 在未来工作中, 我们将进一步提高算法在大规模稀疏数据集上的处理效果, 提高算法在现实工业领域的适应性.
| [1] |
Sisinni E, Saifullah A, Han S, et al. Industrial Internet of Things: Challenges, opportunities, and directions. IEEE Transactions on Industrial Informatics, 2018, 14(11): 4724-4734. DOI:10.1109/TII.2018.2852491 |
| [2] |
常建龙, 曹锋, 周傲英. 基于滑动窗口的进化数据流聚类. 软件学报, 2007, 18(4): 905–918.
|
| [3] |
杨春宇, 周杰. 一种混合属性数据流聚类算法. 计算机学报, 2007, 30(8): 1364–1371.
|
| [4] |
沙乐天, 肖甫, 陈伟, 等. 面向工业物联网环境下后门隐私泄露感知方法. 软件学报, 2018, 29(7): 1863–1879.
|
| [5] |
Youn J, Shim J, Lee SG. Efficient data stream clustering with sliding windows based on locality-sensitive hashing. IEEE Access, 2018, 6: 63757–63776.
|
| [6] |
王桂玲, 韩燕波, 张仲妹, 等. 基于云计算的流数据集成与服务. 计算机学报, 2017, 40(1): 107–125.
|
| [7] |
Growe GA. Comparing algorithms and clustering data: Components of the data mining process [Master’s Thesis]. Allendale: Grand Valley State University, 1999.
|
| [8] |
陈华辉, 施伯乐, 钱江波, 等. 基于小波概要的并行数据流聚类. 软件学报, 2010, 21(4): 644–658.
|
| [9] |
Aggarwal CC, Yu PS, Han JW, et al. A framework for clustering evolving data streams. In: Freytag JC, Lockemann P, Abiteboul S, et al., eds. Proceedings 2003 VLDB Conference. Amsterdam: Elsevier, 2003. 81–92.
|
| [10] |
Baer A, Casas P, D’Alconzo A, et al. DBStream: A holistic approach to large-scale network traffic monitoring and analysis. Computer Networks, 2016, 107: 5–19.
|
| [11] |
Islam K, Ahmed M, Zamli KZ. A buffer-based online clustering for evolving data stream. Information Sciences, 2019, 489: 113–135.
|
| [12] |
Chen YX, Tu L. Density-based clustering for real-time stream data. Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Jose: ACM, 2007, 133-142. |
| [13] |
Amini A, Saboohi H, Wah TY, et al. A fast density-based clustering algorithm for real-time Internet of Things stream. The Scientific World Journal, 2014, 2014: 926020.
|
| [14] |
Amini A, Saboohi H, Herawan T, et al. MuDi-Stream: A multi density clustering algorithm for evolving data stream. Journal of Network and Computer Applications, 2016, 59: 370–385.
|
| [15] |
Aggarwal CC, Han JW, Wang JY, et al. A framework for projected clustering of high dimensional data streams. In: Nascimento MA, Özsu MT, Kossmann D, et al., eds. Proceedings 2004 VLDB Conference. Amsterdam: Elsevier, 2004. 852–863.
|
| [16] |
Ntoutsi I, Zimek A, Palpanas T, et al. Density-based projected clustering over high dimensional data streams. Proceedings of the 2012 SIAM International Conference on Data Mining. Anaheim: Society for Industrial and Applied Mathematics, 2012. 987–998.
|
| [17] |
Xiao RL, Su JW, Du X, et al. SFAD: Toward effective anomaly detection based on session feature similarity. Knowledge-Based Systems, 2019, 165: 149–156.
|
| [18] |
Ng RT, Han JW. CLARANS: A method for clustering objects for spatial data mining. IEEE Transactions on Knowledge and Data Engineering, 2002, 14(5): 1003–1016.
|
| [19] |
Haque A, Khan L, Baron M. SAND: Semi-supervised adaptive novel class detection and classification over data stream. Proceedings of the 30th AAAI Conference on Artificial Intelligence. Phoenix: AAAI Press, 2016. 1652–1658.
|
| [20] |
Hyde R, Angelov P, MacKenzie AR. Fully online clustering of evolving data streams into arbitrarily shaped clusters. Information Sciences, 2017, 382–383: 96–114.
|
| [21] |
Halim Z, Khattak JH. Density-based clustering of big probabilistic graphs. Evolving Systems, 2019, 10(3): 333–350.
|
| [22] |
Maia J, Junior CAS, Guimarães FG, et al. Evolving clustering algorithm based on mixture of typicalities for stream data mining. Future Generation Computer Systems, 2020, 106: 672–684.
|
 2022, Vol. 31
2022, Vol. 31



