在现实生活中存在大量需要优化的问题, 且随着时代的发展, 这些问题的特征也在不断改变, 从最简单的线性问题, 到现在的多模态问题, 问题的求解难度不断上升, 由此有学者提出群智能算法. 群智能算法通过模拟生物的群体行为, 群体中的个体通过学习不断改变自身位置和搜索方向, 使个体往更好的方向进化, 进而达到种群群体进化的效果. 经典的群智能算法有粒子群算法(PSO)^[1]、萤火虫算法(FA)^[2]、蚁群算法(ACO)^[3]、狼群算法(WPA)^[4]、混合蛙跳算法(SFLA)^[5] 和进化算法(EAS)^[6]等, 群智能算法现已广泛应用于各个领域^[7-10].

蜉蝣算法(mayfly algorithm, MA)^[11]是Zervoudakis和Tsafarakis在2020年提出的一种新型的群智能算法. MA从蜉蝣的飞行和交配过程中得到启发并遵循了达尔文进化理论中的交叉、变异、选择和适应决策. 对于求解简单问题具有较好的寻优能力, 但由于MA不具备良好的跳出局部最优的性能, 且在迭代前期, 惯性系数较小, 雄雌蜉蝣增速较慢导致种群整体进化效率较低, 而在迭代后期, 雄蜉蝣婚礼舞蹈系数、雌蜉蝣飞行系数和惯性系数的减小导致雄雌蜉蝣移动缓慢. 因此, 在高维复杂问题上, MA体现出较为乏力的寻优能力. 在低维问题上, 收敛速度较慢, 收敛性较差. 为增强算法跳出局部最优的能力和提升种群整体进化速度, 本文提出偏移进化蜉蝣优化算法(migration evolutionary mayfly algorithm, MEMA). MEMA在MA基础上添加了一项新策略, 从种群的进化角度出发, 剔除种群中进化性能较差的蜉蝣, 并以特殊方式生成进化性能较好的蜉蝣以此来加快种群进化速度从而使算法快速趋向目标问题的最优解. 本文将引用MA、PSO、ABC^[12]、RPSO ^[13]、IOABC^[14]和本文所提算法, 通过不同函数特性随机抽取benchmark标准测试函数, 进行综合性能对比, 验证算法的有效性.

1 蜉蝣算法简介

MA的灵感来源于蜉蝣的飞行和交配过程. 雄蜉蝣皆群居于水面之上, 雄蜉蝣进行移动时, 将受到种群整体和自身的影响向更优方向进发. 每过一段时间, 雄蜉蝣会通过舞动来吸引雌蜉蝣, 雌蜉蝣则会随机飞向雄蜉蝣进行交配. 交配产生若干个子代蜉蝣, 极少数子代蜉蝣会发生变异. MA中, 雄蜉蝣和子代蜉蝣参与寻优, 即作为解空间中的候选解决方案. 随后, 对种群中所有个体通过精英保留策略保留较好个体, 形成新种群进行下一轮迭代.

算法最初的时候会随机产生雄蜉蝣和雌蜉蝣, 每一只蜉蝣的位置都是随机的. 由D维向量表示的蜉蝣的位置 $ {x}_{i}=\left\{{x}_{1}, {x}_{2}, {x}_{3}, \cdots , {x}_{D}\right\} $ , 速度表示为 $ {V}_{i}=\left\{{V}_{1}, {V}_{2}, $ $ {V}_{3}, \cdots , {V}_{D}\right\} $ , 每次迭代通过在当前位置上加上速度来进行位置更改.

1.1 雄性蜉蝣的位置更新

雄性蜉蝣是群居的生物, 每只雄蜉蝣的位置根据自己的情况以及种群整体的情况来调整, 雄蜉蝣一般在水面上进行上下移动, 假设蜉蝣不能快速移动, 雄蜉蝣的速度为:

$ v_{ij}^{t + 1} = \left\{\begin{split} &g \cdot v_{ij}^t + {a_1}{{\text{e}}^{ - \beta r_p^2}}\left( {pbes{t_{ij}} - x_{ij}^t} \right) + {a_2}{{\text{e}}^{ - \beta r_g^2}}\left( {gbes{t_{ij}} - x_{ij}^t} \right),\\ &\;\;\;\;\;\;\;\;\;\;{\text{if}}\;f\left( {{x_i}} \right) > f(gbest) \\ &{g \cdot v_{ij}^t + d \cdot r,\;{\text{if}}\;f(gbest) \leqslant f({x_i})} \end{split} \right. $

(1)

其中, $ {v}_{ij}^{t+1} $ 为蜉蝣 $ i $ 在 $ j $ 维度 $ t $ 时刻的速度, $ {x}_{i}^{t} $ 为时间步长为 $ t $ 时, 蜉蝣 $ i $ 在搜索空间中的位置, $ a_1 $ 为种群学习系数, $ a_2 $ 为个体学习系数, $ {pbest}_{ij} $ 为蜉蝣 $ i $ 曾经到过最好位置, $ {gbest}_{j} $ 为全局最佳位置, $ \;\beta $ 为蜉蝣的能见度系数, $ g $ 为惯性权重, $ d $ 为舞蹈系数, $ r $ 为范围内的随机值 $ \in \left[-\mathrm{1, 1}\right] $ , $ {r}_{p} $ 代表当前位置与 $ {pbest}_{ij} $ 的笛卡尔距离. $ {r}_{g} $ 代表当前位置与 $ {gbest}_{j} $ 的笛卡尔距离.

雄雌蜉蝣的移动, 通过在当前位置添加速度 $ {v}_{i}^{t+1} $ 来改变位置. 假设 $ {x}_{i}^{t} $ 是在时间步长为 $ t $ 时蜉蝣 $ i $ 在搜索空间中的位置, 公式如下:

$ x_i^{t + 1} = x_i^t + v_i^{t + 1} $

(2)

笛卡尔距离公式为:

$ \left\| {{x_i} - {X_i}} \right\| = \sqrt { \displaystyle\sum\nolimits_{j = 1}^n {{{\left( {{x_{ij}} - {X_{ij}}} \right)}^2}} } $

(3)

1.2 雌性蜉蝣的位置更新

雌蜉蝣会寻找适应值更好雄蜉蝣繁衍后代, 即雌蜉蝣将被适应值更好的雄蜉蝣所吸引, 所以雌蜉蝣会向更好雄蜉蝣靠近. MA中种群雄雌蜉蝣的相互吸引定性为最优匹配, 即最优雄蜉蝣与最优雌蜉蝣相互吸引, 次优雄蜉蝣与次优雌蜉蝣相互吸引, 以此类推. 若对应雄蜉蝣的适应值更差, 雌蜉蝣将选择随机向周围飞行. 雌蜉蝣的速度的计算公式为:

$ v_{ij}^{t + 1} = \left\{ \begin{split} &{g \cdot v_{ij}^t + {a_2}{{\text{e}}^{ - \beta r_{mf}^2}}\left( {x_{ij}^t - y_{ij}^t} \right), \;{\text{if}}\;f\left( {{y_i}} \right) > f\left( {{x_i}} \right)}\\ &{g \cdot v_{ij}^t + fl \cdot r, \;{\text{if}}\;f\left( {{y_i}} \right) \leqslant f\left( {{x_i}} \right)} \end{split}\right. $

(4)

其中, $ {y}_{ij}^{t} $ 为雌蜉蝣 $ i $ 对应的雄蜉蝣 $ i $ 的位置, $ {r}_{mf} $ 是雌性蜉蝣与雄性蜉蝣的笛卡尔距离, $ fl $ 是一个随机飞行系数.

1.3 蜉蝣交配行为

MA采用最优匹配的机制来抽取雄雌蜉蝣进行交配产生后代, 公式如下:

$\left\{ { \begin{split} {\textit{offs}1} =& L \cdot male + (1 - L) \cdot female\\ {\textit{offs}2} =& L \cdot female + (1 - L) \cdot male \end{split} } \right.$

(5)

其中, ${\textit{offs}1}$ 为第一个子代, ${\textit{offs}2}$ 为第二个子代, $ male $ 为雄蜉蝣, $ female $ 为雌蜉蝣, $ L $ 为 $ \left[-1, 1\right] $ 的随机值.

1.4 子代蜉蝣突变

MA引入了高斯变异^[15], 假设种群数量为N, 设定变异因子为m, 则子代蜉蝣中发生变异个体为 $ ⌊N \cdot m⌋ $ , 变异子代蜉蝣的随机一个维度将发生突变, 突变公式为:

$ {{{\textit{offs}}_{n}}} = {{{\textit{offs}}_{n}}} + \sigma \cdot {N_n}(0, 1) $

(6)

其中, $ {\textit{offs}}_{n} $ 为被选中的子代 $ {\textit{offs}} $ 的n维度, $ \sigma $ 为正态分布的标准差, $ {N}_{n}\left(\mathrm{0, 1}\right) $ 为均值为0, 方差为1的标准正态分布.

1.5 动态惯性权重

为了平衡全局探索能力和局部搜索能力, MA加入了动态惯性权重. 在迭代过程中, 蜉蝣的惯性权重将线性减少小, 公式如下:

$ g = {g_{\text{max} }} - \frac{{{g_{\text{max} }} - {g_{\text{min} }}}}{{ite{r_{\text{max} }}}} \cdot iter $

(7)

其中, $ g $ 为惯性权重, ${g}_{\text{max}}$ 是最大惯性权重, ${g}_{\text{min}}$ 是最小惯性权重, $ iter $ 为迭代次数, ${iter}_{\text{max}}$ 为最大迭代次数, $ iter $ 为迭代次数.

算法前期, 较大的 $ g $ 能更好地满足全局探索能力增加算法的收敛速度, 算法后期, 较小的 $ g $ 增加局部搜索能力提高算法的搜索精度.

1.6 婚礼舞蹈系数与随机飞行系数

为了寻找更好的解, 蜉蝣算法引入婚礼舞蹈系数, 当雄蜉蝣适应值大于全局最优时, 将进行随机移动以寻找更优解, 引入飞行系数, 当雌蜉蝣未被雄蜉蝣吸引时, 会向四周随机飞行寻找更好的雄蜉蝣. 婚礼舞蹈系数和随机飞行系数会随迭代次数减小以此减少蜉蝣步长, 增加局部搜索能力, 在算法后期提高收敛精度, 公式如下:

$ {d_t} = {d_1} \cdot d_{\text{damp}{\rm{ }}}^t, \;0 < {d_{\text{damp}{\rm{ }}}}< 1 $

(8)

$ f l_{t}=f l_{1} \cdot f l_{{\text{damp} }}^{t}, 0<f l_{ {\text{damp} }}<1 $

(9)

其中, ${d}_{t}$ 与 ${fl}_{t}$ 为 $ t $ 时刻的婚礼舞蹈系数和随机飞行系数, ${d}_{\text{damp}}$ 与 ${fl}_{\text{damp}}$ 为衰减参数.

2 偏移进化蜉蝣优化算法

MA算法在迭代前期, 种群较快收束于当前全局最优位置, 不利于种群整体进化, 在迭代中后期, 易出现早熟收敛现象. 对这个问题提出MEMA, 添加年龄到蜉蝣的属性中, 剔除群体中较为年长且进化程度较低的蜉蝣, 并在该个体附近重新生成新个体保证种群完整性, 同时对该蜉蝣进行指向性动态进化训练, 促进蜉蝣良性进化, 提升种群整体利用率, 提升算法寻优性能.

2.1 偏移进化机制

抽象蜉蝣良性进化的思想为算法的偏移进化机制, 在每次迭代后, 记录种群中雄蜉蝣的进化次数, 由于当蜉蝣进化次数超过一定次数时会存在适应值较差的个体, 为了排除进化2次到3次存在的偶然性, 而4次以上会使适应值较差的浮游在外徘徊次数过多浪费进化次数, 所以选取4次当蜉蝣数进化次数. 超过4次且适应值较差时, 说明该蜉蝣的进化速度始终在跟随整体的进化疲于奔向最优位置, 判定这样的解为失效解, 不具备较好进化能力对算法求解帮助较小. 剔除该蜉蝣并引入新蜉蝣, 从原蜉蝣的位置上进行一次偏移操作, 生成新蜉蝣. 新蜉蝣出现位置为:

$ mayfl{y_w} = mayfl{y_w} + W $

(10)

其中, $ {mayfly}_{w} $ 为被剔除蜉蝣的位置, $ W $ 为拉伸因子, 公式为:

$ W = rand \cdot (Upper - Lower) $

(11)

其中, $ Lower $ 为解空间下限, $ Upper $ 为解空间上限 $ rand $ 为 $( 0, 1 ]$ 的随机值.

为了保证新蜉蝣是优秀的个体且能有效地对种群进化起到帮助. 在加入种群前, 将对新蜉蝣进行随机次数的进化. 规定该蜉蝣会根据速度调节因子 $ \rho $ 进行指向性动态进化训练, 但不会超过当前种群进化次数, 其公式为:

$ \rho=[ {rand\cdot iter} ] $

(12)

新蜉蝣在加入种群前的进化移动与种群进化移动相同, 通过在当前位置 $ {\textit{z}}_{{i}{j}}^{{t}} $ 添加速度 $ {v}_{i}^{t+1} $ 来改变位置. 但更改速度的变化为:

$v_{ij}^{t + 1} = \left\{ \begin{split} &g \cdot v_{ij}^t + \frac{1}{\rho } \cdot \left( {gbes{t_j} - {\textit{z}}_{ij}^t} \right) + \frac{1}{\rho } \cdot \left( {pbes{t_{ij}} - {\textit{z}}_{ij}^t} \right),\\ &\;\;\;\;\;\;\;\;\;\;\;\;{\text{if}}\;f\left( {{{\textit{z}}_i}} \right) > f(gbest) \\ &{g \cdot v_{ij}^t + d \cdot r,\;{\text{if}}\;f(gbest) \leqslant f\left( {{{\textit{z}}_i}} \right)} \end{split} \right. $

(13)

根据速度公式, 在速度调节因子 $\; \rho $ 的影响下, 蜉蝣将进行分段寻找, 重力因子 $ g $ 的存在, 可以减小前一次进化速度的影响, 同时蜉蝣的速度受到 $ gbest $ 和 $ pbest $ 两个位置因子影响, 若蜉蝣找到比偏移后的初始位置更优的位置, 将受到上一次速度的影响继续向前前进一段距离, 之后受到两个位置因子的影响快速减速, 并反向加速回到更新后的全局最优位置附近, 否则将进行先加速后减速的分段寻找. 这一过程蜉蝣将仔细搜索更新后的全局最优位置的附近位置以期能将失效个体转换为引导种群进化的个体, 填补MA算法的缺陷, 增加算法收敛性能. 这些策略都是为了能更好地适应复杂的自然环境, 让其算法在保持多样性的条件下让其在全局搜索与局部搜索方面更为灵活.

2.2 MEMA算法流程

Step 1. 初始化参数.

Step 2. 初始化雄雌蜉蝣位置与速度, 计算并找出当前最优解.

Step 3. 根据式(1), 式(2), 式(4)更新雄雌性蜉蝣速度与位置.

Step 4. 所有蜉蝣根据当前适应值排序.

Step 5. 根据式(5)生成后代, 并根据变异可能性和式(6)随机产生变异后将其后代随机变成雄蜉蝣或者雌蜉蝣.

Step 6. 根据种群的适应值, 对雄雌蜉蝣进行排序, 用当前更优解代替劣解.

Step 7. 根据式(8)和式(9)更新舞蹈系数和随机飞行系数, 根据式(7)更新惯性权重.

Step 8. 若超过4次且能力较差, 则根据式(10)和式(11)产生新蜉蝣, 根据式(12)产生随机进化次数, 根据式(13)进化新蜉蝣, 将淘汰的个体替换.

Step 9. 判断是否到达迭代上限, 若是, 转Step 10, 若否, 转Step 3.

Step 10. 输出当前最优解.

3 实验及数据比对 3.1 实验环境

实验中所使用的软硬件参数如下:

(1) 操作系统: Windows 10;

(2) 硬件参数: Intel(R) Core(TM) i7-8750H CPU @ 2.20 GHz 2.21 GHz 8 GB RAM 内存;

(3) 编译环境及工具: Matlab 2018a.

3.2 测试函数

为了说明算法的普遍适用性, 本文为突出该算法的全面性随机抽取了标准benchmark测试函数中6个具有不同特点的函数(见表1).

首先抽取两个典型的单峰函数Sphere函数和Ackley函数, 其中Sphere函数常用于检验算法的收敛效率, 而Ackley函数是一个梯度式的函数, 在高维问题上, 算法收敛将会非常慢, 常用于检验算法的全局收敛速度.

其次抽取两种底部较平缓的单峰函数Powell Sum函数和Rosenbrock函数, 前一种单峰函数底部较平, 导致算法接近最优值附近区域时, 寻优较慢, 可以用于检验算法寻优效率. Rosenbrock函数是病态单峰函数, 也称为香蕉函数. 函数面可以看作为陡坡, 底部较为平缓, 最优值位于陡坡底部, 底部区域很容易找到, 但由于底部的值变化不大, 要找到全局最优很困难, 一般用于检验算法的局部搜索能力.

最后抽取两个经典的多峰函数Schwefel 2.22函数和Rastrigin函数. Schwefel 2.22函数较为平滑, 但全局最优值位于定义域的界限处. Rastrigin函数是一个多模态多峰函数, 具有大量的局部最小值, 尤其在高维问题上, 易使算法陷入局部最优, 常用于检验算法跳出局部最优的能力.

将MEMA与MA^[11]、ABC^[12]、IQABC^[14]、PSO^[1]、RPSO^[13] 5种算法进行对比, 来测试算法的性能.

3.3 参数设置

设置迭代次数为500次, 所有算法的种群数量都为40, MEMA的参数设置为: 最大惯性权重为1.5, 最小惯性权重为0.4, 婚礼舞蹈系数为1, 婚礼舞蹈系数的衰减系数为0.8, 随机飞行系数为1, 随机飞行系数的衰减系数为0.99, 子代数量为20, 变异可能性为0.01, 种群学习参数a₁为1.0, 蜉蝣个体学习参数a₂为1.5, 其他算法的参数设置参考文献内容.

实验将偏移进化蜉蝣优化算法(MEMA)与蜉蝣算法(MA), 蜂群算法(ABC), 改进蜂群算法(IQABC), 粒子群算法(PSO)和改进粒子群算法(RPSO)进行对比, 为避免因随机因素造成算法结果影响, 因此本文对每个测试函数独立运行100次实验取平均值作为算法的最终结果以降低随机数对结果的影响. 为了综合考虑算法的有效性, 记录了6种算法的平均值, 最优解, 最劣解和方差.

为了更全面地验证各算法在低维及高维空间的有效性, 本文将从低维和高维进行算法测试. 低维我们取10维, 数据见表2, 高维我们取100维, 数据见表3.

由表2中数据可见, 在6个10维的测试函数上，MEMA所找到的最优值与最劣值均能达到测试函数的全局最优解, 说明算法的收敛精度相较于对比算法更强. 时可以看出MEMA方差有5个都趋于0, 对于F3和F6函数未收敛完成的测试函数, 相比较其他5种算法, MEMA在收敛精度和算法稳定性上也都体现了卓越的性能.

对于表3中的数据, 同样的, 对于10维的问题中可以收敛完成的测试函数, MEMA在100维的问题上也完成收敛, 充分体现了MEMA对于解决高维问题的优异性能, 对于F3和F6函数未能有效完成收敛, 但是MEMA相较于其他的算法体现了较强的能力寻优能力和寻优稳定性. 因此表现了MEMA在求解高维问题时更能体现出算法的寻优能力.

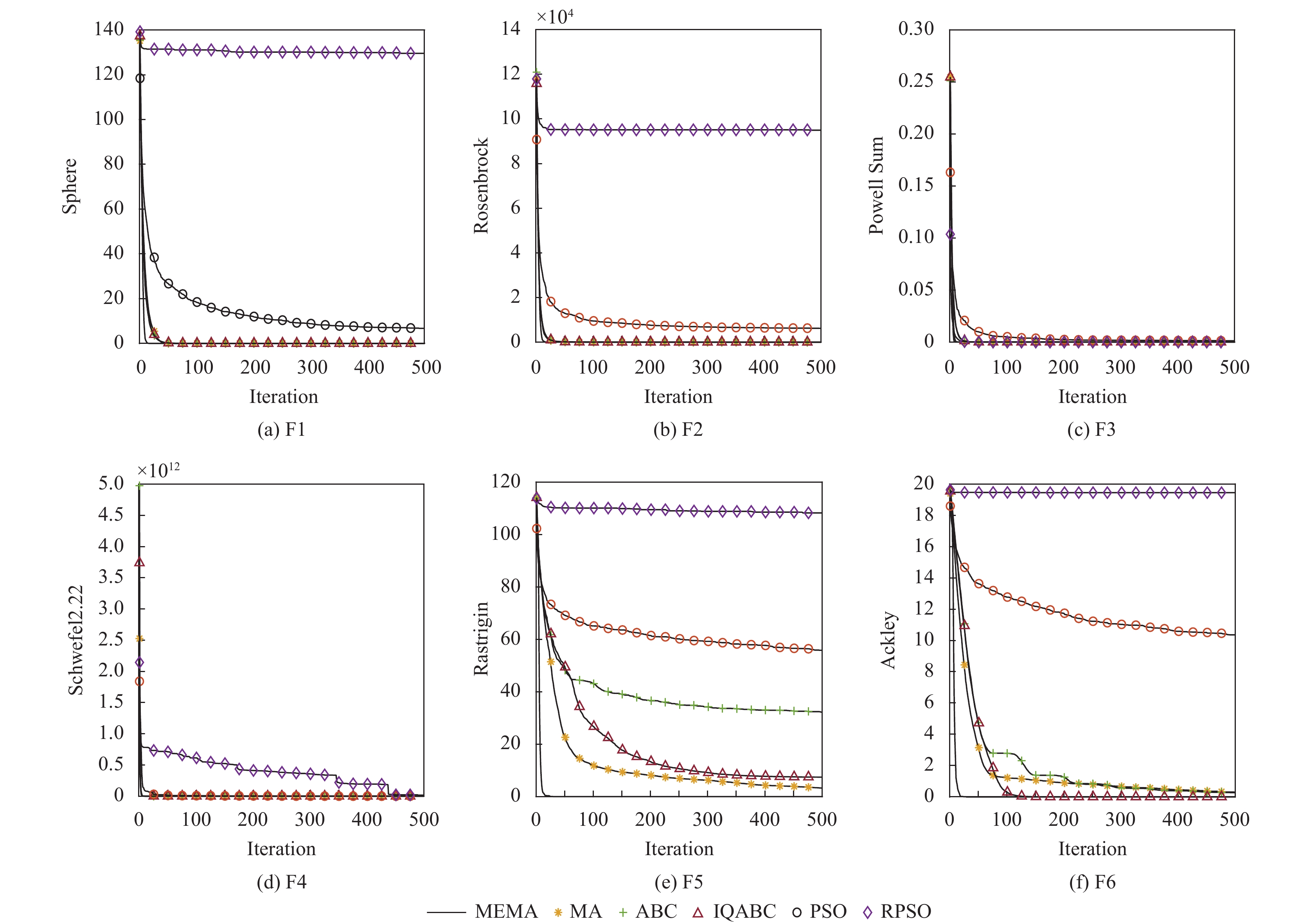
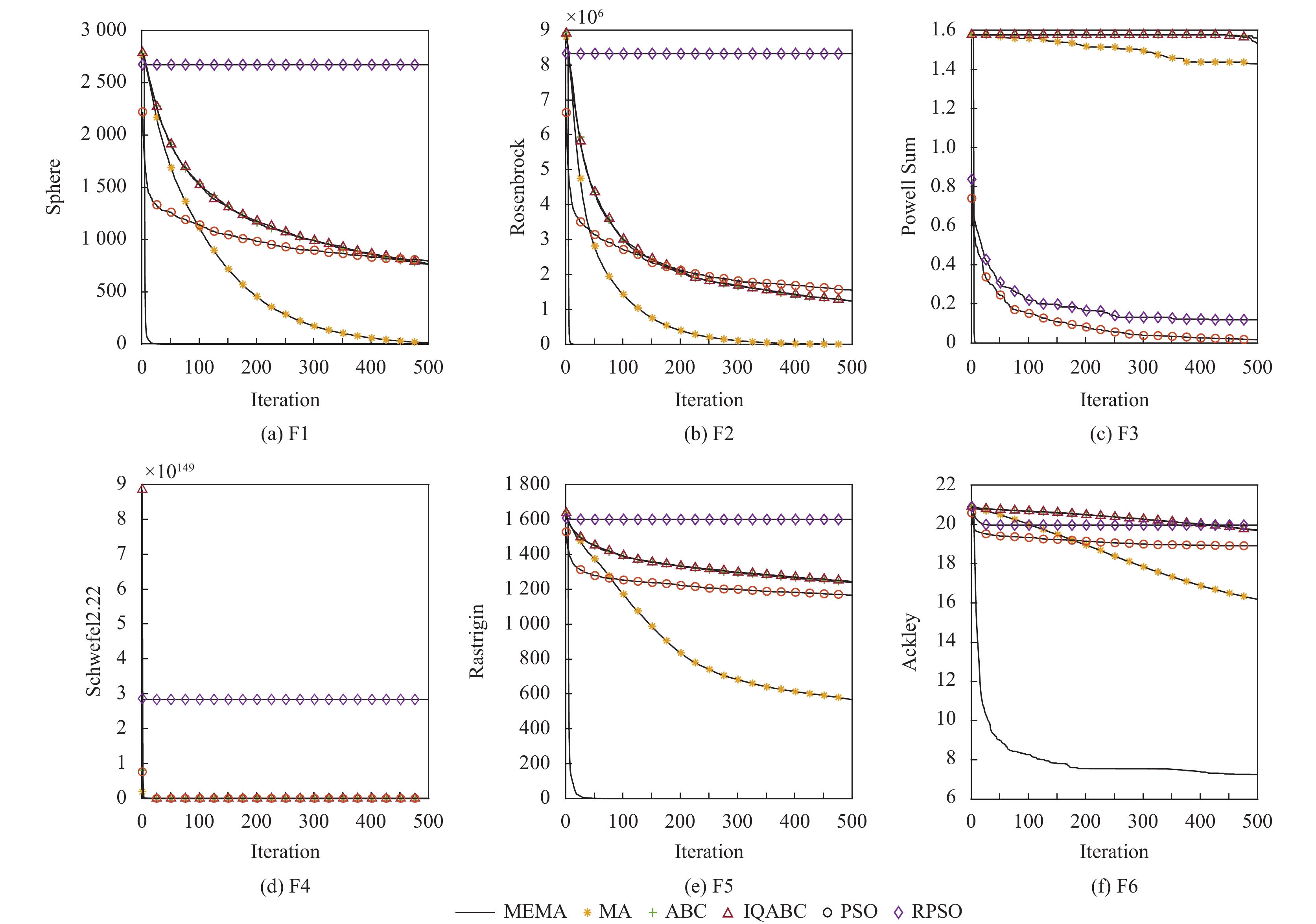
综上数据结果可得, MEMA相比较其他算法, 对于问题的处理能力更加出色, 说明在MA中加入生命周期的属性, 将生命周期较长且进化能力较弱的个体替换为更优个体, 可以有效地将蜉蝣的利用率提升, 提升种群整体进化速度. 为了清晰的体现算法的收敛效率, 同样采用图1与图2画出了在10维与100维的问题上不同函数的收敛曲线. 同样采用低维和高维两种维度进行算法测试. 低维我们取10维, 数据见图1, 高维我们取100维, 数据见图2.

结合表2、表3的数据和图1、图2的收敛曲线可以得出, 对于对比函数, 其他5种算法在收敛速度上明显低于MEMA. 在图1的低维问题上F1函数在迭代25次时完成收敛, F2函数在迭代50次左右时完成收敛. 图1中F5函数在其他算法都没有找到最优解时, MEMA大约20次的时候就找到了最优解. 在图2高维问题上难以在短时间内收敛完成, 而MEMA除F6都在迭代50次左右完成了收敛并达到全局最优值, 而F6也能在图中可以看出当其他对比算法都陷入局部最优时, MEMA还能继续向下收敛, 且该函数为单峰函数, 函数面较平, 在最优值附近区域较小, 较为考验算法的收敛速度, 充分说明了在高维问题上MEMA求解效率快, 寻优精度高. 从图2中F5可以看出, 其他测试算法由于全局搜索能力较慢, 难以快速接近最优解, 而MEMA迭代50次左右就可以快速接近最优值. 对于100维的收敛曲线图可以看到在收敛速度上MEMA远超其他算法. 对于F1、F2、F4、F5函数, MEMA在迭代50次内, 已经收敛完成, 证明算法充分利用了蜉蝣群体中的较劣蜉蝣, 提升了算法的收敛性能.

3.4 运行效率

为验证MEMA的寻优能力, 我们设计运行效率的实验, 因为篇幅原因, 我们随机抽取4个benchmark测试函数, 假设算法在求解精度达到 $ {10}^{-20} $ 时, 判定为算法寻找到最优解, 停止算法运行, 若未找到, 则运行算法直到迭代上限500次, 通过测试CPU运行时间, 得出算法运行时间, 最快运行时间标黑, 数据见表4.

从数据表上看, MEMA的CPU运行时间远小于其他5种算法, 也表明在实际优化方面找到最优值的概率会大幅增加. 即证明MEMA的寻优能力优于其他算法.

4 结束语

本文分析了蜉蝣算法难以有效利用失效蜉蝣的缺点, 引入了偏移进化后的蜉蝣去替换原有物种中失效个体, 在陷入局部极值时能够快速的跳出循环, 已趋于最优解空间, 以此来加快算法收敛效率并提高算法收敛性, 最终提出了基于偏移进化的改进型蜉蝣优化算法MEMA. 本文从多方面对算法性能进行实验, 使用6个具有典型代表的benchmark标准测试函数, 将MEMA与MA、ABC、PSO、IQABC、RPSO五种算法进行对比, 证实了改进后的该算法无论在高纬度还是低维度反面都可以有效地进行全局收敛, 并且在图中也能更为直观地看出全局收敛能力能是远超于其他算法的. 为了证明该算法的效率方面的情况, 设计了运行时间比对实验, 实验结果表明, MEMA算法不但结构简洁, 而且针对测试函数集表现出良好的寻优性能, 在收敛精度和收敛速度等方面均具有明显优势. 后期研究方向为提出相应的离散化算法及多目标优化算法.