当今世界互联网快速发展, 数据海量化是互联网技术发展的必然结果[1]. 如何快速、高效、可靠地存储这些数据资源成为研究热点和面临的巨大挑战. 传统的集中式存储将数据集中存放在专用服务器或者专用磁盘阵列中, 存储海量数据时存在诸多瓶颈, 例如系统性能、存储成本和可扩展性. 分布式存储系统将海量数据存储在多个廉价存储设备中, 海量存储能力、高吞吐量、高可用性、高可扩展性和低成本等突出优势使分布式存储系统成为海量数据的有效存储手段. 但是实际的分布式存储系统中不可避免地会出现节点故障, 如何高效地修复故障节点来保障分布式存储系统的高可靠性和高可用性成为目前急需解决的关键问题[2, 3].
现有的复制和纠删码策略能修复分布式存储系统中的节点故障, 但都存在各自的缺陷. 随后, Dimakis等人将网络编码应用到分布式存储系统中, 提出了再生码的概念[4], 显著降低了故障节点的修复带宽开销. 再生码虽然能有效降低故障节点修复时的带宽开销, 但没有考虑磁盘I/O开销和修复局部性. 为了确保修复故障节点较低修复带宽开销的同时, 需要连接的存活节点数也较少, Papailiopoulos等人提出了局部修复码(locally repairable codes, LRC)[5]. 进一步, Hao等人和Wang等人分别研究了局部修复码的构造以及协作局部修复码[6, 7].
再生码和局部修复码在故障节点修复过程中涉及大量有限域运算, 计算复杂度较高. 为了进一步降低计算复杂度和修复带宽开销, El Rouayheb等人提出一种精确修复的最小带宽再生码——部分重复(fractional repetition, FR)码[8]. 目前对 FR码的研究主要有基于组合设计构造FR码[9], 基于序列构造FR码[10], 基于二分图构造局部修复 FR码[11], FR 码的修复消耗最小化[12]. 这些构造算法复杂, 并且大多只能构造同构的 FR码, 不能得到异构的 FR码. Silberstein等人基于组合设计和正则图, 提出了一种达到最大码率的 FR 码的构造方法[13], 但其重复度受 FR 码结构的约束, 不能适用于任意参数. 基于Hadamard 矩阵构造的异构部分重复码[14, 15]修复复杂度和修复带宽开销都有所降低. 基于矩阵变换和可调节环的部分重复码构造[16]可以大范围的选择参数, 构造结构简单直观. Zhu等人提出基于组合设计的FR码, 可以调整存储节点的数量和节点的存储容量[17]. 进一步, Zhu等人对一般好的部分重复码的重复度限和重构度限进行了讨论[18-21]. 在实际的分布式存储系统中, 数据存储的结构多为异构的, 并且需要动态存储, 即在增加或减少数据时, 自动调节数据的存储分布.
为了解决上述问题, 本文构造了一种基于节点共边的异构部分重复码(heterogeneous fractional repetition codes based on node common edge, HFRC-NCE). 具体地, 结合节点共边的特性, 将热数据存储在多点共边上, 将冷数据存储在两点共边上, 使得热数据具有较高的重复度, 同时各个节点存储的数据容量不同, 实现数据的动态存储和异构存储. 性能分析表明, 与文献[8]基于完全图和文献[22]基于部分正则图构造的部分重复码相比, 虽然HFRC-NCE的存储开销和修复带宽开销略大, 但其构造简单, 减小了文件的重构度, 节点的修复选择度更高, 节点存储的数据容量更加多样性, 使得系统能更高效地修复故障节点.
1 点共边和部分重复码 1.1 点共边图

|
图 1 |
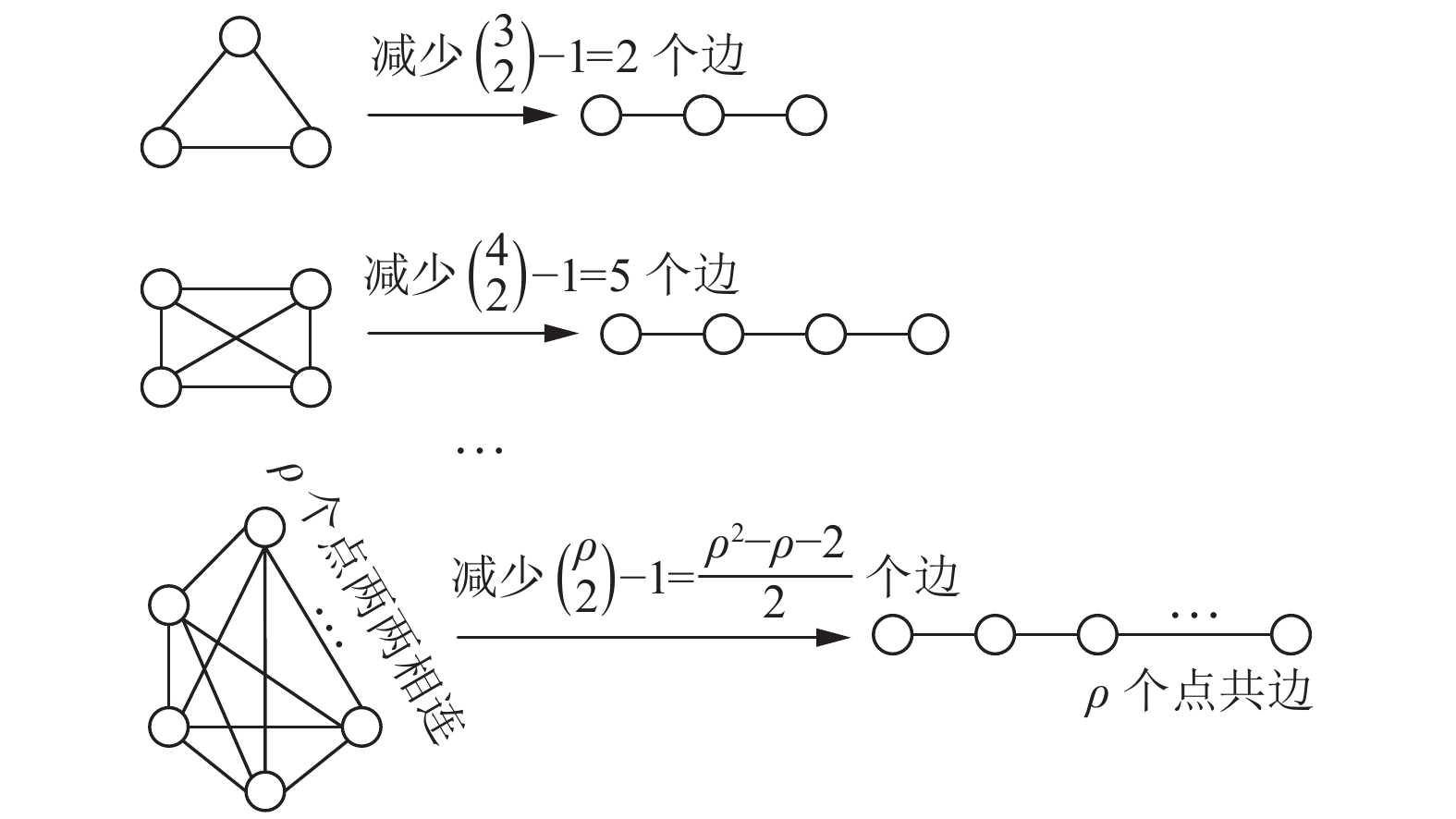
图2为
| $ \left( \begin{gathered} n \hfill \\ 2 \hfill \\ \end{gathered} \right) - \sum\nolimits_{\rho = 3}^n {\left( {\left( \begin{gathered} \rho \hfill \\ 2 \hfill \\ \end{gathered} \right){P_\rho } - {P_\rho }} \right)} = \theta $ | (1) |
| $ \sum\nolimits_{\rho = 2}^n {{P_\rho }} = \theta $ | (2) |
|
图 2 多点共边时减少的边数 |
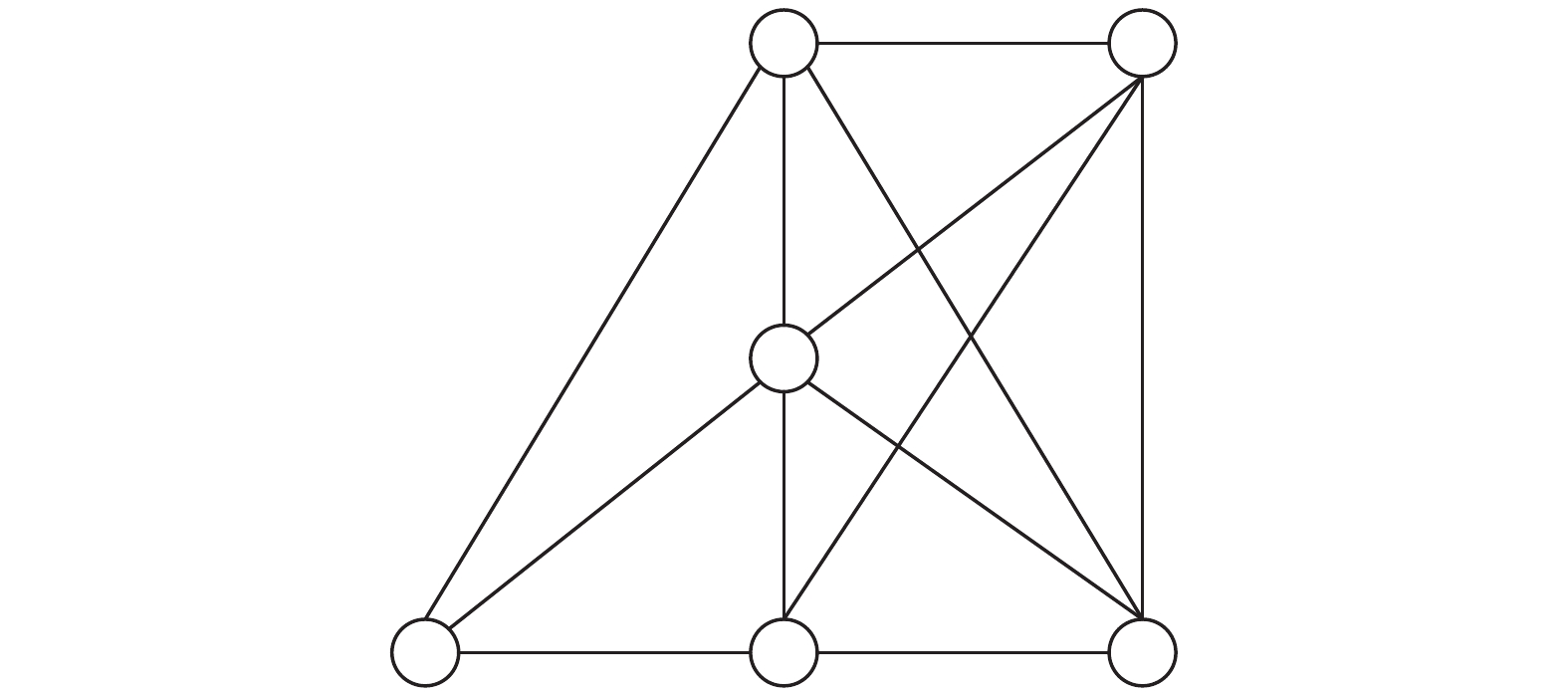
具体地以图3中的6阶图为例, 图中共有9条边,
|
图 3 |
1.2 部分重复码
部分重复码的实质是由外部的最大距离可分码(maximum distance separable, MDS)和内部重复码构成, 首先将原始文件分成
图4为基于完全图构造的部分重复码, 由外部的

|
图 4 基于完全图构造的
|
2 基于节点共边的异构部分重复码 2.1 基于节点共边的异构部分重复码构造
在实际的分布式存储系统中, 存储节点的存储容量大多异构. 为了满足分布式存储系统存储容量异构的特点, 结合节点共边的特性, 按照热数据重复度高和冷数据重复度低的原则构造异构部分重复码. 具体步骤如下.
步骤1. 首先将原始文件分成
步骤2. 设
步骤3. 通过已知的节点个数
具体地, 通过例1来说明构造的过程.
例1. 首先将原始文件分成
本文异构部分重复码是基于节点共边来构造的, 因此当节点发生故障时, 可以简单直观的通过图中的数据分布来修复节点, 当节点故障时只需连接图中相邻的存活节点进行修复, 下面分单节点故障和多节点故障进行讨论.

|
图 5 |
单节点故障修复: HFRC-NCE每个数据块最小的重复度为2, 即每条边的数据块最少存储在两个节点上, 故当单个节点发生故障时可从相邻的存活节点下载数据块进行修复, 并且当故障节点存储的数据块位于
多节点故障修复: HFRC-NCE每个数据块最大的重复度为4, 即每条边的数据块最多存放在4个节点上, 故最多能同时修复3个故障节点, 存在以下3种情况:
(1) 当同时修复3个故障节点时, 这3个节点应在同一个
(2) 当同时修复2个故障节点时, 这2个节点应在同一个
(3) 当故障节点不在同一个
图5中的节点1、2和3同时发生故障时, 节点1、2和3中的数据块1均可连接节点4下载数据块1进行修复, 节点1、2和3中的其他数据块可连接相邻的存活节点下载相应的数据块进行修复. 当节点5和6同时发生故障时, 节点5和6可以通过连接存活节点1、2、3和4下载相应的数据块进行修复. 当节点3和6同时发生故障时, 由于节点3和6不在同一多点共边上, 数据块8没有存活节点可供下载, 故不能同时修复节点3和6.
3 性能分析本节主要分析HFRC-NCE的节点修复选择度、节点存储容量、重构度、存储开销和修复带宽开销, 并与完全图和部分正则图构造的部分重复码进行对比.
3.1 节点修复选择度修复故障节点可选的方案数, 叫做该节点的修复选择度. 基于节点共边的异构部分重复码的节点修复选择度与各个数据块的重复度

|
图 6 节点故障的最大修复选择度对比 |
如图5当节点1、2、3中的一个发生故障时, 单节点的修复选择度为3; 当节点5、6中的一个发生故障时, 单节点的修复选择度为2; 当节点4发生故障时, 单节点的修复选择度为6. 当节点1和2同时故障时, 节点修复选择度为2; 当节点1和6同时故障时, 由于节点1在4点共边上, 节点6在3点共边上, 导致数据块6没有存活节点供其下载修复, 无法进行多节点修复.
基于完全图和部分正则图构造的部分重复码, 单节点的节点修复选择度为1, 并且当2个及以上节点故障时均不能进行修复. 因此HFRC-NCE提高了单节点及多节点的节点修复选择度, 并增加了故障节点可修复的个数.
3.2 节点存储容量节点存储容量及每个节点存储的数据块容量, 表1为完全图和部分正则图构造的部分重复码和HFRC-NCE节点存储容量的对比.
| 表 1 不同构造部分重复码存储容量的对比 |
通过部分节点的存储容量对比发现HFRC-NCE的节点存储容量更加多样化, 更适用于实际的分布式存储系统中.
相对于静态存储, 动态存储更适用于实际的分布式存储系统, HFRC-NCE在增删原始文件
用
通过表2可以得出, 在节点个数相同的情况下, HFRC-NCE的最小重构度
| 表 2 不同参数下文件的重构度 |
3.4 存储开销和修复带宽开销
存储开销为各个节点存储数据块所需的空间与原始文件

|
图 7 存储开销对比 |
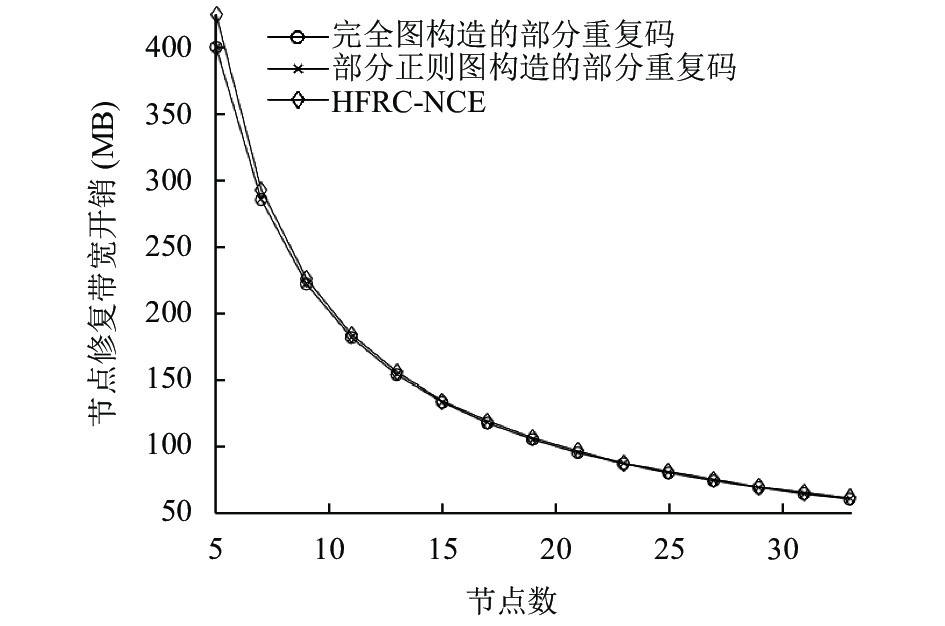
修复带宽开销为修复故障节点时所需下载的数据量的大小.
7阶完全图构造的部分重复码故障节点的修复带宽开销为
|
图 8 节点修复带宽开销对比 |
3.5 构造算法运算复杂度
衡量一个算法的好坏, 其算法运算复杂度是一个重要的指标. 本文构造的HFRC-NCE码, 在构造时只需根据已知的节点数和边数结合式(1)和式(2)求出两点共边和多点共边的情况, 之后将冷数据和热数据块分别存储在边上, 构造出的HFRC-NCE码简单直观. 本文的构造与文献[13]相比, 文献[13]运用大量组合设计的知识, 所需判断的情况过多, 加大运算复杂度, 因此本文的算法复杂度更优.
4 结论当前部分重复码的构造大多为同构的并且为静态存储, 不太适用于实际的分布式存储系统. 本文结合节点共边的特性, 并将实际分布式系统的冷热数据块相结合, 构造的HFRC-NCE简单直观, 便于进行快速的节点修复. 通过与完全图和部分正则图构造的部分重复码对比, 可以发现, HFRC-NCE虽然具有较高的存储开销和修复带宽开销, 但能实现更多故障节点的修复, 降低了文件的重构度, 提高了节点的修复选择度, 使节点容量更加多样化, 并且在增删原始数据时, 能快速地调整节点的存储分布, 实现动态存储.
| [1] |
Dai XM, Zhang ZY, Bai BM, et al. Pattern division multiple access: A new multiple access technology for 5G. IEEE Wireless Communications, 2018, 25(2): 54–60.
|
| [2] |
王意洁, 许方亮, 裴晓强. 分布式存储中的纠删码容错技术研究. 计算机学报, 2017, 40(1): 20.
|
| [3] |
Li CD, Zhou ZH, Zhai XP. On a class of multi-source distributed storage with exact repair. IEEE Access, 2018, 6: 20704–20711.
|
| [4] |
Dimakis AG, Godfrey PB, Wu YN, et al. Network coding for distributed storage systems. IEEE Transactions on Information Theory, 2010, 56(9): 4539–4551.
|
| [5] |
Papailiopoulos DS, Dimakis AG. Locally repairable codes. Proceedings of 2012 IEEE International Symposium on Information Theory. Cambridge: IEEE, 2012. 2771–2775.
|
| [6] |
Hao J, Xia ST, Shum KW, et al. Bounds and constructions of locally repairable codes: Parity-check matrix approach. IEEE Transactions on Information Theory, 2020, 66(12): 7465–7474.
|
| [7] |
Wang J, Yan ZY, Li KC, et al. Local codes with cooperative repair in distributed storage of cyber-physical-social systems. IEEE Access, 2020, 8: 38622–38632.
|
| [8] |
El Rouayheb S, Ramchandran K. Fractional repetition codes for repair in distributed storage systems. Proceedings of the 2010 48th Annual Allerton Conference on Communication, Control, and Computing. Monticello: IEEE, 2010. 1510–1517.
|
| [9] |
Olmez O, Ramamoorthy A. Fractional repetition codes with flexible repair from combinatorial designs. IEEE Transactions on Information Theory, 2016, 62(4): 1565–1591.
|
| [10] |
Benerjee KG, Gupta MK. On dress codes with flowers. Proceedings of 2015 7th International Workshop on Signal Design and its Applications in Communications (IWSDA). Bengaluru: IEEE, 2015. 108–112.
|
| [11] |
Su YS. Optimal pliable fractional repetition codes that are locally recoverable: A bipartite graph approach. IEEE Transactions on Information Theory, 2019, 65(2): 985–999.
|
| [12] |
Itani M, Sharafeddine S, Elkabbani I. Practical single node failure recovery using fractional repetition codes in data centers. Proceedings of the 2016 IEEE 30th International Conference on Advanced Information Networking and Applications (AINA). Crans-Montana: IEEE, 2016. 762–768.
|
| [13] |
Silberstein N, Etzion T. Optimal fractional repetition codes based on graphs and designs. IEEE Transactions on Information Theory, 2015, 61(8): 4164–4180.
|
| [14] |
孙伟, 沈克勤, 张鑫楠, 等. 异构部分重复码的构造. 计算机系统应用, 2021, 30(2): 226–230.
|
| [15] |
王静, 孙伟, 何亚锦, 等. 基于Hadamard矩阵构造部分重复码. 电子科技大学学报, 2021, 50(2): 173–179.
|
| [16] |
沈克勤, 孙伟, 何亚锦, 等. 基于矩阵变换和可调节环的部分重复码构造. 计算机系统应用, 2020, 29(12): 187–193.
|
| [17] |
Zhu B, Li H, Li SYB. General fractional repetition codes from combinatorial designs. IEEE Access, 2017, 5: 26251–26256.
|
| [18] |
Zhu B, Shum KW, Li H. On the duality of fractional repetition codes. Proceedings of 2017 IEEE Information Theory Workshop. IEEE, 2017. 56–60.
|
| [19] |
Zhu B. A study on universally good fractional repetition codes. IEEE Communications Letters, 2018, 22(5): 890–893.
|
| [20] |
Zhu B, Shum KW, Li H, et al. On the optimal reconstruction degree of fractional repetition codes. Proceedings of 2019 IEEE International Symposium on Information Theory. Paris: IEEE, 2019. 1557–1561.
|
| [21] |
Zhu B, Shum KW, Li H. Fractional repetition codes with optimal reconstruction degree. IEEE Transactions on Information Theory, 2020, 66(2): 983–994.
|
| [22] |
Hosung P, Young-Sik K. Construction of Fractional Repetition Codes with Variable Parameters for Distributed Storage Systems. Entropy, 2016, 18(12): 441.
|
 2022, Vol. 31
2022, Vol. 31



