2. 海洋石油工程(青岛)有限公司, 青岛266520
2. Offshore Oil Engineering (Qingdao) Co. Ltd., Qingdao 266520, China
随着互联网技术的发展, 在线教育以其打破课堂时空限制等优势越来越受到人们的关注, 尤其是新冠疫情爆发以来, 人们对在线教育的需求大大增加. 中国互联网络信息中心报告显示: 2020年3月, 我国在线教育用户规模达4.23亿, 较2018年底增长110.2%, 占网民整体的46.8%. 然而, 随着在线教育的发展, 信息过载现象愈发严重, 如何使用户在短时间内找到适合自己的学习资源便成了一项巨大的挑战. 为了解决信息过载的问题, 科研人员提出了推荐系统的概念, 通过对信息的个性化推荐, 提高了人们的用户体验[1].
有关推荐系统算法的研究较多, 主要分为3类: 基于内容的推荐算法、协同过滤的推荐算法和混合的推荐算法. 许多在线教育网站采用传统的协同过滤的推荐算法[2], 其基本思想是利用已有的用户选课信息来构建相似用户群体, 进而进行课程的推荐, 但传统的协同过滤算法存在冷启动和数据稀疏性等问题[3].
由于深度学习具有强大的非线性映射能力, 在处理高维数据时, 可以有效地将其映射到低维空间从而提取高层次的特征, 随着近几年深度学习的发展, 利用深度学习进行个性化推荐也得到了广泛的应用[4-6]. 由于自编码器具有强大的隐特征学习能力, 能够有效处理数据的稀疏性问题[7]. 另外, 由于用户在进行选课时往往会考虑到之前学过的课程, 用户的选课序列具有明显的时序特点, LSTM (long short-term memory, 长短期记忆网络)具有强大的时序建模能力, 能够有效处理时间序列数据. 根据上述特性, 本文利用LSTM改进自编码器, 将其应用于在线教育的课程推荐领域, 根据用户的课程学习历史来推荐之后的学习课程.
2 国内外研究现状 2.1 协同过滤推荐算法协同过滤算法是根据用户的历史数据划分用户群体, 根据群体内其他用户的偏好来为其进行推荐, 分为两大类: 基于用户的协同过滤推荐和基于物品的协同过滤推荐.
刘国丽等人[8]提出了一种融合专家信任的协同过滤推荐算法, 在专家信任度计算公式中引入了项目平衡因子, 提高了算法的推荐准确率. Li等人[9]设计了一个应用协同过滤算法的个性化在线教育平台, 实验验证了平台的性能和功能的有效性. 为了解决在物联网情境下的推荐问题, Cui等人[10]提出了一种结合时间相关系数和改进的K-means聚类方法的推荐模型, 实验结果表明了其在物联网情境下的优越性能.
2.2 基于深度学习的推荐算法随着深度学习的发展, 越来越多的研究人员将深度学习方法应用到推荐系统上. 利用深度学习的非线性映射能力, 对协同过滤算法中的用户矩阵和物品矩阵进行建模, 使模型具有非线性表达能力.
王素琴等人[11]提出了一种基于LSTM和课程关联分类的推荐模型, 首先利用GSP (generalized sequential pattern mining algorithm) 算法和谱聚类算法对课程进行分组, 然后利用LSTM进行课程的时间序列建模, 最后利用Softmax函数对课程进行分类, 实验结果表明与协同过滤等算法相比, 该算法具有更高的推荐准确性. 卜祥鹏[12]提出了一种基于GRU (gated recurrent unit, 门控循环单元)和课程关联关系的推荐模型, 结合课程之间的关联关系, 利用GRU和Softmax函数进行课程推荐, 实验结果表明与协同过滤或仅考虑课程关联的推荐算法相比, 推荐的准确率更高. Sedhain等人[13]利用自编码器将数据映射到非线性隐空间, 实验证明与MF (matrix factorization, 矩阵分解)和CF (collaborative filtering, 协同过滤)相比, 具有更低的均方误差. Strub[3]结合评价信息和诸如用户属性和物品描述等辅助信息, 利用自编码器进行矩阵的分解, 通过实验验证了所提方法的有效性.
3 相关概念 3.1 符号表示及问题定义假设在当前的在线教育系统中, 共有
长短期记忆网络是一类特殊的循环神经网络, 最早由Hochreiter和Schmidhuber为了解决传统循环神经网络梯度消失的问题而提出[14]. 不同于前馈神经网络跟普通的循环神经网络, 长短期记忆网络不仅可以处理点数据(例如图片), 还可以处理间隔和延迟非常长的序列数据(例如语音跟视频). 长短期记忆网络在诸如连笔字识别[15]、语音识别[16]以及时间序列数据异常检测[17]等任务中取得了优秀的成果. 其结构如图1.
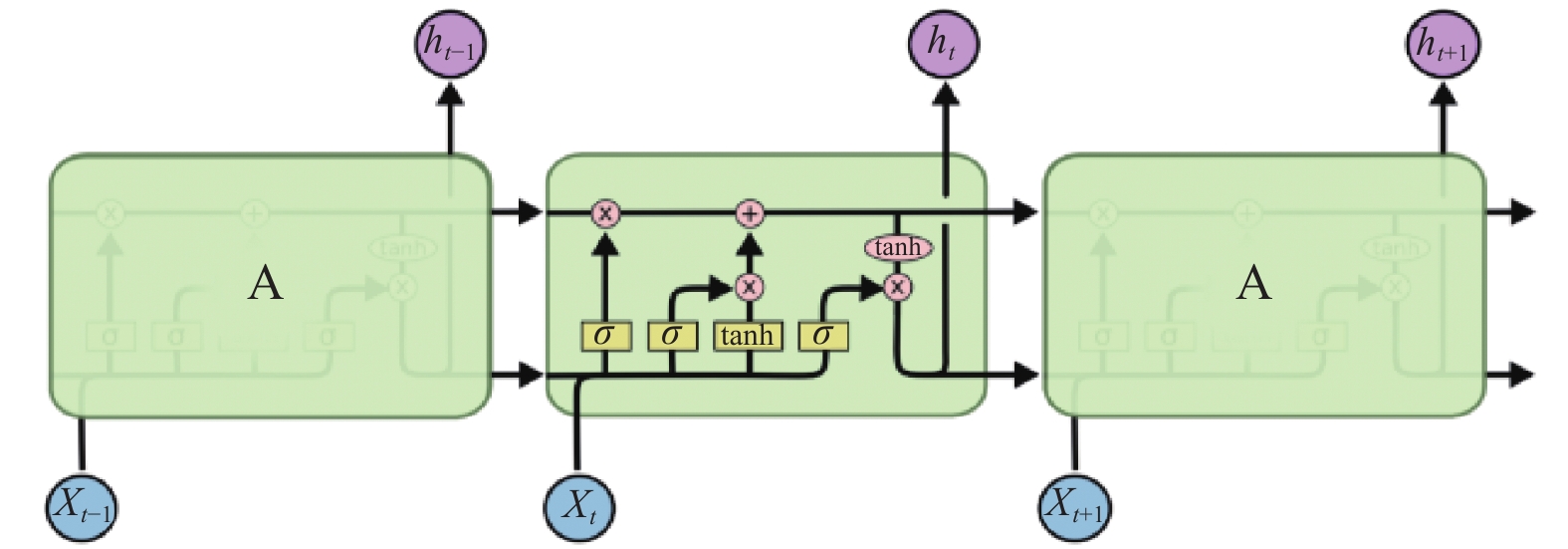
|
图 1 LSTM网络结构[18] |
长短期记忆网络主要由3个称为门的特殊结构来控制神经元的状态, 这3个门分别称为遗忘门、输入门跟输出门.
长短期记忆网络的工作由3个阶段完成:
(1)遗忘阶段. 该阶段来决定神经元需要遗忘哪些信息, 对输入的信息进行选择性抛弃.
(2)选择记忆阶段. 该阶段来决定给神经元添加哪些信息.
(3)输出阶段. 该阶段来决定神经元的哪些信息会被输出.
3.3 自编码器自编码器是一种以无监督学习的方法来学习数据编码的人工神经网络, 其特点是学习目标跟输入数据相同, 一般用途是通过训练神经网络来忽略无关信息以实现对数据的降维.
自编码器由两部分组成: 对输入数据进行压缩编码的编码器和将编码重建为输入数据的解码器. 其基本结构如图2所示.
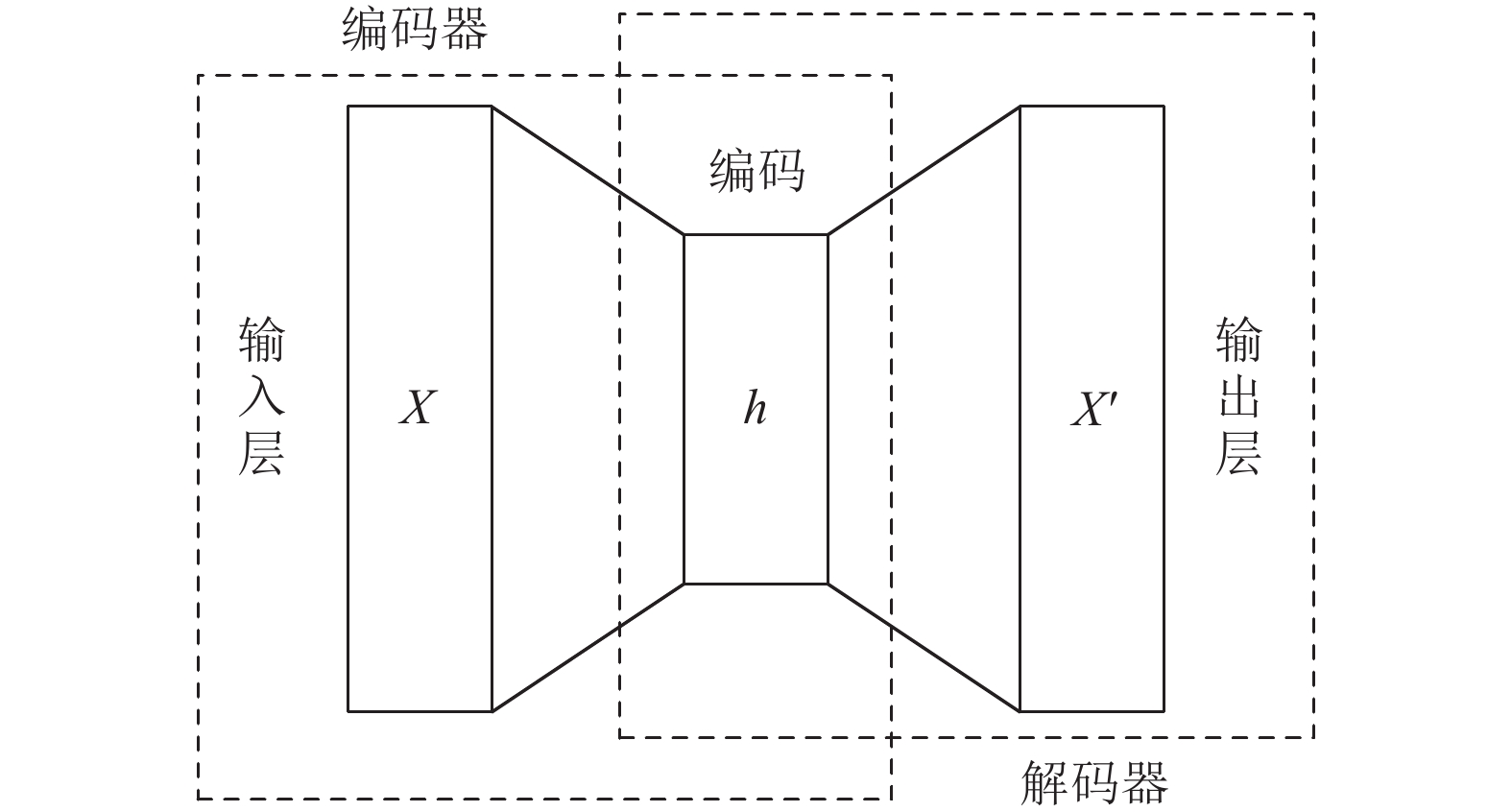
|
图 2 自编码器网络结构 |
对于编码器映射φ和解码器映射ψ有:
| $ \varphi :X \to F $ | (1) |
| $ \psi :F \to X $ | (2) |
| $ \varphi , \psi = \mathop {\text{argmin} }\limits_{\varphi , \psi } {\left\| {x - \psi \left[ {\varphi \left( x \right)} \right]} \right\|^2} $ | (3) |
自编码器在编码阶段, 将输入
| $ h = f(Wx + b) $ | (4) |
f为激活函数, 常用的有Sigmoid函数和ReLU函数, W是输入x的权重矩阵, b为偏置单元. 在训练过程中通过反向传播算法来更新W和b.
在解码阶段, 将h映射到输出,
| $ {x'} = {f'}({W'}h + {b'}) $ | (5) |
通过最小化重构误差(例如均方误差), 来训练自编码器:
| $ \begin{split} L(x, {x'}) &= {\left\| {x - {x'}} \right\|^2}\\ &= {\left\| {x - {f'}({W'}(f(Wx + b)) + {b'})} \right\|^2} \end{split} $ | (6) |
为了对用户选课数据的时序性建模, 利用LSTM替换自编码器中的前馈神经网络, 类似于RNN Encoder-Decoder[19]和 EncDec-AD[20], 将二者相结合.
所提时序特征提取方法如图3所示.

|
图 3 时序特征提取方法 |
本文提出的时序特征提取方法包括输入层、编码层、LSTM层、解码层和输出层5部分. 首先对输入数据进行预处理, 包括数据增强和按窗口划分序列, 随后将每一个序列送入编码器得到特征向量, 再将此特征向量作为LSTM网络的输入, 最后将LSTM的输出送入解码器, 得到对原始数据窗口下一个窗口的重建. 通过最小化重构误差进行训练, 训练完成后, 提取LSTM网络输出作为提取的时序特征.
(1)对原始的时序数据进行预处理, 将处理好后的数据输入到输入层.
预处理过程中采用了数据增强(data augmentation)技术, 通过添加高斯噪音来提高模型的准确率.
| $ {X'} = X + \gamma * {\sigma ^2} * {randn} (m) $ | (7) |
其中,
然后, 将添加噪音的数据以长度为
| $ {w_t} = \left[ {{x_{t - p + 1}}, {x_{t - p + 2}}, \cdots, {x_t}} \right] $ | (8) |
其中,
(2)将
| $ {W_t} = \left[ {{w_{t - (k - 1) \times p}}, {w_{t - (k - 2) \times p}}, \cdots, {w_t}} \right] $ | (9) |
| $e_t^i = {{Encoder}} (w_t^i)\;\;\; {\rm{for}}\; i = 1, 2, \cdots, k $ | (10) |
| $ {E_t} = [e_t^1, e_t^2, \cdots, e_t^k] $ | (11) |
(3)训练LSTM网络, 用一个序列
| $ \left[ {\hat e_t^2, \hat e_t^3, \cdots, \hat e_t^k} \right] = {LSTM} ([e_t^1, e_t^2, \cdots, e_t^{k - 1}]) $ | (12) |
LSTM的计算可以按照以下公式展开:
| $ {f_t} = \sigma ({W_f} \cdot [{h_{t - 1}}, {x_t}] + {b_f}) $ | (13) |
| $ {i_t} = \sigma ({W_i} \cdot [{h_{t - 1}}, {x_t}] + {b_i}) $ | (14) |
| $ {\hat C_t} = {\rm{tanh}} ({W_c} \cdot [{h_{t - 1}}, {x_t}] + {b_c}) $ | (15) |
| $ {C_t} = {f_t} * {C_{t - 1}} + {i_t} * {\hat C_t} $ | (16) |
| $ {O_t} = \sigma ({W_o} \cdot [{h_{t - 1}}, {x_t}] + {b_o}) $ | (17) |
| $ {h_t} = {O_t} * {\rm{tanh}} ({C_t}) $ | (18) |
其中,
应用梯度裁剪(gradient clipping)[21]来解决LSTM中的梯度爆炸问题. 通过将超过阈值的梯度设定为固定值来使梯度值保持在合理水平. 更确切地说, 在梯度
| $ {\rm{if}}\left\| g \right\| > v $ | (19) |
| $ g \leftarrow \frac{{gv}}{{\left\| g \right\|}} $ | (20) |
其中,
采用真实值跟LSTM预测值之间的均方误差(mean square error, MSE)作为损失函数, MSE计算公式如式(21)所示:
| $ {\textit{MSE}} = \frac{1}{{k - 1}}\sum\nolimits_{i = 1}^{k - 1} {{{\left( {e_t^i - \hat e_t^{i + 1}} \right)}^2}} $ | (21) |
其中
(4) 利用解码器将LSTM的输出重构为时间序列窗口.
| ${\hat w_{t - (k - i) \times p}} = {Decoder} (\hat e_t^i)\;\;\;{\rm{for}}\; i = 2, 3, \cdots,k $ | (22) |
经过上一步提取到数据的时序特征后, 将LSTM的输出作为输入, 经过Softmax函数, 得到模型最后的推荐结果. 如图4所示.

|
图 4 进行课程推荐 |
| $ {y_u} = {{Softmax}}({W_u} \cdot h + {b_u}) $ | (23) |
采用MOOC真实数据集[22], 共458454条选课记录, 包含82535位用户和1 302门课程. 每条记录包含用户id、选课时间、课程id、课程名称、课程类别等属性.
5.2 数据预处理(1)首先, 将原始数据数据简化为三元组(用户id, 选课时间, 课程id).
(2)其次, 从82535位用户中, 剔除选修课程数量少于10门的用户, 剩余130812条数据, 8 268位用户.
(3)然后, 再按照用户分组, 共分为8 268个组, 在每个组内按照选课时间升序进行排序.
(4)最后, 按照(用户id, 课程id时间序列)合并组内数据, 得到最终数据集, 共计8 268条数据.
5.3 评价指标本文采用Top-N推荐系统中常用的查准率(precision, P)、查全率(recall, R)、F1-分数(F1-Score, F1)3个评价指标来衡量所提方法的推荐性能, 表达式如下.
| $ {{P}} = \frac{{\displaystyle\sum\nolimits_{u \in U} {\left| {{{R}}\left( u \right) \cap {{T}}\left( u \right)} \right|} }}{{\displaystyle\sum\nolimits_{u \in U} {\left| {{{R}}\left( u \right)} \right|} }} $ | (24) |
| $ {{R}} = \frac{{\displaystyle\sum\nolimits_{u \in U} {\left| {{{R}}\left( u \right) \cap {{T}}\left( u \right)} \right|} }}{{\displaystyle\sum\nolimits_{u \in U} {\left| {{{T}}\left( u \right)} \right|} }} $ | (25) |
| $ {{{F}}_1} = \frac{{2 \times {{P}} \times {{R}}}}{{{{P}} + {{R}}}} $ | (26) |
其中,
对于Top-N课程推荐问题, 本文取
| 表 1 N=1时实验对比 |
| 表 2 N=3时实验对比 |
| 表 3 N=10时实验对比 |
(1)在同一组对比实验内, 所提方法在查准率、查全率、F1-Score3个指标上的表现均要优于协同过滤算法和基于传统的自编码器的推荐算法. 当N=1时, 与CF算法相比, 准确率提高22.8%, 召回率提高26.2%, F1-Score提高24.6%; 与AE算法相比, 准确率提高9.9%, 召回率提高7.7%, F1-Score提高8.7%. 当N=3时, 与CF算法相比, 准确率提高15.5%, 召回率提高12.7%, F1-Score提高14.1%; 与AE算法相比, 准确率提高8.5%, 召回率提高7.4%, F1-Score提高7.9%. 当N=10时, 与CF算法相比, 准确率提高13.3%, 召回率提高14.2%, F1-Score提高13.8%; 与AE算法相比, 准确率提高3.1%, 召回率提高2.6%, F1-Score提高2.9%. 实验结果表明, 基于深度学习方法的推荐算法性能表现要优于传统的算法, 这是因为深度学习算法可以提取更深层次的数据特征. 本文所提方法由于采用了LSTM对数据的时序特征进行建模, 因此效果也要优于基于传统的自编码器的推荐算法.
(2)不同对比实验组间, 随着N的增大, 模型的3个性能评价指标也越来越高, 这是因为随着推荐课程的数量增加, 包含用户喜欢的课程的概率也越来越大.
6 结论与展望本文针对在线教育的课程推荐问题, 提出了一种基于改进自编码器的在线课程推荐模型. 首先, 利用长短期记忆网络改进自编码器, 使得模型可以提取数据的时序性特征; 然后, 利用提取到的数据特征进行在线教育的课程推荐; 最后, 在真实的MOOC数据集上进行实验验证, 实验结果表明所提方法与协同过滤算法和基于传统的自编码器的推荐算法相比, 具有更高的准确性.
但是, 本文工作仍存在以下不足: 在LSTM网络中, 有众多的超参数需要手动设置, 仅凭个人经验难以找到最合适的数值, 接下来将研究如何利用神经网络搜索, 去自动寻找最优的超参数.
| [1] |
Zhang S, Yao LN, Sun AX, et al. Deep learning based recommender system: A survey and new perspectives. ACM Computing Surveys, 2019, 52(1): 5. |
| [2] |
Yang B, Lei Y, Liu JM, et al. Social collaborative filtering by trust. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1633–1647.
|
| [3] |
Strub F, Gaudel R, Mary J. Hybrid recommender system based on autoencoders. Proceedings of the 1st Workshop on Deep Learning for Recommender Systems. Boston: ACM, 2016. 11–16.
|
| [4] |
陈征, 宋轩, 杜先瑞, 等. 基于多图神经网络的个性化推荐模型. 中国传媒大学学报(自然科学版), 2020, 27(6): 14–18.
|
| [5] |
郭旦怀, 张鸣珂, 贾楠, 等. 融合深度学习技术的用户兴趣点推荐研究综述. 武汉大学学报(信息科学版), 2020, 45(12): 1890–1902.
|
| [6] |
徐亚军, 郭俭. K12学习平台个性化学习资源推荐. 计算机系统应用, 2020, 29(7): 217–221.
|
| [7] |
Strub F, Mary J. Collaborative filtering with stacked denoising autoencoders and sparse inputs. NIPS Workshop on Machine Learning for eCommerce. Montreal, 2015.
|
| [8] |
刘国丽, 廉孟杰, 于丽梅, 等. 融合专家信任的协同过滤推荐算法. 计算机系统应用, 2021, 30(4): 160–167.
|
| [9] |
Li J, Ye Z. Course recommendations in online education based on collaborative filtering recommendation algorithm. Complexity, 2020, 2020: 6619249. |
| [10] |
Cui ZH, Xu XH, Xue F, et al. Personalized recommendation system based on collaborative filtering for IoT scenarios. IEEE Transactions on Services Computing, 2020, 13(4): 685–695.
|
| [11] |
王素琴, 吴子锐. 利用LSTM网络和课程关联分类的推荐模型. 计算机科学与探索, 2019, 13(8): 1380–1389.
|
| [12] |
卜祥鹏. 基于GRU和课程关联关系的推荐模型. 软件, 2020, 41(6): 137–142.
|
| [13] |
Sedhain S, Menon AK, Sanner S, et al. Autorec: Autoencoders meet collaborative filtering. Proceedings of the 24th International Conference on World Wide Web. Florence: ACM, 2015. 111–112.
|
| [14] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735–1780.
|
| [15] |
Graves A, Liwicki M, Fernández S, et al. A novel connectionist system for unconstrained handwriting recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(5): 855–868.
|
| [16] |
Sak H, Senior A, Beaufays F. Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition. arXiv: 1402.1128, 2014.
|
| [17] |
Malhotra P, Vig L, Shroff G, et al. Long short term memory networks for anomaly detection in time series. 23rd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning. Bruges: ESANN, 2015. 89–94.
|
| [18] |
Staudemeyer RC, Morris ER. Understanding LSTM—a tutorial into long short-term memory recurrent neural networks. arXiv: 1909.09586, 2019.
|
| [19] |
Cho K, Van Merriënboer B, Gulcehre C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv: 1406.1078, 2014.
|
| [20] |
Malhotra P, Ramakrishnan A, Anand G, et al. LSTM-based encoder-decoder for multi-sensor anomaly detection. arXiv: 1607.00148, 2016.
|
| [21] |
Pascanu R, Mikolov T, Bengio Y. On the difficulty of training recurrent neural networks. Proceedings of the 30th International Conference on International Conference on Machine Learning. Atlanta: JMLR, 2013. III-1310–III-1318.
|
| [22] |
Zhang J, Hao BW, Chen B, et al. Hierarchical reinforcement learning for course recommendation in MOOCs. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1): 435–442.
|
 2022, Vol. 31
2022, Vol. 31



