近年来, 云计算[1]作为一种新的计算模型, 吸引了人们的广泛关注. 云存储作为云计算的重要组成部分, 已经被人们以极大优势频繁地用于存储数据. 比如, 数据所有者不再需要处理大量的数据, 无论数据使用者所处何地, 查阅资料都很方便. 由于云存储有很多优势, 越来越多的用户选择将他们的数据存储在知名的云服务器(CSP)上. 例如, 大家所熟知的谷歌、微软等大型网络公司均有云存储的服务; 在国内, 百度云和微云则是市场占有量最大的存储云. 此外, 通过CSP提供的数据存储和共享服务, 使人们可以很轻松地进行团队合作. 更具体地说, 一旦用户在云端创建了共享数据, 用户群内的每个用户不仅可以访问和修改共享数据, 还可以与群内其他人共享最新版本的数据. 虽然数据存储和共享服务使数据所有者可以方便地访问、修改和共享用户群内的数据, 以致用户从这种数据管理方式中受益匪浅, 但是数据外包到云上进行存储的方式也引发了严重的安全问题. 首先, 一旦用户数据被外包到CSP上, 用户失去了对数据的直接控制权[2], 这使得用户担心CSP是否正确地存储了用户数据. 例如, CSP可能由于软件或者硬件故障[3, 4]遭受内部敌手或者外部敌手的攻击. 其次, 恶意的CSP可能删除极少被访问的数据以节省存储空间或者掩盖数据被损坏的事实以维持自身的良好声誉. 因此, 如何保证用户外包数据的完整性[5-8]是至关重要的问题之一.
为了解决数据完整性问题, 一些基于传统密码学的公开审计方案[5,9,10]被提出. 其中, 用户的公、私钥是通过数字证书发放, 通信效率低, 计算量大, 证书的管理成本高. 为了解决复杂的证书管理问题, Shamir等人[11]引入基于身份的密码体制概念. 在基于身份的密码体制中, 用已知的身份信息作为公钥, 来避免使用公钥证书. 之后, 基于身份的可证明数据拥有方案[12-18]被提出, 但是这些方案[12-18]大多利用双线性对技术和映射到点的哈希函数来实现完整性认证, 需要昂贵的时间和通信成本, 造成很大的计算和存储负担.
为了在实现数据共享服务的同时, 高效实现用户可撤销, 本文提出了一种高效的隐私保护可证明数据拥有方案. 首先, 所提方案采用基于椭圆曲线密码学[19, 20]实现了无对认证, 并且不使用映射到点的哈希函数, 极大地减少了通信和计算代价[21, 22]. 其次, 所提方案采用中国剩余定理[23]实现了高效安全的用户撤销[24, 25], 在实现隐私保护的同时, 保证方案的高效性. 最后, 在设定的实验模型下, 给出了所提方案的计算和通信成本分析, 证明所提方案的效率高于已知方案[15-17].
1 背景知识 1.1 椭圆曲线椭圆曲线密码学的概念是由Miller[19]和Koblitz[20]基于椭圆曲线提出. 定义
中国剩余定理[23]是一种古老的求解相同余数的方法, 它是数论中的重要定理. 设定
| $ \left\{ \begin{gathered} \alpha = va{r_1}\boldsymbolod {k_1} \hfill \\ \alpha = va{r_2}\boldsymbolod {k_2} \hfill \\ \qquad \quad \vdots \hfill \\ \alpha = va{r_n}\boldsymbolod {k_n} \hfill \\ \end{gathered} \right. $ |
(1) 椭圆曲线离散对数问题(ECDL问题): 假定
(2) 椭圆曲线离散对数(ECDL假设) : 任何概率多项式时间算法都不能以不可忽略的概率解决ECDL问题.
(3) 计算性Diffie-Hellman问题(CDH问题): 假定
(4) 计算性Diffie-Hellman假设(CDH假设): 概率多项式时间算法都不能以不可忽略的概率解决CDH问题.
1.4 系统模型所提方案的系统模型图, 如图1所示. 其中, 共有5个参与者, 包括密钥生成中心(KGC), 车辆用户(
(1) RSU: 路边单元, 是具有足够计算能力的雾设备, 可以及时处理每个车辆用户的传感器产生的信息, 并将其上传到CSP. 在本文中看作车辆用户群的群管理者GM, 后续内容不再赘述.

|
图 1 系统模型图 |
(2)
(3) KGC: 密钥生成中心, 是一个完全可信的参与者, 具有强大的计算和存储能力, 负责初始化整个系统以生成主密钥和公共参数, 并且为用户群生成和分配群私钥.
(4) CSP: 云服务器, 是一个半可信实体, 具有强大存储空间和计算能力. 云服务器在接收到第三方审计者发来的审计请求时, 为第三方审计者生成相应的审计证据. 所有数据都存储在云服务器中, 所有的用户通过云服务器实现数据共享服务.
(5) TPA: 第三方审计者, 作为一个半可信的实体, 接受用户群的审计委托, 向云服务器发送审计询问, 并根据云服务器返回的证据确定共享数据是否完整存储在云服务器中.
1.5 安全需求作为一个基于身份的共享数据云存储审计方案, 需要满足下面的安全需求:
公开审计: TPA能够代表用户认证CSP中存储的数据的完整性.
存储正确性: 如果用户, TPA和CSP都是诚实的, 并且正确地执行了指定的算法, 那么CSP生成的证据能够通过TPA的完整性认证.
安全用户撤销: 确保被撤销的用户无法像CSP上传数据和数据标签.
数据隐私保护: TPA在审计阶段不能获得CSP中存储的任何数据.
2 本文方案方案由7个算法组成, 包括系统建立算法, 密钥生成算法, 标签生成算法, 挑战生成算法, 证据生成算法, 证据认证算法, 和用户撤销算法.
2.1 系统建立算法由KGC执行, 输入安全参数
(1)给定一个安全参数
(2)随机选择
(3)选择密码学安全的哈希函数:
KGC保存主密钥
由KGC, 群管理者GM和合法的车辆群用户
(1)在接收到GM的身份
(2) GM接收到
(3) GM随机选择
(4) GM随机选择
(5) 每个
给定原始文件
(1)将原始文件
(2)对于每个
当收到来自
随机选择
在接收到来自TPA的挑战消息之后, 由CSP执行:
(1) 计算
(2) 计算
给定
(1) 对于所有的
(2) 如果等式成立, 说明CSP正确存储了用户的数据, 发送“成功”给
当用户群内有用户离开或者由于不合法的行为被撤销时, 由群管理者GM和合法群用户执行:
(1) 当用户
(2) GM选择一个新的部分私钥
(3) 车辆群用户
由所提方案可知, 如果TPA和CSP都是诚实的, 并且正确地执行了指定的算法, 且
| $ \begin{split} a =& \displaystyle\sum\limits_{j = 1}^c {{w_j} \cdot {\sigma _{{v_j}}} \cdot P} \hfill \\ =& \displaystyle\sum\limits_{j = 1}^c {{w_j} \cdot ({r_{{v_j}}} \cdot {m_{{v_j}}} + sk \cdot H(I{D_F}||pk||{R_{{v_j}}})) \cdot P} \hfill \\ =& \displaystyle\sum\limits_{j = 1}^c {{w_j} \cdot {r_{{v_j}}} \cdot {m_{{v_j}}} \cdot P} + \sum\limits_{j = 1}^c {{w_j} \cdot sk \cdot H(I{D_F}||pk||{R_{{v_j}}}) \cdot P} \hfill \\ =& b + pk \cdot \displaystyle\sum\limits_{j = 1}^c {{w_j} \cdot H(I{D_F}||pk||{R_{{v_j}}})} \hfill \\ \end{split} $ |
由于等式成立, 因此, 所提方案是正确的.
3.2 方案安全性分析(1)公开审计: 所提方案中, TPA能够代表用户对CSP发起审计挑战, 并且可以通过系统公开参数, 用户群的公钥
(2)存储正确性: 通过对方案的正确性分析, 我们得到, 如果用户, TPA和CSP都是诚实的, 并且正确地执行了指定的算法, 那么CSP生成的证据能够通过TPA的完整性认证.
(3)安全的用户撤销: 每当有群用户离开, 新的群用户加入和不合法的群用户被撤销时, 都生成新的用户群私钥
(4)数据隐私保护: 在TPA对CSP进行审计的过程中, TPA不能从
为了满足80 bit的安全性, 对于现存方案[15-17], 选择双线性对
| 表 1 密码运算的运行时间 |
| 表 2 计算代价对比 |
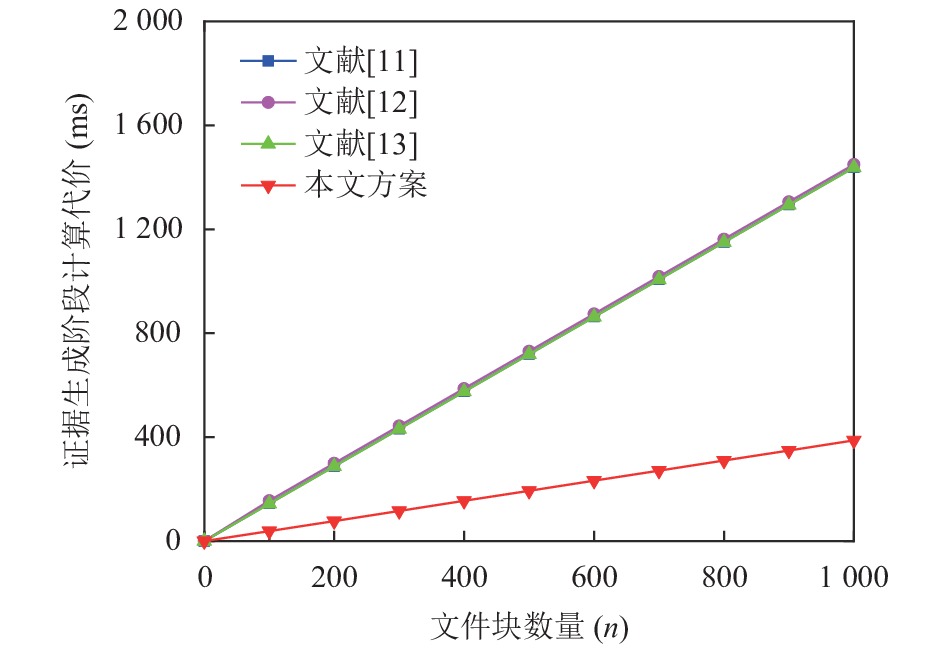
图2–图4分别表示标签生成阶段, 证明生成阶段和证据认证阶段的计算代价比较. 正如图2–图4显示, 所提方案的计算代价明显低于已知方案[15-17]. 并且, 随着文件块数量
为满足80 bit的安全性,

|
图 2 标签生成的计算代价比较 |
|
图 3 证据生成的计算代价比较 |
|
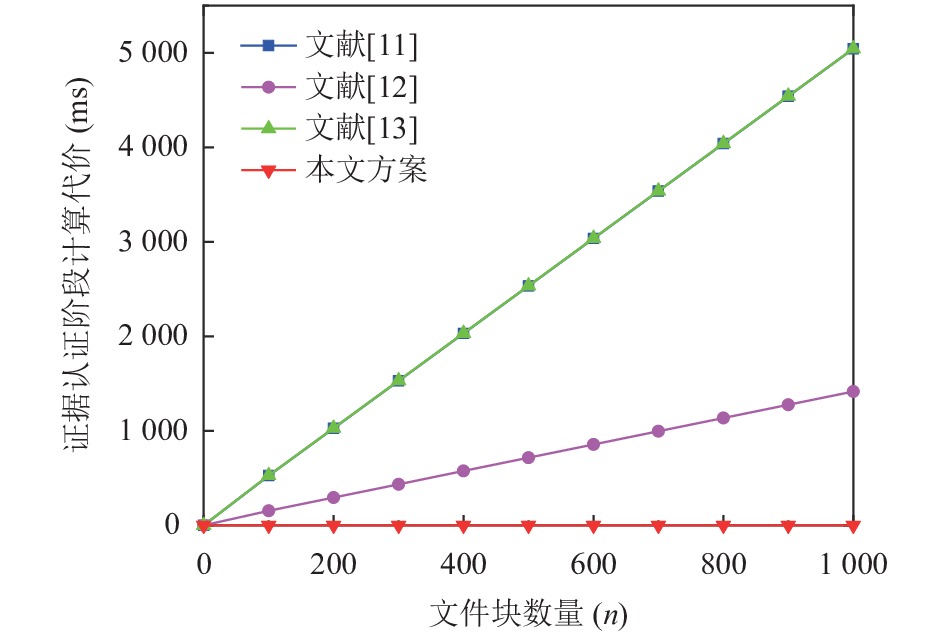
图 4 证据认证的计算代价比较 |
| 表 3 通讯数据对比 (bit) |
如表3所示, 首先, 从TPA到CSP, 现存方案[15–17]有相同的
其次, 从CSP到TPA, 现存方案[15-17]的通信代价都保持不变, 分别为1 184 bit, 672 bit, 672 bit, 320 bit. 因此, 在证据生成阶段, 所提方案的通信代价明显低于已知方案[15-17].
4 结论与展望为了解决复杂的证书管理问题, 一些基于身份的可证明数据拥有方案被提出. 但是, 这些方案大都采用昂贵的双线性对运算和映射到点的哈希函数, 具有很大的通信和计算代价. 本文采用椭圆曲线技术和中国剩余定理技术提出了一种高效的隐私保护可证明数据拥有方案, 在保证方案隐私和效率的同时, 实现了高效安全的用户撤销. 安全性分析表明, 所提方案能够满足基于身份的可证明数据拥有方案的安全需求. 计算代价和通信代价的分析表明, 与现存方案[15-17]相比, 所提方案具有较低的通信和计算代价. 在本文的基础上, 可进一步研究用户如何以更低的代价将数据和标签上传到多个CSP上, 以及防止如何进一步防止CSP和TPA的合谋攻击.
| [1] |
Armbrust M, Fox A, Griffith R, et al. A view of cloud computing. Communications of the ACM, 2010, 53(4): 50-58. DOI:10.1145/1721654.1721672 |
| [2] |
Li J, Ye H, Wang W, et al. Efficient and secure outsourcing of differentially private data publication. Proceedings of the 23rd European Symposium on Research in Computer Security. Barcelona: Springer, 2018. 187–206.
|
| [3] |
Li JG, Wang Y, Zhang YC, et al. Full verifiability for outsourced decryption in attribute based encryption. IEEE Transactions on Services Computing, 2020, 13(3): 478-487. DOI:10.1109/TSC.2017.2710190 |
| [4] |
Ali M, Khan SU, Vasilakos AV. Security in cloud computing: Opportunities and challenges. Information Sciences, 2015, 305: 357-383. DOI:10.1016/j.ins.2015.01.025 |
| [5] |
Ateniese G, Burns R, Curtmola R, et al. Provable data possession at untrusted stores. Proceedings of the 14th ACM Conference on Computer and Communications Security. Virginia: ACM, 2007. 598–609.
|
| [6] |
白国靖. 云计算环境下数据完整性验证方案的研究与设计[硕士学位论文]. 重庆: 重庆邮电大学, 2012.
|
| [7] |
Shacham H, Waters B. Compact proofs of retrievability. Proceedings of the 14th International Conference on the Theory and Application of Cryptology and Information Security. Melbourne: Springer, 2008. 90–107.
|
| [8] |
王珺翔. 可证明数据持有模型与方案的研究[硕士学位论文]. 上海: 上海交通大学, 2013.
|
| [9] |
Ateniese G, Di Pietro R, Mancini LV, et al. Scalable and efficient provable data possession. Proceedings of the 4th International Conference on Security and Privacy in Communication Netowrks. Istanbul: ACM, 2008. 9.
|
| [10] |
Sebé F, Domingo-Ferrer J, Martinez-Balleste A, et al. Efficient remote data possession checking in critical information infrastructures. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(8): 1034-1038. DOI:10.1109/TKDE.2007.190647 |
| [11] |
Shamir A. Identity-based cryptosystems and signature schemes. Workshop on the Theory and Application of Cryptographic Techniques. Aarhus: Springer, 1984. 47–53.
|
| [12] |
Wang HQ, He DB, Yu J, et al. Incentive and unconditionally anonymous identity-based public provable data possession. IEEE Transactions on Services Computing, 2019, 12(5): 824-835. DOI:10.1109/TSC.2016.2633260 |
| [13] |
Li YN, Yu Y, Min GY, et al. Fuzzy identity-based data integrity auditing for reliable cloud storage systems. IEEE Transactions on Dependable and Secure Computing, 2019, 16(1): 72-83. DOI:10.1109/TDSC.2017.2662216 |
| [14] |
Yang GY, Yu J, Shen WT, et al. Enabling public auditing for shared data in cloud storage supporting identity privacy and traceability. Journal of Systems and Software, 2016, 113: 130-139. DOI:10.1016/j.jss.2015.11.044 |
| [15] |
Wang C, Wang Q, Ren K, et al. Privacy-preserving public auditing for data storage security in cloud computing. 2010 Proceedings IEEE INFOCOM. San Diego: IEEE, 2010. 1–9.
|
| [16] |
Yu Y, Au MH, Ateniese G, et al. Identity-based remote data integrity checking with perfect data privacy preserving for cloud storage. IEEE Transactions on Information Forensics and Security, 2017, 12(4): 767-778. DOI:10.1109/TIFS.2016.2615853 |
| [17] |
Zhang Y, Yu J, Hao R, et al. Enabling efficient user revocation in identity-based cloud storage auditing for shared big data. IEEE Transactions on Dependable and Secure Computing, 2020, 17(3): 608-619. DOI:10.1109/TDSC.2018.2829880 |
| [18] |
王佳硕. 云存储中可证明数据持有性研究[硕士学位论文]. 成都: 西南交通大学, 2018.
|
| [19] |
Miller VS. Use of elliptic curves in cryptography. Conference on the Theory and Application of Cryptographic Techniques. Bruges: Springer, 1985. 417–426.
|
| [20] |
Koblitz N. Elliptic curve cryptosystems. Mathematics of Computation, 1987, 48(177): 203-209. DOI:10.1090/S0025-5718-1987-0866109-5 |
| [21] |
Boneh D, Lynn B, Shacham H. Short signatures from the Weil pairing. International Conference on the Theory and Application of Cryptology and Information Security. Gold Coast: Springer, 2001. 514–532.
|
| [22] |
Schnorr CP. Efficient signature generation by smart cards. Journal of Cryptology, 1991, 4(3): 161-174. DOI:10.1007/BF00196725 |
| [23] |
Katz J, Lindell Y. Introduction to Modern Cryptography. Taylor and Francis, 2007.
|
| [24] |
Wang BY, Li BC, Li H. Panda: Public auditing for shared data with efficient user revocation in the cloud. IEEE Transactions on Services Computing, 2015, 8(1): 92-106. DOI:10.1109/TSC.2013.2295611 |
| [25] |
Jiang T, Chen XF, Ma JF. Public integrity auditing for shared dynamic cloud data with group user revocation. IEEE Transactions on Computers, 2016, 65(8): 2363-2373. DOI:10.1109/TC.2015.2389955 |
| [26] |
Shamus Software. Multiprecision Integer and Rational Arithmetic Cryptographic Library (MIRACL). https://github.com/miracl/MIRACL. (2019-06-10).
|
 2022, Vol. 31
2022, Vol. 31



