自深度学习兴起以来, 将人工智能技术应用于如工程、医学等传统行业是近年的热门研究方向^[1-3]. 但传统行业往往面临由样本收集难度大、成本高、涉及个人隐私等原因导致难以收集到足以代表总体的样本数量进行深度学习的阻碍.

解决小样本问题的方法大致上分为: 半监督学习^{[4, 5]}、转导推理学习^[6]、主动学习^[7]和虚拟样本^{[8, 9]}. 其中, 半监督学习具有样本获取相对容易的优势, 其主要思想是结合未标记样本辅助有标签训练样本进行学习, 利用无标签样本的分布信息, 提高模型的泛化能力. 主动学习则是通过主动查询, 标记最重要的样本, 辅助原样本的分类学习, 其困难在于如何确定和标记样本的重要性. 而虚拟样本法通过对样本特征采取一定假定生成新样本, 是降低小样本问题的影响的直观方法, 达到扩充原有样本集的目的.

虚拟样本法主要分为基于专家先验知识构造样本、基于扰动的思想构造虚拟样本以及基于研究领域的分布函数生成虚拟样本^[10]. 例如程彬^[11]通过颜色空间变化、文本区域变换、背景区域变换来合成新的场景文字图像, 提高场景文本检测算法的准确度和泛化能力; 温津伟等^[12]利用对人脸轮廓线的先验知识, 构造特征矢量, 并且通过计算原样本中人脸角度变化后的特征矢量变化关系, 构造新样本. 上述方法需要对样本有详细的先验知识, 适用性有限. 而加入扰动的虚拟样本构造方法^[13]普适性更强, 而且易于操作. 但是该方法只保证了样本生成的合理性, 并没有兼顾广泛性, 生成的样本属性基本与原有样本相同, 只提高了对输入特征自身误差的宽容性.

大多数机器学习算法在测试样本的表现依赖于训练样本集分布满足i.d.d. (independent and identically distributed)假设. 天然样本的不均衡分布普遍存在, 并且稀少类样本通常更为重要, 若直接对不均衡的原样本进行训练, 算法会认为样本多的类别更重要. 一种解决思路是提高稀少类的重要程度, 例如更改样本集各类型样本配比的SMOTE算法^[14]和对各类别按占比赋予不同的错分代价的METACOST算法^[15].

以上方法普遍有不能同时兼顾合理性和广泛性等缺点, 而基于变分自编码器(VAE)的虚拟样本法, 有不对样本集分布采取强制假定, 准确拟合样本集分布的特点. 研究表明, VAE用作扩充稀有类样本数量时, 使样本集各类别趋于均衡, 能有效缓解不均衡数据类别的问题^[16].

VAE通过抽样标准高斯分布的潜变量生成新样本, 对生成样本的特性是无控的. 为此, Sohn等^[17]提出的CVAE在训练时融入标签信息, 使生成过程能定向至对应标签. 更为灵活、丰富的控制生成方式则是通过提炼潜变量的语义后, 直接控制潜变量生成特定属性的样本. 例如Higgins等提出的β-VAE^[18]、Kim等提出的FactorVAE^[19]以及对β-VAE的改进型方法β-TCVAE^[20]对VAE的潜变量进行特征解耦(feature disentanglement), 使各潜变量能独立代表样本的一类属性, 然后通过枚举法提取一系列涵盖潜变量的取值空间的潜变量值及其对应解码后的样本, 观测各潜变量的改变带来解码样本的变化, 见图1.

然而仅对于图像类样本可采用枚举加主观判断的方法提炼潜变量的语义, 对于数值和文字类输入特征很难通过可视化表达观察出各潜变量的语义. 因此, 本文提出一种基于输入特征与潜变量的依赖关系统计的方法, 准确测出对各潜变量敏感(依赖关系高)的输入区域, 然后通过输入区域内特征的共性, 确定潜变量的语义, 实现可控地生成特定属性的样本, 灵活地扩充原有样本集.

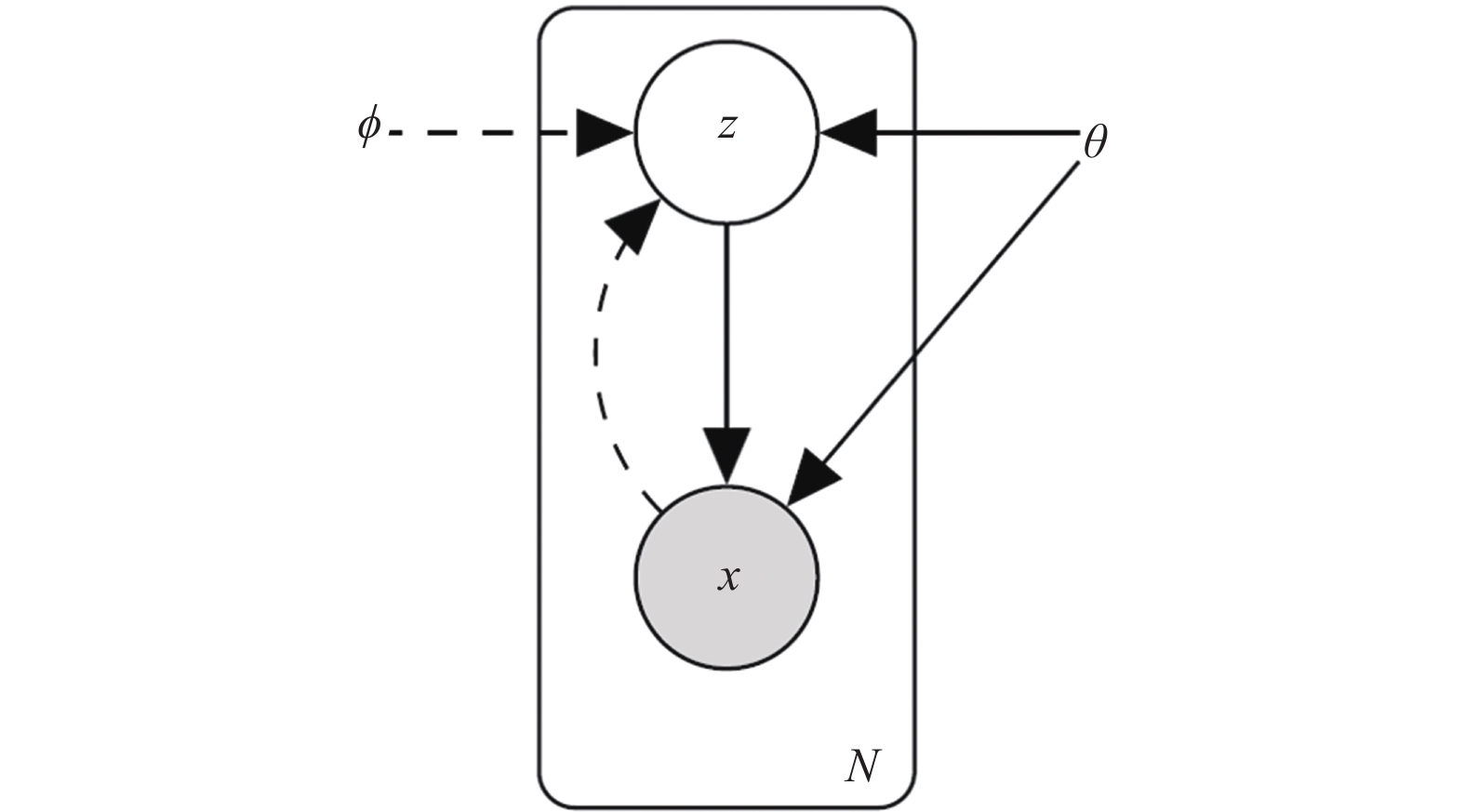
1 VAE潜变量语义提炼算法的原理 1.1 变分自编码器(VAE)介绍

变分自编码器(VAE)^[21]是一种包含潜变量的生成模型, 它利用神经网络训练得到编码器和解码器, 通过标准高斯分布的潜变量Z加一个足够复杂的函数映射(由神经网络求解)得到任何输入特征的分布, 进而输出原样本集中不包含的数据, 标准VAE模型见图2.

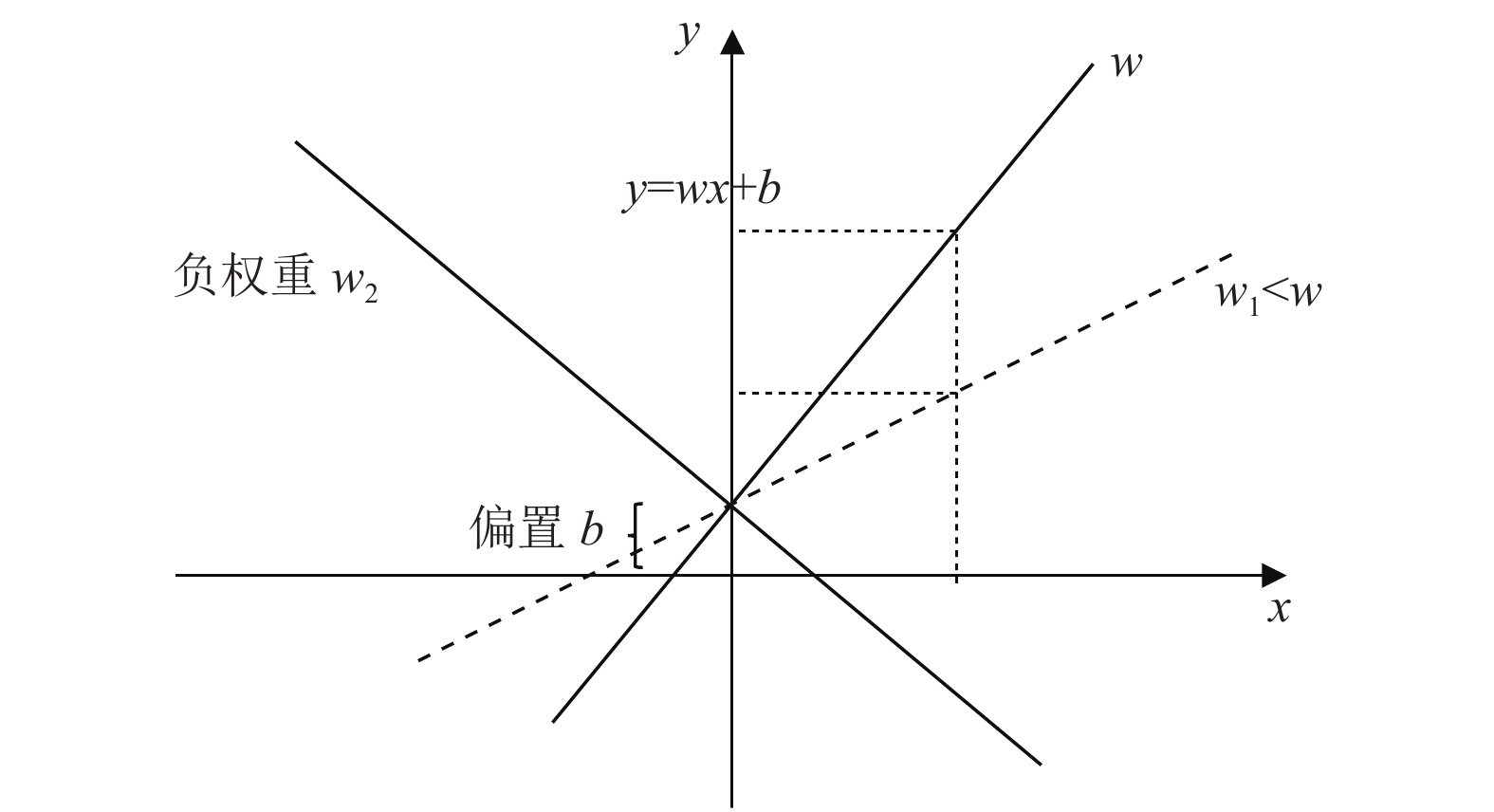
1.2 权重作为依赖关系度量的合理性证明

输入特征经过“黑箱子”神经网络与潜变量连接, 通过利用神经网络的权重作为输入特征与潜变量相关性的度量, 通过统计各输入特征对各潜变量的贡献度, 即可获取输入特征与VAE潜变量的依赖关系. 神经网络的神经元激活计算公式 $ y=w \cdot x+b $ 可看作线性映射. 偏置b代表的是对原始输入特征值偏离的矫正; 权重w代表的是该神经元的激活对上游神经元连接传递值的敏感程度, 见图3. 因此, 权重可用于反映各层神经元的连接强度. 权重的正负号反映互相连接的两神经元的正/负相关关系; 权重的绝对值大小反映该相关关系的强弱. 因此, 以权重的绝对值作为两神经元连接强弱的度量.

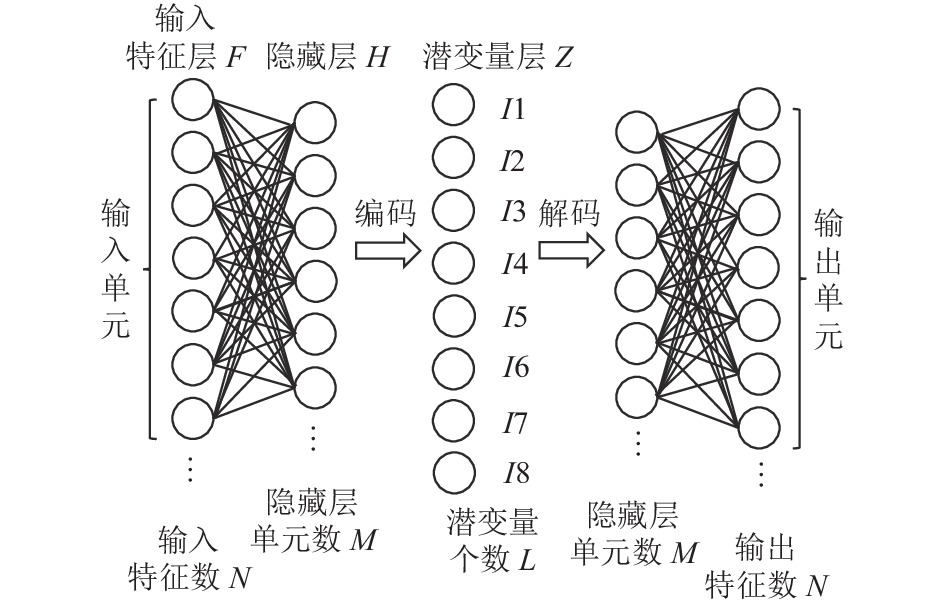
VAE架构如图4所示, 由于与VAE隐藏层连接的是潜变量的分布 $ Z-N(\mu, \sigma) $ (两个并行的潜变量层μ与σ), 通过重参数化技巧 $ {\textit{z}}=\mu+\sigma \odot e $ 得出潜变量Z的值. 因为潜变量Z层是计算层, 不与隐藏层直接相连, 能代表潜变量Z的是其分布均值μ. 因此, 各隐藏层单元Hi对潜变量Z的贡献度等价于各隐藏层单元Hi对潜变量分布均值μ的贡献度.

1.3 输入特征与潜变量依赖关系的量化统计

单个输入特征对潜变量的贡献度可表示为其所有从该输入特征到该潜变量的路径上的权重绝对值的乘积之和. 表达式为:

$ C_{i, j}=\sum_{1}^{m} \prod_{1}^{n}\left|W_{n}\right| $

(1)

其中, i为输入特征, j为潜变量, m为输入特征i到潜变量j的路径数, n为该段路径包含的权重个数.

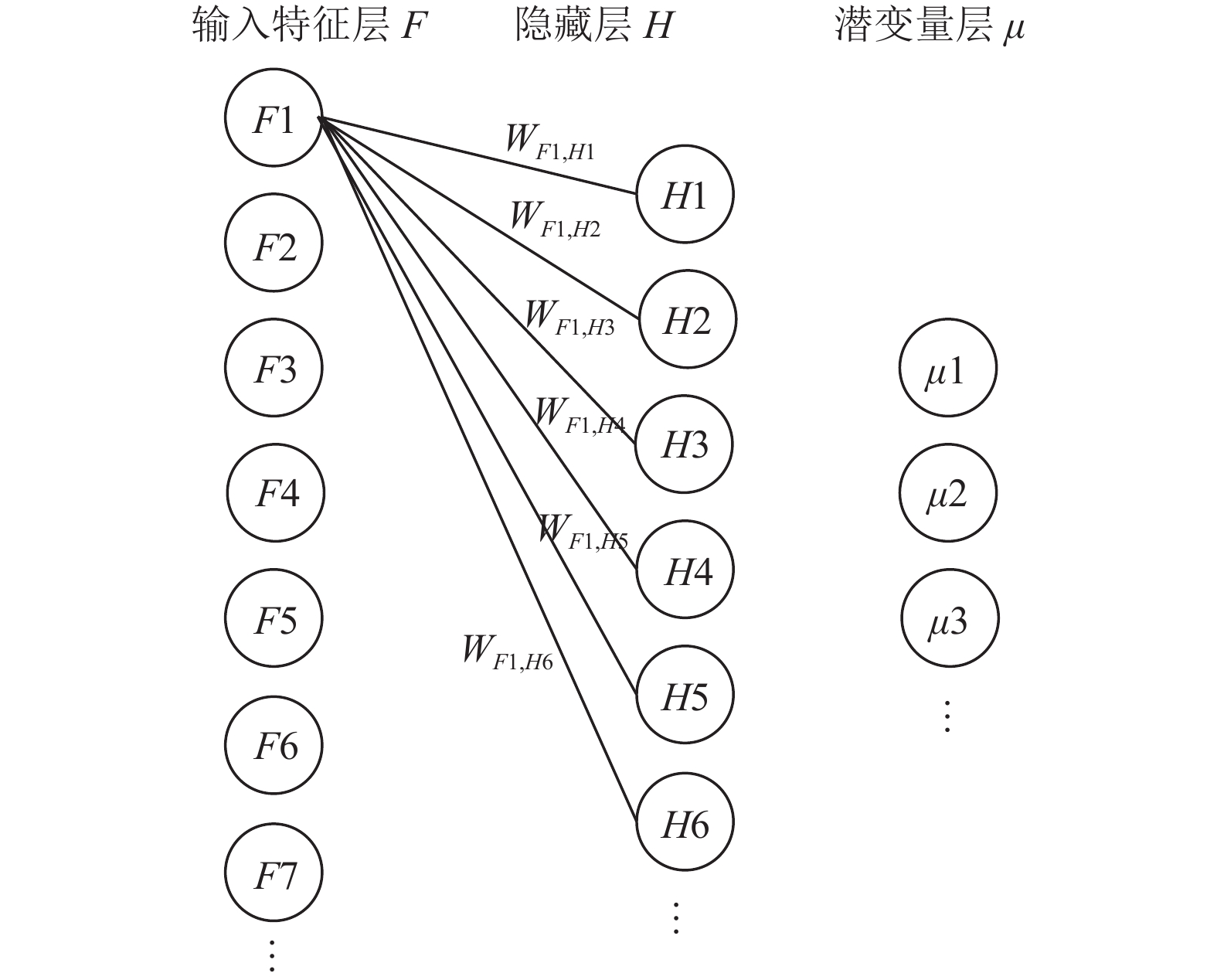
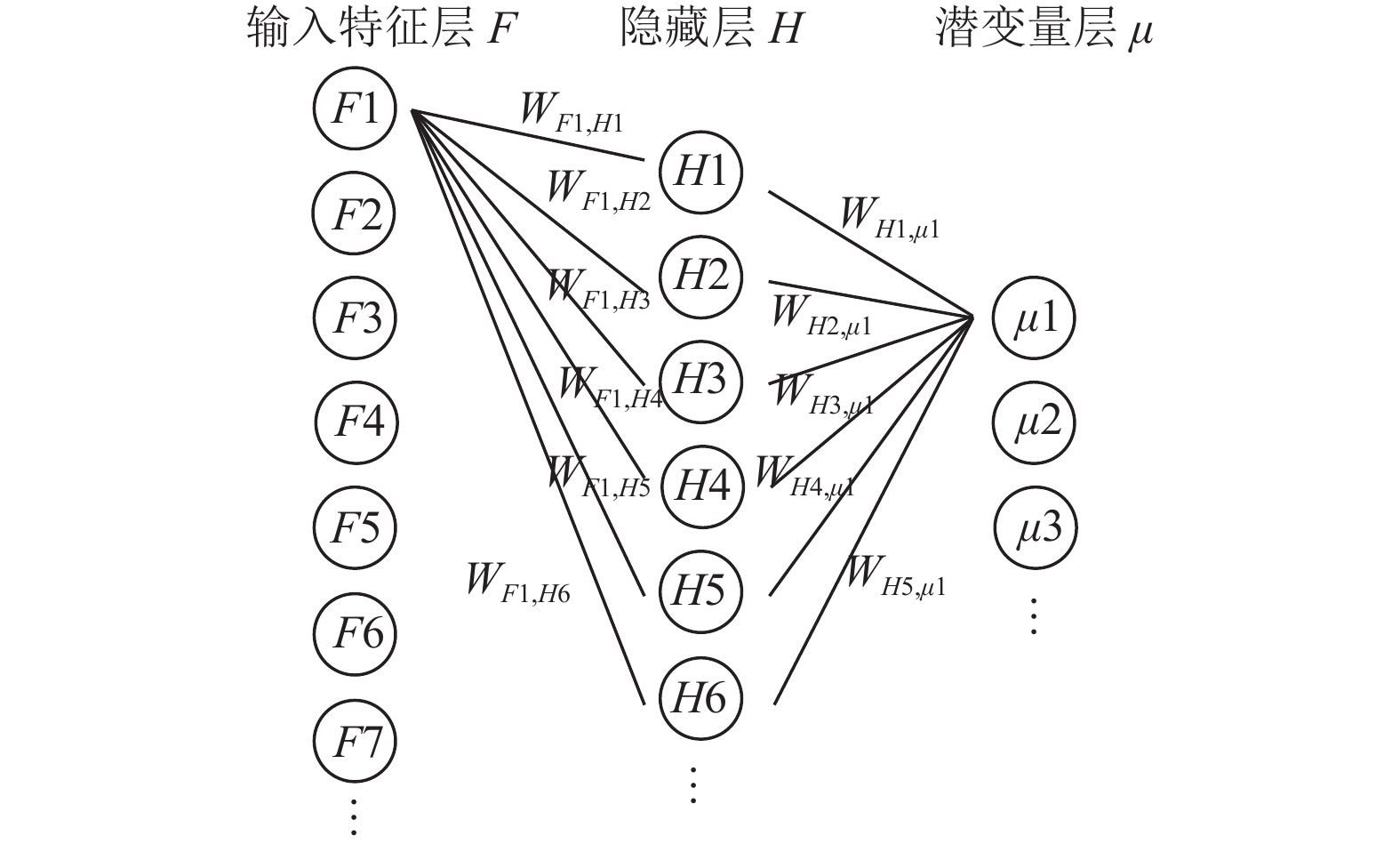
为消除输入特征本身的取值范围的影响(偏置一定程度会消除该影响), 贡献度的测量采用相对贡献度的度量方式, 即单个输入特征对所有潜变量的贡献度之和为1. 编码/解码神经网络可以拥有任意数量、大小的隐藏层, 本文以一层隐藏层的编码/解码神经网络为例, 列出贡献度计算公式. 另输入特征个数为N, 隐藏层单元个数为M, 潜变量个数为L. 输入层各单元与隐藏层各单元的连接权重记为W_Fi,Hj, 隐藏层各单元与潜变量层的连接权重记为W_Hj,Zk, 第i个输入特征F对第j个隐藏层单元H的贡献度(见图5)可写为:

$ {C_{Fi, Hj}} = \frac{{\left| {{W_{Fi, Hj}}} \right|}}{{\displaystyle\sum\limits_{j = 1}^M {\left| {{W_{Fi, Hj}}} \right|} }} $

(2)

以此类推, 第j个隐藏层单元H对第k个潜变量分布均值μ的贡献度为:

${C_{Hj, \mu k}} = \frac{{\left| {{W_{_{Hj, \mu k}}}} \right|}}{{\displaystyle\sum\limits_{k = 1}^L {\left| {{W_{_{Hj, \mu k}}}} \right|} }} $

(3)

因此, 第i个输入特征F对第k个潜变量分布均值μ的贡献度(见图6)可写为:

$ {C_{Fi, \mu k}}\frac{{\displaystyle\sum\limits_{j = 1}^M {\left| {{C_{Fi, Hj}}} \right|\left| {{C_{Fi, \mu k}}} \right|} }}{{\displaystyle\sum\limits_{k = 1}^L {\displaystyle\sum\limits_{j = 1}^M {\left| {{C_{Fi, Hj}}} \right|\left| {{C_{Hj, \mu k}}} \right|} } }} $

(4)

1.4 潜变量语义提炼的原理

通过贡献度计算, 得出输入特征与潜变量的依赖关系后, 以相关关系的强弱决定与各潜变量有强依赖关系的输入特征集. 当输入特征数量不多时, 通过观察潜变量对应的输入特征集, 以专家知识归纳出输入特征集的共性作为语义是较为准确的. 当输入特征数量多, 难以通过观察归纳出共性时, 本文给出一种语义与潜变量统计匹配算法, 能完成给定语义下的最优匹配, 并给出匹配明晰度作为预先给定语义与潜变量实际语义偏差的度量.

(1)语义与输入特征的依赖关系

由于潜变量的实际语义是未知的, 已知的是潜变量与各输入特征的依赖关系. 因此, 通过建立预定义的语义与输入特征的相关关系, 即把属于该语义范畴的输入特征定义为与该语义相关. 根据先验知识, 有依赖关系的填1, 无依赖关系时填0, 得出语义与输入特征的依赖关系矩阵R_j,k.

$ R_{j, k}= \begin{array}{rcccccc} & { F1 } & F 2 & F 3 & F 4 & F 5 & \cdots \\ I 1 & 0 & 0 & 1 & 1 & 1 & \cdots \\ I 2 & 1 & 0 & 0 & 1 & 0 & \cdots \\ I 3 & 1 & 0 & 1 & 0 & 0 & \cdots \\ I 4 & 0 & 1 & 0 & 1 & 1 & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array} $

(5)

代表潜变量与各输入特征的依赖关系的贡献度矩阵C_{i, k}由式(4)计算得出, 如下所示:

$C_{i, k} = \begin{array}{rcccccc} & { F1 } & F 2 & F 3 & F 4 & F 5 & \cdots \\ \mu 1 & {C_{\mu 1, F1}} & {C_{\mu 1, F2}} & {C_{\mu 1, F3}} & {C_{\mu 1, F4}} & {C_{\mu 1, F5}} & \cdots \\ \mu 2 & {C_{\mu 2, F1}} & {C_{\mu 2, F2}} & {C_{\mu 2, F3}} & {C_{\mu 2, F4}} &{C_{\mu 2, F5}} & \cdots \\ \mu 3 & {C_{\mu 3, F1}} & {C_{\mu 3, F2}} & {C_{\mu 3, F3}} & {C_{\mu 3, F4}} & {C_{\mu 3, F5}} & \cdots \\ \mu 4 & {C_{\mu 4, F1}} & {C_{\mu 4, F2}} & {C_{\mu 4, F3}} & {C_{\mu 4, F4}}& {C_{\mu 4, F5}} & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array} $

(6)

由于贡献度矩阵和依赖关系矩阵中的潜变量和语义均表达为对输入特征的相关关系, 因此可以通过寻找和语义与输入特征相关关系最相近的潜变量, 进行语义与潜变量的匹配. 完成一对匹配后将其从待匹配矩阵中去除, 如此循环直到匹配完成.

(2)语义与潜变量的匹配算法

语义和潜变量的相近度采用“距离”衡量, 即潜变量μi与各输入特征Fk的贡献度减去语义Ij与各输入特征Fk的依赖度. 由于贡献度矩阵C_i,k的计算值范围为(0, 1), 均值在1除以潜变量个数附近, 与依赖关系矩阵R_i,j的取值(0或1)绝对距离较远. 换言之, 输入特征对各潜变量贡献度的变化幅度相对于依赖关系矩阵的取值差别较大, 使贡献度的差异淹没在与依赖关系矩阵的绝对距离差中. 因此, 需将贡献度矩阵的取值转换为与依赖关系矩阵同一量级, 其中一个方法是将各输入特征对所有潜变量的相对贡献度大于均值的取1, 其余取0. 潜变量μi与语义Ij的相对距离D_i,j数学表达式为:

$ D_{i,j}=\frac{\displaystyle\sum_{k=1}^{N}\left|[C]_{i,k}-[R]_{j,k}\right|}{\displaystyle\sum_{j=1}^{L} \displaystyle\sum_{k=1}^{N}\left|[C]_{i,k}-[R]_{j,k}\right|} $

(7)

距离矩阵D_i,j示意如下:

$D_{i, j}= \begin{array}{rccccc} & I 1 & I 2 & I 3 & I 4 & \cdots\\ \mu 1 & 0.11 & 0.23 & 0.15 & 0.17 & \cdots\\ \mu 2 & 0.34 & 0.12 & 0.24 & 0.32 & \cdots\\ \mu 3 & 0.23 & 0.42 & 0.36 & 0.16 & \cdots\\ \mu 4 & 0.14 & 0.25 & 0.16 & 0.28 & \cdots\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array} $

(8)

由相对距离的特性可知, 相对距离的均值为1/N, N为潜变量个数. 所有潜变量匹配的平均值与1/N对比即可反映匹配的准确度. 因此, 本文给出明晰度MI作为匹配准确性的度量, 计算公式为:

$ \begin{split} M I =\left(\dfrac{\dfrac{1}{N}-\dfrac{1}{N} \displaystyle\sum D_{i, j}}{\dfrac{1}{N}}\right) \times 100 {\text{%}} =\left(1-\sum D_{i, j}\right) \times 100 {\text{%}} \end{split} $

(9)

明晰度MI取值为0%~100%, 明晰度为0表示VAE训练得出的潜变量与输入特征的依赖关系与由先验知识确定的语义与输入特征的依赖关系完全不一致. 反之, 明晰度为100%代表VAE训练匹配得出和由先验知识确定的语义(潜变量)与输入特征的依赖关系完全吻合. 由此可判断语义提炼和匹配的准确度.

算法1. 潜变量—语义匹配算法

Require: 潜变量μi与语义Ij的相对距离矩阵D_i,j

While 还有潜变量未匹配 do

　　从相对距离矩阵D_i,j搜索最小值

　　抹去该最小值对应的行μi与列Ij, 并完

　　成第i个潜变量与第j个语义的匹配

End while

明晰度MI计算: $\scriptstyle \left( {1 -\sum {{D_{i,j}}} } \right) \times 100{\text{%}}$

1.5 最优参数搜索

VAE模型的训练是基于神经网络反向传播的原理, 通过预测标签与真实标签的误差来计算用于更新各层权重的梯度, 是以最小化损失(loss)为目标的优化过程. 为使生成的潜变量与输入特征的依赖关系趋近于基于先验知识确定的语义与输入特征的依赖关系, 在VAE的损失函数里加入明晰度的约束项, 让神经网络搜索能生成满足训练样本分布的模型参数的同时最大化明晰度.

明晰度本身的数量级不一定与VAE的损失函数对应, 且过早加入明晰度到损失函数会影响VAE的生成效果. 因此, 通过追踪作为训练进度指示的KL散度, 确定模型充分训练与过拟合的临界点. 然后重新训练模型至接近临界点后停止训练, 构建镜像模型并代入停止训练时的权重与偏置, 并在损失函数里加上明晰度的约束项后继续训练模型, 让神经网络进行微调, 在不影响模型生成能力的前提下, 自动搜索出让模型训练得出的依赖关系与先验知识预定义的依赖关系接近的参数. 更新后的损失函数为:

$ { loss }= { reconstruction\_loss }+KL\_loss + MI\_loss $

(10)

明晰度约束项表达式为:

$ MI\_{loss}=\eta\left(\frac{1}{M I}\right) $

(11)

$ \eta=\dfrac{ { reconstruction }\_{loss}^{\prime}+KL\_{loss }^{\prime}}{4\left(\dfrac{1}{{MI}^{\prime}}\right)} $

(12)

其中, ${ reconstruction\_loss }^{\prime}$ 和 ${KL\_loss}^{\prime}$ 是停止训练时VAE模型的重构误差和KL散度, $M I^{\prime}$ 是提取停止训练时的权重计算的明晰度. 接近充分训练时, 重构误差和KL散度基本趋于稳定. η为数量级调谐因子, 因为VAE训练时应以能生成满足训练样本分布的样本的能力优先, 所以另明晰度约束项的最大数值仅为停止训练时VAE模型损失的1/4.

1.6 可控的虚拟样本生成

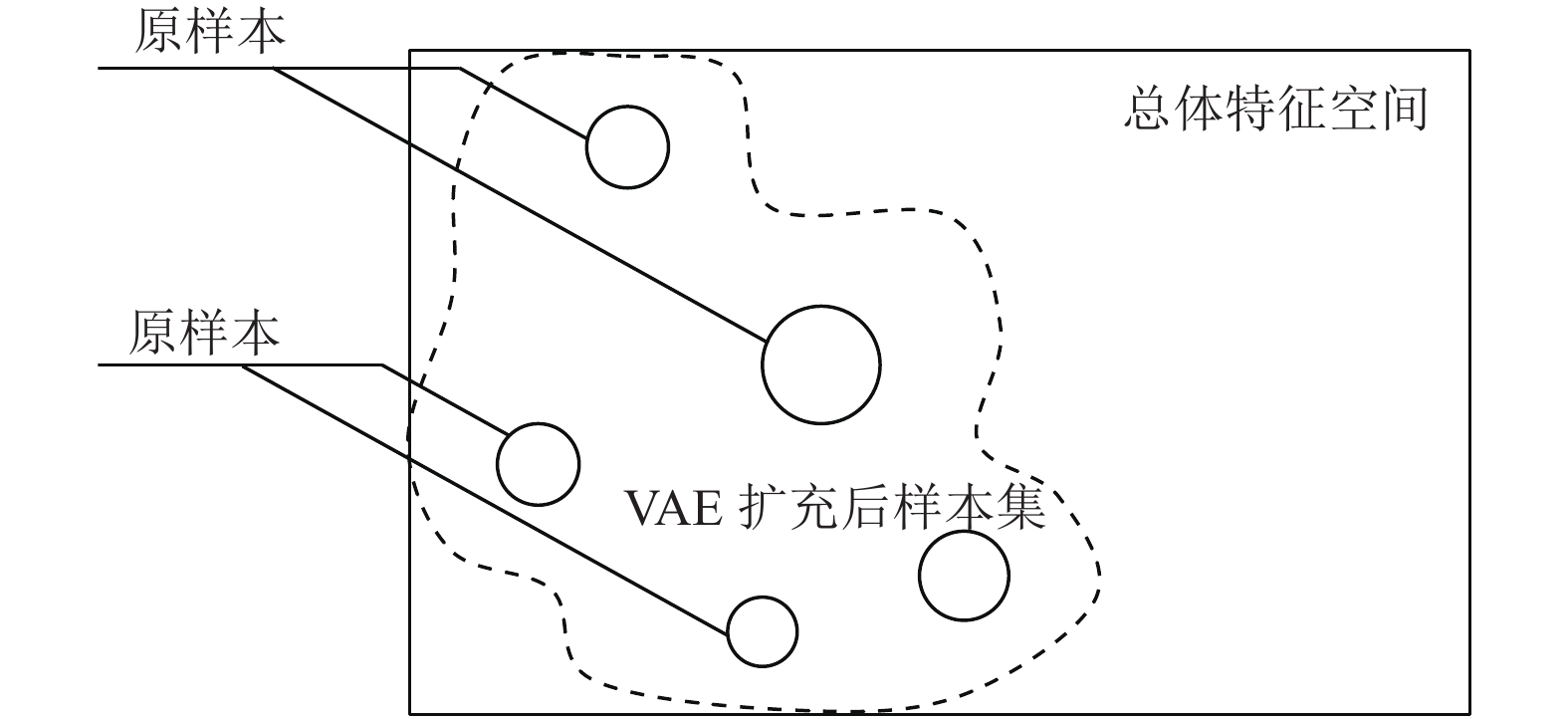
通过VAE模型生成的新样本均满足原样本集分布, 而且可以生成原样本集没有但统计意义上存在的新样本, 以标准高斯分布扩充潜变量空间后解码得到的新样本集示意图见图7.

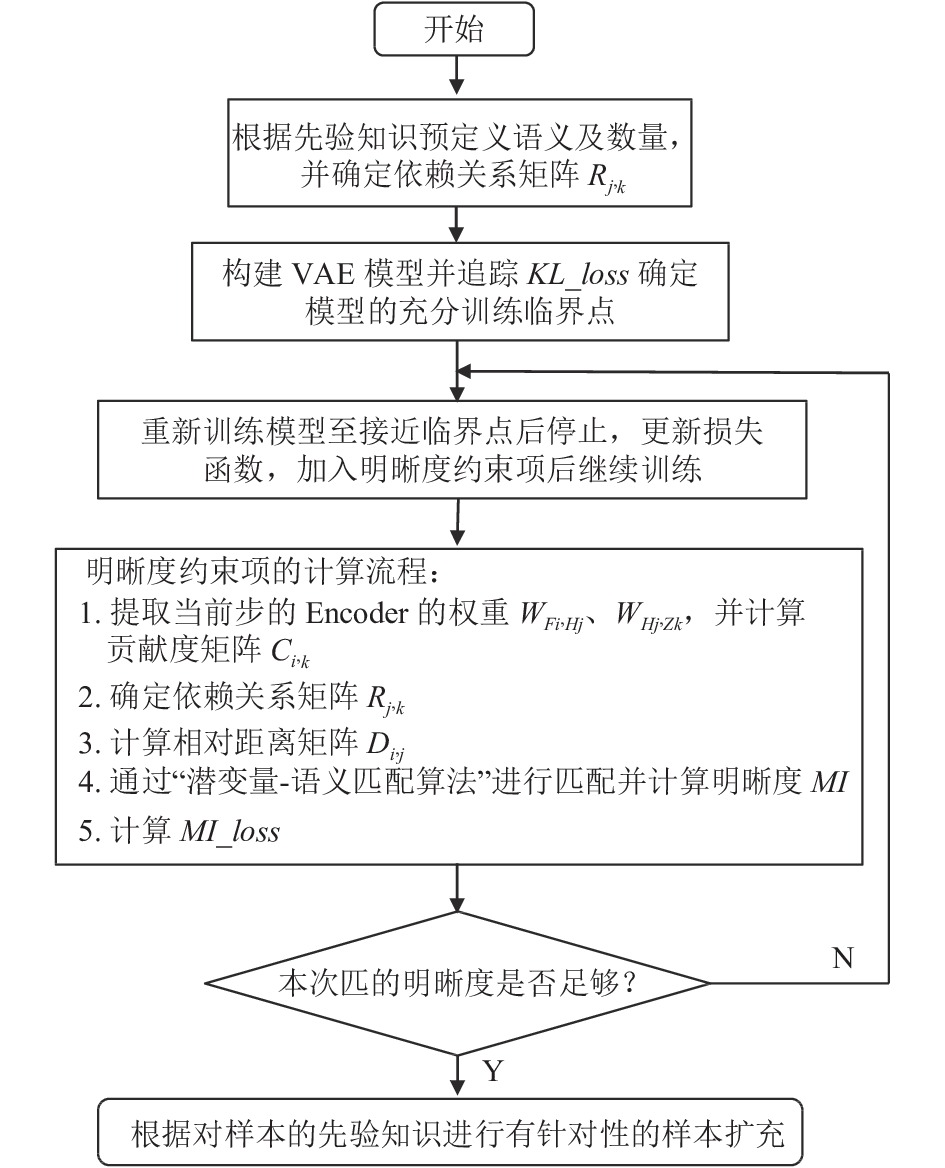
本文提出的基于VAE潜变量语义提炼的虚拟样本生成法提供一种可控、定向地生成特定属性的样本的策略. 结合先验知识, 可灵活解决小样本、样本不均衡的问题. 算法流程图如图8所示.

2 案例应用

以民用建筑结构安全数据库的样本扩充为例, 说明基于VAE潜变量语义提炼的虚拟样本生成法流程以及语义提炼效果. 从该数据库抽取30个房屋信息记录, 提取45个结构安全相关的房屋信息作为输入特征. 表1列出部分房屋及输入特征记录.

据先验知识预定义8个结构安全相关的语义后, 构建VAE模型并进行训练至明晰度满足精度要求, 如表2.

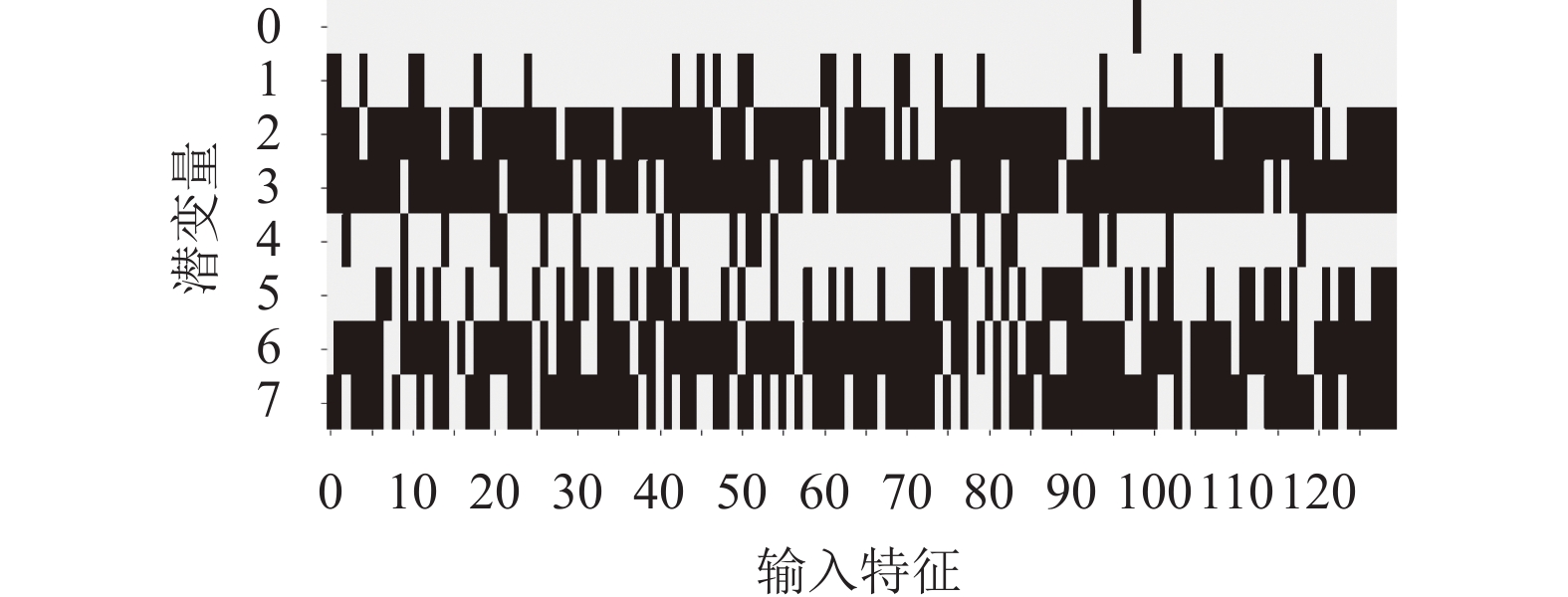
然后根据算法流程图, 进行模型学习和匹配的明晰度计算. 其中, 根据式(4)计算出输入特征对潜变量分布均值的贡献度矩阵C_i,k的二值化结果如图9所示, 由于数据输入类型为混合类型, 包含连续值、二值型以及独热编码, 因此经独热编码转换后输入特征扩张至130个, 由先验知识确定的语义与输入特征的依赖关系矩阵亦由程序进行对应转换.

得到贡献度矩阵C_i,k后, 与由先验知识得出的语义与输入特征依赖关系矩阵根据式(7)进行相对距离计算. 距离越小时, 语义与潜变量越相近. 距离D_i,j的可视化矩阵如图10.

应用“潜变量-语义匹配算法”为每个潜变量匹配最优语义并计算当前匹配的明晰度, 匹配结果详见表3.

模型训练完成后的匹配明晰度为:

$MI=\left(1-\displaystyle\sum D_{i, j}\right) \times 100 {\text{%}}=70.4 {\text{%}}$ , 表明该模型的潜变量经语义提炼和匹配后与先验知识预定义的对应关系相近, 采用该模型进行定向样本生成时准确度较高, 满足精度需求.

3 结论与展望

本文提出的基于VAE潜变量语义提炼的样本扩充方法, 利用了VAE能拟合输入特征分布的特点, 能产生合理且具有广泛性的样本, 一定程度上, 补充原有训练集没有出现但统计意义上存在的样本属性. 避免了采用其他样本生成技术会带来样本不合理和容易过拟合的缺点. 通过对融入特征解耦的VAE训练得到的相互独立的潜变量进行语义提炼, 能实现更灵活且有针对性的样本扩充.

潜变量语义的提炼本质上是一种主观的方法, 依赖于对样本集的先验知识, 包括β-VAE^[18]、FactorVAE^[19]、β-TCVAE^[20]等均采用枚举观察法匹配根据先验知识确定的语义和潜变量. 本文给出了当样本集为数据或文字, 枚举观察法不适用时的潜变量语义提炼策略, 以统计权重作为依赖关系度量的方法, 揭示各潜变量对应的输入特征集, 根据输入特征集的共性, 即可得出该潜变量控制的样本属性. 尤其当输入特征数量多, 难以通过观察归纳出共性作为语义时, 语义与潜变量统计匹配算法能完成给定语义下的最优匹配, 并给出匹配明晰度作为预先给定语义与潜变量实际语义偏差的度量.

该匹配方法存在一定缺点, 预定义语义与潜变量实际语义不一定相符, 需根据匹配的明晰度调整预定义语义及数量, 最终不一定能得出高准确率的匹配.

揭示出样本固有特征的语义对人工智能在各行业的应用有重要意义. 下一步将继续优化语义提炼算法, 得出能广泛适用于各种样本类型且匹配准确率高的算法.