2. 南京航空航天大学 高安全系统的软件开发与验证技术工信部重点实验室, 南京 211106;
3. 软件新技术与产业化协同创新中心, 南京 210023
2. Key Laboratory of Safety-Critical Software, Ministry of Industry and Information Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China;
3. Collaborative Innovation Center of Novel Software Technology and Industrialization, Nanjing 210023, China
复杂系统[1]是一种包含很多相互作用子系统的系统. 它具有非线性、高不确定性、高维度、多层次以及高相关性的特点. 空气动力系统[2]、股票市场系统[3]、暴雨洪涝人口风险系统[4]就是一些的复杂系统例子. 为研究自然、工程和社会科学中的现象与原理, 探究这些复杂系统的内在性质, 人们对复杂系统建模并利用计算机对它们进行仿真与实验, 并让实验能够尽可能地接近真实世界, 不断向着复杂化发展. 比如, 在武器装备领域, 为了测定直航鱼雷[5]在不同复杂想定下的打击范围和命中能力, 需要做大量的仿真实验. 为了让实验能在较小的代价下执行, 需要进行高效实验设计. 但复杂系统的特点会给复杂系统实验设计带来非线性、相关性、不确定性和规模性等问题[6], 传统的实验设计方法只能部分解决这些问题, 例如: 完全析因设计[7]适用于非线性系统, 但需要的实验样本和实验次数非常多; 响应面设计[8]用于分析系统中因子间的相互作用, 但当因子数量增多时, 计算量会急剧增加; 为了降低实验中的不确定性, 可以通过大量的随机重复抽样设计, 但这同样的会极大地增加实验规模. 以上问题都会使得复杂系统实验设计最终走向规模性, 即产生维度灾难[9]. 正交设计[10]、均匀设计[11]、拉丁超立方设计[12]这类遵循“充满空间”性质的实验设计方法虽然可以通过优化实验取样来缩减实验规模, 但仅在均匀空间中最有效, 对复杂系统实验设计效率的提升有限. 因此, 迫切需要一种适用于复杂系统、可以大幅提高实验效率的实验设计方法.
变分自编码器(variational auto-encoder, VAE)[13]是一种借鉴变分推断原理的深度神经网络, 凭借其优秀的性能, 近年来在图像处理[14]、语音识别[15]、文本生成[16]等应用领域取得了巨大的成功. 变分自编码器作为一种生成模型, 含有多个隐藏层, 包括了编码器、解码器和隐变量空间. 编码器可以将复杂分布的样本数据投影到简单的隐变量空间, 实现对样本数据的特征提取. 而解码器可以通过还原在隐变量空间里取样的数据, 生成新的样本. 和一般生成模型只考虑重构损失函数不同的是, 变分自编码器同时考虑了重构损失函数和KL损失函数, 使得生成的样本具有更强的泛化能力, 可以提高样本空间取点的覆盖率, 这给复杂系统实验设计带来了新的思路: 一方面, 如图1所示, 将复杂系统实验的输入样本和输出响应结果一同作为实验历史记录数据训练变分自编码器, 通过生成新的实验样本, 综合考虑复杂系统实验输入样本
(1) 通过适应随机采样, 防止出现过拟合;
(2) 隐变量空间具有良好的分布性质, 易于抽样处理;
(3) 生成的样本点是在隐变量空间采样得到, 可以通过调整采样来进行优化.

|
图 1 提高实验设计效率的思路是使这3个分布尽可能充满空间 |
基于上述分析, 本文提出一种基于VAE的实验设计方法, 将复杂系统实验历史记录数据投影到一个满足正态分布的隐变量空间, 并通过对隐变量空间采样生成新的实验设计方案. 实验结果表明, 本文实验设计方法系统性地解决了复杂系统自身特性导致的实验设计规模性问题.
本文接下来的内容安排如下: 第1节详细阐述了本文的方法; 第2节介绍了实验有效性的评价方法; 第3节通过一个直航鱼雷命中模型的案例对本文方法进行了验证并展示与分析了实验结果; 第4节总结了全文并得出了结论.
1 一种基于变分自编码器的复杂系统实验设计方法本节首先形式化定义了待解决问题, 然后详细介绍了本文方法的总体架构和各模块内容.
1.1 问题定义复杂系统的特性可以表示为其输入到输出的一个函数:
实验设计目的之一是提高实验设计取样的有效性, 即在相同实验样本数量的情况下, 提高选取样本的准确性. 对于待比较的不同实验设计方法, 令每种实验设计方法产生
| $ RMSE = \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^k {{{\left( {{{{{\boldsymbol{y}}}}_i} - {{{{{\boldsymbol{y}_i'}}}}}} \right)}^2}} }}{k}} $ | (1) |
| $ MRE = \max (\left| {{{{{\boldsymbol{y}}}}_i} - {{{{{\boldsymbol{y}_i'}}}}}} \right|) $ | (2) |
| $ MAE = \frac{{\displaystyle\sum\limits_{i = 1}^k {\left| {{{{{\boldsymbol{y}}}}_i} - {{{{{\boldsymbol{y}_i'}}}}}} \right|} }}{k} $ | (3) |
| $ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^k {{{({{{{\boldsymbol{y}}}}_i} - {{{{{\boldsymbol{y}_i'}}}}})}^2}} }}{{\displaystyle\sum\limits_{i = 1}^k {{{({{{{\boldsymbol{y}}}}_i} - {{\bar {\boldsymbol{y}}}})}^2}} }} $ | (4) |
在式(4)中,
基于变分自编码器的实验设计方法的总体架构如图2所示, 它包含了3个模块.

|
图 2 总体架构 |
实验需求确定了实验的背景、对象、参数以及属性的取值范围和概率分布, 为本实验设计方法的输入. 实验设计方案即实验样本集
基于变分自编码器的实验设计方法各个模块的作用和总体步骤如下.
(1) 依据实验需求, 设计并实施实验, 得到初次的实验历史记录集.
(2) 数据预处理模块将实验历史记录集转化成变分自编码器可以使用的实验历史记录向量集.
(3) 网络学习模块将此实验历史记录向量集用作训练集, 训练变分自编码器.
(4) 实验设计模块在训练好的变分自编码器的隐变量空间里采样, 利用解码器还原采样点生成实验样本, 输出复杂系统实验设计方案.
(5) 对输出的复杂系统实验设计方案实施实验, 并将得到的实验历史记录加入原先的实验历史记录集, 得到新的实验历史记录集, 然后回到步骤(2)进行下一轮的实验设计, 使得实验设计取样得到进一步的优化.
1.3 数据预处理模块变分自编码器的训练集需要向量化或数值化的样本, 但是实验历史记录并不一定都满足这个条件. 在训练变分自编码器的过程中, 为了能让损失函数更容易收敛到最佳结果, 需要防止样本中有因子取值范围过大或存在极端值的情况. 为此需要对实验历史记录进行数据预处理.
对于实验历史记录中无序离散值的属性来说, 需要对它进行独热编码. 对于有序离散值的属性需要对它进行标签编码.
而对于实验历史记录中连续数值, 防止取值范围过大或有极端值情况的策略是使用Minmax归一化:
| $ {{\rm{Minmax}}} ({{{\boldsymbol{O}}}}) = \frac{{{{{{\boldsymbol{X}}}}_i} - {{{{\boldsymbol{X}}}}_{\min}}}}{{{{{{\boldsymbol{X}}}}_{\max}} - {{{{\boldsymbol{X}}}}_{\min}}}} $ | (5) |
其中,
因此, 在数据预处理模块, 对于复杂系统实验历史记录集
(1) 判断实验历史记录每个因子的类型.
1) 对实验历史记录中的有序离散取值的属性进行标签编码;
2) 对实验历史记录中的无序离散取值的属性进行独热编码;
3) 对实验历史记录中的连续数值的属性进行归一化.
(2) 对步骤(1)中得到的结果进行向量组装, 得到数据预处理后的实验历史记录.
数据预处理后的实验历史记录记为
本文方法用Python库SciKit-Learn[17]的preprocessing模块的OneHotEncoder方法、LabelEncoder方法和MinMaxScaler方法实现数据的独热编码、标签编码和归一化.
1.4 网络学习模块网络学习模块的主体部分是变分自编码器.
变分自编码器由编码器
编码器和真实后验概率分布
| $ {{{KL}}} ({q_\phi }({{{\boldsymbol{{\textit{z}}}}}}|{{{\boldsymbol{x}}}})\parallel {p_\theta }({{{\boldsymbol{{\textit{z}}}}}}|{{{\boldsymbol{x}}}})) = {{{{E}}} _{{q_\phi }({{{\boldsymbol{{\textit{z}}}}}}|{{{\boldsymbol{x}}}})}}\log \frac{{{q_\phi }({{{\boldsymbol{{\textit{z}}}}}}|{{{\boldsymbol{x}}}})}}{{{p_\theta }({{{\boldsymbol{{\textit{z}}}}}}|{{{\boldsymbol{x}}}})}} $ | (6) |
整个变分自编码器训练就是要去优化编码器模型的参数
| $ \phi , \theta = \mathop {\arg \min }\limits_{\phi , \theta } {{{KL}}} ({q_\phi }({{{\boldsymbol{{\textit{z}}}}}}|{{{\boldsymbol{x}}}})\parallel {p_\theta }({{{\boldsymbol{{\textit{z}}}}}}|{{{\boldsymbol{x}}}})) $ | (7) |
定义生成模型
| $ {{{L}}} (\theta , \phi ) = \underbrace {{{{KL}}} ({q_\phi }({{{\boldsymbol{{\textit{z}}}}}}|{{{\boldsymbol{x}}}})|{p_\theta }({{{\boldsymbol{{\textit{z}}}}}}))}_{{{{KL}}} - {\rm{loss}}} - \underbrace {{{{{E}}} _{{q_\phi }({{{\boldsymbol{{\textit{z}}}}}}|{{{\boldsymbol{x}}}})}}{{\rm{lb}}} {p_\theta }({{\hat {\boldsymbol{x}}}}|{{{\boldsymbol{{\textit{z}}}}}})}_{{{\rm{Reconstruction}}} - {\rm{loss}}} $ | (8) |
其中, 第一项是变分自编码器的KL损失函数, 第二项是变分自编码器的重构损失函数.
当完成对变分自编码器的训练后, 就可使用解码器生成新的样本. 网络学习模块的结构如图3所示.

|
图 3 网络学习模块结构 |
由于当输入样本的维度不高时, 使用深度生成模型变分自编码器不一定能很好地学习出样本的内在性质, 为了获得更精确的学习效果, 需要酌情增加输入样本的维度. 网络学习模块在常规变分自编码器结构中增加了输入层和输出层. 输入层的作用是将输入样本的维度扩大
网络学习模块的输入是经过数据预处理的实验历史记录集
实验设计模块在由网络学习模块求出的隐变量空间里做抽样实验设计, 将原本分布不均的复杂系统实验历史记录空间投影到低维的服从标准正态分布的隐变量空间. 因为训练中引入了随机的扰动, 这个过程可以确保与原始实验样本编码的潜在位置靠近的每个点都能被解码为与原始实验历史记录类似的实验历史记录, 从而迫使隐变量空间能够连续地有意义. 隐变量空间中任意两个相邻的点都会被解码为高度相似的实验历史记录. 隐变量空间的连续性以及低维度, 使得隐变量空间非常适合进行抽样. 实验设计模块结构如图4所示.
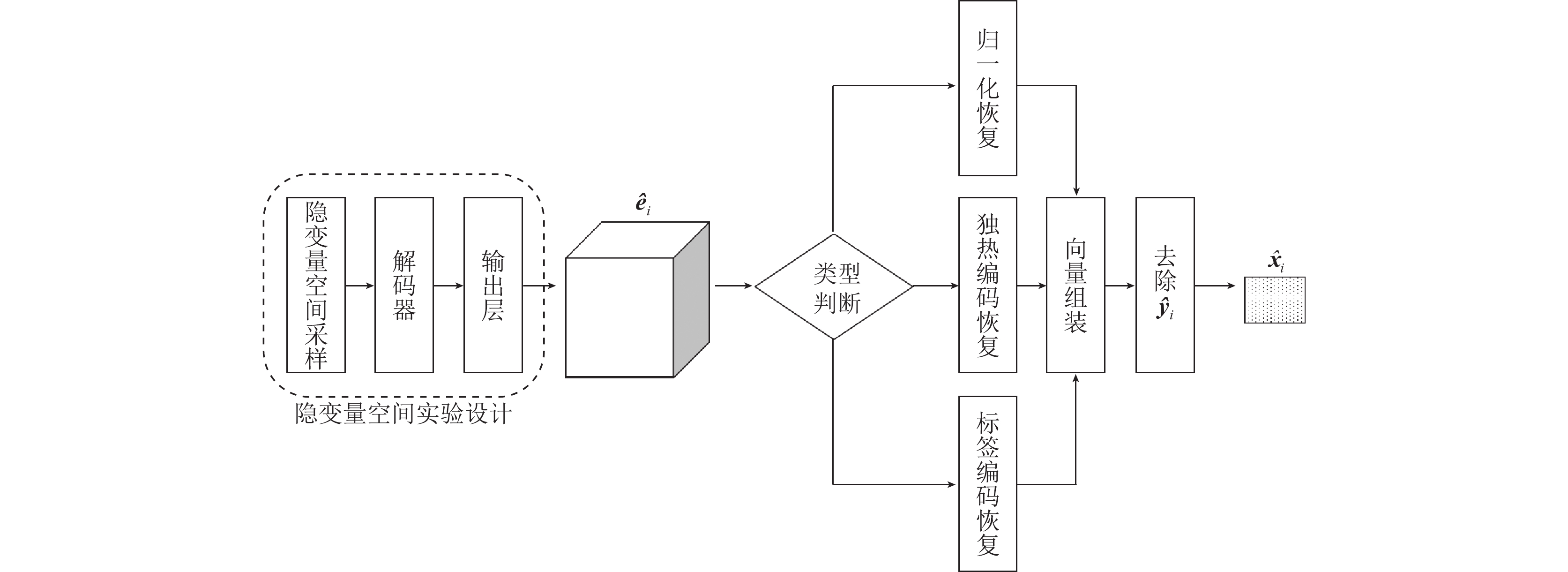
|
图 4 实验设计模块结构 |
实验设计模块在隐变量空间里做实验设计, 相当于对隐变量
为了要让
(1) 判断样本向量中各个部分原先属于哪个属性并进行恢复;
1) 对样本向量中经过归一化的部分进行归一化恢复;
2) 对样本向量中经过独热编码的部分进行独热编码恢复;
3) 对样本向量中经过标签编码的部分进行标签编码恢复;
(2) 对步骤(1)中得到的结果进行向量组装, 得到经过恢复后的实验样本.
在Python里, 这些恢复函数可以用各自原函数的inverse_transform方法实现. 经过恢复后的实验历史记录形如
依据实验设计需求, 如果实验需要做
为评价本文实验设计方法的有效性, 可用生成的实验样本和它们对应的实验响应去拟合真实复杂系统, 并评估其误差. 由于支持向量回归(support vector regression, SVR)模型[19]在表达式形式未知和小样本的情况下具有良好的性能, 这里选用SVR来进行拟合.
SVR是支持向量机[20]在回归问题上的应用, 将输入映射到高维空间, 并用一个或一组超平面来对样本点进行回归. 假定在高维空间中, 样本点是可以通过如下的线性函数拟合的:
| $ {{\hat {\boldsymbol{y}}}} = \hat f({{{\boldsymbol{x}}}}) = {{{\boldsymbol{w}}}} \cdot {{{\boldsymbol{x}}}} + {{{\boldsymbol{b}}}} $ | (9) |
其中,
| $ {{{L}}} ({{{\boldsymbol{y}}}}, \hat f({{{\boldsymbol{x}}}})) = {\left\| {{{\boldsymbol{w}}}} \right\|^2}/2 + C\sum\limits_{i = 1}^N {(\xi _i^ - + \xi _i^ + )} $ | (10) |
其中,
| $ {{{\boldsymbol{w}}}}, {{{\boldsymbol{b}}}} = \mathop {\arg \min }\limits_{{{{\boldsymbol{w}}}}, {{{\boldsymbol{b}}}}} {{{L}}} ({{{\boldsymbol{y}}}}, \hat f({{{\boldsymbol{x}}}})) $ | (11) |
SVR虽然将输入样本映射到了高维空间, 但向量内积在原空间上更容易被计算出来, 因此在高维空间上的向量内积运算使用核函数技巧[21]. 常见的核函数包括: 线性核、多项式核、径向基核和Sigmoid核.
利用SVR对实验设计评价方法如下:
首先, 在原始样本空间中采样
然后, 对每一个待测实验设计方法
对每一个
将测试集中每个
最后比较每种模拟的复杂系统的对测试集中所有
本节选取了几种常用的实验设计方法作为基线, 然后介绍了所使用的复杂系统模型和实验设置. 最后通过实验得出了结果并对其进行了分析.
3.1 基线基线实验设计选择拉丁超立方、K-means[22]和Maximin[23]实验设计方法与本文方法相比较, 因为它们是常用的实验设计方法且支持在连续区间内的实验取点. 上述的这些基线实验设计方法可以通过Python实验设计库doepy (
直航鱼雷在现代战争中是反制敌方舰船和潜水艇的有力武器, 为了能提高直航鱼雷的命中率和增加直航鱼雷的打击范围, 需要考虑多种影响直航鱼雷发射的因素, 建立直航鱼雷的命中模型并通过大量的仿真实验, 得到清晰的影响直航鱼雷的命中率和打击范围的关键因素和它们之间的关系, 从而可以为实际作战中直航鱼雷的战术运用提供指导.
本文实验选用文献[24]中的直航鱼雷命中模型作为本文实验设计方法验证的复杂系统. 直航鱼雷命中模型的响应
在本文实验中,
| $ \varphi = \arcsin \left(\frac{V}{{{V_T}}}\sin X\right) $ | (12) |
整个直航鱼雷命中模型的方程如式(13)所示:
| $ {y_Q} = 20.1168 \times (D - \Delta D)\dfrac{{\sin (\varphi - \Delta \varphi + \Delta \beta ) - \dfrac{{V - \Delta V}}{{{V_T} - \Delta {V_T}}}\sin (X - \Delta \beta + \Delta C)}}{{\sin (X + \varphi - \Delta \varphi + \Delta C)}} $ | (13) |
在本次实验中, 变分自编码器的隐变量空间的维度
对每一种待测实验设计方法, 生成的实验设计方案
实验结果如图5所示. 图5是不同实验设计方法在不同样本数下分别按图5(a) RMSE、图5(b) MRE、图5(c) MAE、图5(d) R2决定系数这些指标对直航鱼雷命中模型拟合效果比较的折线图.
从实验结果可以看出, 对直航鱼雷命中模型的拟合, 不论是在小样本还是在一定样本数下, 本文方法均优于K-means实验设计方法, Maximin实验设计方法与拉丁超立方实验设计方法. 只有当样本数
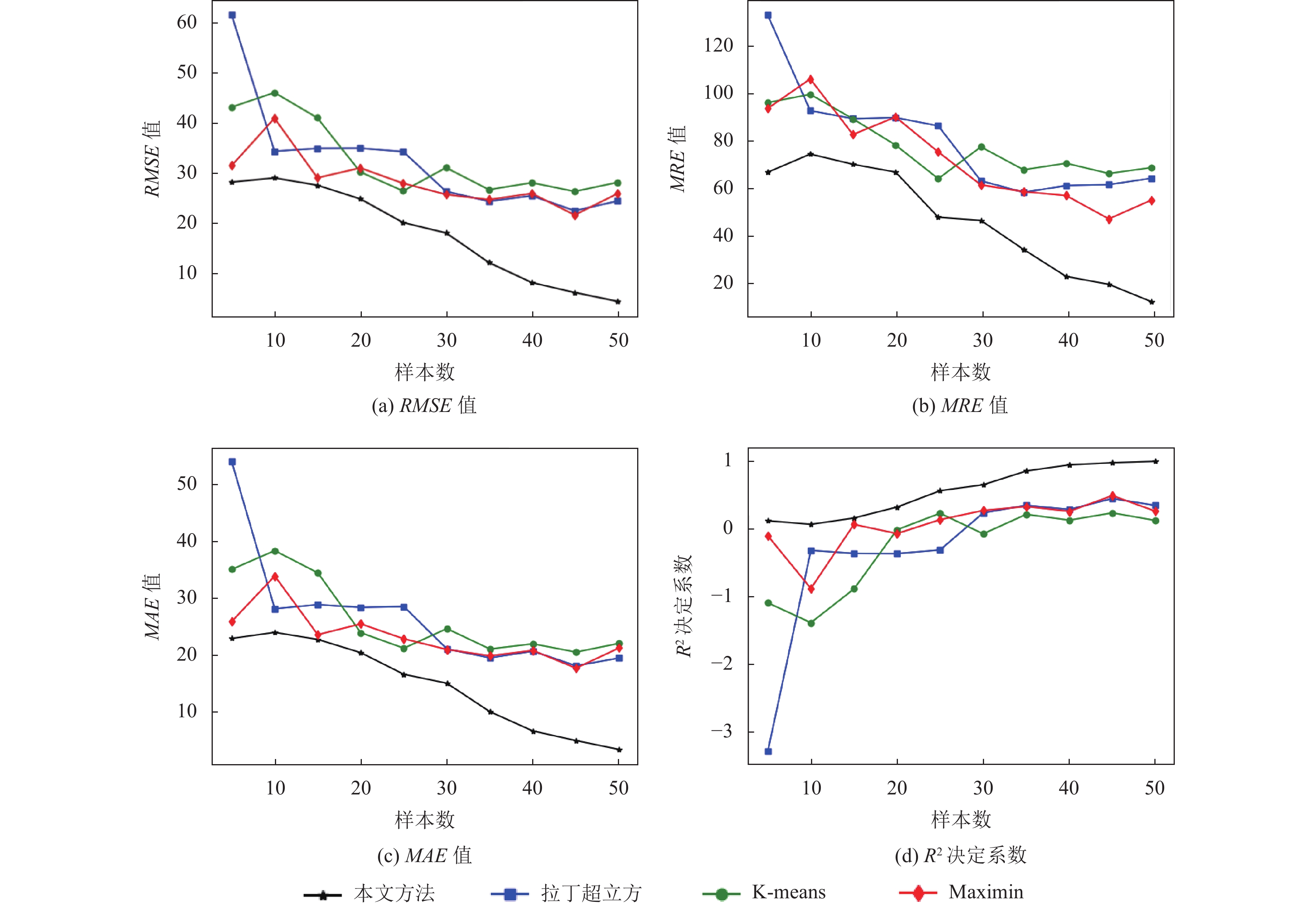
|
图 5 不同实验设计方法在不同指标不同样本数下对直航鱼雷命中模型拟合效果的比较 |
表1是各个实验设计方法的指标在低于或高于特定值时最少所需的样本数
综上所述, 本文实验设计方法可以提高在复杂系统中的实验设计效率, 在拟合复杂系统时, 本文实验设计方法随着样本数的增加也不会产生显著的过拟合, 即使在小样本的情况下, 本文方法也能得到比较优秀的实验设计方案.
4 结论本文为解决复杂系统实验设计中非线性、不确定性、高相关性和规模性导致的维度灾难问题, 提出了一种基于变分自编码器的复杂系统实验设计方法. 首先, 给出了基于变分自编码器的复杂系统实验设计方法的总体结构, 详细介绍了每个子模块的目的和它们的功能, 并给出了评价实验设计优劣的方法. 然后, 本文通过对实际的直航鱼雷命中模型的拟合, 对本文方法、拉丁超立方、K-means和Maximin实验设计方法进行了比较实验. 最后, 得出了本文方法可以提高复杂系统实验效率的结论.
|
表 1 各个实验设计方法的指标在低于或高于特定值时最少所需的样本数
|
| [1] |
万秋生. 复杂仿真实验设计与监控技术研究[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2012.
|
| [2] |
Hsu MC, Akkerman I, Bazilevs Y. Finite element simulation of wind turbine aerodynamics: Validation study using NREL Phase VI experiment. Wind Energy, 2014, 17(3): 461-481. DOI:10.1002/we.1599 |
| [3] |
卞曰瑭, 刘夏群, 李金生. 基于网络混合学习策略的股市投资者行为演化模型及仿真. 运筹与管理, 2019, 28(11): 156-168. |
| [4] |
郭啸天, 李文波, 王海雷, 等. 基于ABM与ABS的暴雨洪涝人口风险动态模拟. 计算机系统应用, 2015, 24(12): 10-17. DOI:10.3969/j.issn.1003-3254.2015.12.002 |
| [5] |
Jomon G, Jojish JV, Santhanakrishnan T. System of systems architecture for generic torpedo defence system for surface ships. Advances in Military Technology, 2019, 14(2): 307-319. DOI:10.3849/aimt.01330 |
| [6] |
谢晓天. 复杂仿真系统高效实验方法研究[硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [7] |
Shokri A. Application of Sono-photo-Fenton process for degradation of phenol derivatives in petrochemical wastewater using full factorial design of experiment. International Journal of Industrial Chemistry, 2018, 9(4): 295-303. DOI:10.1007/s40090-018-0159-y |
| [8] |
Yolmeh M, Jafari SM. Applications of response surface methodology in the food industry processes. Food and Bioprocess Technology, 2017, 10(3): 413-433. DOI:10.1007/s11947-016-1855-2 |
| [9] |
Bessa MA, Bostanabad R, Liu Z, et al. A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Computer Methods in Applied Mechanics and Engineering, 2017, 320: 633-667. DOI:10.1016/j.cma.2017.03.037 |
| [10] |
Feng GZ, Lei SY, Guo YJ, et al. Optimisation of air-distributor channel structural parameters based on Taguchi orthogonal design. Case Studies in Thermal Engineering, 2020, 21: 100685. DOI:10.1016/j.csite.2020.100685 |
| [11] |
Feng ZK, Niu WJ, Cheng CT. Optimizing electrical power production of hydropower system by uniform progressive optimality algorithm based on two-stage search mechanism and uniform design. Journal of Cleaner Production, 2018, 190: 432-442. DOI:10.1016/j.jclepro.2018.04.134 |
| [12] |
Ma P, Zhou YC, Shang XB, et al. Firing accuracy evaluation of electromagnetic railgun based on multicriteria optimal Latin hypercube design. IEEE Transactions on Plasma Science, 2017, 45(7): 1503-1511. DOI:10.1109/TPS.2017.2705980 |
| [13] |
Kingma DP, Welling M. Auto-encoding variational Bayes. arXiv: 1312.6114, 2014.
|
| [14] |
Hou XX, Shen LL, Sun K, et al. Deep feature consistent variational autoencoder. Proceedings of 2017 IEEE Winter Conference on Applications of Computer Vision. Santa Rosa: IEEE, 2017. 1133–1141.
|
| [15] |
Hsu WN, Zhang Y, Glass J. Unsupervised domain adaptation for robust speech recognition via variational autoencoder-based data augmentation. Proceedings of 2017 IEEE Automatic Speech Recognition and Understanding Workshop. Okinawa: IEEE, 2017. 16–23.
|
| [16] |
Semeniuta S, Severyn A, Barth E. A hybrid convolutional variational autoencoder for text generation. Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing. Copenhagen: Association for Computational Linguistics, 2017. 627–637.
|
| [17] |
Pedregosa F, Varoquaux G, Gramfort A, et al. Scikit-learn: Machine learning in Python. The Journal of Machine Learning Research, 2011, 12: 2825-2830. |
| [18] |
翟正利, 梁振明, 周炜, 等. 变分自编码器模型综述. 计算机工程与应用, 2019, 55(3): 1-9. DOI:10.3778/j.issn.1002-8331.1810-0284 |
| [19] |
Mohammadi B, Mehdizadeh S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm
. Agricultural Water Management, 2020, 237: 106145. DOI:10.1016/j.agwat.2020.106145 |
| [20] |
林香亮, 袁瑞, 孙玉秋, 等. 支持向量机的基本理论和研究进展. 长江大学学报(自科版), 2018, 15(17): 48-53. |
| [21] |
肖建, 于龙, 白裔峰. 支持向量回归中核函数和超参数选择方法综述. 西南交通大学学报, 2008, 43(3): 297-303. DOI:10.3969/j.issn.0258-2724.2008.03.001 |
| [22] |
Shakeel PM, Baskar S, Dhulipala VRS, et al. Cloud based framework for diagnosis of diabetes mellitus using K-means clustering. Health Information Science and Systems, 2018, 6(1): 16. DOI:10.1007/s13755-018-0054-0 |
| [23] |
Pronzato L. Minimax and maximin space-filling designs: Some properties and methods for construction. Journal de la Société Française de Statistique, 2017, 158(1): 7-36. |
| [24] |
孙华春, 李长文, 李海玲. 直航鱼雷命中概率模型与仿真. 舰船电子工程, 2009, 29(12): 138-141. DOI:10.3969/j.issn.1627-9730.2009.12.038 |
 2022, Vol. 31
2022, Vol. 31


