随着我国基础设施建设的需求和数量的不断扩大, 巨大数量的基础设施需要定期检查评估以确保其安全性和可靠性. 近年来利用结构健康监测(SHM)技术管理基础设施成为研究人员关注的热点. 以模态分析为中心的基于结构动力学的振动方法是民用、机械和航空结构健康监测、模型表征和更新最广泛使用的技术之一[1].
桥梁结构的模态分析需要通过分析传感器的振动数据来确定模态特性, 传统的传感器多为接触式传感器, 如加速度计, 通过直接固定在结构表面上进行测量. 这种方法通常非常精确并具有高动态范围, 人们也可以通过使用应变仪来测量动态应变[2]. 但接触式传感器在许多人类难以到达的结构处安装困难、费时且昂贵, 并且对于长期监测而言, 传感器的传输电缆或电池维护也是一个挑战. 最近非接触式传感器系统用于结构振动测量, 如微波遥感[3], 数字图像处理[4], 激光多普勒技术[5, 6]和基于视频序列的光流分析[7]. 这些方法的优点在于传感器不需固定在结构上, 并且随着消费级相机的普及和算法的改进, 基于计算机视觉的位移测量技术越来越受到研究人员关注.
目前在结构位移检测领域内应用较多的方法有模板匹配、数字图像相关技术(DIC)、SIFT特征点匹配、传统Lucas-Kanade光流神经、基于深度学习的光流等方法. 例如Ye等人[8]通过在桥梁上使用专用的视觉标记如二维码或LED灯进行模板匹配监测大跨度桥梁的结构位移, 这种方法的限制是仍需在结构表面添加人工目标. Mazzoleni等人[9]通过DIC第一次在土木结构上估算人群引起的垂直动荷载. Khuc等人[10]研究使用尺度不变特征变换SIFT方法进行结构位移测量, 和传统传感器之间的最大差异小于5%. Zhao等人[11]结合支持相关滤波算法与Kanade-Lucas-Tomasi (KLT)算法测量斜拉桥的位移, 但仅在KLT算法上较为鲁棒. Dong等人[7]提出一种基于神经网络Flownet2的全场光流法位移计算方法, 比传统的光流算法具有更高的精度.
人眼感知运动的范围是有限度的, 对于视频中许多幅度微小的运动, 人眼无法感知. 最近, 一种用于可视化肉眼看不见的微小运动的运动放大算法受到关注, 基于欧拉的运动放大和基于相位的运动放大算法类似于流体流动分析的欧拉框架[12-14], 即跟踪图像中每一像素在不同帧中亮度的变化. Wadhwa等人[13]通过复数可操纵金字塔将图像分解为多尺度的相位和幅值图, 再通过放大系数放大不同帧之间的相位差, 将放大后的相位叠加对图像进行重构, 放大了微小位移. 2015年, Chen等人[15]结合基于局部相位的光流技术[16], 将基于相位的运动放大算法拓展为一种可以量化微小运动的光流法, 并用于悬臂梁的模态识别. 2017年, Chen等人[17]测量了校园建筑顶部距离超过175 m的天线塔, 识别出0.21 mm的谐振振幅, 小于1/170像素. Cha等人[18]通过卡尔曼滤波降低了基于相位的光流法的噪声. Shang等人[19]通过基于运动放大的光流法进行人行天桥的多点模态频率和振型测量, 误差均小于4%. 基于相位的光流法在微小位移测量方面显示出巨大的应用潜力.
目前基于相位的光流法在桥梁结构振动检测方面应用较少, 本文受以上研究启发, 并根据Diamond等人[2]对基于相位运动放大的光流法精确度的验证研究, 提出了一种基于相位的改进光流法计算结构微小位移的方法. 本文选择基于相位的运动放大方法中的构造的复数可操纵金字塔中的第一层y方向滤波器来计算局部相位, 利用局部相位轮廓不变性求得视频中运动结构的像素位移时间历程, 再通过比例因子将像素位移转换为实际位移. 并在实验室通过搭建简支梁模型进行振动测量实验并与传感器进行对比, 验证了本文方法的性能.
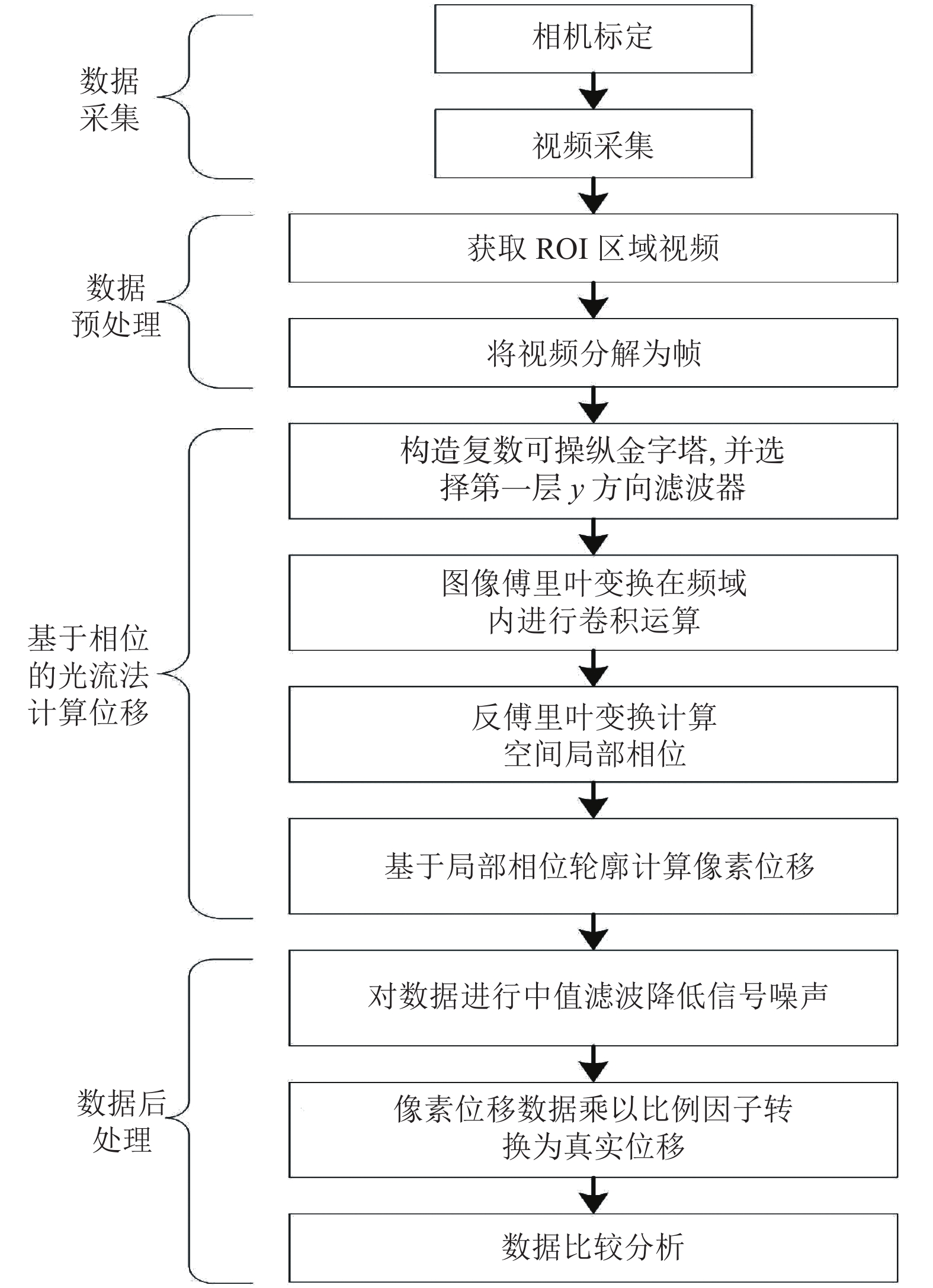
1 结构微小振动位移计算方法设计 1.1 位移测量系统流程本文提出的基于相位的光流法计算结构微小位移实验流程如图1所示, 大致可分为4个步骤: 数据采集、数据预处理、基于相位的光流法计算位移和数据后处理. 首先进行相机标定, 建立二维图像和三维真实世界之间的对应关系, 并通过相机采集结构振动视频数据. 接着进行数据预处理, 采集的视频需要进行裁剪选择出感兴趣(region of interest , ROI)区域, 目的是降低运算量. 并将视频拆解为帧, 因为位移计算是计算第一帧和第n帧之间的位移. 第3步就是计算像素位移, 采用改进的基于相位的光流法计算振动的像素位移. 最后是数据的后处理, 算法要对像素位移数据进行降噪处理, 并将像素单位的位移转换为物理单位的位移并进行数据结果分析.
1.2 相机标定相机标定是为了估计投影过程. 在基于视觉的结构位移测量研究中, 常用的方法主要有3种: 比例因子法、全投影矩阵法和平面单应矩阵法[7]. 当相机和镜头的轴垂直于运动平面时, 比例因子计算为真实世界物体尺寸与图像尺寸的比率. 如果在基于视觉的位移测量系统中应用比例因子, 则径向失真可以忽略不计的假设必须成立. Dong等人[7]建议使用径向畸变可忽略不计的变焦镜头, 以避免现场应用中繁琐的摄像机固有矩阵校准工作. 本文中所使用的数码相机具有失真校正功能, 且本文实验中相机镜头光轴垂直于物体运动平面, 因此选择比例因子法将运动结构的像素运动转换为毫米的物理单位.
|
图 1 实验流程图 |
1.3 滤波器构造
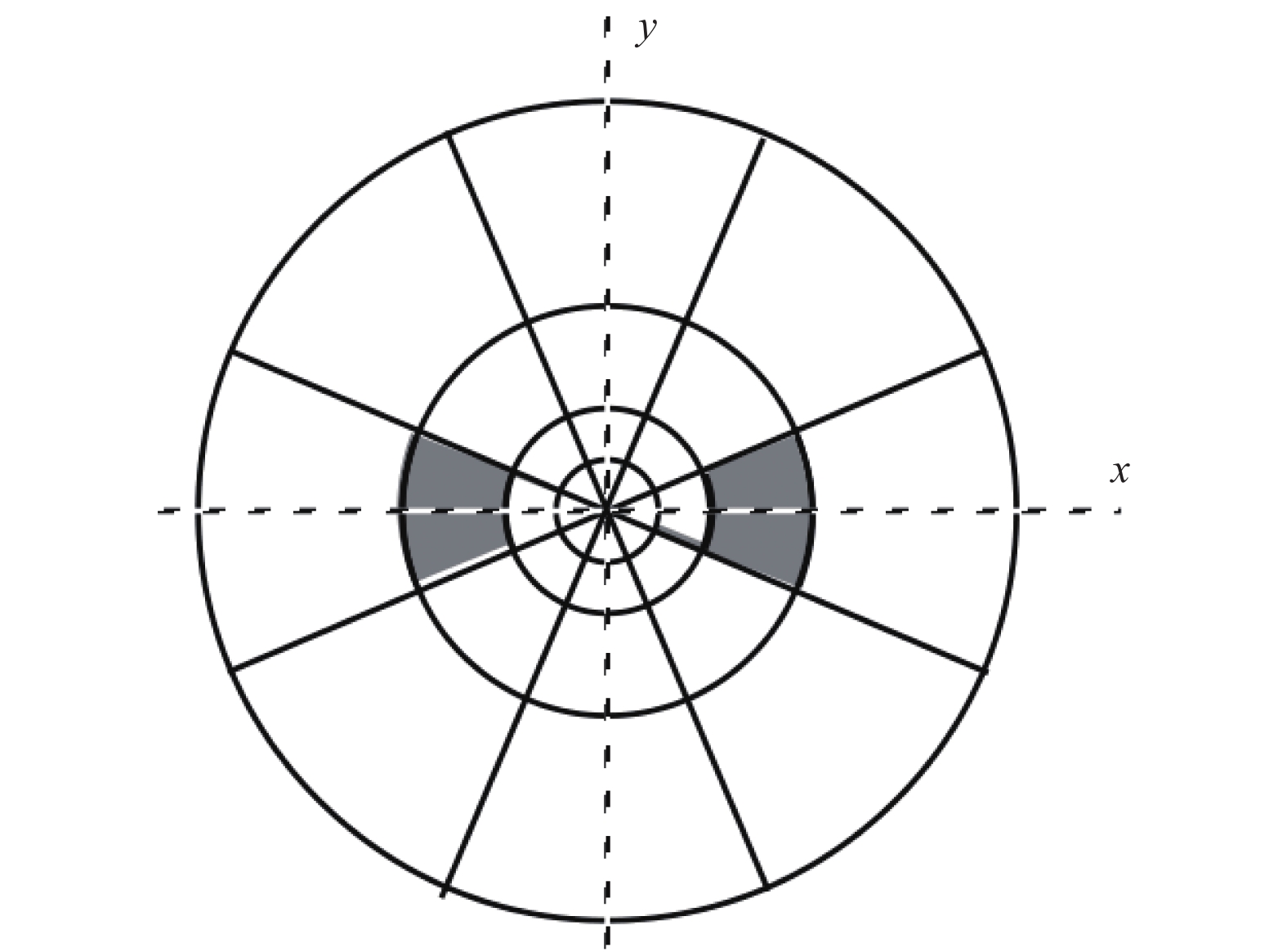
可操纵金字塔(steerable pyramid)是一种过完备变换, 根据空间比例、方向和位置分解图像. 变换的基函数类似于Gabor小波, 由高斯包络加窗的正弦曲线, 并且是可操纵的[20]. 可操纵金字塔的定向频带
|
图 2 可操纵金字塔进行的光谱分解理想化说明 |
可控金字塔是通过递归地将图像分割成一组定向子带和一个低通残留带来实现的. 转换的系统图如图3所示, H表示高通滤波, L表示低通滤波, B表示带通滤波, 低通部分通过递归的方式进行子项分解.

|
图 3 图像分解示意图 |
在傅里叶域中, 滤波器构造公式[22]如下:
| $ \left\{ {\begin{split} &L(r, \theta ) = \left\{ {\begin{array}{*{20}{l}} {2\cos \left(\dfrac{\pi }{2}{{\log }_2}\left(\dfrac{{4r}}{\pi }\right)\right), } \\ {2, } \\ {0, } \end{array}} \right.\begin{array}{*{20}{c}} {\dfrac{\pi }{4} < r < \dfrac{\pi }{2}} \\ {r \leqslant \dfrac{\pi }{4}} \\ {r \geqslant \dfrac{\pi }{2}} \end{array} \hfill \\ & {B_k}(r, \theta ) = H(r){G_k}(\theta ), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k \in [0, K - 1] \hfill \\ \end{split} } \right.$ | (1) |
带有径向和角度部分:
| $ \left\{ {\begin{split} H(r) = &\left\{ {\begin{array}{*{20}{l}} {\cos \left(\dfrac{\pi }{2}{{\log }_2}\left(\dfrac{{2r}}{\pi }\right)\right), } \\ {1, } \\ {0, } \end{array}} \right.\begin{array}{*{20}{l}} {\dfrac{\pi }{4} < r < \dfrac{\pi }{2}} \\ {r \geqslant \dfrac{\pi }{2}} \\ {r \leqslant \dfrac{\pi }{4}} \end{array} \hfill \\ {G_k}(\theta ) = & \left\{ {\begin{array}{*{20}{l}} {{\alpha _K}{{\left[ {\cos \left(\theta - \dfrac{{\pi k}}{K}\right)} \right]}^{K - 1}}, } \\ {0, } \end{array}} \right.\begin{array}{*{20}{c}} {\left| {\left. {\theta - \dfrac{{\pi k}}{K}} \right|} \right.} \\ {\rm{otherwise}} \end{array} \hfill \\ \end{split} } \right.$ | (2) |
其中,
复数可操纵金字塔(complex steerable pyramid, CSP)的转换函数只包含相应的实部可控金字塔滤波器的正频率, 即
本文通过时域卷积定理进行滤波, 即时域内的卷积对应频域内的乘积, 如式(3)所示:
| $ F[{f}_{1}(t)*{f}_{2}(t)]={F}_{1}(\omega ) \cdot {F}_{2}(\omega ) $ | (3) |
在基于相位的视频运动放大中, 局部相位需要进行放大叠加以形成重构图像. 但在本文中, 计算的是局部相位轮廓随时间偏移形成的位移, 实验设计为y方向垂直振动的简支梁振动模型, 因此选择复数可操纵金字塔第一层y方向的滤波器, 即
基于相位的光流法是由Chen等人[15]新提出的一种结构位移计算方法, 适用于无背景杂波的微小像素位移计算. Wadhwa等人[13]首次提出了一种基于相位的运动放大算法, 通过构造的复数可操纵金字塔滤波器对图像亮度进行滤波, 计算出局部空间相位和幅值, 局部空间相位信号在时间上被傅立叶变换分解成一系列代表谐波运动的正弦曲线. 相位信号随后在时间上被带通滤波、放大并重新组合以形成运动放大视频. Wadhwa等人[14]又通过里斯变换进行改进加快了运算速度. Chen等人[15]受基于相位的运动放大启发, 利用局部相位在时间上的恒定轮廓的运动[16, 23]来计算相应的位移信号.
空间局部相位和局部振幅是类似于傅立叶级数系数的相位和振幅的量. 相位控制基函数的位置, 而振幅控制其强度. 在傅里叶变换的情况下, 相位对应于全局运动. 局部相位提供了一种计算局部运动的方法[16]. 对于视频数据, 如式(4)所示, 由
| $ {A_\theta }(x, y, {t_0}){{\rm{e}}^{i{\phi _\theta }(x, y, {t_0})}} = I(x, y, {t_0}) \otimes (G_2^\theta + iH_2^\theta ) $ | (4) |
位移信号是从局部相位在时间上的恒定轮廓的运动中获得的[16, 23], 可以表示为:
| $ {\phi _\theta }(x, y, t){\text{ = }}m $ | (5) |
其中, m表示常数, 意味着随着时间的推移相位的局部相位恒定轮廓不变, 某个方向的位移信号就是局部相位轮廓在第一帧和当前帧之间的移动距离, 在实际计算中仅考虑和坐标轴x,y平行的两个方向的分量, 式(6)是通过关于时间的微分获得的方程式.
| $ \left( {\dfrac{{\partial {\phi _\theta }(x, y, t)}}{{\partial x}}, \dfrac{{\partial {\phi _\theta }(x, y, t)}}{{\partial y}}, \dfrac{{\partial {\phi _\theta }(x, y, t)}}{{\partial t}}} \right) \cdot (u, v, 1) = 0 $ | (6) |
其中, u和v表示图像x,y轴方向上的速度. 通过求解式(6)可得:
| $\left\{ { \begin{split} u = & - \frac{{\partial {\phi _0}(x, y, t)}}{{\partial t}}\Bigg/\left( {\frac{{\partial {\phi _0}(x, y, t)}}{{\partial x}}} \right) \hfill \\ v = & - \frac{{\partial {\phi _{\pi /2}}(x, y, t)}}{{\partial t}}\Bigg/\left( {\frac{{\partial {\phi _{\pi /2}}(x, y, t)}}{{\partial y}}} \right) \hfill \\ \end{split}} \right. $ | (7) |
其中,
| $ \Delta y = - \dfrac{{\alpha \left( {{\phi _{\pi /2}}(x, y, {t_n}){{ - }}{\phi _{\pi /2}}(x, y, {t_0})} \right)}}{{\beta \left( {\dfrac{{\partial {\phi _{\pi /2}}(x, y, t)}}{{\partial y}}{\text{ + }}\eta } \right)}} $ | (8) |
其中,
通过多次实验发现, 在算法计算过程中, 由于图像噪声的影响, 位移时程数据中会出现某些超出正常范围值得尖峰噪声, 因此选择中值滤波进行降噪处理, 滤波器尺寸为1×3. 最后通过比例因子将像素单位的位移转换为以毫米为单位的真实物理位移, 并于其他方法进行比较. 在接下来的章节中, 将通过实验室实验来验证所提出的改进算法的可行性和性能.
2 实验与结果分析 2.1 实验设置本文的实验环境为实验室搭建的简支梁模型, 如图4所示, 图4(a)为简支梁模型, 左侧为固定端, 右侧为滑动端; 图4(b)为传感器固定位置, 为简支梁左侧1/4位置处, 传感器下方箭头指向的像素点为选择进行计算的点, 位于简支梁的边缘, 将传感器的数据作为参考标准; 图4(c)为激励源, 使用橡皮锤在简支梁右侧10 cm处轻轻敲击, 产生振动源. 两个底座固定在同一木板上, 简支梁是一组总长150 cm, 宽30 mm, 厚度为2 mm的钢条组成, 在简支梁中部可通过改变螺丝松紧度来模拟桥梁损伤, 但本文实验目标是验证振动位移测量方法的性能, 因此将螺丝旋转至固定.

|
图 4 实验室搭建的简支梁模型 |
本文中进行视频采集的设备为Canon EOS-1D X Mark II相机, 摄像模式参数为1920×1080的分辨率和120 fps的帧率, 光照条件为稳定的室内光源. 相机通过三脚架和云台固定, 与简支梁和传感器处于同一水平面上, 且镜头正对简支梁和传感器, 距离简支梁模型1.3 m, 以免因夹角产生计算误差. 本文中使用的为891-4型超低频测振仪垂直传感器, 传感器的采样频率为200 Hz, 用来测量竖直方向的速度作为参考数据, 并在最后的实验比对阶段进行积分处理, 振动数据采集设备如图5所示, 图5(a)为视频采集设备, 图5(b)为振动传感器数据采集仪和采集软件.

|
图 5 振动数据采集设备 |
本文使用的位移真值近似值由用于超低频或低频振动测量的891-4型拾振器获得, 通过传感器测量的速度积分计算位移, 该传感器的速度分辨率为1.6×10–6 m/s, 速度灵敏度为1.738 mV/mm/s, 位移分辨率为1.6×10–6 m, 传感器采样率为200 Hz. 本文认为由891-4型拾振器采集的原始位移数据属于更高一级的位移测量方法, 因此选择此数据作为振动位移的真值近似值.
2.2 实验结果与分析为了验证本文方法的性能, 选取了两种基于神经网络的光流方法进行对比, 文献[24]中的Flownet2.0网络是一种经典的基于神经网络的光流方法, 性能追平了传统光流方法, 文献[25]中的基于循环全对场变换(recurrent all-pairs field transforms, RAFT)的神经网络是截止2020年最为先进的深度学习光流方法, 两种网络具体结构见文献[24, 25], 几种方法均选择同一像素进行位移计算.
在简支梁上选取点并放置振动传感器作为参照, 使用本文方法及深度学习光流方法计算简支梁振动位移, 本文方法与其他光流方法的数据可视化对比如图6所示, 横坐标为图像帧数, 纵坐标为真实位移, 单位为mm. 视频中简支梁结构振动振幅不超过1个像素. 将传感器数据降采样为120 Hz, 手动进行传感器和相机的时间对齐, 将两者数据进行同步, 选择了1 300个数据点进行对比. 图6(a)为总的1 300个数据, 为了更直观的展示方法差异, 选择部分数据进行展示, 图6(b)为200–400帧数据可视化对比, 图6(c)为800–1 000帧的可视化对比, 从中可以看出本文方法位移时程序列明显更加平滑.
本文采用两种评价参数作为性能指标, 一是皮尔森相关系数(Pearson correlation coefficient), 是两组位移时程数据的协方差和标准差的商, 用于衡量算法数据与传感器数据的相关程度, 相关系数越大, 表示相关程度越高:
| $ {\rho _{X, Y}} = \dfrac{{{\rm{cov}} (X, Y)}}{{{\sigma _X}{\sigma _Y}}} = \dfrac{{E[(X - {\mu _X})(Y - {\mu _Y})]}}{{{\sigma _X}{\sigma _Y}}} $ | (9) |
二是平均绝对误差(mean absolute error, MAE), 用来度量两条位移时程序列间各点的平均偏差程度, MAE越小, 表示偏差程度越小:
| $ MAE = \frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {|\mathop {{y_i}}\limits^\Lambda - {y_i}|} $ | (10) |
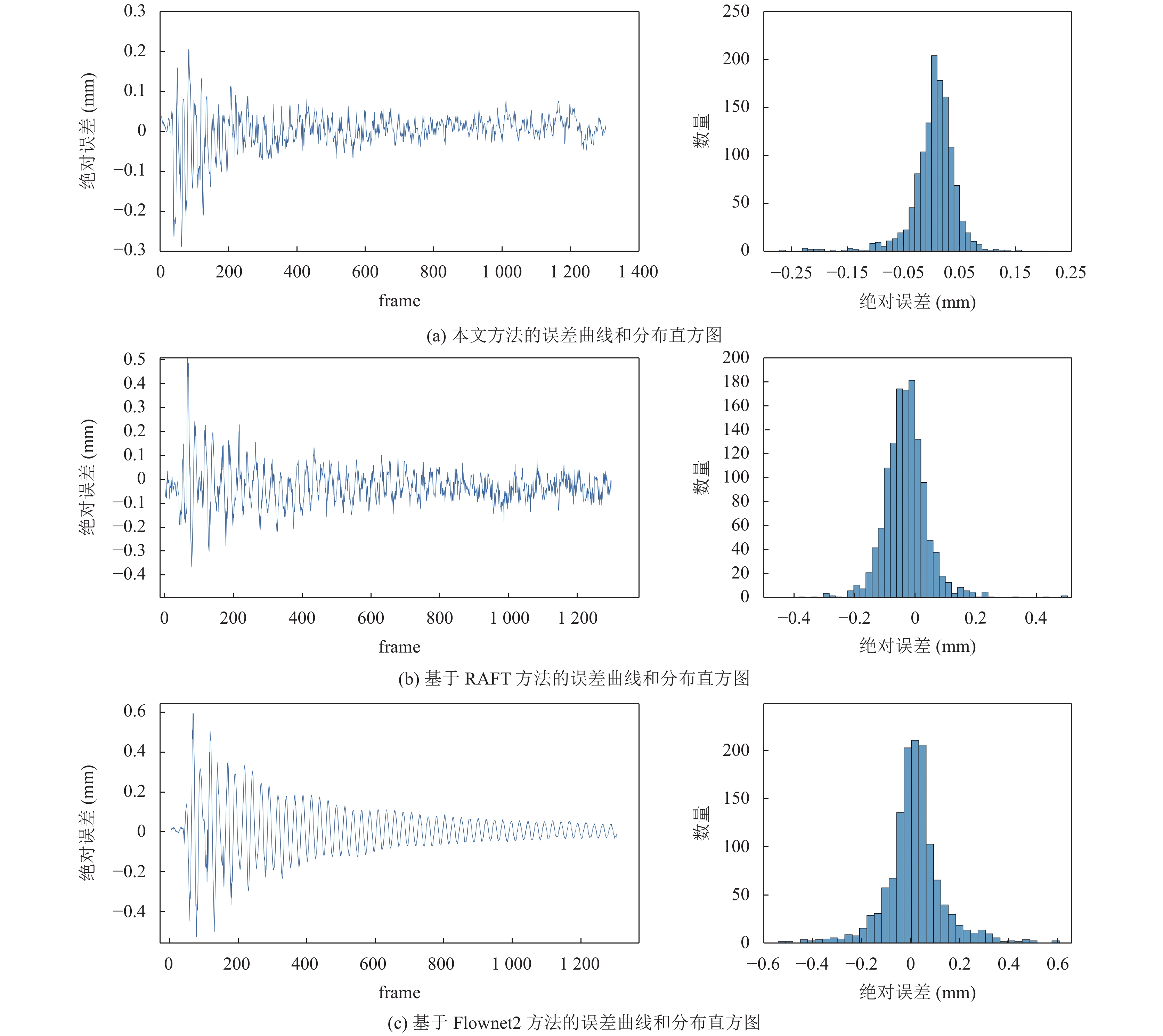
图7展示了3种方法与传感器数据的误差分析可视化图, 左侧为绝对误差的时程曲线, 右侧为绝对误差的分布直方图. 方法的误差服从正态分布, 选择误差的均值、方差、和标准差进行分析. 均值公式、方差、标准差公式分别为:

|
图 6 单次实验各种方法计算位移数据结果可视化比较 |
| $ \begin{array}{l}\\[-5pt] \left\{ {\begin{split} \overline X =& \dfrac{{\displaystyle\sum _{i = 1}^n{X_i}}}{n} \hfill \\ {S^2}{{ = }}&\dfrac{{\displaystyle\sum _{i = 1}^n{{({X_i} - \overline X )}^2}}}{{n{{ - }}1}} \hfill \\ S = &\sqrt {\dfrac{{\displaystyle\sum _{i = 1}^n{{({X_i} - \overline X )}^2}}}{{n{{ - }}1}}} \hfill \\ \end{split} } \right. \end{array}$ | (11) |
Chen等人建议在使用此方法时量程不要超过2个像素单位[15], 在本文实验中, 经过验证, 本方法在位移为3个像素单位内测量较为准确, 因此本文方法量程为3个像素单位, 即单侧位移不超过1.5个像素单位. 测量方法的准确度等级为(最大绝对误差/量程)×100, 本文方法测量的最大绝对误差为0.267 8个像素单位, 最大量程为3个像素单位, 因此本文方法的精确度等级为8.9. 量程较小属于方法的固有缺陷, 这限制了本文方法的应用场景, 但本文方法的优势在于对于微小位移的测量的相关度和误差分析结果均优于现有光流方法.
本文实验通过橡皮锤敲击简支梁产生单次振动, 并重复10次实验, 每次振动的峰-峰值均接近最大量程, 本文方法的10次实验结果如表1. 每次均选择从振动开始的1 300个数据点(每秒120个数据点)进行分析.
接着使用其他两种方法对10次实验进行数据分析和误差分析对比, 结果如表2所示, 本文的方法在稳定光照条件下测得的简支梁振动数据各项指标均优于其他两种光流方法.
综合以上实验结果, 本文基于相位运动放大的结构振动微小位移测量方法在微小振动位移的精确度和稳定性上具有明显优势, 并且通过实验室简支梁振动实验验证了方法的有效性.
3 结论与展望结构健康监测技术对于维护土木建筑结构的安全和可靠性具有重要意义, 基于计算机视觉的技术可以实现在较少用户参与的情况下, 实现土木结构的非接触位移监测. 本文提出了一种改进的基于相位的光流法, 与传统的位移和振动监测测量技术相比, 该方法需要更简单、不太复杂且更具成本效益的硬件. 本文将方法应用于一个实验室搭建的简支梁模型, 它很好地代表了许多类似的相对细长的结构. 本文方法相比于其他光流方法在微小位移检测上具有更好的精确度, 但当视频中的结构出现大的运动(大于3个像素)或者光照剧烈变化时, 该方法并不适用, 这限制了方法的适用范围. 在未来的研究中, 要加强方法对于外界干扰的鲁棒性研究, 扩展方法的适用范围, 提高方法的实用性.
|
图 7 单次误差分析可视化 |
| 表 1 基于相位光流法的10次振动实验数据分析和误差分析 |
| 表 2 不同方法的实验数据和误差分析10组数据均值 |
| [1] |
Doebling SW, Farrar CR, Prime MB. A summary review of vibration-based damage identification methods. The Shock and Vibration Digest, 1998, 30(2): 91-105. DOI:10.1177/058310249803000201 |
| [2] |
Diamond DH, Heyns PS, Oberholster AJ. Accuracy evaluation of sub-pixel structural vibration measurements through optical flow analysis of a video sequence. Measurement, 2017, 95: 166-172. DOI:10.1016/j.measurement.2016.10.021 |
| [3] |
Gentile C, Cabboi A. Vibration-based structural health monitoring of stay cables by microwave remote sensing. Smart Structures and Systems, 2015, 16(2): 263-280. DOI:10.12989/sss.2015.16.2.263 |
| [4] |
Kim SW, Jeon BG, Kim NS, et al. Vision-based monitoring system for evaluating cable tensile forces on a cable-stayed bridge. Structural Health Monitoring, 2013, 12(5–6): 440-456. DOI:10.1177/1475921713500513 |
| [5] |
Cunha A, Caetano E. Dynamic measurements on stay cables of cable-stayed bridges using an interferometry laser system. Experimental Techniques, 1999, 23(3): 38-43. DOI:10.1111/j.1747-1567.1999.tb01570.x |
| [6] |
Nassif HH, Gindy M, Davis J. Comparison of laser Doppler vibrometer with contact sensors for monitoring bridge deflection and vibration. NDT & E International, 2005, 38(3): 213-218. |
| [7] |
Dong CZ, Celik O, Catbas FN, et al. Structural displacement monitoring using deep learning-based full field optical flow methods. Structure and Infrastructure Engineering, 2020, 16(1): 51-71. DOI:10.1080/15732479.2019.1650078 |
| [8] |
Ye XW, Dong CZ, Liu T. Environmental effect on vision-based structural dynamic displacement monitoring. Proceedings of the Second International Conference on Performance-based and Life-cycle Structural Engineering. Brisbane: University of Queensland, 2015. 261–265.
|
| [9] |
Mazzoleni P, Zappa E. Vision-based estimation of vertical dynamic loading induced by jumping and bobbing crowds on civil structures. Mechanical Systems and Signal Processing, 2012, 33: 1-12. DOI:10.1016/j.ymssp.2012.06.009 |
| [10] |
Khuc T, Catbas FN. Computer vision-based displacement and vibration monitoring without using physical target on structures. Structure and Infrastructure Engineering, 2017, 13(4): 505-516. DOI:10.1080/15732479.2016.1164729 |
| [11] |
Zhao J, Bao YQ, Guan ZG, et al. Video-based multiscale identification approach for tower vibration of a cable-stayed bridge model under earthquake ground motions. Structural Control and Health Monitoring, 2019, 26(3): e2314.1-e2314.19. DOI:10.1002/stc.2314 |
| [12] |
Wu HY, Rubinstein M, Shih E, et al. Eulerian video magnification for revealing subtle changes in the world. ACM Transactions on Graphics, 2012, 31(4): 65. |
| [13] |
Wadhwa N, Rubinstein M, Durand F, et al. Phase-based video motion processing. ACM Transactions on Graphics, 2013, 32(4): 80. |
| [14] |
Wadhwa N, Rubinstein M, Durand F, et al. Riesz pyramids for fast phase-based video magnification. 2014 IEEE International Conference on Computational Photography (ICCP). Santa Clara: IEEE, 2014. 1–10.
|
| [15] |
Chen JG, Wadhwa N, Cha YJ, et al. Modal identification of simple structures with high-speed video using motion magnification. Journal of Sound and Vibration, 2015, 345: 58-71. DOI:10.1016/j.jsv.2015.01.024 |
| [16] |
Fleet DJ, Jepson AD. Computation of component image velocity from local phase information. International Journal of Computer vision, 1990, 5(1): 77-104. DOI:10.1007/BF00056772 |
| [17] |
Chen JG, Davis A, Wadhwa N, et al. Video camera–based vibration measurement for civil infrastructure applications. Journal of Infrastructure Systems, 2017, 23(3): B4016013. |
| [18] |
Cha YJ, Chen JG, Büyüköztürk O. Output-only computer vision based damage detection using phase-based optical flow and unscented Kalman filters. Engineering Structures, 2017, 132: 300-313. DOI:10.1016/j.engstruct.2016.11.038 |
| [19] |
Shang ZX, Shen ZG. Multi-point vibration measurement and mode magnification of civil structures using video-based motion processing. Automation in Construction, 2018, 93: 231-240. DOI:10.1016/j.autcon.2018.05.025 |
| [20] |
Simoncelli EP, Freeman WT, Adelson EH, et al. Shiftable multiscale transforms. IEEE transactions on Information Theory, 1992, 38(2): 587-607. DOI:10.1109/18.119725 |
| [21] |
Simoncelli EP, Freeman WT. The steerable pyramid: A flexible architecture for multi-scale derivative computation. Proceedings, International Conference on Image Processing. Washington: IEEE, 1995. 444–447.
|
| [22] |
Portilla J, Simoncelli EP. A parametric texture model based on joint statistics of complex wavelet coefficients. International Journal of Computer Vision, 2000, 40(1): 49-70. DOI:10.1023/A:1026553619983 |
| [23] |
Gautama T, Van Hulle MA. A phase-based approach to the estimation of the optical flow field using spatial filtering. IEEE Transactions on Neural Networks, 2002, 13(5): 1127-1136. DOI:10.1109/TNN.2002.1031944 |
| [24] |
Ilg E, Mayer N, Saikia T, et al. FlowNet 2.0: Evolution of optical flow estimation with deep networks. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 1647–1655.
|
| [25] |
Teed Z, Deng J. RAFT: Recurrent all-pairs field transforms for optical flow. Proceeding of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 402–419.
|
 2022, Vol. 31
2022, Vol. 31



