2. 苏州科技大学 江苏省建筑智慧节能重点实验室, 苏州 215009;
3. 苏州科技大学 苏州市移动网络技术与应用重点实验室, 苏州 215009
2. Jiangsu Province Key Laboratory of Intelligent Building Energy Efficiency, Suzhou University of Science and Technology, Suzhou 215009, China;
3. Suzhou Key Laboratory of Mobile Network Technology and Application, Suzhou University of Science and Technology, Suzhou 215009, China
能源与环境是当今世界的两大热点问题, 越来越受到人们的关注. 为了避免能源消耗和全球变暖的有害影响, 研究人员正在寻找减少建筑物能源消耗的方法[1]. 据统计, 供暖、通风和空调系统是主要的能源消耗大户. 建筑行业最终能耗的细分表明, 供暖、通风和空调系统分别占住宅和商业建筑总能耗的34%–40%[2]. 因此, 如何在不牺牲舒适性的前提下减少供热和制冷能耗是实现建筑节能必须考虑的问题.
最近10年, 建筑物的舒适性和能源管理已经成为人们关注的研究热点. 能源优化方法建立在建筑供热和制冷系统运行模型的基础上, 目前已经提出多种方法用于建筑热舒适控制和节能优化. 优化方法主要分为基于模型和基于数据驱动两种[3, 4]. 基于模型的方法旨在用简化的数学模型对建筑物中的能耗控制进行建模. 然而, 为建筑能量流建立精确的物理模型非常困难, 并且计算也十分昂贵[5]. 此外, 不同的建筑环境可能需要不同的模型, 很难建立一种适用于所有建筑环境的通用模型. 因此, 目前多使用数据驱动的方法进行能耗优化研究.
强化学习(reinforcement learning, RL)是一种用来在线求解最优控制策略的机器学习方法[6], 其可以通过与环境的交互试错来学习最优控制策略. 最近有很多关于智能建筑的研究, 通过强化学习方法学习的控制策略设计智能控制器, 使其感知建筑状态和环境条件, 调整模型参数, 优化建筑能耗. Wei等人基于模拟软件EnergyPlus, 利用强化学习算法控制建筑内设备以达到优化建筑能耗的目的[7]. Kim等人使用马尔科夫决策过程对能量管理系统进行建模, 提出一种基于强化学习的能量管理算法, 以降低未来未知信息下目标能源建筑的运行成本[8]. 胡龄爻等人提出一种强化学习自适应控制方法——RLAC, 该方法具有较快的收敛速度以及较好的收敛精度[9].
虽然能耗控制技术已经有不少研究, 但是在训练建筑能耗系统设定排放温度时, 会存在获得奖赏稀疏的情况. 为了解决这种问题, 构建一个建筑能耗模型来模拟某建筑的能耗, 采用基于自监督网络的DDPG (deep deterministic policy gradient)算法[10]将建筑能耗优化问题转化为马尔科夫决策过程进行求解, 并比较不同控制器的节省能耗和排放温度设定点, 实验结果证明, 采用基于自监督网络的DDPG方法可以更好地观测数据特性、学习最佳控制策略, 降低建筑能耗, 同时将建筑中的环境条件保持舒适.
1 相关理论 1.1 马尔科夫决策过程马尔科夫决策过程(Markov decision process, MDP)可以用来对强化学习问题进行建模, 通常用一个四元组
强化学习是一种通过Agent与环境的交互, 根据获得的奖赏或惩罚学习最优策略, 从而获得最大期望累计奖赏的学习方法. 策略一般用
| $ {V^\pi }(s) = \displaystyle\sum\limits_{a \in A} {\pi (s, a)\displaystyle\sum\limits_{s' \in S} {T(s, a, s')} } [R(s, a, s') + \gamma {V^\pi }(s')] $ | (1) |
| $ \begin{split} {Q^\pi }(s, a) = & \sum\limits_{s' \in S} {T(s, a, s')} \left[ {R(s, a, s') } \right. \hfill \\ & + \gamma \sum\limits_{a' \in A} {\pi (s', a)}\left. { {Q^\pi }(s', a')} \right] \end{split} $ | (2) |
折扣率 γ 决定未来奖赏的当前价值, 取值范围为(0, 1]. 如果当前策略是最优策略, 则对应的最优值函数如式(3)、式(4)所示:
| $ {V^{\text{*}}}(s) = \mathop {\max }\limits_{a \in A} \sum\limits_{s' \in S} {T(s, a, s')\left[ {R(s, a, s') + \gamma {V^{\text{*}}}(s')} \right]} $ | (3) |
| $ {Q^{\text{*}}}(s, a) = \sum\limits_{s' \in S} {T(s, a, s')} \left[ {R(s, a, s') + \gamma \mathop {\max }\limits_{a' \in A} {Q^*}(s', a')} \right] $ | (4) |
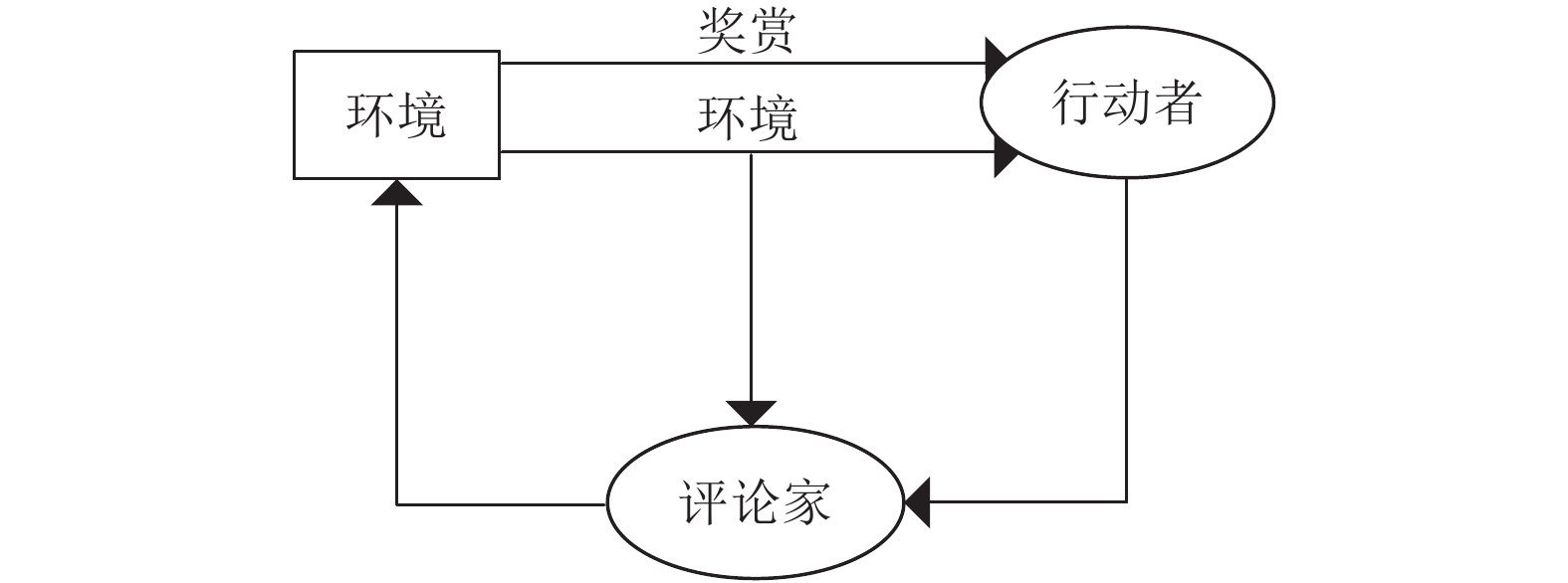
DDPG算法基于行动者—评论家(actor-critic, AC)框架, 如图1所示.
和传统的AC结构不同, 其Critic网络预估的是Q值而不是V值, 并通过最小化损失函数L来更新值函数的参数
| $ L = \frac{1}{N}\sum\nolimits_i {({y_i} - Q({s_i}, {a_i}|{\theta ^Q})} {)^2} $ | (5) |
其中,
| $ {y_i} = {r_i} + Q'({s_{i + 1}}, \mu '({s_{i + 1}}|{\theta ^{\mu '}})|{\theta ^{Q'}}) $ | (6) |
Actor部分采用确定性策略梯度(deterministic policy gradient, DPG)的方式[11], 使用梯度下降方法进行更新, 继而输出一个确定的动作
| $ \begin{split} {\nabla _{{\theta ^\mu }}}J = \dfrac{1}{N}\displaystyle\sum\limits_i {{\nabla _a}Q(s, a|{\theta ^Q})} {|_{s = {s_i}, a = \mu ({s_i})}} {\nabla _{{\theta ^\pi }}}\mu (s|{\theta ^\mu }){|_{{s_i}}} \end{split}$ | (7) |
DDPG算法在Actor和Critic中都有估值网络和目标网络, 在训练过程中只需要估值网络的参数, 而目标网络的参数由估值网络每隔一段时间进行软更新, 其参数按照式(8)进行更新:
| $ \left\{ {\begin{array}{l} {\theta ^{Q'}} \leftarrow \tau {\theta ^Q} + (1 - \tau ){\theta ^{Q'}} \hfill \\ {\theta ^{\mu '}} \leftarrow \tau {\theta ^\mu } + (1 - \tau ){\theta ^{\mu '}} \hfill \\ \end{array}} \right. $ | (8) |
其中,
|
图 1 DDPG算法原理框图 |
1.3 强化学习中的稀疏奖赏问题
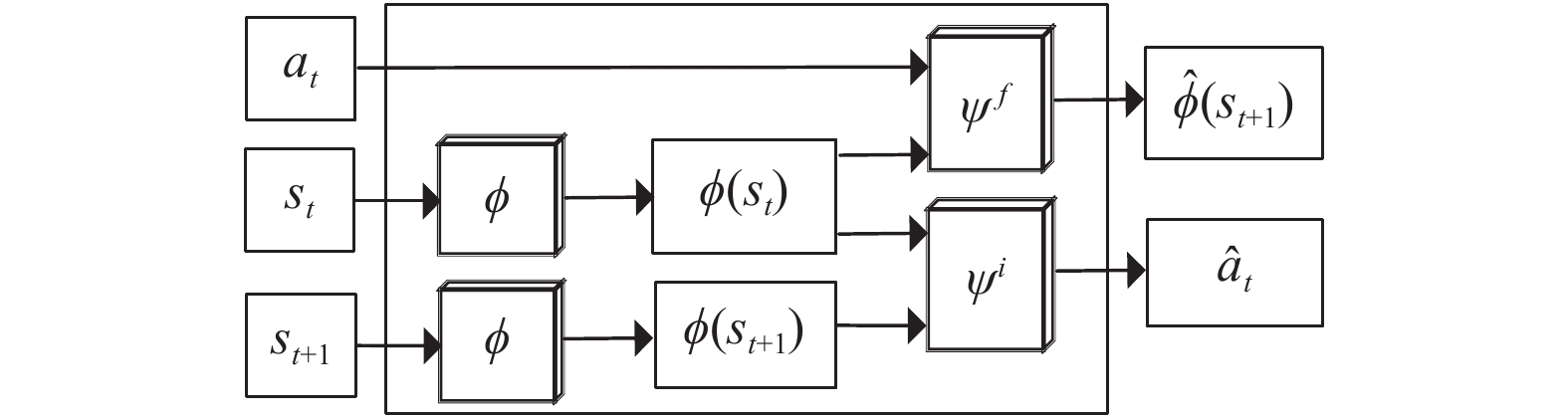
将强化学习用于实际应用问题时, 可能会出现奖赏稀疏的问题, 即多数时候Agent没有办法得到奖赏. 如果环境中奖赏非常稀疏, 会导致Agent学习缓慢, 不积极地探索更多未知的状态, 从而很难学会选择合适的动作. 目前, 好奇心机制是解决稀疏奖赏(sparse reward)问题很好的一个途径, 其通过引入内在好奇心模块(intrinsic curiosity module, ICM), 增加一个好奇心的内在奖赏
|
图 2 ICM模型 |
其工作原理为: 通过特征提取层
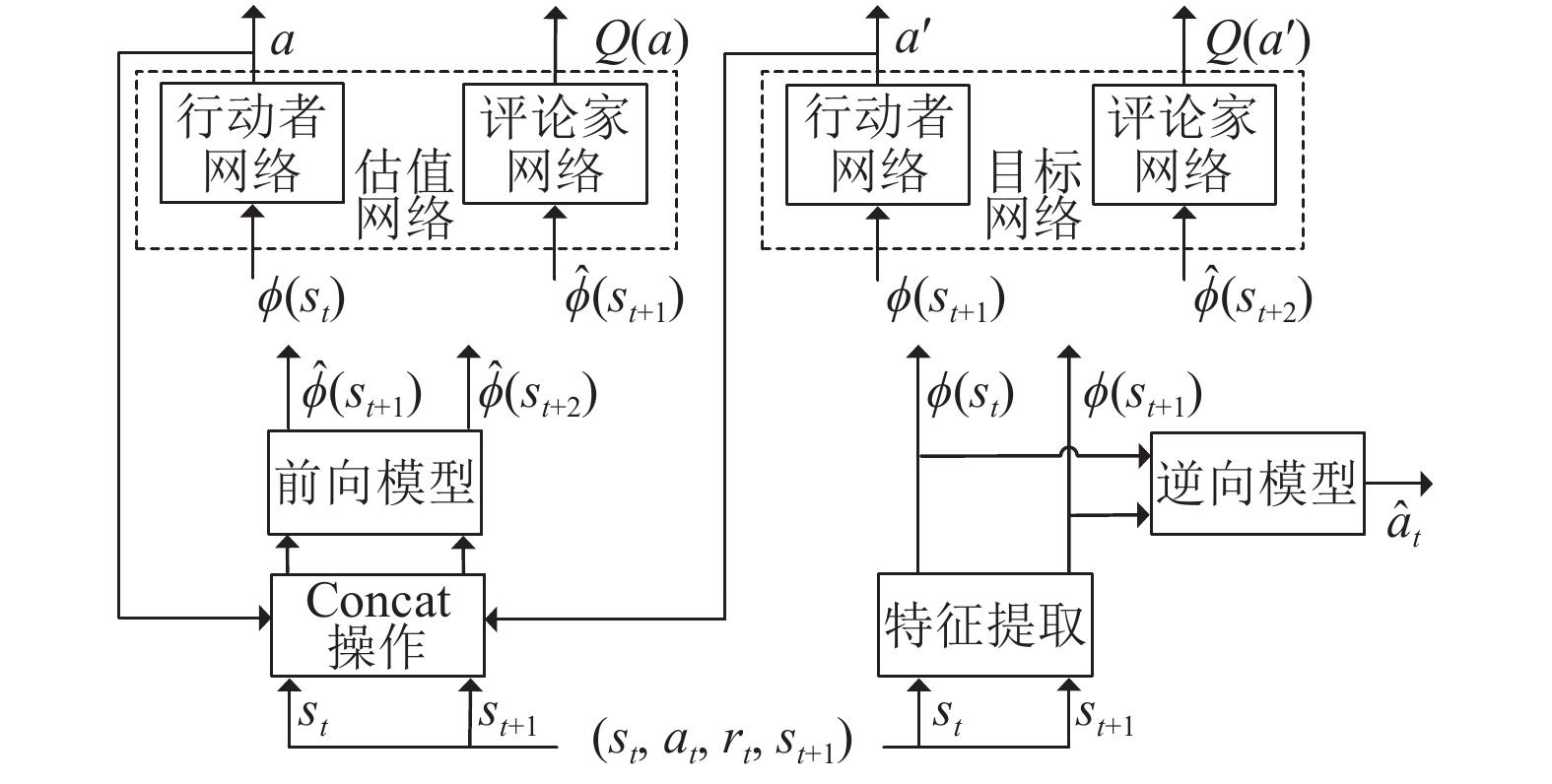
为了使Agent在奖赏稀疏的情况下保持好奇心且积极探索, 更好的提取原始数据中真正有用的信息, 文献[10]提出了一种基于自监督网络的DDPG算法. 输入状态特征
| $ {a_t} = {\mu _{{\theta ^\pi }}}(\phi ({s_t})) $ | (9) |
通过
|
图 3 基于自监督网络的DDPG算法流程图 |
该算法中行动者和评论家网络的目标函数分别定义为式(10)和式(11):
| $ \begin{split} & {\nabla _{{\theta ^\pi }}}J =\hfill \\ &\frac{1}{N}\sum\limits_i {{\nabla _{{\theta ^\pi }}}\mu (\phi (s)|{\theta ^\mu }){|_{\phi ({s_i})}}} {\nabla _a}Q(\phi (s), a|{\theta ^Q}){|_{\phi (s) = \phi ({s_i}), a = \mu (\phi ({s_i}))}} \end{split} $ | (10) |
| $ \begin{split} L =& \frac{1}{N}\sum\nolimits_i {\left( {{r_i} + \gamma {Q^{'}}(\phi ({s_{i + 1}}), \mu '(\phi ({s_{i + 1}}|{\theta ^{\mu '}})|{\theta ^{Q'}}} \right.} \hfill \\ & {\left. { - Q((\phi ({s_i}), {a_i}|{\theta ^Q})} \right)^2} \hfill \\ \end{split} $ | (11) |
文献[10]提出一种基于自监督网络的DDPG算法, 并通过实验证明该算法的有效性, 能够较好地解决实际任务训练过程中存在的奖赏稀疏问题, 现将其应用于建筑能耗控制问题中.
当人们处在密闭空间时, 保持令人舒适的室内空气环境尤其重要. 设计控制器调节空气处理装置(air handling unit, AHU)的排放温度, 将空气释放到建筑物之前对空气进行加湿或者除湿, 以达到使人感到舒适的程度, 然后送入房间[13]. 一般设定建筑中期望的空气湿度水平为50%时, 人体感觉舒适. 通常, 空气以18 ℃–25 ℃释放到建筑中. AHU的子系统中, 冷却、预热和再热盘管是其主要能源消耗者. 设定AHU的工作模式为: 当室外温度低于12 ℃时, 预热盘管将进入的冷空气加热到预定的设定点; 当室外温度高于12 ℃时, 使用冷却盘管对空气进行除湿, 冷凝多余的水分. 再加热和预热设定值都取决于运行模式, 同时排放温度由基于强化学习的控制器定义.
虽然在保持建筑条件舒适以及优化建筑能耗方面已经有不少研究, 但大都忽略了控制器设定动作后响应延迟带来的问题. 在大型建筑中, 空气处理装置作用的空间区域很大, 设定排放温度后系统需要较长时间响应并达到效果, 即行动和反馈之间存在时差, 这期间Agent获得的奖赏存在延迟, 很难进行探索和学习, 从而就会导致稀疏奖赏的问题.
因此, 采用基于自监督网络的DDPG算法[10]解决描述的建筑能耗控制问题. 首先单独训练自监督网络部分, 结合状态和动作变量, ICM模块中的前向模型以此来预测下一个状态特征向量, 并将预测误差作为鼓励Agent产生好奇心的内在奖赏, 较好地引导Agent在奖赏稀疏环境下的探索, 从而解决奖赏稀疏问题. 然后, 使用数据驱动的方法模拟建筑中的供暖和制冷能耗, 并且为环境的状态空间和动作空间设置上下界. 再构建供热和制冷系统基于物理的仿真环境, 研究控制动作变化后对应的建筑能耗. 之后, 将基于自监督网络的DDPG算法与上述环境进行交互, 学习最优策略, 最优策略充当控制器, 用于实时调节空气处理装置中除湿空气的排放温度设定点. 也就是说, 将比较基于建筑控制器设定值消耗的能耗和使用这个环境的强化学习控制器设定值消耗的能耗. 将描述的建筑能耗优化问题作为一个MDP来解决.
2.2 环境建模(1)状态
设定状态
(2)动作
根据历史数据, 排放温度设置在18–25 ℃之间能够使人体保持一定舒适度. 因此, 设定Agent选择动作的范围为(18 ℃, 25 ℃), 对该范围的数值进行采样. 然后将状态特征向量
(3)奖赏
奖赏函数包括两部分:
t时间间隔内建筑物消耗的历史能耗
| $ {r_1} = E_t^{\rm{old}} - E_t^{\rm{pre}} $ | (12) |
建筑物内控制器建议的排放温度用
| $ {r_2} = - \dfrac{{\left| {set{\kern 1pt} {a_t}{{ - }}set{\kern 1pt} {a_0}} \right|}}{{set{\kern 1pt} {a_0}}} $ | (13) |
所以, 总的奖赏函数为:
| $ r(\phi ({s_t}), {a_t}) = (E_t^{\rm{old}} - E_t^{\rm{pre}}){\kern 1pt} + \lambda \times\left( - \frac{{\left| {set{\kern 1pt} {a_t}{{ - }}set{\kern 1pt} {a_0}} \right|}}{{set{\kern 1pt} {a_0}}}\right) $ | (14) |
奖赏函数第1部分的目的是为更低的能耗提供更高的奖赏. t时刻, 建筑物响应强化学习控制器的动作后, 消耗能量
设置控制动作
参数
将基于自监督网络的DDPG算法[10]应用于建筑能耗控制问题中. 用基于ICM模块的附属网络处理输入的状态
算法1. 基于自监督网络的DDPG算法的建筑能耗控制
1) 初始化估值网络的参数
2) 初始化Replay Buffer: R;
3) for episode=1, N do
4) fort=1, Tdo
5) 通过策略函数
6) 将得到的交互数据
7) 将状态
8) 将
9) 利用当前以及下一步的状态动作对
10) 从重放缓冲区R中采样M个序列;
11) 根据式(10)计算策略网络中关于
12) 根据式(11)计算价值函数并更新参数
13) end for
14) 更新目标网络
15) end for
3 实验结果与分析为验证该算法在实际应用问题中的有效性, 利用基于自监督网络的DDPG方法解决建筑能耗系统运行时存在的奖赏稀疏问题.
3.1 实验设置实验的监测数据来源于某环境学院项目, 其中包括环境变量: 室外空气温度(℃)、室外空气相对湿度(RH)、时间t时的太阳辐照度(瓦特/m2), 以及从建筑物自动化系统中每5 min采样一次的空气处理装置的排放温度设定点(℃)和建筑物消耗的总能量(J). 实验将数据集分为两部分, 用两个月数据对模型进行训练, 再用一周数据测试方法的应用性能. 在训练期间设定不同的参数 λ 进行实验, 结果显示设置参数
选取均方误差(mean-square error, MSE)、均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)和平均绝对百分比误差(mean absolute percentage error, MAPE)作为衡量指标:
| $ {\textit{MSE}} =\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{y'_i}})}^2}} $ | (15) |
| ${\textit{RMSE}} = \sqrt {\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{y'_i}})}^2}} } $ | (16) |
| $ {\textit{MAE}} = \frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {|{y_i} - {{y'_i}}|} $ | (17) |
| ${\textit{MAPE}} =\frac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\frac{{|{y_i} - {{y'_i}}|}}{{{y_i}}}} \times 100{\text{%}} $ | (18) |
其中, n表示相关参数样本的数量,
MSE可以评价实际数据与预测数据之间的误差; RMSE又称标准误差, 该指标对一组预测数据中特大特小误差反应十分敏感, 所以RMSE能够很好地反映出预测的准确性; MAE表示所有单个预测值与算术平均值的偏差的绝对值的平均; 而相对误差MAPE评估预测值的误差与实际值之间的比例. 这4个评估指标从不同的角度衡量了预测模型的效果, 以上4个评估指标值越小, 表明对应方法的性能越好.
表1为采用不同控制器设置的排放温度后能耗预测的评估值, 分别列出MSE、RMSE、MAE、MAPE的值, 充分展示各自的性能.
| 表 1 不同控制器能耗预测的误差对比 |
从各项衡量指标可以看出, 通过基于自监督网络的DDPG方法学习最优策略, 该策略充当RL控制器设置排放温度, 预测数据集的供热和制冷能耗, 该方法的预测精度优于建筑控制器, 取得了较好的结果.
目前, 建筑能源控制系统中的空气排放温度通常由建筑人员确定, 建筑人员根据环境湿度在不同的时间设定不同建筑区域的排放值, 并编程到系统中. 但是, 这种预先设置排放温度的方式效率低下, 当环境变化时不能及时响应并作出改变, 且未能以节能的方式实施. 例如, 当AHU在较高的温度下释放除湿空气, 但建筑中的某些区域需要将它们冷却到较低的温度时, 就会导致不必要的能源消耗. 而基于RL的控制器使用动态能量和环境模型学习一个控制策略, 该策略不断调整排放温度设置点以减少建筑能耗.
在训练阶段, 代理设置排放温度后与环境交互, 并观察立即奖赏和下一个状态. 每隔一段时间, 从重放缓冲区R随机采样一批经验, 使用式(10)训练Critic网络. 重新评估评论家网络的权重, 根据式(8)更新Actor网络的权重. 每个训练情节结束时, 观察当前的Actor-Critic网络是否积累了比以前更高的回报. 如果是, 此时目标达到最优值, 说明基于强化学习的控制器比在建筑中实施的控制器学习到更好的控制策略, 将网络权重保存为当前最佳值.
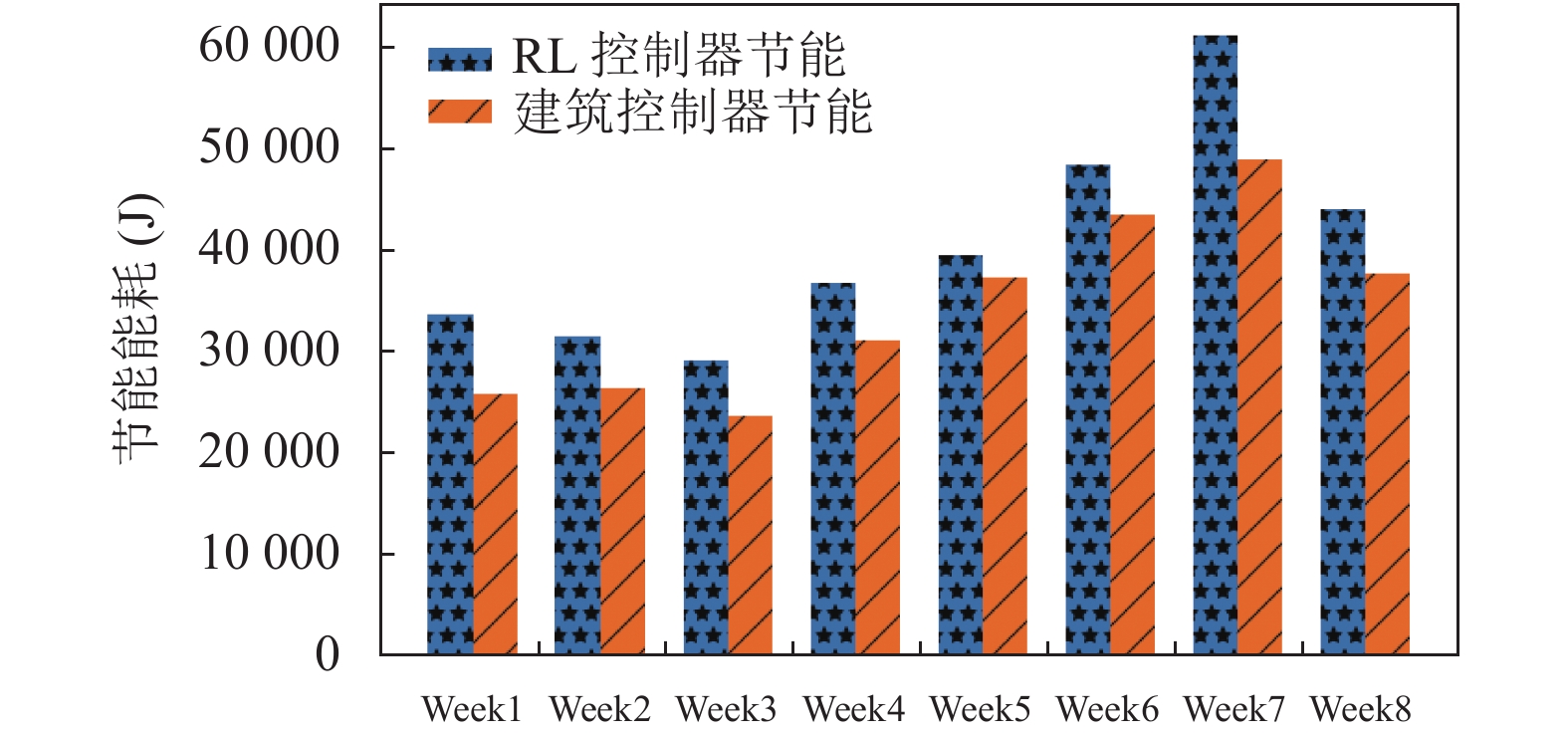
图4主要展示RL控制器和建筑控制器的训练效果. 从图中可以看出, RL控制器的节省能耗始终高于建筑控制器, 并且随着训练时间的增加, 能够达到更好的节能效果.
|
图 4 RL与建筑控制器节能效果比较 |
接下来, 用最佳权重加载Actor-Critic网络, 并在测试数据上使用学习的控制策略评估各自的性能. 将基于RL控制器推荐的排放温度设定值所产生的能耗, 与采用建筑控制器设定排放温度所产生的能耗进行对比, 如图5所示, 图中横坐标的时间步长以5分钟为间隔.
分析图5得出, 当室外温度低于12 ℃时, 控制器进入预热模式并产生能耗; 反之, 控制器调整再热设定值并消耗能量. 总体看来, 不论是RL控制器, 还是建筑控制器, 都能够根据环境条件调整空气处理装置的工作模式, 保证舒适性, 但使用RL控制器推荐的排放温度尽可能地降低了峰值能耗. 然而, 两种控制器设定的排放温度相差并不大. 这表明, 在保证舒适性的前提下, 通过对建筑控制器的固定时间表进行少量调整, 可以显著的减少能耗, 即使用RL控制器建议的排放温度产生的能耗值更低.
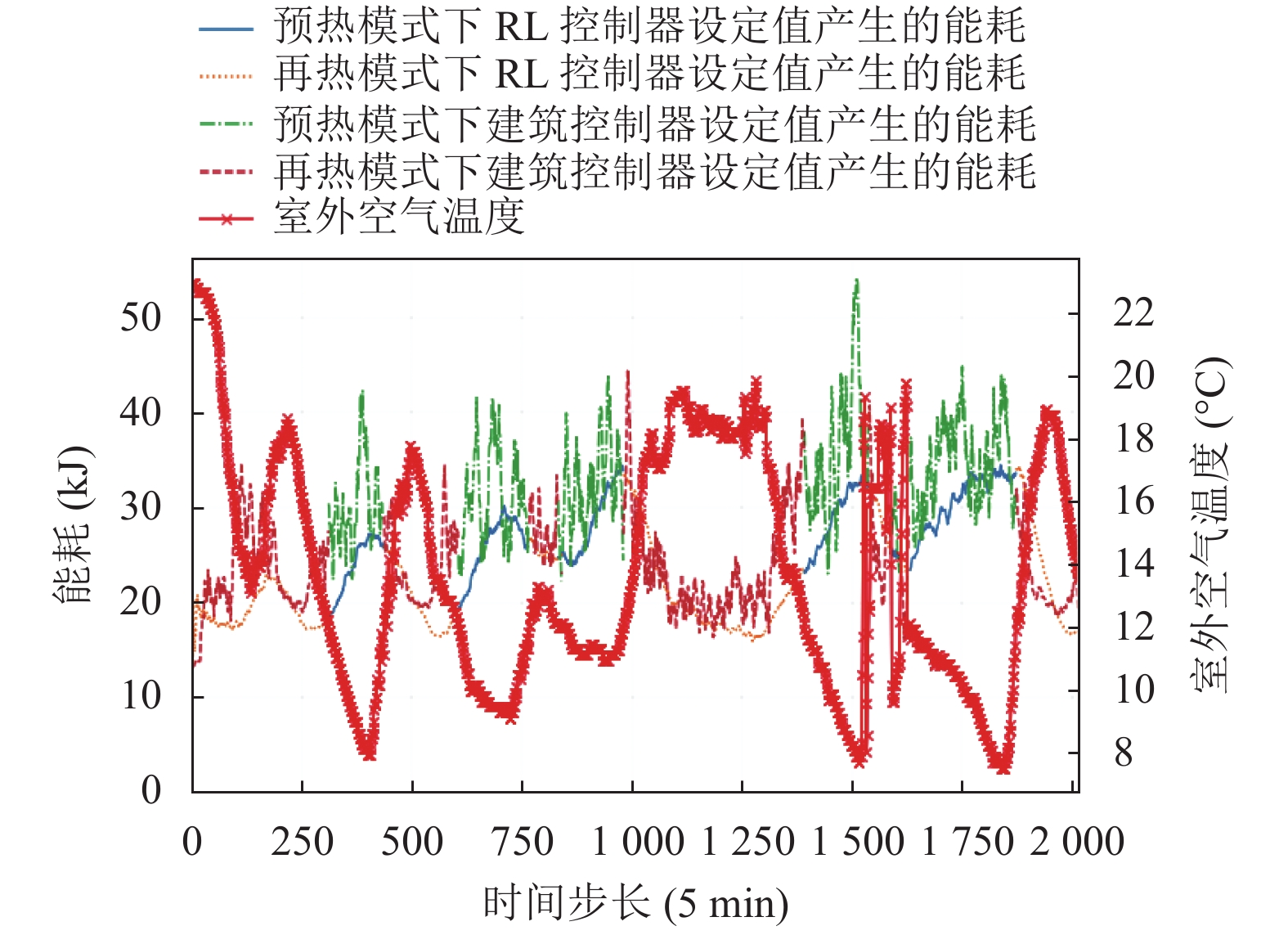
|
图 5 RL和建筑控制器推荐设定值产生能耗的比较 |
式(13)表明, RL控制器推荐的排放温度偏离建筑控制器推荐的设定温度时, 奖赏函数第二部分
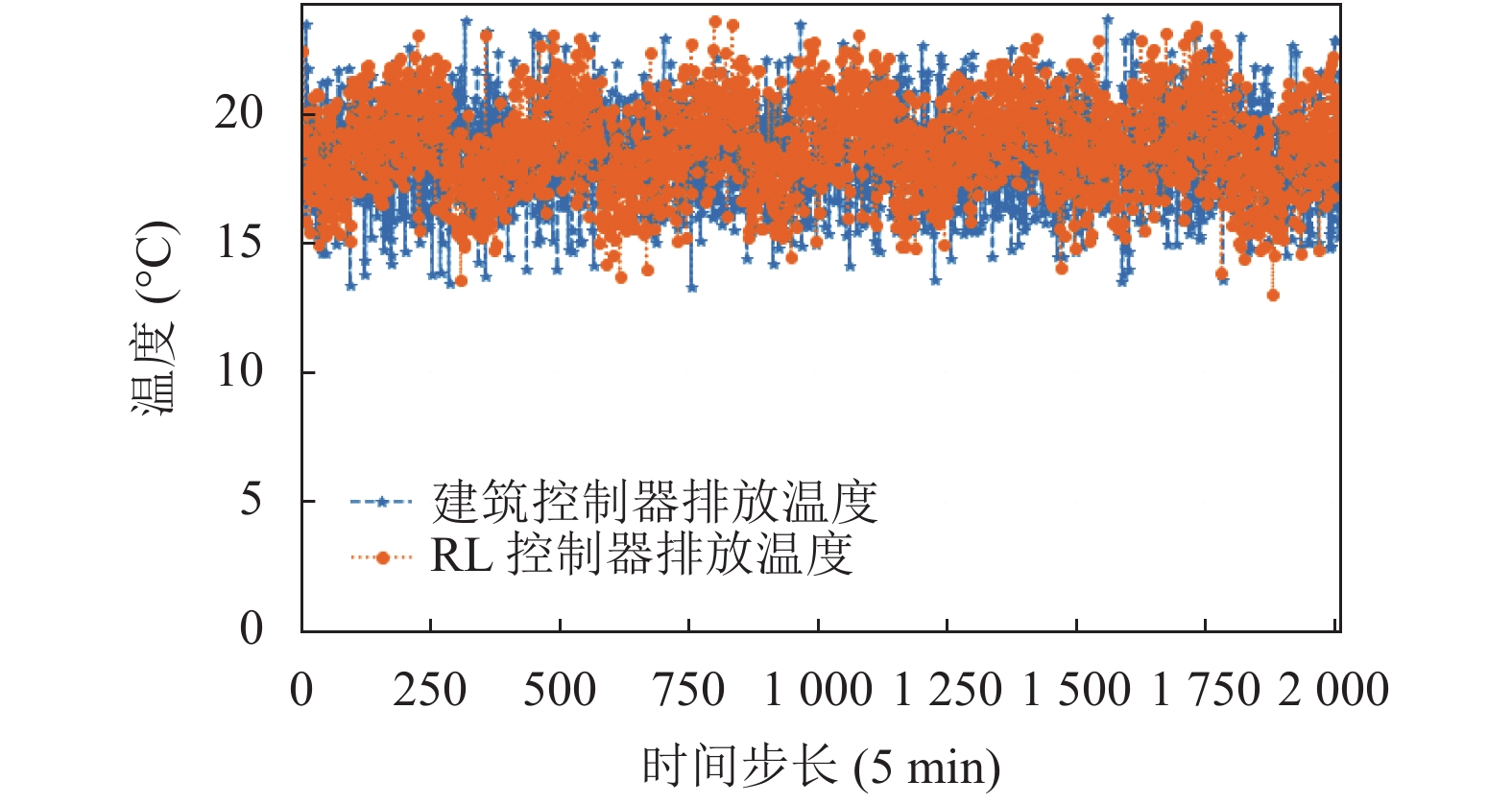
|
图 6 RL和建筑控制器推荐排放温度设定值的比较 |
训练阶段, 通过大量迭代逐步提升动作—价值Q函数, RL控制器已经学习到所能达到的最佳策略, 将环境变量作为输入数据, 希望最小化建筑的总能耗, 对空气处理装置的排放温度进行调整, 将其视为控制变量以实现能耗减少. 测试期内, 使用该策略选择控制动作, 得到基于RL控制器和建筑控制器设定排放温度产生的供热和制冷总能耗, 结果如图7所示, 对其进行进一步的分析.
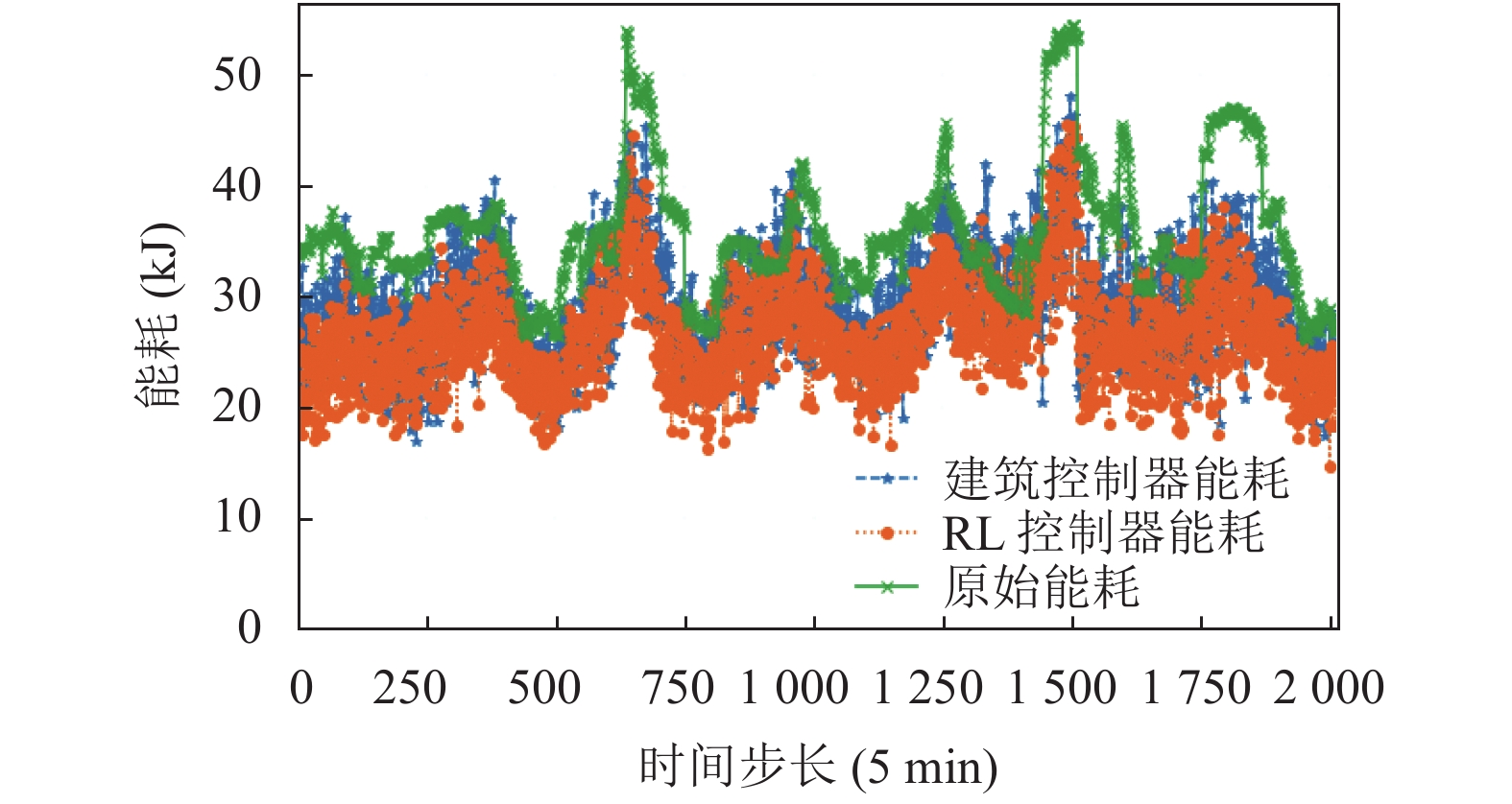
|
图 7 基于RL和建筑控制器控制的总能耗比较 |
从图7中可以看出, 和建筑控制器产生的总能耗相比, 基于自监督网络的DDPG方法学习的RL控制器产生的能量, 始终比建筑控制器的产生的能耗少. 再结合图6的实验结果, 说明确保排入建筑中的空气满足人体的舒适度条件时, 采用基于RL方法的控制器设定排放温度能够达到更好的节能效果.
表2显示RL控制器和控制器分别执行5次所对应的节能量. 在整个测试期, 基于RL方法设定排放温度的控制器平均每周可以节省能耗为43.826 1 kJ, 而建筑控制器平均每周的节能量只有21.668 7 kJ. 表明采用RL控制器建议的设定值可以获得显著的节能.
| 表 2 5次实验的节能能耗(kJ) |
4 结论与展望
本文将基于自监督网络的DDPG算法应用到建筑能耗控制问题中. 通过提取建筑周围环境状态的更多特征, 使Agent在出现奖赏稀疏问题时能够保持好奇心, 增加探索. 然后对建筑的随机能量进行优化, 目标是在一段时间内降低总能耗, 同时满足建筑内保持舒适空气条件的要求. 通过对建筑物周围环境进行建模, 使用基于自监督网络的DDPG方法学习最优策略, 基于该RL方法的控制器可以学习建筑内空气处理装置的最佳可能排放温度, 结果显示设计的控制器具有较好的性能.
本文主要研究建筑内某一区域的能耗控制问题, 从结果可以看出, 将基于自监督网络的DDPG方法运用于建筑节能领域可以获得明显的节能效果. 下一步, 将考虑继续完善能量模型, 并和其他控制方法进行比较, 同时, 预计进一步研究如何设置不同区域的控制参数, 以更好地调节建筑内的舒适度并减少能耗.
| [1] |
Berardi U. A cross-country comparison of the building energy consumptions and their trends. Resources, Conservation and Recycling, 2017, 123: 230-241. DOI:10.1016/j.resconrec.2016.03.014 |
| [2] |
Amasyali K, El-Gohary NM. A review of data-driven building energy consumption prediction studies. Renewable and Sustainable Energy Reviews, 2018, 81: 1192-1205. DOI:10.1016/j.rser.2017.04.095 |
| [3] |
Naug A, Ahmed I, Biswas G. Online energy management in commercial buildings using deep reinforcement learning. 2019 IEEE International Conference on Smart Computing (SMARTCOMP). Washington: IEEE, 2019. 249–257.
|
| [4] |
Zhao HX, Magoulès F. A review on the prediction of building energy consumption. Renewable and Sustainable Energy Reviews, 2012, 16(6): 3586-3592. DOI:10.1016/j.rser.2012.02.049 |
| [5] |
Huang H, Chen L, Hu E. Model predictive control for energy-efficient buildings: An airport terminal building study. 11th IEEE International Conference on Control & Automation (ICCA). Taichung: IEEE, 2014. 1025–1030.
|
| [6] |
Lillicrap TP, Hunt JJ, Pritzel A, et al. Continuous control with deep reinforcement learning. arXiv: 1509.02971, 2015.
|
| [7] |
Wei TS, Wang YZ, Zhu Q. Deep reinforcement learning for building HVAC control. Proceedings of the 54th Annual Design Automation Conference 2017. Austin: ACM, 2017. 22.
|
| [8] |
Kim S, Lim H. Reinforcement learning based energy management algorithm for smart energy buildings. Energies, 2018, 11(8): 2010. DOI:10.3390/en11082010 |
| [9] |
胡龄爻, 陈建平, 傅启明, 等. 一种面向建筑节能的强化学习自适应控制方法. 计算机工程与应用, 2017, 53(21): 239-246. DOI:10.3778/j.issn.1002-8331.1702-0217 |
| [10] |
Zhang GH, Chen HL, Li JX. Efficient DDPG via the self-supervised method. 2020 Chinese Control and Decision Conference (CCDC). Hefei: IEEE, 2020. 4636–4642.
|
| [11] |
Silver D, Lever G, Heess N, et al. Deterministic policy gradient algorithms. Proceedings of the 31st International Conference on International Conference on Machine Learning. Beijing: ACM, 2014. I-387–I-395.
|
| [12] |
Pathak D, Agrawal P, Efros AA, et al. Curiosity-driven exploration by self-supervised prediction. 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW). Honolulu: IEEE, 2017. 488–489.
|
| [13] |
Lee KP, Cheng TA. A simulation-optimization approach for energy efficiency of chilled water system. Energy and Buildings, 2012, 54: 290-296. DOI:10.1016/j.enbuild.2012.06028 |
 2022, Vol. 31
2022, Vol. 31



