2. 山东大学 前沿交叉科学青岛研究院, 青岛 266237
2. Institute of Frontier and Interdisciplinary Science, Shandong University, Qingdao 266237, China
基于模糊推理的空调智能控制系统是利用模糊推理算法作为数学工具, 用计算机来实现对空调的智能控制, 其本质上是一种非线性的智能控制系统. 其特点主要有: 不需要建立精确的数学模型, 利用模糊规则对环境温度参数进行模糊推理以实现自动化控制; 具有较强的鲁棒性, 对参数变化不灵敏, 抗干扰能力强; 基于模糊规则进行控制, 用文字语言代替数学变量, 更加简单方便. 基于以上优于常规控制策略的显著特点, 模糊推理在工业控制领域, 家用电器自动化领域等行业中解决了传统控制方法难以解决的控制问题. 另一方面, 模糊控制系统在理论和应用领域都还没形成完整的研究体系, 缺乏更深入的研究和进展, 因此, 对模糊推理控制系统的研究对自动控制和工业过程自动化的进一步发展都具有非常重要的意义.
基于模糊推理的空调智能控制系统首先对温度参数进行定义, 设置模糊变量、模糊术语、模糊值等, 规定了在一定温度范围内人体感受及人体感受的程度. 接下来, 对该系统进行规则库构建, 该系统的规则库主要是针对冷热阀门的开关、通风口尺寸的大小变化以及风速变化进行建立, 将外界温度的准确数值传递给模糊推理系统. 准确的温度参数经过模糊化、模糊规则匹配、去模糊化等步骤, 产生准确的控制指令, 控制指令传递给空调控制器, 进行相应的精确控制.
本文主要内容如下:
(1)空调智能控制概述. 本部分主要介绍空调智能控制领域的相关研究, 以及与本文所提出的基于模糊推理的空调智能控制系统的相关研究.
(2)相关模糊理论. 本部分主要介绍模糊控制技术所需要的相关模糊理论, 包括模糊变量、模糊集合、隶属度函数、模糊集合运算等.
(3)模糊控制技术方法. 本部分主要介绍模糊控制系统的主要技术步骤, 包括精确参量模糊化、模糊规则库构建、模糊推理和去模糊化4部分组成.
(4)实验验证. 本部分主要利用Java的FuzzyJ Tooklit第三方工具包对基于模糊推理的空调智能控制系统进行了模拟实现, 同时将实验结果与PID模拟实验结果进行对比, 从对比结果中可以明显看出模糊推理在空调温度控制领域的表现优于PID算法.
(5)模糊控制系统实现. 基于模糊推理的空调智能控制系统在本部分利用Matlab的Mamdani模型和Java的FuzzyJ Toolkit第三方包进行了模拟实现, 并在原有模拟控制系统的基础上对该控制系统进行可视化, 利用Java进行GUI界面的编写, 实现系统的可视化交互.
(6)结束语. 本部分主要简要总结了全文研究内容, 并提出了基于模糊推理的空调智能控制系统的不足, 同时对下一步的研究工作进行了展望.
1 空调智能控制概述随着社会的发展, 人们生活水平提高, 对空调的控制效果也提出了更高的要求. 黄志远等[1]对家用变频空调的节能原理以及控制方法进行了介绍, 其中就包括分段定点控制、PID控制和模糊逻辑控制等智能控制方法; 文丹[2]提出基于迭代优化的空调温湿度控制算法, 在保证空调送风温度的基础上, 实现室内负荷的变更与控制系统应对外界随机干扰的需求; 于军琪等[3]提出了一种群智能控制系统适用的并联水泵优化算法, 解决了中央空调系统中并联水泵优化算法在群智能控制方面适应性不足的问题; 王彦等[4]针对中央空调的控制提出了自适应Smith预估补偿控制方案, 仿真研究表明, 当参数发生变化时, 该方案具有较好的控制性能.
模糊推理是基于模糊逻辑的思想发展起来的推理机制, 模糊逻辑是利用语言文字来计算的逻辑. 1965年, 美国加利福尼亚大学教授Zadeh[5]提出“隶属函数”概念来定量描述事物Fuzzy性的模糊集合理论; 1973年, Zadeh[6]定义了模糊控制器; 1974年, 英国工程师Mamdani[7]首次将模糊集合理论应用到蒸汽机控制中; 1985年Kiszka等[8]提出了模糊系统稳定性理论; 1988年Dubois和Prade[9]提出了模糊近似推理. 在国内, 越来越多的研究者将模糊推理应用到生活的各个领域: 白云飞等[10]通过模糊推理实现了对蜂群中蜂王的识别; 孙博[11]利用模糊推理技术实现了雷达机动目标跟踪, 将这一技术从理论层面成功应用到军事领域; 梁娟等[12]利用自适应神经模糊推理系统和比例积分微分实现了一种机器人控制方法, 实验结果表明, 该方法能很好地控制并联机器人末端机械手的运动; 袁小平等[13]利用优化的模糊PID控制器改善了电动汽车驱动器控制系统中量化因子和比例因子自调节能力; 陈果等[14]采用变论域模糊PID控制提高了导管机器人的相应速度、定位精度与稳定性, 为血管介入手术导管机器人的控制提供良好的理论依据.
在利用模糊逻辑对空调进行控制的研究中, 赵巍等[15]尝试将模糊控制与PID控制结合, 对空调冰蓄冷进行控制; 朱如春[16]将神经网络与模糊控制结合, 对智能变频空调控制系统进行了一系列研究; 徐今强等[17]提出了一种鲁棒自适应两级模糊比例-积分-微分控制器, 解决了变频多联机空调运行特性复杂的问题, 实验证明该控制方法和控制器控制温度时可获得优良的动静态控制性能. 但是, 这些复合式空调控制系统目前技术尚未成熟, 并不适合广泛应用到工业生产中. 模糊控制与传统的PID控制相比参数控制更精确, 空调能耗更低, 且易于推广到大规模工业生产, 所以基于模糊推理的空调智能控制系统更具有实用价值.
2 相关模糊理论 2.1 模糊集合与隶属度函数经典集合论可以很好地表达分界线明确的关系, 但是自然界中有许多分界线不明确的事物关系, 例如温度的高低、产品质量的好坏等. 这种界限不明确的关系不能用经典集合论来表达, 所以人们引入了模糊集合论[18]的概念, 通过隶属度的方式来表达自然界中的模糊关系.
在模糊集合论中, 论域Z中的元素z与论域Z上的某一集合
| $ {\textit{Z}} \to \left[ {0,1} \right] $ | (1) |
| $ \mu_{{X}'} : {\textit{Z}}\to {\mu }_{{X}'}\left({\textit{z}}\right) $ | (2) |
其中,
假设论域Z上有
交运算:
| $ {\mu _{{X'} \cap Y'}}\left( {\textit{z}} \right) = {\mu _{{X'}}}\left( {\textit{z}} \right) \wedge {\mu _{{Y'}}} $ | (3) |
并运算:
| $ {\mu _{{X'} \cup Y'}}\left( {\textit{z}} \right) = {\mu _{{X'}}}\left( {\textit{z}} \right) \vee {\mu _{{Y'}}} $ | (4) |
补运算:
| $ {\mu _{{\bar X'}}}\left( {\textit{z}} \right) = 1 - {\mu _{{X'}}}\left( {\textit{z}} \right) $ | (5) |
| $ {\mu _{{\bar Y'}}}\left( {\textit{z}} \right) = 1 - {\mu _{{Y'}}}\left( {\textit{z}} \right) $ | (6) |
其中,
本文利用模糊控制系统对环境温度进行处理最终生成空调控制器的控制方案, 控制方案包括了冷热阀门的开关状态、通风口的开放尺寸以及风速大小. 一个模糊控制系统由精确参量模糊化、模糊规则库构建、模糊推理和去模糊化4部分组成, 模糊控制系统结构如图1所示.

|
图 1 模糊控制系统结构框架 |
3.2 参数模糊化
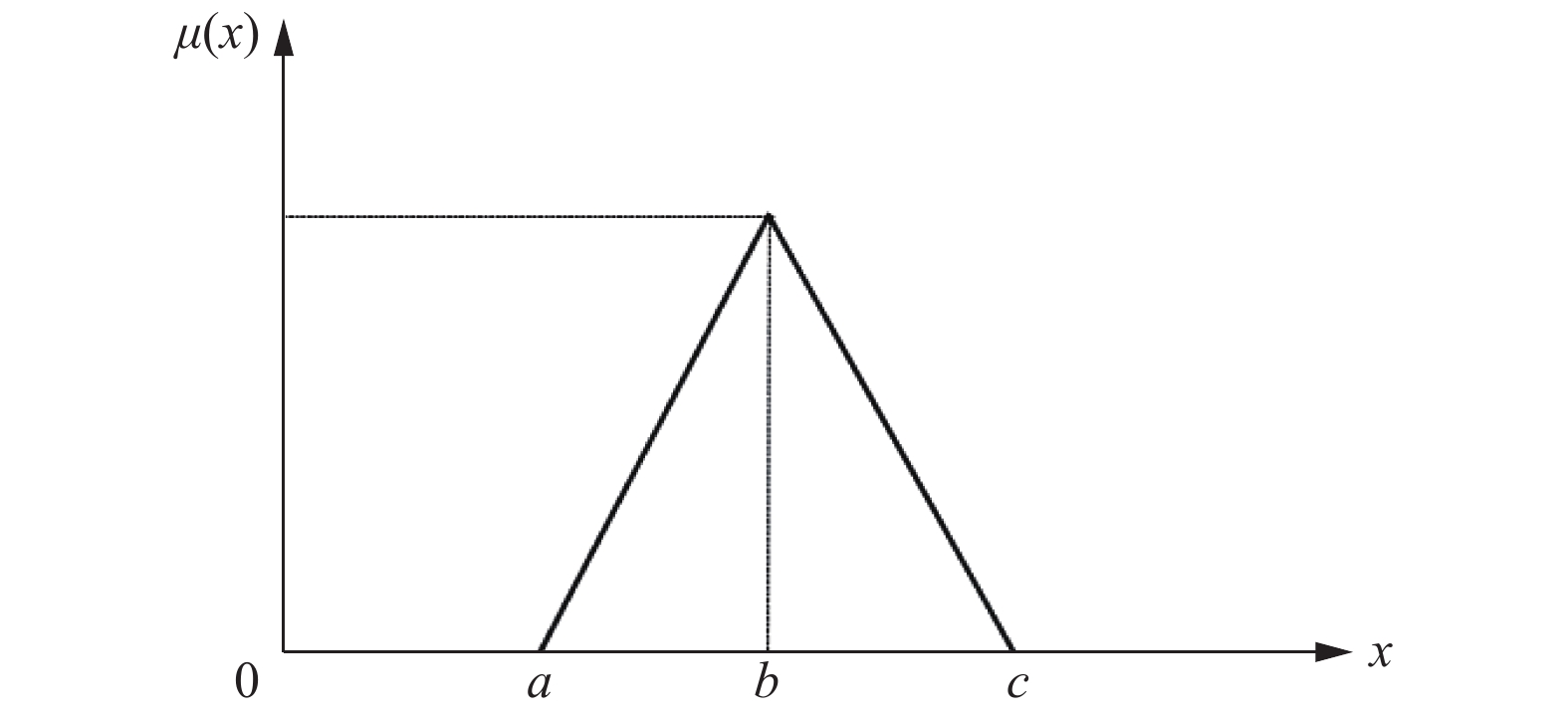
模糊化是将输入的精确参数通过隶属度函数转换成模糊集的过程. 隶属度函数是把输入变量对应到模糊集合中某个介于0和1之间的值, 求出隶属度, 隶属度函数的形式常见的有三角隶属函数、梯形隶属函数和高斯隶属函数. 在本文提出的基于模糊推理的空调智能控制系统中对输入的温度数值和输出的通风口尺寸以及风速大小均选择了三角隶属函数来实现模糊化. 三角隶属函数公式如下:
| $ \mu \left( x \right){\text{ = }}\left\{ \begin{gathered} 0, \;\;\;{x \leqslant a} \hfill \\ \frac{{x - a}}{{b - a}}, \;\;\; {a < x \leqslant c} \hfill \\ \frac{{c - x}}{{c - b}}, \;\;\; {b < x \leqslant c} \hfill \\ 0, \;\;\; {x > c} \hfill \\ \end{gathered} \right. $ | (7) |
三角隶属函数图如图2所示.
|
图 2 三角隶属度函数 |
在空调控制系统控制冷热空气阀门的开关及通风口开放尺寸的过程中, 包含了大量精确的温度数据, 这些温度数据经过分析后可以被粗略定义为寒冷、凉爽、舒适、温暖、炎热等多种人体感觉. 对于不同群体而言, 不同的温度范围对应着不同的人体感觉, 而温度范围又可以无限细分. 于是, 本文结合了大部分人的实际感受来定义温度参数. 根据调查, 人的舒适感取决于人体的热平衡. 影响热平衡的因素有很多, 比如环境温度、相对湿度、人体附近的空气流速、人的年龄和健康状况等, 因此, 舒适感是主观与客观多种因素综合作用后人产生的主观感受. 同时, 本文也考虑到人体健康的问题. 室内外温差太大, 会使人进出时气温骤变, 容易患病感冒, 因此室内外温差不易太大, 一般在5–10 ℃为宜.
为了更直观地表示在不同温度下的人体感觉, 本文在一定温度范围内设定人体感觉的程度, 该程度可由0.0到1.0来划分(0.0表示一定不, 1.0表示一定), 人体感觉暂分为寒冷(cold)、凉爽(cool)、舒适(OK)、温暖(warm)和炎热(hot) 5种, 环境温度的隶属度函数如图3所示.

|
图 3 温度隶属度函数 |
空调通风口尺寸是模糊控制的输出参数, 与环境温度一样需要进行模糊化处理. 假设一个空调的通风口完全打开时尺寸为长500 mm×宽300 mm, 如果把空调通风口当作标准矩形来处理, 那么空调通风口在变化状态下, 通风口的长度保持不变, 只有通风口的宽度在变化, 所以本文以通风口的宽度变化来描述通风口尺寸的变化. 本文把通风口开合程度分为完全开放(all)、大部分开放(almost)、半开放(half) 3种状态. 如表1所示.
| 表 1 通风口尺寸定义(mm) |
通风口尺寸的隶属度函数如图4所示.

|
图 4 通风口尺寸隶属函数 |
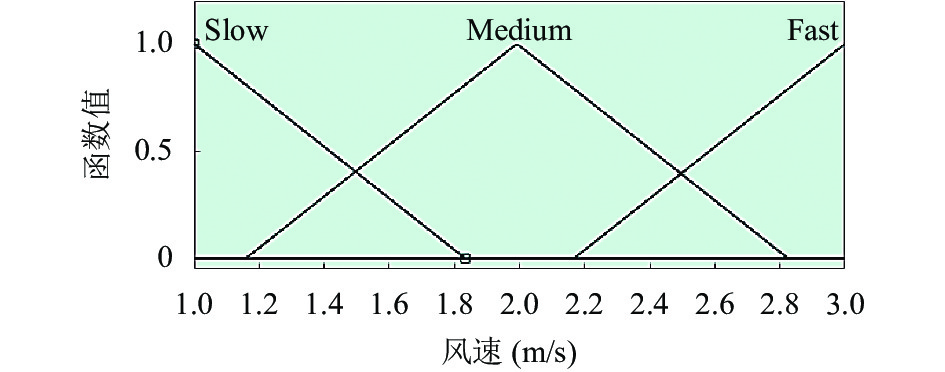
空调风速是模糊控制的另一个输出参数, 同样需要进行模糊化处理. 经调查, 家用空调的出风速度为1–3 m/s. 本文将空调风速分为快速(fast)、中等(medium)、慢速(slow) 3种状态, 如表2所示.
| 表 2 空调风速定义(mm) |
空调风速的隶属度函数如图5所示.
|
图 5 空调风速隶属函数 |
3.3 模糊规则库构建
将精确参数模糊化后要构建一组规则存放在模糊规则库中, 模糊规则采用“If A Then B”的形式, 可表示为:

|
图 6 模糊规则 |
3.4 模糊推理
模糊推理主要是将模糊集根据模糊规则进行推理运算. 首先将模糊化后的输入变量按照模糊规则通过运算进行近似推理得到单规则推理结果, 然后将各推理结果叠加得到最终推理结果. 常见的模糊推理模型有Tsukamoto模型、Mamdani模型和TSK模型, 本文利用Mamdani模型对空调控制系统进行模糊推理, 将在第5.1节中详细阐述. 推理规则的运算选择与模糊算子的确定有一定的联系, 目前世界上多数使用最大最小法和最大乘积法等算法[19], 模糊推理规则表达式形式如下:
| $ {K_i}\xrightarrow{{{Y_1}\left( {{\omega _{i1}}} \right){Y_2}\left( {{\omega _{i2}}} \right)\cdots{Y_m}\left( {{\omega _{im}}} \right)}}Z\left( \lambda \right), {\text{ }}i = 1, 2, \cdots, m $ | (8) |
其中,
| $ {R^1}:{\rm{If}}{\text{ }}{x_1}{\text{ }}{\rm{is}}{\text{ }}{{{A}}_1}{\text{ }}{\rm{Then}}{\text{ }}{y_1}{\text{ }}{\rm{is}}{\text{ }}{C^1} $ | (9) |
| $ {R^2}:{\rm{If}}{\text{ }}{x_1}{\text{ }}{\rm{is}}{\text{ }}{{{A}}_2}{\text{ }}{\rm{Then}}{\text{ }}{y_2}{\text{ }}{\rm{is}}{\text{ }}{C^2} $ | (10) |
输入变量模糊化后得到
去模糊化是将模糊推理结果通过运算得到精确输出结果的过程. 去模糊化的方法主要有重心法、面积中心法、均值最大法等, 本文提出的控制系统采用重心法来对模糊推理结果进行去模糊化, 重心法公式如下:
| $ {y'} = \frac{{\int {y\mu \left( y \right)dy} }}{{\int {\mu \left( y \right)dy} }} $ | (11) |
本部分主要利用Java的FuzzyJ Toolkit第三方工具包[20]对基于模糊推理的空调智能控制系统进行了模拟实现, 该工具包是在Jess专家系统的基础上, 将Java代码和Jess专家系统融合到一起的模糊推理工具, 利用前向规则快速匹配Rete算法, 推理效率高. 首先, 本文规定温度输入的范围为–10 ℃到40 ℃, 这是根据我国空调使用率高的地区的年温度范围而制定的, 符合大多数人对环境温度的要求. 其次, 将不同环境温度下人体感受分为cold、OK、hot三类, 将通风口尺寸分为all、almost、half三类, 将空调风速分为fast、medium、slow三类, 使用三角隶属度函数公式将精确的温度参数模糊化. 然后, 利用If…Then原则构建相应的模糊规则库, 部分模糊规则库示例如表3所示.
| 表 3 空调控制系统部分模糊规则库 |
最后, 将输入的环境温度与建立的模糊规则库进行匹配得到模糊集合, 模糊集合经过去模糊化得到精确的空调控制指令. 本系统将模糊推理结果利用窗口界面进行了输出, 部分输出结果如表4所示.
| 表 4 部分输出结果 |
通过输出结果可以直观地看到, 基于模糊推理的空调智能控制系统在输入温度参数从零下10 ℃到40 ℃的过程中, 冷空气阀门先关闭后开启, 热空气阀门先开启后关闭, 通风口尺寸经历了由大到小再变大的过程, 空调风速经历了由快变慢再变快的过程. 注意到本系统设置通风口尺寸最小为100 cm2, 这是因为在现实生活中通风口完全关闭则空调将停止运行, 在某一温度下用户只需要冷热阀门同时关闭但并不希望空调完全关闭, 而且通风口由关闭到打开的过程会增加空调控制器的控制时间, 造成控制不精确和能源消耗大的问题, 因此本系统不设置空调通风口完全关闭的情况. 另外, 由输出结果可以看到, 冷热阀门的开启和关闭情况属于布尔类型, 也就是说冷热阀门只有开启和关闭两种状态, 从这一点无法体现出模糊推理控制系统的精确度. 但是, 在通风口尺寸一列, 温度每发生变化, 通风口尺寸就会相应地发生变化, 这些变化幅度不大而且每一条控制指令的通风口尺寸都精确到小数点7位以后(温度为20 ℃时除外), 这就体现出该系统对温度参数精确的调节.
同时, 考虑到不同个体对温度的感官差异大, 只是依赖通风口尺寸的控制显然不够严谨, 因此我们在系统中引入空调风速这一输出参量. 当环境温度低, 让人体感受到寒冷, 空调的通风口尺寸变大的同时空调风速会加快. 而环境温度使人感觉舒适时, 空调通风口尺寸变小同时空调风速会减慢. 从输出结果中可看出, 空调风速的变化精确到小数点后两位, 同时随环境温度的改变空调风速的变化幅度相对平稳, 空调通风口尺寸与空调风速的结合, 可以成功解决传统空调控制算法参数调节困难, 调节效果差以及非线性、滞后性、突变性等问题, 很好地改善空调控制效果.
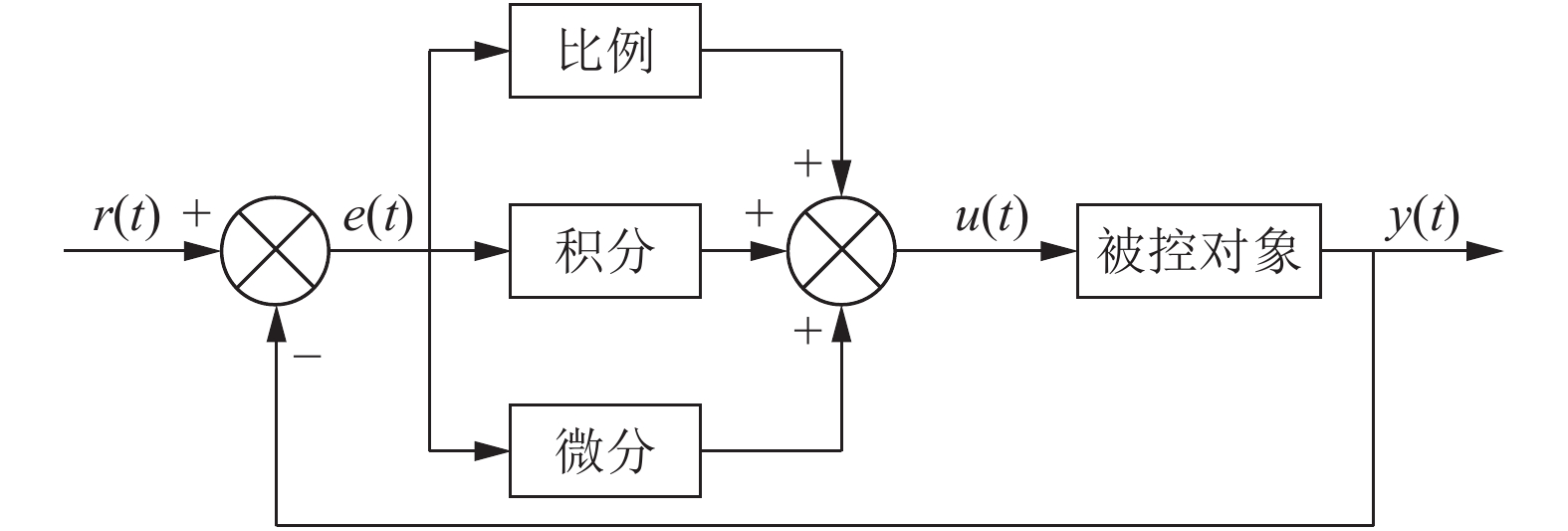
4.2 模糊控制与PID控制对比 4.2.1 PID算法介绍PID算法是集比例(proportion)、积分(integral)、微分(differential) 3部分于一体的控制算法, PID控制的实质就是根据输入的偏差值, 按照比例、积分、微分的函数关系进行运算, 运算结果用以控制输出[21]. PID控制分为位置型控制算法和增量型控制算法, 其中位置型控制算法公式为:
| $ \mu \left( k \right) = {K_p}e\left( k \right) + {K_i}\sum\limits_{j = 0}^k {{e_j} + {K_d}\left( {{e_k} - {e_{k - 1}}} \right)} $ | (12) |
增量型控制算法公式为:
| $ \Delta {\mu _k} = {\mu _k} - {\mu _{k - 1}} = {K_p}\left( {{e_k} - {e_{k - 1}} + \frac{T}{{{T_1}}}{e_k} + {T_d}\frac{{{e_k} - 2{e_{k - 1}} - {e_{k - 2}}}}{T}} \right) $ | (13) |
其中,
本部分将PID算法在对空调通风口的控制这一角度进行了简单实现并与模糊控制算法进行对比. 设定参数
|
图 7 PID控制流程 |
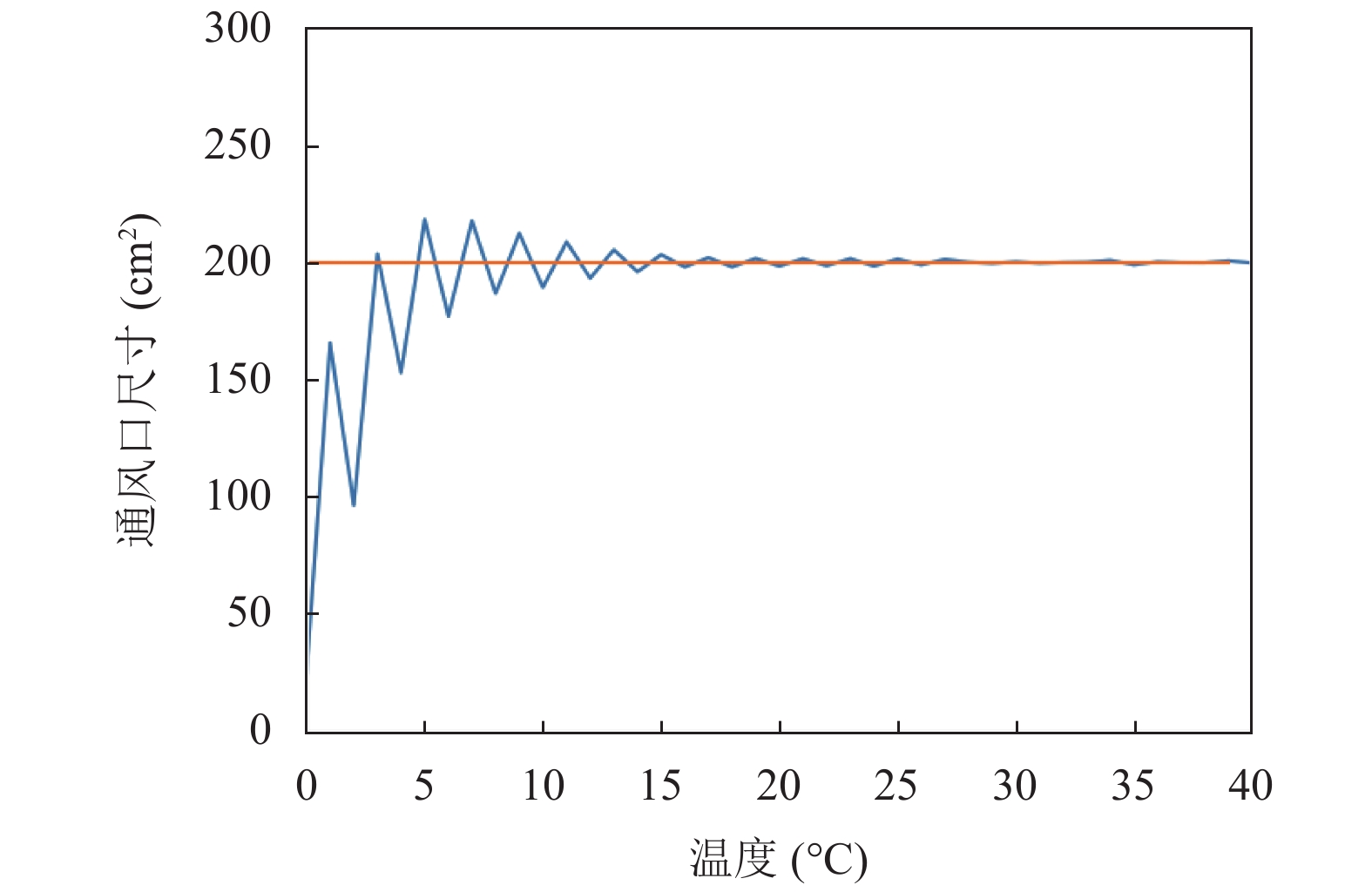
|
图 8 PID控制输出结果 |
据图8可发现, 当温度从0 ℃增加到40 ℃, PID控制的通风口尺寸由小迅速变大再减小, 最后逐渐稳定到200 cm2, 这说明PID控制在前期温度发生小幅度改变时通风口尺寸变化幅度过大, 而到后期温度上升幅度较大时通风口尺寸的变化幅度几乎忽略不计. 将PID控制结果与本文实现的模糊控制结果进行对比, 为了更直观地观察到两种控制算法在0–40 ℃对通风口尺寸的控制变化, 本文将两组数据制成折线图, 如图9所示.
由图9不难发现, PID算法在0–40 ℃变化过程中对通风口尺寸的控制是先在短时间内迅速将通风口开放至某一尺寸, 然后在该尺寸上来回波动, 但波动幅度很小. 环境温度在0–40 ℃的过程中, 人体感受大约会经历寒冷、凉爽、舒适、温暖、炎热5个阶段, PID算法所控制的通风口尺寸在5 ℃左右达到最大值, 突变性会迅速改变环境温度, 给人体感官造成不适. 随着温度升高, 通风口尺寸几乎未发生变化, 空调只是机械地感应环境温度, 通过出冷热风来使环境温度符合设定的温度. 在这个过程中, 空调控制系统并不关心人体感受, 所以PID控制算法对空调的控制与人体感受无实质关联.

|
图 9 PID与模糊推理对比 |
模糊推理算法则是感知环境温度后, 将环境温度参数模糊化为人体感受, 比如寒冷、舒适、炎热等, 依据已建立的模糊规则库, 来调节通风口尺寸. 要注意的是, 模糊推理算法持续感知环境温度, 并不断重复模糊化、模糊推理、去模糊化的步骤, 使空调通风口尺寸一直处于动态变化的过程中, 如此, 模糊控制的空调控制系统会将环境温度适中控制在使人体感觉为舒适的程度.
除了通风口尺寸外, 本文还引入了空调风速作为另一个输出参量, 在本部分实验验证中并未涉及该参量, 仅用通风口尺寸这一输出参量对PID算法和模糊推理算法进行了简单对比. 通过对比可得, 模糊推理算法在对空调控制上可以解决PID控制参数调节不精确, 控制效果不佳, 大滞后性等问题, 控制效果明显优于PID算法.
5 模糊控制系统实现 5.1 Mamdani模型实现本文利用Matlab的模糊逻辑工具箱[22]对空调控制系统进行了模糊推理过程的实现. 首先, 定义环境温度数值为输入变量, 冷阀门开关、热阀门开关及通风口尺寸为输出变量, 设定环境温度的论域范围为
最后选择重心法进行去模糊化, 得到推理结果如图11所示.

|
图 10 模糊规则库 |

|
图 11 模糊推理结果 |
从图11可以观察出, 当环境温度为0 ℃时, 冷阀门推理结果为0.33, 认为冷阀门处于关闭状态, ; 热阀门推理结果为0.67, 认为热阀门处于开启状态; 通风口尺寸推理结果为151, 属于大部分开放状态; 空调风速为2.05, 属于中速状态. 在Input栏内输入准确温度即可得到对应的推理结果.
5.2 FuzzyJ Toolkit可视化基于模糊推理的空调智能控制系统已利用Matlab的Mamdani模型和Java的FuzzyJ Toolkit第三方包进行了模拟实现, 具体内容已在第5.1节和第4节中详细阐述. 本章将在原有模拟控制系统的基础上对该控制系统进行可视化, 利用Java进行GUI界面的编写, 实现系统的可视化交互. 本章分为用户管理、温度输入、温度监测3部分.
5.2.1 用户管理本系统与MySQL数据库相连接, 对登录系统的用户进行管理. 用户名和密码均由管理员设置并发送给用户, 用户在登录界面输入正确的用户名和密码进入系统主界面.
5.2.2 温度输入温度输入功能是本系统的核心功能, 主要操作流程为:
1) 点击“温度输入”按钮, 进入温度输入界面.
2) 在温度输入框内输入
3) 点击再次计算按钮回到温度输入界面继续输入温度, 点击“关闭页面”按钮即可关闭当前页面.
本模块通过输入某一范围内的温度数值, 可以得到该温度下空调冷热阀门状态, 通风口的精确尺寸及空调风速.
5.2.3 温度监测温度监测功能的目的是记录某天温度的变化及系统对空调控制器控制方案的变化, 用户输入目标日期后点击“温度数据”或“控制器响应数据”即可分别通过折线图和导出csv文件的方式获得该日的温度或控制器数据信息. 温度监测功能的主要作用是为了帮助管理员随时获取某日的温度及控制器数据信息, 检查系统是否出现问题以便及时维修.
6 结论与展望目前, 空调成为家居工作必不可少的一部分, 传统的PID控制算法存在参数调节不精准, 突变性等问题, 而使用模糊推理算法对空调进行控制则可以很好地解决PID算法的缺点, 并且模糊推理算法更加智能化, 更符合当代人的需要, 为此, 本文提出了一种基于模糊推理的空调智能控制机制, 与传统控制算法进行实验对比后, 得出模糊控制效果明显优于传统控制算法.
目前, 有很多研究提出复合式控制算法, 这些算法经仿真实验验证的确对空调控制性能有较好的改善. 但是这些复合式算法无论从成本还是技术成熟性角度都不适合进行大规模工业生产. 而模糊推理算法技术已相对成熟, 对空调的控制效果明显优于传统的PID算法的控制效果, 适合进行大规模工业空调的生产, 所以这必将成为空调控制领域的一个热点研究.
基于模糊推理的空调智能控制系统尚有几点不足之处:
1) 对温度参数进行定义时, 不同年龄、不同地域、不同生活习惯的人群对温度带来的人体感觉不同.
2) 本文实现的模拟控制系统的模糊规则库内的规则简单化, 不符合自然界复杂多变的环境变化.
针对以上问题, 提出改进方法:
1) 按照年龄、地域等类别收集更多的人群信息, 将温度参数定义尽可能详细化, 同时可让用户自主选择此时的身体感受, 通过空调遥控装置向控制系统发送信号, 使控制效果更加理想.
2) 不断丰富和更新规则库内的规则, 适应自然界复杂多变的环境变化, 使空调能更精确地控制环境温度.
下一步的研究将重点关注模糊推理与其他机器学习算法相结合, 并将其应用到空调智能控制领域, 力求提高空调控制的精准性、有效减少空调控制能耗.
| [1] |
黄志远, 徐象国, 邵俊强. 家用空调节能控制算法综述. 家电科技, 2019(05): 58-61+89. |
| [2] |
文丹. 基于迭代优化的空调温湿度控制算法. 现代电子技术, 2020, 43(24): 38-41. |
| [3] |
于军琪, 张瑞, 赵安军, 钱薛艮, 刘奇特. 中央空调系统并联水泵节能优化群智能控制算法. 控制理论与应用, 2020, 37(10): 2155-2162. DOI:10.7641/CTA.2020.90543 |
| [4] |
王彦, 刘宏立, 王超. 中央空调系统中自适应Smith预估补偿器的研究. 计算机应用研究, 2011, 28(01): 58-60+71. DOI:10.3969/j.issn.1001-3695.2011.01.014 |
| [5] |
Zadeh LA. Fuzzy sets. Information & Control, 1965, 8(3): 338-353. |
| [6] |
Zadeh LA. Outline of a New Approach to the Analysis of Complex Systems and Decision Processes. IEEE Transactions on Systems, Man and Cybernetics. 1973, SMC-3(1): 28–44.
|
| [7] |
Mamdani E. Applications of fuzzy algorithm for control of a simple dynamic plant. Proceedings of IEEE, 1974, 121. |
| [8] |
Kiszka JB, Kochańska ME, Sliwińska DS. The influence of some fuzzy implication operators on the accuracy of a fuzzy model—Part I. Fuzzy Sets & Systems, 1985, 15(3): 223-240. |
| [9] |
Dubois D, Prade H. The treatment of uncertainty in knowledge-based systems using fuzzy sets and possibility theory. International Journal of Intelligent Systems, 2010, 3(2): 141-165. |
| [10] |
白云飞, 张翔, 林建. 基于改进的形态学二次重建蜜蜂蜂王模糊识别方法. 计算机应用与软件, 2020, 37(11): 139-145. DOI:10.3969/j.issn.1000-386x.2020.11.024 |
| [11] |
孙博. 基于模糊推理的雷达机动目标跟踪[博士学位论文]. 大连: 大连海事大学, 2020.
|
| [12] |
梁娟, 赵开新, 陈伟. 自适应神经模糊推理结合PID控制的并联机器人控制方法. 计算机应用研究, 2016, 33(12): 3586-3590. DOI:10.3969/j.issn.1001-3695.2016.12.016 |
| [13] |
袁小平, 金鹏, 周国鹏. 基于改进QPSO算法的电动汽车模糊控制器参数优化. 计算机应用研究, 2019, 36(12): 3690-3696. |
| [14] |
陈果, 刘金根, 韩世鹏. 基于导管机器人的变论域模糊PID控制研究. 计算机应用研究, 2018, 35(2): 471-474, 482. DOI:10.3969/j.issn.1001-3695.2018.02.032 |
| [15] |
赵巍, 李房云. 基于预估模糊PID的冰蓄冷空调控制系统. 现代电子技术, 2019, 42(20): 26-28, 32. |
| [16] |
朱如春. 基于模糊神经网络算法智能变频空调控制系统的研究[博士学位论文]. 苏州: 苏州大学, 2007.
|
| [17] |
徐今强, 冯自平. 变频多联机空调模糊逻辑控制及仿真研究. 计算机应用研究, 2008, 25(10): 3155-3157. DOI:10.3969/j.issn.1001-3695.2008.10.082 |
| [18] |
裴道武. 关于模糊逻辑与模糊推理逻辑基础问题的十年研究综述. 工程数学学报, 2004, 21(2): 249-258. DOI:10.3969/j.issn.1005-3085.2004.02.020 |
| [19] |
Garibaldi JM, 陈虹宇, 李小双. 差异与学习: 模糊系统与模糊推理. 智能科学与技术学报, 2019, 1(4): 319-326. |
| [20] |
Orchard R. Fuzzy reasoning in Jess: The fuzzyj toolkit and fuzzyjess. Proceedings of the ICEIS 2001. Setubal: National Research Council of Canada, 2001. 533–542.
|
| [21] |
张烨. 大空间中央空调PID控制算法. 南京师范大学学报(工程技术版), 2007, 7(2): 37-40. |
| [22] |
祝杨菲. 基于模糊推理系统的浙江省滑坡灾害地图制图综合研究[博士学位论文]. 金华: 浙江师范大学, 2019.
|
 2022, Vol. 31
2022, Vol. 31



