频谱感知作为认知无线电的关键技术 (cognitive radio, CR)是解决频谱资源匮乏和授权频段利用率低下这一矛盾最有潜力的通信技术之一[1, 2]. 无线通信信号的统计特性一般呈现周期性变化, 具有循环平稳特征, 而噪声作为随机变量不具备该特征. 本文正是通过分析授权用户信号的循环平稳特征来判断授权用户是否存在, 该方法稳健性高, 能有效减少噪声对检测性能带来的影响.
授权用户信号具有分布在多个循环频率上的多个循环平稳特征, 由于受阴影衰落影响, 采用单一循环频率检测不足以充分利用信号的多循环平稳特征; 同时单认知用户的检测不足以克服信道衰落, 隐藏终端等不利因素对检测性能带来的影响. 文献[3]改进了一种基于主用户随机到达的循环平稳检测方法, 该方法是通过将检测周期内后半部分瞬时采样值累加到前半部分来提高检测性能, 但该算法存在虚警概率偏高的缺点; 文献[4]提出了一种基于多个循环频率的联合循环谱感知方法, 较单个循环频率检测提高了检测性能; 文献[5]研究了一种基于循环平稳的能量检测法, 该方法利用某一循环频率截面的能量来检测信号, 但没有充分利用信号的多循环平稳特征, 也没有考虑各认知节点处判决结果的可信度.
针对现有问题, 本文提出了一种基于无线环境图信息辅助的频谱检测方法. 无线环境图可以看作是对复杂无线环境的一种数字化抽象, 能够反应信道参数、无线信号、网络拓扑等多维无线环境信息, 其根本目的是为认知无线电设备和网络提供全面的信息支持[6]. REM所包含的信息有: 地理位置分布; 必须遵循的频谱监管制度; 频谱机会; 合适的信道模型; 阴影衰落分布以及干扰源等; REM获取无线环境信息主要依赖于:位置意识、地理环境意识、射频环境意识、移动和跟踪意识、政策意识、功能意识等[7, 8].
本文正是利用REM提供的授权与认知用户之间的位置信息计算各认知用户处的权值, 通过加权融合来提高检测结果的可信度. 第1步在多个认知用户处分别选取多个相同的循环频率进行循环平稳检测, 通过比较不同循环频率处谱相关函数幅值与门限值的大小来判断授权用户是否存在, 通过判决融合得到各认知用户处的检测结果; 第2步采用集中式协作检测[9], 将各认知用户处的检测结果与根据授权用户发射台和认知用户之间的位置信息计算的各节点处权值进行加权融合, 从而得到最终检测结果. 联合多个循环频率参与检测的难点和挑战在于如何确定具体参与检测的循环频率, 根据信号谱相关理论可知循环频率在二倍载波频率处具有较强的循环平稳特征, 因此可以选择此处的循环频率参与检测, 本文则是通过计算接收信号的循环谱, 选取二倍载波频率处循环谱值较高的多个循环频率参与检测来改善检测性能.
1 基于谱相关的频谱检测原理 1.1 通信信号的谱相关特性常用通信信号的调制方式主要包括有BPSK, QPSK, QAM等, 因受调制、编码、采样等处理使信号具备了一定的统计特性. 当某一通信信号的均值和自相关函数均存在周期性, 且周期性与信号的周期一致, 则称信号
| $ {R_x}\left( \tau \right) = \sum\limits_{\alpha \in \Omega } {R_x^\alpha \left( \tau \right)} {{\rm{e}}^{j2\pi {{ }}x{{ }}t}} $ | (1) |
其中, 傅里叶系数
| $ {R}_{x}^{\alpha }\left(\tau \right)=\frac{1}{T}\displaystyle {\int_{ - \frac{T}{2}}^{\frac{T}{2}}{R}_{x}}\left(t+\frac{\tau }{2}\text{, }t-\frac{\tau }{2}\right){\rm{e}}^{-j2\pi \alpha {}t}dt $ | (2) |
把循环自相关函数的傅里叶变换定义为谱相关函数, 对
| $ S_x^\alpha \left( f \right) = \frac{1}{T}\int_{ - \frac{T}{2}}^{\frac{T}{2}} {R_x^\alpha \left( \tau \right)} {{\rm{e}}^{ - j2\pi {{ }}f{{ }}\tau }}d\tau $ | (3) |
频谱感知的主要目的是在保证授权用户正常通信的前提下, 实现对频谱空洞快速准确的检测. 通常频谱感知问题被建模成一个二元假设检测问题:
| $ y\left( t \right) = \left\{ \begin{gathered} n\left( t \right),{\text{ }}{{{{H}}}_{{\text{ 0}}}}{\text{ }} \hfill \\ \omega {\text{ }}x\left( t \right) + n\left( t \right),{\text{ }}{{{{H}}}_{{\text{ 1}}}}{\text{ }} \hfill \\ \end{gathered} \right. $ | (4) |
其中,
噪声作为随机变量, 在处理过程中不会出现周期性变化, 因此就不具备循环平稳特征, 所以通过检测信号是否具备循环平稳特征, 就可以有效区分噪声和信号. 假设信号与噪声相互独立, 对式(4)应用循环平稳特征检测, 可得式(5)所示的频谱检测模型:
| $ S_y^\alpha \left( f \right) = \left\{ \begin{gathered} S_n^0\left( f \right),\;\;\;\;\;\;\; \;\;\;\;\;\;\; \;\;\;\;\;\;\; \;\;\;\;\;\;\; \;\;\;\;\;\;\; \;\;\;\;\;\alpha = {\text{0 }}, {{{H}}_{\text{0}}} \hfill \\ {\left| {H\left( f \right)} \right|^2}S_x^0\left( f \right) + S_n^0\left( f \right),\;\;\;\;\;\;\;\;\;\;\;\;\alpha = {\text{0 }},{{{H}}_{\text{1}}} \hfill \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\; \;\;\;\;\;\;\; \;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\; \alpha \ne {\text{0 }},{{{H}}_{\text{0}}} \hfill \\ H\left( {f + \frac{\alpha }{2}} \right){H^*}\left( {f - \frac{\alpha }{2}} \right)S_x^\alpha \left( f \right),\;\,\,\alpha \ne {\text{0 }},{{{H}}_{\text{1}}} \hfill \\ \end{gathered} \right. $ | (5) |
式中,
分析式(5)可知, 通过判断
| $ \left\{ {\begin{array}{l}|{S}_{y}^{\alpha }\left(f\right)| \gt \lambda \text{, }{{H}}_{\text{1}}\\ |{S}_{y}^{\alpha }\left(f\right)|\leqslant \lambda \text{, }{{H}}_{\text{0}}\end{array} } \right.$ | (6) |
其中,
对认知用户接收的信号进行采样得到离散信号
| $ S_y^\alpha \left( f \right) = \frac{1}{{MN}}\sum\limits_{m = 1}^M {Y_m\left( {f + \alpha } \right)} {Y_m^*}\left( {f - \alpha } \right) $ | (7) |
其中,
当接收信号中只含有噪声时, 式(7)可表示为:
| $ S_n^\alpha \left( f \right) = \frac{1}{{MN}}\sum\limits_{m = 1}^M {} W_m\left( {f + \alpha } \right){W_m^*}\left( {f - \alpha } \right) $ | (8) |
其中,
| $ E\left[ {S_n^\alpha \left( f \right)} \right] = \frac{1}{{MN}}\sum\limits_{m = 1}^M {E\left[ {W_m\left( {f + \alpha } \right){W_m^*}\left( {f - \alpha } \right)} \right]} $ | (9) |
令
| $ \begin{split} & E\left[{Z}^{\alpha }\left(\alpha \right){\left({Z}^{\alpha }\left(\alpha \right)\right)}^{*}\right]\\ &=E\left[W\left(\alpha \right){W}^{*}\left(-\alpha \right){W}^{*}\left(\alpha \right)W\left(-\alpha \right)\right]\\ &=E\left[{W}\left(\alpha \right){W}^{*}\left(-\alpha \right)\right]E\left[{W}^{*}\left(\alpha \right)W\left(-\alpha \right)\right]\\ &\quad +E\left[W\left(\alpha \right){W}^{*}\left(\alpha \right)\right]E\left[{W}^{*}\left(-\alpha \right)W\left(-\alpha \right)\right]\\ &\quad +E\left[{W}\left(\alpha\right) {W}\left(-\alpha \right)\right]E\left[{{W}}^{\text{*}}\left(-\alpha \right){W}^{*}\left(\alpha \right)\right]\\ &=\left\{ {\begin{array}{l}\text{2}{\sigma }^{\text{4}}{N}^{2}{\left(1-\dfrac{\left|m-n\right|}{p}\right)}^{2}{\rm{e}}^{j4\pi \alpha \left(m-n\right)/p},\left|{m-n}\right|\leqslant p-1\\ \text{0},\left|{m-n}\right|\geqslant p\end{array}} \right.\end{split} $ | (10) |
其中,
| $ \begin{split} & {V_{s1}} = Var\left( {S_n^\alpha \left( 0 \right)} \right) \\ & \;\;\;\;\;\;= \frac{{2{\sigma ^4}}}{{{M^2}}}\left[ {M + \sum\limits_{i = 1}^{p - 1} {2\left( {M - i} \right){{\left( {1 - \frac{i}{p}} \right)}^2}\cos \left( {{{4i\pi \alpha } \mathord{\left/ {\vphantom {{4i\pi \alpha } p}} \right. } p}} \right)} } \right] \end{split} $ | (11) |
可以证明
当
| $ \begin{split} {V_{s2}} &= Var\left( {S_n^\alpha \left( f \right)} \right) \\ & = \frac{{{\sigma ^4}}}{{{M^2}}}\left[ {M + \sum\limits_{i = 1}^{p - 1} {2\left( {M - i} \right){{\left( {1 - \frac{i}{p}} \right)}^2}\cos \left( {{{4i\pi \alpha } \mathord{\left/ {\vphantom {{4i\pi \alpha } p}} \right. } p}} \right)} } \right] \\ \end{split} $ | (12) |
| $ {p_s}\left( r \right) = \frac{r}{{\sigma _s^2}}{{\rm{e}}^{{{ - r} \mathord{\left/ {\vphantom {{ - r} {2\sigma _s^2}}} \right. } {2\sigma _s^2}}}} , {r \geqslant 0} $ | (13) |
其中,
| $ \lambda = \sqrt {2\sigma _s^2\ln \left( {\frac{1}{{{p_f}}}} \right)} $ | (14) |
给定噪声功率和虚警概率, 根据式(14)可以得到循环平稳特征检测的判决门限值.
2 信息辅助的协作频谱感知 2.1 多循环频率信息融合本文方法的第一步为: 各认知用户在接收信号
| $ {{P}}_d^j = 1 - \prod\limits_{i = 1}^n {(1 - } {P_{di}}) $ | (15) |
图1为多循环频率检测融合框图, 式(15)中
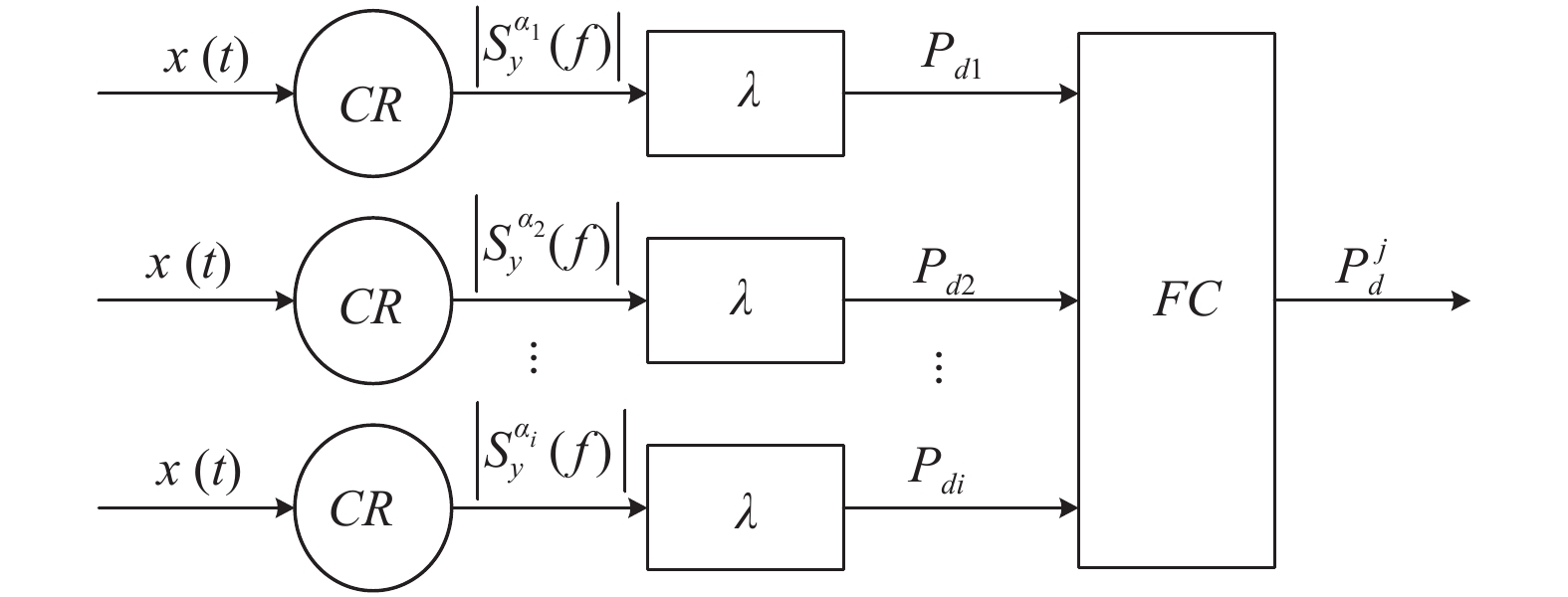
|
图 1 多循环频率检测融合框图 |
2.2 多认知用户协作加权融合
本文方法的第2步为: 将各认知用户处的检测结果与对应的权值进行加权融合, 得出最终的检测结果. 权值根据无线环境图提供的授权用户与认知用户之间的位置信息计算得出. 在协作检测中, 各认知用户分布在不同的空间位置上, 因此各认知用户所处的无线环境也略有差异, 这就导致各认知用户所做判决对最终检测结果的影响也不相同. 在理论分析中通常会选取认知节点处授权用户信号的信噪比作为影响度因子, 但在实际应用中很难获取. 实际通信中, 在不考虑多径和衰落的前提下, 认知节点处接收信号的信噪比与收发双方之间的距离成负相关, 认知用户与授权用户之间的距离越近其信噪比越高, 可靠性也就越高.
本文考虑实际应用场景, 假设认知用户能接收到授权用户信号且位置均固定, 认知无线网络利用认知用户和授权用户之间的位置分布构建一个REM, REM中包含有授权用户与认知用户之间的位置信息, 利用该位置信息能计算出授权用户到认知节点的距离. 因此可利用REM提供的授权用户与认知用户的距离信息作为认知节点处的权值, 二者之间的距离越小权重越大, 距离越大权重越小. 定义权重值[11]为:
| $ {P_d} = 1 - \prod\limits_{j = 1}^n {{W_{lj}}(1 - } P_d^j) $ | (16) |
其中,

|
图 2 多认知用户协作加权融合框图 |
2.3 位置信息辅助的频谱检测流程
基于循环谱的多循环频率加权协作频谱感知步骤总体分为3步, 如图3所示.
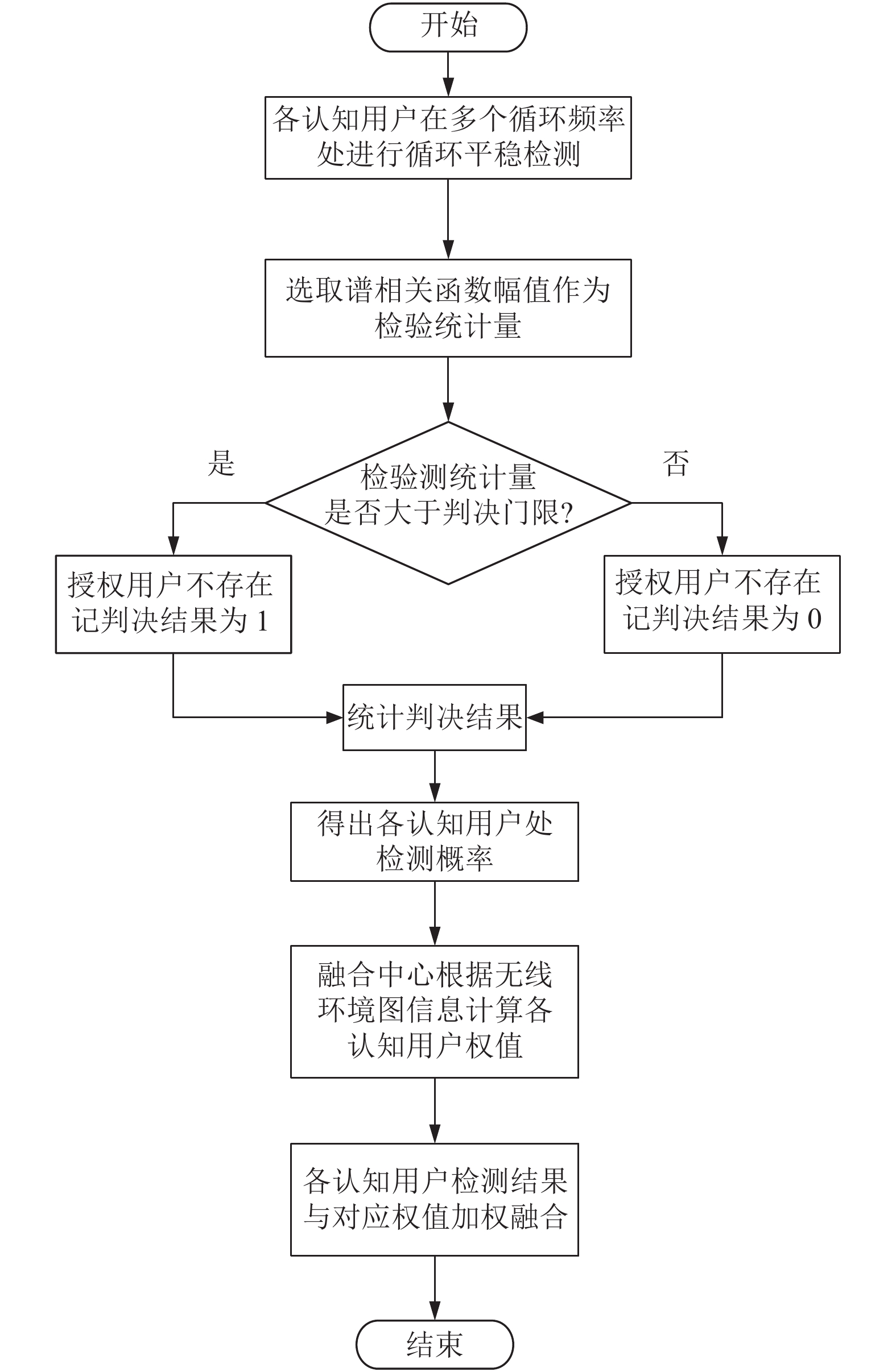
|
图 3 信息辅助的加权协作频谱感知流程图 |
步骤1. 各认知用户在不同循环频率处计算相应的谱相关函数幅值
步骤2. 根据REM储存的授权用户与认知用户之间的距离计算各认知用户的权重值
步骤3. 将各认知用户的检测结果乘以权值
构建蒙特卡洛仿真模型, 假设授权用户调制方式为
图5所示为
图6为在
由图6可知, 就整体检测性能而言, 联合循环频率数越多其检测性能越好. 在同一虚警概率条件下, 5个循环频率的联合检测性能优于3个循环频率的联合检测和单循环频率检测. 联合检测的循环频率个数越多, 检测概率越快达到1. 在频谱感知中为保证授权用户的正常通信, 认知用户的虚警概率应满足小于等于0.1. 当虚警概率为0.1时, 5个循环频率联合检测比3个循环频率联合检测的检测概率大约提升了6.1%, 比单个循环频率检测概率大约提升了17.8%. 综上可知, 充分利用授权用户信号在不同循环频率处的多个循环平稳信息能有效改善检测性能, 在一定程度上提高了检测概率.

|
图 4 BPSK信号循环谱图 |

|
图 5 BPSK信号循环谱
|
图7为在
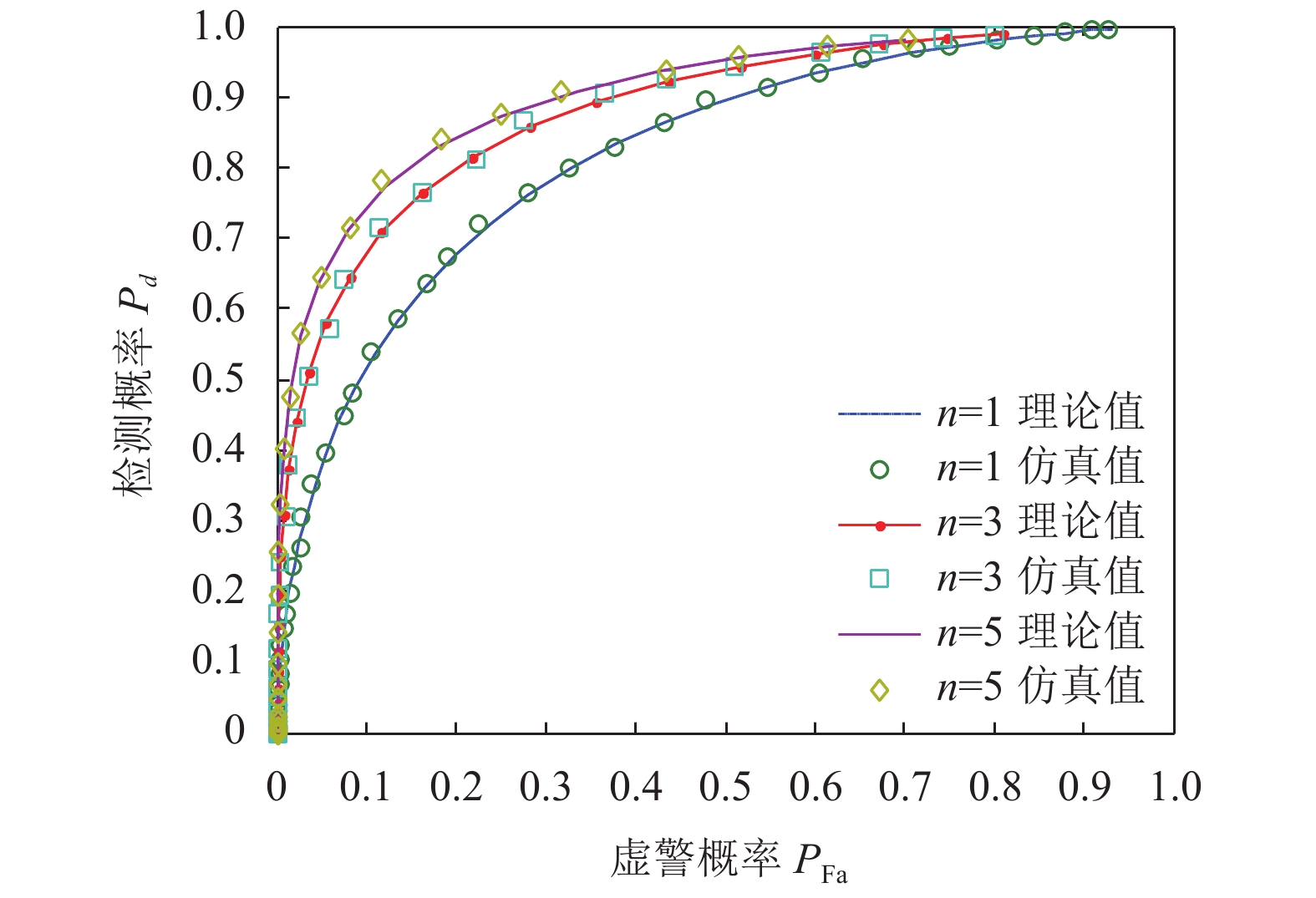
|
图 6 不同循环频率个数联合检测仿真图 |
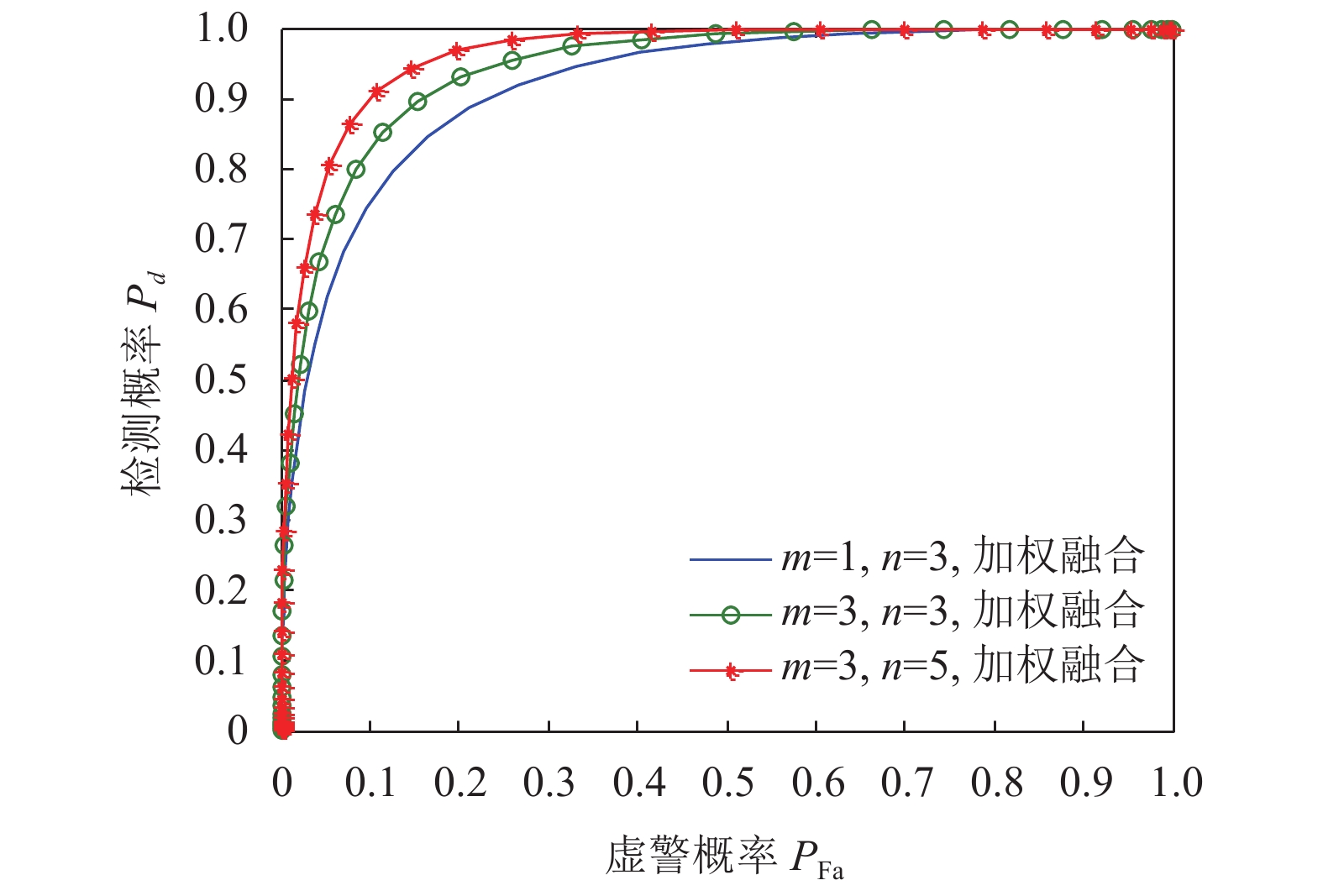
|
图 7 多循环频率协作加权融合检测性能 |
图8为在

|
图 8 两种检测方法的性能对比 |
4 结论
本文方法主要通过判断不同循环频率处谱相关函数幅值与门限值的大小来判断授权用户是否存在, 同时通过对信号多个循环平稳特征以及空间上多个授权信息的充分利用来提高检测概率, 考虑到各认知节点处实时信噪比难以获取的问题, 本文根据REM提供的认知用户与授权用户之间的距离信息来计算各认知节点的权值, 通过加权融合来进一步提高检测结果的可靠性. 仿真结果表明该检测方法在低信噪比环境下有着良好的检测性能, 同时不需要考虑认知用户自身信噪比信息, 更适用于实际通信中的频谱检测.
| [1] |
Zhou M, Wang TY, Wang SW. Spectrum sensing across multiple service providers: A discounted Thompson sampling method. IEEE Communications Letters, 2019, 23(12): 2402-2406. DOI:10.1109/LCOMM.2019.2941717 |
| [2] |
Jin M, Guo QH, Xi JT, et al. On spectrum sensing of OFDM signals at low SNR: New detectors and asymptotic performance. IEEE Transactions on Signal Processing, 2018, 65(12): 3218-3233. |
| [3] |
马彬, 方源, 谢显中. 一种主用户随机到达情况下改进的循环平稳特征检测算法. 电子与信息学报, 2017, 37(7): 1531-1537. |
| [4] |
张瑜, 马惠珠. 一种基于多个循环频率的联合循环谱感知方法. 应用科技, 2010, 37(2): 16-19. DOI:10.3969/j.issn.1009-671X.2010.02.005 |
| [5] |
Han DM, Liu H. An energy detection based on cyclostationary. 2011 7th International Conference on Wireless Communications, Networking and Mobile Computing. Wuhan: IEEE, 2011. 1–4.
|
| [6] |
Mao DL, Shao W, Qian ZP, et al. Constructing accurate radio environment maps with kriging interpolation in cognitive radio networks. 2018 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC). Xuzhou: IEEE, 2018. 1–3.
|
| [7] |
Zhao YP, Raymond D, Da Silva C, et al. Performance evaluation of radio environment map-enabled cognitive spectrum-sharing networks. MILCOM 2007-IEEE Military Communications Conference. Orlando: IEEE, 2007. 1–7.
|
| [8] |
Nuallain EO, Anderson C. Real-time radio environment mapping for cognitive radio. 2014 National Wireless Research Collaboration Symposium. Idaho Falls: IEEE, 2014. 64–68.
|
| [9] |
Kim J, Choi JP. Sensing coverage-based cooperative spectrum detection in cognitive radio networks. IEEE Sensors Journal, 2019, 19(13): 5325-5332. DOI:10.1109/JSEN.2019.2903408 |
| [10] |
包亚萍, 蒋利, 朱晓梅. 基于循环谱的多循环频率加权合作频谱检测. 数据采集与处理, 2012, 27(2): 248-253. DOI:10.3969/j.issn.1004-9037.2012.02.020 |
| [11] |
Chen Y, Zhang H, Hu H, et al. A new cooperative spectrum sensing with radio environment map in cognitive radio networks. Proceedings of 2015 International Conference on Intelligent Computing and Internet of Things. Harbin: IEEE, 2015. 40–43.
|
 2022, Vol. 31
2022, Vol. 31


