不同支配关系的NSGA-III算法在机器人制造单元调度问题中的应用

引用本文

李晓辉, 高铎, 杨晰, 刘元东, 赵毅, 董媛. 不同支配关系的NSGA-III算法在机器人制造单元调度问题中的应用. 计算机系统应用, 2022, 31(2): 279-284.http://www.c-s-a.org.cn/1003-3254/8336.html

Li XH, Gao D, Yang X, Liu YD, Zhao Y, Dong Y. Application of NSGA-III Algorithm Based on Different Dominance Relations in Robotic Cell Scheduling Problem. Computer Systems and Applications, 2022, 31(2): 279-284(in Chinese).http://www.c-s-a.org.cn/1003-3254/8336.html

不同支配关系的NSGA-III算法在机器人制造单元调度问题中的应用

李晓辉¹, 高铎¹, 杨晰², 刘元东¹, 赵毅¹, 董媛¹

1. 长安大学电子与控制工程学院, 西安 710054;
2. 陕西航天时代导航设备有限公司, 宝鸡 721099

收稿日期：2021-04-20; 修改日期：2021-05-28; 采用时间：2021-06-08; csa 在线出版时间：2022-01-17

基金项目：国家重点研发项目(2020YFB1600400)

通讯作者：董媛 yuandong@chd.edu.cn.

摘要：随着经济的发展, 机器人制造单元对制造行业的生产效率和生产质量有很大提高. 相对于传统的柔性制造单元, 带机器人搬运的车间的调度问题还考虑了加工物料的搬运环节. 因此, 生产调度所面临的问题越来越复杂. 针对Pareto支配关系在高维多目标优化中的支配能力不足, 本文将 Lorenz支配和CDAS支配分别与NSGA-III算法相结合, 并首次应用到带机器人制造单元的高维多目标车间调度问题上来. 考虑到现代生产过程的复杂化, 本文提出对最大完工时间、加工总能耗、交货期提前量、延迟量、生产总成本等多个目标同时进行优化, 用于确定机器人工作时操作状态和搬运顺序, 提高生产效率. 通过实验发现基于Lorenz支配和CDAS支配的NSGA-III算法在该生产调度问题上比传统的NSGA-III在解的收敛性和均匀性上表现更优.

关键词: NSGA-III 机器人制造单元调度高维多目标优化不同支配关系

Application of NSGA-III Algorithm Based on Different Dominance Relations in Robotic Cell Scheduling Problem

LI Xiao-Hui¹, GAO Duo¹, YANG Xi², LIU Yuan-Dong¹, ZHAO Yi¹, DONG Yuan¹

1. School of Electronics and Control Engineering, Chang’an University, Xi’an 710054, China;
2. Shaanxi Aerospace Times Navigation Equipment Co. Ltd., Baoji 721099, China

Abstract: With the development of economy, robotic of economy, robotic cells have greatly improved the production efficiency and quality of the manufacturing industry. Compared with that of the traditional flexible manufacturing cells, the scheduling problem of shops with robot handling also involves material handling. As a result, the production scheduling problem is becoming increasingly complex. In view of the lack of dominance of the Pareto dominance relation in high-dimensional multi-objective optimization, the Lorenz domination and CDAS domination are combined, respectively, with the non-dominated sorting genetic algorithm-III (NSGA-III) algorithm in this study and applied for the first time to the high-dimensional multi-objective scheduling of shops with robotic cells. Considering the complexity of modern production processes, this study proposes to optimize multiple objectives, such as maximum completion time, total processing energy consumption, delivery lead time, delivery delay time, and total production cost, at the same time to determine the operating state and handling sequence of the robot and improve production efficiency. Experiments show that on the abovementioned production scheduling problem, the NSGA-III algorithm based on Lorenz domination or CDAS domination performs better than the traditional NSGA-III algorithm in the solution convergence and uniformity.

Key words: NSGA-III robotic cell scheduling high-dimensional multi-objective optimization different dominance relations

由于机器人制造单元对制造行业的生产效率和生产质量有很大提高, 近30年来, 生产调度问题^[1]已成为国内外自动控制领域、计算机科学等领域的研究热点. 现代智能制造市场的需求越来越个性化、多样化, 使传统的量产模式受到了极大的挑战. 机器人制造单元在实现量产的同时, 能够保持小批量定制生产的灵活性, 能够更好地适应当前智能制造发展的需求, 而合理的优化调度是机器人制造单元整体控制的一个重要方面. 制造企业为了在激烈的竞争环境中生存和发展, 需要提供能够满足客户各种需求的资源调度方案. 单一目标的寻优已经满足不了人们日常生活的需要, 工业上对于优化目标个数增多的要求使得求解问题的难度显著增加. 目前, 调度问题的理论和实践方法研究, 仍不能满足现实生产需求. 传统的优化算法在解决复杂多目标问题中^[2-5]常常效率低下, 难以达到预期. 智能优化算法^[6-9]通常是基于非劣解概念基础上的现代启发式算法, 具有更好的处理高维多目标问题的能力. 因此, 在经典车间调整理论的基础上, 本文要针对Pareto支配关系在高维多目标优化中的支配能力不足, 将另外两种支配关系与NSGA-III算法相结合去对生产调度问题进行求解去解决机器人制造单元优化上的多目标协同调度优化问题.

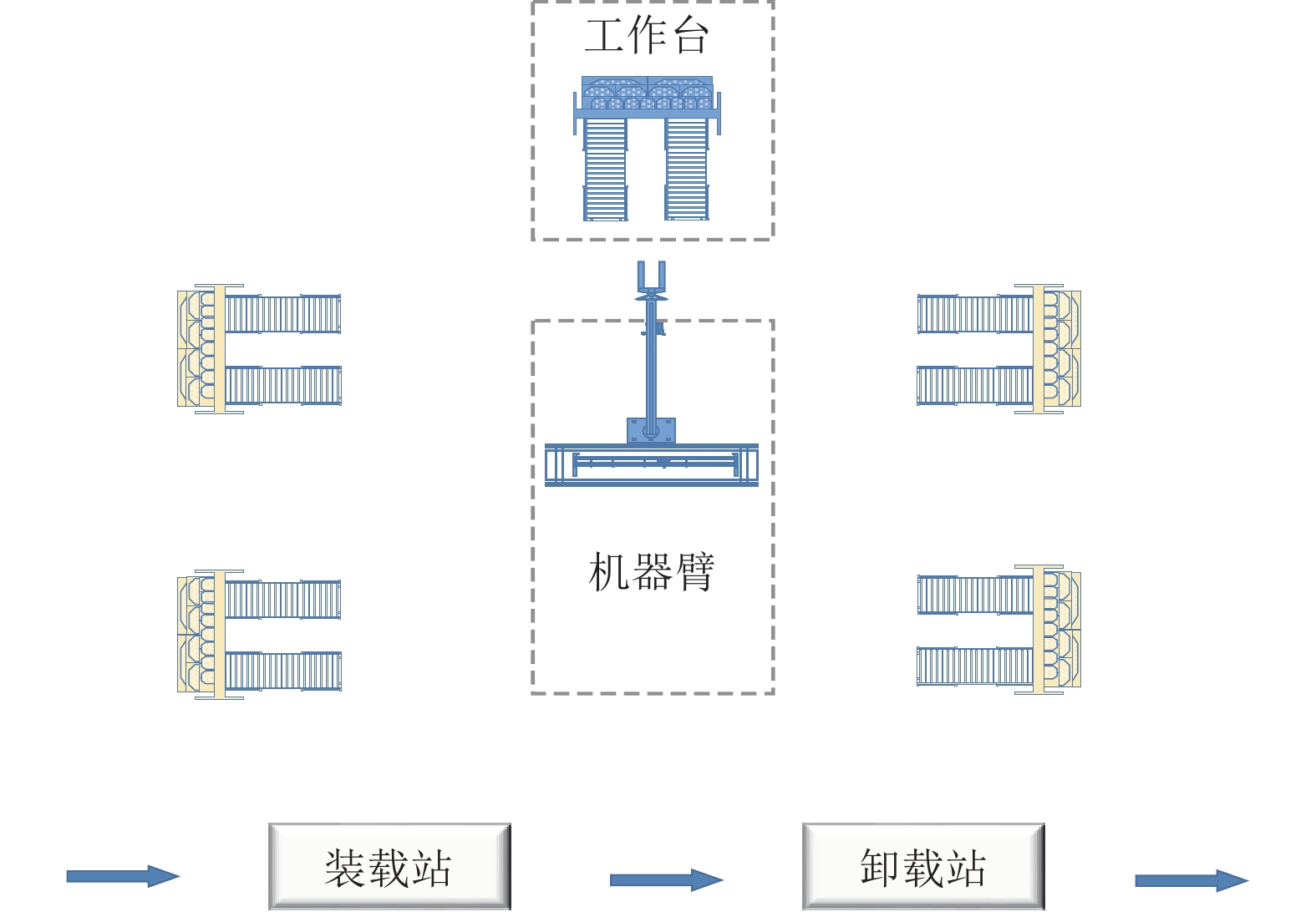
1 问题描述

本文主要研究的是有关job-shop 类型的机器人的智能制造车间的搬运问题. Job-shop 类型的机器人制造单元主要由加工站、搬运机器人和控制系统等组成. 根据车间调度的工业路线特点, 可将job-shop 类型的机器人制造单元调度过程描述为: 有 $ n $ 个工件 $ J=\{{J}_{1}, $ $ {J}_{2}, \cdots , {J}_{n}\} $ 将在 $ m $ 台加工机器 $M=\{{M}_{1}, M_{2}, \cdots , {M}_{m}\}$ 上进行加工, 其中 $ {M}_{0} $ 为装载站兼卸载站. 每个工件 $ {J}_{i} $ 有 $ p $ 道加工工序 $ {O}_{ij}=\{{O}_{i1}, {O}_{i2}, \cdots , {O}_{ip}\} $ , 且每个工件都有预先设定好的工序加工顺序, 所有的工序都严格按照预定的加工工序顺序在 $ m $ 台机器上进行. 现已知每道工序的加工时间、每道工序对应的加工机器和任意两台机器之间的搬运时间. 如图1所示: 调度基本过程可描述为, 首先, $ n $ 个工件在 $ {M}_{0} $ 上等待加工, 当加工任务开始时, 机器手按照工序顺序, 当工件处于装载区或工件上一道工序已完成时, 从该工件所在位置上取走工件并搬运到该工件下一道工序对应加工机器上, 根据当前加工机器状态决定是否开始加工. 当最后一道加工工序完成后并由机器手将该工件搬运至卸载站上时, 则为加工任务结束.

图 1 以搬运机械人为中心的制造单元

近年来, 在生产过程中人们越来越关注能够使多项决策目标都能得到满足的生产调度方案. 通常考虑多个目标共同优化的方案. 同时, 由于对环境问题的重视, 本文又引入了加工总能耗, 生产总成本等一系列的绿色调度目标. 以下是本文要优化的5个目标:

1) 最大完工时间:

$ C_{\rm{max}}={\rm{max}}\left({C}_{i}\right),\; i=\mathrm{1, 2}, \cdots , N $

(1)

2) 加工总能耗:

$ \begin{split} {E}_{\rm{total}}=&\sum\nolimits_{i=1}^{M}\left(\sum\nolimits_{j=1}^{{N}_{i}}{t}_{ij}{P}_{m, i}+{t}_{i, {\rm{idle}}}{P}_{i, {\rm{idle}}}\right)\\ &+\sum\nolimits_{i=1}^{{N}_{b}}{t}_{b, i}{P}_{b}+{t}_{b, {\rm{idle}}}{P}_{b, {\rm{idle}}} \end{split} $

(2)

3) 交货期提前量:

$ ET=\sum\nolimits_{j=1}^{N}{(DT}_{j}-{RT}_{j}), \;{DT}_{j} > {RT}_{j} $

(3)

4) 交货期延迟量:

$ LT=\sum\nolimits_{j=1}^{N}{(RT}_{j}-{DT}_{j}), \;{DT}_{j} < {RT}_{j} $

(4)

5) 生产总成本:

$ {C}_{\rm{total}}={cost}_{e}{E}_{\rm{total}}+\sum\nolimits_{i=1}^{M}\sum\nolimits_{j=1}^{{N}_{i}}{t}_{ij}{C}_{u, i} $

(5)

其中, 最大完工时间指所有工件完成加工后的总加工时间, $ N $ 为工序总数; $ {C}_{i} $ 为第 $ i $ 个工件的完工时间. 加工总能耗指调度过程中机器加工总功率与机器手搬运总功率之和. M为机器总个数; $ {N}_{i} $ 为第 $ i $ 个机器上的加工工序数; $ {t}_{ij} $ 为第 $ i $ 个机器上第 $ j $ 道工序的加工时间; $ {P}_{m, i} $ 为第 $ i $ 个机器的加工功率; ${t}_{i, {\rm{idle}}}$ 为第 $ i $ 台机器空载时间; ${P}_{i, {\rm{idle}}}$ 为第 $ i $ 台机器空载功率; $ {N}_{b} $ 为机器手搬运次数; $ {t}_{b, i} $ 为第 $ i $ 次搬运所花费的时间; $ {P}_{b} $ 为机器手拌搬运功率; ${t}_{b, {\rm{idle}}}$ 为机器手空载时间; ${P}_{b, {\rm{idle}}}$ 为机器手空载功率. 交货期为制造企业交付加工产品的时间. 若工件在理想交货时间前完成生产则为提前, 在理想交货时间后完成则为延迟. $ N $ 为工件个数; $ {DT}_{j} $ 为第 $ j $ 工件的理想交货时间; $ {RT}_{j} $ 为第 $ j $ 工件的实际交货时间. 生产总成本为加工所需电费与机床使用成本之和. $ {cost}_{e} $ 为电价(单位能耗成本); ${E}_{\rm{total}}$ 为加工总能耗; $ {C}_{u, i} $ 为第 $ i $ 台机器单位时间的使用成本.

2 算法描述

NSGA-III^[10]是Deb和Jain在2014年提出来的用于处理多个优化目标的进化优化算法. 其主要思路是在NSGA-II的基础上引入了参考点机制, 对于那些非支配并且接近参考点的种群个体进行保留, 相比NSGA-II拥有优秀的处理更高维度目标的能力.

2.1 NSGA-III基本算法流程

本文以NSGA-III的算法基本框架, 全局搜索以遗传算法为基础, 使用了一种符合调度问题特点的交叉变异策略, 并提出了两种更改支配关系的改进措施. 改进后的NSGA-III将具有更好的处理高维数据的能力, 用于解决本文所提出的机器人制造单元的高维多目标调度问题. NSGA-III的算法流程如下.

Step 1. 初始化, 随机产生大小为 $ N $ 的父代种群 $ Pt $ . 更新操作, 父代通过交叉、变异产生大小为 $ N $ 的子代种群 $ Qt $ , 合并为大小为 $ 2N $ 的种群 $ Rt=Pt+Qt $ .

Step 2. 计算目标值, 通过非支配排序, 将 $ Rt $ 划分为不同的非支配层 $(F1, F2,\cdots)$ .

Step 3. 选择优先级高的非支配子集保留到下一代, 用 $ St $ 来保留. 设 $ Fl $ 为临界层, 临界层为加上该层解数目大于等于 $ N $ 时的非支配层. 若数目等于 $ N $ 则 $St= St\cup Fi, $ $ i=\mathrm{1, 2}, \cdots, l$ , 否则 $St= St\cup Fi, i=\mathrm{1, 2}, \cdots, l-1$ . 令 $ Pt+1= $ $ St $ . 用 $ K=N-\left|Pt+1\right| $ 来记录需要从 $ Fl $ 中补充的解的个数.

Step 4. 每一维度最大值作为极值点, 最小值作为理想点, 对每个解的目标值做归一化处理.

Step 5. 以极值点构造超平面, 产生均布的 $ C (M+ $ $ H-1, H) $ 个参考点, M为维度数, H为每维分割份数.

Step 6. 对 $ St $ 中和 $ Fl $ 层中每个解找出距离最近的参考点分别进行关联.

Step 7. 对于 $ St $ 中关联少的参考点, 找出Fl层对应参考点关联的一个最近的解进行补充. 每添加一个解, 就将该解从 $ Fl $ 中删除, 并将 $ St $ 中关联解的个数更新排序. 重复Step 7直至补充K个解.

Step 8. 返回Step 2, 直至迭代次数达到预设值, 对当前解集进行非支配排序找出第一非支配层的解作为最终解集.

2.2 改进的NSGA-III

随着目标数量的增加, 算法对解的选择压力变小, 基于Pareto支配, 解之间很难存在支配关系, 这导致解集中很大部分的解都是非支配的. 而算法本身就强调保留种群中的非支配解, 所以在每一代种群中, 就没有太多的空间来保留新解. 这样就减缓了算法的搜索过程, 使算法效率变得低下. 使用改变支配关系的方法, 将解的目标值进行调整, 可以扩大每个解的支配空间, 从而提高解之间的区分度. 本文分别将Lorenz支配和CDAS支配与NSGA-III结合来进行优化. 第2.2.1节和第2.2.2节分别介绍了 Lorenz支配和CDAS支配.

2.2.1 Lorenz支配

$\left\{ { \begin{split} f\left(x\right)=&\left[{f}_{1}\left(x\right), {f}_{2}\left(x\right), \cdots , {f}_{m}\left(x\right)\right]\\ f{'}\left(x\right)=&\bigg[{f}_{1}\left(x\right), {f}_{1}\left(x\right)+{f}_{2}\left(x\right), {f}_{1}\left(x\right)+{f}_{2}\left(x\right)\\ &+{f}_{3}\left(x\right), \cdots , \sum\nolimits_{i=1}^{m}{f}_{i}\left(x\right)\bigg] \end{split}} \right. $

(6)

Lorenz支配(式(6))是将标准化后的每一个解的目标值, 按照从小到大进行排列, 之后在一个新列表里, 第 $ i $ 个位置存放前 $ i $ 个目标值的和 $ (i=\mathrm{1, 2}, \cdots , m) $ , $ m $ 为维度数. 所有解的目标值 $ f\left(x\right) $ 都用Lorenz修改过后, 用此新的目标值 $f{'}\left(x\right)$ 来进行非支配排序, 修改过支配关系后, 每个解的支配空间将会变大, 每个解之间就有更好的区分度.

如图2所示是一个双目标的例子, 对于解 $ S $ , 基于Pareto支配区域为(a), 经Lorenz支配 $ S $ 的支配空间增加到(a)、(b)、(c). 图2中, X 是一个解序列所求出对应的目标值的坐标.

2.2.2 CDAS支配

$ \left\{ {\begin{split} &{\varphi }_{i}=S\times\pi\\ &{f}_{i}{{'}}\left(x\right)=\frac{r\times\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{i}+{\varphi }_{i})}{{\rm{sin}}{\varphi }_{i}}, \;i=\mathrm{1, 2}, \cdots , m \end{split}} \right.$

(7)

CDAS支配(式(7))如图3所示, 式中, $ r $ 为该解的目标值点与原点之间的距离; $ {\omega }_{i} $ 为该点与原点连线和第i维的夹角; $ {\varphi }_{i} $ 为该点与第 $ i $ 维上一个可控的夹角, 其大小由系数 $ S $ 控制. 当 $ S=0.5 $ 时, CDAS支配与Pareto支配效果相同; 当 $ S < 0.5 $ 时, CDAS支配将使原目标值点的支配区域扩大; 当 $ S > 0.5 $ 时, CDAS支配将使原目标值点的支配区域变小. 图3中, X是一个解序列所求出对应的目标值的坐标.

图 2 Lorenz支配关系

图 3 解x修改前后第i维目标值

通过试验发现, 当 $ S $ 取0.25时, 求解多目标优化问题的效果最佳. 此时根据CDAS支配将原目标值 $ f\left(x\right) $ 修改为 $f{'}\left(x\right)$ , 扩大该解的支配区域.

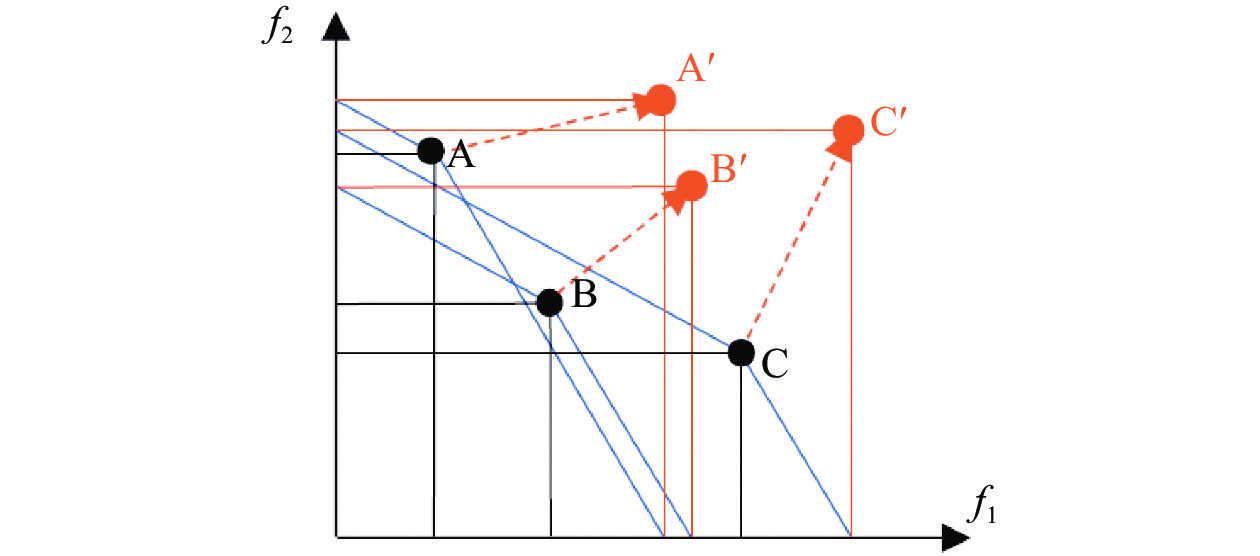
以双目标优化问题为例, 如图4所示, 当 $ S=0.5 $ , 即Pareto支配关系下解A、B、C是互不支配的. 取 $ S=0.25 $ , 增大扩张角, 从图中虚线部分可以看到每个解的支配区域都有所扩大, 解之间出现了更细微的序值分布, 此时, 3个解从互不支配变为解B支配解C.

3 实验分析

为了验证本文提出的改进算法的有效性, 通过对本文算法与传统的NSGA-Ⅲ算法进行对比. 并从以下3个方面来测试算法性能.

1)收敛性: 反映解集与真实Pareto前沿趋近程度.

2)多样性: 反映是否所得的Pareto最优解集中的解都分布在 Pareto 前沿上.

3)均匀性: 反映所得的Pareto最优解集中的解在目标空间中分布的均匀程度.

本次实验采用世代距离GD (generational distance)、反向世代距离IGD (inverted generational distance)和间距Spacing作为评价算法性能的指标. 其中, GD用于评价解集收敛性, IGD用于评价解集收敛性和多样性的综合性能, Spacing评价解集均匀程度.

本文提出的改进优化算法以 PyCharm Python 3.8 为开发工具编程实现, 其中相关参数设置如下: 实验设计环境和配置为Intel(R)Core(TM) i5-7300HQ CPU@2.50、8.00 GB RAM、Windows 10 64位操作系统. 交叉概率设为1.0, 变异概率设为0.5, 迭代次数设为50, 种群大小设为40. 表1中, I_nd表示案例编号,J表示该案例工件个数,M表示加工机器台数, S表示加工工序总数, 上标1为C-NSGA-III算法测试结果, 上标2为L-NSGA-III算法测试结果, 上标3为NSGA-III算法测试结果, 下标AVG为均值, SD为标准差, MIN为最小值. 本文挑选了由小到中到大型的案例共10个进行了实验, 用来测试本文所提出的算法的性能, 各案例均按照一定规则随机生成. 每个案例运行10次, 取均值作为测试结果.

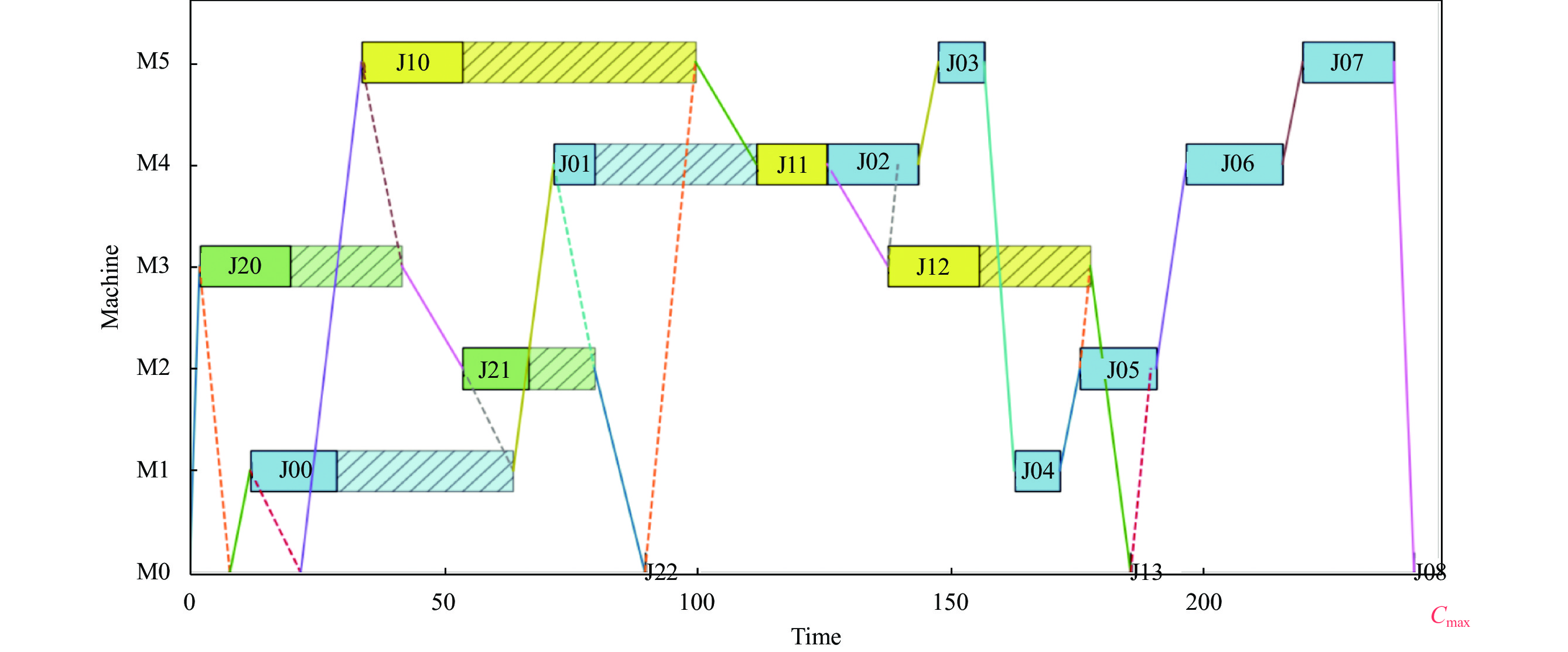
为了更好的描述最优方案的调度过程, 可以通过甘特图来分析工件的加工顺序与机器人的搬运顺序, 如图5为案例CS-3-16-5的甘特图. 该案例包含3个工件, 5台加工机器, 16道工序. 图中, 横坐标为时间轴, 纵坐标为加工机器序号, M0为装载卸载站. 纯色矩形代表加工过程, 虚线矩形代表工件在当前机器上的等待时间, 实线代表机器人带载过程, 虚线代表空载过程. “J00”代表工件0的第0道工序, 之后以此类推. 则案例CS-3-16-5的加工过程可描述为: 机器人将工件2从M0搬出至M3进行工序J20的加工, 搬运后机器人返回至M0开始搬运工件0至M1进行工序J00的加工, 随后返回M0搬运工件1至M5加工工序J10. 随后机器人转至M3取走在M3上完成加工的且已在输出缓冲区上等待的工件2, 搬运至M2加工工序J21. 以此类推, 直到所有工件加工结束.

图 4 CDAS修改后解支配关系

表1、表2、表3分别为C-NSGA-III、L-NSGA-III和NSGA-III算法在GD、IGD、Spacing上的对比结果. 通过对比可以得出, C-NSGA-III和L-NSGA-III都在GD上表现良好, 在绝大部分案例上数值都小于NSGA-III, 且标准差不大, 说明改进算法较为稳定. 在GD最小值上, C-NSGA-III始终为0, 总体可得两种改进算法在收敛性上都要优于NSGA-III. 但在IGD值上, NSGA-III几乎始终占优, 说明C-NSGA-III和L-NSGA-III在多样性上会变差, 分析原因是两算法均加大了支配空间, 它们的解相当于Pareto关系下的解的子集, 所以解的多样性会变差. 比较Spacing值可知, 两改进算法在解集均匀程度上, 较优于NSGA-III. 总体来说, C-NSGA-III和L-NSGA-III算法有效地提升了解集的收敛性和均匀性, 在多样性上表现一般.

图 5 案例CS-3-16-5甘特图

表 1 C-NSGA-III、L-NSGA-III与NSGA-III算法GD指标对比表

I_nd	J	M	S	GD¹_AVG	GD¹_SD	GD¹_MIN	GD²_AVG	GD²_SD	GD²_MIN	GD³_AVG	GD³_SD	GD³_MIN
1	3	5	16	0.002 9	0.002 6	0.000 0	0.004 7	0.002 5	0.002 0	0.007 4	0.003 5	0.001 8
2	4	4	23	0.001 8	0.001 1	0.000 0	0.001 5	0.000 7	0.000 5	0.007 9	0.003 6	0.003 9
3	7	5	40	0.001 5	0.001 4	0.000 0	0.000 8	0.000 8	0.000 0	0.004 5	0.002 1	0.001 7
4	8	6	55	0.004 8	0.005 9	0.000 0	0.011 2	0.007 8	0.000 0	0.014 1	0.006 2	0.004 8
5	11	6	74	0.003 1	0.002 7	0.000 0	0.006 3	0.006 2	0.000 0	0.007 8	0.006 5	0.000 0
6	12	6	86	0.002 6	0.003 1	0.000 0	0.002 8	0.001 8	0.000 0	0.005 3	0.004 1	0.001 1
7	14	8	95	0.009 6	0.007 6	0.000 0	0.007 4	0.004 6	0.000 0	0.011 6	0.008 5	0.000 0
8	16	8	97	0.005 6	0.003 9	0.000 0	0.004 7	0.004 3	0.000 0	0.007 4	0.004 6	0.000 0
9	19	10	107	0.003 2	0.005 5	0.000 0	0.015 7	0.012 0	0.000 0	0.008 0	0.008 2	0.000 0
10	20	9	135	0.019 6	0.032 2	0.000 0	0.021 0	0.028 3	0.000 0	0.022 2	0.014 0	0.000 0

表 1 C-NSGA-III、L-NSGA-III与NSGA-III算法GD指标对比表

表 2 C-NSGA-III、L-NSGA-III与NSGA-III算法IGD指标对比表

I_nd	J	M	S	IGD¹_AVG	IGD¹_SD	IGD¹_MIN	IGD²_AVG	IGD²_SD	IGD²_MIN	IGD³_AVG	IGD³_SD	IGD³_MIN
1	3	5	16	0.149 1	0.043 5	0.090 6	0.126 1	0.056 0	0.061 8	0.053 7	0.019 0	0.026 7
2	4	4	23	0.219 4	0.045 9	0.155 4	0.113 3	0.031 2	0.073 8	0.059 3	0.024 7	0.028 7
3	7	5	40	0.166 2	0.038 3	0.079 7	0.107 0	0.036 5	0.059 5	0.065 3	0.027 3	0.026 2
4	8	6	55	0.293 1	0.128 3	0.118 8	0.254 2	0.119 2	0.085 6	0.093 2	0.028 8	0.041 1
5	11	6	74	0.245 1	0.042 5	0.165 7	0.282 4	0.091 8	0.158 9	0.096 8	0.035 0	0.052 6
6	12	6	86	0.278 6	0.085 1	0.172 8	0.176 2	0.054 7	0.072 2	0.080 3	0.030 6	0.031 5
7	14	8	95	0.280 7	0.109 1	0.132 8	0.210 6	0.084 0	0.111 8	0.108 7	0.034 0	0.060 4
8	16	8	97	0.227 9	0.062 7	0.133 6	0.230 9	0.042 0	0.151 2	0.106 5	0.048 4	0.048 1
9	19	10	107	0.260 9	0.070 5	0.191 0	0.306 5	0.113 0	0.189 4	0.125 5	0.075 3	0.044 9
10	20	9	135	0.343 4	0.110 7	0.125 7	0.269 5	0.083 6	0.155 9	0.185 4	0.150 6	0.036 8

表 2 C-NSGA-III、L-NSGA-III与NSGA-III算法IGD指标对比表

表 3 C-NSGA-III、L-NSGA-III与NSGA-III算法Spacing指标对比表

I_nd	J	M	S	S¹_AVG	S¹_SD	S¹_MIN	S²_AVG	S²_SD	S²_MIN	S³_AVG	S³_SD	S³_MIN
1	3	5	16	0.049 6	0.036 9	0.010 8	0.046 4	0.025 5	0.018 8	0.107 2	0.048 6	0.044 1
2	4	4	23	0.031 2	0.015 4	0.010 8	0.033 0	0.011 3	0.013 4	0.082 8	0.038 5	0.054 6
3	7	5	40	0.028 5	0.016 2	0.006 8	0.029 3	0.016 9	0.010 7	0.087 3	0.040 3	0.048 8
4	8	6	55	0.053 2	0.036 8	0.009 8	0.058 9	0.022 8	0.022 2	0.086 7	0.020 1	0.058 0
5	11	6	74	0.043 9	0.015 5	0.025 9	0.051 8	0.016 9	0.022 9	0.078 1	0.015 6	0.054 7
6	12	6	86	0.035 4	0.015 9	0.013 4	0.038 7	0.013 9	0.017 5	0.076 5	0.039 9	0.046 7
7	14	8	95	0.053 7	0.028 6	0.029 7	0.062 1	0.024 9	0.023 5	0.085 9	0.024 0	0.059 3
8	16	8	97	0.044 0	0.014 8	0.027 3	0.052 5	0.022 9	0.031 8	0.078 0	0.019 5	0.050 3
9	19	10	107	0.059 4	0.033 6	0.012 9	0.062 5	0.037 7	0.013 1	0.108 2	0.035 0	0.066 8
10	20	9	135	0.061 2	0.031 6	0.018 1	0.076 8	0.046 0	0.034 7	0.102 5	0.049 1	0.017 6

表 3 C-NSGA-III、L-NSGA-III与NSGA-III算法Spacing指标对比表

4 结论与展望

本文针对研究机器人制造单元的多目标协同调度问题, 同时优化5个目标: 最大完工时间, 加工总能耗, 交货期提前量, 交货期延迟量及生产总成本. 针对job-shop的特点, 分别将Lorenz支配和CDAS支配与NSGA-III结合来进行优化并将结果与NSGA-III进行比较, 证明该算法有效.

参考文献

[1]	Haimes YY, Lasdon LS, Wismer DA. On a bicriterion formulation of the problems of integrated system identification and system optimization. IEEE Transactions on Systems, Man, and Cybernetics, 1971, SMC-1(3): 296-297. DOI:10.1109/TSMC.1971.4308298
[2]	Zadeh LA. Optimality and non-scalar-valued performance criteria. IEEE Transactions on Automatic Control, 1963, 8(1): 59-60. DOI:10.1109/TAC.1963.1105511
[3]	Coello CAC. Evolutionary multi-objective optimization: A historical view of the field. IEEE Computational Intelligence Magazine, 2006, 1(1): 28-36. DOI:10.1109/MCI.2006.1597059
[4]	Escamilla J, Salido MA, Giret A, et al. A metaheuristic technique for energy-efficiency in job-shop scheduling. The Knowledge Engineering Review, 2016, 31(5): 475-485. DOI:10.1017/S026988891600031X
[5]	Dai M, Tang DB, Giret A, et al. Energy-efficient scheduling for a flexible flow shop using an improved genetic-simulated annealing algorithm. Robotics and Computer-Integrated Manufacturing, 2013, 29(5): 418-429. DOI:10.1016/j.rcim.2013.04.001
[6]	May G, Stahl B, Taisch M, et al. Multi-objective genetic algorithm for energy-efficient job shop scheduling. International Journal of Production Research, 2015, 53(23): 7071-7089. DOI:10.1080/00207543.2015.1005248
[7]	Subulan K. An interval-stochastic programming based approach for a fully uncertain multi-objective and multi-mode resource investment project scheduling problem with an application to ERP project implementation. Expert Systems with Applications, 2020, 149: 113189. DOI:10.1016/j.eswa.2020.113189
[8]	Soto C, Dorronsoro B, Fraire H, et al. Solving the multi-objective flexible job shop scheduling problem with a novel parallel branch and bound algorithm. Swarm and Evolutionary Computation, 2020, 53: 100632. DOI:10.1016/j.swevo.2019.100632
[9]	Zhu ZW, Zhou XH. An efficient evolutionary grey wolf optimizer for multi-objective flexible job shop scheduling problem with hierarchical job precedence constraints. Computers & Industrial Engineering, 2020, 140: 106280.
[10]	Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535