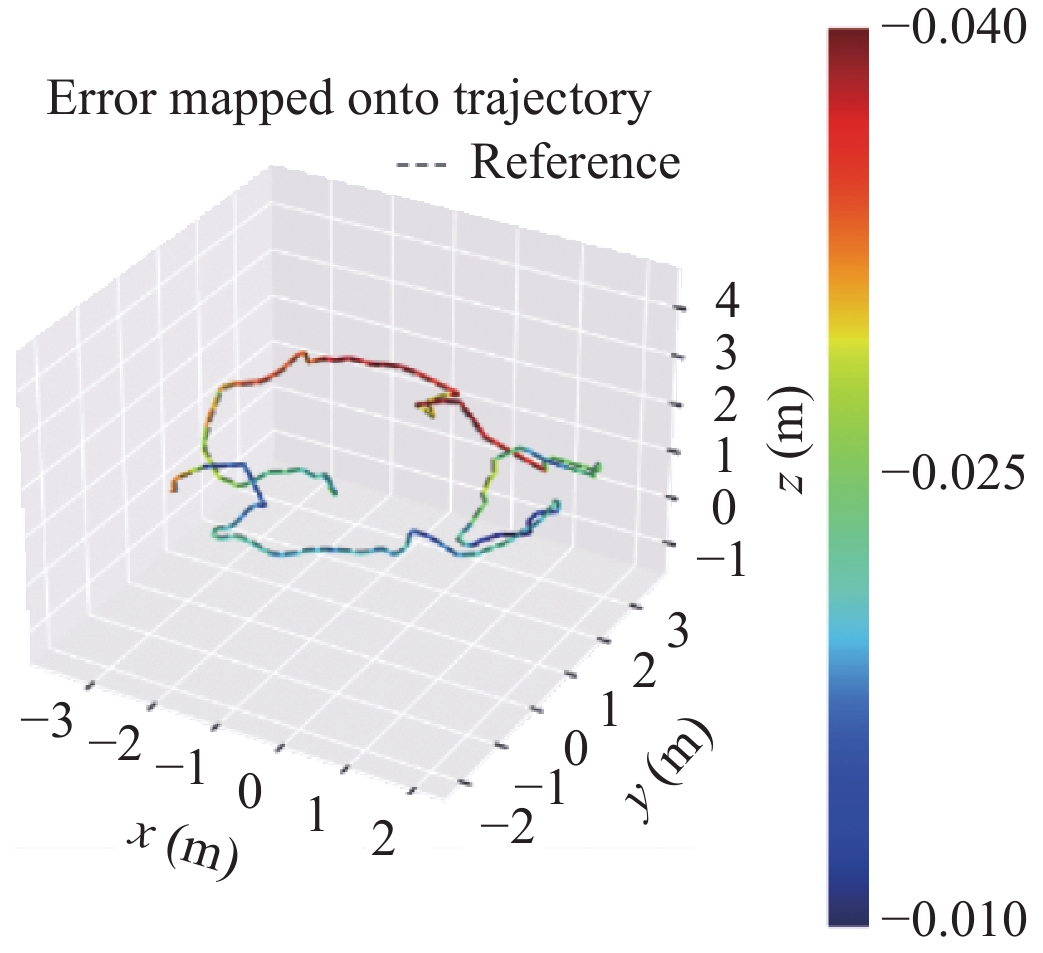
在计算机领域, 运动状态估计有着广泛的应用场景, 涉及机器人导航、自动驾驶、虚拟现实以及增强现实等诸多领域. 在众多传感器融合方案中, 视觉与惯性传感器融合更好的鲁棒性. 一方面, 相机传感器能够提供丰富的环境视觉信息, 以便进行环境定位、回环检测以及三维重建等; 另一方面, 惯性传感器(inertial measurement unit, IMU)可直接提供自身运动信息, 可恢复真实尺度信息, 重力方向以及自身姿态信息.
由于光照信息变化、弱纹理以及运动模糊等外部环境因素, 从而导致视觉跟踪失败. 而IMU预积分估计可有效弥补纯视觉跟踪效果, 从而有效改善运动跟踪性能.
然而, 对于单目惯性视觉运动估计仍存在些许问题会影响实际应用. 一是系统初始化问题, 由于缺少直接距离(深度)信息, 很难将单目视觉跟踪系统与惯性估计相结合. 二是单目惯性视觉问题是高度非线性的, 数值迭代求解方面仍面临着挑战以及位姿估计在长时间运动下的轨迹漂移问题. 为此, 希望运动状态估计系统在已知空间位置进行初始化, 并缓慢移动. 基于以上两点, 限制了运动状态估计在实际中的应用.
目前, 以单目视觉为基础的里程计以及同步定位与地图构建(simultaneous localization and mapping, SLAM)等领域有着很多优秀的研究工作. 如首次采用多线程方法的PTAM[1], 以及后续改进的SVO[2]、LSD-SLAM[3]以及ORB-SLAM[4]等.
一般的单目惯性测量, 如Weiss[5]和Lynen[6], 采用松耦合的方式, 将视觉信息与IMU信息作为独立模块计算. 松耦合采用扩展卡尔曼滤波, IMU作为状态变量, 视觉信息用于更新变量. 更进一步, 则是采用扩展卡尔曼滤波[5, 7, 8]或图优化算法[9, 10], 将图像信息与IMU信息联合优化. MSCKF[11]是著名的基于扩展卡尔曼滤波EKF的惯性视觉里程计, 通过相机姿态作为状态变量, 并使用多角度相机的多相机视图来形成约束更新. 为实现一致处理时间, 基于图优化的视觉惯性里程计(visual inertial odometry, VIO)方法通常采用边缘化窗口外的状态与测量值, 在最近状态的有限窗口进行数据优化. 由于迭代求解非线性系统的高计算量, 很难实现实时计算.
根据视觉信息处理方式, 位姿优化可分为最小化光流误差的直接法[2,3,11]和基于最小化重投影误差的非直接方法[7,9,12]. 直接法需要较好的初始值估计, 而非直接法则需要更多的计算资源进行特征提取与匹配. 目前, 非直接法因算法成熟及鲁棒性受到更多的应用, 而直接法的优势则是可像素操作并可使密集匹配变得更加容易.
通常IMU数据的获取频率远远超过相机图像数据. 为此提出了很多方法计算高频IMU数据测量. 最直接的方法采用EKF方法将IMU数据作为状态变量进行计算[5, 11]. 在图优化算法中, 采用IMU预积分方式避免IMU积分重计算. 这种方法是由Lupton等[13]第一次提出, 采用欧拉角参数化旋转变量. Forster等[10, 14]通过添加IMU残差校正进一步提升了预积分方法.
香港科技大学提出以稀疏光流法跟踪特征点为前端, 采用IMU预积分与视觉构建紧耦合框架-VINS-Mono单目视觉SLAM系统[15], 解决了视觉与IMU尺度对齐, 重力方向、IMU数据残差等问题. Campos等[16]在2020年提出第一个支持纯视觉、视觉-惯性以及多地图的实时SLAM系统, 可在单目、双目和RGB-D相机上利用针孔或鱼眼成像模型运行. Campos等在单目-惯性初始化[17]对IMU进行了残差计算, 恢复了单目相机尺度, 并对齐到惯性系.
本文方法采用惯性传感器数据与相机图像数据以紧耦合策略构建联合状态变量, 通过最小化加权重投影误差与惯性运动误差在移动端实现实时位姿优化计算. 紧耦合策略可有效保证全局轨迹位姿一致性, 减小漂移误差. 在移动端可实时并行采集IMU数据与相机图像数据, 在保证实时性的同时, 可获得更小误差参数的重建轨迹位姿.
2 位姿优化方法传统纯视觉位姿优化算法一般采用相机图像信息, 首先对相机进行参数标定, 获取包含相机焦距等参数在内的内参矩阵信息; 而后对所获取图像进行特征提取、匹配, 建立图像关键帧; 根据同一场景图像间的对极几何约束关系, 求解出对应基础矩阵或本质矩阵; 对基础矩阵或本质矩阵进一步分解, 可求解出的相机在两幅图像间的旋转、位移; 而后通过计算特征点重投影误差进行位姿优化, 获取相机轨迹位姿信息.
本文方法在传统纯视觉位姿优化算法上, 增加了惯性传感器数据对轨迹位姿测量约束, 并采用加权视觉重投影误差与惯性运动误差更加优化求解出相机位姿轨迹信息. 优化方法主要内容如下.
惯性运动测量单元在惯性坐标系B下, 在
在世界坐标系
| $ \left\{ {\begin{split} & R_{WB}^{k + 1} = R_{WB}^k{\rm{exp}}\left(\left(w_B^k - b_g^k\right)\Delta t\right) \hfill \\ & v_{WB}^{k + 1}{\text{ = }}v_{WB}^k + R_{WB}^k\left(a_B^k - b_g^k\right)\Delta t \hfill \\ & P_{WB}^{k + 1} = P_B^k + v_{WB}^k\Delta t + R_{WB}^k\left(a_B^k - b_g^k\right)\Delta {t^2} \hfill \end{split} } \right.$ | (1) |
本文提出采用紧耦合的方式, 将IMU数据与图像信息数据紧密结合在一起, 通过联合优化方式求解. 基于Mur-Artal等[18]提出的采用ORB特征点的实时ORB-SLAM系统, 采用初始定义两个关键帧之间的运动变化, 旋转变量差值
| $\left\{ { \begin{split} & R_{WB}^{i + 1} = R_{WB}^i\Delta {R_{i,i + 1}}{\rm{exp}}\left(J_{\Delta R}^gb_g^i\right) \hfill \\ & v_{WB}^{i + 1}{\text{ = }}v_{WB}^i + R_{WB}^i\left(\Delta {v_{i,i + 1}}{\text{ + }}J_{\Delta {{v}}}^gb_g^i + J_{\Delta v}^ab_a^i\right) \hfill \\ & P_{WB}^{i + 1}{\text{ = }}P_B^i + v_{WB}^i\Delta {t_{i,i + 1}} + R_{WB}^i\left(\Delta {P_{i,i + 1}}{\text{ + }}J_{\Delta p}^gb_g^i + J_{\Delta p}^ab_a^i\right) \hfill \end{split}} \right. $ | (2) |
其中,
基于已实现的实时ORB-SLAM系统, 可运行在大尺度场景中, 重建局部地图以便跟踪与映射, 并可构建真实环境的点云地图. 本文方法可实现在预设帧率下的传感器姿态、速度以及IMU误差的位姿跟踪计算代替原始单目跟踪系统. 根据初始的ORB-SLAM系统, 预计算得到相机位姿之后, 局部地图中的地图点可投影与对应帧图像中的关键点相匹配. 相较于之前关键帧
| $ \left\{ {\begin{split} & \varepsilon = \left\{ {R_{WB}^j,P_{WB}^j,v_{WB}^j,b_g^j,b_a^j} \right\} \hfill \\ & {\varepsilon ^*} = \mathop {\arg \min }\limits_\varepsilon \left(\lambda \sum\limits_k {{E_{\rm{proj}}}(k,j) + \mu {E_{\rm{IMU}}}(i,j)} \right) \hfill \end{split} } \right.$ | (3) |
其中,
而基于ORB特征点的重投影误差函数
| $ \left\{ {\begin{split} & {E_{\rm{proj}}}(k,j) = \rho \left({({x^k} - \pi (X_C^k))^{\rm{T}}}{\Sigma _k}\left({x^k} - \pi \left(X_C^k\right)\right)\right) \hfill \\ & X_C^k = {R_{CB}}R_{BW}^j\left(X_W^k - P_{WB}^j\right) + {P_{CB}} \hfill \end{split}} \right. $ | (4) |
其中,
| $\left\{ { \begin{split} & {E_{\rm{IMU}}}(i,j) = \rho \left(\left[e_R^{\rm{T}}e_v^{\rm{T}}e_p^{\rm{T}}\right]{\Sigma _I}{\left[e_R^{\rm{T}}e_v^{\rm{T}}e_p^{\rm{T}}\right]^{\rm{T}}}\right) + \rho \left(e_b^{\rm{T}}{\Sigma _R}{e_b}\right) \hfill \\ & {e_R} = \ln\left({\left(\Delta {R_{ij}}{\rm{exp}}\left(J_{\Delta R}^gb_g^j\right)\right)^{\rm{T}}}R_{BW}^iR_{WB}^j\right) \hfill \\ & {e_v} = R_{BW}^i\left(v_{WB}^j - v_{WB}^i\right) - \left(\Delta {v_{ij}} + J_{\Delta v}^gb_g^j + J_{\Delta v}^ab_a^j\right) \hfill \\ & {e_p} = R_{BW}^i\left(P_{WB}^j - P_{WB}^i - v_{WB}^i\Delta {t_{ij}}\right) - \left(\Delta {p_{ij}} + J_{\Delta p}^gb_g^j + J_{\Delta p}^ab_a^j\right) \hfill \\ & {e_b} = {b^j} - {b^i} \hfill \end{split} } \right.$ | (5) |
其中,
当第
紧耦合的实时位姿优化方法整体流程如下: 1) 预处理采用张正友标定法进行相机标定; 2) 采用相机图像数据与惯性传感器数据作为实时输入, 对图像信息进行特征提取、匹配; 3) 根据对极几何约束求解出初始相机位姿, 并预积分计算两帧间的惯性运动数据; 4) 构建联合状态变量, 最小化加权重投影误差与惯性运动误差求解出相机位姿信息并保存; 5) 实时输入新的图像数据与惯性运动数据进行迭代算法求解.
3 实验分析为了更好的衡量评价本文提出的移动端位姿优化方法, 采用EuROC数据集[22]进行系统评估与误差分析. EuRoC数据集使用MAV采集了两个不同房间及一个工业环境, 总共11组数据, 并根据照明、纹理、运动快慢以及模糊程度分为简单、中等、困难3等级数据组. 此数据集的良好特性使得可以很好的检验评估类似惯性视觉的位姿轨迹系统, 数据测试时仅采用单目图像(左目)作为视觉图像流输入, IMU数据流输入以及真实轨迹参照.
在计算完成位姿轨迹后, 采用位姿轨迹文件TUM导出, 采用evo轨迹评测对重建位姿进行误差评价. 假设真实的运动轨迹为T, 预估轨迹为
| $ {e_i} = {\left\| {\ln {{(T_i^{ - 1}{T_{ei}})}^V}} \right\|_2} $ | (6) |
则根据两条轨迹的均方根(root mean square error, RMSE)误差为:
| $ {\textit{RMSE}}(e) = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {e_i^2} } $ | (7) |
为确定重投影误差和IMU误差的最佳权重系数, 针对

|
图 1 RMSE 评测结果 |
由图1可知, 当
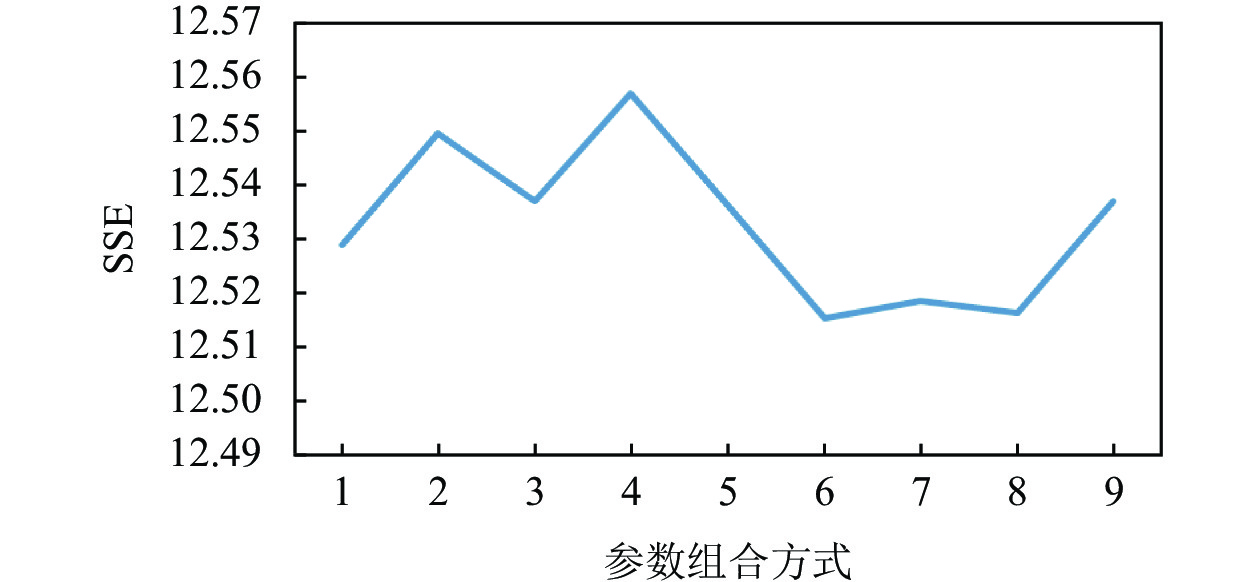
|
图 2 SSE 评测结果 |
从EuRoC数据集中选取了6组对比实验数据, 评估位姿优化系统的精确性与稳定性, 通过计算RMSE(轨迹误差), 不同方法计算结果如表1所示.
从表1可见, 在不同数据集上, 采用视觉信息与IMU数据同时约束方法的轨迹重建方法较仅采用纯视觉方法的ORB-SLAM2获取的轨迹效果均好. 香港科技大学提出的VINS-Mono视觉惯性里程计, 对相机轨迹的重建的效果较ORB-SLAM方法较好.
| 表 1 不同算法的数据集RMSE评测结果 |
而本文提出的位姿优化算法在EuRoC的6个数据集上的表现整体偏好, 除MH_01_easy数据库集误差相差0.115之外, 其他数据集表现均优于其他方法, 轨迹误差更小, 更加接近真实的轨迹位姿, 取得较好的相机轨迹效果.
通过上述分析可见, 本文提出的算法在相机轨迹重建效果较好, 提供了一种新的位姿优化方式.
由于ORB-SLAM2并没有采用IMU数据处理, 仅采用纯视觉方式进行相机位姿重建, 缺少一个尺度因子, 故评测绝对误差时不与考虑.
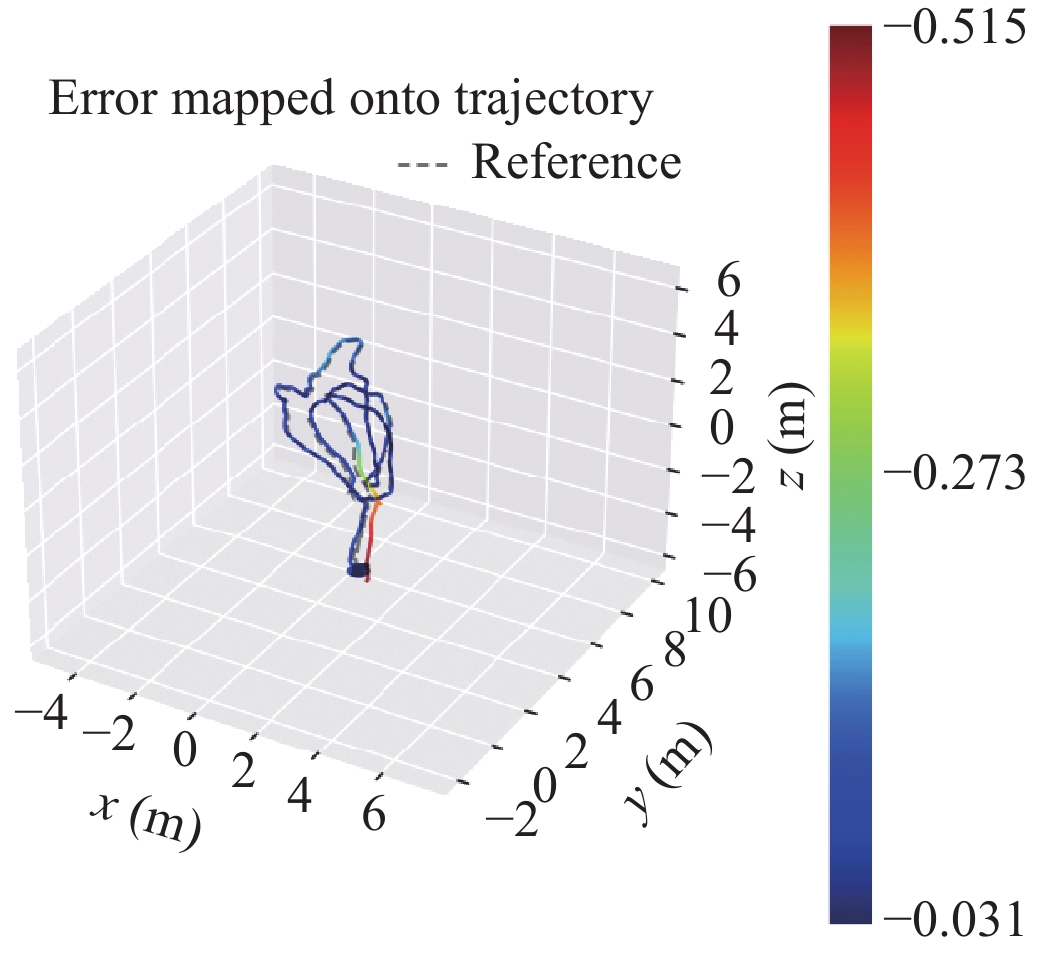
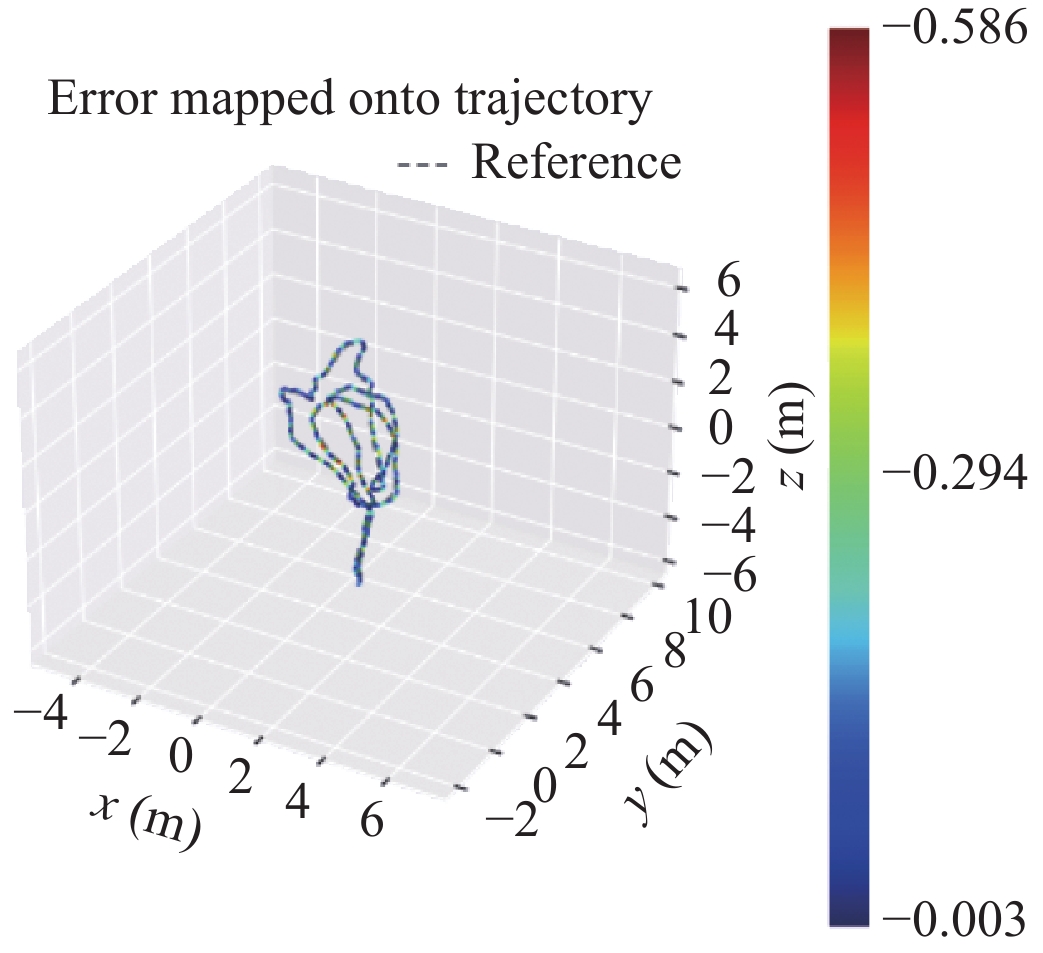
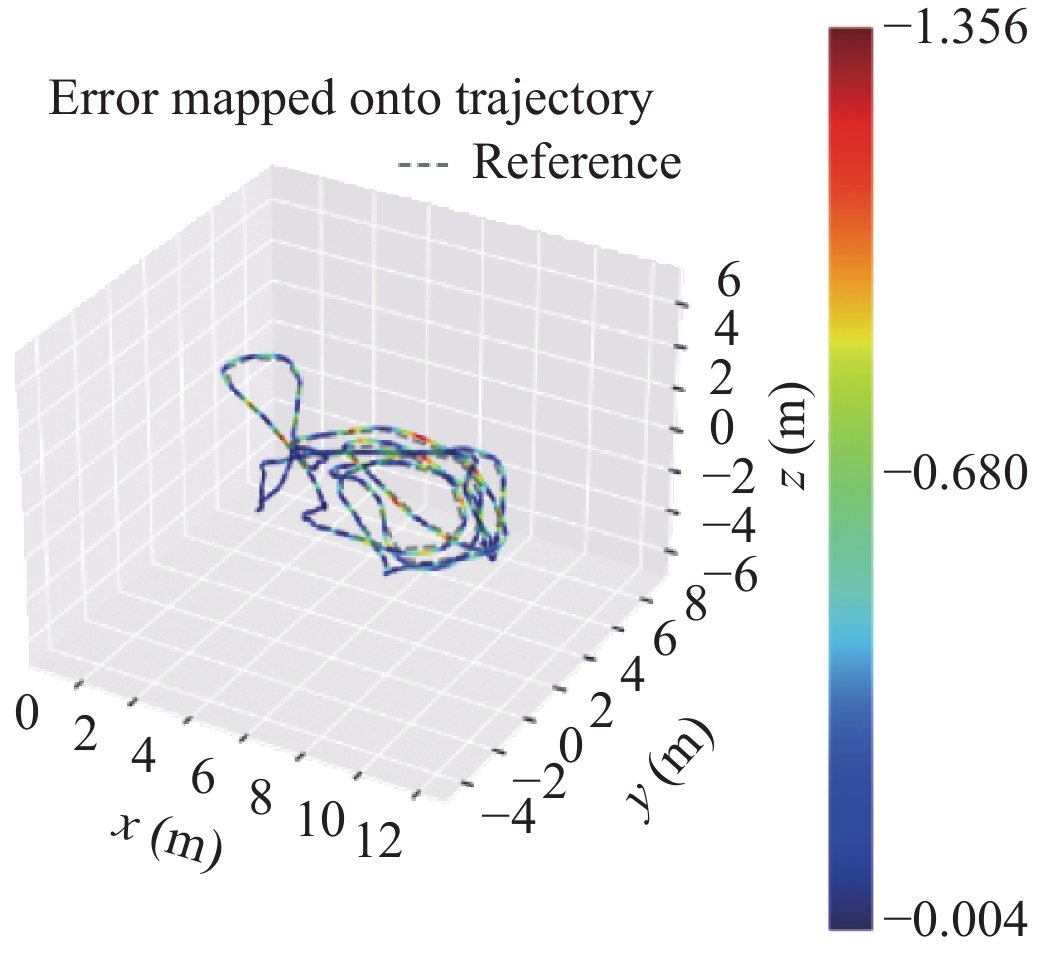
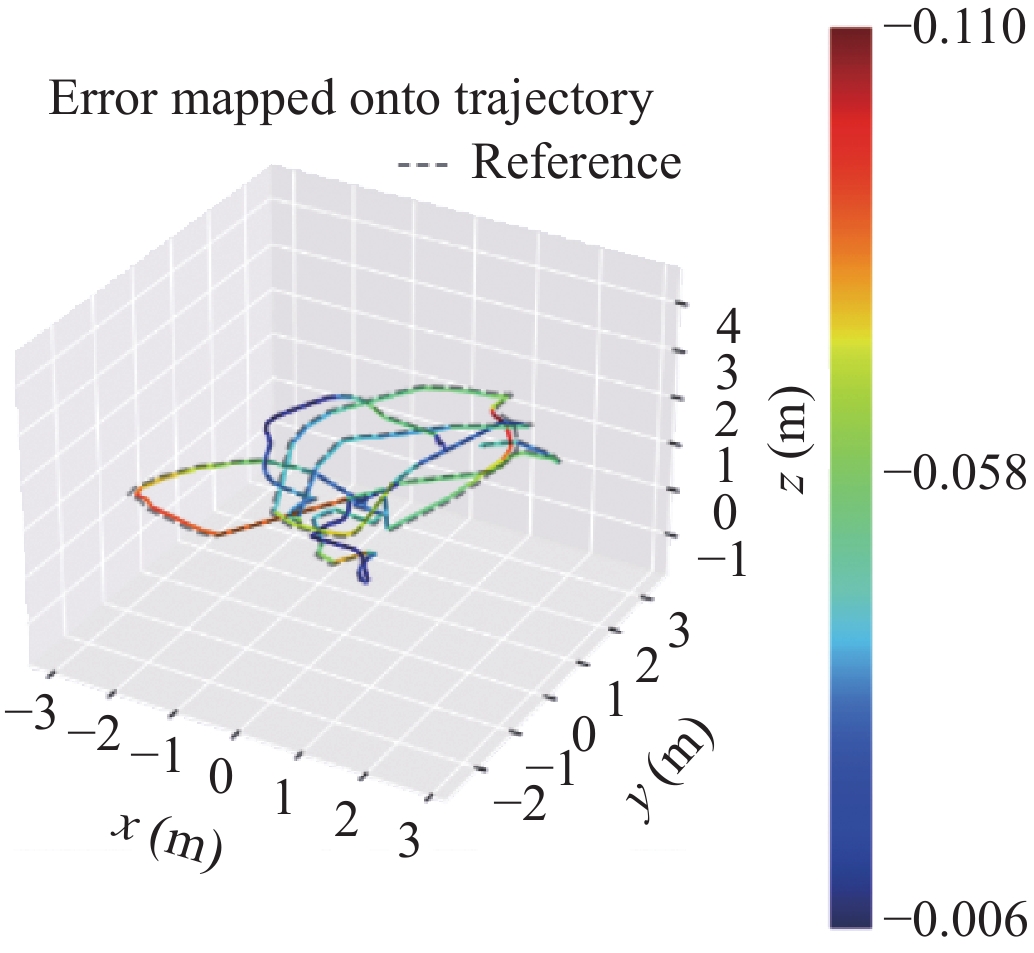
对3种不同的重建方法采用EVO评测轨迹的真实误差, 效果如表2.
将不同方法的重建相机位轨迹与数据集的真实轨迹作比较, 验证重建相机轨迹的重建效果.
结合表1, 根据表2可知, 3种方法在重建轨迹误差相差不大的情况下, 展现出不同的轨迹误差分布. 从表2中的轨迹图可知, ORB-SLAM3虽然均方根误差较大, 轨迹误差分布均匀, 说明对轨迹处理的综合性能较好, 可处理更多种的轨迹情况, 鲁棒性更好. 而VINS-Mono与本文方法呈现两种不同的误差浮动表现. 本文方法在相机移动位移幅度较大时, 误差显著浮动提升, 归其原因在位移较大时, IMU数据积分误差较大, 而优化方法给予更高的权重比, 不能很好的优化计算大位移时的位姿轨迹. 基于VINS-Mono初始化算法, 采用松耦合的传感器融合方法, 在轨迹重建的初始阶段对相机位姿轨迹的重建效果较差, 相机轨迹误差较大.
4 结论与展望本文提出了一种可实时运行在移动端的紧耦合惯性视觉位姿优化方法. 可根据实时相机图像数据与惯性运动数据计算载体在自身所构建地图中的位置, 并可获得优化后的相机位姿信息, 为后续三维重建工作提供可靠相机姿态信息, 更好地为三维重建服务.
实验证明, 本文提出位姿优化方法, 相较于ORB-SLAM3基于IMU最大后验估计的SLAM系统和VINS-Mono视觉惯性里程计, 在相同数据集下, 具有更高的尺度还原性以及轨迹准确性.
| 表 2 不同算法绝对轨迹误差 |
该位姿优化方法也存在不足, 在位移较大时, IMU数据不能很好的积分优化, 导致局部轨迹误差较大. 这需要探索更好的IMU数据模型, 以期修正较长时间下大位移的IMU数据误差问题, 达到更好的相机轨迹还原. 本方法并过于依赖ORB-SLAM系统进行初始化, 初始化时间较ORB-SLAM2系统略长.
未来工作预期利用移动端的多相机镜头信息(类似双目)以及景深镜头信息, 加以融合求解, 优化IMU数据模型. 以期通过更加精确的传感器与视觉信息数据模型完成初始化, 紧耦合优化计算, 提高整个系统精确性与稳定性.
| [1] |
Klein G, Murray D. Parallel tracking and mapping for small AR workspaces. Proceedings of the 6th IEEE and ACM International Symposium on Mixed and Augmented Reality. Nara: IEEE, 2007. 225–234.
|
| [2] |
Forster C, Pizzoli M, Scaramuzza D. SVO: Fast semi-direct monocular visual odometry. Proceedings of 2014 IEEE International Conference on Robotics and Automation (ICRA). Hong Kong: IEEE, 2014. 15–22.
|
| [3] |
Engel J, Schöps T, Cremers D. LSD-SLAM: Large-scale direct monocular SLAM. Proceedings of the 13th European Conference on Computer Vision. Zurich: Springer, 2014. 834–849.
|
| [4] |
Mur-Artal R, Montiel JMM, Tardós JD. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Transactions on Robotics, 2015, 31(5): 1147-1163. DOI:10.1109/TRO.2015.2463671 |
| [5] |
Weiss S, Achtelik MW, Lynen S, et al. Real-time onboard visual-inertial state estimation and self-calibration of mavs in unknown environments. Proceedings of 2012 IEEE International Conference on Robotics and Automation. Saint Paul: IEEE, 2012. 957–964.
|
| [6] |
Lynen S, Achtelik MW, Weiss S, et al. A robust and modular multi-sensor fusion approach applied to MAV navigation. Proceedings of 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems. Tokyo: IEEE, 2013. 3923–3929.
|
| [7] |
Li MY, Mourikis AI. High-precision, consistent EKF-based visual-inertial odometry. The International Journal of Robotics Research, 2013, 32(6): 690-711. DOI:10.1177/0278364913481251 |
| [8] |
Bloesch M, Omari S, Hutter M, et al. Robust visual inertial odometry using a direct EKF-based approach. Proceedings of 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Hamburg: IEEE, 2015. 298–304.
|
| [9] |
Leutenegger S, Lynen S, Bosse M, et al. Keyframe-based visual-inertial odometry using nonlinear optimization. The International Journal of Robotics Research, 2015, 34(3): 314-334. DOI:10.1177/0278364914554813 |
| [10] |
Forster C, Carlone L, Dellaert F, et al. On-manifold preintegration for real-time visual-inertial odometry. IEEE Transactions on Robotics, 2017, 33(1): 1-21. DOI:10.1109/TRO.2016.2597321 |
| [11] |
Mourikis AI, Roumeliotis SI. A multi-state constraint Kalman filter for vision-aided inertial navigation. Proceedings of 2007 IEEE International Conference on Robotics and Automation. Rome: IEEE, 2007. 3565–3572.
|
| [12] |
Usenko V, Engel J, Stückler J, et al. Direct visual-inertial odometry with stereo cameras. Proceedings of 2016 IEEE International Conference on Robotics and Automation (ICRA). Stockholm: IEEE, 2016. 1885–1892.
|
| [13] |
Lupton T, Sukkarieh S. Visual-inertial-aided navigation for high-dynamic motion in built environments without initial conditions. IEEE Transactions on Robotics, 2012, 28(1): 61-76. DOI:10.1109/TRO.2011.2170332 |
| [14] |
Forster C, Carlone L, Dellaert F, et al. IMU preintegration on manifold for efficient visual-inertial maximum-a-posteriori estimation. Technical Report, Atlanta: Georgia Institute of Technology, 2015.
|
| [15] |
Qin T, Li PL, Shen SJ. VINS-Mono: A robust and versatile monocular visual-inertial state estimator. IEEE Transactions on Robotics, 2018, 34(4): 1004-1020. DOI:10.1109/TRO.2018.2853729 |
| [16] |
Campos C, Elvira R, Rodríguez JJG, et al. ORB-SLAM3: An accurate open-source library for visual, visual-inertial and multi-map SLAM. arXiv: 2007.11898, 2021.
|
| [17] |
Campos C, Montiel JMM, Tardós JD. Inertial-only optimization for visual-inertial initialization. Proceedings of 2020 IEEE International Conference on Robotics and Automation (ICRA). Paris: IEEE, 2020. 51–57.
|
| [18] |
Mur-Artal R, Tardós JD. ORB-SLAM2: An open-source SLAM system for monocular, stereo, and RGB-D cameras. IEEE Transactions on Robotics, 2017, 33(5): 1255-1262. DOI:10.1109/TRO.2017.2705103 |
| [19] |
Ghadi M, Laouamer L, Nana L, et al. A novel zero-watermarking approach of medical images based on Jacobian matrix model. Security and Communication Networks, 2016, 9(18): 5203-5218. DOI:10.1002/sec.1690 |
| [20] |
Wang Y, Hu SQ, Wu SD. Object tracking based on Huber loss function. The Visual Computer, 2019, 35(11): 1641-1654. DOI:10.1007/s00371-018-1563-1 |
| [21] |
Kümmerle R, Grisetti G, Strasdat H, et al. G2o: A general framework for graph optimization. Proceedings of 2011 IEEE International Conference on Robotics and Automation. Shanghai: IEEE, 2011. 3607–3613.
|
| [22] |
Burri M, Nikolic J, Gohl P, et al. The EuRoC micro aerial vehicle datasets. The International Journal of Robotics Research, 2016, 35(10): 1157-1163. DOI:10.1177/0278364915620033 |
 2022, Vol. 31
2022, Vol. 31