2. 黑龙江东部节水设备有限公司, 绥化 152001
2. Heilongjiang Water Saving in the East Co. Ltd., Suihua 152001, China
随着我国农业与经济的发展, 智慧农业对农田起到了至关重要的作用, 精准灌溉已经成为农业生产和生活的重要因素, 而实现对农作物精准灌溉, 对农作物土壤湿度进行精准预测至关重要[1]. 土壤湿度是旱涝评价的重要参考, 对地表能量、降雨再分配、水资源管理、农业灌溉等方面都有重要影响[2]. 土壤湿度过低, 会导致土壤干旱, 对植物的光合作用产生严重影响, 甚至导致植物干枯死亡; 土壤湿度过高, 会导致植物根部缺氧, 严重时会导致植物根部腐烂[3, 4]. 通过对农作物土壤湿度的精准预测可以准确地反映农作物土壤的水分含量状况, 从而为实现精准灌溉提供了科学决策的依据和方法.
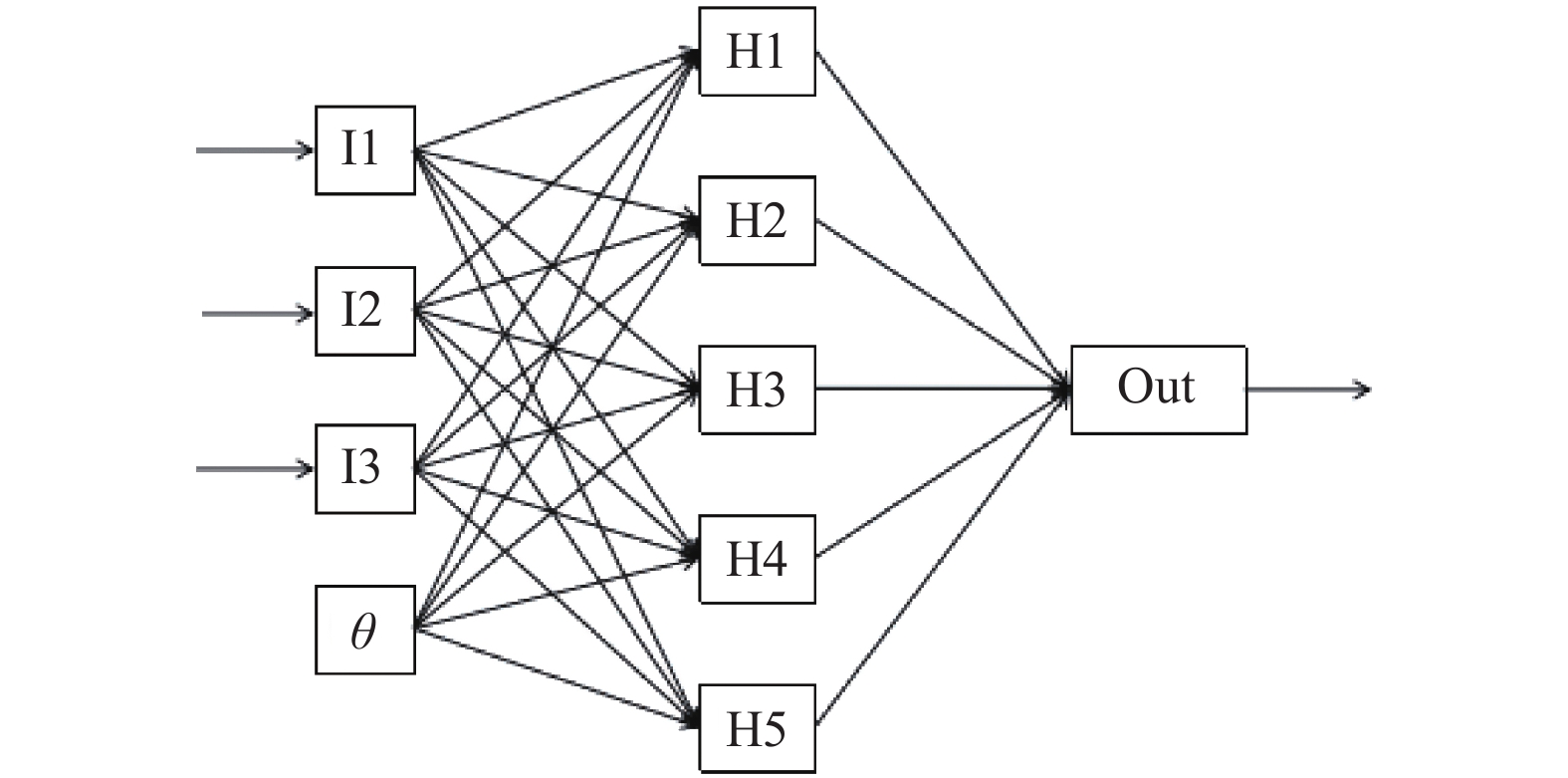
1 基本理论 1.1 BP神经网络算法BP (back propagation)神经网络算法是一种典型的多层前馈神经网络, 它通过误差逆向传播算法来进行学习训练[5-7]. BP神经网络是目前使用最为广泛, 结构最为直观并且工作原理最为容易理解的神经网络, 它的结构简单, 可塑性强, 且拥有较强的数据拟合能力[8-10]. BP神经网络主要包含输入层、隐含层和输出层, 在训练过程中, 神经网络不断调整输入层与隐含层以及隐含层和输出层之间的权值和阈值[11, 12], 当神经网络输出值与目标值一致或者达到迭代次数时训练停止, 这种神经网络拥有较强的泛化能力, 神经网络的结构原理如图1所示.
|
图 1 BP神经网络结构原理 |
BP神经网络的计算公式如式(1)–式(3)所示:
| $ f_s(u) = \frac{1}{{1 + \mathop e\nolimits^{ - u} }} $ | (1) |
| $ u_j = \sum\limits_{i = 1}^n {w_{ij}x_i - o_j} $ | (2) |
| $ p = f_s\left(\sum\limits_{j = 1}^n {w_jo_j + \theta } \right) $ | (3) |
式(1)为神经元的激励函数, 采用的是Sigmoid函数, 式(2)为神经元的输入数据经过加权值求和之后与阈值相减,
常规的BP神经网络主要采用数据正向传播, 误差反向传播的方式, 根据误差值采用梯度下降的方法对网络的权值和阈值进行修正, 从而不断使误差下降到预期数值, 权值和阈值的修正如式(4)和式(5)所示:
| $ w(k + 1) = w(k) - \beta \frac{{\partial E}}{{\partial w}} $ | (4) |
| $ \theta (k + 1) = \theta (k) - \beta \frac{{\partial E}}{{\partial \theta }} $ | (5) |
式(4)和式(5)为权值和阈值修正的公式, E表示神经网络的输出值与目标值的误差,
遗传算法(genetic algorithm, GA)最早是由美国的Holland于20世纪70年代提出[13], 该算法是根据大自然中生物体进化规律而设计提出的[14]. 它的工作原理是首先对输入数据进行编码, 之后通过一定的概率进行选择、交叉和变异运算直到选择出适应度最大的个体作为目标值输出, 之后停止运算.
1.2.2 适应度函数的选择适应度函数是衡量种群中个体适应能力大小的标准, 一般情况下, 会将训练目标函数选作遗传算法的适应度函数, 本算法中采用误差平方的倒数作为适应度函数, 如式(6)和式(7)所示:
| $ E = \frac{1}{2}{\sum\limits_{j=1}^{n} {(\mathop P\nolimits_j^{k - 1} (w, x) - y_j)} ^2} $ | (6) |
| $ F(j) = \frac{1}{{E(j)}} $ | (7) |
式(6)中, E为误差函数, P为整体输出, w为权矢量, x为输入矢量; 式(7)中, F为适应度, j为迭代次数.
1.2.3 选择算子的改进传统的遗传算法在工作过程中经常采用“轮盘赌”的方式, 种群中个体被选中的概率是随机的, 这种选择方式很有可能丢掉最优个体, 在实际的运算过程中会产生较大的误差. 因此, 本文对选择算子进行改进, 首先将种群个体利用排序法进行重新排列, 重新排序之后个体被选择的概率如式(8)和式(9)所示:
| $ {{s}} = \frac{{{{{p}}_{\text{0}}}}}{{{{1 - (1 - }}{{{p}}_{\text{0}}}{{\text{)}}^{{a}}}}} $ | (8) |
| $ p = s{(1 - {p_0})^{b - 1}} $ | (9) |
式(8)和式(9)中, a为遗传算法中种群的数量, p0为最优个体可能被选择的概率, s为将p0进行标准化后的值, b为在对种群重新排列后第n个个体所在的位置.
1.2.4 交叉算子的改进传统的遗传算法在工作过程中一般会将交叉概率设为0.3–0.8之间的一个常数. 在运算过程中, 交叉概率设置过高会提高遗传算法的全局搜索能力, 但染色体的适应能力会有所下降, 而交叉概率设置得过低会降低遗传算法的全局搜索能力和收敛速度. 本文对交叉算子进行改进, 在算法迭代过程中会根据适应度的变化来调整交叉概率的变化, 改进的交叉概率如式(10)所示:
| $ {{{P}}_{{j}}} = \left\{ {\begin{array}{*{20}{l}} {{P_{{{j{\rm{max}}}}}}, }&{F < {F_{{\rm{mean }}}}}\\ {{P_{{{j{\rm{max}}}}}} - \dfrac{{{P_{{{j}}\max }} - {P_{{{j\min}}}}}}{{{n_{\max }}}} \times n, }&{F \geqslant {F_{{\rm{mean }}}}} \end{array}} \right. $ | (10) |
其中, F为种群中两个进行交叉的个体的最大适应度, Fmean为整个种群的平均适应度, n为遗传算法在当前工作过程中的迭代次数,nmax为遗传算子在工作过程中的最大迭代次数, 在遗传算法初始化时可以将最小交叉概率Pjmin设置为0.3, 最大交叉概率Pjmax设置为0.8.
1.2.5 变异算子的改进传统的遗传算法在工作过程中一般会将变异概率设为0.001–0.1之间的一个常数. 在遗传算法运算初期, 种群个体的适应度相对平均适应度较低, 所以需要将变异的概率设为较小的值, 从而保留染色体中基因优良的个体. 在遗传算法运算的后期, 种群个体的适应度相对高于平均适应度, 因此需要将变异的概率设为较大的值来提高遗传算法的局部搜索能力. 本文对变异算子进行改进, 在遗传算法运算过程中会根据适应度的变化来调整变异概率的值, 改进的变异概率如式(11)所示:
| $ {P_{{b}}} = \left\{ {\begin{array}{*{20}{l}} {{P_{{{b}}\min }}, }&{F < {F_{{\rm{mean }}}}}\\ {{P_{{\mathop{\rm bmax}\nolimits} }} - \dfrac{{{P_{{{b\max }}}} - {P_{{{b\min}}}}}}{{{n_{\max }}}} \times n, }&{F \geqslant {F_{{\rm{mean }}}}} \end{array}} \right. $ | (11) |
其中, F为种群中两个进行变异的个体的最大适应度, Fmean为整个种群的平均适应度, n为遗传算法在当前工作过程中的迭代次数,nmax为遗传算子在工作过程中的最大迭代次数, 在遗传算法初始化时可以将最小变异概率Pbmin设置为0.001, 最大变异概率Pbmax设置为0.1.
2 改进遗传算法优化BP神经网络预测模型 2.1 预测模型的设计框架BP神经网络的初始权值和阈值对训练的结果有着很大的影响, 并且在训练过程中容易陷入局部最优, 因此为了提高BP神经网络的预测精度以及避免BP神经网络陷入局部最优的问题, 引入了改进遗传算法对BP神经网络的权值和阈值进行优化. 传统遗传算法的选择概率、交叉概率和变异概率使用的是固定的常数, 这样在训练的前期和后期容易产生局部最优解, 为了解决这个问题, 对选择算子、交叉算子和变异算子的概率进行了改进, 通过判断当前适应度值从而对选择概率、交叉概率和变异概率进行调整. 随着适应度值的不断变化, 预测模型的选择概率、交叉概率和变异概率会随之产生变化, 使预测模型能够将各个参数调整为模型最佳的状态, 形成了改进遗传算法优化BP神经网络预测模型.
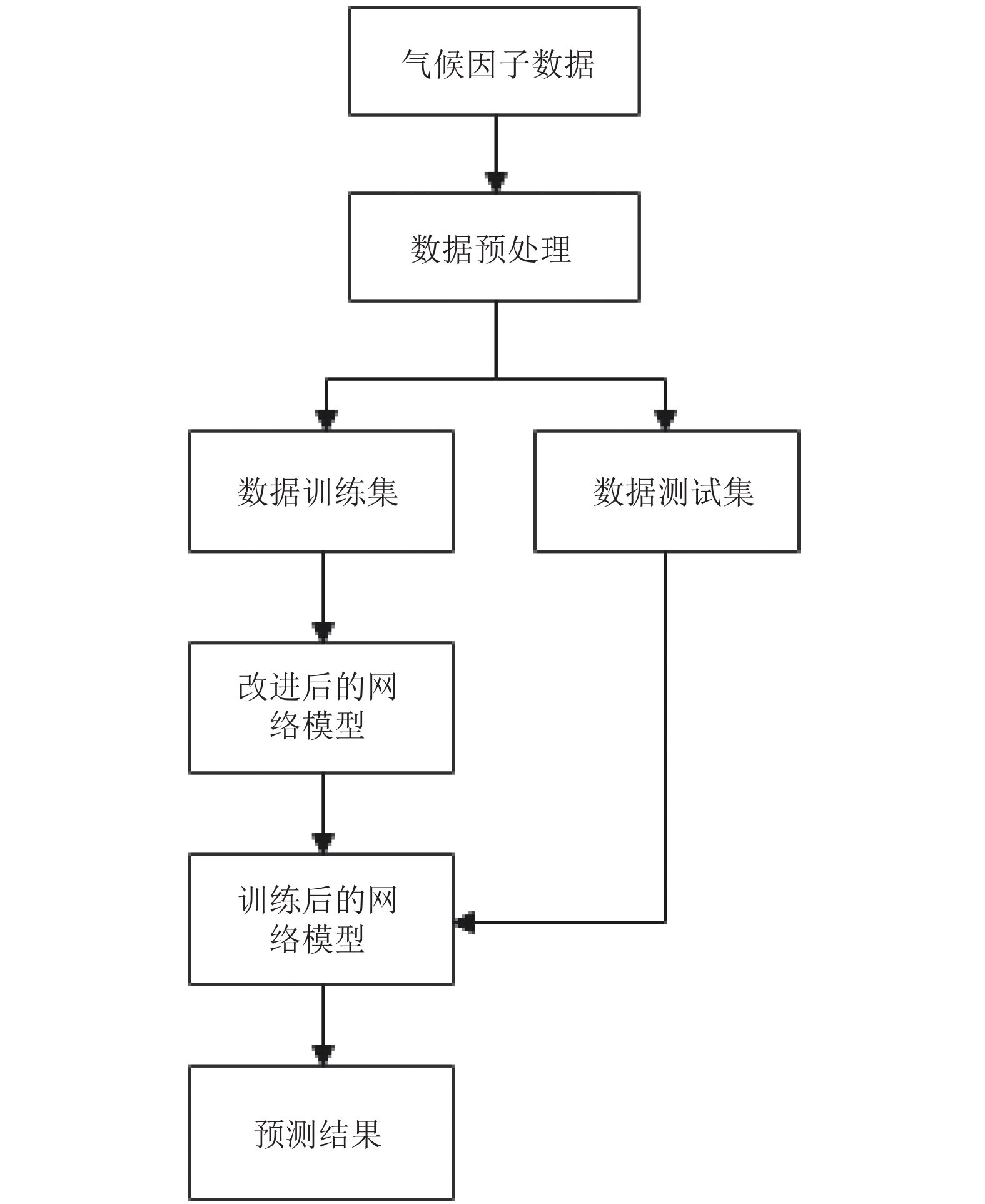
在改进遗传算法优化BP神经网络预测模型中, 具体操作流程包括以下几个方面, 首先通过传感器对空气温度、空气湿度和光照强度3种气象数据进行采集; 其次, 对采集数据进行预处理, 由于采集后的数据可能存在错误数据, 将3组数据中的最大值和最小值去除, 并根据实际数据进行插值处理, 得到正确的气象数据; 再次, 将预处理的数据分为两组, 一组作为训练集, 另一组作为测试集. 最后将训练集数据导入预测模型中对预测模型进行训练, 再将测试集导入训练好的预测模型中进行预测评估. 改进遗传算法优化BP神经网络预测模型的设计框架如图2所示.
|
图 2 改进遗传算法优化BP神经网络框架图 |
2.2 预测模型的设计流程
实验所使用的软件平台为Matlab R2018a, 计算机硬件为Windows 7系统, CPU频率为2.50 GHz, 内存为8 GB, 硬盘为500 GB. 将改进的遗传算法与BP神经网络结合, 建立了基于改进遗传算法优化BP神经网络, 提高了预测模型的预测精度. 改进遗传算法优化BP神经网络流程图如图3所示.

|
图 3 改进遗传算法优化BP神经网络流程图 |
3 实验仿真分析 3.1 预测模型的参数设置
进行预测模型的训练之前, 要对预测模型的参数进行设置, 在Matlab R2018a软件平台下构建基于改进遗传算法优化BP神经网络模型, 对改进遗传算法优化BP神经网络预测模型的相关参数进行设置, 输入层的节点数设置为3个, 隐含层的节点数设置为9个, 输出层的节点数设置为1个, 激活函数采用的是Sigmoid函数, 神经网络的迭代次数为1 000.
3.2 预测模型的误差评估为了测试预测模型的精确度, 采用MAE (平均绝对误差)、MAPE (平均绝对百分率误差)以及RMSE (均方根误差)3种误差分析方法对预测模型的精确度进行评估, 从而验证预测模型的准确性. 3种误差公式如式(12)、式(13)、式(14)所示.
| $ MAE = \frac{1}{N}\sum\limits_{i = 1}^N {|y_i - m_i|} $ | (12) |
| $ MAPE = \frac{1}{N}\sum\limits_{i = 1}^N {\frac{{|y_i - m_i{\text{|}}}}{{y_i}}} $ | (13) |
| $ RMSE = \sqrt {\sum\limits_{i = 1}^N {{{(y_i - m_i)}^2}} } $ | (14) |
实验数据来自黑龙江省哈尔滨市呼兰区玉米种植基地, 基地采用农业物联网技术, 通过物联网技术对种植基地的各种气象数据进行采集, 将采集的数据进行处理后, 选取1 000组环境气象数据作为本文的试验数据, 试验数据包括空气温度、空气湿度和光照强度. 试验将1 000组数据分为两部分, 随机选取980组数据作为预测模型的训练数据, 剩余20组数据作为测试数据, 表1为部分试验数据.
| 表 1 部分采集数据 |
3.4 实验仿真结果
使用处理后的训练数据对模型进行训练, 将训练后的预测模型通过测试集数据测试, 并将BP神经网络、遗传算法优化BP神经网络和改进遗传算法优化BP神经网络的测试结果进行对比, 数据预测结果如图4所示.
图4(a)、图4(b)和图4(c)分别是BP神经网络、遗传算法优化BP神经网络和改进遗传算法优化BP神经网络的预测结果对比图, 由图可知改进遗传算法优化的BP神经网络预测效果最好, BP神经网络预测效果最差.

|
图 4 各个模型预测误差 |
通过测试集数据对预测模型进行预测后, 分别计算各个模型的相对误差, 误差对比情况如表2所示.
表3为模型预测误差, 通过各个预测模型的结果计算它们的MAE、MAPE以及RMSE 三种误差, 从表3能够看出, IGA-BP模型的预测精度最高,MAE、MAPE以及RMSE分别是0.014 2、0.000 4和0.063 4, 与BP预测模型相比分别提高了3.13%、0.11%和14.02%; 与GA-BP模型相比分别提高了2.55%、0.09%和11.4%, 所以IGA-BP预测模型的预测质量更高.
| 表 2 各个模型预测结果 |
| 表 3 模型预测误差比较 |
通过对训练结果的分析, 改进的遗传算法优化的BP神经网络具有更好的稳定性和精确性, 对BP模型、GA-BP模型和IGA-BP模型输出的相对误差可以得出, IGA-BP模型的相对误差普遍较小; 对3种预测模型的MAE、MAPE以及RMSE进行分析可以得出IGA-BP模型的预测效果更精准.
4 结论与展望本文提出了一种土壤湿度预测模型, 该模型具有良好的预测性能, 能够提高土壤湿度的预测精度, 为土壤湿度的预测提供了新的模型和方法. 该模型的具体实施步骤是: (1)对数据进行预处理, 初始化BP神经网络, 从而获得初始权值和阈值; (2)对初始权值和阈值进行编码, 导入改进的遗传算法模型中并且初始化遗传算法; (3)通过改进的遗传算法能够得到最优的权值和阈值, 从而提高了预测模型的精确性. 本文通过对黑龙江省哈尔滨市呼兰区玉米种植基地采集的数据进行训练, 之后取20组数据对模型进行测试, 结果显示本文提出的土壤预测模型具有更高了预测精度.该模型还有很多不足之处, 比如该模型的适应性有待提升, 对环境气候不同地区的预测可能会产生误差, 因此未来的改进方向是如何更好地适应不同地区土壤环境预测, 对干湿度不同地区的土壤湿度进行准确预测.
| [1] |
孙浩然, 孙琳, 毕春光, 等. 基于粒子群与模拟退火协同优化的农田物联网混合多跳路由算法. 智慧农业(中英文), 2020, 2(3): 98-107. |
| [2] |
王冰玉. 基于神经网络灰色模型的农田土壤湿度预测研究. 节水灌溉, 2020(7): 32-35. DOI:10.3969/j.issn.1007-4929.2020.07.007 |
| [3] |
Ignace DD. Determinants of temperature sensitivity of soil respiration with the decline of a foundation species. PLoS One, 2019, 14(10): e0223566. DOI:10.1371/journal.pone.0223566 |
| [4] |
张绪成, 马一凡, 王红丽, 等. 不同耕作方式对旱地全膜双垄沟播玉米产量和水分利用的影响. 生态学报, 2021, 41(9): 3603-3611. |
| [5] |
张峰峰, 张欣, 陈龙, 等. 采用改进遗传算法优化神经网络的双目相机标定. 中国机械工程, 2021, 32(12): 1423-1431. DOI:10.3969/j.issn.1004-132X.2021.12.005 |
| [6] |
闫春, 厉美璇, 周潇. 基于改进的遗传算法优化BP神经网络的车险欺诈识别模型. 山东科技大学学报(自然科学版), 2019, 38(5): 72-80. |
| [7] |
周婧, 白云龙, 张小宝, 等. 基于MEA-BP神经网络的土壤养分评价模型. 中国农机化学报, 2020, 41(2): 231-236. |
| [8] |
彭彬彬, 闫献国, 杜娟. 基于BP和RBF神经网络的表面质量预测研究. 表面技术, 2020, 49(10): 324-328, 337. |
| [9] |
魏良良, 丁祥, 蔡甜, 等. 基于BP神经网络与改进遗传算法的泵站优化调度. 水电能源科学, 2019, 37(5): 168-171. |
| [10] |
张然, 刘敏, 张启坤, 等. 一种基于SA-SOA-BP神经网络的网络安全态势预测算法. 小型微型计算机系统, 2020, 41(10): 2157-2163. DOI:10.3969/j.issn.1000-1220.2020.10.022 |
| [11] |
Zhao Z, Chen WH, Wu XM, et al. LSTM network: A deep learning approach for short-term traffic forecast. IET Intelligent Transport Systems, 2017, 11(2): 68-75. DOI:10.1049/iet-its.2016.0208 |
| [12] |
Kuremoto T, Kimura S, Kobayashi K, et al. Time series fore-casting using a deep belief network with restricted Boltzmann machines. Neurocomputing, 2014, 137: 47-56. DOI:10.1016/j.neucom.2013.03.047 |
| [13] |
Holland J. Adaptation in natural and artificial systems: An introductory analysis with application to biology. Control & Artificial Intelligence, 1975. |
| [14] |
宋尧, 仰燕兰, 叶桦. 改进遗传算法在MSPSP问题中的验证. 计算机系统应用, 2020, 29(10): 235-241. DOI:10.15888/j.cnki.csa.007591 |
 2022, Vol. 31
2022, Vol. 31


