1 背景和目标 1.1 课题背景

省域地理范围房产权利登记和交易活动中所形成的历年数据记录是反映我国经济社会活动的重要大数据基础资源. 我们在承担广东省应用型科技研发专项资金重点项目“省域房地产交易数据资源云同步及大数据规模化应用”过程中, 获得了海量的广东省域房地产交易法定业务实录大数据资源. 然而, 这些过往业务所产生的历史和现状大数据的直接使用, 只能发挥其档案查询、数据统计和现态监控的数据支持作用, 对于省级房地产主管部门进行房地产市场预警预报, 开展住房和房地产管理政策、产业发展和住房建设规划的研究和制定等并无前瞻性的帮助. 就我国房地产大数据应用意义而言, 省域区划是我国社会治理和政治经济特色的最大综合管治(包括监管服务与行业调控)单元. 特别是, 广东省作为我国第一经济大省, 2019年全省实现地区生产总值107 671.07亿元(仅低于世界排行第12名的韩国), 其中全年新增房地产开发投资15 852.16亿元^[1], 加上城镇与房产为依托的各行各业的经济产值则总量更为巨大. 因此在宏观层面研究广东省域房产大数据并深化其应用具有重要的现实意义. 本文拟通过建立基于人工智能的系统平台, 全程实现对既有积累的海量房产法定业务大数据资源做可视化呈现并面向未来进行建模预测, 以探索实现直观地显示预示广东省域城乡建设、城镇发展的某些重要指标(如房产或房屋建筑面积和套数)的时空演化过程, 为研究广东省域城乡建设、区划经济的布局趋势, 科学有效地辅助支持各相关城市开发建设管理决策和省域房地产市场宏观调控等工作服务.

1.2 前期工作

在“十三五”期间, 我们一直从事广东省域房产大数据相关工作, 具备了进一步开展房产大数据深度智慧应用的基础.

1.2.1 房产大数据基础平台及数据资源开发建设

建立“(房产)行业数据云同步枢纽平台系统”: 实现了可覆盖全省各市房地产交易登记数据的同步归集. 提供了包括同步系统节点规划管理、安装配置, 分块流水线处理、单和双向同步(全量/增量, 乐观/谨慎校验策略, 同步块及分组调适)、并发控制、指标映射、多属性主键归一、敏感字段Hash, 以及同步正确性保障等较齐全的同步枢纽平台功能.

建立“HBDP (housing big data platform)省房屋大数据计算集群及作业调度系统”^[2]: 集群采用Hadoop分布式文件存储架构, 选用Hive管理元数据, 供用户利用Spark SQL进行房屋大数据分布式交互分析, 参见图1.

归集省域房产交易登记数据资源: 形成全省房产交易与产权管理数据大字典1 137页(省和各市卷合编), 入库各市4 108个原始表、92 871列字段、9.07亿条记录, 约203.7 GB数据量. 析出房产单元约1 551.4万套(其中, 住宅831.8万套, 有房屋建成年份的约1 200万套)、产权人827万. 梳理8市网签和预售系统楼盘表共935.4万户和22 790个房地产项目的数据.

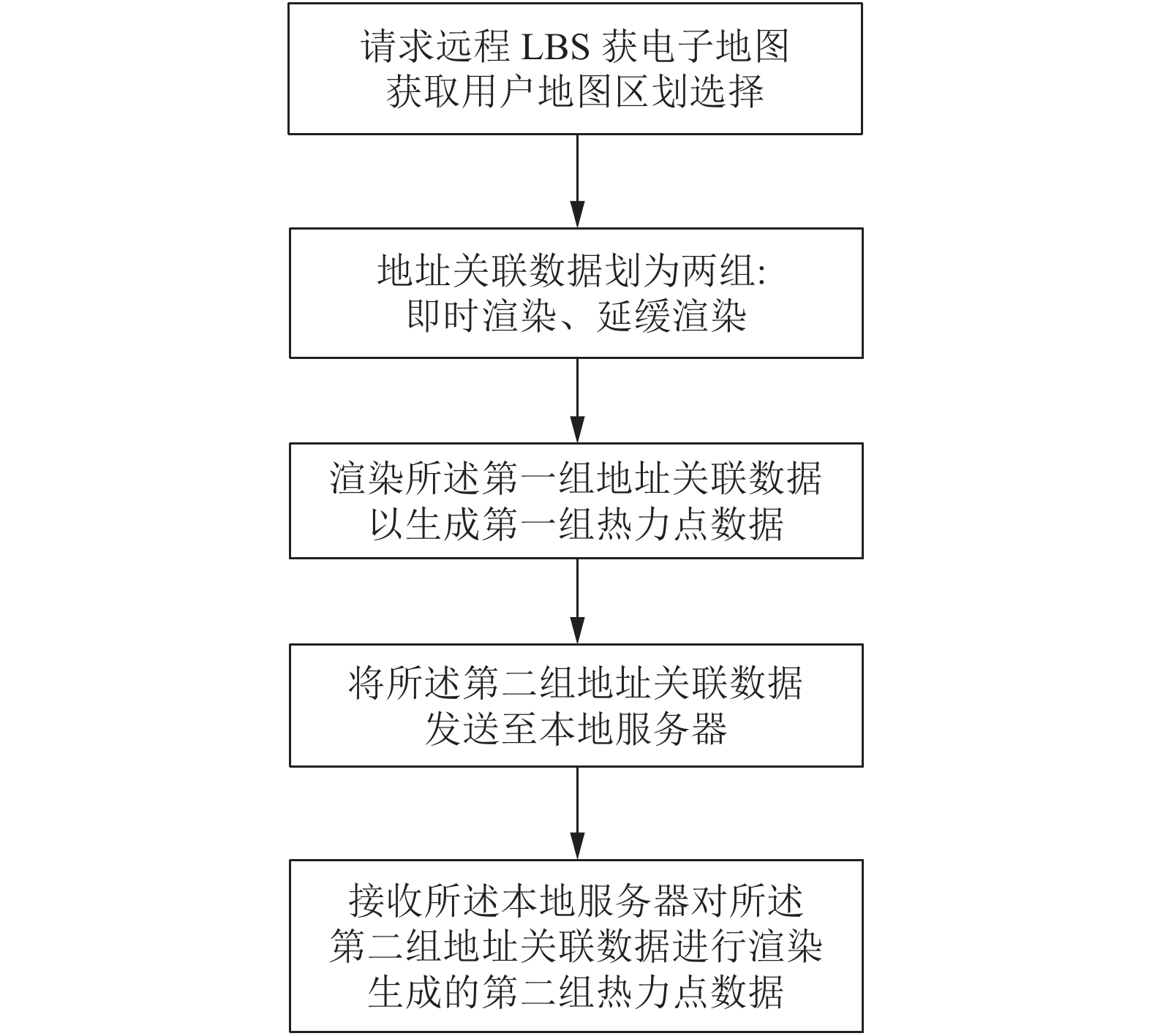
1.2.2 海量地址关联数据的热力图渲染优化研发

地址关联数据的地理分布热力图呈现通常是依托基于位置服务 (location-based service, LBS)公共平台进行二次开发实现. 现有方案是将所有地址关联数据在本地进行整理后按照固定的格式全部上传至LBS服务提供商的远程服务器, 由远程服务器处理后返回本地进行呈现. 但是, 在处理海量数据时, 该方案由于互联网带宽和PC浏览器处理能力的限制, 实际响应慢, 用户体验差. 对此, 我们通过实践探索, 创造性实现了“一种地址关联数据处理方法、用户终端和服务器”^[3], 它依据用户选择的需求参数和应用的地图属性, 将输入的海量地址关联数据划分成即时渲染(第1组)和延缓渲染(第2组)两组数据, 使得第1组的数据能迅速在客户端呈现, 同时第2组数据的落图渲染计算在本地服务器(集群)同步进行. 这种前后两组计算结合能显著地提高海量地址关联数据落图渲染呈现的响应速度, 改善了相关应用的用户体验, 解决了一般PC端网页浏览器在交互式播放海量地址关联数据渲染所普遍遇到的显示滞卡问题. 具体参见图2.

1.3 课题目标 1.3.1 省域房产大数据热力图系统总体构成

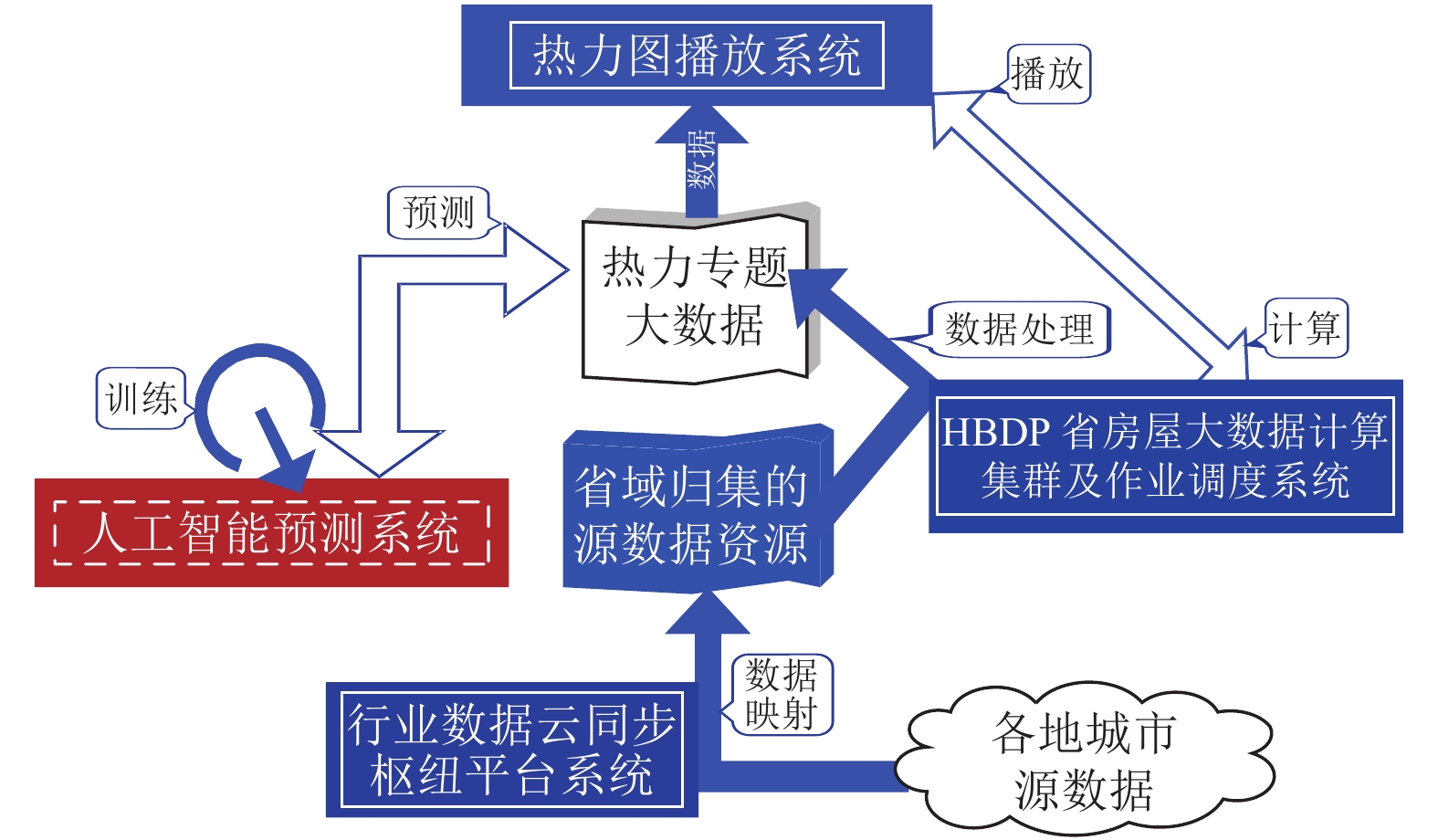
系统总体由两大部分构成, 参见图3.

第一部分是基础设施部分, 它由负责数据归集和专题数据生产的系统构成: 首先由“(房产)行业数据云同步枢纽平台系统”同步归集广东省域各地城市源数据, 然后, 经由“HBDP省房屋大数据计算集群及作业调度系统”计算生成适用于热力图渲染播放的热力值专题大数据对象. 本文术语“房屋”与“房产”可相互通用, 具体沿继使用习惯.

第二部分是热力图播放和预报部分, 它由“热力图播放系统”和“人工智能预测系统”构成. 其中, “人工智能预测系统”为本文研发的重点, 它提供人工智能建模预测功能, 负责使用已有的热力值数据训练模型并产生预测输出.

1.3.2 关键研发任务—人工智能预测系统

在前述总体框架, 待研发实现的是“人工智能预测系统”. 而该系统的关键在于如何有效地实现“省域房产大数据热力值预测计算”的核心课题任务上. 基于我们所能掌握的广东省域房产大数据资源限于2018年之前的原始数据, 我们将本文主要课题任务的实质性研发内容具体地明确为: 如何利用人工智能算法对既获得的已知的广东省各市截至2017年的房产登记和交易业务等历史记录的指标数据(房产套数和面积)的热力值, 建立可重复使用的时序预测模型系统, 特别是, 近期实现预测后来2018–2023年指标数据热力值; 据此, 为将来具备条件(获得后继年份数据资源)时, 滚动地推广应用至更多的未知数据年份.

2 技术问题归结与预测建模设计

针对上节提出的主要课题任务, 我们首先从计算机系统开发建设与应用的角度出发, 细化和明确所拟要研究解决的实质技术问题及其技术路线. 具体地, 本文课题的核心研发内容主要包括以下3方面: 1)关键指标及其计算问题的归结; 2)总体计算处理框架设计; 3)时序预测模型设计与实现.

2.1 问题归结

(1)房产热力值的定义

所谓热力图就是关于地理区域单元上的计算指标的值即“热力值”的地图渲染. 具体地, 本课题所研究的房产热力值是关于一个地理区域内的房产指标(套数和面积)的统计量的数值.

(2)时序数据计算任务定义

本文处理的房产指标热力值是具有时间属性的, 从而可构成时序序列. 相应的时序数据计算任务包括: 一是由原始房产业务记录导出可直接计算房产热力值的房产单元记录; 二是由已知的一系列年份的房产单元记录数据集计算出对应地理区域的房产指标(套数和面积)的热力值(可直接在百度地图上标识渲染成热力图); 三对地理区域后继年份的未知房产指标热力值进行预测计算. 为简化起见, 只对套数和面积两个基本指标进行预测.

鉴于房产数据的变化规模与频度的实际情况, 本文所考虑的时序单位明确为“年份”.

原始房产业务记录化为如下房产单元记录格式:

<房产单元>(经度, 纬度, 建成年份, 套数|面积, 城市)

其中, 经度和纬度坐标是用房产单元坐落地址调用“百度开放平台”Web服务API的地理编码服务(又名Geocoder)^[4]获得. 例如, 以房产单元坐落 “广州市越秀区豪贤路102号”调用百度Geocoder, 可获得经纬度坐标{113.281 270 035 554 5, 23.136 617 015 096 8}.

我们所讨论的房产热力值是关于具体地理区域内的所有<房产单元>个数(称作“套数”)或面积的统计值的数量指标. 欲将房产热力值落在百度地图上渲染显示, 就必须将其与地理区域的坐标相关联. 为简单起见, 我们采取地理区域中心点的经度和纬度来标识地理区域, 从而有如下的房产指标热力属性关系:

<区域房产热力>(经度, 纬度, 年份, 热力值, 城市)

其中, “热力值”是该(经度, 纬度)所标识区域截止于“年份”的期末实有房产单元的“套数|面积”统计数(假设房产房屋建成后一直存在, 则它代表历年直至该“年份”期末的累计数, 以下均采用此假设).

(3)时序计算区域的网格化处理

为确定最基本的地理区域单元, 也为了细化计算处理、减少随机噪音影响, 我们将广东省全域(东沙群岛除外)分成 $ M \times M $ 个矩形区域( $ M > 0 $ ), 称作“M分网格”. 每个网格区域可用经其左下角点的网格线的行号和列号来唯一标识: 网格 $ (x,y) $ 代表以第x列、第y行(0≤x＜M, 0≤y＜M)网格线的交点为其左下角的矩形网格区域.

网格 $ (x,y) $ 区域的年房产热力值(套数|面积)按房产房屋建成年份排列构成如下时序:

1)网格 $ (x,y) $ 房产套数累计时序:

$ {{\boldsymbol{T}}_{x,y}} = \{ {{\boldsymbol{T}}_{x,y,1}},\;{{\boldsymbol{T}}_{x,y,2}},\; \cdots \} $

其中, $ {{\boldsymbol{T}}_{x,y,i}} $ 为第i年 $ (x,y) $ 区域累计房产套数.

2)网格 $ (x,y) $ 房产套数增量时序:

$ \Delta {{\boldsymbol{T}}_{x,y}} = \{ \Delta {{\boldsymbol{T}}_{x,y,1}},\;\Delta {{\boldsymbol{T}}_{x,y,2}},\; \cdots \} $

其中, $ \Delta {{\boldsymbol{T}}_{x,y,i}} $ 为第i年 $ (x,y) $ 区域新增房产套数, 可由下式计算:

$ \Delta {{\boldsymbol{T}}}_{x,y, i}={{\boldsymbol{T}}}_{x,y,i}-{{\boldsymbol{T}}}_{x,y,i-1} $

3)网格 $ (x,y) $ 房产面积累计时序:

$ {{\boldsymbol{A}}_{x,y}} = \{ {{\boldsymbol{A}}_{x,y,1}},\;{{\boldsymbol{A}}_{x,y,2}},\; \cdots \} $

其中, $ {{\boldsymbol{A}}_{x,y,i}} $ 表示第i年 $ (x,y) $ 区域累计房产面积.

4)网格 $ (x,y) $ 房产面积增量时序:

$ \Delta {{\boldsymbol{A}}_{x,y}} = \{ \Delta {{\boldsymbol{A}}_{x,y,1}},\;\Delta {{\boldsymbol{A}}_{x,y,2}},\; \cdots \} $

其中, $ \Delta {{\boldsymbol{A}}_{x,y,i}} $ 表示第i年 $ (x,y) $ 区域新增房产面积, 可由下式导出:

$ \Delta {{\boldsymbol{A}}_{x,y,i}} = {{\boldsymbol{A}}_{x,y,i}}\; - {{\boldsymbol{A}}_{x,y,i - 1}} $

进一步, 在更大的尺度上, 对于某个城市c, 我们得到市级房产热力值统计值序列如下:

1)市级房产套数累计时序:

$ {{\boldsymbol{T}}^c} = \{ {\boldsymbol{T}}_1^c,\;{\boldsymbol{T}}_2^c,\; \cdots \} $

其中, $ {\boldsymbol{T}}_i^c $ 表示第i年城市c累计房产套数.

2)市级房产套数增量时序:

$ \Delta {{\boldsymbol{T}}^c} = \{ \Delta {\boldsymbol{T}}_1^c,\;\Delta {\boldsymbol{T}}_2^c,\; \cdots \} $

其中, $ \Delta {\boldsymbol{T}}_i^c $ 表示第i年城市c新增房产套数, 可由下式导出:

$ \Delta {\boldsymbol{T}}_i^c = {\boldsymbol{T}}_i^c - {\boldsymbol{T}}_{i - 1}^c $

3)市级房产面积累计时序:

$ {{\boldsymbol{A}}^c} = \{ {\boldsymbol{A}}_1^c,\;{\boldsymbol{A}}_2^c,\; \cdots \} $

其中, $ {\boldsymbol{A}}_i^c $ 表示第i年, 城市c累计房产面积.

4)市级房产面积增量时序:

$ \Delta {{\boldsymbol{A}}^c} = \{ \Delta {\boldsymbol{A}}_1^c,\;\Delta {\boldsymbol{A}}_2^c,\; \cdots \} $

其中, $ \Delta A_i^c $ 表示第i年城市c新增房产面积, 可由下式导出:

$ \Delta {\boldsymbol{A}}_i^c = {\boldsymbol{A}}_i^c - {\boldsymbol{A}}_{i - 1}^c $

本课题的基本预测计算任务可归结为两个:

预测1: 给定网格区域 $ (x,y) $ 的房产套数n年时序数据 $ \{ {{\boldsymbol{T}}_{x,y,1}},\;{{\boldsymbol{T}}_{x,y,2}},\; \cdots ,\;{{\boldsymbol{T}}_{x,y,n}}\} $ , 预测下一年(第n+1年)该区域累计房产套数 $ {{\boldsymbol{T}}_{x,y,n + 1}} $ .

预测2: 给定网格区域 $ (x,y) $ 的房产面积n年时序数据 $ \{ {{\boldsymbol{A}}_{x,y,1}},\;{{\boldsymbol{A}}_{x,y,2}},\; \cdots ,\;{{\boldsymbol{A}}_{x,y,n}}\} $ , 预测下一年(第n+1年)该区域累计房产面积 $ {{\boldsymbol{A}}_{x,y,n + 1}} $ .

显见, 通过逐年向前移动时序数据, 就可实现: 利用过去一段时间房产数据的变化, 对未来一段时间内的房产数据进行预测.

2.2 总体处理框架设计

根据上节的分析, 课题的基本科学技术问题在于建立时序预测模型: 利用过去一段时间内某事件(房屋建成事件)的时间特征来预测未来一段时间内该事件的特征(房产套数或面积)—这种时间序列数据预测.

鉴于房产套数和建筑面积的预测的建模都是类同的, 本文仅需阐述房产套数的预测模型.

实践上, 我们先直接对广东省域(由于东沙群岛无房地产项目, 本文研究的广东省域不包括东沙群岛)各网格单元应用深度神经网络建立预测模型. 结果所产生的预测误差普遍过大, 且无法调优模型将误差降到合理程度. 这是因为, 全省各市房地产源数据集的房产热力指标值的地理空间和时间区间的分布相当不均匀, 并且在时间和空间上存在不同程度的数据样本不足. 因此, 我们提出“网格累计量预测+市域增量预测修正”的总体预测建模计算框架. 具体工作思路如下.

1)对广东省域地图做M分网格, 将其中的任意网格看作独立单元, 运用基于深度神经网络的预测模型对其房产套数时序数据进行独立预测, 获得其下一时序点套数的预测值.

2)考虑到实际上同一城市的不同区域间受共同的城市发展内在关系影响, 彼此间应存在某些关联或约束, 我们在模型中进一步引入同城数据约束修正来提高预测结果的合理性和准确性.

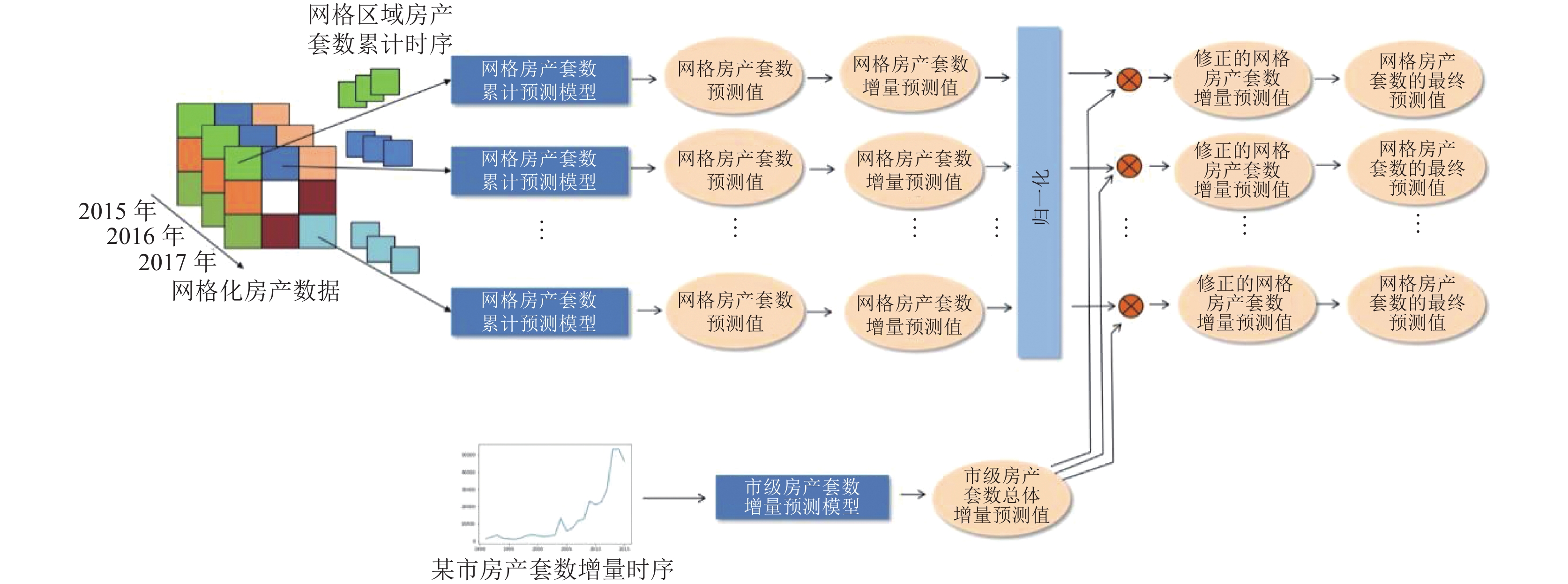
总体处理框架如图4所示. 具体过程如下.

1)市域网格预测

将同属一个城市的所有网格区域筛滤出来, 然后将每个网格区域 $ (x,y) $ 的房产累计套数年份时序 $ \{ {{\boldsymbol{T}}_{x,y,1}},\;{{\boldsymbol{T}}_{x,y,2}},\; \cdots ,\;{{\boldsymbol{T}}_{x,y,n}}\} $ 输入到基于深度神经网络的网格房产套数累计预测模型. 该预测模型输出下一个时序年份该区域房产套数累计 $ {{\boldsymbol{T}}_{x,y,n + 1}} $ 的预测值 $ {\overline {\boldsymbol{T}} _{x,y,n + 1}} $ . 根据 $ {\overline {\boldsymbol{T}} _{x,y,n + 1}} $ , 计算出对应的房产套数增量的预测值:

$ {\overline {\Delta {\boldsymbol{T}}} _{x,y,n + 1}} = {\overline {\boldsymbol{T}} _{x,y,n + 1}} - {{\boldsymbol{T}}_{x,y,n}} $

对同属城市c的每个区域 $ (x,y) $ 的房产套数增量预测值进行归一化, 得到:

$ {Norm} {\text{(}}{\overline {\Delta {\boldsymbol{T}}} _{x,y,n + 1}}{\text{)}} = \frac{{{{\overline {\Delta {\boldsymbol{T}}} }_{x,y,n + 1}}}}{{\displaystyle\sum\nolimits_{{\text{(}}u,v{\text{)}} \in {\Omega _{\text{c}}}} {{{\overline {\Delta {\boldsymbol{T}}} }_{u,v,n + 1}}} }} $

其中, $ {\Omega _c} $ 表示所有属于城市c的网格区域 $ (u,v) $ 的集合.

2)市域全局修正

用同城全域数据作为约束对 $ {\overline {\Delta {\boldsymbol{T}}} _{x,y,n + 1}} $ 值进行修正. 为此, 先计算出该市全域房产套数增量时序 $ \{ \Delta {\boldsymbol{T}}_1^c,\;\Delta {\boldsymbol{T}}_2^c,\; \cdots , $ $ \;\Delta {\boldsymbol{T}}_n^c\} $ , 将该时序输入到基于深度神经网络的市级房产套数增量预测模型, 得到下一个时序年份该市房产套数增量 $ \Delta {\boldsymbol{T}}_{n + 1}^c $ 的预测值 $ \overline {\Delta {\boldsymbol{T}}} _{n + 1}^c $ . 以此同城全域增量预测值 $ \overline {\Delta {\boldsymbol{T}}} _{n + 1}^c $ 作为全局约束, 对该市网格区域 $ (x,y) $ 的房产套数增量预测值 $ {\overline {\Delta {\boldsymbol{T}}} _{x,y,n + 1}} $ 做修正:

$ {\overline{\overline {\Delta {\boldsymbol{T}}}} _{x,y,n + 1}} = \overline {\Delta {\boldsymbol{T}}} _{n + 1}^c \cdot {Norm} {\text{(}}{\overline {\Delta {\boldsymbol{T}}} _{x,y,n + 1}}{\text{)}} $

由此修正后的房产套数增量的预测值, 得到该网格区域的累计房产套数最终预测值:

$ {\overline{\overline {\boldsymbol{T}}} _{x,y,n + 1}} = {\overline{\overline {\Delta {\boldsymbol{T}}}} _{x,y,n + 1}} + {{\boldsymbol{T}}_{x,y,n}} $

实际操作上, 整个工作路线包括如下基本步骤:

1)数据预处理: 对原始数据进行清洗、网格映射、序列提取、数据规范化, 获得网格区域房产套数累计时序、网格区域房产面积累计时序、市级房产套数增量时序、市级房产面积增量时序.

2)使用网格区域房产套数累计时序, 训练图4中的网格房产套数累计预测模型^[5,6].

3)使用市级房产套数增量时序, 训练图4中的市级房产套数增量预测模型.

4)使用网格区域房产面积累计时序, 训练网格房产面积累计预测模型(与套数预测模型类似, 省略).

5)使用市级房产面积增量时序, 训练市级房产面积增量预测模型(与套数预测模型类似, 省略).

6)应用图4所示的预测过程对2018–2023年的房产套数进行预测, 输出规定格式的数据.

7)对2018–2023年的房产面积进行预测, 输出规定格式的数据(与步骤6)类似, 省略).

训练数据资源限于2018年之前的原始数据.

2.3 时序预测模型设计

前节的总体处理框架设计关键在于图4中的网格房产累计套数(或面积)预测模型和市级房产套数(或面积)增量预测模型设计—它们都是基于深度神经网络的时序预测模型设计. 众所周知, 在人工智能深度学习算法中^[7,8], 正如卷积神经网络主要用于图像数据建模, 循环神经网络(recurrent neural networks, RNN)主要用于时序数据建模. 但是, 传统的RNN在长期依赖方面存在梯度消失的问题, 也就是会遗忘时间序列距离比较远的信息. 1997年, Hochreiter和Schmidhuber提出了传统RNN的一种变形: 长短时记忆网络(long short term memory, LSTM)^[9]. LSTM通过引入3种门限(遗忘门限、输入门限和输出门限)而获得学习长期依赖的能力, 即具有学习时间序列距离较远信息的能力. 尽管LSTM相对于RNN更加复杂, 但因为它可以适应更长的时间序列数据, 我们用LSTM对已知的过往年份房产热力数据进行时序特征抽取, 并对这些特征进行时序预测^[10], 然后用全连接层(fully connected layers, FC)^[11]神经网络再将时序预测得到的特征数据回归映射成房产指标热力数据.

图4中的网格房产累计套数(或面积)预测模型和市级房产套数(或面积)增量预测模型均采用如图5所示的(LSTM→FC)房产数据时序预测模型设计: 先用LSTM对输入的n年份时序数据 $ \{ {{\boldsymbol{X}}_1},\;{{\boldsymbol{X}}_2},\; \cdots ,\;{{\boldsymbol{X}}_n}\} $ 进行特征抽取和预测, 输出该时序数据隐含的时序特征的抽象表达向量的预测值(不直接是房产指标热力值本身); 然后, 将LSTM模型的输出向量作为后面FC的输入, 经由FC做非线性变换后, 输出下一年份(第n+1年)的房产热力值 $ {{\boldsymbol{X}}_{n + 1}} $ 的预测值 $ {\hat {\boldsymbol{X}}_{n + 1}} $ .

2.4 预测建模技术实现

(1)技术选型

我们选择在谷歌公司的TensorFlow开源机器学习平台上实现预测建模^[12]. 在TensorFlow平台上, 我们使用 Keras^[13]这种直观的高阶API来构建和训练机器学习模型, 这样能够快速迭代模型并轻松地调试模型.

鉴于为省域房产大数据热力图预测而构建和训练机器学习模型需要频繁地进行大规模CPU-heavy的张量数值计算, 一般CPU难以承担. 于是, 我们配置强力的加速计算协处理器, 即引入具有比CPU更加强大密集数据计算能力的GPU来参加计算. 但是, 传统的访问GPU模式(如依赖图像API接口来实现GPU访问)无法将GPU强大的密集数据计算能力用于图像处理之外的用途. NVIDIA发明的CUDA (compute unified device architecture)编程模型采用了一种全新的计算体系结构来使用GPU硬件资源, 可让软件开发者在应用程序中能充分地利用CPU和GPU各自的优点, 特别是充分利用GPU强大的计算能力加速大规模密集数据计算^[14]. NVIDIA已将CUDA实现成一套实用编程环境, 并且可通过对应的SDK集成到更高级别的机器学习框架中. 其中, cuDNN就是CUDA的一个专门用于TensorFlow神经网络运算加速的SDK^[15]. 因此, 我们采用TensorFlow+CUDA+cuDNN的开发环境来运行调试深度神经网络.

(2)算法部署

TensorFlow平台选择Python作为表达和控制模型训练的语言. Python是数据科学家和机器学习专家用的最舒适的高级语言, 籍用其NumPy^[16]库的丰富计算资源, 可以很容易地在Python中进行各种海量数据高性能预处理计算, 然后输送给TensorFlow进行真正CPU-heavy计算. 所以我们采用Python语言进行编程. 具体环境部署上, 使用Anaconda安装和管理Python相关包—Anaconda提供最便捷的方式来使用Python进行数据科学计算和机器学习^[17]. 算法部署主要包括模型训练和生成数据两部分.

模型训练部分的目录部署: data文件夹: 存放预处理后的数据, model文件夹: 存放训练好的模型; Python可执行代码文件“网格累计(套数|面积)模型训练.py”用于网格累计(套数|面积)模型的训练, “登记单市模型训练.py”与“网签单市模型训练.py”分别用于对单个城市的登记与网签数据增量模型进行训练.

生成数据部分的目录部署: Python可执行代码文件“登记面积数据生成.py”“登记套数数据生成.py”“网签面积数据生成.py”和“网签套数数据生成.py”分别对登记数据面积、登记数据套数、网签数据面积、网签数据套数进行预测, 并会将结果分别保存在dj_area(登记面积)、dj_count (登记套数)、wq_area (网签面积)、wq_count (网签套数)目录下.

(3)训练预测模型

训练好的模型存放在model 文件夹下. 如果一个市的数据发生大幅变动, 则需重新训练. 训练命令语法格式为:

Python + 运行脚本名称 + argv1 + argv2 + argv3

其中, argv1 代表预处理后的数据集名, argv2 代表城市名称, argv3 代表热力指标名称(套数或面积). 若训练过程误差不下降, 则需重新运行脚本—可能是模型参数随机初始化或者训练样本过少造成的.

(4)生成预测数据

在数据生成代码所在目录, 使用Python命令:

Python + 运行脚本名称 + argv1

其中, argv1 代表预处理后的数据集名. 运行结果除在指定的文件夹下生成套数|面积热力图预测数据的JSON格式文件外, 还在当前目录下生成相应的CSV格式文件. JSON格式的输出数据可直接用于热力图渲染, CSV格式的输出数据便于做大数据分析.

3 预测模型应用 3.1 处理模式和建模设定 3.1.1 数据压缩落图

原始房产数据极其庞大, 难以全部在百度地图上落图显示, 必须先进行压缩映射预处理并生成相应的训练数据集后, 才能应用预测模型对网格区域累计房产热力值(套数、面积)进行预测.

压缩映射: 将原始数据记录的经纬度坐标精度降低(将经纬度小数点后13位有效数字四舍五入至小数点后仅保留5位有效数字), 然后去掉重复值. 本课题所有房产地址的经纬度坐标均取自百度地图公开数据, 原始精度为小数点后13位有效数字.

“房产登记簿数据”共有12 476 111条房屋建成年代记录. 压缩映射得到353 464 条不同经纬度坐标的记录, 每条记录包含聚集计算出来的热力值属性(套数|面积).

“房产网签数据”共有6 076 778条新建房屋年份记录. 压缩映射得到50 242条不同经纬度坐标的记录.

3.1.2 数据网格映射

基于经纬度网格的房产指标数据热力图必须先将落在同一个网格中的各个房产原始数据记录归化成网格数据: 用网格中间点的经纬度坐标作为网格坐标, 网格区域中所有房产的指标统计值(如总建筑面积或总房产套数)作为网格的房产指标值.

再进一步将网格数据规范化, 即, 将所有网格数据映射成一个 ${Y} \times M \times M$ 点的张量 $ {\boldsymbol{Z}} $ ( $ {Y} $ 为房屋建成年份的最大时间跨度, $ M $ 为网格划分数):

对于任一条略去“城市”属性的网格房产数据记录 $ {\text{(}}{{lon} _q},la{t_q},yea{r_q},coun{t_q}{\text{)}} $ | $ 1 \leqslant {q} \leqslant m $ , m为网格数据记录总数, $ {\text{(}}{{lon} _q},la{t_q}{\text{)}} $ 为对应网格的经纬度, $ coun{t_q} $ 为该网格区域在年份 $ yea{r_q} $ 的房产统计指标增量值, 则其到张量 ${\boldsymbol{Z}}$ 的映射由式(1)–式(3)计算:

张量Z的第1维度坐标 $ k $ 可通过式(1)求得:

$ k = yea{r_q} - y_{\rm min} $

(1)

其中, $y_{\rm min}$ 代表所有记录年份中的最小值.

张量Z的第2维度横坐标 $ i $ 可通过式(2)求得:

$ i = \frac{{{\rm{(}}lo{n_q} - lo{n_{\min }}{\rm{)}} \times M}}{{lo{n_{{\rm{max}}}} - lo{n_{{\rm{min}}}}}} $

(2)

其中, $lon_{\rm{min}}$ 和 $lon_{\rm{max}}$ 分别代表广东省经度范围(东沙群岛除外)的最小值和最大值.

张量Z的第3维度纵坐标 $ j $ 可通过式(3)求得:

$ j = \frac{{{\text{(}}la{t_q} - lat_{\rm{min}} {\text{)}} \times {M} }}{{lat_{\rm{max}} - lat_{\rm{min}} }} $

(3)

其中, $lat_{\rm{min}}$ 和 $lat_{\rm{max}}$ 分别代表广东省纬度范围(东沙群岛除外)的最小值和最大值.

最后, $ {\boldsymbol{Z}} $ 任意点 $ {\text{(}}k,i,j{\text{)}} $ 的数值 $ {{\boldsymbol{Z}}_{{k} ,i,j}} $ 由下式计算:

$ {{\boldsymbol{Z}}_{{k} ,i,j}} = \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{Z}}_{{k} - 1,i,j}} + coun{t_q},\; {{}}k > 0{{}}} \\ {coun{t_q},\; {{}}k = 0{{}}} \end{array}} \right. $

这样, Z_k,i,j (0≤k≤Y, 0≤i＜M, 0≤j＜M)代表网格 $ {\text{(}}i,{j} {\text{)}} $ 里累计至第 $ k $ 年末的房产套数或面积统计值.

3.1.3 网格数目选择

网格越细化(网格划分M越大), 网格化后的坐标点越多, 反之亦然.

首先, 我们选定广东省全域(东沙群岛除外)经、纬度范围:

[lon_min, lon_max]= [110.177, 116.885]

[lat_min, lat_max]= [20.334, 25.313]

然后, 就省域房产登记簿数据集, 计算网格划分数M与房产数据集网格化后其坐标点数目的关系, 结果见图6.

由图6可见, 网格化后数据集经纬度坐标点数目随着M的增大而增加, 但当M达到7 000后, 坐标点数目增长逐渐减弱, 说明: 此后网格划分继续细化对于网格化近似精度的提高其作用逐渐趋无. 若在获得较高的网格化近似精度的同时, 又兼顾算法的性能(网格化后坐标点越少就越好), 推荐M = 7000的网格化.

3.1.4 滑窗切分处理

对于长的时序数据序列一般采用滑窗法进行数据切分预测, 即限定一个滑动窗口, 依次将其顺时序向前移动一定步长来切取数据子序列用以预测后继若干时序值: 对于已知数据序列 $ {\text{(}}{{\boldsymbol{X}}_1},\;{{\boldsymbol{X}}_2},\; \cdots ,\;{{\boldsymbol{X}}_{N} }{\text{)}} $ , 取滑窗跨度L(L<N), 滑动步长S, 初始切取 $ {\text{(}}{{\boldsymbol{X}}_1},\;{{\boldsymbol{X}}_2},\; \cdots ,\;{{\boldsymbol{X}}_{L} }{\text{)}} $ 来预测 ${{\boldsymbol{X}}_{L{\text{+1}}}},\;{{\boldsymbol{X}}_{{L} {\text{+}}2}},\; \cdots ,\;{{\boldsymbol{X}}_{L{\text{+}}P}}$ (P<L), 向前滑动第1步, 切取 $ {\text{(}}{{\boldsymbol{X}}_{1 + {S} }},\;{{\boldsymbol{X}}_{2 + {S} }},\; \cdots ,\;{{\boldsymbol{X}}_{L + S}}{\text{)}} $ 预测 ${{\boldsymbol{X}}_{L{{ + }}{S} {{ + 1}}}}, {{\boldsymbol{X}}_{{L} {{ + }}{S} {{ + }}2}}, \cdots , {{\boldsymbol{X}}_{L{{ + }}{S} {{ + }}P}}$ , 接着滑动第2步, 重复前步类似的过程, 如此滑动预测, 直至第k步 $(L + k \times S + 1) \leqslant {N} \wedge (L + (k + 1{\text{)}} \times $ $ S + 1) > {N}$ .

鉴于要预测的年末实有房产套数和面积是不断增长的数值, 为降低解空间的取值范围, 我们将滑窗内 ${L}$ 个时点序列 $ {\text{(}}{{\boldsymbol{X}}_1},\;{{\boldsymbol{X}}_2},\; \cdots ,\;{{\boldsymbol{X}}_{L} }{\text{)}} $ 各项数据规范化为相对于其第1时点的增量值: $ {\text{(}}{{\boldsymbol{X}}_1} - {{\boldsymbol{X}}_1},\;{{\boldsymbol{X}}_2} - {X_1},\; \cdots ,\;{{\boldsymbol{X}}_{L} } - {{\boldsymbol{X}}_1}{\text{)}} $ , 以加快神经网络学习过程收敛.

3.1.5 建模参数取值

根据以上设计建立模型后, 我们针对本课题应用实际进行优化. 经测试后确定:

1) “网格房产累计预测模型”(参见图4中的“网格房产套数累计预测模型)的参数如表1所示.

2) “市级房产增量预测模型”(参见图4中的“市级房产套数增量预测模型)的参数如表2所示—只对全市域总增量值进行预测, 不用做网格划分.

3.2 房产数据预处理

通常不是所有的原始数据都可直接用于神经网络模型. 在此数据预处理是必须的.

3.2.1 数据清洗

数据清洗过程包括对缺失值、异常值进行处理.

缺失值处理: 对于缺失房屋建成年份、坐落地址或面积数值的数据, 直接舍弃, 因为这些数据对于时序预测没有意义; 对于缺失城市属性的数据, 可以根据房产坐落确定地理位置, 不会对预测结果产生影响.

异常值处理: 主要针对面积数值为零的原始数据—对此类数据记录直接舍弃.

3.2.2 数据集准备

深度学习算法需要切取历史时序数据进行训练和测试. 全部房产数据记录经网格数据映射存储在三维张量 $ {\boldsymbol{Z}} $ 中. 令 $ {\Omega _c} $ 为城市c所有网格的集合, 则从 $ {\boldsymbol{Z}} $ 中切取: 1)矩阵序列 $ {\text{(}}{{\boldsymbol{Z}}_1},\;{{\boldsymbol{Z}}_2},\; \cdots ,\;{{\boldsymbol{Z}}_{Y} }{\text{) | }}{{\boldsymbol{Z}}_{k} }{\text{ = \{ }}{{\boldsymbol{Z}}_{{k} ,i,j}}{\text{|(}}{i} ,{j} {\text{)}} \in {\Omega _c}{\text{\} }} $ $ {\text{(1}} \leqslant {k} \leqslant {Y} {\text{)}} $ , 2)数据序列 ${\text{(}}{{\boldsymbol{Z}}_{1,i,j}},{{\boldsymbol{Z}}_{2,i,j}}, \cdots ,{{\boldsymbol{Z}}_{{V} ,i,j}}{\text{)|}}{\boldsymbol{V}}{\text{ = }}{\rm{max}}{\text{(}}{l} {\text{)}}$ , $ \forall {{\boldsymbol{Z}}_{{l} ,{i} ,{j} }} \ne {\text{null(1}} \leqslant {l} \leqslant {Y} {\text{)}} $ , $ \forall {\text{(}}{i} ,{j} {\text{)}} \in {\Omega _c} $ 作为预测模型训练与测试的候选数据集.

对于每一份数据集来说, 均需要划分训练集与测试集. 训练集是模型学习时用的数据集, 是确定模型参数用的; 测试集则是检验模型性能时用的数据集. 在时序数据预测问题中, 训练集与测试集不能交叉. 训练集就类似考生平常做的习题, 测试集类似考试的题目, 后者是衡量一个模型泛化能力的数据集.

若测试集序列太短, 将不足以评价和调校预测模型. 结合各城市房产单元数据集的房屋建成年份时序范围的实际(详见表3), 我们取每个市至少最后5个年份的数据作为其评价模型的测试集, 即要具备最近5+3年(加上3年滑窗跨度)的原始数据. 这样绝大多数城市数据满足要求, 只有个别城市例外—在表3中用*标注: 佛山市房产登记簿仅有2012–2016年的数据; 梅州市、惠州市和茂名市的网签数据分别只有6、7和6个年份的.

具体以某市为例说明:

1)用最近1993–2017年数据进行预测评价:

输入2012年以前数据, 预测2013年的环比增量.

输入2013年以前数据, 预测2014年的环比增量.

输入2014年以前数据, 预测2015年的环比增量.

输入2015年以前数据, 预测2016年的环比增量.

输入2016年以前数据, 预测2017年的环比增量.

2)然后, 将预测结果与真实数据进行比较评价.

计算及评价结果见图7. 图中, 预测数据序列在2012年及之前的年份直接使用真实数据.

3.3 预测数据集生成

房产登记簿数据: 其落图压缩后得到的353 464 条不同经纬度坐标的数据记录网格化后, 落至81 240个经纬度网格上, 用于生成其预测模型的训练数据集.

房产网签数据: 其落图压缩后得到50 242条不同经纬度坐标的数据记录网格化后, 落到3 514个经纬度网格上, 用于生成其预测模型的训练数据集.

对于已知房产时序数据 $ {seq} = {\text{(}}{{\boldsymbol{X}}_1},{{\boldsymbol{X}}_2}, \cdots ,{{\boldsymbol{X}}_{L} }{\text{)}} $ , 将其规范为 $ {\text{(}}{{\boldsymbol{G}}_1},{{\boldsymbol{G}}_2}, \cdots ,{{\boldsymbol{G}}_{L} }{\text{)|}}{{\boldsymbol{G}}_{k} } = {{\boldsymbol{X}}_{k} } - {{\boldsymbol{X}}_1}{\text{(1}} \leqslant k \leqslant {L} {\text{)}} $ 后, 放入房产数据预测模型预测出 $ L+1 $ 年份相对于时序首年的热力值增量 $ {{\boldsymbol{G}}_{{L} + 1}} $ , 即可预测出至 ${{ L}} + 1 $ 年份的全量值:

$ {{\boldsymbol{X}}_{{L} + 1}} = {{\boldsymbol{X}}_1} + {{\boldsymbol{G}}_{{L} + 1}} $

将 $ {{\boldsymbol{X}}_{{L} + 1}} $ 加入已知序列得 ${seq} := {seq} + {\text{(}}{{\boldsymbol{X}}_{{L} + 1}}{\text{)}}$ . 再从新的 $ {seq} $ 最后面切取长度为L的子序列, 并对此子序列重复上述过程, 就可逐年推进预测未知年份的数据. 我们将一个年份的预测数据存储成一个文件, 以(经度, 纬度, 年份, 预测全量值)格式输出到JSON和CSV文件中. 其中, “预测全量值”代表直到该“年份”年末, (经度, 纬度)所标识区域的房产统计指标的历史累计值.

4 误差评价与学习校正

预测模型的评价指标采用平均绝对百分误差(mean absolute percentage error, MAPE):

$ {MAPE} = \frac{{100 {\text{%}} }}{{n} }\sum\limits_{i = 1}^n {\left| {\frac{{{{y} _i} - {y_i} '}}{{{{y} _i}}}} \right|} $

其中, n表示序列样本的个数, $ {y_i} $ 表示真实值, $ {y_i} ' $ 表示预测值. 平均绝对百分误差反映了预测值对真实值的偏离程度. 优化方法采用Adam (adaptive moment estimation)算法^[18]. Adam是一种自适应调节学习率的方法. 它利用梯度的一阶矩估计和二阶矩估计动态调整预测模型每个参数的学习率. Adam的优点主要在于经过偏置校正后, 每一次迭代学习率都有个确定范围, 使得参数比较平稳. 我们设定学习率 $ \alpha = 0.001 $ , 取每个市最后5年真实数据作为评价模型的测试集.

误差评价可按以下指标衡量:

1)预测增量相对于真实增量的误差MAPE-I.

2)预测全量相对于真实全量的误差MAPE-T.

对于深度学习过程校正: 增量和全量预测模型分别使用MAPE-I和MAPE-T进行偏置校正.

对于最终预测结果评价: 考虑到本课题是以预测各市年末实有房产数(累计全量数)为目标, 我们使用MAPE-T进行误差评价.

测试评价表明, 不同市的训练样本的数量和质量、环比变化梯度对于预测误差的影响是不同的, 详见表4. 表中佛山市的登记簿和梅州、惠州、茂名3市的网签数据因真实数据序列太短无法进行深度学习, 不能进行预测, 误差评价不适用(标记为NA). 此外, 个别市的训练数据样本较小, 年份实际增量波动较大, 预测效果相比其他市较差(例如, 湛江、茂名两市的登记簿数据预测, 以及韶关和汕尾两市的网签数据预测), 甚至出现极端误差情况(例如云浮市的网签数据预测). 但从整体结果来看, 我们的模型还是能捕捉到各市的房产指标数据的基本变化, 平均误差大多数在5%以下, 绝大多数在10%以下. 这说明, 针对性建立和训练的预测模型是有效的, 达到预期的目的.

5 图效展示

以广州市房屋登记簿时序数据预测为例. 我们用已知的1958–2017年历史数据记录, 对其各网格单元区域未知的2018–2023年各年年末房屋套数热力值进行预测. 然后将广州市各网格区域所有年份的年末实有房屋套数热力值在百度地图落图呈现—调用百度地图LBS服务, 渲染成市域房屋统计指标数据地理分布热力值图^[19], 并在此基础上提供正反时序的各年度热力图播放, 供观察比较. 为简便起见, 我们仅取广州市房屋套数分布热力图局部情况为例进行前后两两环比, 限于篇幅, 仅以图8和图9例示. 目测可见, 随着预测年份推延, 全市实有累计房屋套数的地理分布热力值增加趋势具有如下特征: 开始变化明显, 后来逐渐减弱. 这里的一个原因是随着预测年份的增长, 模型的预测值准确度下降, 预测结果趋同; 另一个原因是每当热力图图斑开始呈现高亮度色时, 后来的热力值增加对于图斑的增强作用会显著减弱. 图示目测效果大体与我们对广州市近年城市建设区域发展的直观预期相符.

6 结束语

(1)应用集成方面, 本文基于深度神经网络机器学习的广东省域房产大数据热力图人工智能预测系统, 与广东省域“(房产)行业数据云同步枢纽平台系统”^[20]、“HBDP省房屋大数据计算集群及作业调度系统”和“热力图播放系统”配合使用, 全面实现了可从过往已知的至后来未知的广东省域房产登记和交易大数据指标的热力图年时序播放展示, 有助于从时空维度俯瞰城市建设演化过程, 为城市资源和区划经济规划等相关的宏观管理活动提供历史和前瞻性的大数据参考, 也可作为满足人们对城市具体属性未来演变的预见愿望的行业大数据直观应用的实践范例.

(2)技术创新方面, 本文提出“网格累计量预测+市域增量预测修正”的总体预测建模计算框架, 相对于常规直接应用深度神经网络机器学习模型, 不但在建模前期引入了网格粒度调选环节, 为简化计算量提供选项, 更重要的是有效地将细化的局部预测与全局宏观预测修正结合, 较好地化解了因各地网格单元源数据样本质量参差不齐而引起的模型训练预测误差过大问题, 创造条件来调优应用长短时记忆与全连接层网络AI深度学习模型. 这样, 即使在网格单元样本时间和空间数据质量不理想情况下, 仍然实现了课题的技术目标: 系统产生的预测数据可直接应用于百度热力图呈现, 预测模型的可评测应用误差总体囿于合理范畴, 相应数据结果可视化符合人们目测预期.