铁路移动通信系统是铁路安全运营的核心之一, 其安全状况直接关系到高速铁路列车能否安全运行, LTE-R通信系统与现有高速铁路客运专线使用的 GSM-R 移动通信系统相比较, 具有更大带宽、系统架构扁平化和业务处理质量高等优点[1, 2]. 2018年, 中国铁道科学研究院在京沈客运专线上领导了LTE-R系统在高速条件下的动态测试, 并计划根据测试结果逐步建立标准规格和相关的安全评估基础[3]. 因此, 深入研究LTE-R通信系统安全风险评估, 对于高效展开基于LTE-R通信的应用, 寻找其薄弱环节, 对降低铁路安全事故发生可能性、提高列车安全运行效率具有举足轻重的意义.
目前, 对于铁路信号系统的安全性和控制研究理论较多, 但对信号系统中子系统通信系统部分安全风险评估方法少. 文献[4]使用云模型实现定性和定量分析并且以图形形式反映出来, 具有形象和直观, 但不能分析风险变化; 文献[5]使用多层次模型解决了具有多个属性和对象的复杂问题, 但操作时候主观判断难以量化, 解决方案的排名是不稳定的; 文献[6]使用灰色模糊理论通常使用灰色关联度反映总体间灰色关系, 但在说明关系时只在意在定量特性; 文献[7]利用可靠性框图、故障树和马尔科夫模型法来综合分析, 只定量的分析了不同应用场景下的LTE-R通信系统的可靠性. 上述分析方法主要反映了对象之间特定的随机、模糊和灰色等不确定性的关系, 没有关注风险动态变化或不确定性信息到确定性信息的链接和转换. 针对上述不足, 本文应用集对可拓对铁路通信系统进行风险评估. 集对分析理论是将确定性和不确定性因素转化为可预测的数学模型, 通过描述因素间的同一性、差异性和对立性的进行不确定性分析的方法. 结合可拓学理论, 从基于物元的角度, 使用可拓-集对评估模型, 对LTE-R 通信系统的安全性进行风险评估. 为LTE-R通信系统的风险评估提供了新的思路, 有助于提高通信系统运营期间的安全性管理能力以及通信系统时风险管控应对能力.
1 集对可拓评估理论 1.1 基本原理集对分析[8]在三分原则基础上分析集合间的同异反程度, 可拓学[9]采用物元变换和可拓联系度来定量描述事物的数量和质量变化. 可拓集合的正域、临界和负域, 与集对理论中同异反相似. 集合对和可拓集合论域可分为如图1 所示关系, 当数据处于由讨等级组成的可拓集合标准正域中时, 定义为集对同一性; 将位于过渡正域定义为集对的差异性, 而将负域定义为集对对立性[10].

|
图 1 集对同异反与可拓集合论域关系图 |
1.2 集对可拓模型构建
设N1, N2,…,Nk (k=1, 2, 3,…,K)为所有风险评估对象类别, Cj为第j(j=1,2,3,…,m)评估指标, vjk为评估对象类别Nk对于指标Cj量值,由物元概念得风险级别k指标值的同征物元为Rk为:
| $ {R_k} = \left( {{N_k},{C_j},{V_k}} \right) = \left[ {\begin{array}{*{20}{c}} {{N_k}}&{{C_1}}&{{V_{1k}}} \\ {}&{{C_2}}&{{V_{2k}}} \\ {}& \vdots & \vdots \\ {}&{{C_m}}&{{V_{mk}}} \end{array}} \right] $ | (1) |
其中, Vk=<ajk, bjk>为评估对象Nk对评估指标Ci量值范围, 则经典域RK构成:
| $ \begin{split} {R_K} &= \left[ {\begin{array}{*{20}{c}} N&{{N_1}}&{{N_2}}& \cdots &{{N_K}} \\ C&{{V_1}}&{{V_2}}& \cdots &{{V_K}} \end{array}} \right] \\ &=\left[ {\begin{array}{*{20}{c}} N&{{N_1}}&{{N_2}}& \cdots &{{N_K}} \\ {{C_1}}&{\left\langle {{a_{11}},{b_{11}}} \right\rangle }&{\left\langle {{a_{12}},{b_{12}}} \right\rangle }& \cdots &{\left\langle {{a_{1K}},{b_{1K}}} \right\rangle } \\ {{C_2}}&{\left\langle {{a_{21}},{b_{21}}} \right\rangle }&{\left\langle {{a_{22}},{b_{22}}} \right\rangle }& \cdots &{\left\langle {{a_{2K}},{b_{2K}}} \right\rangle } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{C_m}}&{\left\langle {{a_{m1}},{b_{m1}}} \right\rangle }&{\left\langle {{a_{m2}},{b_{m2}}} \right\rangle }& \cdots &{\left\langle {{a_{mK}},{b_{mK}}} \right\rangle } \end{array}} \right] \end{split}$ | (2) |
相应节域Rm为:
| $ {R_m} = \left[ {\begin{array}{*{20}{c}} N&{{C_1}}&{{V_{1d}}} \\ {}&{{C_2}}&{{V_{2d}}} \\ {}& \vdots & \vdots \\ {}&{{C_m}}&{{V_{md}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} N&{{C_1}}&{\left\langle {{a_{1d}},{b_{1d}}} \right\rangle } \\ {}&{{C_2}}&{\left\langle {{a_{2d}},{b_{2d}}} \right\rangle } \\ {} & \vdots &{\vdots} \\ {}&{{C_m}}&{\left\langle {{a_{md}},{b_{md}}} \right\rangle } \end{array}} \right] $ | (3) |
其中, Vk=<ajk, bjk>为评估指标Cj量值范围. 则同征物元体Rp(p=1,2,3,…, P) 为:
| $ {R_P} = = \left[ {\begin{array}{*{20}{c}} P&{{p_1}}&{{p_2}}& \cdots &{{p_P}} \\ {{C_1}}&{{v_{11}}}&{{v_{12}}}& \cdots &{{v_{1P}}} \\ {{C_2}}&{{v_{21}}}&{{v_{22}}}& \cdots &{{v_{2P}}} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{C_m}}&{{v_{m1}}}&{{v_{m2}}}& \cdots &{{v_{mP}}} \end{array}} \right] $ | (4) |
由可拓集合与集对理论, 分析图1知: 当评估样本j指标处于风险等级k(k=1, 2, 3,…, K), 则与等级k集对关系为同, 可由可拓集合X0=<Fj,k, Fj,k–1 >标准正域表示, 对应的联系隶属度关系为:
| $ {\mu }_{k}\left({x}_{ij}\right)=\left\{ {\begin{array}{ll} \dfrac{2\left({F}_{j,k+1}-{x}_{ij}\right)}{{F}_{j,k+1}-{F}_{j,k}},\hfill & {x}_{ij}\geqslant\dfrac{{F}_{j,k}+{F}_{j,k+1}}{2}\hfill \\ \dfrac{2\left({x}_{ij}-{F}_{j,k}\right)}{{F}_{j,k+1}-{F}_{j,k}},\hfill & {x}_{ij} < \dfrac{{F}_{j,k}+{F}_{j,k+1}}{2}\hfill \end{array} } \right.$ | (5) |
其中, Fj,k和Fj,k+1为左右限值; μk(xij)为i对等级k中j指标的隶属度.
当样本i评估j指标处于评估等级k的相邻k–1(k>2)或k+1等级, 则与等级k的集对关系为异, 可由可拓过渡正域X1=<Fj,k–1,Fj,k >或 X2=<Fj,k–1,Fj,k+2 >表示, 相应的联系隶属度为:
| $ {\mu _k}\left( {{x_{ij}}} \right) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{\rho \left( {{x_{ij}},{X_0}} \right)}}{{\rho \left( {{x_{ij}},X} \right) - \rho \left( {{x_{ij}},{X_0}} \right)}},\;\;\;\rho \left( {{x_{ij}},X} \right) \ne \rho \left( {{x_{ij}},{X_0}} \right)} \\ { - \rho \left( {{x_{ij}},{X_0}} \right)\rho \left( {{x_{ij}},X} \right) = \rho \left( {{x_{ij}},{X_0}} \right),\;\;\;\;{x_{ij}} \in {X_0}} \\ { - 1,\quad \rho \left( {{x_{ij}},X} \right) = \rho \left( {{x_{ij}},{X_0}} \right),{x_{ij}} \in {X_0},{x_{ij}} \in X} \end{array}} \right. $ | (6) |
| $ \rho \left( {{x_{ij}},{X_0}} \right) = \left| {{x_{ij}} - \frac{{{F_{j,k}} + {F_{j,k + 1}}}}{2}} \right| - \frac{{{F_{j,k + 1}} - {F_{j,k}}}}{2} $ | (7) |
| $ \rho \left( {{x_{ij}},X} \right) = \left| {{x_{ij}} - \frac{{{F_{j,k - 1}} + {F_{j,k + 2}}}}{2}} \right| - \frac{{{F_{j,k + 2}} - {F_{j,k - 1}}}}{2} $ | (8) |
其中, Fj,k–1和Fj,k+2为左右限值, 样本i与评估等级k组成可拓正域距ρ(xij,X), 标准正域距为ρ(xij,X0). 在式(7)和式(8)中, k=1时, 则Fj,k−1= Fj,k, k=K时, 则Fj,k+2= Fj,k−1.
当样本j指标与评估等级k关系不满足上述两种情况, 则其与评估等级k集对关系为对立, 其联系隶属度为μk(xij)=−1. 基于评估指标权重, 可得隶属度计算模型μk为:
| $ {\mu _k} = \sum\limits_{j = 1}^M {{w_j}} {\mu _k}({x_{ij}}) $ | (9) |
其中, wj为指标权重. 按上式求得集成隶属度越大, 则表示与某风险等级越匹配, 故评定准则为:
| $ k = \max \left\{ {{\mu _1},{\mu _2},{\mu _3}, \cdots ,{\mu _m}} \right\} $ | (10) |
其中, k为评估结果风险等级.
2 改进层次分析法指标计算权重 2.1 基本原理改进层次分析法将传统的AHP方法与区间数学方法相结合, 采用三标度法对影响因素进行重要性比较, 比较矩阵更可靠、合理, 运用数学手段对比较矩阵中的相关影响因素进行优化, 将比较矩阵转换成一致性矩阵, 避免一致性检验等复杂计算步骤[11, 12].
2.2 权重计算过程使用三标度法构造重要性比较矩阵, 比较矩阵A为:
| $ A = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}} \\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nn}}} \end{array}} \right] $ | (11) |
其中,
| $ {a}_{ij}=\left\{\begin{array}{l}0,\hfill \\ 1,\hfill \\ 2,\hfill \end{array}\begin{array}{l}表示影响因素j比影响因素i重要\\ 表示影响因素j与影响因素i同等重要\\ 表示影响因素i比影响因素j重要\end{array}\right. $ | (12) |
根据矩阵A=(aij)n×n通过相关变换构造判断矩阵B=(bij)n×m, 计算比较因子cm, 计算公式见式(13).
| $ \left\{ {\begin{array}{*{20}{l}} {{s_i} = \displaystyle\sum\limits_{j = 1}^n {{a_{ij}}}, i = 1,2,3, \cdots ,n} \\ {{s_{\max }} = \max \left\{ {{s_i}} \right\}} \\ {{s_{\min }} = \min \left\{ {{s_i}} \right\}} \\ {{c_{{m}}} = \dfrac{{{s_{\max }}}}{{{s_{\min }}}}} \end{array}} \right. $ | (13) |
| $ {C}_{ij}=\left\{ {\begin{array}{ll} \dfrac{{s}_{i}-{s}_{j}}{{s}_{\mathrm{max}}-{s}_{\mathrm{min}}}\left({c}_{m}-1\right)+1,\hfill & {s}_{i}\geqslant{s}_{j}\hfill \\ {\left[\dfrac{\left|{s}_{i}-{s}_{j}\right|}{{s}_{\mathrm{max}}-{s}_{\mathrm{min}}}\left({c}_{{m}}-1\right)+1\right]}^{-1},\hfill & {s}_{i} < {s}_{j}\hfill \end{array}} \right. $ | (14) |
最优传递矩阵(cij)n×m为:
| $ {c_{ij}} = \frac{1}{n}\sum\limits_{k = 1}^n {\left( {\lg \frac{{{b_{ik}}}}{{{b_{jk}}}}} \right)} $ | (15) |
最优一致传递矩阵元素为:
| $ {{{d}}_{ij}} = {10^{{c_{ij}}}} $ | (16) |
方根法相对权重计算:
| $ \overline {{w_i}} = \sqrt[n]{{\prod\limits_{j = 1}^n {b_{ij}^\prime } }},i,\;j = 1,2, \cdots ,n $ | (17) |
其中, bij′为判断矩阵每一行元素, 归一化得:
| $ {w_i} = \overline {{w_i}} /\sum\limits_{i = 1}^n {\overline {{w_i}} } ,\;i = 1,2, \cdots ,n $ | (18) |
则改进AHP获得的指标权重为:
| $ {w^\prime } = \left[ {{w_1},{w_2}, \cdots ,} \right.\left. {{w_n}} \right]_{}^{{\rm{T}}} $ | (19) |
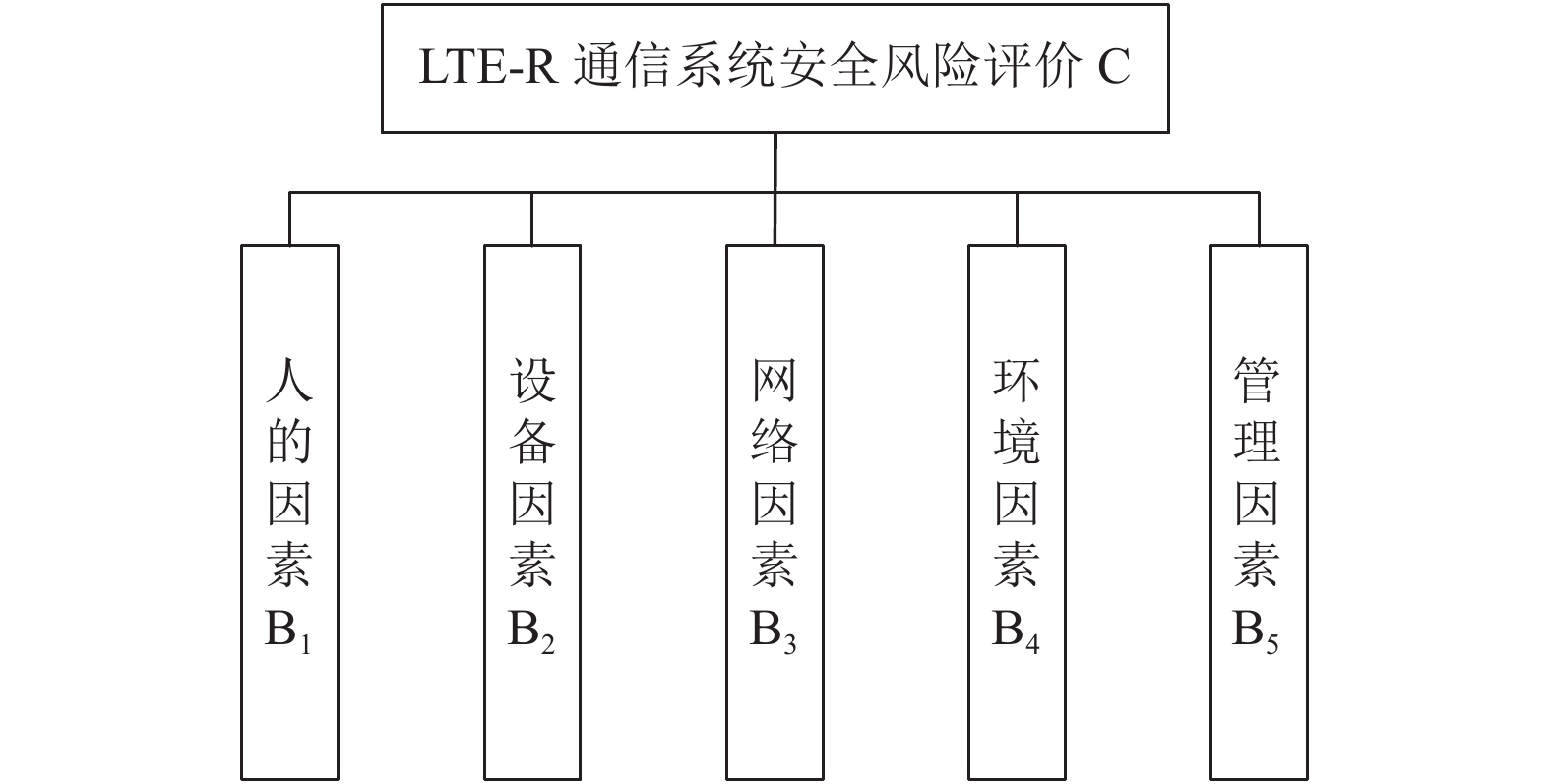
国内外目前对LTE-R通信系统进行安全分析主要从铁路系统RAMS[13, 14]方面研究, 以此为基础, 根据文献[15]建立的LTE-R通信系统安全评估指标, 只针对一级指标主要影响因素进行分析, 如图2所示.
|
图 2 LTE-R通信系统风险评估体系 |
3.2 评估步骤
基于集对可拓-改进层次分析法的铁路通信系统安全风险评估步骤如下:
1)由通信系统实际情况, 确定评估指标和评估标准, 设置评估条件集M={M1, M2, M3,…,Mn}中 Mi=(Ci, Vi)征元(Vi为特征Ci的量值域)构建风险集对.
2)集对分析结合可拓论域,确定风险等级联系隶属度形式.
3)可拓-集对分析确定联系隶属度形式.
4)改进层次分析法权重值计算, 确定评估样本与每个特征元的对应类别的隶属关系值.
5)按照风险隶属度判定风险等级, 评估流程如图3所示.

|
图 3 评估流程 |
3.3 通信系统安全风险经典域与节域确定
根据 5个主要风险指标状况, 专家分析后按照满分为100分成5个风险等级, 风险等级具体描述和具体分类标准见表1和表2.
| 表 1 各风险状态具体描述 |
| 表 2 评估标准等级 |
因此, LTE-R 通信系统风险评估指标的同征物元体Rk和节域Rm如下:
| $ {R_k} = \left[ {\begin{array}{*{20}{c}} N&{{N_1}}&{{N_2}}&{{N_3}}&{{N_4}}&{{N_5}} \\ {{C_1}}&{\langle 0,20\rangle }&{\langle 21,40\rangle }&{\langle 41,60\rangle }&{\langle 61,80\rangle }&{\langle 81,100\rangle } \\ {{C_2}}&{\langle 0,20\rangle }&{\langle 21,40\rangle }&{\langle 41,60\rangle }&{\langle 61,80\rangle }&{\langle 81,100\rangle } \\ {{C_3}}&{\langle 0,20\rangle }&{\langle 21,40\rangle }&{\langle 41,60\rangle }&{\langle 61,80\rangle }&{\langle 81,100\rangle } \\ {{C_4}}&{\langle 0,20\rangle }&{\langle 21,40\rangle }&{\langle 41,60}&{\langle 61,80\rangle }&{\langle 81,100\rangle } \\ {{C_5}}&{\langle 0,20\rangle }&{\langle 21,40\rangle }&{\langle 41,60\rangle }&{\langle 61,80\rangle }&{\langle 81,100\rangle } \end{array}} \right], \;\;\;\;\;\;\;{R_m} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} N \\ {} \end{array}} \\ {} \\ {\begin{array}{*{20}{c}} {} \\ {} \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{C_1}} \\ {{C_2}} \end{array}} \\ {{C_3}} \\ {{C_4}} \\ {{C_5}} \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\langle 0,100\rangle } \\ {\langle 0,100\rangle } \end{array}} \\ {\langle 0,100\rangle } \\ {\langle 0,100\rangle } \\ {\langle 0,100\rangle } \end{array}} \end{array}} \right] $ |
根据建立的铁路无线通信系统运营风险评估系统, 结合高速铁路通信系统运营考核数据以及相关专家经验, 得到5组样本数据, 见表3.
| 表 3 LTE-R 通信系统评估指标值 |
由实例实测数据可以构成待评同征物元体:
| $ {R_m} = \left[ {\begin{array}{*{20}{c}} N&{{P_1}}&{{P_2}}&{{P_3}}&{{P_4}}&{{P_5}} \\ {{C_1}}&{23}&{25}&{27}&{21}&{24} \\ {{C_2}}&{73}&{69}&{75}&{75}&{78} \\ {{C_3}}&{33}&{31}&{29}&{35}&{37} \\ {{C_4}}&{35}&{36}&{38}&{37}&{39} \\ {{C_5}}&{19}&{21}&{18}&{22}&{25} \end{array}} \right] $ |
根据图2及式(5)–式(8)可得指标隶属度, 其中第1组数据为例说明计算过程.
1) C1(p11)=23时, 位于评估等级标准K∈(0–20)相邻K–1等级内, 隶属度μk(p11)=−0.15; 位于评估等级标准K∈(21–40)等级内, μk(p11)=0.3; 位于评估等级标准K∈(41–60)相邻K–1等级内, μk(p11)=−0.85; 位于评估等级K∈(61–80)相邻K+3等级内, μk(p11)=−1; 位于评估等级K∈(81–100)相邻K+4等级内, μk(p11)=−1.
2) C2(p12)=73时, 位于评估等级标准K∈(0–20)相邻K–3等级内, μk(p12)=−1; 位于评估等级标准 K∈(21–40)相邻K–2等级内, μk(p12)=−1; 位于评估等级标准K∈(41–60)相邻K–1等级内, μk(p12)=−0.65; 位于评估等级K∈(61–80)等级内, μk(p12)=0.7; 位于评估等级K∈(81–100)相邻K+1等级内, μk(p12)=−0.35.
3) C3(p13)=33时, 位于评估等级标准K∈(0–20)相邻K–1等级内, μk(p13)=−0.65; 位于评估等级标准K∈(21–40)等级内, μk(p13)=−0.7; 位于评估等级标准K∈(41–60) 相邻K+1等级内, μk(p13)=−0.35; 位于评估等级K∈(61–80)相邻K+2等级内, μk(p13)=−1; 位于评估等级相邻K+3等级内, μk(p13)=−1.
4) C4(p14)=35时, 位于评估等级标准K∈(0–20)相邻K–1等级内, μk(p14)=−0.63; 位于评估等级标准K∈(21–40)等级内, μk(p14)=0.5; 位于评估等级标准K∈(41–60)相邻K+1等级内, μk(p14)=−0.25; 位于评估等级K∈(61–80)相邻K+2等级内, μk(p14)=−1; 位于评估等级K∈(81–100) 相邻K+3等级内, μk(p14)=−1.
5) C5(p15)=19时, 位于评估等级标准K∈(0–20)等级内, μk(p15)=0.1; 位于评估等级标准K∈(21–40)相邻K+1等级内, μk(p15)=−0.05; 位于评估等级标准 K∈(41–60)相邻K+2等级内, μk(p15)=−1; 位于评估等级K∈(61~80)相邻K+3等级内, μk(p15)=−1; 其位于评估等级K∈(81–100)相邻K+4等级内, μk(p15)=−1.
4.3 权重计算根据式(12)及专家相关意见对图1中5个因素C=(B1,B2,B3,B4,B5)评估指标两两比较重要性, 得到基于改进AHP法的两两比较矩阵A如下:
| $ {A_{}} = \left[ {\begin{array}{*{20}{c}} 1&2&0&2&2 \\ 0&1&0&0&2 \\ 2&2&1&2&2 \\ 0&2&0&1&2 \\ 0&0&0&0&1 \end{array}} \right] $ |
由式(13)–式(15)得最优一致矩阵D:
| $ D = \left[ {\begin{array}{*{20}{r}} {1.00}&{4.17}&{0.51}&{2.04}&{8.13} \\ {0.24}&{1.00}&{0.12}&{0.49}&{1.95} \\ {1.95}&{8.13}&{1.00}&{3.98}&{15.85} \\ {0.49}&{2.04}&{0.25}&{1.00}&{3.98} \\ {0.12}&{0.13}&{0.06}&{0.25}&{1.00} \end{array}} \right] $ |
由式(16)–式(19)可得基于改进AHP法指标权重值, 如表4所示.
| 表 4 评估指标权重值 |
4.4 通信系统安全风险级别判定
根据样本1数据与权重,结合式(9)–式(10)求出样本1数据的最大联系隶属度μk=0.210, 其他4组数据详细计算结果如表5所示, 根据表1风险状态等级, 5组数据验证通信系统风险等级为Ⅱ级(低风险), 和其他文献研究及现场情况结果相符.
4.5 模型评估方法有效性分析为验证本文方法的可行, 将耦合方法的评估结果与云模型方法[4]和灰色模糊理论[9]对比验分析证. 方法对比结果如图4和表6所示, 评估结果为较低风险, 对比所示, 两者方法与本文分析结果相同, 说明了集对分析与可拓学耦合方法的准确性.

|
图 4 安全评估云 |
| 表 5 风险等级确定 |
| 表 6 风险评估算法对比 |
5 结束语
针对现有高速铁路中LTE-R通信系统安全评估方法不足问题, 基于集对可拓与改进层次分析法方法建立了LTE-R通信系统风险评估模型, 结果表明, 该方法来评估LTE-R 通信系统风险是有效可行的. 用改进层次分析法使指标权重更加合理科学; 集对可拓耦合方法可以真实反映LTE-R通信系统实际风险等级品评估过程中的不确定性, 改进了传统集对分析联系度计算方法, 分析思路清晰, 易于计算.
通过分析具体实例, 进一步丰富了LTE-R通信系统安全评估方法内容, 为系统建立LTE-R通信系统安全评估方法和过程提供了参考意义.
| [1] |
He RS, Ai B, Wang GP, et al. High-speed railway communications: From GSM-R to LTE-R. IEEE Vehicular Technology Magazine, 2016, 11(3): 49-58. DOI:10.1109/MVT.2016.2564446 |
| [2] |
张怡. 简谈铁路通信系统向LTE-R的发展与演进. 铁路通信信号工程技术, 2016, 13(1): 18-20. DOI:10.3969/j.issn.1673-4440.2016.01.005 |
| [3] |
Solanki, Kratika Chouhan. High speed railway mobile communication system based on 4G LTE technology. International Journal of Scientific Research in Science, Engineering and Technology, 2020, 3(8): 452-457. |
| [4] |
陈永刚, 周净毓, 戴乾军, 等. 基于组合赋权-云模型的LTE-R系统的安全评估研究. 铁道科学与工程学报, 2019, 16(12): 3110-3118. |
| [5] |
腾辉. LTE-R通信系统安全设计与评估技术研究[硕士学位论文]. 北京: 北京交通大学, 2012.
|
| [6] |
Ma DD, Hu LL, Liu K. Safety evaluation of high speed railway LTE-R communication system based on AHP and fuzzy comprehensive evaluation. 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS). Changsha: IEEE, 2019. 211–214.
|
| [7] |
马得途. 基于LTE-R的车车通信技术及可靠性研究[硕士学位论文]. 兰州: 兰州交通大学, 2018.
|
| [8] |
蒋云良, 赵克勤. 集对分析在人工智能中的应用与进展. 智能系统学报, 2019, 14(1): 28-43. |
| [9] |
汪明武, 周天龙, 叶晖, 等. 基于联系云的地下水水质可拓评价模型. 中国环境科学, 2018, 38(8): 3035-3041. DOI:10.3969/j.issn.1000-6923.2018.08.032 |
| [10] |
李文军, 杨春燕, 汤龙, 等. 可拓学中相关关系的变换方法研究. 智能系统学报, 2019, 14(4): 619-626. |
| [11] |
Yue Z, Xu G, Feng L, et al. Study on safety evaluation for tailing reservoirs based on the IAHP-fuzzy comprehensive evaluation. 2012 IEEE 3rd International Conference on Emergency Management and Management Sciences (ICEMMS). Beijing: IEEE, 2013. 1–6.
|
| [12] |
赵梦兰. 基于改进层次分析法的山区桥梁建设风险影响评价. 公路与汽运, 2020(5): 158-160. DOI:10.3969/j.issn.1671-2668.2020.05.041 |
| [13] |
European Committee for Electrotechnical Standardization. BS EN 50126: 1999 Railway applications-the specification and demonstration of reliability, availability, maintainability and safety (RAMS). Brussels: European Committee for Electrotechnical Standardization, 1999.
|
| [14] |
赵佳琦. 高速铁路LTE-R系统服务质量测试与评估[硕士学位论文]. 北京: 北京交通大学, 2019.
|
| [15] |
马迪迪. 基于高速铁路LTE-R通信系统安全风险评估技术研究[硕士学位论文]. 兰州: 兰州交通大学, 2019.
|
 2022, Vol. 31
2022, Vol. 31



