2. 广西民族大学 广西混杂计算与集成电路设计分析重点实验室, 南宁 530006
2. Guangxi Key Laboratory of Hybrid Computation and IC Design Analysis, Guangxi University for Nationalities, Nanning 530006, China
旅行商(TSP)问题是数学领域组合优化中著名的NP难题之一, 又称旅行推销员问题[1]. 该问题的求解一直是学术界研究的热点问题. 旅行商问题的表述比较容易, 但对于路径的优化求解比较困难. 对于TSP问题求解的传统方法有蛮力法、动态规划法、分枝限界法等[2], 但当TSP问题的规模较大时, 传统算法往往不能解决. 针对大规模的TSP问题, 近年来兴起的群体智能优化算法在该问题的求解中得到了很好的应用.
群体智能优化算法是一种基于概率而进行随机搜索的进化算法, 通过模拟昆虫、鱼群、鸟群、兽群等生物的觅食方式, 对群体之间信息的交流进行抽象, 从而快速找到问题的最优解[3]. “群体智能”的概念最早由Beni和Wang在文献[4]中提出. 之后群体智能优化算法得到迅速的发展, 最具代表性的是1991年Colorni和Dorigo提出的蚁群算法(ACO)[5]以及1995年Kennedy和Eberhart提出的粒子群优化算法(PSO)[6]. 在此之后, 群体智能算法的灵感来源主要有3个方面: 1)单纯动物个体的觅食行为; 2)单纯动物个体的社会行为; 3)生物群体的觅食行为与社会行为. 专家学者因此提出了许多群体智能优化算法, 例如2003年Eusuff等提出的混合蛙跳算法(SFLA)[7]、2009年Karaboga等提出的人工蜂群算法(ABC)[8]、2008年Yang提出的萤火虫优化算法(GSO)[9], 2014年Mirjalili等提出的灰狼优化算法(GWO)[10]与2016年提出的鲸鱼优化算法(WOA)[11]等.
对于群体智能优化算法在优化问题上的应用也得到了进一步的研究与发展[12], 针对旅行商问题的求解, Mahi等提出了一种求解标准TSP的混合算法PSO-ACO-3-opt[13], Geng等提出了一种有效的基于模拟退火(SA)和贪婪搜索技术的局部搜索算法来求解TSP问题[14], Jolai和Ghanbari提出了一种改进的人工神经网络(ANN)方法来求解TSP[15]等.
麻雀搜索算法(SSA)是Xue等[16]2020年新提出的元启发式群体智能优化算法. 研究表明[17], 相对于其他的群体智能优化算法在收敛速度、搜索精度、稳定性方面有明显的优势. 但是, 在搜索接近全局最优时, 存在种群的多样性减少, 容易陷入局部最优等问题. 本文通过对其改进, 并应用在旅行商问题的求解中, 获得了较好的结果.
本文对麻雀搜索算法的搜索策略与算法的基本流程进行研究分析, 针对SSA容易陷入局部最优问题, 通过改进发现者与侦查者的位置更新公式, 引入高斯变异策略, 提出一种改进的麻雀搜索算法(ISSA). 将ISSA算法与基本SSA算法、粒子群优化算法(PSO)、鲸鱼优化算法、灰狼优化算法使用6个基准测试函数进行性能对比测试实验, 验证ISSA算法的有效性, 最后将其应用在旅行商问题的求解中, 验证ISSA算法与SSA算法对于求解TSP问题的可行性与优越性.
1 麻雀搜索算法麻雀搜索算法是受麻雀群体的捕食与反捕食行为启发得来. 麻雀的觅食过程遵循发现者-跟随者模型, 同时引入麻雀对于捕食者的预警机制. 麻雀群体种有发现者、跟随者、预警者3种角色. 种群中适度值较高的麻雀作为发现者, 负责找到食物并且为其他麻雀提供食物的方位. 除去作为发现者的麻雀, 其他个体则为跟随者, 跟随发现者进行觅食. 同时, 跟随者会监视发现者, 并对其进行食物的掠夺提高自己的适应度, 从而成为发现者. 在麻雀群体中, 存在一定数量的预警者, 当预警值大于安全值时, 预警者会发出叫声为其他麻雀提供信号, 逃离危险区域, 防止被捕食. 麻雀搜索算法中麻雀角色具体位置更新公式如下:
麻雀种群中的发现者的位置更新公式为:
| $X_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {X_{i,j}^t \cdot \exp \left( { - \dfrac{i}{{\alpha \cdot ite{r_{\max }}}}} \right),}&{{R_2} < ST}\\ {X_{i,j}^t + Q \cdot L,}&{{R_2} \geqslant ST} \end{array}} \right. $ | (1) |
其中, 麻雀种群中发现者所占的比例为10%–20%, 式中t为当前的迭代数,
麻雀种群中跟随者的位置更新公式为:
| $X_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {Q \cdot \exp \left( {\dfrac{{{X_{\rm{worst}}} - X_{i,j}^t}}{{{i^2}}}} \right),}&{i > \dfrac{n}{2}}\\ {X_p^{t + 1} + \left| {X_{i,j}^t - X_p^{t + 1}} \right| \cdot {A^ + } \cdot L,}&{\rm{otherwise}} \end{array}} \right. $ | (2) |
其中,
麻雀种群中预警者的位置更新公式如下:
| $ X_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {X_{\rm{best}}^t + \beta \cdot \left| {X_{i,j}^t - X_{\rm{best}}^t} \right|,}&{{f_i} > {f_g}}\\ {X_{i,j}^t + K \cdot \left( {\dfrac{{\left| {X_{i,j}^t - X_{\rm{worst}}^t} \right|}}{{\left( {{f_i} - {f_w}} \right) + \varepsilon }}} \right),}&{{f_i} = {f_g}} \end{array}} \right. $ | (3) |
其中, 预警者所占的比例为10%–20%,
麻雀搜索算法的基本算法步骤如下:
步骤1. 初始化最大迭代次数, 种群数量N, 发现这比例PD, 侦察者比例SD、警戒阈值R2.
步骤2. 计算麻雀种群的适度值并进行排序, 找出当前最差适度个体与最优适度值个体.
步骤3. 应用式(1)对发现者进行位置更新.
步骤4. 应用式(2)对跟随者进行位置更新.
步骤5. 应用式(3)对预警者进行位置更新.
步骤6. 完成当前迭代, 得到新的位置.
步骤7. 计算当前麻雀种群的适度值, 如果优于之前位置, 更新麻雀种群位置.
步骤8. 判断是否满足最大迭代次数或者精度要求, 若是, 结束迭代输出最优结果, 否则返回步骤3.
2 改进的麻雀搜索算法麻雀搜索算法在接近全局最优时, 会出现种群多样性减少, 容易陷入局部最优, 出现早熟现象的缺点[17]. 为此, 本文对麻雀搜索算法中发现者与侦查者的位置更新进行改进, 引入高斯变异策略对全局最优解进行扰动, 具体改进策略如下.
2.1 改进发现者更新位置为了使SSA算法能够避开向原点收敛的弊端, 将算法向最优位置跳跃的操作转换为向最优位置的移动, 将式(1)进行如下修改:
| $ X_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {X_{i,j}^{t + 1} \cdot (Q + 1)},&{{R_2} < ST}\\ {X_{i,j}^{t + 1} + Q},&{{R_2} \geqslant ST} \end{array}} \right. $ | (4) |
其中, Q+1为均差为1, 方差为1的正态随机分布数. Q为标准正态随机分布数.
2.2 改进预警者更新位置为了让预警者发现危险后能够逃离到最优的安全位置, 提高算法的全局搜索能力, 将式(3)进行如下修改:
| $ X_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {X_{i,j}^{t + 1} \cdot \beta \cdot (X_{i,j}^t - X_{\rm{best}}^t)},&{{f_i} = {f_g}}\\ {X_{i,j}^{t + 1} + \beta \cdot (X_{\rm{worst}}^t - X_{\rm{best}}^t)},&{{f_i} \ne {f_g}} \end{array}} \right. $ | (5) |
如果该麻雀处于最优位置, 则逃离到最优位置与最差位置之间的随机位置, 否则逃离到自己与随机位置之间的随机位置,
引入高斯变异算子对每次迭代得到的全局最优解进行扰动, 避免算法陷入局部最优, 出现早熟现象的缺点, 同时也能够维持种群个体的多样性[18]. 高斯变异算子如下:
| $ X_{\rm{gauss}}^{t + 1} = X_{\rm{gbest}}^t \cdot (1 + Gaussian(\alpha )) $ | (6) |
其中,
具体策略方式的使用贪婪规则如下所示:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_{\rm{gbest}}} = X_{i,j}^{t + 1}\begin{array}{*{20}{c}}, {} \end{array}\begin{array}{*{20}{c}} {}&{f(X_{i,j}^{t + 1}) \lt f(X_{\rm{gauss}}^{t + 1})} \end{array}} \\ {{X_{\rm{gbest}}} = X_{\rm{gauss}}^{t + 1}\begin{array}{*{20}{c}}, {}&{f(X_{i,j}^{t + 1}) \geqslant f(X_{\rm{gauss}}^{t + 1})} \end{array}} \end{array}} \right. $ | (7) |
步骤1. 初始化最大迭代次数, 种群数量N, 发现者比例PD, 侦察者比例SD、警戒阈值R2.
步骤2. 计算麻雀种群的适度值并进行排序, 找出当前最差适度个体与最优适度值个体.
步骤3. 应用改进式(4)对发现者进行位置更新.
步骤4. 应用式(2)对跟随者进行位置更新.
步骤5. 应用改进式(5)对预警者进行位置更新.
步骤6. 完成当前迭代, 得到新的位置.
步骤7. 使用高斯变异算子(6)对全局最优位置进行高斯变异, 使用贪婪规则(7)判断是否更新最优位置.
步骤8. 判断是否满足最大迭代次数或者精度要求, 若是, 结束迭代输出最优结果, 否则返回步骤3.
3 算法性能测试为验证改进的麻雀搜索算法能够改善原算法的缺点, 证明其有效性. 本文将ISSA与基本麻雀搜索算法、粒子群优化算法、鲸鱼优化算法、灰狼优化算法使用6个基准测试函数进行对比实验.
本文实验所使用的操作系统为Windows 10专业版64位, 实验软件为Matlab R2019b, 处理器Intel(R) Core(TM)i5-5257U CPU @ 2.70 GHz.
3.1 参数设置在相同的实验环境下, 设置种群数量为30, 最大迭代次数为1 000, 对每一个测试函数进行独立的20次实验, 每一个测试的优化算法均用文献[4,10,11,17]中所给出的原始参数值如表1. 6个基准测试函数分别为表2的单峰基准测试函数, 表3的多峰基准测试函数, 表4的固定尺寸的多峰基准测试函数.
3.2 算法性能测试实验结果分析5种算法优化6个基准测试函数的最优值、最差值、平均值对比结果如表5所示, 最优结果由粗体标出. 从收敛曲线图(图1、图2)可以看出, ISSA在优化单峰函数时的性能是最好的, 有很强的全局搜索能力. 从收敛曲线图(图3、图4)可以看出在优化多峰函数时, 改进后的麻雀搜索算法的收敛速度随着迭代次数的增多逐渐加快, 能够快速收敛到最优值, 没有出现早熟现象. 总体结果由表5可以看出, 改进的麻雀搜索算法在处理含有多个局部最优解的问题上, 相对于其他3种优化算法性能更好. 从收敛曲线图(图5、图6)可以看出, 在处理固定尺寸的多峰测试函数时, 5种算法的收敛速度基本相同, 都是在每次迭代的最开始就快速收敛. 但在优化测试函数时, 改进麻雀搜索算法的收敛速度相对于其他算法更快.
由上述实验结果可知, 通过改进麻雀搜索算法中发现者与侦察者的位置更新公式, 有效的提高了SSA的全局搜索能力, 加快了寻优与收敛的速度. 通过引入高斯策略, 通过贪婪规则对全局最优解进行扰动, 能够明显改善SSA算法容易陷入局部最优, 出现早熟现象的缺点. 综上所述, 证明了改进的麻雀搜索算法的有效性.
| 表 1 算法的初始参数 |
| 表 2 单峰基准测试函数 |
| 表 3 多峰基准测试函数 |
| 表 4 固定尺寸的多峰基准测试函数 |
4 ISSA求解旅行商问题 4.1 问题描述
旅行商问题是经典的组合优化NP问题, 又称之为旅行推销员问题, 最早由Flood在1956年提出, 在运筹学和理论计算机科学中具有非常重要的地位[19].
旅行商问题可以描述为一个商品的推销员要在若干城市之间推销商品, 该推销员从某一个城市出发, 需要经过所有的城市之后回到出发地. 问题是如何选择行进路线才能够使得总行程最短[20].
设城市的集合为顶点集
| $ f = \min \sum {{d_{({v_i},{v_{i + 1}})}} + {d_{({v_n},{v_1})}}} $ |
本实验采用tsplib中的burma14、A280和Eil51的TSP数据对本文提出的改进的麻雀搜索算法与基本麻雀搜索算法、进行仿真实验结果与文献[21,22]给出的数据进行对比. 每个算法对TSP数据进行20次独立实验. 设置的初始参数为: 种群麻雀的个数为100, 最大迭代次为1 000, 各算法的具体参数按表1给出.
| 表 5 5种算法的20次实验结果 |

|
图 1 |

|
图 2 |

|
图 3 |

|
图 4 |
4.3 实验结果分析
各算法20次独立实验的最优值、平均值、迭代次数如表6所示. 图7–图9为ISSA求解3种TSP问题的最优路径图. 从表6的实验结果可以看出, ISSA算法与SSA算法在求解TSP问题时, 与其他群体算法相比能在更少的迭代次数与时间内求得最优路径, 并且最优解相对更好. 体现出求TSP问题时的优越性, 并且改进后的麻雀搜索算法相对于基本麻雀搜索算法的求解速度更快, 路径更短.

|
图 5 |

|
图 6 |
综上所述, 麻雀搜索算法在求解TSP问题时, 与其他群体智能算法相比时间更短, 收敛次数更少, 因此有更好的优越性, 并且改进后的麻雀搜索算法相对于基本麻雀搜索算法的收敛速度更快、路径相对更优, 说明了改进的有效性.
5 结论与展望本文对2020年最新提出的麻雀搜索优化算法[16]的原理、种群位置更新策略、算法流程进行了分析, 针对麻雀搜索算法在接近全局最优时, 会出现种群多样性减少, 容易陷入局部最优, 出现早熟现象的缺点, 改进发现者与侦察者的位置更新公式, 引入高斯变异策略对全局最优解进行扰动. 通过对比实验结果表明, 在全局搜索能力与收敛性方面, 改进麻雀搜索算法的性能明显优于其他算法, 验证了改进的麻雀搜索算法有效性.
| 表 6 TSP问题求解实验结果 |

|
图 7 Burma14最优路径图 |
|
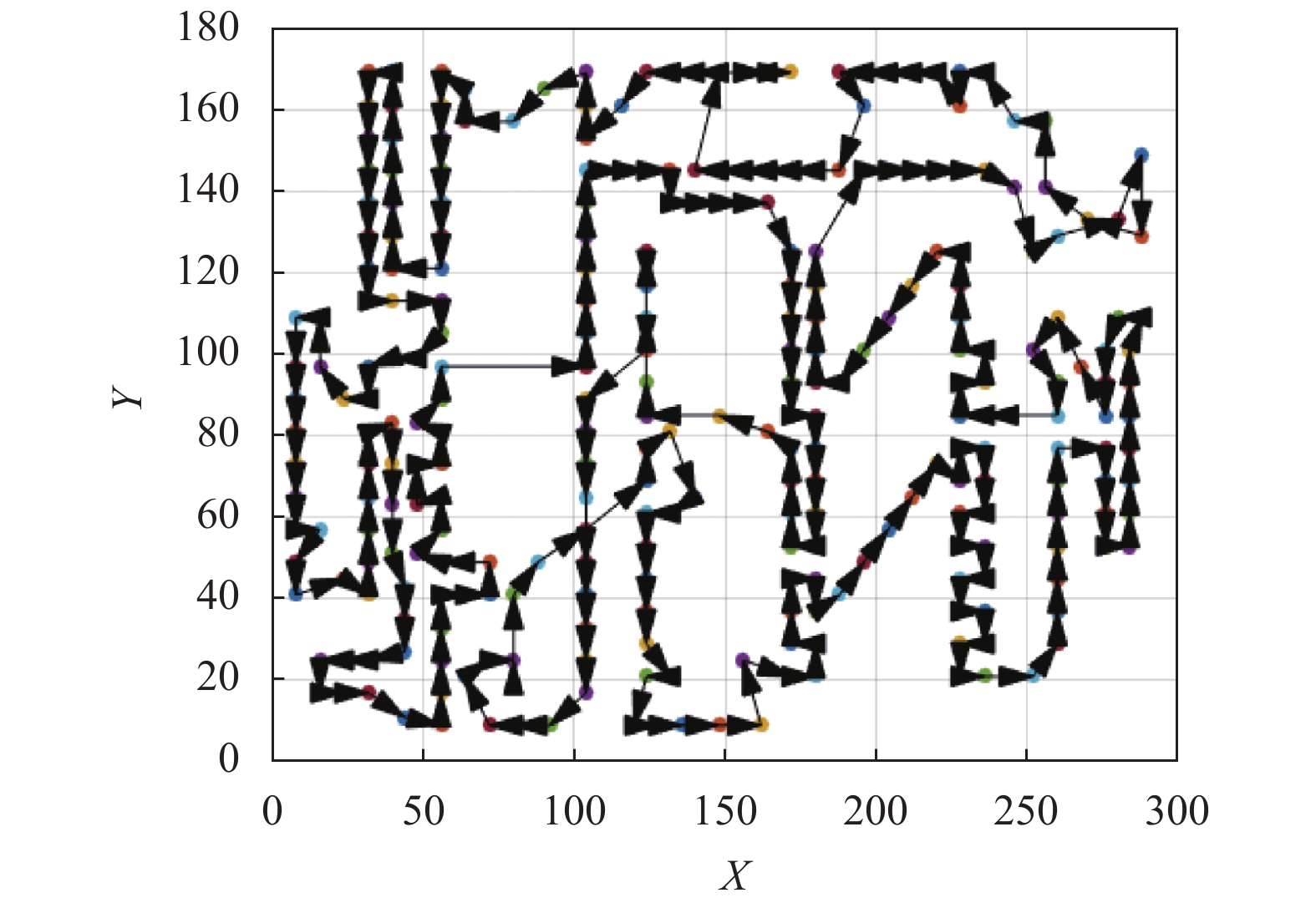
图 8 A280最优路径图 |

|
图 9 Eil51最优路径图 |
在旅行商求解问题中, 改进的麻雀搜索算法提供了一种新的优化方法, 通过仿真实验可以看出改进麻雀搜索算法对于最优路径算法与其他群体智能优化算法相比更有具优越性.
相信随着麻雀搜索算法的不断发展与改进, 麻雀搜索算法将在人工智能领域中的组合优化、计算智能、图像处理、数据挖掘领域将发挥巨大的优势.
| [1] |
黄岚, 王康平, 周春光, 等. 粒子群优化算法求解旅行商问题. 吉林大学学报(理学版), 2003, 41(4): 477-480. DOI:10.3321/j.issn:1671-5489.2003.04.012 |
| [2] |
朱继生. 混合人工蜂群算法求解旅行商问题[硕士学位论文]. 南宁: 广西大学, 2020.
|
| [3] |
莫愿斌, 刘贺同, 王勤. 智能优化算法的综述教学研究. 科技创新导报, 2008(13): 2-3. DOI:10.3969/j.issn.1674-098X.2008.13.002 |
| [4] |
Beni G, Wang J. Swarm intelligence in cellular robotic systems. Proceedings of NATO Advanced Workshop on Robots and Biological Systems. Tuscany: Springer, 1989. 26–30.
|
| [5] |
Colorni A, Dorigo M, Maniezzo V. Distributed optimization by ant colonies. Proceedings of the 1st European Conference on Artificial Life. Paris: ECAL, 1991. 134–142.
|
| [6] |
Kennedy J, Eberhart R. Particle Swarm Optimization. IEEE, 1995.
|
| [7] |
Eusuff MM, Lansey KE. Optimization of water distribution network design using the shuffled frog leaping algorithm. Journal of Water Resources Planning and Management, 2003, 129(3): 210-225. |
| [8] |
Karaboga D, Akay B. A comparative study of artificial bee colony algorithm. Applied Mathematics and Computation, 2009, 214(1): 108-132. |
| [9] |
Yang XS. Nature-inspired Metaheuristic Algorithms. UK: LuniverPres, 2008.
|
| [10] |
Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007 |
| [11] |
Mirjalili S, Lewis A. The whale optimization algorithm. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 |
| [12] |
李雅丽, 王淑琴, 陈倩茹, 等. 若干新型群智能优化算法的对比研究. 计算机工程与应用, 2020, 56(22): 1-12. DOI:10.3778/j.issn.1002-8331.2006-0291 |
| [13] |
Mahi M, Baykan ÖK, Kodaz H. A new hybrid method based on particle swarm optimization, ant colony optimization and 3-opt algorithms for traveling salesman problem. Applied Soft Computing, 2015, 30: 484-490. DOI:10.1016/j.asoc.2015.01.068 |
| [14] |
Geng XT, Chen ZH, Yang W, et al. Solving the traveling salesman problem based on an adaptive simulated annealing algorithm with greedy search. Applied Soft Computing, 2011, 11(4): 3680-3689. DOI:10.1016/j.asoc.2011.01.039 |
| [15] |
Jolai F, Ghanbari A. Integrating data transformation techniques with Hopfield neural networks for solving travelling salesman problem. Expert Systems with Applications, 2010, 37(7): 5331-5335. DOI:10.1016/j.eswa.2010.01.002 |
| [16] |
Xue JK, Shen B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Systems Science & Control Engineering, 2020, 8(1): 22-34. |
| [17] |
吕鑫, 慕晓冬, 张钧, 等. 混沌麻雀搜索优化算法. 北京航空航天大学学报, 2021, 47(8): 1712-1720. |
| [18] |
莫愿斌, 刘付永, 张宇楠. 带高斯变异的人工萤火虫优化算法. 计算机应用研究, 2013, 30(1): 121-123. DOI:10.3969/j.issn.1001-3695.2013.01.029 |
| [19] |
Flood MM. The traveling-salesman problem. Operations Research, 1956, 4(1): 61-75. DOI:10.1287/opre.4.1.61 |
| [20] |
杨启文, 阮姗娜, 陈俊风, 等. 群体智能在旅行商问题中的应用综述. 自动化技术与应用, 2016, 35(8): 1-6, 17. |
| [21] |
高珊, 孟亮. 贪婪随机自适应灰狼优化算法求解TSP问题. 现代电子技术, 2019, 42(14): 46-50, 54. |
| [22] |
周永权, 黄正新, 刘洪霞. 求解TSP问题的离散型萤火虫群优化算法. 电子学报, 2012, 40(6): 1166-1170. |
 2022, Vol. 31
2022, Vol. 31



