伴随着我国的人口数量增长和国民经济水平提高, 在近年来, 居民的汽车使用量一直在不断的增加. 因此, 人们大量地利用机器与摄像头来识别车辆, 车牌等信息, 达到检测识别车辆收费, 测速等目的. 但在很多情况下, 例如在遮挡、阴影、相机噪音、光线变化和天气状况等复杂环境条件下, 拍摄的车牌图片质量往往不尽人意, 这也使得后续的处理过程变得愈加艰巨. 因此, 利用深度学习技术对模糊的车牌图片进行修复、重建, 方便机器或者人对拍摄的车辆进行后续的定位或其他操作, 从而帮助人们更好地实现社会交通智能管理.
1.1 国内外研究现状对于失真度较高的图片进行重建这一领域来说, 可以大致的分为以下3种方法: 1)最早被学者提出的方法是基于插值的图像重建[1], 虽然这方法简单、而且重建图像速度较快, 但是这种方法会引起锯齿、振铃等人工效应缺点, 因此很快被人所抛弃. 2)基于重构的方法[2]是针对插值方法的缺点所提出的一种方法, 但是该算法操作复杂, 精度低, 也不值得学者进行研究. 3)基于深度学习的图像超分辨率重建(super-resolution, SR)[3]作为一门能丰富图像细节, 对失真图像进行较高质量还原的图像处理技术, 在国外学者提出后, 便引起了图片修复相关领域的研究员们的高度关注. Dong等人[4]首次在图像超分辨率重建运中用卷积神经网络(CNN). Kim等人[5, 6]的研究中, 通过增加卷积网络的深度和引入残差学习结构, 提高模型中的收敛率问题. Zhang的团队[7]利用了残差密集结构, 该模型有助于从卷积层中提取出图像特征. Ledig等人[8]对GAN做出了改进, 并将模型的命名为SRGAN. 最近, 在文献[9]中, Wang等人首次引入residual-in-residual dense block (RRDB), 并应用于生成对抗网络中, 而且重新设计了感知损失函数的输出形式.
本文共由6节组成. 第1节主要介绍了图像修复重建领域算法的相关背景, 前人研究成果, 以及论文规划. 第2节介绍了GAN的原理和本文模型研究算法的贡献. 第3节对本文提出一种新的网络模型进行详细的介绍. 第4节将本文提出的模型应用于中国停车场数据集(CCPD)中, 并分析了实验结果的优点与不足. 第5节结合网络模型结构与实验结果进行相关的讨论, 在第6节中做了总结, 并提出对今后工作的展望.
2 生成对抗网络原理生成对抗网络是Goodfellow等人[10]在2014年提出的一种基于无监督的深度学习模型, 该模型能够学习大量的数据样本之间的复杂的联系, 从而输出与真实数据相似的机器数据. 如图1所示, 该网络由两部分组成: 生成器(generator)+鉴别器(discriminator). 生成器主要用于生成机器数据, 而鉴别器主要用于判断数据的真假. 在双方的不断对抗训练中, 最终使得该模型输出极其符合现实意义的数据, 并达到纳什均衡[11].
在原始的GAN网络中, 鉴别器的主要功能在于对数据进行二分类的判别, 判断真或假. 对于输入的图片, 我们设置其标签为1, 否则为0. 而生成模型G通过不断训练尝试生成相似的“机器数据”, 使得判别模型D判别该数据为真, 所以其损失函数可以定义为:
| $ \underset{D}{\mathrm{min}}\underset{G}{\mathrm{max}}V \left( D, G \right) = -{E}_{x \sim {P}_{r}} \left[\mathrm{ln} \left(D\right( x)\right] - {E}_{{\textit{z}} \sim {P}_{{{{\textit{z}}}}}} \left[\mathrm{ln}( 1 - D(G\left({\textit{z}}\right) ) \right] $ | (1) |
其中, Pr是代表真实数据, Pz是代表假设的机器数据.

|
图 1 生成对抗网络原理图 |
我们在前人研究的基础上, 提出了一种新的基于生成对抗网络的图片重建模型, 本文的主要贡献有以下几点: 1)我们采用RRDB对图片进行高级特征的提取, 在图片重建阶段我们采用渐进式上采样网络. 2)引入马尔可夫判别器(Markovian discriminator, PatchGAN)[12]作为GAN的鉴别器, 利用其输出为矩阵的这一特点, 引导生成器进行更高质量、更多细节的图像重建. 3)对车牌而言, 我们将重点关注车牌字母方向与边缘等高级特征, 采用MSE (内容损失)与最小化VGG的混合作为模型的损失函数. 4)引入峰值信噪比(PSNR)[13]与结构相似度(SSIM)等多种评价指标, 对模型重建图像进行客观评价.
同时, 我们还与目前较新的图像超分辨方法进行对比. 首先, 在生成器方面, 与罗会兰等人[14]提出的生成对抗网络相比, 我们运用了密集连接的残差采样块进行高级特征采样. 其次, 在鉴别器方面, 相较于传统GAN的判别器[15], 本文判别器允许任意大小的图像作为输入, 网络设计更加灵活. 最后, 在损失函数方面, 与徐姝琪等人[16]运用TV损失联合相比, 我们重点关注车牌这一特殊图像的高级特征, 如车牌边缘、字母方向等, 采用MSE与最小化VGG的混合函数作为模型的损失函数.
3 本文网络模型 3.1 生成器模型对于车牌图像分辨率不足导致无法识别, 现有超分辨率算法重建的车牌图像依然存在字符扭曲, 字符断裂等问题. 因此, 在生成器模型阶段, 我们打算采用一种基于密集残差网络(dense-connected residual sampling network DRSN)的车牌超分辨率重建算法. 整体网络结构如图2所示.
由图2可以知道, 生成器网络包含3个模块, 分别为初始化特征提取模块, 密集连接的残差采样模块, 图像重建模块.
3.1.1 初始化特征提取模块| $ {F}_{-1}={H}_{FE1}\left({I}^{LR}\right) $ | (2) |
| $ {f}_{D}^{1}={F}_{0}={H}_{FE2}\left({F}_{-1}\right) $ | (3) |
式(1)中, HFE1表示为卷积核为3×3卷积层, 主要目的在于将车牌图像特征从空间维度映射到特征维度, 用于提取车票的形状边缘信息. HFE2是一个卷积核为1×1的卷积层, 用于对HFE1提取到的特征进行降维, 同时提取关键信息. F0表示初始化特征提取模块所提取到的特征, 同时也是密集残差连接模块的输入[17].
3.1.2 密集连接的残差采样块在更高级的特征提取模块, 本文采用了密集连接的残差采样块. 该模块由多个残差密集块(RRDB)链接而成. 密集连接的残差采样模块使得不同RRDB之间的存在着连续记忆. 一个RRDB可以链接所有后续的RRDB块, 传递并保留图像信息, 从而使状态延续传递. 其次, 密集连接的残差采样块同时具有密集与残差网络两者的优良特性, 将全局特征和局部特征融合形成连续的记忆机制.
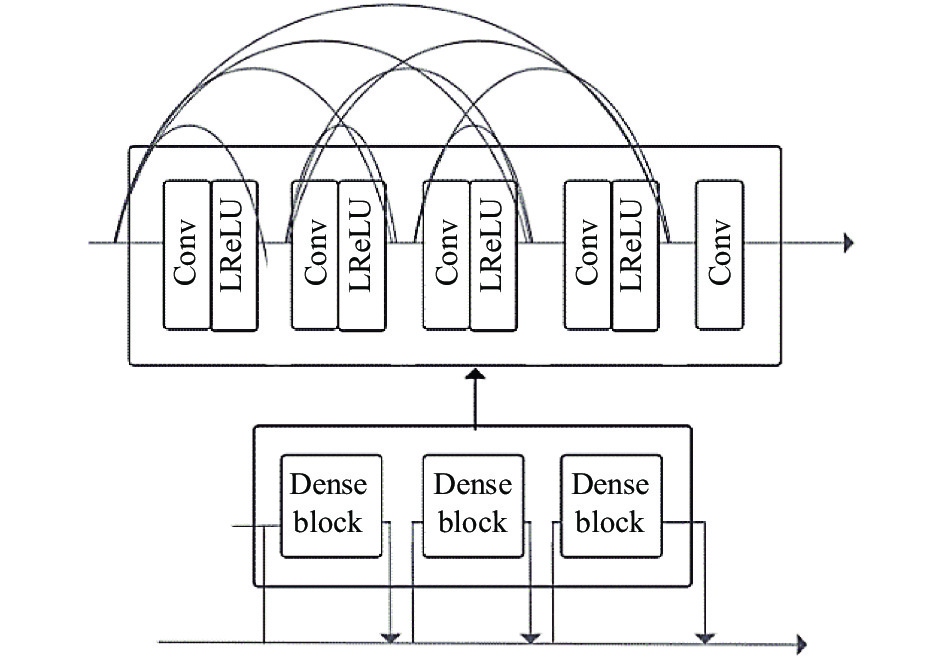
1个RRDB由3个dense block (DB)块组成. 1个DB块了存在着5个卷积核(Conv)与4个激活函数(Leaky-ReLU), 每个卷积核大小都为7×7. 它们密集地连接在一起, 形成了残差密集网络中的dense block, 整体结构如图3所示.
3.1.3 图像重建模块本文采取渐进式上采样实现车牌重建模块. 对比普通的上采样网络, 渐进式上采样采用子亚像素卷积实现. 这是因为子亚像素卷积能提高更多更细节的上下文信息. 在子亚像素卷积中, 我们假设亚像素图像的长、宽(设为h, w), 和采样因子r, 通过普通的卷积来产生h×w×r×r亚像素图像. 我们将亚像素图像按顺序进行重组, 得到高分辨率的图像. 结构如图4所示.
3.2 鉴别器模型鉴别器借鉴了PatchGAN[18]的思想, 将输入映射为N×N的矩阵M, 其中, 矩阵上每一个元素Mi,j对应原图中某个特定图像块(Patchi, j), 通过取鉴别器网络矩阵的均值作为最终判断结果, 设定阈值输出0或者1. 鉴别器设计选用卷积核大小为 4×4, 步幅为2的卷积层, 共6层, 用于增加感受野大小, 加强模型探索重要信息的能力, 同时利用全局池化操作去缩减特征规模, 提高网络计算速度.鉴别器的模型架构如图5所示.
3.3 损失函数我们采用MSE与最小化VGG的混合作为模型的损失函数.
在ESRGAN[9]中, 作者定义了一种新的VGG损失函数, 该函数有利于突出原始图像的特征. VGG损失定义如式(4):
| $ \begin{split} VGG(Y) =& \frac{1}{{{W_{i, j}}{H_{i, j}}}}\sum\limits_{x = 1}^{{W_{{{i}}, j}}} {} \sum\limits_{y = 1}^{{H_{i, j}}} ({\Phi _{i, j}}{{({I^{HR}})}_{x, y}} \\ &- {\varPhi _{i, j}}{{({G_{\theta G}}({I^{LR}}))}_{x, y}})^2 \end{split} $ | (4) |
其中, Wi, j和Hi, j表示VGG中特征图的尺寸,IHR表示高分辨率图像尺寸,
内容损失的作用使生成器的上采样网络在重建车牌时注意图像的高级特征, 如车牌边缘, 方向, 事实证明, 这是十分有利于车牌重建的.
整体的损失函数如式(5):
| $ \begin{split} Loss= & 0.01\times \frac{1}{n} {\sum }_{i = 1}^{n} \left|\right| VGG \left(\widehat{Y}\right) - VGG\left(Y\right)|{|}_{2} \\ &+ \frac{1}{n}{\sum }_{i=1}^{n} \left|\right|\widehat{Y} - Y|{|}_{2} \end{split} $ | (5) |
其中,

|
图 2 生成器网络结构图 |
|
图 3 残差密集网络结构图 |
4 实验结果和分析 4.1 实验过程
本文实验在CPU为CPU Intel Xeon E5-2689C2, GPU为NVIDIA GTX970, 显存为16 GB, 操作系统为Windows 10的主机上进行. 模型学习率初始化为10–5, 经过不断调整, 最终发现模型的最佳的学习率为10–3.
本项目采用的数据集来自于中国停车场数据集(CCPD)[19], 该数据集包含了大量的不同背景下的车牌照片, 数据集包含将近30万张图片. 显然, 我们应该对数据集进行筛选, 筛选掉亮度与对比度较差的图片. 最终, 我们选取了1 000张作为实验测试数据集. 其中, 800张车牌图片用于模型训练, 100张图片用于模型测试, 剩下的100张用于模型验证.

|
图 4 渐进式上采样网络结构图 |

|
图 5 鉴别器模型结构图 |
4.2 实验结果
我们的算法与目前较为先进的图像重建技术如Bicubic、SRCNN[20]、ESPCNN、EDSR[21]进行客观数据PSNR、SSIM的对比. 结果见表1和表2.
| 表 1 测试图像集超分辨率重建结果比较 |
| 表 2 典型图像实验结果对比 |
由表1可得, 基于深度学习的SR算法明显优越于Bicubic传统算法, 且基于GAN的算法较某些基于CNN的算法可以获得更高的PSNR、SSIM值, 具有更好的图像重建效果. 比较于Bicubic 和 ESPCNN, 本文模型重建车牌能获得较大的PSNR、SSIM 值.
由表2可以看出, 我们从测试集中选取了背景色调不同的4张图片作为典型图片, 并利用不同的算法进行重建, 效果如图6–图9所示. 相比于基于ESPCNN的重建算法和基于Bicubic的重建算法, 本文模型算法的PSNR、SSIM值有大幅度提高. 本文算法的平均 PSNR 值大约提升 2.0–4.0 dB, SSIM值大约提升0.01–0.04. 相比于EDSR、SRCNN等较为先进的算法, 本文算法模型的PSNR、SSIM值提升得并不明显. 这显然是美中不足的, 这需要我们后续对模型进行改进.

|
图 6 典型示例图1重建效果 |

|
图 7 典型示例图2重建效果 |

|
图 8 典型示例图3重建效果 |

|
图 9 典型示例图4重建效果 |
其次, 我们不仅在PSNR, SSIM方面对模型的优越性进行了验证, 我们还对算法的运行效率进行了测试. 由表3可看出, 基于Bicubic的重建算法耗时最短, 这是与它的简单插值方式有关. 相比于卷积神经网络中的ESPCNN, 我们的算法大约缩短了0.08 s, 同时PSNR值提高了1 dB左右, 最后, 在多种基于GAN框架算法中, 本文算法处理数据的平均速度最高.
| 表 3 各算法在同一图片上重建运行时间比较 |
综上所述, 本文提出的模型在保证重建精准度接近于国内外主流模型的前提下, 花费了较少的重建时间, 这是十分具有现实意义的.
5 讨论我们采用残差密集网络, 便于获取各网络层提取到的图像特征以保留图像更多的高频信息, 同时用渐进式上采样方式以提升大缩放因子下超分辨率重建效果. 同时在鉴别器模型上, 我们借鉴了马尔可夫判别器(PatchGAN), 将鉴别器设计成6层全卷积神经网络, 用于增加视觉感受野大小, 便于丰富重建后图像的细节. 其次, 我们的算法平均耗时较少, 基于CNN框架算法模型重建图片的平均耗时较多, 这是因为CNN包含了大量的卷积计算, 导致图像重建耗时较多.
接着, 我们从多维度去对本文算法进行评价. 我们引入PSNR、SSIM作为图像超分辨率重建评判指标, 根据表1、表2的数据显示, 我们的算法数值达到了目前主流算法的平均值以上, 但目前处于顶级的算法模型来说, 例如SRCNN、EDSR, 本文模型算法还是存在较大的差距, 我们通过粗略的分析是认为模型的判别器设计层数较少, 无法很好的高效率的区别机器数据和真实数据. 但是, 值得说明的是, 我们模型花费的时间也处于一个较低的值, 这是我们算法的一个的优势.
6 总结利用深度学习对图像进行重建不仅发展的速度极快, 而且修复后图像的效果要比传统技术修复要好. 本文在基于GAN网络上, 引入了残差密集网络以及渐进式上采样方法, 在车牌超分辨率重建模型上取得了令人满意的效果. 首先, 模型利用了密集残差网络对车牌图像进行高级, 核心特征的提取, 加强了特征的传播, 其次, 运用渐进上采样的方式重建大尺度因子图像. 最后, 算法采用基于PatchGAN的鉴别器更加精准地判断, 从而引导生成器更高质量、高细节的图像重建. 实验部分表明: 与其他 SR 算法相比较, 在花费较少的时间代价的情况下, 模型输出的图片具有PSNR、SSIM等参考值较高和较少的边缘阴影等优点. 未来研究工作的重点在于进一步优化网络结构, 降低训练的难度, 推进使得车牌重建算法早日运用于实际生活.
| [1] |
Zhou F, Yang WM, Liao QM. Interpolation-based image super-resolution using multisurface fitting. IEEE Transactions on Image Processing, 2012, 21(7): 3312-3318. DOI:10.1109/TIP.2012.2189576 |
| [2] |
Lin ZC, Shum HY. Fundamental limits of reconstruction-based superresolution algorithms under local translation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(1): 83-97. DOI:10.1109/TPAMI.2004.1261081 |
| [3] |
Lian QS, Zhang W. Image super-resolution algorithms based on sparse representation of classified image patches. Acta Electronica Sinica, 2012, 40(5): 920-925. |
| [4] |
Dong C, Loy CC, He KM, et al. Image super-resolution using deep convolutional networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-307. DOI:10.1109/TPAMI.2015.2439281 |
| [5] |
Kim J, Lee JK, Lee KM. Accurate image super-resolution using very deep convolutional networks. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas: IEEE, 2016. 1646–1654.
|
| [6] |
Kim J, Lee JK, Lee KM. Deeply-recursive convolutional network for image super-resolution. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas: IEEE, 2016. 1637–1645.
|
| [7] |
Zhang YL, Tian YP, Kong Y, et al. Residual dense network for image restoration. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(7): 2480-2495. DOI:10.1109/TPAMI.2020.2968521 |
| [8] |
Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017. 105–114.
|
| [9] |
Wang XT, Yu K, Wu SX, et al. ESRGAN: Enhanced super-resolution generative adversarial networks. European Conference on Computer Vision. Munich: Springer, 2018. 63–79.
|
| [10] |
Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: ACM, 2014. 2672–2680.
|
| [11] |
Ratliff LJ, Burden SA, Sastry SS. Characterization and computation of local Nash equilibria in continuous games. 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton). Monticello: IEEE, 2013. 917–924.
|
| [12] |
Isola P, Zhu JY, Zhou T, et al. Image-to-image translation with conditional adversarial networks. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 1125–1134.
|
| [13] |
Lai CX, Chen Y, Wang TY, et al. A machine learning approach for magnetic resonance image-based mouse brain modeling and fast computation in controlled cortical impact. Medical & Biological Engineering & Computing, 2020, 58(11): 2835-2844. |
| [14] |
罗会兰, 敖阳, 袁璞. 一种生成对抗网络用于图像修复的方法. 电子学报, 2020, 48(10): 1891-1898. |
| [15] |
胡蕾, 王足根, 陈田, 等.一种改进的SRGAN红外图像超分辨率重建算法. 系统仿真学报, 2021, 33(09): 2109–2118.
|
| [16] |
徐姝琪, 杨会成, 潘玥, 等. 基于生成对抗网络的面部修复. 平顶山学院学报, 2020, 35(5): 54-59. DOI:10.3969/j.issn.1673-1670.2020.05.012 |
| [17] |
郝元杰. 单幅车牌图像超分辨率重建算法研究[硕士学位论文]. 西安: 西安邮电大学, 2020.
|
| [18] |
Lan ZZ, Lin M, Li XC, et al. Beyond Gaussian pyramid: Multi-skip feature stacking for action recognition. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston: IEEE, 2015. 204–212.
|
| [19] |
Xu ZB, Yang W, Meng AJ, et al. Towards end-to-end license plate detection and recognition: A large dataset and baseline. Proceedings of the 15th European Conference on Computer Vision (ECCV). Munich: Springer, 2018. 261–277.
|
| [20] |
Keys R. Cubic convolution interpolation for digital image processing. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(6): 1153-1160. DOI:10.1109/TASSP.1981.1163711 |
| [21] |
Li FB, He X, Wei ZH, et al. Multiframe infrared image super-resolution reconstruction using generative adversarial networks. Infrared and Laser Engineering, 2018, 47(2): 17-24. |
 2022, Vol. 31
2022, Vol. 31



