无人机具有易于部署, 灵活性高以及制造成本低等优势, 常被用来部署在各种民用场景中, 其中包括精准农业, 清理海洋废弃物, 包裹投递, 自然灾害后恢复网络服务以及搜索与搜救[1-5]. 基于无人机的灾后搜救也由之前的单机式搜救逐渐发展到小型的多机群式搜救[6], 大幅度提高了搜救效率.
在早期, 无人机辅助搜救的目标多是针对目标位置已知的情况[7-9], 无人机只需要规划飞行路线抵达目标所在位置即可. 实际搜救过程中在搜索目标之前对于任务区域的信息知之甚少, 复杂的室内环境对于无人机的避障能力提出了巨大的挑战. 如何使无人机群对环境无任何先验知识的前提下进行自主决策是个值得研究的问题. 为此, 文献[10]将基于模型的强化学习算法应用到无人机的自主导航领域, 极大提高了无人机自主决策能力. 在无人机最佳路径规划方向, 文献[11]考虑了奖励与惩罚机制, 使得无人机在不断地尝试飞行中选择最佳路径从而到达目标位置. 考虑到无人机在复杂环境中状态值爆炸式的增多, 为解决大容量的状态值问题, 文献[12]提出了基于神经网络的分布式DQN算法, 以控制无人机在未知环境中进行目标搜索与目标跟踪. 针对大规模的搜索环境, 需要多台无人机设备进行协作完成搜索任务, 文献[13]提出一种异构多智能体算法, 以控制多台无人机在复杂的环境中以协作的方式最大程度上完成搜索任务.
为组织合作的、智能的、适应复杂环境下的无人机群, 本文提出了一种基于多智能体强化学习的控制策略. 首先将多无人机搜救任务进行建模处理, 将其转化为具有完全回报函数的分散的部分可观的马尔可夫决策过程; 其次提出了基于集中学习分散执行的多智能体强化学习方法, 利用了Double-DQN算法对Dec-POMDP进行了求解; 最后利用蒙特卡洛方法对本方案进行通用性测试. 结果表明本文方案在搜救成功率方面所具备的优势, 能够在大型的救援环境中出色的完成搜救任务.
1 问题概述与系统模型 1.1 问题概述本文考虑了这样一个场景, 某大型图书馆发生火灾, 无人机群进入图书馆以协作的方式迅速对馆内受害人员进行搜索. 具体地, 无人机群的搜索任务环境如图1所示. 该图模拟了复杂的室内环境, 为简化训练模型, 假设无人机飞行过程中高度恒定为h(不包括起飞与降落操作), 飞行速度恒定为V. 受害者的手机可作为其位置信息传感器随时发出其位置信息, 其通信模式为: 无人机通过发射一种激活信号, 受害者持有的终端设备接受此信号后通过反向散射(back scatter)方式向无人机发送位置数据[14], 由于每个手机设备反射功率的不同会导致无人机只有在一定范围内才能采集位置信息.

|
图 1 无人机室内搜救模型 |
任务区域内随机布置了3台无人机与7名位置随机的受害者. 无人机从停机坪(充电站位置)出发后, 分别对受害者位置信息进行采集, 受限于电池容量的影响, 无人机群须在电量耗尽之前返航到充电站位置进行充电操作, 对于没能在电量耗尽之前安全返航进行充电操作的所提方案将其作为惩罚加入奖励函数中.
为将地图进行合理的建模, 本方案将地图分割为
在本文中, 所提方案考虑到现实场景, 将无人机与受害者之间的通信链路建模为视距(line of sight, LOS)与非视距(none-line of sight, NLOS)的点对点信道模型[15], 在该信道模型下本文定义在时间为
| $ {R}_{{j}}(n)={\mathrm{log}}_{2}\left(1+\frac{{P}_{j}}{{\sigma }^{2}}\cdot {d}_{j}{(n)}^{-{\alpha }_{e}\cdot{10}^{{\eta }_{e}/10}}\right) $ | (1) |
其中,
本系统模型的主要研究目标是使得无人机团队在一定约束条件下能够最大化的从搜救区域中搜集受害者的位置信息. 这些约束条件主要分为两部分, 一部分来自无人机设备自身的条件约束, 例如电池容量. 另一部分来自环境对无人机设备的约束. 例如室内门墙等障碍物、无人机与无人机之间避免碰撞以及无人机的起落位置(充电位置).
对无人机群进行建模, 定义第
| $ A({p_i}(t)) = \left\{ {\begin{array}{*{20}{l}} {\{ hover,east,north,west,south,charging\} ,} \;{{p_i}(t) \in \mathbb{Z}}\\ {[0,0, - h]/\{ hover,east,north,west,south,charging\} ,} \;{{\text{otherwise}}} \end{array}} \right. $ | (2) |
| $ \left\{\;\; {\begin{split} &hover = {[0,0,0]^{\rm{T}}} \hfill \\ &east = {[c,0,0]^{\rm{T}}} \hfill \\ &north = {[0,c,0]^{\rm{T}}} \hfill \\ &west = {[ - c,0,0]^{\rm{T}}} \hfill \\ &south = {[0, - c,0]^{\rm{T}}} \hfill \\ &charging = {[0,0, - h]^{\rm{T}}} \hfill \end{split} } \right.$ | (3) |
第
无人机
| $ {\lambda _i}(t + 1) \in \left\{ {\begin{array}{*{20}{l}} {0,} \;{{a_i}(t) = {{[0,0, - h]}^{\rm{T}}} \vee {\lambda _i}(t) = 0}\\ {1,} \;{{\rm{otherwise}}} \end{array}} \right. $ | (4) |
对于本模型中的无人机剩余电量, 第
| $ {E_i}(t + 1) = \left\{ {\begin{array}{*{20}{l}} {{E_i}(t) - 1,}\;{{\lambda _i}(t) = 1} \\ {{E_i}(t),}\; {{\text{otherwise}}} \end{array}} \right. $ | (5) |
对于无人机的动作策略的优化本质上是对无人机的接收信息的吞吐量最大化, 无人机群与受害者持有的设备之间通信时遵循标准的时分多址模型(TDMA), 在任务时间
| $ \mathop {\max }\limits_{{x_i}{a_i}(t)} \sum\limits_{t = 0}^T {\sum\limits_{i = 1}^I {{B_i}(t)} } $ | (6) |
| $ {B_i}(t) = {\lambda _i}(t)\sum\limits_{n = \beta t}^{\beta (t + 1) - 1} {\sum\limits_{j = 1}^J {{q_{i,j}}(n){R_{i,j}}(n)} } $ | (7) |
其中,
强化学习作为机器学习的一个重要分支, 其核心是智能体与特定环境的重复交互, 学习如何在未知环境中执行最优策略[16]. 在当前状态
本文针对多无人机协作问题定义了同质的、非通信的、简单合作的无人机群. 同质性是指每台无人机设备具有相同的构造结构, 相同的动作空间以及任务领域; 非通信是指无人机之间没有直接的通信, 即无人机不能协调它们的动作以及进行有关的通信, 但都能感知与其他无人机之间位置信息, 并可利用这种感知到的位置信息对无人机进行监管维护; 简单合作是指无人机团队共同收集的位置数据可添加到每一台无人机的回报函数中, 这就使得他们有一个共同的目标. 在多智能体训练阶段, 每台无人机与环境不断地交互进行自身的策略优化, 之后将它们的经验数据集中起来, 通过组建神经网络数据库来训练控制系统, 最后将训练好的控制系统部署到每台无人机设备上.
2.1 部分可观的马尔可夫决策过程本节将无人机团队与环境交互的问题转换为部分可观的马尔可夫决策过程. 一个Dec-MDP通常是由一个七元组组成
状态(
动作(
| $ \mathop {{a_i}}\limits^\vartriangle (t) = \left\{ {\begin{array}{*{20}{l}} {{{[0,0,0]}^{\rm{T}}},}\;\mathbb{R} \\ {{a_i}(t),}\; {\rm{otherwise}} \end{array}\begin{array}{*{20}{l}} \\ \end{array}} \right. $ | (8) |
在区域
| $ \left\{ {\begin{array}{*{20}{l}} {{p_i}(t) + {a_i}(t) \in \{ \mathbb{C},\mathbb{N}\} } \\ { \vee {p_i}(t) + {a_i}(t) = {p_k}(t) \wedge {\lambda _k}(t) = 1} \\ {\forall k,k \ne i} \end{array}} \right. $ | (9) |
即时奖励(
| $ {\psi _i}(t) = \tau \sum\limits_{j = 1}^J {({D_j}(t + 1) - {D_j}(t))} $ | (10) |
路径规划奖励主要用于惩罚无人机在飞行过程中不执行安全动作空间, 为诱导无人机优化最短飞行路径来搜集受害者的位置信息, 定义方法如下:
| $ {\theta _i}(t) = \left\{ {\begin{array}{*{20}{l}} {\theta + \delta ,} \;{{a_i}(t) \ne \mathop {{a_i}}\limits^\vartriangle (t)}\\ {\delta,} \;{\rm{otherwise}} \end{array}} \right. $ | (11) |
其中, 当无人机的动作空间不符合安全动作空间时, 给出惩罚
即时充电奖励强迫无人机在电量耗尽之前返航进行充电, 对于没有即时返航的无人机给予值为
| $ {\omega }_{i}(t)=\left\{\begin{array}{l} \omega ,\;{E}_{i}(t+1)=0\wedge {p}_{i}(t+1)={[·,·,h]}^{\rm{T}}\\ 0,\;{\rm{otherwise}} \end{array}\right. $ | (12) |
综上3部分, 总即时奖励为以上3部分奖励之和, 即:
| $ {R_i}(t) = {\psi _i}(t) + {\theta _i}(t) + {\omega _i}(t) $ | (13) |
观测结果(
| $ {f_{\rm{2D}}}(x) = \left[ {\begin{array}{*{20}{c}} {1/c}&0&0 \\ 0&{1/c}&0 \end{array}} \right]x $ | (14) |
式(15)与式(16)分别将受害者与无人机的位置经过投影函数
| $ {\widehat L_j}(t) = {f_{\rm{2D}}}({L_j}(t)) $ | (15) |
| $ {\widehat p_i}(t) = {f_{\rm{2D}}}({p_i}(t)) $ | (16) |
带有位置信息
| $ {f_{\rm{observation}}}:{P_{\rm{location}}} \times {Q_{\rm{information}}} \to O $ | (17) |
式(18), 式(19), 式(20)分别将无人机的位置信息与该位置对应的运动状态和剩余电量在映射函数
| $ {O_{{\lambda _i}(t)}} = {f_{\rm{observation}}}(\{ {\widehat p_i}(t)\} ,\{ {\lambda _i}(t)\} ) $ | (18) |
| $ {O_{{E_i}(t)}} = {f_{\rm{observation}}}(\{ {\widehat p_i}(t)\} ,\{ {E_i}(t)\} ) $ | (19) |
| $ {O_{{D_j}(t)}} = {f_{\rm{observation}}}(\{ {\widehat L_j}(t)\} ,\{ {D_j}(t)\} ) $ | (20) |
将上述所有的图层作为无人机的观测结果输入到本文神经网络架构中, 式(21)为无人机的观测结果:
| $ {O_i}(t) = ({M_i}(t),{O_{{\lambda _i}(t)}},{O_{{E_i}(t)}},{O_{{D_j}(t)}}) $ | (21) |
本文的无人机群在大型室内空间中执行任务, 如将Q值表示为数值表格是不可取的, 文献[17]应用了经验回放等方面的技术, 将Q-Learning与神经网络结合起来, 完美的解决了大状态空间问题. 经验池的主要功能是解决相关性与非静态分布问题, 具体方法是通过将每个时刻智能体与环境交互的样本
DQN算法的主要目标是保证估计值网络输出的值
| $ {{TargetQ}}=r+\gamma \underset{{a}^{\prime }}{\mathrm{max}}Q({s}^{\prime },{{{a}}}^{\prime };\theta ) $ | (22) |
基于上述的目标值, 定义DQN的损失函数公式, 求
| $ L(\theta ) = E[{({{{TargetQ}}} - Q(s,a;\theta ))^2}] $ | (23) |
具体地, DQN算法的流程如图2所示.
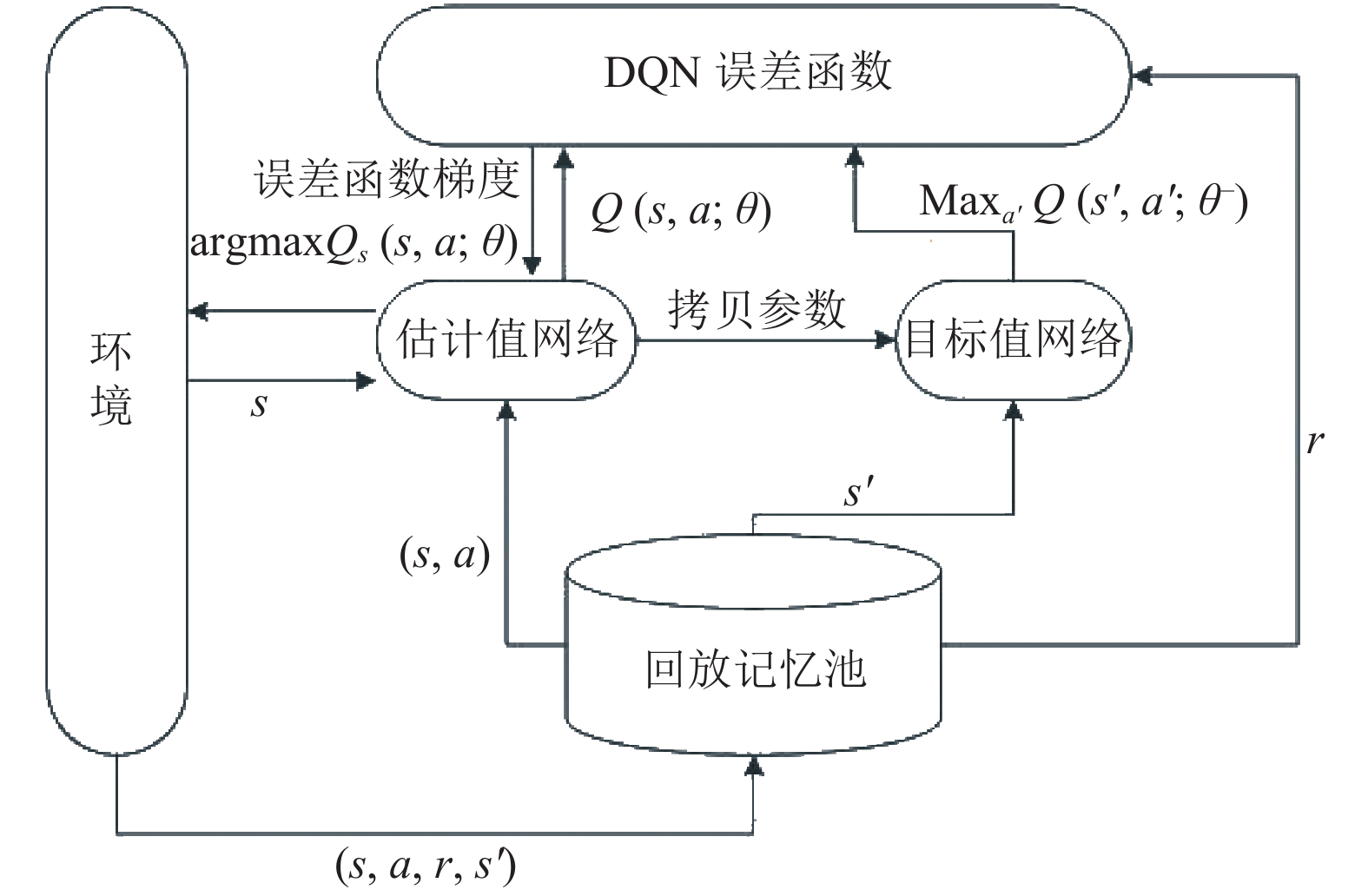
|
图 2 DQN算法流程图 |
3 无人机团队路径规划算法 3.1 Double DQN (DDQN)算法
本文利用DDQN算法对无人机团队路径规划进行训练, 不同于DQN算法, DDQN算法克服了Q-Learning算法固有的缺陷即过估计问题, 而在DQN算法中此问题也没有得到有效解决, 为解决过估计问题Double DQN算法将动作的选择和动作的评估分别用不同的值函数来实现如图3所示, 具体如下:
通过网络(main-net)获得最大值函数的动作a, 然后通过目标网络(target-net)获得上述动作a所对应的
| $ {{{TargetQ}}} = r + \gamma Q(s',{{{\rm{argmax}}} _a}({Q_{\rm{main}}}(s',a))) $ | (24) |
基于目标网络
| $ L(\theta ) = E[{({{{TargetQ}}} - {Q_{\rm{main}}}(s,a;\theta ))^2}] $ | (25) |
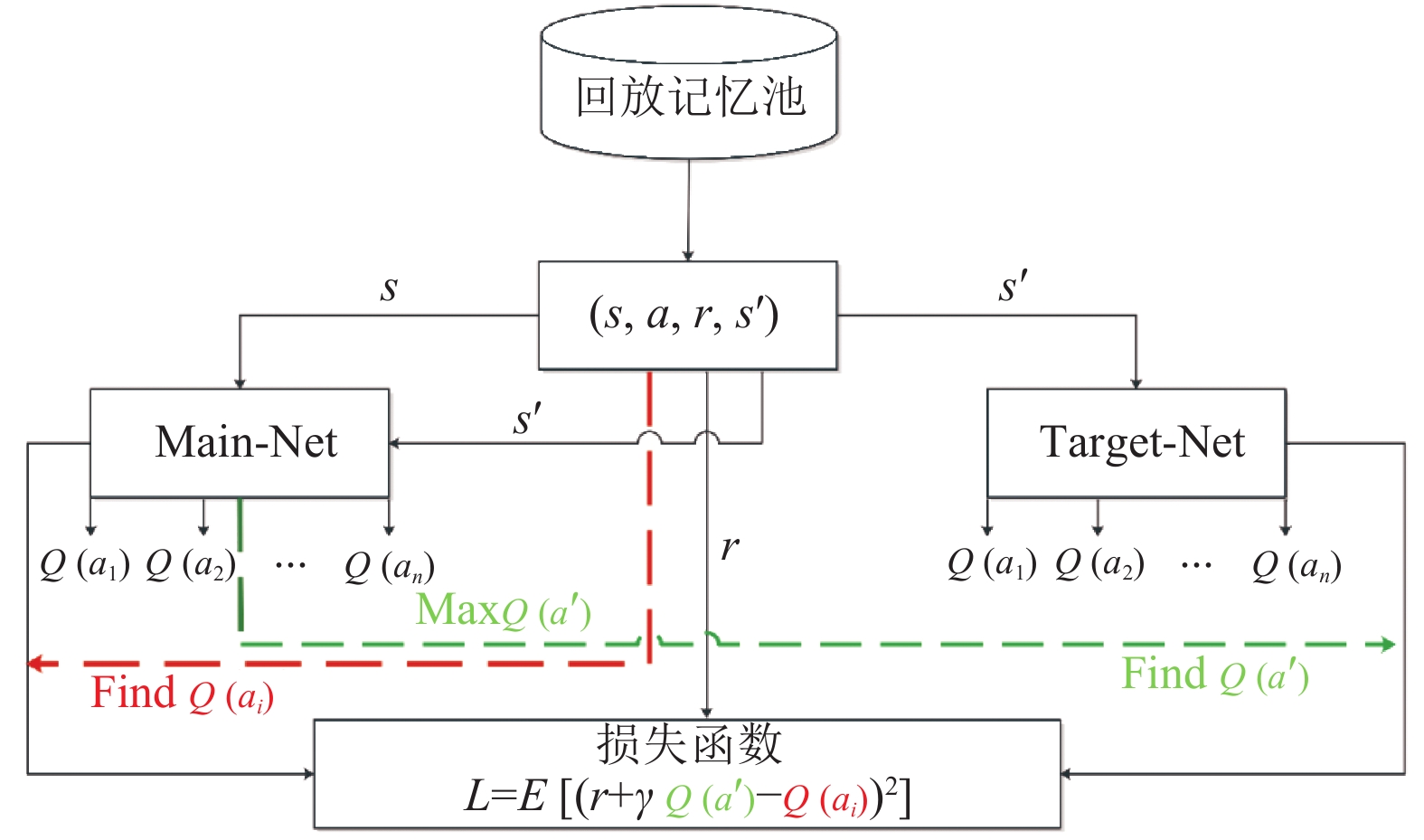
|
图 3 DDQN损失函数构造流程 |
3.2 Double DQN神经网络
如图4所示, 本文构建了该神经网络架构. 将上述处理的4幅信息图层堆叠起来组成状态信息图作为观测值传入卷积核为5×5的卷积层1和2, 然后通过激活函数
利用
| $ P({a_i}|s) = \frac{{{{\rm{e}}^{{V_i}}}}}{{\displaystyle\sum\nolimits_i^6 {{{\rm{e}}^{{V_i}}}} }} $ | (26) |
| $ {V_i} = \frac{{{Q_\theta }(s,{a_i})}}{\beta } $ | (27) |
通过贪婪策略得到
| $ \pi (s) = \arg \max {Q_\theta }(s,a) $ | (28) |
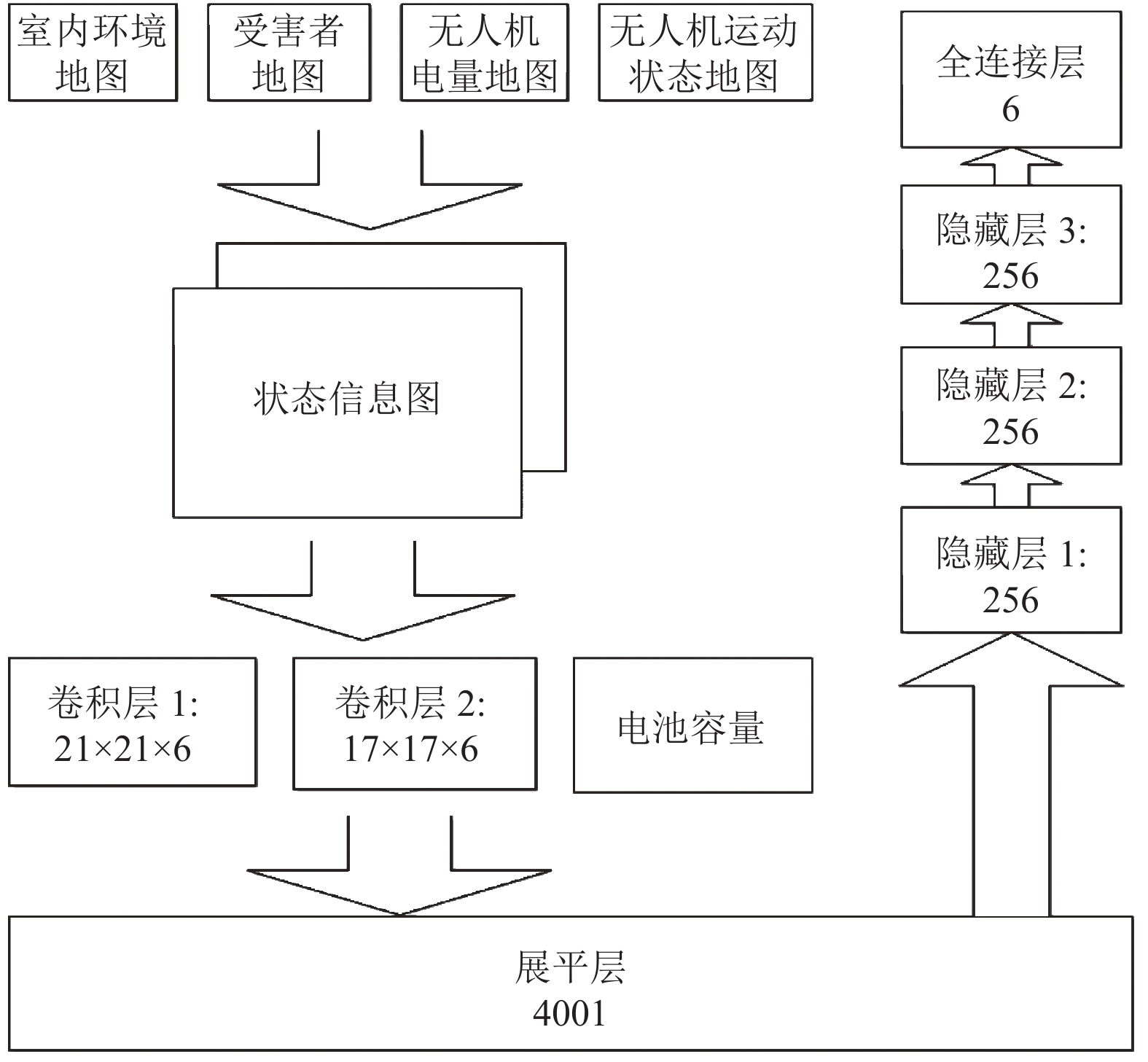
|
图 4 神经网络架构 |
4 仿真分析
本节对所提方案进行仿真与分析, 且与传统算进行对照, 最后验证了本文所提方案所具备的优势. 本文考虑了320 m × 320 m的无人机搜索区域, 无人机团队在所提方案的训练后在室内搜救路径规划如图5所示.

|
图 5 无人机团队搜救路径 |
在该室内区域随机分布了9位受害者, 为达到较好搜救效果, 本方案为其配备由3台无人机设备组成的搜救机群. 无人机的起落位置, 充电站都在图5中蓝色区域. 将不同的受害者用不同颜色的小圆圈表示. 所飞行的路径轨迹由图5中带箭头的线段表示, 不同路径颜色则代表此时的无人机正在搜集与本颜色所对应受害者的位置信息. 固定其飞行高度为10 m, 飞行速度为1 m/s, 考虑到飞行区域为室内区域, 设定路径损耗参数
相比于传统方案, 所提方案优势在于加入充电操作、引入多智能体、适用大状态搜救场景3方面, 为验证3方面所具备的优势, 分别使用所提方案与传统的算法对本文场景进行了无人机群的路径规划训练. 经过3 000 000次的训练迭代, 所提方案使得累计回报值得到显著提升.
| 表 1 仿真参数设置 |
本文方案加入充电模块, 相比于未加入此模块的传统方案训练所得的累计回报对比如图6所示.

|
图 6 两种方案的训练回报对比 |
在图6中, 所提方案累计回报值增长较快, 最终达到收敛. 可以明显看出加入充电模块的回报值明显高于传统方案. 这种比较说明了本文方案能够快速的适应搜救场景, 且能高效的进行辅助搜救, 因此本文方案更加有效.
为说明所提方案在大状态环境的适用性, 将本文室内搜救场景下的受害者的数量以及部署的无人机集群规模进行逐步增大, 观测其对于搜救率的影响. 如图7所示, 随着受害者人数的增加对同一规模集群其搜救率并没有出现明显的骤降, 之所以出现下降趋势是由于在整个搜救场景中受害者的位置被随机的放置, 受害者人数的增加导致无人机的碰撞概率增大最终导致无人机集群更加复杂的路径规划, 因此使得搜救成功率有所下降.

|
图 7 所提方案对于大状态环境下的搜救率 |
在图7中, 由2台无人机组成的集群搜救成功率明显低于其他集群, 主要原因是在大范围与复杂的搜救场景中, 2台无人集群缺乏搜索覆盖能力, 存在搜索盲区导致搜救率下降. 如果采取由4台无人机组成的集群进行搜救任务, 当环境中存在4位以下受害者时能达到最佳搜救效果, 然而随着受害者人数增加到5位以上时, 搜救成功率明显低于由3台无人机组成的搜救集群. 这是因为环境中存在4位以下受害者时, 由4台无人机组成的搜救集群具有较强的搜救覆盖能力且不需要执行复杂的路径规划, 受害者人数增加到5人以上时, 4台无人机集群虽具有较强的覆盖能力, 但在一定范围的搜索环境下, 无人机设备数量的增多以及受害者人数的上升势必会导致复杂的路径规划, 对于无人机之间的避免碰撞以及单程电池容量提出了巨大挑战. 考虑到本文实际的模拟场景以及设备成本, 最终选择3台无人机作为搜救集群, 并达到了最优的搜救效果.
本文对随机场景进行了1 000次蒙特卡洛迭代, 所得性能指标用于评估多智能体在搜救任务中的优势, 图8可以明显看出, 在搜救场景中部署多台无人机设备使得搜救成功率得到了显著提高, 传统的单智能体方案在搜救区域增大时缺乏搜救覆盖能力, 如其经常在某一个固定区域搜救然后直接返回着陆位置, 造成其他区域位置的受害者无法得到救援, 最终导致搜救能力下降.
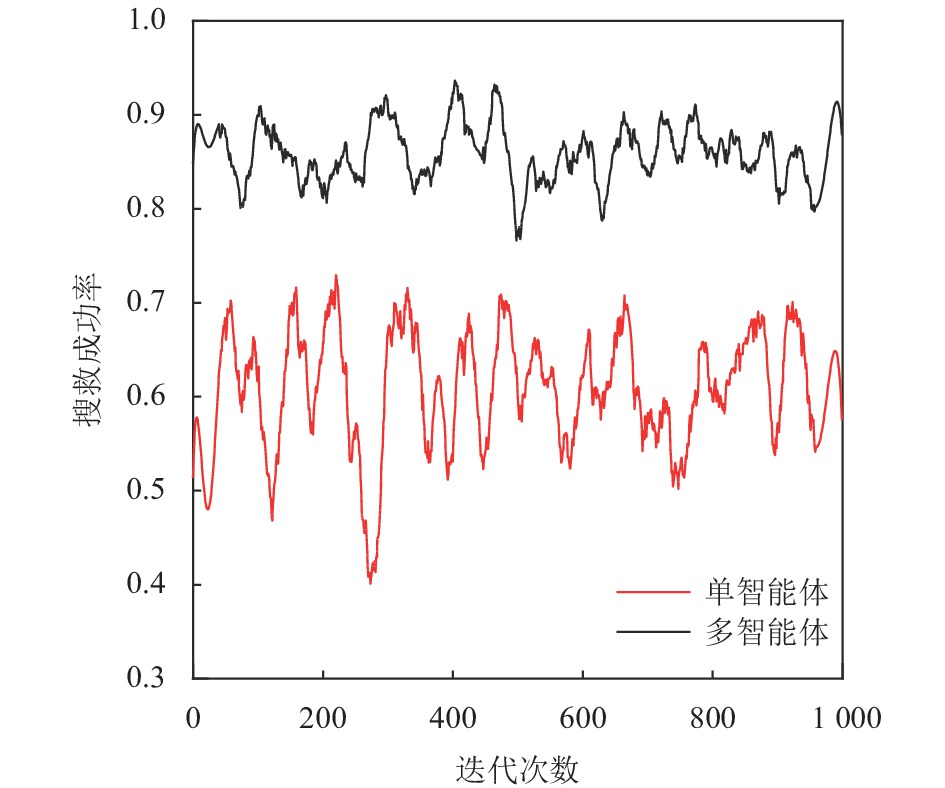
|
图 8 多智能体与单智能体搜救率对比 |
5 总结
本文研究了无人机群协作进行辅助搜救的问题, 搜救的区域是发生火灾的大型室内场景. 为提高无人机群的搜救能力本文引入了一种多智能体强化学习方案, 该方案基于DDQN算法来优化无人机团队的飞行路径, 解决了无人机群在不确定环境下的搜救问题, 在搜救过程中无人机群受限于电池容量, 所提方案又引入了充电模块, 从而最大程度的完成对受害者位置信息的搜集. 除此之外, 本文还详细描述了将搜救的模型转化为部分可观的马尔可夫决策的过程. 对于未来的工作, 无人机速度控制以及飞行高度的扩展是重要的探索方向, 这种扩展可以使无人机团队适应更为复杂的搜救场景.
| [1] |
Zeng Y, Zhang R, Lim TJ. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Communications Magazine, 2016, 54(5): 36-42. DOI:10.1109/MCOM.2016.7470933 |
| [2] |
Pham HX, La HM, Feil-Seifer D, et al. Reinforcement learning for autonomous UAV navigation using function approximation. 2018 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR). Philadelphia: IEEE, 2018. 1–6.
|
| [3] |
Chowdhury MU, Bulut E, Guvenc I. Trajectory optimization in UAV-assisted cellular networks under mission duration constraint. 2019 IEEE Radio and Wireless Symposium (RWS). Orlando: IEEE, 2019. 1–4.
|
| [4] |
Chowdhury MU, Erden F, Guvenc I. RSS-based Q-learning for indoor UAV navigation. 2019 IEEE Military Communications Conference (MILCOM). Norfolk: IEEE, 2019. 121–126.
|
| [5] |
Ezuma M, Erden F, Anjinappa CK, et al. Detection and classification of UAVs using RF fingerprints in the presence of Wi-Fi and Bluetooth interference. IEEE Open Journal of the Communications Society, 2019, 1: 60-76. |
| [6] |
Zhang YM, Mehrjerdi H. A survey on multiple unmanned vehicles formation control and coordination: Normal and fault situations. 2013 International Conference on Unmanned Aircraft Systems (ICUAS). Atlanta: IEEE, 2013. 1087–1096.
|
| [7] |
Bertuccelli LF, How JP. Search for dynamic targets with uncertain probability maps. 2006 American Control Conference. Minneapolis: IEEE, 2006. 6.
|
| [8] |
Bourgault F, Furukawa T, Durrant-Whyte HF. Decentralized Bayesian negotiation for cooperative search. Proceedings 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566). Sendai: IEEE, 2004. 2681–2686.
|
| [9] |
沈延航, 周洲, 祝小平. 基于搜索理论的多无人机协同控制方法研究. 西北工业大学学报, 2006, 24(3): 367–370.
|
| [10] |
Imanberdiyev N, Fu CH, Kayacan E, et al. Autonomous navigation of UAV by using real-time model-based reinforcement learning. 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV). Phuket: IEEE, 2016. 1–6.
|
| [11] |
Gandhi D, Pinto L, Gupta A. Learning to fly by crashing. 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Vancouver: IEEE, 2017. 3948–3955.
|
| [12] |
Venturini F, Mason F, Pase F, et al. Distributed reinforcement learning for flexible UAV swarm control with transfer learning capabilities. Proceedings of the 6th ACM Workshop on Micro Aerial Vehicle Networks, Systems, and Applications. Ontario: ACM, 2020. 10.
|
| [13] |
Liu CH, Dai ZP, Zhao YN, et al. Distributed and energy-efficient mobile crowdsensing with charging stations by deep reinforcement learning. IEEE Transactions on Mobile Computing, 2021, 20(1): 130-146. DOI:10.1109/TMC.2019.2938509 |
| [14] |
Zhang Y, Li B, Gao FF, et al. A robust design for ultra reliable ambient backscatter communication systems. IEEE Internet of Things Journal, 2019, 6(5): 8989-8999. DOI:10.1109/JIOT.2019.2925843 |
| [15] |
Narayanan S, Renzo MD, Graziosi F, et al. Distributed spatial modulation: A cooperative diversity protocol for half-duplex relay-aided wireless networks. IEEE Transactions on Vehicular Technology, 2016, 65(5): 2947-2964. DOI:10.1109/TVT.2015.2442754 |
| [16] |
Sutton RS, Barto AG. Reinforcement learning: An introduction. IEEE Transactions on Neural Networks, 1998, 9(5): 1054. |
| [17] |
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning. Nature, 2015, 518(7540): 529-533. DOI:10.1038/nature14236 |
 2022, Vol. 31
2022, Vol. 31


