不平衡数据是指在一个数据集中, 某一类别数据的样本数量远远大于其他类别样本的数量, 其中, 样本数量较少的类别被称为少数类(或称为正类), 类别数量较多的类被称为多数类(或称为负类). 类不平衡是一个现实生活中普遍存在的现象, 如故障检测、医学诊断、信用卡欺诈检测、软件缺陷检测、互联网攻击识别等. 传统的分类方法如感知机^[1]、决策树^[2]、朴素贝叶斯模型^[3]、Logistic回归^[4]、支持向量机^[5]等, 众多的方法都是为了提高分类模型的性能而设计提出, 但是不平衡数据的出现会导致训练得到的分类器对多数类的感知能力强于对少数类的感知能力, 这对诸如医学诊断、信用卡欺诈检测等应用场景是十分不利的, 因此, 如何提高不平衡数据集的分类器性能已经成为机器学习领域的热点问题, 众多解决不平衡数据问题的新方法也不断被提出.

目前, 解决非平衡数据集的方式主要有两种: 一种是从算法的改进入手, 该方式从生成新的分类策略、分类器集成^[6]、代价敏感^[7]、特征选择^[8]等方面进行改进; 另一种是从数据集的处理入手, 这也是重要的处理不平衡问题的方式, 主要采用包括欠采样^[9]、过采样^[10]、训练集划分等降低数据集的不平衡程度. 其中, 欠采样方法容易造成有用信息的丢失, 过采样方法容易造成分类器的过拟合^[11]. 本文由此出发, 从生物遗传理论^[12]中得到启发, 利用“近亲”(同类临近数据)生成有相似特性而又和“父类”不完全相同的少数类数据, 在平衡两类数据的同时又极大降低传统方法中过拟合的现象.

1 相关工作

解决数据不平衡问题时, 在数据处理方面, 采样的方式分为非启发式采样和启发式采样, 本文提出的合成少数类样本是典型的启发式方法. 此外, 启发式过采样方法还结合了K近邻准则(K-nearest neighbor,KNN)^[13]、邻域清理准则(neighborhood cleaning rule, NCL)^[14]、OSS(one-sided selection)^[15]和 IRUS (inverse random under sampling)^[16]等.

Chawla等在2002年提出了少数类样本合成技术, 即SMOTE (synthetic minority over-sampling technique) ^[17]. 此方法与随机过采样方法不同, 它是通过在少数类样本与其k个最近邻居连线上合成新样本, 合成公式如下:

$ {x_{\rm{new}}} = x + rand(0,1) \times \left( {\widetilde x - x} \right) $

(1)

使用传统的SMOTE算法会增加子集群的大小, 生成的每个数据实例都属于指定的集群, 加剧了类内的数据不平衡. 该方法中对实例点A和B进行过采样, 生成的点会落到各自的簇中, 估计的决策边界会向实例密集的群靠近, 而不是向实际边界靠近. 正如Barua的结论: 这些问题的出现是因为这些方法选择了所有k个最近的邻居, 而忽略了数据点与这些邻居间的位置关系和距离关系.

随后, Freund等提出了AdaBoost算法^[18], 是一种经典的集成算法, 该算法相对传统算法具有更好的泛化能力, 更高的分类精度. Chawla等将SMOTE方法和AdaBoost.M2 算法相结合, 在每次迭代中引入合成样本, 提出SMOTEBoost分类算法^[17]. Kinoshita等提出了联合随机降采样与Boosting的RUSBoost算法^[19], 是SMOTEBoost的变形. 李克文等^[20]提出基于 RSBoost的不平衡数据分类方法, 该方法采取 SMOTE过采样和随机降采样, 再将其与Boosting 算法相结合对数据进行分类: 李雄飞等提出一种新的不平衡数据学习算法PCBoost^[21], 每次迭代初始, 考虑属性特征, 合成新的少数类样本, 平衡训练信息.

上述研究中, 各种改进过采样的方法改善了类间的数据不平衡, 一定程度上提高了分类器的性能, 虽然较原生AdaBoost方法取得了较大的进步, 但仍然需要继续关注和改进, 进一步提高不平衡数据的分类精度. 本文提出的改进方法充分考虑了类间和类内的不平衡, 使少数类边界最大化, 更好地模拟数据的分布, 提高样本的总体质量.

2 基于遗传理论的不平衡数据过采样方法 2.1 染色体遗传理论

根据基础生物学和遗传学, 位于染色体上的基因是遗传的基本单位, 受精卵形成过程中, 有父母双方各一半染色体等量组合, 这就是染色体遗传理论.

引入集合M=(m_1, m_2, m_3, …, m_q)和F=(f_1, f_2, f_3, …, f_q)分别代表来自父母双方的一对染色体, A、B为控制个体性状的等位基因, 新个体产生过程中同源染色体上的等位基因彼此分离, 非同源染色体上的非等位基因自由组合, 如图1所示. 生物遗传理论的发现对生物学、农业等领域都掀起了巨大的轰动, 对该理论的应用取得了重大的成果. 生物学家通过基因工程得到了更高产, 抵抗灾害能力更强的作物极大促进了人类社会生产力的发展. 从中得到启发, 我们可以通过相似性度量来分离数据样本, 合理的对有缺陷的类进行过采样. 与遗传理论不同的是: 遗传理论强调基因对个体性状的影响, 而用于采样方法中的遗传理论强调个体的多样性; 遗传理论中, 生成新的个体后父类个体逝去, 而该采样方法中, 父类数据个体和子数据个体会同时存在于集合中.

2.2 基于遗传理论的过采样原理

利用染色体遗传理论, 将缺陷模块的特征指标作为染色体. 改进的过采样方法分为3个阶段: 首先, 分离出少数类与多数类样本, 并按照少数类样本相对本类样本的马氏距离进行降序排列; 将已排序少数类样本从中心点分割为两份数据集, 并依次为相应数据集中的每个实例分配唯一标签; 最后, 从两个分区中选择有相同唯一标签的实例求均值生成新的实例. 算法1列出了整个过程.

算法1. 基于遗传理论的过采样算法

(1) 将数据集按照少数类与多数类进行划分获得集合N_min、N_maj;

(2) 计算可使数据集达到平衡的所需合成的少数类样本数T, 并记k为少数类样本集样本数;

(3) 建立容纳合成数据的集合 $\scriptstyle {X_{\rm{new}}}$ , 初始化为空;

(4) 建立记录合成数据数量的数据集 $\scriptstyle {X_{{\rm{new}}c}}$ , 初始化为空;

(5)计算N_min中样本的马氏距离D²;

(6)创建马氏距离矩阵N_mindist, 将数据按照递减顺序进行存储;

(7)确定中间实例N_mid;

(8)将N_mindist以N_mid为界分为两个子集, 分别记为N_bin1={x₁, x₂, x₃, …, x_mid}和N_bin2={x_min+1, x_min+2, x_min+3, …, x_k}, 其中 $\scriptstyle {x_i} \in {N_{\rm{midist}}}$ ;

(9)为 $\scriptstyle {x_i} \in {N_{\rm{bin1}}}$ 和 $\scriptstyle {x_i} \in {N_{\rm{bin2}}}$ 中的样本按次序分配标签 $\scriptstyle {l_i} $ , $\scriptstyle i = 1,\;2,\;3, \cdots ,\;{\rm{mid}}$ ;

(10) for $\scriptstyle i = 1,\;2,\;3, \cdots ,\;{\rm{mid}}$

(11)

　1)选择 $\scriptstyle {N_{\rm{bin1}}}$ 和 $\scriptstyle {N_{\rm{bin2}}}$ 中标签相同的样本 $\scriptstyle {l_i} $ , 如 $\scriptstyle {x_a}\left( {{l_i}} \right) = = {x_b}\left( {{l_i}} \right) $ ;

　2)通过取 $ {x_a},{x_b} $ 均值生成少数类样本x

　3)将x添加到 $\scriptstyle {X_{\rm{new}}}$ 中, 增加 $\scriptstyle {X_{{\rm{new}}c}}$

(12) end for

(13)如果 $\scriptstyle {X_{{\rm{new}}c}} < T$ , 将 $\scriptstyle {X_{\rm{new}}}$ 中的实例与每个父 $\scriptstyle {N_{\rm{bin}}}$ 中的实例配对, 并重复步骤(10)–(12)来创建两个不同的集合 $\scriptstyle {X}_{{\rm{new}}[j]}\left(j=1, 2, \cdots \right)$ . 如果仍然 $\scriptstyle {X_{{\rm{new}}c}} < T$ , 将当前的每一个 $\scriptstyle {X_{\rm{new}}}$ 集合与它的直接父集合进行配对后, 然后将其与祖先集合进行配对, 并为后续迭代重复步骤(10)–(12);

(14)如果 $\scriptstyle {X_{{\rm{new}}c}} \geqslant T$ , 将 $\scriptstyle {X_{\rm{new}}}$ 中的所有样本赋值为少数类(defective)的标签, 并添加到数据集N中.

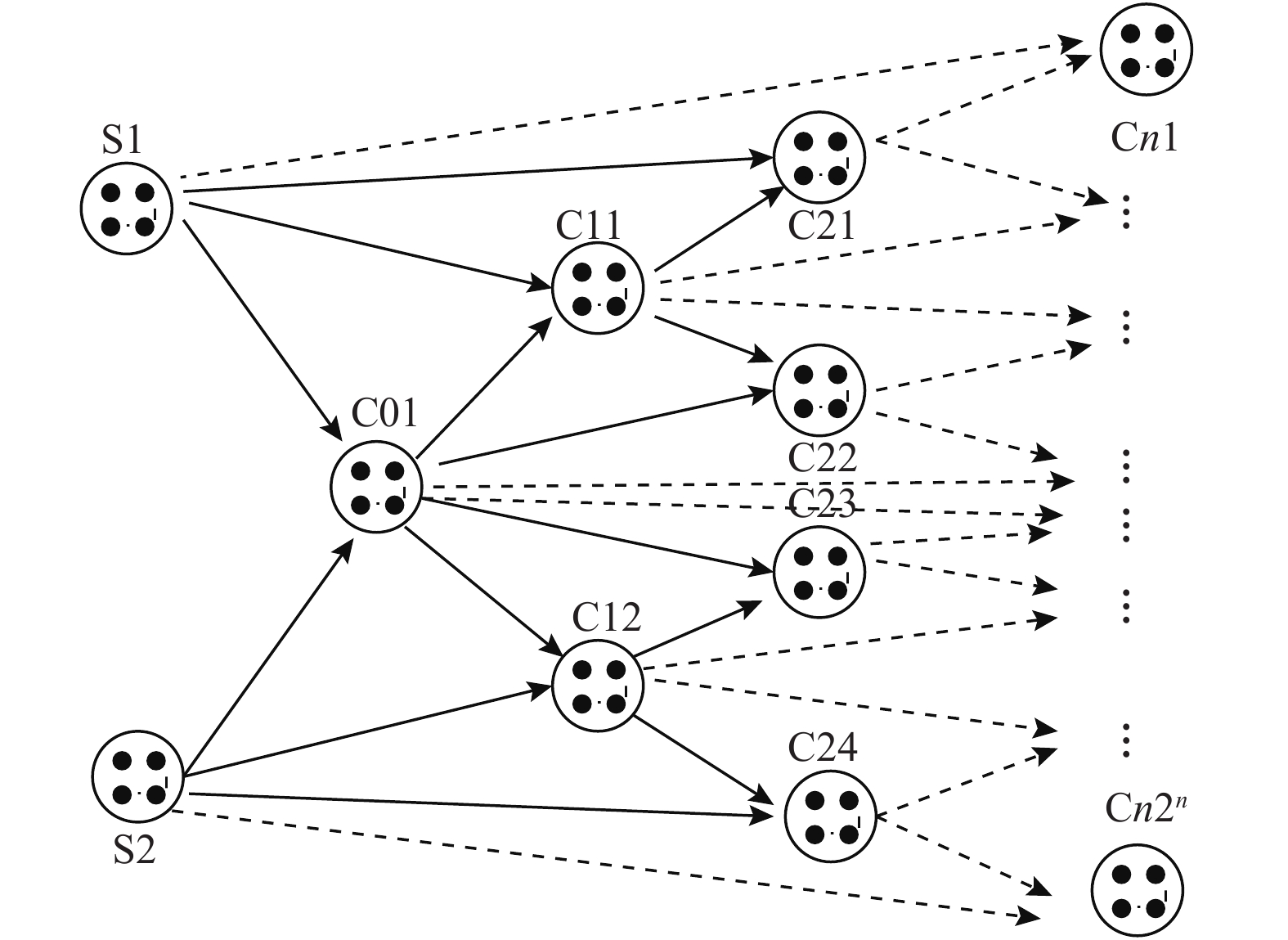
图解(图2)过程如下: 第1步, 根据数据点的马氏距离找到起始双亲即S1和S2, 合成新样本C01, 为了防止传统SMOTE方法中的渗透现象, 设定初始父节点作为边界, 将后续生成的子节点限定在父类的范围内, 如果需要更多的实例, 在第2代中, 利用新生成的实例分别与父节点(S1、S2)继续生成新的节点. 在第3代中, 如果子节点和直接父节点配对生成的样本小于所需的样本数量, 则利用祖父节点与当前节点继续配对生成新的节点, 当前层级的所有配对情况均已完成后若仍不满足样本需求, 则继续按照此规则进行下一层级新样本的生成直至满足所需样本数量. 从第1代开始, 调用的是算法1的步骤(10)–(14).

实例点x=(x_1, x₂, x₃, …, x_n)^T与实例点y=(y_1, y₂, y₃, …, y_n)^T之间的马氏距离可表示为: ${d_m}\left( {\overrightarrow x ,\overrightarrow y } \right) = $ $ \sqrt {{{\left( {\overrightarrow x - \overrightarrow y } \right)}^{\rm{T}}}M_{}^{ - 1} {\left( {\overrightarrow x - \overrightarrow y } \right)} }$ (其中, M是多维随机变量的协方差矩阵, 它的幂为–1表示求其逆矩阵), 我们使用这个度量将数据点进行降序排列, 以便于我们区分出数据点离中心点的距离. 将本文所提出的过采样方法记为GOS (genetic over-sampling)算法, 其执行过程如下:

GOS算法的流程图如图3所示. 基于P_fp的值, 算法计算要生成的合成数据实例的数量, 对已生成但不需要的数据进行剔除. 最后一层以上的合成数据点全部存储至最终数据集中. 冗余数据的删除从所生成的最后一层数据开始, 方法是将完成所需最终集的剩余数据样本量除以该层上的样本总数得到选择概率P_c. 然后以概率值P_c在最后一层中选择保留样本, 这意味着上一级别的每个样本可为所需新生成数据作出相同贡献.

基于所设定的两个分区, 新生成的实例与其父实例是密切相关的, 两个分区之间的顺序限定保证了子实例的遵循父实例的趋势, 新的实例就被限制在了少数类样本的边界之内, 同时避免了样本的重叠现象. 相对于KNN, 改进算法所生成的样本分布更加均匀, 携带的信息量更大.

3 实验分析 3.1 实验设置

为验证本文遗传过采样算法的表现, 探究分类预测模型能否借助本文采样方法提升预测精度, 实验部分将本文方法(GOS)同SMOTE、Borderline-SMOTE、随机过采样(ROS), 和非采样方法(None)进行比较. 实验数据集采用UCI公共数据集中的数据, 数据详情如表1所示, 其中Yeast数据集中将EM1、EXC、VAC 作为正类, CYT、NUC、MIT 作为负类; Ecoli数据集中将第2、4、5、6类作为正类, 其余作为负类.

实验结果的评价指标采用召回率及几何平均值G-mean, 其表达式如式(2)、式(3)所示, 式中变量含义如表2所示. 其中, 召回率越高, 则说明分类器对少数类样本的识别性能越好, 可以反映出分类器对少数类样本的识别敏感度; G-mean值弥补了召回率作为评价指标的片面性, 该评价公式将少数类的识别准确率和多数类的识别准确率同时考虑在内, 可更加综合的反映出算法的总体预测分类性能.

$ Recall = \frac{{TP}}{{TP + FP}} $

(2)

$ G {\textit{-}} mean = \sqrt {\frac{{TP}}{{TP + FN}} \times \frac{{TN}}{{TN + FP}}} $

(3)

对实验数据的准备主要包括预处理、备份、数据划分. 具体为首先经过对实验数据执行集成、规约、变换等预处理后将6个数据集进行复制备份至5份, 分别采用5种采样方式进行采样得到目标实验数据集, 对每个数据集按照4:1的比例划分训练集和测试集, 而后, 分别在3种分类模型(BP、SVM、决策树)的作用下进行测试, 以对比各采样方式在不同分类模型中对最终结果的影响, 其中每项最终实验数据均采用10折交叉验证的方式产生. 其中, 采用3种对比算法的目的是减小实验结果的偶然性, 提升实验结果的说服力.

3.2 实验结果分析

经过对比试验, 各分类算法在不同采样方式的作用下产生的分类结果如表3、表4所示, 表3为各算法在召回率(Recall)评价中的表现. 由表中数据可以看出, 由于数据集Breast Cancer和Hepatitis平衡率较高, 采样算法甚至无需执行, GOS采样方式对其召回率的提升并不明显, 除了SMOTE采样方式下的BP实验结果和Borderline-SMOTE采样方式下的SVM实验结果外, 本文采样方式下的分类结果和相对应的分类算法所获取的次优结果相比, 仍然以最低1%, 最高4%的优势取得最优的召回率值; 对于数据集Spambase和Steel Pastry, 其不平衡率相对加剧, GOS采样方式对其召回率的提升相对明显, 和次优结果相比平均提升了4.1%; Yeast和Ecoli数据集的平衡率最低, GOS采样方法对各算法的召回率性能提升也最为明显, 达到了4.8%. 表3数据表明采样方法可以提升算法对正类样本的错分概率, 有效缓解不平衡数据对算法性能的影响.

表4为各分类算法在不同采样方式的作用下取得的G-mean值, 从表中数据可得, Breast Cancer和Hepatitis两个较为平衡的数据集在SMOTE和Borderline-SMOTE采样方法中以BP分类算法和SVM分类算法取得了1%优势, 这是由于采样方法对数据集的改变较弱, 实验结果主要取决于原始数据, 采样对算法性能提升不明显; 除此之外, 本文采样法下的算法均取得了最优的G-mean值. 表4的实验结果进一步印证了本文算法的有效性.

对本文所提出方法的表现更为优异的原因进行简要分析, 这可以归因于该方法所生成的样本在少数类边界内简洁且同原样本的分布更为相似, 扩散更加均匀. 从样本多样性角度考虑, 通过计算重采样数据样本中少数类中每个度量的多样性, 每个指标的多样性计算使用香农多样性指数来评价, 通过该评价指标我们发现GOS对样本多样性的增加是最为明显的.

4 总结与展望

本文针对现行分类算法对不平衡数据集的正类数据预测性能偏低的情况提出一种基于遗传思想的过采样方法, 该方法在不改变数据分布的前提下, 通过合成少数类数据实例来平衡数据集中的正负样本成分. 该采样方式避免了常见合成方式会产生错误或重复的数据导致高负类率的情形, 马氏距离的使用确保了合成数据不会跨越分类算法的决策边界. 通过在6个公共数据集上使用3种分类模型, 将本文方法和其他4种采样方法进行比较, 经90个实验组合结果验证, 本文采样方式在召回率和G-mean两个评价指标上均取得了综合最优的结果, 证明了本文采样方式的有效性. 在未来的研究中, 对GOS在多分类模型中的引入应用可进一步扩展该采样法方法的应用价值.