2. 中交隧道工程局有限公司, 北京 100102;
3. 长安大学 公路学院, 西安 710064
2. CCCC Tunnel Engineering Co. Ltd., Beijing 100102, China;
3. School of Highway, Chang’an University, Xi’an 710064, China
当前, 国内隧道建设进程处于高速发展阶段, 且正由东部转站中西部. 在复杂山区地形下, 隧道施工存在高风险、管理难、施工方式落后等诸多问题. 通过各类传感器可以辅助监测隧道的施工及安全状态, 并为管理和施工者提供合理决策. 针对实时监测量仅能反映出隧道当前的各项安全指标, 对于未来可能出现的潜在风险并没有前瞻性的不足, 国内外诸多学者开展了针对隧道地表下沉量、拱顶下沉量和周边收敛量等预测研究, 并取得了一定的研究成果. 总体而言, 对于隧道变形预测的方法主要有经验法、回归分析法、灰色系统理论模型、人工神经网络等. 对于经验法, 因为存在较大的主观性, 现已采用较少, 多为辅助使用, 回归分析法介于只适用于一些静态数据的处理, 因此很难用于隧道沉降这种动态的模型分析, 灰色理论法, 该法于1982年由邓聚龙教授提出[1], 最早被用于农业和经济领域, 随着经济建设的发展, 逐步被运用于土木工程领域, 并在建筑物的沉降、边坡的长期变形预测、混凝土长期强度的变化的预测等方面取得一定成果, 如胡亮等[2]对高速公路隧道进行灰色理论模型预测, 贾承辉等[3]基于激光断面仪运用灰色理论对隧道进行变形预测, 胡达[4]、张锦等[5]基于改进灰色理论模型对隧道围岩变形进行监测, 并取得较好的监测效果. 但随着实际工程应用的增多以及对该理论研究的深入, 诸多学者发现, 灰色理论对数据的要求较高, 要求数据具备指数递增或单调性, 在很大程度上限制了它在具有非线性变形特点的隧道上的应用.
基于数字技术的发展, 人们对神经网络的研究越来越深入, 目前, 各类人工智能算法已经得到突飞猛进的进步, 包括经典的BP神经网络以及新型的诸如长短期记忆人工神经网络(LSTM)等深度学习算法在计算机视觉、语音识别、文本分类等领域都得到了广泛的应用并取得了良好的效果. 在隧道监测领域也有部分应用, 例如, 廖小辉等[6]基于BP神经网络分析预测了混凝土的抗压强度变化, 赵挚南等[7-9] 结合数值分析软件研究了基于BP神经网络邻近地铁基坑土体参数反演规律的变化, 且取得了较好的分析结果. 武铁路[10]以广州地铁7号线为例, 采用深度学习方法对破碎带盾构施工沉降进行预测分析, 并分析了预测结果与实测值来验证预测模型的有效性. 曾学宏等[11]将LSTM网络应用于地铁隧道的沉降变形分析, 并取得了较高的预测精度. 孙钧等[12-15]将人工神经网络和智能模糊逻辑应用于施工变形预测, 且已经在上海沿江通道中得到阶段性试验应用.
然而, 相较于回归分析、支持向量机等经典方法, 人工神经网络在隧道施工安全状态监测领域应用的研究仍较为欠缺[16-18]. 目前人工神经网络在隧道施工安全状态监测领域应用已经得到验证, 但是目前的研究主要是将人工神经网络运用在参数明确、机械化程度高的盾构隧道工程中, 对爆破等施工因素引起的隧道地表下沉预测研究较少; 且现有监测方法多为基于时间序列的指标预测, 鲜有文献将隧道指标的监测特征区域作为人工神经网络的分析、拟合和预测对象.
鉴于此, 本文提出了一种基于特征区域(feature region, FR)神经网络的隧道地表沉降状态预测模型. 通过采集白家庄隧道栾川端的地表观测数据对所提方法的预测性能进行算例分析, 以此检验基于时空特征区域神经网络的施工隧道沉降量预测方法的准确性和可靠性.
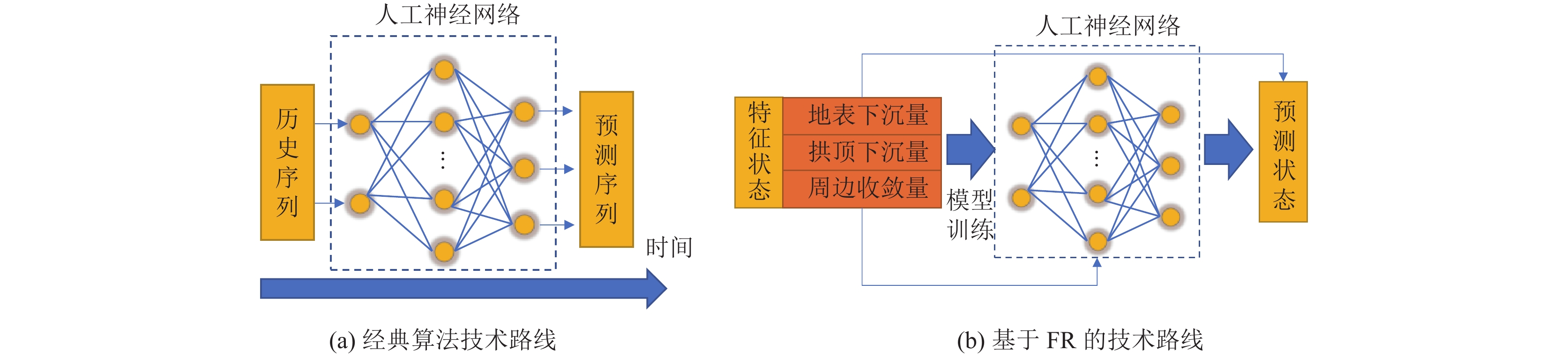
1 基于FR神经网络的构建 1.1 建模思想在隧道领域, 基于神经网络构建的模型越来越多, 总结来说主要有对围岩的变形预测、隧道地表沉降的预测、隧道岩体位移的预测、隧道支护形式的稳定性的评价等, 更具体的来说, 以往对隧道的变形方面的预测都是基于时间特性的预测, 但传统的基于时间序列的隧道地表沉降量预测方法多数只考虑了时间特性, 而在时空特征等方面却很少有考虑, 而实际隧道的变形却是一个随时空变化的动态变形过程, 这种过程不仅融合了时间特性, 更是与周边环境气候等多因素相关, 因此, 为准确预测隧道的沉降量, 预测模型的关注量融合了隧道时空特征的监测状态, 而非单一时间序列下的指标. 经典预测算法的技术路线和基于FR的技术路线对比图如图1所示.
|
图 1 技术路线对比 |
基于FR的人工神经网络隧道特性状态预测步骤为: 首先, 基于大量实测隧道监测历史数据筛选能够代表隧道施工状态的特征变量, 并借助多源数据融合提取关键变量; 其次, 通过人工神经网络(BP神经网络、LSTM神经网络)训练学习诸如地表下沉量、拱顶下沉量和周边收敛量等隧道特性数据的典型演化趋势; 最后, 依据训练后的神经网络做出空间特征度量的状态预测, 为隧道监测即施工管理规划提供合理建议与参考.
需要说明, 上述隧道特征量的筛选主要用到K-means聚类方法: 首先, 随机选取k个聚类中心, 并计算各特征点与聚类中心的多维空间距离; 其次, 依据计算结果为各特征点分配簇, 并计算簇心; 随后, 迭代计算特征点群的空间距离, 确定相应的簇及簇心, 直至满足终止条件; 最后, 当各特征点距离簇心的全局误差平方和满足设定要求后, 终止迭代计算. 特征区域可以反映出沉降量、收敛量等的平均演化特征, 减小神经网络的计算复杂度.
1.2 空间特征度量为衡量个体特征点之间的相关性, 常采用如下两种距离计算方法, 即切比雪夫距离和曼哈顿距离. 个体特征点在多维空间中的无量纲距离越远就表明个体差异性越大.
(1)切比雪夫距离(CD)
CD的具体计算公式如式(1)所示:
| $ CD(E,U): = \mathop {\lim }\limits_{q \to \infty } {\left( {\sum\limits_{j = 1}^m {{{\left| {{{{e}}_j} - {u_j}} \right|}^k}} } \right)^{1/k}} = \max \left| {{{e}}_{\mathop j\limits_{} }} - {u_j} \right|,j\in m $ | (1) |
(2)曼哈顿距离(MD)
MD的具体计算公式如式(2)所示:
| $ MD(E,U): = \sum\limits_{j = 1}^m {\left| {{e_j} - {u_j}} \right|} $ | (2) |
网络架构图如图2所示, 网络隐藏层选用tansig函数, 输出层选用purelin函数. 对于BP神经网络, 隐藏层神经网络的个数选择如经验公式(3).
| $ L = \sqrt {I + O} + \delta $ | (3) |
其中, L为网络隐藏层节点数, I为输入层数, O为输出层数, δ为经验选取值, 一般取值在1–10之间.
定义网络传播误差为:
| $ E{\text{ = }}\frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{k = 1}^K {{{({p_{n,k}} - {{\hat p}_{n,k}})}^2}} } $ | (4) |
其中,
| $ \begin{split} \frac{{\partial E}}{{\partial w}}& = \sum\limits_i {\sum\limits_j {\frac{{\partial E}}{{\partial x_{ij}^ + }}} } \frac{{\partial y_{ij}^ + }}{{\partial x_{pq}^ + }} \\ &= \sum\limits_i {\sum\limits_j {{\delta _{ij}}\frac{\partial }{{\partial x_{pq}^ + }}\left(\sum\limits_p {\sum\limits_q {w_{pq}^ + y_{i + p,j + q}^ + + {b^ + }} } \right)} } \\ &= \sum\limits_i {\sum\limits_j {{\delta _{ij}}y_{i + p,j + q}^ - } } \end{split} $ | (5) |

|
图 2 神经网络架构图 |
图2所示神经网络的输入为隧道地表下沉量的观测平均值、相对变化值和累计变化值经聚类后的监测量. 隐藏层依据经验公式(3)选择神经元个数为10. 输出层的输出量分别为沉降量的观测平均值、相对变化值和累计变化值的预测值.
2 工程实例 2.1 数据来源此工程采用的数据均来源于河南省郑西高速栾双段白家庄隧道栾川端的左线和右线地表实时观测数据, 隧道左线桩号ZK104+214–ZK105+526, 全长1 312 m; 右线桩号K104+116–K105+416, 全长1 300 m, 为河南省郑西高速栾双段在建隧道群中最长隧道, 隧道地处于华北陆块南缘与秦岭构造带的结合部位, 大部分位于昆仑–秦岭构造带东段, 在该段岩片北边界附近常见古生代辉长闪长岩及斜长花岗岩侵入体成带分布, 它们是二郎坪群火山活动晚期的同源岩浆侵入活动产物, Ⅳ、Ⅴ级围岩居多, 且岩体性质较不稳定, 在隧道开挖过程中, 常伴有围岩脱落等情况, 容易造成超挖等现象, 被工程建设称为 “最难啃的骨头”, 因此, 隧道采用台阶法开挖, 并严格遵守短进尺、弱爆破原则.
为防止隧道因爆破等施工因素引起隧道较大的变形沉降, 提出了基于特征区域神经网络的隧道地表沉降状态预测模型进行案例分析, 以准确对隧道开挖过程中可能出现的变形进行准确及时预测. 数据采集时段为2019年8月25日–2019年9月14日, 每日观测3次, 最终的监测数据取为3次观测的平均值. 数据分别采集自桩号K104+116-2.1、K104+126-1.2和K104+126-1.3.
2.2 隧道地表下沉量监测量(1)桩号K104+116-2.1传感器
表1为隧道右线栾川端桩号K104+116-2.1传感器的地表下沉量监测数据. 施工状态的监测数据可以反映出隧道当前的安全状态, 若超出预警值则需要及时停止施工, 重新评估设计方案及施工. 但传感器的监测数据是实时反映隧道当前安全指标, 并不具备前瞻性和预测性.
| 表 1 隧道右线栾川端地表下沉量测记录表(桩号K104+116-2.1) |
(2)桩号K104+126-1.2传感器
表2为隧道右线栾川端桩号K104+126-1.2传感器的地表下沉量监测数据. 在实际隧道施工中, 传感器需在各受力关键部位多点安放, 来综合反映出隧道总体情况. 因此文中另选取同一隧道的不同部位传感器进行监测分析.
(3)桩号K104+126-1.3传感器
表3为隧道右线栾川端桩号K104+126-1.3传感器的地表下沉量监测数据. 为防止预测算法仅适用于特定传感器数据, 而不具有普适性, 即出现过拟合现象. 加设桩号K104+126-1.3传感器为预测结果进行验证分析.
| 表 2 隧道右线栾川端地表下沉量测记录表(桩号K104+126-1.2) |
| 表 3 隧道右线栾川端地表下沉量测记录表(桩号K104+126-1.3) |
3 结果与分析
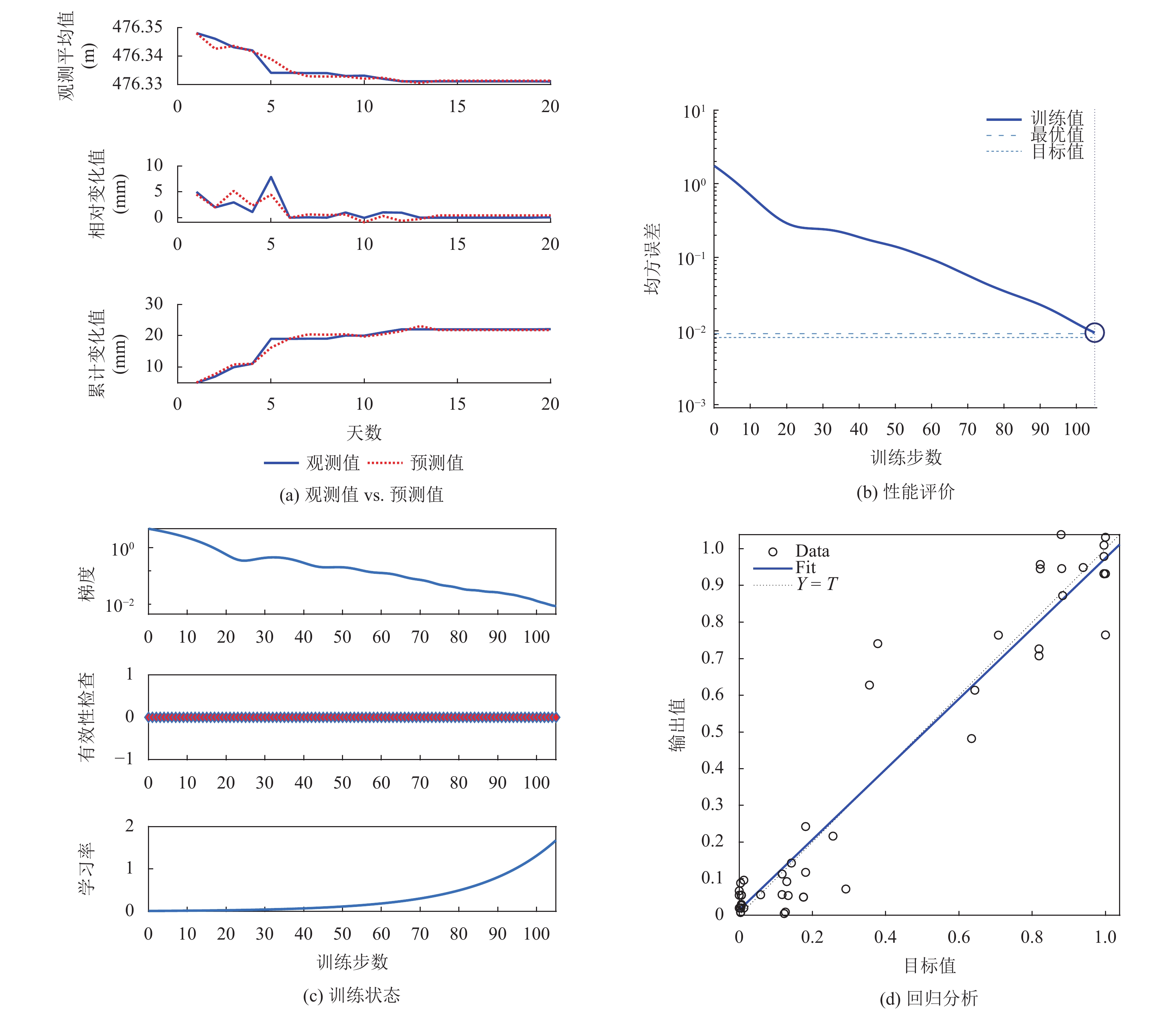
图3显示了桩号K104+116-2.1传感器数据采用与预测结果. 图3(a)分别对比了沉降量的观测平均值、相对变化值与累计变化值的观测量和相应的预测量. 实线代表每天的实际观测量, 虚线代表依据历史观测数据预测到的沉降及其变化量. 图3(b)显示神经网络训练曲线、最优训练结果和目标, 结果显示在105代达到了最优训练表现, 即0.009 510 5. 图3(c)显示了神经网络的训练状态, 在105代即结束代的梯度和学习率分别为0.017 479和1.678 3. 图3(d)为网络回归分析, 结果显示拟合数据与训练数据间的相关度为0.971 5, 即具有较高的相关性.
|
图 3 桩号K104+116-2.1传感器数据预测结果 |
为了确保所提预测模型的可靠性, 另选择桩号K104+126-1.2传感器数据进行验证分析. 图4显示了桩号K104+126-1.2传感器数据采用与预测结果. 图4(a)分别对比了沉降量的观测平均值、相对变化值与累计变化值的观测量和相应的预测量. 实线代表每天的实际观测量, 虚线代表依据历史观测数据预测到的沉降及其变化量. 图4(b)显示神经网络训练曲线、最优训练结果和目标, 结果显示在122代达到了最优训练表现, 相比于图3的结果迭代次数有所延长. 最优训练结果为0.009 827 5, 相比于图3所示结果0.009 510 5, 性能有轻微降低. 图4(c)显示了神经网络的训练状态, 在122代即结束代的梯度和学习率分别为0.009 592 4和3.846 8, 可以看出学习率相比于图3(c)步长较长, 可能在优化过程中产生了振荡. 图4(d)为网络回归分析, 结果显示拟合数据与训练数据间的相关度为0.950 24, 总体来说仍具有较高的相关性.

|
图 4 桩号K104+126-1.2传感器数据预测结果 |
同理, 选择桩号K104+126-1.3传感器数据进行验证分析. 图5显示了桩号K104+126-1.3传感器数据采用与预测结果. 图5(a)分别对比了沉降量的观测平均值、相对变化值与累计变化值的观测量和相应的预测量. 实线代表每天的实际观测量, 虚线代表依据历史观测数据预测到的沉降及其变化量. 图5(b)显示神经网络训练曲线、最优训练结果和目标, 结果显示在333代达到了最优训练表现, 训练迭代次数均超出图3和图4所示结果. 最优训练结果为0.009 927 9. 图5(c)显示了神经网络的训练状态, 在122代即结束代的梯度和学习率分别为0.005 818 2和3.694 4, 可以看出学习率相比于图3(c)步长较长, 可能在优化过程中产生了振荡. 图5(d)为网络回归分析, 结果显示拟合数据与训练数据间的相关度为0.961 93, 相关性介于图3与图4之间, 预测的鲁棒性基本稳定.
综上所述, 针对桩号K104+116-2.1、桩号K104+126-1.2和K104+126-1.3的隧道地表沉降量传感数据均有较准确的预测效果, 且预测结果也具有一定的鲁棒性, 未出现过拟合情况, 可应用于实际隧道施工的监测管理过程.

|
图 5 桩号K104+126-1.3传感器数据预测结果 |
4 结论与展望
本文对时空特征区域神经网络在施工隧道沉降量预测中的应用展开了深入的研究和分析, 并以此提出了一种基于特征区域的神经网络隧道状态监测模型, 且依据白家庄隧道实例地表下沉量对未来的演化趋势做出合理预测, 得出以下几点结论.
(1)基于特征区域的神经网络模型能够有效融合多维空间特征量, 预测结果具有精准性和鲁棒性的特点, 并能解决传统神经网络易出现过拟合的现象.
(2)基于特征区域的神经网络模型相比于经典技术路线能更合理准确地预测出隧道地表下沉量, 在隧道管理施工领域有一定应用价值.
| [1] |
邓聚龙. 灰色控制系统. 华中工学院学报, 1982(3): 9–18.
|
| [2] |
胡亮. 基于灰色理论的高速公路隧道围岩变形预测方法及应用. 交通标准化, 2013(9): 103-105. |
| [3] |
贾承辉. 基于灰色理论的隧道围岩变形预测. 科技视界, 2015(17): 258-259. DOI:10.3969/j.issn.2095-2457.2015.17.208 |
| [4] |
胡达, 黄小林, 何杰. 基于改进灰色理论模型的隧道围岩变形预测. 公路工程, 2017, 42(5): 72-75, 84. DOI:10.3969/j.issn.1674-0610.2017.05.015 |
| [5] |
张锦, 陈林, 赖祖龙. 改进遗传算法优化灰色神经网络隧道变形预测. 测绘科学, 2021, 46(2): 55-61, 77. |
| [6] |
廖小辉, 黄新, 施俊玲, 等. 基于BP网络的再生混凝土抗压强度的预测模型. 南京林业大学学报(自然科学版), 2010, 34(5): 105-108. |
| [7] |
赵挚南, 年帅, 郝龙, 等. 基于BP神经网络邻近地铁基坑土体参数反演分析. 施工技术, 2020, 49(S1): 661-663. |
| [8] |
Xiao Z, Ye SJ, Zhong B, et al. BP neural network with rough set for short term load forecasting. Expert Systems with Applications, 2009, 36(1): 273-279. DOI:10.1016/j.eswa.2007.09.031 |
| [9] |
Jin W, Li ZJ, Wei LS, et al. The improvements of BP neural network learning algorithm. Proceedings of the 2000 5th International Conference on Signal Processing. Beijing: IEEE, 2000. 1647–1649.
|
| [10] |
武铁路. 基于深度学习的破碎带盾构施工沉降预测分析. 隧道建设, 2019, 39(2): 197-203. DOI:10.3973/j.issn.2096-4498.2019.02.003 |
| [11] |
曾学宏, 赵义花. LSTM网络在地铁隧道沉降预测中的应用研究. 甘肃科学学报, 2019, 31(6): 117-122. |
| [12] |
孙钧, 温海洋. 人工智能科学在软土地下工程施工变形预测与控制中的应用实践—理论基础、方法实施、精细化智能管理(示例). 隧道建设, 2020, 40(1): 1-8. DOI:10.3973/j.issn.2096-4498.2020.01.001 |
| [13] |
曾德建, 刘维, 杜宇本. 基于人工神经网络的顺层偏压隧道变形预测. 路基工程, 2020(3): 170-174. |
| [14] |
王铁生, 张利平, 华锡生. 地铁隧道施工变形预测研究综述. 水利水电科技进展, 2003, 23(5): 62-65. DOI:10.3880/j.issn.1006-7647.2003.05.022 |
| [15] |
李永林, 冯学钢, 姜云, 等. 隧道工程围岩大变形及预测预报研究. 现代隧道技术, 2005(5): 49-54, 62. |
| [16] |
宋臻. 基于支持向量机的盾构施工地表沉降预警系统研究[硕士学位论文]. 赣州: 江西理工大学, 2017.
|
| [17] |
张云毅, 李江灵, 穆岩松, 等. 岩溶破碎带盾构下穿建筑物沉降分析及控制. 施工技术, 2019, 48(3): 80-83, 93. |
| [18] |
高蔚. 基于深度学习的再生混凝土抗压强度预测. 混凝土, 2018(11): 58-61, 70. DOI:10.3969/j.issn.1002-3550.2018.11.015 |
 2022, Vol. 31
2022, Vol. 31



