2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
随着互联网成为社会生产生活所依赖的关键基础设施, 科研活动也越来越依赖网络设施的深度支持. 科研活动需要产生和处理的数据规模急剧增长, 对网络设施快速传输处理数据的需求也不断提高. 例如引力波的发现就有赖于科学家们长达5个月的观测和跨洲际高速网络对观测数据的采集和传输提供强有力支撑, 科研活动越来越依赖数据、计算和网络传输的深度融合, 海量科研数据快速产生, 需要科研专用高速网络的支持. 经过多年发展, 国内外已建立了较为完善的科研专网长期服务科研活动, 例如美国的ESNET[1]、Internet2[2]、欧洲GEANT[3], 国内的科研专网有中国科技网CSTNet[4]和中国教育网CERNet[5]. 我国目前已建成和即将建成的大科学装置基础设施总量约为55个左右, 随着大科学装置运行活动频度增加、科学采样指标的扩展和采样频率加快, 如FAST、BESIII、JUNO、LHAASO、散裂中子源等大科学装置每年都将产生PB级的海量异构化数据需要快速传输和处理, 需要更高质量、大带宽、低延迟的科研专网服务支撑, 促进我国高能物理、气象观测、生物信息、生命科学、天文联测、遥感观测、高性能网格计算等科学领域不断发展. 随着高速科研专网的建设和发展, 支持了科研用户实现从原有的自一级站点获取数据转化为与遍布世界各地的二级站点共享数据的战略转变. 网络节点数量和网络流量规模的急剧膨胀, 科研应用类型也越来越丰富多样. 传统的IP架构已无法应对高负载业务接入的需求, 科研专网正不断探索向软件定义网络(SDN)等新型架构演进的可行性, 以使网络具备更灵活的调度能力和扩展能力. 软件定义网络技术通过数据平面和控制平面的分离为网络管理控制提供了极大的自由度, 而灵活的网络控制能力与精准快速的网络链路流量预测能力结合能为网络运行管理提供更进一步降低人工干预需求的可能性. 科研专网的链路流量预测对科研观测传输窗口保障、带宽资源预留配置、数据分发传输调度等方面起着至关重要的作用. 建立有效的科研专网链路流量预测模型, 能在更灵活数据转发控制技术的辅助下更有效支持链路资源调度的更优决策, 还可以帮助科研专网动态评估当前链路中资源使用情况和网络运行状况、预测未来流量变化趋势、对专网链路建设规划提供决策辅助以及为科研用户提供更好的传输服务质量.
2 相关工作链路流量是当前链路负载的一种数值表征, 是链路所属网络节点间流量矩阵的最基本组成单元. 链路流量预测的方法是根据流量特性设计流量模型以刻画实际流量的突出特征, 用以进行研究和分析. 预测模型可以通过输入历史流量数据然后输出对未来流量的预判. 流量预测的本质是总结历史流量特征, 推演未来流量特征的过程. 当前流量预测模型研究主要分为线性流量预测模型和非线性流量预测模型两类. 常见的线性流量预测模型有泊松模型[6]、马尔科夫模型[7]、自回归模型[8]等. 互联网发展早期, 网络节点数量少、规模小、拓扑简单、应用单一, 因此泊松模型等线性模型在此类场景下应用取得了一定的成绩, 但是随着网络流量复杂度的提高, 泊松模型与流量观察值出现明显差异. 马尔科夫模型随着时间尺度的拉大则趋向于一个稳定的与初始无关的状态, 使用马尔科夫模型仅能对临近的短时间段流量有效. 自回归模型是时间平稳序列预测模型, 在非时间平稳序列中则准确率不高. 线性预测模型的本质是刻画网络流量的短相关特征, 短相关特性是在不同的时间尺度上有不同的特性, 但是在长相关特性上有一定缺陷. 随着网络规模继续发展且流量组成复杂度增加, 学术界发现了流量的自相似性, 由此提出了各种非线性流量预测模型, 常见比如有分形布朗运动模型[9]、分形自回归整合移动平均模型[10]和基于小波的模型[11]. 分形布朗运动模型能够完美描述流量的自相似性, 但不能描述序列的短相关性, 因此不能对同时具有长相关性和短相关性的序列建模. 分形自回归模型可以同时很好地描述流量的长相关性和短相关性, 但该模型复杂且参数较多, 计算资源开销过大. 小波分析模型可以突出研究对象的特征, 但在选取小波基函数时需要满足小波变换系数之间相互独立, 因此小波基的选取会影响模型的实际效果. 随着机器学习的蓬勃发展, 学术界利用机器学习优越的非线性映射能力应用于流量预测领域取得一定的效果, 非线性流量模型进入了新的发展阶段, 比较典型的模型有支持向量机回归[12]、循环神经网络模型[13]等. 支持向量机模型通过穷举搜索和对比实验进行模型寻优, 这在很大程度上会影响支持向量机的泛化能力[14]. 由于梯度爆炸和梯度消失的存在, RNN神经网络不能完美的保持记忆, 需要通过引入长期记忆和短期记忆解决梯度爆炸和梯度消失的问题[15, 16].
互联网系统经过多年发展到当前, 网络链路流量的组成更具多样性和复杂性, 流量特征不再表现为简单的短相关, 以往基于线性流量模型无法很好的描述和适配当前网络流量特征. 当前非线性的流量预测模型未过多考虑不同时刻间的数据特征之间的前后关系, 在特定的网络场景中, 自变量解释因变量的变化的能力不足, 最终影响整个模型的拟合, 导致模型效果一般, 因此不能满足复杂特征的链路流量预测. 为了提取流量内部的深层细粒度特征, 高效拟合特定网络的流量特征, 本文针对LSTM模型加以改进, 提出并实现了一种新的面向科研专网的链路流量预测模型: AE-栈式混合LSTM模型, 该模型由自编码器、双向LSTM模型、单向LSTM模型和全连接层组成. 自编码器可以压缩输入数据的特征维度, 获取输入数据中最稳定的特征, 较大幅度提升了流量特征的提取能力, 双向LSTM模型学习输入不同时刻数据之间的前向联系和后向联系, 构建更高级别的特征. 通过自编码器和双向LSTM模型的协同挖掘不同时刻的数据特征之间的前后依赖关系, LSTM具有单元内部的自循环和隐藏层单元的外循环, 可更好适配时间序列的长期依赖性.
2.1 自编码器模型自编码器(AutoEncoder, AE)是一种半监督学习或无监督学习的具备表征学习能力的神经网络模型, 可以被广泛应用于异常检测和输入信息降维. 自编码器模型的功能是将输入信息作为学习目标, 利用反向传播算法对输入信息进行表征学习[17]. 此模型的关键特点在于输出维度远小于输入维度, 对序列数据的降维能力比较强大. 自编码器模型通过约束信息条件让潜在特征空间中的潜在特征e(x)具有价值属性, 使得中间层从数据中发现更稳健信息和更关键特征, 防止模型仅仅学习输入与输出之间的恒等关系, 即是在编码器层面限制e(x)的特征维度使其小于输入x的特征维度. 自编码器的这种高强度降维的转换过程必然会使最后的输出结果相对于输入序列而言存在一定的信息损失, 形成中间层的有损信息特征表示, 但最终解码器中的输出特征是同自编码器的输入的特征大致相同, 因此在编解码的过程中, 序列数据会经历高低维度的线性转换或者非线性转换, 自编码器在数据经历有损转换和有损恢复的过程中, 能够学习到数据中的最重要且稳定的特征, 同时实现数据降噪.
为了解决科研专网链路流量的时序数据预测的问题, 本文基于自编码器的基础模型优化设计了“宽-窄-宽”的网络结构, 通过自监督的学习方式完成链路网络流量数据的特征转换和特征表示. 本文设计的自编码器模型具体结构如图1(a)所示, 编码器由前3层全连接网络组成, 解码器由后2层全连接网络组成, 其中每一层全连接网络的具体组成结构如图1(b)所示, 包含Batch Norm层、全连接层和激活层. 给定网络流量数据
| $ f:x \to h $ | (1) |
| $ g:h \to x $ | (2) |
| $ f,g = {\rm{arg\;min}}_{f,g}{(x - g(f(x)))^2} $ | (3) |

|
图 1 自编码器AE模型结构图 |
2.2 AE-栈式混合LSTM模型设计
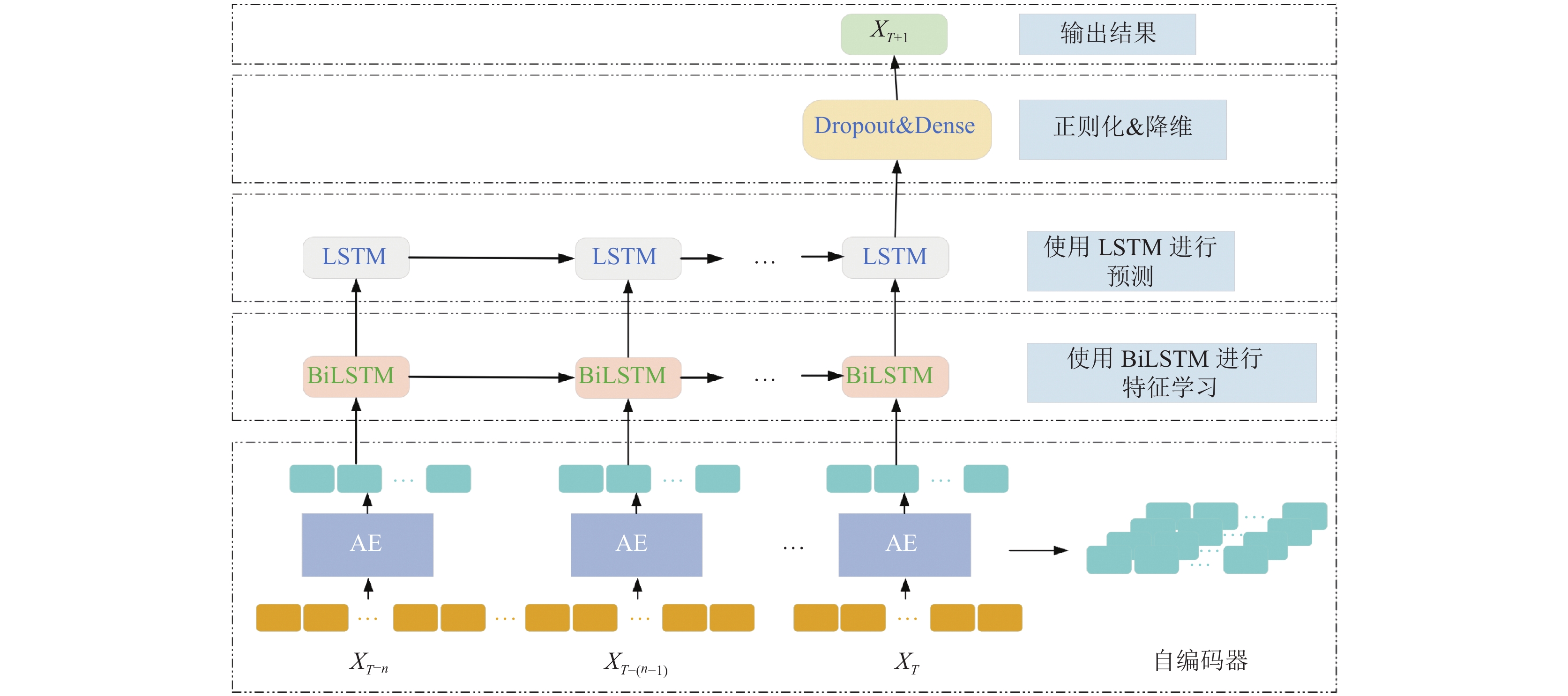
LSTM神经网络模型是基于循环神经网络进行改进的, 在处理时间序列数据时具有比较好的效果. LSTM神经网络模型的输出信息与当前时刻的信息、当前时刻的期记忆和当前时刻细胞状态(长期记忆)决定, 因此在序列预测上得到了广泛的应用. 有研究证明, 具有多个隐藏层的深层LSTM体系结构可以构建更高级别的序列数据特征表示, 从而可以更加高效地对序列数据进行预测[18]. 文献[19]将BiLSTM作为隐藏层单元来获取不同时刻数据特征之间的前后依赖关系, 进而进行对交通流量的预测. 科研专网的链路流量预测需要预测模型更好的捕获当前链路流量中的突发性、周期性和趋势性的关键特征, 同时还需要考虑链路流量的内部深层细粒度特征, 兼顾不同时刻数据特征的前后依赖关系, 为了更好的解决此问题, 本文将自编码器AE、单向LSTM神经网络、双向LSTM神经网络和全连接BP神经网络组成一种综合预测模型, 用于挖掘科研专网链路流量中的深层显著重要特征, 模型的逻辑结构图如图2所示.
图2中的自编码器AE模型的主要作用是对历史链路流量进行有损压缩和有损恢复, 进而获得输入数据中最重要和最稳定的信息; 图2的双向LSTM(BiLSTM)层的具体结构如图3所示, 其主要作用是在自编码器的基础上, 进一步学习数据的前后向依赖关系, 从而构建更高级别的特征表示; 图2中的LSTM网络层的主要作用是在已构建的数据特征之上完成对链路流量的预测; 全连接层的主要作用是通过降维的方式输出预测结果, 其中添加dropout层的意义是可以有效缓解过拟合的发生, 在一定程度上达到正则化的效果.
|
图 2 AE-栈式混合LSTM模型逻辑结构示意图 |

|
图 3 双向LSTM模型结构示意图 |
3 模型实证分析 3.1 真实数据采集和数据集整理
本文实验采用的科研专网真实的链路流量数据, 数据采集来自中国科技网(CSTNet)的全国骨干网真实生产环境中随机抽取的某一链路关联节点的SNMP数据, 采集时间周期跨度为315天. SNMP协议是互联网工程任务组(Internet Engineering Task Force, IETF)定义的一套专门用来管理网络设备的网络管理协议. 表1为中国科技网的SNMP数据属性, 其中hostId属性和hostname属性唯一标识一台监测机器设备, portNo属性标识端口号, inFlowValue属性是经过此设备端口的上行流量数目, outFlowValue属性是经过此设备端口的下行流量数目, inPackageValue属性是经过此设备端口的下行报文数目, outPackageValue属性是经过此设备端口下的下行报文数目, datetime属性是产生此条SNMP数据的时间点.
| 表 1 中国科技网(CSTNet)的SNMP数据属性 |
中国科技网CSTNet的监测节点每5 min生成一条SNMP数据记录, 因此每天24 h中产生288条数据记录. 图4为7天内和2天内的指定链路下行流量展示图, 如图4所示, 链路流量的特征在局部范围内具有一定的随机性、突发性甚至无序性, 但是在全局范围内具有一定的周期性、趋势性和自相似性. 在流量区间内, 0:00–6:00链路实时流量处于下降趋势, 6:00–8:00网络流量总量处于上升趋势, 8:00–21:00在某个区间震荡, 21:00–24:00处于下降趋势.
实验所采用数据均来源于中国科技网骨干网真实生产环境内某链路节点, 采集过程符合隐私不可逆脱敏要求, 仅提取设备端口数据包转发的流量计数信息, 不涉及和接触数据包流向信息. 经过数据整理和比对去除了少量异常数据点, 同时对序列数据中的少量缺失值做了完整化处理, 本文采用加权移动平均法对缺失点附近的前3个时刻和后3个时刻取值, 然后取均值进行填充, 经过数据预处理后, 最终投入实验的链路流量数据共有90 720条.
数据采集集中后因为覆盖的维度范围较大, 会使模型收敛时难以获取全局最优解, 也会造成部分指标忽视, 因此类数据需要使用进行归一化处理才能使用. 本文通过Min-Max归一化(Min-Max normalization)对输入的采集数据进行处理, 对集中的数据进行特征缩放, 确保模型在求得最优解过程中比较平缓, 更容易收敛到模型的最优解. Min-Max归一化也叫离差归一化, 具体公式见式(4), 该方法没有假设数据符合某种数学分布模型, 是对原始数据的线性变化, 将数据映射到[0, 1]区间里.
| $ newX{\text{ = }}\frac{{X{{ - }}min}}{{max{{ - }}min}} $ | (4) |

|
图 4 链路网络流量数据展示图 |
3.2 模型实证过程
在本应用场景下通过新型预测模型做目标链路的流量预测时, 需要确定对预测模型的输入和输出的粒度尺度, 也就是确定输入已获取的过去多长时间的链路流量给预测模型来期望预测模型输出可用的未来多长时间内的预测结果. 根据科研专网的实际运行需求, 一般来说, 预测结果的预期一般以一个完整的自然日为通常分析粒度, 因此本文需要确定的是如果需要预测未来一个自然日的链路流量, 则需要输入的历史数据的度量应为多少为宜. 预测过程的特征选择模式如图5所示, 图5中上部的方块“Model”表示本文提出的AE-栈式混合LSTM模型. 根据现有采集频度, 一天中目标链路获取的SNMP数据有288条, 所以第1–288条是第1个自然日的链路网络流量记录, 第289–576条是第2天的链路网络流量数据, 以此类推; Seq_1, Seq_2, …, Seq_n表示每一次的预测, 且步长为1. 因此需要确定的k值则是所需确认的输入粒度, 同时需要确认模型中具体的参数才能使得本文提出的链路流量预测模型实现最优的预测输出.

|
图 5 特征选择模式 |
本文中自编码器AE模型使用“宽-窄-宽”的网络结构, 第1层网络隐藏单元个数为16, 第2层网络隐藏单元个数为8, 第3层网络隐藏单元个数为4, 第4层网络隐藏单元个数为8, 第5层网络隐藏单元个数为16. 其中的输入参数为归一化后的前k天的SNMP数据的拼接, 拼接方法表示为如下:
| $ \begin{array}{l} [Inflo{w_{t - k}},Outflo{w_{t - k}},Inpackag{e_{t - k}},\\ Outpackag{e_{t - k}}, \cdots ,Inflo{w_{t - 1}},Outflo{w_{t - 1}},\\ Inpackag{e_{t - 1}},Outpackag{e_{t - 1}}] \end{array} $ |
自编码器的输出结果为栈式混合LSTM模型的输入参数, 栈式混合LSTM模型的具体参数如图6所示, 本模型由BiLSTM网络、LSTM网络、dropout层, 全连接层和激活层共同构成. 在输入参数经过的BiLSTM中, 第1个LSTM网络设置了96个隐藏单元, 第2个LSTM网络设置了120个隐藏单元. 设置BiLSTM网络主要是为了进一步挖掘目标链路流量序列数据中的深层次高级特征, 学习输入序列数据的前后依赖关系; 紧随BiLSTM网络的是一个单向LSTM网络, 该网络设置了120个隐藏单元; 接着进入dropout层, 每次随机删掉20%的隐藏神经单元, 输出单元不变; 最后一层进入全连接层经过ReLU激活函数输出.
在本文中设计实验来确定使用过去多少天的链路流量去预测未来一天的链路流量,使用k值表示过去的天数. 下文阐述探究k的最优值的过程, 实验中使用不同的模型性能评价指标, 梯度下降算法选用Adagrad算法, Adagrad算法是Duchi在2011年提出的参数自适应梯度下降算法[20], 该算法的主要思想是初始时需要设定一个全局的学习率, 接下来会自适应且独立地训练模型中的参数, 给偏导数大的参数设置较大的学习率, 给偏导数小的参数设置较小的学习率. 为了测试不同的初始学习率为模型训练带来的影响, 本文中设置的初始学习率分别有0.001, 0.002, 0.01, 0.02, 同时数据集按照4:1的比例划分训练集和测试集. 训练过程有300个epoch, 每10个epoch在测试集上验证模型效果.
接下来测试k的取值, 将k的取值从2变化至10, 其中RMSE的变化如图7所示. 从图7中可以明显看出, 当k值为4时, 本文的AE-栈式混合LSTM模型的预测性能最好, 同时也可以看出, 模型的预测性能并不是随着输入参数维度的增加而不断提升, 当输入维度增加至一定程度时, 模型的预测性能将不再变化, 甚至会变差.

|
图 6 栈式混合LSTM结构示意图 |

|
图 7 k值的取值测试 |
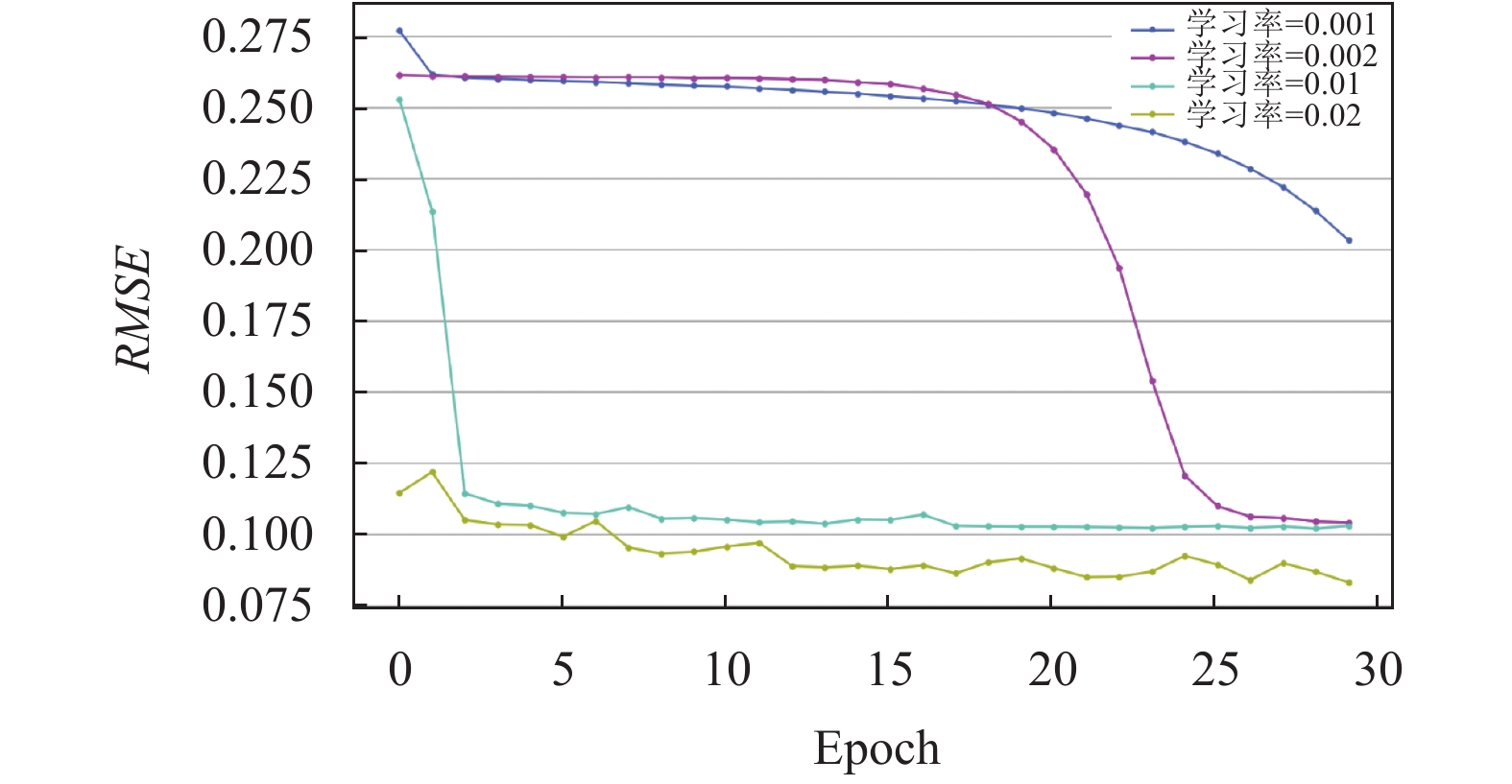
通过上述实验过程以及讨论分析, 本文中的k值确定为4为最优解, 即确定预测模型输入为使用前4天的链路流量, 然后模型输出未来1天的链路流量预测结果. 当k值为4时, 模型训练过程如图8所示, 最终模型在不同学习率下的性能指标参数如表2所示, 当学习率为0.001和0.002时, 由于初始学习率过小, 不会错过局部最优值, 但是此时也意味着模型需要花费更多的时间进行收敛, 图8中显示过小的学习率并没有收敛到最优值, 当学习率(lr)为0.02时, 模型收敛效果最好.
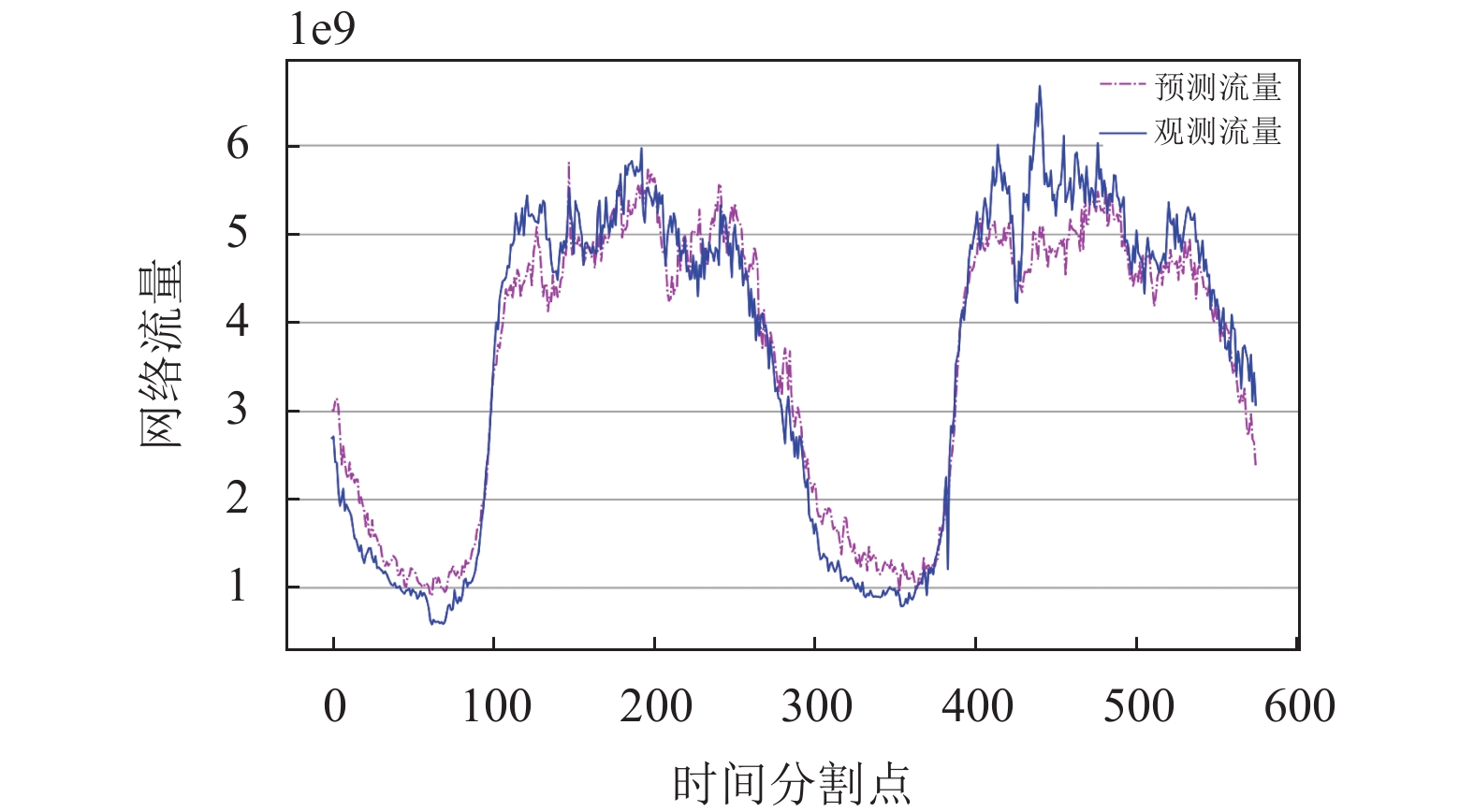
接下来模型设置参数k值为4时, 输入中国科技网采集的真实流量数据, 模型输出具体的预测结果对比观测值如图9所示. 图9中展示了未来2天内的链路网络流量预测效果, AE-栈式混合LSTM模型能够拟合曲线的趋势走向且流量预测值比较贴合于流量观测值.
3.3 差值评价指标链路流量预测是回归类型问题的一种, 在训练模型和评价模型的阶段, 需要一系列可量化的指标来评价拟合训练数据达到模型最优解和评价该最优解下模型的性能. 预测问题多用真实值和预测值之间的差值指标来评价预测模型的优劣, 而常见的模型评价指标有均方误差(mean squared error, MSE)、均方根误差(root mean squared error, RMSE)、平均绝对误差(mean absolute error, MAE)、平均绝对百分比误差(mean absolute percentage error, MAPE)、对称平均绝对百分比误差(symmetric mean absolute percentage error, SMAPE)和可决系数(R-squared, R2). 相关标准定义和计算方法如下.
|
图 8 k=4时的不同学习率下的RMSE对比图 |
| 表 2 k=4时的模型评价指标 |
|
图 9 k=4时AE-栈式混合LSTM模型链路流量预测对比 |
均方误差: 是真实值与预测值之间误差平方的期望值, 是一种衡量平均误差较方便的方法, 式(5)是MSE的定义. MSE经常被作为损失函数, 在模型训练和测试过程中, 不断降低MSE值是模型优化的目标.
| $ {\textit{MSE}} = \frac{1}{N}\sum\limits_{i=1}^N {{{({y_i} - {{\hat y}_i})}^2}} $ | (5) |
均方根误差: 用来衡量真实值与预测值之间的偏差, 其本质是均方误差的算术平方根, 式(6)是RMSE的定义. RMSE经常被用来作为模型测试的指标, RMSE越小, 表示模型拟合的越精准.
| $ {\textit{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i=1}^N {{{({y_i} - {{\hat y}_i})}^2}} } $ | (6) |
平均绝对误差: 用来衡量真实值与预测值之间的偏差绝对值, 其定义如式(7)所示, 相比均方根RMSE, 平均绝对误差MAE对离群点没有那么敏感, 对误差样本惩罚较小. MAE越小, 模型越精准.
| $ {\textit{MAE}} = \frac{1}{N}\sum\limits_{i=1}^N {|{y_i} - {{\hat y}_i}|} $ | (7) |
平均绝对百分比误差: 是一种常见的误差测量统计方式, 其定义如式(8)所示, 其本质是平均绝对误差MAE的标准化. MAPE的取值范围是[0, +∞], MAPE越小, 表示模型效果越好, 当MAPE的值为0时, 表示该模型是完美模型; MAPE越大, 表示模型效果越差, 当MAPE的值等于或超过100%时, 表示该模型是劣质模型.
| $ {\textit{MAPE}} = \frac{{100{\text{%}} }}{N}\sum\limits_{i=1}^N {\left|\frac{{{y_i} - {{\hat y}_i}}}{{{y_i}}}\right|} $ | (8) |
对称平均绝对百分比误差: MAPE的取值范围是[0, +∞], 对于低预测, 即预测值低于观测值的情况, 平均绝对百分比误差MAPE不会超过100%, 但是高预测, 即预测值高于观测值的情况, MAPE没有预测上限. 因此MAPE指标会对高预测施加更大的惩罚, 即MAPE指标更加偏向于预测不足而不是过度预测的模型. MAPE是不对称的, 因此引入了能克服不对称性问题的SMAPE指标加以解决, 相关公式如式(9)所示.
| $ {\textit{SMAPE}}=\frac{100{\text{%}}}{N}\sum\limits_{{i=1}}^{N}{\dfrac{2|{{y}_{i}}-{{{\hat{y}}}_{i}}|}{{}{(|{{y}_{i}}|+|{{{\hat{y}}}_{i}}|)}\\{}\;}} $ | (9) |
可决系数: 反映了因变量和自变量的关联程度, 也即可决系数反映了因变量随自变量变化的可靠程度. 上述的衡量方法的缺陷是没有预测上限, 可决系数的公式如式(10)所示, 它的取值范围是[0, 1]. 可决系数R2越大, 表示模型效果越好, 当R2的值为1时, 表示自变量能够完全解释关于因变量的变化; 可决系数R2越小, 表示模型效果越差, 当R2的值为0时, 表示自变量不能解释关于因变量的变化.
| $ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{i=1}^N {{{({y_i} - {{\hat y}_i})}^2}} }}{{\displaystyle\sum\limits_{i=1}^N {{{({y_i} - {{\bar y}_i})}^2}} }} $ | (10) |
针对本文提出的新型预测模型的效果评价, 使用了标准LSTM神经网络、小波神经网络和Seq2Seq模型3种不同类型的模型与之通过实验进行对比验证, 具体过程和结果分析如下.
标准LSTM神经网络设置了120个隐藏单元, 最后由一个全连接层降维输出预测结果. 小波神经网络为3层网络结构, 第1层和第2层网络的隐藏单元数量均为96, 第3层网络的隐藏单元数量为1, 作用为降维输出结果, 其中激活函数选用Morlet母小波基函数, 如式(11)所示. Seq2Seq模型中的RNN模型具体选用门控神经网络GRU, 其中的GRU隐藏神经单元数量分别为96和16. 对上述3种模型均使用Adagrad算法对模型进行训练, 设置300个epoch, 每10个epoch在测试集上验证模型效果.
| $ y = {\rm{cos}}(1.75x){{\rm{e}}^{ - \frac{{{x^2}}}{2}}} $ | (11) |
本文提出的AE-栈式混合LSTM模型与小波神经网络、Seq2Seq模型和LSTM模型在同等设定条件下的验证实验结果按照不同的差值评价指标的对比情况如表3所示, 结果显示在中国科技网的验证环境中, 同等条件下本文提出的新型预测模型与其他3种不同类型的预测模型相比, 按6种差值指标考察结果均为最优.
| 表 3 模型性能对比 |
在R2指标上, 新模型比小波神经网络提高了0.14, 比LSTM模型提高了0.21, 这表明新模型能够更好的挖掘链路流量的内部深层细粒度特征, 特征作为自变量能够解释链路流量的变化.
在SMAPE指标上, 新模型相比于LSTM模型下降了10.88%, 说明新模型给出的流量预测值与流量观测值之间的残差较小, 流量预测值更加接近流量观测值, 说明本新模型在科研专网的真实数据集上具有更优的表现.
4 结束语科研专网主要服务于各个不同学科的科研应用数据传输, 流量特征相比通用大众网络而言流量特征更具复杂性, 数据类型更具多样性, 应用面向更具广泛性, 传输质量要求更具敏感性. 现有的预测模型不能很好地拟合业务流量的变化趋势, 针对这种不足, 本文提出了一种新型的基于自编码器的栈式混合LSTM模型来针对科研专网的链路流量进行预测, 在国内典型的科研专网CSTNet的真实生产网运行数据验证环境中证明了与标准LSTM、小波模型、Seq2Seq等其他预测模型相比较, 预测结果的精度更优.
在新型科研范式的推动下, 科研数据的流量特征仍然会发生更复杂的变化, AE-栈式混合LSTM模型目前还不支持增量训练, 后续工作需要针对此点进行改进. 对于科研专网不断演化的数据, 模型如能进一步支持增量训练, 使模型根据新数据按照周期自动地进行调整, 更新模型相关参数时支持增量训练可以节约更多的时间成本.
| [1] |
ESnet. http://www.es.net/. [2020-12-23].
|
| [2] |
Internet2. USA. https://www.internet2.edu/. [2020-12-24].
|
| [3] |
GÉANT. https://www.geant.net. [2020-12-24].
|
| [4] | |
| [5] |
CERNet. http://www.cernet.edu.cn. [2020-12-24].
|
| [6] |
Bonald T. The Erlang model with non-Poisson call arrivals. ACM SIGMETRICS Performance Evaluation Review, 2006, 34(1): 276-286. DOI:10.1145/1140103.1140309 |
| [7] |
薛可, 李增智, 刘浏, 等. 基于ARIMA模型的网络流量预测. 微电子学与计算机, 2004, 21(7): 84-87. DOI:10.3969/j.issn.1000-7180.2004.07.022 |
| [8] |
Shim C, Ryoo I, Lee J, et al. Modeling and call admission control algorithm of variable bit rate video in ATM networks. IEEE Journal on Selected Areas in Communications, 1994, 12(2): 332-344. DOI:10.1109/49.272884 |
| [9] |
Mandelbrot B. Self-similar error clusters in communication systems and the concept of conditional stationarity. IEEE Transactions on Communication Technology, 1965, 13(1): 71-90. DOI:10.1109/TCOM.1965.1089090 |
| [10] |
Beran J, Sherman R, Taqqu MS, et al. Long-range dependence in variable-bit-rate video traffic. IEEE Transactions on Communications, 1995, 43(2–4): 1566-1579. |
| [11] |
Flandrin P. Wavelet analysis and synthesis of fractional Brownian motion. IEEE Transactions on Information Theory, 1992, 38(2): 910-917. DOI:10.1109/18.119751 |
| [12] |
Noble WS. What is a support vector machine?. Nature Biotechnology, 2006, 24(12): 1565-1567. DOI:10.1038/nbt1206-1565 |
| [13] |
Cho K, Van Merriënboer B, Gulcehre C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation. Proceedings of 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). Doha: Association for Computational Linguistics, 2014. 1724–1734.
|
| [14] |
王雪松. 改进支持向量机的网络流量预测. 计算机系统应用, 2017, 26(3): 230-233. DOI:10.15888/j.cnki.csa.005668 |
| [15] |
Gers FA, Schmidhuber J, Cummins F. Learning to forget: Continual prediction with LSTM. Proceedings of the 1999 Ninth International Conference on Artificial Neural Networks. Edinburgh: IEEE, 1999. 850–855.
|
| [16] |
Sutskever I, Vinyals O, Le QV. Sequence to sequence learning with neural networks. Advances in Neural Information Processing Systems. 2014: 3104–3112.
|
| [17] |
Bengio Y, Courville A, Vincent P. Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(8): 1798-1828. DOI:10.1109/TPAMI.2013.50 |
| [18] |
LeCun Y, Bengio Y, Hinton G. Deep learning. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [19] |
Cui ZY, Ke RM, Pu ZY, et al. Deep bidirectional and unidirectional LSTM recurrent neural network for network-wide traffic speed prediction. arXiv: 1801.02143, 2018.
|
| [20] |
Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 2011, 12(7): 2121-2159. |
 2022, Vol. 31
2022, Vol. 31


