1 引言

作为成功的人工智能范例, AlphaGo^[1]利用神经网络和树搜索, 于2016年打败世界围棋冠军, 鼓舞了众多人工智能研究者. 然而, 在AlphaGo成功的背后, 它使用了多达30万局对弈作为训练数据, 让我们不禁思考现实中大数据的质量和可获得性如何. 实际上, 情况并不乐观: 由于行业竞争、手续复杂等因素, 大多数行业只拥有有限或者低质的数据, 这阻碍了人工智能和机器学习技术的应用^[2]. 同时, 数据泄露问题危害着社会权益, 对此国内外出台相关法律条例进行规范, 如中国先后发布《中华人民共和国网络安全法》《中华人民共和国数据安全法》和《中华人民共和国个人信息保护法》, 加强对数据安全和个人信息的保护^[3]. 在本文中, 我们将拥有数据的实体称为用户. 随着国内外隐私监管的加强, 不同用户的数据流通受到阻碍, 使用户逐渐成为“数据孤岛”^[4]. 对于以上场景, 用户的有限数据沟通不畅, 无法集中在一处训练, 因此用户的数据和算力得不到充分利用, 难以训练出表现良好的机器学习模型, 研究者开始探索如何在不泄露数据隐私的前提下破解“数据孤岛”困境^[5].

联邦学习由谷歌提出, 作为面向数据孤岛和隐私保护的解决方案, 具体指在不泄露数据隐私的前提下基于分布在多个设备上的数据集构建机器学习模型^[6]. 最初联邦学习引起了一些科技公司的兴趣, 比如谷歌和苹果拥有大量移动端用户, 因此希望通过部署联邦学习系统来改善它们的服务^[7]. FedAvg^[8]作为联邦学习的基准算法, 已经得到广泛的研究与应用. FedAvg在用户数据是独立同分布(independent and identically distributed, IID)且平衡的情况下表现良好, 而这种完美数据在现实场景中很少见. 有研究表明数据的异质性减缓了FedAvg的收敛速度^[9]. 非IID是异质的典型情况, 即用户的数据并不服从同一分布, 若用户仍训练公共模型, 学习效果可能不佳. 除此之外, 用户数据量也可能是不平衡的.

有研究尝试通过创建为用户共享的数据子集以改进对非IID数据的训练^[10], 但直接分配数据给用户有隐私泄露的风险, 不符合联邦学习的前提. 文献[11]提出了一种新算法, FedProx, 来克服联邦学习中的异质性, FedProx在FedAvg的目标函数上增加了近端项, 限制每轮用户更新的参数不过多偏离全局参数. 文献[12]证明了局部随机梯度下降(stochastic gradient descent, SGD)在数据同质和异质时的复杂度, 并提供了最优步长和最优局部迭代次数的值. 但上述工作关注所有用户的数据, 学到的是公共模型, 不同用户应用公共模型时会产生相同输出, 难以学习它们之间的差异, 因此有必要探索能有效处理用户数据异质性的联邦学习算法.

为帮助解决上述问题, 有研究者提出个性化联邦学习, 即不同用户在联邦学习框架下学习不同模型^[13]. 元学习是实现个性化联邦学习的有效方法, 思想是学习如何去学习, 可用来学习不同任务的最优初始化参数^[14]. 一般而言, 优化模型时模型初始化参数作为超参数, 常需要人为设置, 再进行若干次迭代得到表现良好的模型参数, 但人为设置的初始化参数具有随意性, 可能离最优参数的距离很远, 需迭代成千上万次才能达到不错的效果, 而经学习的初始化参数更靠近最优参数, 可能仅需迭代几次就能获得好的模型.

文献[15]提出了一种模型不可知的元学习算法(model-agnostic meta-learning, MAML), 该算法适用于任何使用SGD训练的模型. MAML表现良好, 但它需要梯度的高阶信息, 这很耗费计算内存, 并且会减缓计算速度. 继MAML之后, 文献[16]提出了一种只需梯度一阶信息的元学习方法——Reptile. 结合MAML和FedAvg, 文献[17]提出了一种新的算法, Per-FedAvg, 将FedAvg与MAML相结合为用户学习更优的模型初始化参数, 该算法在异质任务上实现了良好的性能, 但需要用户在每次迭代过程中计算MAML的梯度, 这涉及高阶导数信息, 对于用户的算力和内存有较高的要求.

联邦学习背景下, 数据孤岛的数据量往往较大, 而每个用户拥有的数据量较少, 应尽可能采取运算效率高的方法学习. 比如移动端训练时移动设备只拥有很小的算力和内存, 难以承载过于复杂的训练过程; 在线学习时应及时响应需求, 训练时间不宜过长. 考虑到用户使用MAML更新参数时需要耗费较多的计算资源, 而Reptile只需计算梯度的一阶信息, 较MAML有计算优势, 更适合上述计算速度和内存受限的场景. 本文结合Reptile与FedAvg, 提出一种新的个性化联邦学习算法, 基于Reptile的个性化联邦学习算法(personalized FedAvg algorithm based on Reptile, Per-FedAvg-Reptile). 中央服务器在每轮更新前随机抽取一定比例的用户参与训练, 被抽取的用户应用Reptile处理多任务并更新参数, 之后中央服务器将用户发来的参数平均聚合, 迭代学习合适的初始化参数. 然后将学到的初始化参数代入用户模型, 用户在自己的数据上进行若干步(甚至只需一步)梯度下降后得到表现良好的个性化模型.

2 相关工作

对于元学习, 考虑优化问题: 找到一组初始化参数向量 $w$ , 使得对于随机采样的任务 $\tau $ 及相应的损失 ${L_\tau }$ , 学习器在几次SGD后即可获得表现良好的模型. 其中 $\tau $ 表示具有相似信息的数据集, 这样我们才可能学习到任务之间的共同信息. 接下来, 将介绍两种最通用的元学习方法来实现这个目标, MAML和Reptile.

2.1 MAML

MAML的目标函数是:

$ \mathop{\rm{min}}\limits_w {\mathbb{E}_{\tau} }\left[ {{L_{\tau , B}}\left( {{{\boldsymbol{U}}_{\tau , A}}({\boldsymbol{w}})} \right)} \right] $

(1)

其中, ${\boldsymbol{w}}$ 是要学习的初始化参数向量, $\tau $ 划分成训练集 $A$ 和测试集 $B$ , ${{\boldsymbol{U}}_{\tau , A}}$ 表示使用 $A$ 的数据多次更新 ${\boldsymbol{w}}$ 后的参数向量, 而 ${L_{\tau , B}}$ 表示使用 $B$ 的数据计算的损失. MAML的工作原理是通过梯度下降优化式(1), 即计算:

$ \begin{split} {{\boldsymbol{g}}_{{\rm{MAML}}}}& = \frac{\partial }{{\partial {\boldsymbol{w}}}}{L_{\tau , B}}({{\boldsymbol{U}}_{\tau , A}}({\boldsymbol{w}})) \\ & = {\boldsymbol{U}}{'_{\tau , A}}({\boldsymbol{w}}){\boldsymbol{L}}{'_{\tau , B}}({{\boldsymbol{U}}_{\tau , A}}({\boldsymbol{w}})) \end{split} $

(2)

式(2)中 ${{\boldsymbol{U}}_{\tau , A}}({\boldsymbol{w}}) = w - \alpha \left( {{{\boldsymbol{g}}_1} + {{\boldsymbol{g}}_2} + \cdots + {{\boldsymbol{g}}_k}} \right)$ (如果 ${\boldsymbol{w}}$ 使用SGD更新了 $k$ 次), 其中, $\alpha $ 是学习率, ${{\boldsymbol{g}}_i}$ 是第 $i$ 次更新的梯度, $i \in \{ 1, \cdots, k\}$ . $ {\boldsymbol{U}}{'_{\tau , A}}({\boldsymbol{w}}) $ 是 $ {{\boldsymbol{U}}_{\tau , A}}({\boldsymbol{w}}) $ 的雅各比矩阵. 注意到, 测试集的最小损失可以通过限制对于训练集的若干次更新来实现, 因此MAML可快速学习新任务. $ {\boldsymbol{U}}{'_{\tau , A}}({\boldsymbol{w}}) $ 涉及高阶导数信息, 其计算量很大. 不过, 其近似算法一阶MAML (first-order MAML, FOMAML)也可达到不错的学习效果. 具体来说, FOMAML使用单位矩阵替换了 $ {\boldsymbol{U}}{'_{\tau , A}}({\boldsymbol{w}}) $ , 即FOMAML使用的梯度是 ${{\boldsymbol{g}}_{{\rm{FOMAML}}}} = {\boldsymbol{L}}{'_{\tau , B}}({{\boldsymbol{U}}_{\tau , A}}({\boldsymbol{w}}))$ .

2.2 Reptile

在本节中, 我们介绍另一个以一阶梯度为基础的元学习算法, 称为Reptile. 像MAML一样, Reptile学习一组初始化参数, 这样当我们在个性化应用阶段优化这些参数时, 学习速度会很快. Reptile的细节如算法1所示.

算法1. Reptile

输入: 任务集合 $\scriptstyle T$ , 初始化参数向量的学习起点 $\scriptstyle {\boldsymbol{w}}$ , 学习率 $\scriptstyle \epsilon$ , 迭代轮数K, 梯度下降步数k

输出: 训练好的初始化参数向量

1) 初始化 $\scriptstyle {\boldsymbol{w}}$ //其为初始化参数向量的学习起点

2) for 迭代轮次 $\scriptstyle = 1, \; 2, \; \cdots , \; K$

3) 从 $\scriptstyle T$ 中抽样任务 $\scriptstyle \tau $

4) 计算 $\scriptstyle \tilde {\boldsymbol{w}} = {\boldsymbol{U}}_\tau ^k({\boldsymbol{w}})$ //代表 $\scriptstyle k$ 步梯度下降

5) 更新 $\scriptstyle {\boldsymbol{w}}\leftarrow {\boldsymbol{w}}+{\epsilon}(\tilde{{\boldsymbol{w}}}-{\boldsymbol{w}})$

6) end for

在每轮的最后一步中, 我们可以将 ${\boldsymbol{w}} - \tilde {\boldsymbol{w}}$ 视为某种梯度. 文献[16]已经用泰勒近似证明了MAML和Reptile计算的梯度可以分为两部分: 一部分用来最小化期望损失, 提升任务的整体学习效果; 另一部分用来最大化任务间的泛化, 所以元学习可以学习到任务的共性. 算法1还可扩展为并行或批处理版本, 每次迭代考虑 $n$ 个任务, 并将初始化参数更新为:

$ {\boldsymbol{w}}\leftarrow {\boldsymbol{w}}+{\epsilon}\frac{1}{n}{\displaystyle \sum _{i=1}^{n}\left({\tilde{{\boldsymbol{w}}}}_{i}-{\boldsymbol{w}}\right)} $

(3)

其中, $ {\tilde {\boldsymbol{w}}_i} = {\boldsymbol{U}}_{{\tau _i}}^k({\boldsymbol{w}}) $ 是第 $i$ 个任务的更新参数. 并行版本和联邦学习处理多用户数据有相似之处, 为将Reptile应用于联邦学习场景提供了可能.

3 基于Reptile的个性化联邦学习算法

在联邦平均中, 我们旨在解决这样一个问题:

$ \mathop {\min }\limits_{_{w \in {\mathbb{R}^d}}} \left\{ {f({\boldsymbol{w}})\mathop = \limits^{{\text{ def }}} \frac{1}{n}\sum\limits_{i = 1}^n {{f_i}} ({\boldsymbol{w}})} \right\} $

(4)

其中, ${\boldsymbol{w}} \in {\mathbb{R}^d}$ 是需要学习的参数向量, ${f_i}:{\mathbb{R}^d} \to \mathbb{R}$ 是用户 $i$ 的损失函数. 假设 ${\mathcal{D}_i} = \left\{ {{\mathcal{X}_i}, {\mathcal{Y}_i}} \right\}$ 是用户 $i$ 拥有的数据, 通常我们取 ${f_i}({\boldsymbol{w}}) = {\mathbb{E}_{(x, y)\sim{p_i}}}[{l_i}({\boldsymbol{w}};x, y)]$ , 其中 ${p_i}$ 是 ${\mathcal{X}_i} \times {\mathcal{Y}_i}$ 的分布, ${l_i}({\boldsymbol{w}};x, y)$ 衡量的是数据点 $(x, y) \in {\mathcal{D}_i}$ 在模型参数为 ${\boldsymbol{w}}$ 时的损失.

如图1所示, 对于FedAvg, 中央服务器每次随机选取部分用户参与参数更新, 用户在本地通过SGD计算梯度信息并传送给中央服务器, 中央服务器平均聚合这些信息来更新模型参数. 注意到, 数据始终保留在用户那里, 所以符合隐私保护的要求.

文献[17]将FedAvg与元学习方法MAML相结合, 提出了FedAvg的个性化变体Per-FedAvg, 在用户更新时用MAML替换SGD, 与FedAvg学习的是模型参数不同, Per-FedAvg学习的是模型的初始化参数, 用户在得到优化的初始化参数后还需在本地数据SGD一次才能获得个性化模型. 理论和实验证明了该算法的有效性. 然而, 如前所述, MAML涉及高阶导数信息, 对于复杂模型, 这在计算代价上是昂贵的. 而Reptile只需要计算一阶导数, 局部更新步数也可灵活设置.

本文将FedAvg与Reptile结合起来, 提出新算法Per-FedAvg-Reptile, 用户更新时只需计算一阶导数, 因此更适合移动端训练、在线学习等计算速度和内存受限的联邦学习场景. 该算法以FedAvg作为框架, 确保用户数据不出本地, 用户通过与中央服务器传递梯度来更新参数, 因此满足隐私保护的要求; 以Reptile作为用户的局部更新, 学习用户的模型初始化参数; 在学习完成之后, 用户以优化的初始化参数为起点, 基于本地的额外数据进行一步梯度下降就能获得个性化联邦学习模型. 新提出的算法细节如算法2所示, 并且可分为以下步骤:

步骤1. 中央服务器初始化 ${{\boldsymbol{w}}_0}$ , 作为训练起点, 设定每轮抽取的用户比例为 $r$ , 对应算法2中的2行.

步骤2. $rn$ 个用户被随机选择, 中央服务器向它们发送参数, 对应算法2中的45行. 考虑到用户可能会突然掉线或暂时退出, 这里不要求所有用户都参与每轮训练.

步骤3. 对于选定的用户 $i$ , 接收参数并赋值给 ${{\boldsymbol{w}}_{{\rm{task}}}}$ , 之后将数据 ${\mathcal{D}_i}$ 划分为 ${\tau _{{\rm{out}}}}$ 批, 每批对应Reptile中的任务, 我们可以理解为学习用户数据的内部共性. 然后, 每批被划分为 ${\tau _{{\rm{in}}}}$ 个更小批, ${\tau _{{\rm{in}}}}$ 次梯度下降的步骤会被执行, 我们得到更新的 ${{\boldsymbol{w}}_{{\rm{task}}\_{\rm{task}}}}$ . ${{\boldsymbol{w}}_{{\rm{task}}}} - {{\boldsymbol{w}}_{{\rm{task}}\_{\rm{task}}}}$ 视为某种梯度, ${{\boldsymbol{w}}_{{\rm{task}}}}$ 以学习率 $\alpha $ 在该梯度上更新, 更新后的参数发给中央服务器, 对应算法2中的11–22行, 即用户执行的部分.

步骤4. 中央服务器平均 $rn$ 组参数作为更新的参数, 对应算法2中的9行, 这意味着整合 $rn \times {\tau _{{\rm{out}}}}$ 个任务的学习信息.

步骤5. 重复步骤2–4直到算法收敛. 通常我们不知道何时收敛, 会事先设置迭代轮数的上限.

若 $r = 1$ , 每轮通信需要所有用户执行 ${\tau _{{\rm{out}}}}$ 次本地更新步骤. ${\boldsymbol{w}}_t^i \in {\mathbb{R}^d}$ 被定义为用户 $i$ 在时间 $t$ 的参数向量, 对于用户 $i$ , 更新过程类似于文献[18]中的局部梯度下降, 可表示为(如果通信从 ${t_0}$ 开始):

$ {{\boldsymbol{w}}}_{t+1}^{i}=\left\{\begin{array}{ll}\dfrac{1}{n}{\displaystyle \sum _{j=1}^{n}\left({{\boldsymbol{w}}}_{t}^{j}-\alpha {{\boldsymbol{g}}}_{t}^{j}\right)}, & t={t}_{p \times {\tau }_{{\rm{out}}}}\text{,  }p\in \{1, 2, \cdots, K \} \\ {{\boldsymbol{w}}}_{t}^{i}-\alpha {{\boldsymbol{g}}}_{t}^{i}, &其他 \end{array} \right. $

(5)

其中, ${\boldsymbol{g}}_t^i = {\boldsymbol{ g}}_{t, {\tau _{{\rm{in}}}}}^i = {\boldsymbol{g}}_{t, {\tau _{{\rm{in}}}} - 1}^i + \nabla {f_i}\left( {{\boldsymbol{w}}_t^i - {\boldsymbol{g}}_{t, {\tau _{{\rm{in}}}} - 1}^i} \right)$ 且 $ {\boldsymbol{g}}_{t, 1}^i = \nabla {f_i}\left( {{\boldsymbol{w}}_t^i} \right) $ . 可以看到, 参数由所有用户进行Reptile更新, 并在通信的时间点进行平均聚合. 算法2的优化方法是梯度下降, 所以可以应用于任何使用梯度下降的模型, 适用面较广.

算法2. Per-FedAvg-Reptile

输入: $\scriptstyle n$ 个用户的数据集合 $\scriptstyle \left\{ {{\mathcal{D}_i} = \left\{ {{\mathcal{X}_i}, {\mathcal{Y}_i}} \right\}} \right\}_{i = 1}^n$ , 初始化参数的学习起点 $\scriptstyle {{\boldsymbol{w}}_0}$ , 学习率 $\scriptstyle \alpha $ , 迭代轮数 $\scriptstyle K$ , 主要超参数: $\scriptstyle r$ , $\scriptstyle {\tau _{{\rm{out}}}}$ , $\scriptstyle {\tau _{{\rm{in}}}}$

输出: 训练好的初始化参数向量

1) 中央服务器执行:

2) 初始化 $\scriptstyle {{\boldsymbol{w}}_0}$ , $\scriptstyle r$

3) for $\scriptstyle k = 1, \cdots , K$

4) $\scriptstyle m \leftarrow {\rm{max}}(rn, 1)$

5) $\scriptstyle {C_k} \leftarrow $ (随机抽取 $\scriptstyle m$ 个用户构成的集合)

6) for 每个用户 $\scriptstyle i \in {C_k}$ 并行

7) $\scriptstyle {\boldsymbol{w}}_{k + 1}^i \leftarrow {\textit{UserUpdate}}(i, {{\boldsymbol{w}}_k})$

8) end for

9) $\scriptstyle {{\boldsymbol{w}}_{k + 1}} \leftarrow \tfrac{1}{{rn}}\sum\limits_{i \in {C_k}} {{\boldsymbol{w}}_{k + 1}^i}$

10) end for

11) 用户执行 $\scriptstyle {\textit{UserUpdate}}(i, {{\boldsymbol{w}}_k})$ :

12) $\scriptstyle {{\boldsymbol{w}}_{{\rm{task}}}} \leftarrow {{\boldsymbol{w}}_k}$

13) $\scriptstyle \mathcal{B} \leftarrow $ (将 $\scriptstyle {\mathcal{D}_i}$ 划分成 $\scriptstyle {\tau _{{\rm{out}}}}$ 个批)

14) for 批次 $\scriptstyle b \in \mathcal{B}$

15) $\scriptstyle B \leftarrow $ (将 $\scriptstyle b$ 划分成 $\scriptstyle {\tau _{{\rm{in}}}}$ 个更小批)

16) $\scriptstyle {{\boldsymbol{w}}_{{\rm{task}}\_{\rm{task}}}} \leftarrow {{\boldsymbol{w}}_{{\rm{task}}}}$

17) for 小批次 $\scriptstyle mb \in B$

18) $\scriptstyle {{\boldsymbol{w}}_{{\rm{task}}\_{\rm{task}}}} \leftarrow {\boldsymbol{U}}_{mb}^1({{\boldsymbol{w}}_{{\rm{task}}\_{\rm{task}}}})$ //在mb上进行一次梯度下降

19) end for

20) $\scriptstyle {{\boldsymbol{w}}_{{\rm{task}}}} \leftarrow {{\boldsymbol{w}}_{{\rm{task}}}} + \alpha ({{\boldsymbol{w}}_{{\rm{task}}\_{\rm{task}}}} - {{\boldsymbol{w}}_{{\rm{task}}}})$

21) end for

22) 返回 $\scriptstyle {{\boldsymbol{w}}_{{\rm{task}}}}$ 给中央服务器

4 实验分析

在本节中, 我们通过模拟数据和真实数据来比较个性化模型的效果. 考虑3种算法: (1)本文提出的新算法Per-FedAvg-Reptile; (2)文献[17]将FedAvg与FOMAML结合的算法Per-FedAvg-FO; (3) FedAvg with one update, 即进行一次额外更新的FedAvg. 由于(1)和(2)训练获得良好的初始化参数后, 还需在用户端梯度下降一次才能获得个性化模型, 为了公平比较, 即使FedAvg学习的不是模型初始化参数, 也将训练好的参数在用户端进行一次梯度下降更新. 70%的用户数据用于训练, 剩下的数据用于测试. 此外, 为了避免模型看到所有的测试数据, 我们将测试数据分成两部分: 30%的测试数据用于梯度下降获得个性化模型, 70%的测试数据用于测试模型的效果. 实验采用PyTorch作为学习框架.

4.1 模拟数据

为了生成异质的模拟数据, 我们参考了文献[11]提出的生成方法. 具体来说, 样本 $\left( {X, Y} \right)$ 根据模型 $y = {\rm{argmax} } ({\rm{Softmax}} ({\boldsymbol{Wx}} + {\boldsymbol{b}}))$ 生成, 其中 ${\boldsymbol{x}} \in {\mathbb{R}^{60}}$ , ${\boldsymbol{W}} \in {\mathbb{R}^{10 \times 60}}$ , ${\boldsymbol{b}} \in {\mathbb{R}^{10}}$ . 对于用户 $i$ , 从 $\mathcal{N}\left( {{u_i}, 1} \right)$ 抽样出 ${W_i}$ 和 ${b_i}$ 的每个元素, 其中 ${u_i}\sim \mathcal{N}(0, \delta )$ ; ${{\boldsymbol{x}}_i}\sim \mathcal{N}\left( {{{\boldsymbol{v}}_i}, {\boldsymbol{\varSigma}} } \right)$ , 其中 ${\boldsymbol{\varSigma}} $ 是对角元素为 ${{\boldsymbol{\varSigma}} _{j, j}} = {j^{ - 1.2}}$ 的对角矩阵, ${{\boldsymbol{v}}_i}$ 的每个元素从 $\mathcal{N}\left( {{B_i}, 1} \right)$ 抽样, ${B_i}\sim N(0, \theta )$ . 用户数据量由均匀分布 $U(100, 1000)$ 抽样取整确定.

通过仔细观察, 可以看出 $\delta $ 的大小影响 ${u_i}$ 的方差, ${u_i}$ 决定用户 $i$ 模型参数的均值, 因此 $\delta $ 控制用户模型之间的差异, 其值越大, 用户模型之间的差异越大; 而 $\theta $ 的大小影响 ${B_i}$ 的方差, ${B_i}$ 决定 ${{\boldsymbol{v}}_i}$ 的均值, ${{\boldsymbol{v}}_i}$ 决定 ${{\boldsymbol{x}}_i}$ 的均值, 因此 $\theta $ 控制用户数据之间的差异, 其值越大, 用户数据的差异越大. 我们改变 $\delta $ , $\theta $ 的值来生成4个异质程度不同的数据集, 表示为模拟数据 $(\delta , \theta )$ , 如图2所示.

假设有 $n = 30$ 个用户协同学习模型, 并且在每次迭代中随机选择 $rn$ 个用户参与训练, 其中 $r = 0.2$ , ${\tau _{{\rm{out}}}}$ 和 ${\tau _{{\rm{in}}}}$ 都被设置为4, 学习率 $\alpha = 0.01$ . 请注意, 算法结果对应的是运行一步梯度下降后所有用户的平均测试精度, 并且我们运行10次实验以获得具有标准差的平均性能^[19], 图2中误差棒的中点为10次实验的平均测试准确率, 数值越大意味着测试准确率越高, 中点到两端的距离为10次测试准确率的标准差, 长度越长意味着测试准确率的波动性越大.

在图2中, 横坐标为迭代次数, 对应算法2中的迭代轮数 $K$ ; 纵坐标为测试准确率, 衡量算法性能. 从图2(a)到图2(d), 由于 $(\delta , \theta )$ 逐渐增大, 用户数据和用户模型的异质程度增加, 学习难度随之加大. 我们可以看到, Per-FedAvg-Reptile的学习折线一直处于上方, 说明新算法在测试准确率上优于其他两种算法; 而且Per-FedAvg-Reptile的误差棒较短, 说明10次实验的测试准确率相当, 性能更具鲁棒性. 当异质程度很显著时, 如图2(d), Per-FedAvg-FO和FedAvg with one update的误差棒长度明显增长, 测试准确率的波动加大, 说明这两种算法缺乏鲁棒性, 而Per-FedAvg-Reptile仍能快速收敛到良好的测试准确率.

4.2 真实数据

为继续验证新方法, 我们在标准数据集MNIST^[20]和CIFAR10^[21]上构建了联邦学习场景. MINST是包括60000个训练样本和10000个测试样本的黑白图像集, 内容是手写数字0–9; CIFAR10是包括50000个训练样本和10000个测试样本的彩色图像集, 内容是10类生活图片. MINST和CIFAR10来源于torchvision中的torchvision.datasets库.

我们考虑文献[19]提出的异质数据划分方法, 为用户分配规模大小和类别比例都不平衡的数据. 具体而言, 假设随机向量 ${{\boldsymbol{p}}_k}\sim {{Dir} _n}(0.5)$ , ${p_{k, i}}$ 为 ${{\boldsymbol{p}}_k}$ 的第 $i$ 个元素, 将 ${p_{k, i}}$ 比例的类 $k$ 样本分配给用户 $i$ .

模型采用包含两个隐藏层的全连接神经网络, 规模分别为80个神经元和60个神经元, 指数线性单元(exponential linear unit, ELU)作为激活函数. 选用更复杂的模型可获得更高精度, 而本文关注的是算法之间的差异, 所以只采用两层神经网络. 我们假设有 $n = 50$ 个用户协同学习模型, 其他超参数与模拟数据相同, 所有算法的结果也是对应运行一步梯度下降后所有用户的平均测试精度, 运行10次试验以获得具有标准差的平均性能. 与MNIST相比, 学习CIFAR10时迭代更多次, 因为它作为彩色图像集更难学习.

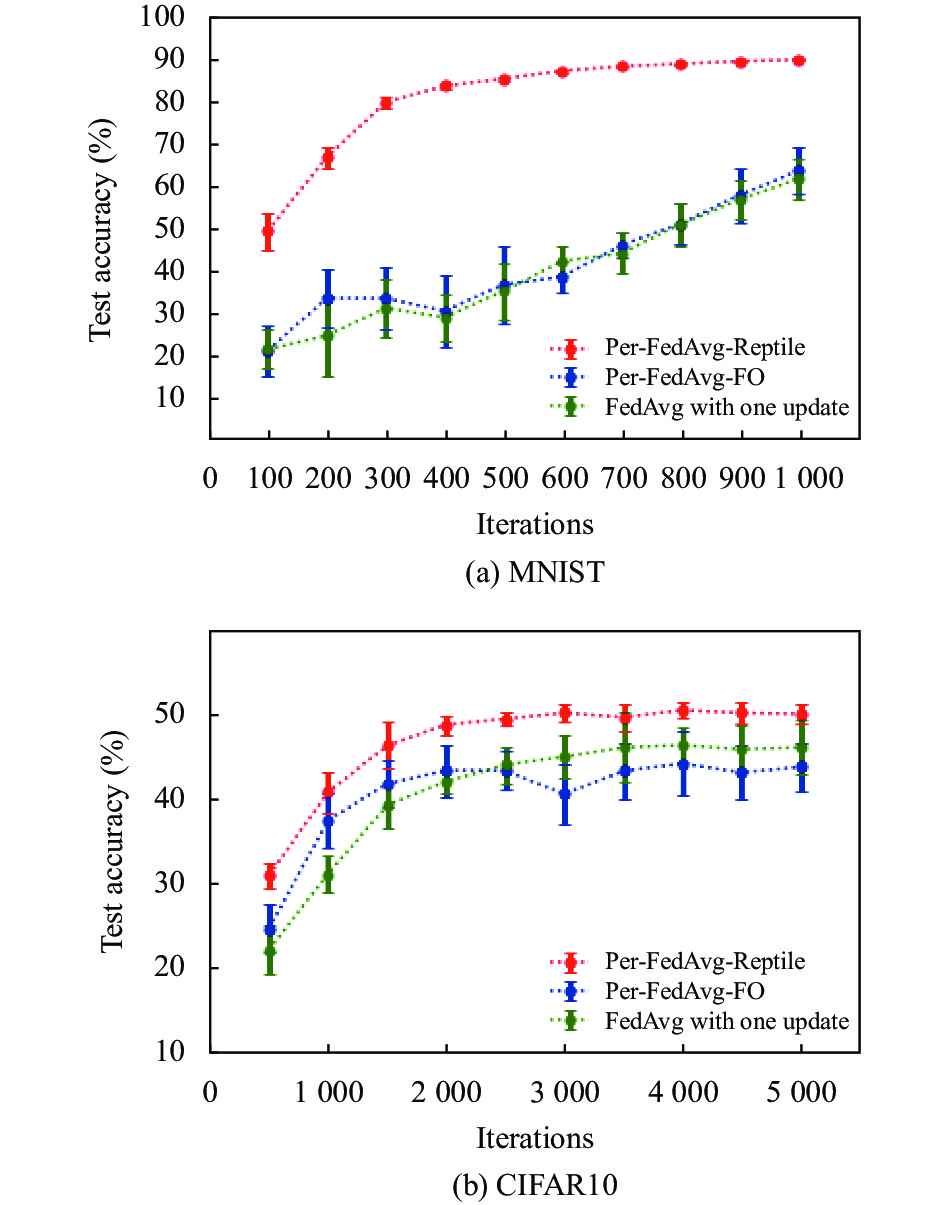
观察图3, 我们可以得出一些结论. 在学习黑白图像集MNIST时, Per-FedAvg-Reptile的学习折线处于上方, 在测试准确率方面明显优于其他两种算法, 而且折线率先趋于平稳说明收敛速度更快; 而在学习彩色图像集CIFAR10时, 3种算法的性能较接近, 我们猜测这和任务的难度有关, 对于更难学的CIFAR10, Per-FedAvg-Reptile的相对优势被压缩了. 但当迭代轮数为5000时, Per-FedAvg-Reptile、FedAvg with one update和Per-FedAvg-FO的误差棒中点分别为50.09%、46.13%和43.77%, 新算法在测试准确率方面仍优于另外两种算法, 且收敛速度更快. 总之, Per-FedAvg-Reptile在收敛速度和测试准确率上都表现更优.

5 结论与展望

本文结合联邦平均和Reptile, 提出了一种新算法Per-FedAvg-Reptile, 旨在学习良好的模型初始化参数, 以期快速学习到个性化联邦学习模型. 我们在模拟数据和真实数据上验证了该算法的有效性, 与现有的两种算法相比, Per-FedAvg-Reptile在收敛速度和测试准确率上表现更好, 可以学习到更加个性化的用户模型. 在未来的研究中, 会考虑3种方向的改进: 现实中, 用户的重要程度可能各不相同, 所以中央服务器可以在聚合用户信息时采取不同权重, 比如按照样本量比例分配权重; 探究新算法中超参数的作用和选择; 分析新算法的收敛性理论.