1 引 言

可见光通信(visible light communication, VLC)将发送信号调制在发光二极管(light emitting diode, LED)中, 通过LED发出高速明暗闪烁信号进行通信^[1]. 室内可见光通信系统中, 收发两端的体积小, 便于安装的同时, 具有干扰小、安全性高、节能环保等优点^{[2, 3]}. 在室内VLC多用户MIMO系统中, 发射端一般由多个LED组成, 接收端有多个用户终端, 在不增加带宽的情况下, 获得更大的系统容量, 还可以使室内通信链路更加稳固, 具有极大的应用前景^[4-6]. 然而, 用户终端能够接收到所有LED发出的信号, MUI的问题也随之而来, 严重地影响了系统性能^{[7, 8]}, 抑制MUI成为室内VLC的研究重点. 在下行链路中, 由于用户设备间协作困难, 所以用户间干扰利用预编码算法在发射端进行消除^[9].

预编码算法在发射端将用户数据进行数据处理, 使得多个用户终端可以利用相同的LED灯阵列且互不干扰进行通信. 在可实现的预编码算法中最具有代表性的是BD预编码算法, 该算法通过两次SVD操作将多用户MIMO信道转化成等价的多个单用户MIMO信道, 完全消除用户间干扰, 但是也导致了较高的复杂度消耗^{[10, 11]}. 在多用户MIMO系统中, 随着数据流以及用户数目的不断增加, 虽然用户终端可以获得更快的数据体验, 然而BD预编码算法的复杂度也急剧增加. BD算法复杂度高的问题严重的限制了其应用场景, 所以不断有改进的算法被提出. Chou等^[12]利用改进的平方根分解法对等效单用户MIMO信道进行块对角化处理, 降低了BD预编码的算法复杂度, 但是在其他方面并没有得到提升. Wu等^[13]提出了一种利用伪逆运算与QR分解代替BD预编码算法中的第一次奇异值分解的方法, 并进一步提出改进方案, 即仅对联合信道矩阵求一次伪逆, 再次降低复杂度. 此外, 巫健^[14]还提出了通过增加一次QR分解中的格拉姆施密特正交化分解来代替伪逆运算的改进方案, 这两种方案本质上是相同的, 虽然降低了复杂度, 但是该算法在误码率上没有得到提升. Zu等^[15]通过将BD预编码算法与格基规约算法相结合, 得到的改进算法在与BD算法进行仿真对比后, 算法复杂度得到降低的同时对系统误码性能也有了一个量级的优化, 但是系统和容量却降低了.

综上所述, 现有文献的低复杂度改进BD算法大多数只是对复杂度进行了降低, 对BD算法的误码率以及系统容量没有得到优化. 为了进一步优化BD算法的系统性能, 本文提出一种基于正交分解的施密特正交化分解与格基规约操作组合的改进BD算法, 不仅降低了算法复杂度, 并且在误码率和系统和容量性能得到了优化.

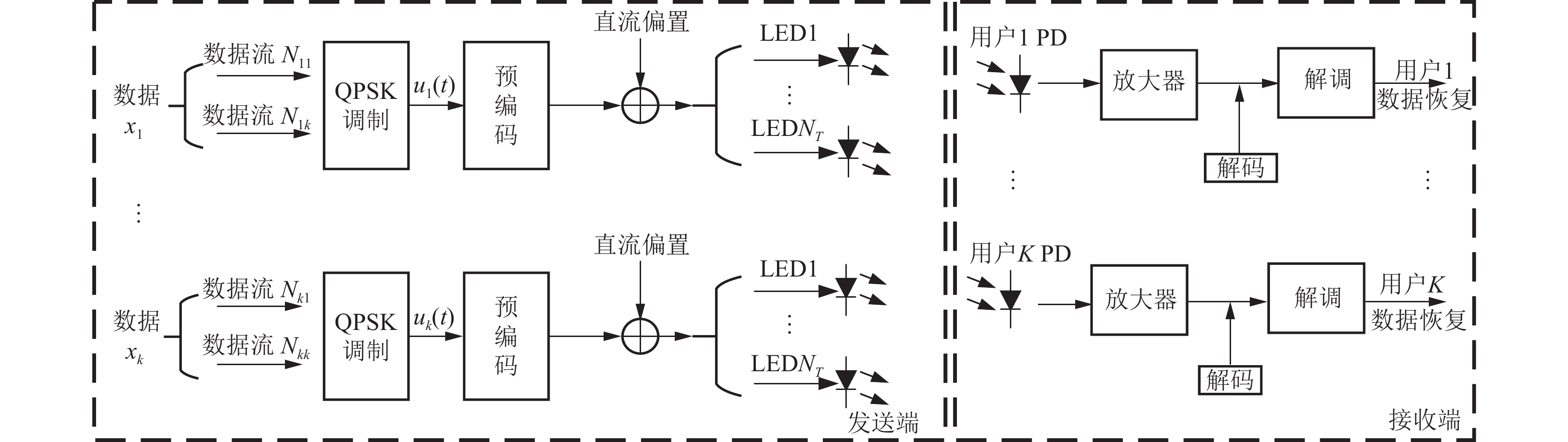
2 系统模型

基于预编码算法的多用户MIMO室内可见光系统模型如图1所示, 由发送端、可见光信道和用户终端组成^[7].

假设系统中有N_T个发射端, K个用户, 每个用户上有N_k个光接收机, 则接收端共有 $ {N}_{R}=\displaystyle \sum _{k=1}^{K}{N}_{k} $ 个, 则用户k的信道矩阵可以用 $ {H_k} \in {\mathbb{C}^{{N_R} \times {N_T}}} $ 表示, 假设全局信道矩阵表示为 $H = {[H_1^{\rm{T}}, H_2^{\rm{T}}, \cdots , H_K^{\rm{T}}]^{\rm{T}}}$ . 用户k的接收信号表示为:

$ {y_k} = {H_k}{W_k}{x_k} + \sum\limits_{j = 1, j \ne k}^K {{H_k}{W_j}{x_j}} + {n_k} $

(1)

其中, x_k表示用户k的发送的原始数据, W_k是用户k的预编码矩阵, n_k表示用户k的高斯白噪声. 此外, 等式右边的第2项代表用户k接收到的来自其它用户的信号, 对自身造成干扰的干扰信号, 是期望被消除的对象.

预编码算法在发射端对MUI进行消除, 核心思想是通过设计一个合理的预编码矩阵W, 再与信道矩阵相乘后, 使每个用户的干扰矩阵均处于该用户的零空间中, 能够有效地消除来自其他用户的数据干扰, 即满足式(2)的约束:

$ {H}_{k}{W}_{j}=0,\; k\ne j\;且\;\text{0}\leqslant k,\; j\leqslant {N}_{R} $

(2)

3 BD预编码算法

BD预编码算法的核心是对每个用户的信道矩阵进行两次SVD运算求解预编码矩阵W, 以达到消除用户干扰以及数据流干扰. 以用户k为例, 在第1次SVD操作中, 对干扰矩阵进行SVD分解, 以此得到消除其他用户干扰的预编码矩阵 $ {W^a} $ ; 第2次SVD操作中, 对等效信道矩阵进行SVD操作后将每个用户的块通道分解为并行信道, 抑制数据流之间的干扰, 令第2个预编码矩阵为 $ {W^b} $ . 因此, 用户k的预编码矩阵为 ${W_k} = {W^a}{W^b}$ , 下面介绍BD算法的具体步骤.

记用户k的补矩阵为 ${\tilde H_k}$ :

$ {\tilde H_k} = [H_1^{\text{T}}, H_2^{\text{T}}, \cdots , H_{k - 1}^{\text{T}}, H_{k + 1}^{\text{T}}, \cdots , H_K^{\text{T}}] $

(3)

其中, $ {H_k} $ 是用户k的信道矩阵.

对 ${\tilde H_k}$ 进行SVD运算:

$ {\tilde H_k} = {\tilde U_k}\left[ {\begin{array}{*{20}{c}} {{{\tilde \Sigma }_k}}&0 \\ 0&0 \end{array}} \right]{[\tilde V_k^{(1)}, \tilde V_k^{(0)}]^{{H}}} $

(4)

其中, $\tilde V_k^{(1)}$ 为 ${\tilde H_k}$ 的前 ${\tilde L_k} = rank({\tilde H_k}) < {N_R} - {N_k}$ 个右奇异向量, $ \tilde V_k^{(0)} $ 包含 ${\tilde H_k}$ 的后 ${N_T} - {L_k}$ 个右奇异值向量, $ \tilde V_k^{(0)} $ 的列构成了 $ {\tilde H_k} $ 零空间的一个正交基.

在第一次SVD运算后, 可得到 $ W_k^a = \tilde V_k^{(0)} $ , 为了获得更大的系统容量, 对等效信道矩进行SVD运算.

记用户k的等效信道矩阵为 ${\bar H _k} = {H_k}W_k^a$ , 对等效信道矩阵 ${\bar H _k}$ 进行SVD运算可得:

$ {\bar H_k} = {H_k}W_k^a = {\bar U_k}\left[ {\begin{array}{*{20}{c}} {{{\bar \Sigma }_k}}&0 \\ 0&0 \end{array}} \right]{[\bar V_k^{(1)}, \bar V_k^{(0)}]^{{H}}} $

(5)

其中, $ \bar V_k^{(1)} $ 表示 $ {\bar H_k} $ 的前 ${\bar L_k} = rank({H_k}W_k^a)$ 个右奇异向量, 则用户k的预编码矩阵的第2部分为:

$ W_k^b = \bar V_k^{(1)} $

(6)

所以, 用户k的最终预编码矩阵 ${W_k}$ 可以表示为:

$ {W_k} = W_k^aW_{^k}^b = \tilde V_k^{(0)}\bar V _k^{(1)} $

(7)

遍历所有的用户, 得到BD算法的预编码矩阵为:

$ W = {W^a}{W^b} = {[\tilde V_1^{(0)}\bar V _1^{(1)}, \cdots , \tilde V_K^{(0)}\bar V _K^{(1)}]^H} $

(8)

同时, 接收矩阵可以表示为:

$ {B_k} = \bar U _k^H $

(9)

4 改进预编码算法

BD算法由于两次SVD操作带来了很高的计算消耗, 并未考虑信道噪声的影响, 提出了改进算法, 对两次SVD操作进行替换, 从而降低算法复杂度, 并且引入信道噪声的影响, 从而优化系统性能. BD算法中第1次SVD操作用QR分解中的GSO正交化代替来求消除多用户干扰, 第2次SVD操作中加入了信道噪声并且利用格基规约操作进行替换. 并将QR分解引入到格基规约技术, 通过对格基规约技术进行QR分解得到单位模矩阵的伪逆, 不用再单独对其进行伪逆操作, 进一步降低算法复杂度. 将这种算法简称GSO-CLLL-BD算法, 其具体步骤如下.

计算补矩阵 ${\tilde H_k}$ 的零空间, 首先对信道矩阵H做LQ分解:

$ {{H = LQ}} $

(10)

其中, L是分解所得到的 $ {N_R} \times {N_R} $ 维下三角形矩阵; Q是分解所得到的 $ {N_R} \times {N_T} $ 维正交矩阵.

信道矩阵的伪逆可以表示为:

$ \begin{split} {H^{\dagger} }& = {H^{{H}}}{(H{H^{{H}}})^{ - 1}} = {Q^{{H}}}{L^{{H}}}{(LQ{Q^{{H}}}{L^{{H}}})^{ - 1}} \\ &= {Q^{{H}}}{L^{ - 1}} = [{Q^{{H}}}{\hat L_1}, {Q^{{H}}}{\hat L_2}, \cdots , {Q^{{H}}}{\hat L_K}] \end{split}$

(11)

因此, 信道矩阵H和其伪逆矩阵 ${{{H}}^\dagger }$ 的乘积可以表示为:

$ \begin{split} H{H^\dagger }& = \left[ {\begin{array}{*{20}{c}} {{H_1}{Q^H}{{\hat L}_1}}&{{H_1}{Q^H}{{\hat L}_2}}& \cdots &{{H_1}{Q^H}{{\hat L}_K}} \\ {{H_2}{Q^H}{{\hat L}_1}}&{{H_2}{Q^H}{{\hat L}_2}}& \cdots &{{H_2}{Q^H}{{\hat L}_K}} \\ \vdots & \vdots & \ddots & \vdots \\ {{H_K}{Q^H}{{\hat L}_1}}&{{H_K}{Q^H}{{\hat L}_2}}& \cdots &{{H_K}{Q^H}{{\hat L}_K}} \end{array}} \right] \\ & = \left[ {\begin{array}{*{20}{c}} {{I_1}}&0& \cdots &0 \\ 0&{{I_2}}& \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{I_K}} \end{array}} \right] \\ \end{split} $

(12)

由式(12), 可以得到:

$ {\tilde H_k}{Q^H}{\hat L_k} = 0 $

(13)

从式(13)说明 ${Q^H}{\hat L_k}$ 处于用户k补矩阵 ${{{\tilde {{H}}}}_k}$ 的零空间中. 此时, 还需要对 ${Q^H}{\hat L_k}$ 进行GSO正交化获取正交矩阵 ${{{G}}_k}$ , ${G_k}$ 为补矩阵 ${\tilde H_k}$ 零空间的正交基. 式(12)可以表示为:

$ \begin{split} H\left[ {{G_1}, {G_2}, \cdots , {G_K}} \right] &= \left[ {\begin{array}{*{20}{c}} {{H_1}{G_1}}&{{H_1}{G_2}}& \cdots &{{H_1}{G_K}} \\ {{H_2}{G_1}}&{{H_2}{G_2}}& \cdots &{{H_2}{G_K}} \\ \vdots & \vdots & \ddots & \vdots \\ {{H_K}{G_1}}&{{H_K}{G_2}}& \cdots &{{H_K}{G_K}} \end{array}} \right] \\ & = \left[ {\begin{array}{*{20}{c}} {{H_1}{G_1}}&0& \cdots &0 \\ 0&{{H_2}{G_2}}& \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{H_K}{G_K}} \end{array}} \right] \end{split} $

(14)

从式(14)可以得知, ${G_k}$ 满足用户零MUI的要求. 记 ${G_k}$ 为用户k的预编码矩阵的前半部分:

$ {{W}}_k^a = {{{G}}_k} $

(15)

在求得预编码矩阵的前半部分后, 用户k的等效信道矩阵可以表示为:

$ {\bar H_k} = {H_k}W_k^a $

(16)

由于传统的BD算法为考虑信道噪声的影响, 因此在接收端, 信道噪声被放大了. 改进算法在进行格基规约操作前, 为了考虑信道噪声, 对用户k的等效信道矩阵 $ {\bar H_k} $ 进行扩展:

$ {\hat H_k} = \left[ {\begin{array}{*{20}{c}} {{{\bar H}_k}}&{\sqrt \alpha {{{I}}_{{N_k}}}} \end{array}} \right] $

(17)

其中, $ \alpha $ 为噪声控制因子.

对扩展矩阵 $ {\hat H_k} $ 进行格基规约操作, 可以得到:

$ {\hat H_k} = {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} _k}T_k^{ - 1} $

(18)

其中, $ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} _k} $ 是通过改进格基规约得到的约减矩阵; $ {T_k} $ 是扩展矩阵 $ {\hat H_k} $ 的单位模矩阵.

由式(18)可以得到约减矩阵表示为:

$ \begin{split} {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{H} }_k} &= {{\hat H}_k}{T_k} = \left[ {\begin{array}{*{20}{c}} {{{\bar H}_k}}&{\sqrt \alpha {I_{{N_k}}}} \end{array}} \right]{T_k} \\ & = \left[ {\begin{array}{*{20}{c}} {{{\bar H}_k}{T_k}}&{\sqrt \alpha {T_k}} \end{array}} \right] \end{split} $

(19)

在传统的格基规约算法中, 求取单位模矩阵需要对等效信道矩阵 $ {\hat H_k} $ 进行伪逆操作^[16], 改进的格基规约算法利用QR分解代替了伪逆操作, 使其复杂度得到了进一步的减小.

扩展等效信道矩阵 ${\hat{{H}} _k}$ 的共轭转置进行QR分解:

$ \hat{H} _k^{H} = \left[ {\begin{array}{*{20}{c}} {{{\bar H}_k}{T_k}} \\ {\sqrt \alpha {T_k}} \end{array}} \right] = {{\hat{Q}} _k}{\hat{R} _k} = \left[ {\begin{array}{*{20}{c}} {\hat{Q} _k^1} \\ {\hat{Q} _k^2} \end{array}} \right]{\hat{R} _k}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {\hat{Q} _k^1{{\hat{R} }_k}} \\ {\hat{Q} _k^2{{\hat{R} }_k}} \end{array}} \right] $

(20)

其中, ${\hat{R} _k}$ 表示 $ {N_k} \times {N_k} $ 的上三角矩阵; ${\hat{Q} _k}$ 表示 $\left({N_k} +\right. \left. {N_k}\right) \times {N_k}$ 的正交矩阵; $\hat{Q} _k^1$ 、 $\hat{Q} _k^{\text{2}}$ 表示矩阵 ${\hat{Q} _k}$ 的前 $ {N_k} $ 和后 $ {N_k} $ 行.

通过式(20)可以求得:

$ \begin{split} \sqrt \alpha {T_k} = &\hat{Q} _k^2{{\hat{R} }_k} \Rightarrow {{\hat{R} }_k} = \sqrt \alpha {(\hat{Q} _k^2)^{ - 1}}{T_k} \\ &\Rightarrow \hat{R} _k^{ - 1} = \frac{1}{{\sqrt \alpha }}T_k^{ - 1}\hat{Q} _k^2 \\ &\Rightarrow {(\hat{R} _k^{ - 1})^{{H}}} = \frac{1}{{\sqrt \alpha }}{(\hat{Q} _k^2)^{{H}}}T_k^{ - 1} \end{split} $

(21)

根据式(21)与式(22), 用户k的预编码矩阵的第2部分为:

$ \begin{split} {{W}}_k^b &= \beta {{H} }_k^\dagger = \beta {{{A}}_k}{\hat{{{H}} }}_k^{{H}}{{{(}}{{{\hat{{H}} }}_k}{\hat{{H}} }_k^{{H}}{{)}}^{ - 1}} \\ &= \beta {{{A}}_k}{{\hat{Q} }_k}{{\hat{R} }_k}{{((}}{{\hat{{Q}}_k}{{\hat{R} }_k}{{{)}}^{{H}}}{{\hat{Q} }_k}{{\hat{R} }_k})^{ - 1}} \\ &= \beta {{{A}}_k}{{\hat{Q} }_k}{{\hat{R} }_k}{{{(}}\hat{R} _k^{{H}}\hat{Q} _k^{{H}}{{\hat{Q} }_k}{{\hat{R} }_k})^{ - 1}} \\ &= \beta {{{A}}_k}{{\hat{Q} }_k}{{{(}}\hat{R} _k^{{H}})^{ - 1}} = \frac{\beta }{{\sqrt \alpha }}{{\hat{Q} }}_k^1{({{\hat{Q} }}_k^2{{)}}^{{H}}}{{T}}_k^{ - 1} \end{split} $

(22)

其中, $ \;\beta $ 表示功率控制因子 $\sqrt {{{N_T}}/ {{{Trace}}({{\hat{H} }^\dagger }{{({{\hat{H} }^\dagger })}^{{H}}})}}$ ; $ {A_k} $ 表示 $\hat{H} _k^{{H}}{({\hat{H} _k}\hat{H} _k^{{H}})^{ - 1}}$ 的上半部分矩阵 $\left[ {\begin{array}{*{20}{c}} {{{{I}}_{{N_k}}}}&{{0_{{N_k} \times {N_k}}}} \end{array}} \right]$ .

遍历所有的用户, 得到BD算法的预编码矩阵为:

$ W = {W^a}{W^b} $

(23)

5 性能分析与仿真

本文采用5 m×5 m×3 m室内模型作为研究对象, 主要参考文献[7]. 发射端由4个LED阵列组成, 每个阵列设置有60×60个LED芯片. 以地面为参考物, 接收平面距地面0.85 m, 其具体仿真参数见表1.

本文选取传统的室内模型分析系统的性能, 如图2所示, UE表示用户位置, AP表示LED位置.

5.1 复杂度分析

在本节中, 对算法复杂度进行分析, 采用浮点操作数(flops)对复杂度进行度量. 分析了BD算法和本文提出的GSO-CLLL-BD算法的复杂度. 首先对两种算法所用到矩阵分解方式所需的浮点数进行了总结, 如表2所示.

从表2中可以看出, QR分解、SVD分解、LQ分解中, SVD操作所产生的浮点运算数是最大的, LQ分解所需的浮点运算数最小, QR分解居中. GSO-CLLL-BD算法利用LQ分解和QR分解来代替SVD分解实现的, 因此较BD算法, 本文提出的GSO-CLLL-BD算法具有更低的复杂度. 下面对两种算法每一步所需的浮点数进行总结.

表3所示为传统BD算法每一步所需要的浮点运算数.

由表3所示, 传统BD算法总共所需浮点运算数为:

$ \begin{split} {\psi _{{\text{BD}}}} = &24{K^2}N_T^2{N_k} - 2K{N_T}{N_k} - 2KN_k^2 \\ &+ (56{K^2} - 40K + 48K){N_T}N_k^2 \\ & + (54{K^3} - 162{K^2} + 216K - 54)N_k^3 \\ = &O({K^2}N_T^2{N_k}) \\ \end{split} $

(24)

参考文献[14]所提出的改进格基规约技术通过QR分解可以直接生成单位模矩阵的伪逆, 可以大大降低运算复杂度. 如表4所示, 为文献[14]所提出的改进格基规约算法的计算复杂度与伪逆操作的复杂度对. 由表4可以看出, 随着矩阵维度的增加, 伪逆运算的浮点运算数急剧增加.

表5所示, 为GSO-CLLL-BD算法每一步所需的浮点运算数.

由表4所示, GSO-CLLL-BD算法总共所需浮点运算数为:

$ \begin{split} {\psi _{{{{\rm{GSO}} {\textit{-}} {\rm{CLLL}} {\textit{-}} {\rm{BD}}}}}} = &(26{K^2} + 8K){N_T}N_k^2 - 4K{N_T}{N_k} \\ &+ \left(\frac{4}{3}{K^3} + 16{K^2}\right)N_k^3 - 2KN_k^2 \\ &+ f + 2K{N_k} \\ = &{\rm O}({K^2}N_k^2{N_T}) \end{split} $

(25)

图3所示, 假设每个用户上的数据流数目为N_k=2, 发射端和接收端的数目相等可看为N_T=KN_k, 比较BD算法和本文提出的改进的GSO-CLLL-BD算法随着用户数目变化时算法总共所需浮点数的变化情况. 由图3可以看出, GSO-CLLL-BD算法在BD算法的基础上再降低了46.7%.

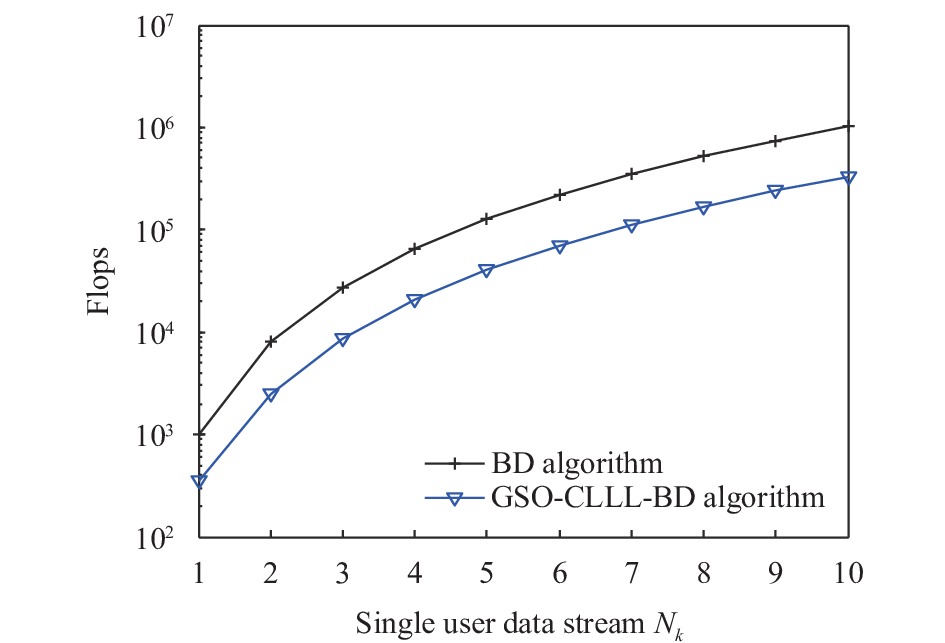
图4所示, 固定用户数目为K=2, 发射天线数目为N_T=KN_k, 比较BD算法和本文所改进的GSO-CLLL-BD算法随着每个用户上数据流数目变化时算法总共所需浮点数的变化情况. 从图4可以看出, 当单用户数据流数目为10时, GSO-CLLL-BD算法在GSO-LDL-BD算法的基础上再降低了40.62%.

5.2 容量分析

以用户k为例, 假设在发射端的数据流采用等功率分配, 在发射端已知信道状态信息的情况下, 其系统容量可以表示为:

$ \begin{split} {{{C}}_k} &= {\log _2}\det \left({{{I}}_k} + \frac{{{\textit{SNR}}_k}}{{{N_k}}}{{{{\bar H}}}_k}{{\bar H}}_k^H \right) \\ &= {\log _2}\det \left({{{I}}_k} + \frac{{{\textit{SNR}}_k}}{{{N_k}}}{{U}}\Lambda {{{U}}^H} \right) \\ &= {\log _2}\det \left({{{I}}_k} + \frac{{{\textit{SNR}}_k}}{{{N_k}}}\Lambda \right) \\ &= \sum\limits_{i = 1}^{{N_k}} {{{\log }_2}\left(1 + \frac{{{\textit{SNR}}_k}}{{{N_k}}}{\lambda _i} \right) } \end{split} $

(26)

其中, SNR_k表示用户接收天线的公共信噪比; $ {\lambda _i} $ 是对 $ {\bar H_k} $ 进行SVD操作后得到的第i个奇异值的平方.

由詹森不等式可以得到^[17]:

$ \begin{split} {C_k} =& \sum\limits_{i = 1}^{{N_k}} {{{\log }_2}\left(1 + \frac{{{\textit{SNR}}_k}}{{{N_k}}}{\lambda _i} \right) }\\ &\leqslant {N_k}{\log _2}\left(1 + \frac{{{\textit{SNR}}_k}}{{{N_k}}}\left(\frac{1}{{{N_k}}}\sum\limits_{i = 1}^{{N_k}} {\lambda _i^2} \right)\right) \end{split} $

(27)

由式(27)可以看出, 当且仅当 $ {\bar H_k} $ 的奇异值相等时( $ {\bar H_k} $ 为正交矩阵), 等号成立时容量达到最大. 当 $ {\bar H_k} $ 的奇异值大小差异越小, 信道容量越接近最大值.

多用户MIMO信道容量可以等价于多个单用户MIMO信道容量之和. 因此, 可以对单用户MIMO信道容量进行分析, 进而对本节所改进的BD算法进行容量仿真. 容量公式采用:

$ C = {\log _2}(\det (I + \sigma _n^{ - 2}HW{W^{{H}}}{H^{{H}}}))({\text{bits/Hz}}) $

(28)

在矩阵论知识中, 通常采用条件数来表示矩阵奇异值的分布情况. 将 $ {\bar H_k} $ 的条件数记为 ${{cond(}}{\bar H_k})$ , 可以表示为:

$ {{cond(}}{\bar H_k}) = \frac{{{\lambda _{\max }}}}{{{\lambda _{\min }}}} $

(29)

当条件数为1时, 该矩阵为正交矩阵, 奇异值相等; 条件数越大, 矩阵奇异值分布越广泛, 正交性也越差. 因此, 采用条件数的分布情况来衡量系统的性能.

图5所示, GSO-CLLL-BD算法的等效信道矩阵 $ {\bar H_k} $ 在格基规约前后, 条件数 $ {\text{cond(}}{\bar H_k}) $ 在对数尺寸的概率密度函数(probability density function, PDF)分布情况. 由图5可以看出, 对等效信道矩阵 $ {\bar H_k} $ 进行格基规约操作后, 其条件数分布更加密集, 均值也更小, 可以得到正交性更好的等效信道矩阵, 从而提高系统性能.

格基规约操作后得到的等效信道矩阵正交性更好. 图6比较了BD算法和GSO-CLLL-BD算法随着信噪变化时系统和容量的变化情况. 与预期结果一致, GSO-CLLL-BD算法较BD算法, 系统容量提高了2–10 bits/Hz.

5.3 误码率对比

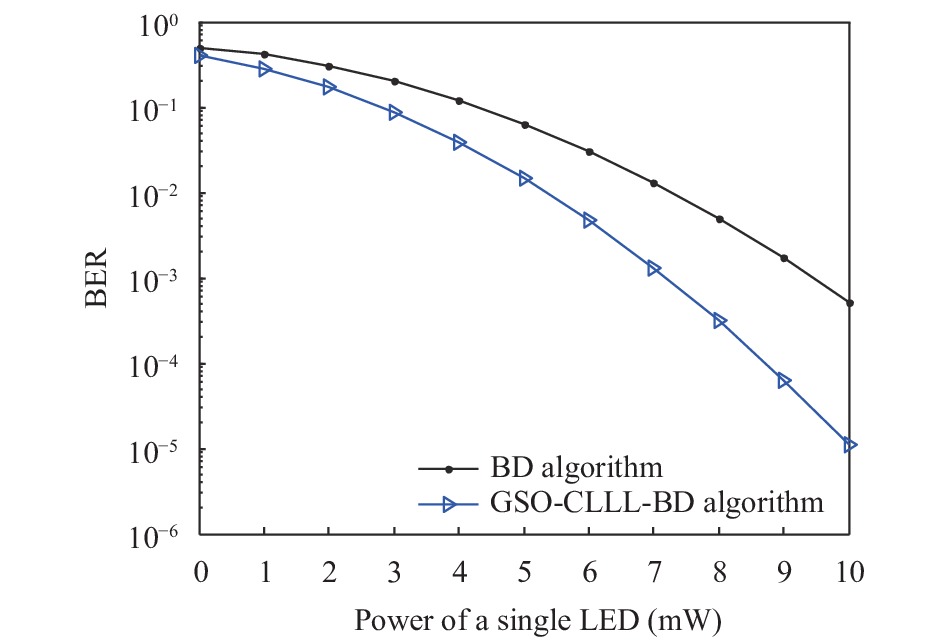
本文提出的GSO-CLLL-BD预编码算法通过格基规约技术来抑制数据流之间的干扰, 在进行格基规约技术前引入了信道噪声, 由图5的分析格基规约操作对等效信道矩阵的正交性也得到了提升, 因此接收端的信号以及干扰加噪声比值达到最大, 以此来优化误码率性能. 图7是本文提出的GSO-CLLL-BD算法与传统BD算法的系统误码率的对比分析, 从图5中可以看出, 当单个LED的功率达到10 mW时, 本文提出算法的误码率可达到10⁻⁵左右, BD预编码算法只能达到10⁻³.

6 结论

本文提出了一种改进BD预编码算法, 该算法通过采用正交分解中的施密特正交化传统BD预编码中的第1次SVD分解, 通过正交性好的格基规约算法代替传统BD算法中的第2次SVD分解. 并从算法复杂度、系统和容量以及系统误码率3个方面对本文所改进的GSO-CLLL-BD算法与BD算法进行仿真对比与分析, 本文提出的改进算法在复杂度上降低了46.7%, 随着用户数目的增加这种优势更明显, 在系统和容量上得到了2–10 bits/Hz的提高, 同时误码率上得到了2个量级的优化.