随着经济文化的迅速发展, 环境污染日益严重和双碳政策的实行, 城市居民开始倾向于绿色出行的交通方式, 网约车合乘出行模式也应运而生. 使用网约车合乘出行, 乘客可受门到门的出行服务, 相较于出租车、传统网约车, 网约车合乘出行成本更低, 更环保; 相较与公交地铁, 网约车合乘出行更舒适、更快捷. 但网约车合乘也存在着诸多问题, 例如合乘路线的不确定性, 容易造成乘客与乘客之间, 乘客与驾驶员之间的纠纷; 合乘成本的不确定性, 因绕行造成的行驶成本, 时间成本等一系列相关成本的承担责任不易界定等. 因此研究网约车合乘模型及其启发式算法十分必要其意义深远.

合乘最早是在1981年被Daganzo等人^[1]提出, 并应于公共交通路网中的交通流均衡分配问题. 但在此文章中应用的合乘需求均为假设, 其构建的模型适应性有待考察. 但合乘这一概念的提出为后续研究工作奠定了理论基础. 2003年, Katzev^[2]提出了一种创新性概念汽车合乘方法, 可以用于解决城市日益严重的交通运输问题. 2007年, Shaheen等人^[3]指出合乘方式是一种灵活的替代方案, 可以满足全球范围内的各种运输需求, 采用出租车合乘可以有效缓解私家车数量的负担, 并详细说明了合乘方式的必要性, 此篇文章使得合乘问题被社会再次关注. 2014年, Huang等人^[4]针对合乘问题提出了智能合乘系统, 提出了一种基于遗传算法的多目标优化问题与模糊控制系统相结合, 来进行合乘路径优化以及车辆匹配. 随着信息通讯技术的不断发展, 合乘逐渐与网约车相结合^[5–11], 并越来越受到国内外学者的注意.

1 问题描述

网约车合乘问题可描述为: 现有若干名乘客存在出行合乘需求, 且乘客的上下车位置坐标已知, 现派出一定数量的车辆为乘客提供合乘服务, 且车辆的负载能力一定. 每辆车均从起点出发, 然后分别行至每位乘客提供上下车地点, 以此来完成乘客的合乘出行. 因此每位乘客相对应的上下车点只能被访问一次, 每辆车在提供服务时所运送的合乘乘客数不能超出车辆的最大负载能力, 车辆须在乘客要求的时间范围内到达乘客要求的上下车点, 并以最小行驶距离成本、等待时间成本以及最大收益额使得司机以最大利润来完成乘客的合乘需求.

2 模型建立 2.1 模型假设

为便于网约车合乘模型的建立, 提出以下基本假设: ① 提供合乘服务的车辆为同一车型, 载重量一定; ② 提供合乘服务的车辆在服务时间窗内只进行从起始点到目的点的运行, 不存在中途折返等情况; ③ 车辆在行驶过程中, 每辆车正在服务的乘客总和不应大于车辆容量; ④ 所有车辆状况良好, 不存在行驶途中车辆抛锚、油量短缺、交通拥堵等特殊情况; ⑤ 所有车辆在行驶过程中均以匀速行驶; ⑥ 不考虑交叉口红绿灯等其他不可抗力因素的影响; ⑦ 每位乘客最多只能被服务一次, 且在被服务期间不存在换乘或取消行程的情况; ⑧ 所有乘客的接送位置和车辆的起终点位置及其之间的距离、服务时间等都是已知的.

2.2 参数与决策变量的含义

设 $ H $ 为车辆集合, 每个车辆 $ h \in H $ , $h = \left\{ {1, 2, \cdots , {n_H}} \right\}$ , ${n_P}$ 表示所有乘坐者的数量, ${n_H}$ 表示待调度车辆的数量. 有向量 $G = \left( {V, A} \right)$ , 其中 $ V = {V_O} \cup V_P^O \cup V_P^D \cup {V_T} $ , $ {V_O} $ 和 $ {V_T} $ 是虚拟节点, 表示所有车辆都需要从 $ {V_O} $ 开始到达终点 $ {V_T} $ , $ {V_O} = \left\{ 0 \right\} $ , $ {V_T} = \left\{ {{n_H} = 2{n_P} + 1} \right\} $ ; $ {V_H} $ 表示车辆当前位置节点, $ {V_H} = \left\{ {1, 2, \cdots , i, \cdots , {n_H}} \right\} $ ; ${m_h}$ 为车辆h最大通行能力, ${q_i}$ 为节点 $i$ 的荷载, $ {q_{{V_O}}} = {q_{{V_T}}} = 0 $ , $ {q_{{V_O}}} = 1 $ , $ {q_{V_O^D}} = - 1 $ ; $Q_i^h$ 为访问点 $i$ 后车辆 $h$ 的负载, ${Q_h}$ 为车辆 $h$ 的容量; $\left[ {{e_i}, {l_i}} \right]$ 为时间窗口, 表示节点i的最早和最晚服务时间, ${t_{ij}}$ 为节点 $i$ 到节点 $j$ 的旅行时间; $c$ 是车辆 $h$ 从节点 $i$ 到节点 $j$ 的距离代价; ${d_{ij}}$ 为节点i到节点 $j$ 的距离; ${w_i}$ 为节点i的等待时间; $f$ 是服务每一个乘坐者所能获得的单位距离收益; $\delta $ 表示单位等待时间的费用.

对于每个乘坐者 $i \in V_P^O$ , 如果乘坐者i被服务, 令 ${s_i} = 1$ ; 如果乘坐者i没有被服务, 则令 ${s_i} = 0$ ; 对于每个弧 $\left( {i, j} \right) \in A$ , 每个车辆 $ h \in H $ , 若车辆 $h$ 从节点 $i$ 到节点 $j$ 旅行, 令 $x_{ij}^h = 1$ . 对于每个节点 $i \in N$ , 每个车辆 $ h \in H $ , 设 $B_i^h$ 为车辆 $h$ 在节点 $i$ 开始的时间, $Q_i^h$ 为车辆 $h$ 访问节点 $i$ 后的负载, ${w_i}$ 为节点 $i$ 的等待时间.

2.3 网约车合乘数学模型

基于上述假设、定义的参数和决策变量, 将网约车合乘问题的数学模型表示为:

$ {\rm{max}}Z = f\sum\nolimits_{i \in V_G^o \cup V_Y^o} {{s_i}{d_{i, {n_P} + i}}} - c\mathop \sum \limits_{h \in H} \mathop \sum \limits_{i \in V} \mathop \sum \limits_{j \in V} {d_{ij}}x_{ij}^h - \delta \mathop \sum \limits_{i \in V} {w_i} $

(1)

约束条件:

$ {s_i} = \mathop \sum \limits_{h \in H} \mathop \sum \limits_{j \in N} x_{ij}^h,\; \forall i \in V_G^O \cup V_Y^O $

(2)

$ \sum _{h\in H}\sum _{j\in V}{x}_{ij}^{h}=1,\; \forall i\in {V}_{H} $

(3)

$ \sum _{i\in V}{x}_{i, {V}_{T}}^{h}=1,\; \forall h\in H $

(4)

$ \mathop \sum \limits_{j \in V} x_{ji}^h - \mathop \sum \limits_{j \in V} x_{ij}^h = 0,\; \forall i \in V_G^O \cup V_G^D \cup V_Y^O \cup V_Y^D,\; \forall h \in H $

(5)

$ \mathop \sum \limits_{h \in H} \mathop \sum \limits_{j \in V} x_{ij}^h \leqslant 1,\; \forall i \in V_G^O \cup V_G^D \cup V_Y^O \cup V_Y^D $

(6)

$ \mathop \sum \limits_{j \in V} x_{i, j}^h - \mathop \sum \limits_{j \in V} x_{{n_P} + i, j}^h = 0,\; \forall i \in V_G^O \cup V_Y^O,\; \forall h \in H $

(7)

$ B_j^h = \mathop \sum \limits_{i \in V} x_{ij}^h\left( {B_i^h + {w_i} + {t_{ij}}} \right),\;\forall j \in V,\;\forall h \in H $

(8)

$ Q_j^h = \mathop \sum \limits_{i \in V} x_{ij}^h\left( {Q_i^h + {q_j}} \right),\;\forall j \in V,\;\forall h \in H $

(9)

$ B_{{V_T}}^h - B_{{V_O}}^h \leqslant {T_h} $

(10)

$ {e_i} \leqslant B_i^h \leqslant {l_i},\; \forall i \in V,\; \forall h \in H $

(11)

$ \max \left\{ {0, {q_i}} \right\} \leqslant Q_i^h \leqslant \min \left\{ {{Q_h}, {Q_h} + {q_i}} \right\},\; \forall i \in V,\; \forall h \in H $

(12)

$ x_{ij}^h \in \{ 0, 1\} ,\; \forall i \in V, j \in V,\; \forall h \in H $

(13)

$ {s_i} \in \{ 0, 1\} ,\; \forall i \in V_G^O \cup V_Y^O $

(14)

目标函数(1)以总利润最大化、成本和等待时间最小为目标^[12–17]. 约束(2)确保送达的乘客被记录. 约束(3)和(4)保证每辆车辆k的路线从车辆起始位置开始, 并在目的地车辆段结束; 约束(5)–(7)保证任何乘坐者最多可送达一次, 送达的每一个乘坐者应在其起始节点处上车, 并在其下车节点处下车. 时间和负荷变量的一致性由约束(8)和(9)保证, 约束(10)对每条路径的持续时间进行约束; 约束(11)和(12)分别施加时间和容量窗口^[18–21]; 约束(13)和(14)是对决策变量 $x_{ij}^h$ 、 ${s_i}$ 的取值范围进行约束.

3 求解网约车合乘模型的遗传算法

遗传算法(genetic algorithm, GA)是一种利用生物世界的自然规律(即适者生存)来寻找最优解空间的随机搜索算法. 该算法通过数学的方式^[22], 利用计算机仿真运算, 将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程^[23].

3.1 染色体编码

车辆总路线编码使用整数编码方式^[24]. 一个染色体即为一个可行解, 染色体被编码为一个整数字符串, 其长度取决于车辆和乘客的数量大小. 每个字符串由几个子字符串组成, 每个子字符串是一个基因序列, 表示其中一辆车从终端开始到行驶结束的总路线. 随机生成染色体, 如图1所示, 其中包含10组乘客, 4辆网约车, 1–10分别为10组乘客的上车点, 11–20分别对应乘客下车点, 并与上车点一一对应. 其中0基因代表区分车辆标记(其数量为车辆数减1).

图1所示染色体为一可行解, 解码后表示为4辆车的行驶路线.

车辆1路线: 5→15→2→12 (车辆1→乘客5上车点→乘客5下车点15→乘客2上车点→乘客2下车点12).

车辆2路线: 3→1→10→20→11→13 (车辆2→乘客3上车点→乘客1上车点→乘客10上车点→乘客10下车点20→乘客1下车点11→乘客3下车点13).

车辆3路线: 7→17→8→4→6→14→18→16 (车辆3→乘客7上车点→乘客7下车点17→乘客8上车点→乘客4上车点→乘客6上车点→乘客4下车点14→乘客8下车点18→乘客6下车点16).

车辆4路线: 9→19 (车辆4→乘客9上车点→乘客9下车点19).

3.2 适应度函数

模型的目标函数为利润最大, 其组成部分为收益、行驶成本和等待时间成本, 为达到利润最大, 要在符合约束条件的情况下尽可能满足最大收益、最小行驶成本和等待时间成本. 设置适应度函数为:

$ F = Length $

其中, F为F适应度值, $Length$ 为每辆车运送每位乘客行驶的距离和. 适应度值越大代表可行解在满足时间窗和车辆载重的情况下所有车辆运送每位乘客行驶的距离和越大, 对应的收益也越大, 从而目标函数值也越大.

3.3 初始解的生成

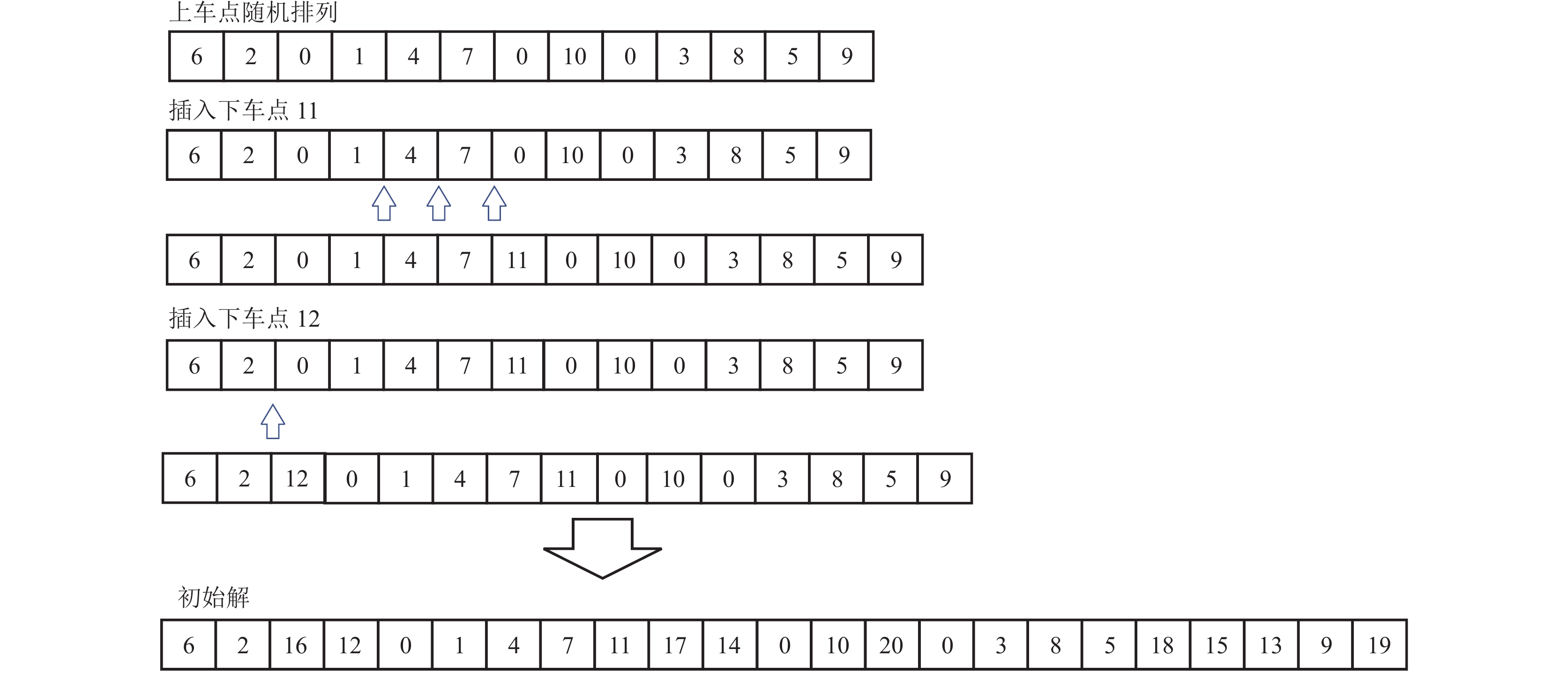
初始解首先通过将乘客上车点和0基因进行随机排列, 将乘客随机与车辆进行匹配, 生成初始基因片段, 而后按照顺序依次将乘客下车点插入. 因乘客上车点与下车点一一对应且车辆只有在上车点接到乘客才能行至对应的乘客下车点, 所以限制了下车点插入的位置. 根据要求下车点只能位于上车点之后, 并且与上车点在同一车辆. 初始解的生成如图2所示, 1–10代表乘客上车点, 11–20代表乘客下车点, 并与上车点一一对应. 第1阶段将上车点和0基因随机排列. 第2阶段按序插入下车点, 首先插入乘客1的下车点11, 可插入位置有3处(箭头处), 随机选择一处插入, 再插入乘客2的下车点12, 可插入位置有一处, 以此类推将下车点按照要求全部插入, 生成初始解.

初始解表示4辆车的行驶路线:

车辆1路线: 6→2→16→12 (车辆1→乘客6上车点→乘客2上车点→乘客6下车点16→乘客2下车点12).

车辆2路线: 1→4→7→11→17→14 (车辆2→乘客1上车点→乘客4上车点→乘客7上车点→乘客1下车点11→乘客7下车点17→乘客4下车点14).

车辆3路线: 10→20 (车辆3→乘客10上车点→乘客10下车点20).

车辆4路线: 3→8→5→18→15→13→9→19 (车辆4→乘客3上车点→乘客8上车点→乘客5上车点→乘客8下车点18→乘客5下车点15→乘客3下车点13→乘客9上车点→乘客9下车点19).

3.4 遗传操作 3.4.1 选择操作

采用锦标赛法进行选择操作, 首先从种群中随机选择一定数量的染色体, 而后在这些染色体中选取适应度最高的染色体进行遗传操作, 对这一过程进行重复操作, 直至子代种群与父代种群的规模相同. 通过这一过程, 可以极大的保持种群的多样性.

3.4.2 交叉操作

交叉操作应用了随机两点交叉的思想, 根据配对和约束原则进行了修改, 其过程如图3所示. 第1阶段, 选择父代染色体中第一辆车的基因片段(用绿色标记的基因)进行交叉操作. 第2阶段, 选中的基因片段交叉在父代染色体前端, 而后全部遗传至子代染色体. 第3阶段, 将子代染色体中重复的基因片段(用蓝色标记的基因)进行删除. 即完成交叉操作.

3.4.3 变异操作

变异操作应用了随机两点突变的思想, 其过程如图4所示. 在父代染色体中, 随机选择两个上车点的基因(例如, 用橙色标记的9, 10), 以及相对应的下车点基因(例如, 用绿色标记的19和20). 子染色体的其余基因从父染色体继承.

4 算例分析 4.1 算例描述

现有可提供合乘服务的车辆4辆, 10组乘客有合乘出行需求, 位置坐标(坐标借鉴使用北京Q汽车制造企业物流园区位置及其4S店位置)如表1所示. 序号0为车辆所在位置, 序号1–10为乘客上车点, 序号11–20为乘客下车点, 上下车点一一对应, 即序号1对应序号11, 序号2对应序号12, 以此类推. 车辆在序号0位置时载重量为0, 经过一个上车点搭载一名乘客, 经过一个下车点车内减少一名乘客. 表1中的最早、最晚时间窗数据均以车辆开始提供服务的时间为基础, 例如乘客1上车点的时间窗为[0, 0.5], 下车点的时间窗[0, 2], 若车辆从8:00开始提供服务, 那须在8:00–8:30到达乘客1的上车点, 在8:00–10:00送乘客1到达下车点位置. 车辆在每个站点接送乘客上下车所用停车时间为0.01小时.

4.2 参数设置

遗传算法参数的合理设置对算法的有效性和计算效率有着重要影响, 算法中的参数种群大小、迭代次数、交叉概率、变异概率、代沟以及各惩罚系数都需进行合理设置. 参数调优和参数控制是启发式算法中确定参数值的两种常用方法. 参数调优是将其他参数固定, 仅变化需要测试的参数, 找到求解效果最好的参数值; 参数控制是将几种参数的值进行变化组合, 找到最优组合方式. 本文使用这参数调优的方法确定各参数值, 如表2所示.

4.3 运行结果

通过上述遗传算法操作及参数设置, 对算例进行求解分析. 实验环境为Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz 1.80 GHz, 操作系统为64位Windows 11, 使用Matlab R2018a进行编程. 求解得到目标函数最大利润为6 906.297 1 元, 运行时间为44.08 s, 车辆行驶总距离为542.648 6 km, 如表3所示. 图5为Matlab运行算例后的迭代图和车辆行驶路线图, 从图5(a)可以看出根据模型所设计的遗传算法在收敛速度和跳出局部最优的能力上表现的十分出色, 根据图5(b)可以看出使用的3辆车的行驶路线, 分别用红、绿、蓝3种颜色表示.

基于乘客合乘需求的节点数据、提供服务的车辆数据以及乘客的时间窗要求, 应用设计的遗传算法求解网约车合乘模型, 得出最优合乘路线有3条如表4所示, 分别为: 车辆1起点→乘客2上车点→乘客2下车点12; 车辆2起点→乘客6上车点→乘客7上车点→乘客5上车点→乘客3上车点→乘客7下车点17→乘客5下车点15→乘客4上车点→乘客8上车点→乘客6下车点16→乘客9上车点→乘客3下车点13→乘客1上车点→乘客8下车点18→乘客9下车点19→乘客4下车点14→乘客1下车点11; 车辆3起点→乘客10上车点→乘客10下车点20.

5 结论与展望

本文就网约车合乘出行模式, 建立了一般合乘的数学模型, 并根据合乘模型的特点和约束条件, 设计了所对应的遗传算法对算例进行了求解, 从而验证了模型和算法的可行性和有效性. 在算法中设计了交叉算子和变异算子, 使种群保持多样性, 尽可能跳出局部最优解, 获得更优的可行解. 模型未考虑不同车型的情况, 下一步研究可考虑不同载重的车型车辆. 自2019年国内外新冠肺炎病毒的爆发, 疫情不断影响和改变着城市居民的日常生活. 在疫情时代的大背景下, 下一步的研究方向也可将模型与疫情相结合, 考虑乘客的风险等级, 车辆是否进行消毒等情况.