2. 衢州学院 电气与信息工程学院, 衢州 324000
2. College of Electrical and Information Engineering, Quzhou University, Quzhou 324000, China
随着数据挖掘方法在各产业中的繁荣发展, 用户数据可以被更加充分地利用以提升生产效率以及用户体验[1]. 然而, 在这些被大规模使用的数据中可能包含用户的隐私信息, 例如个人医疗健康报告[2], 家庭收入与消费记录[3], 以及商业营销数据[4]等. 因此, 大数据应用中的用户隐私问题受到了越来越多的关注[5]. 为了有效地防止用户隐私数据泄露, 发展关于隐私保护的大数据工具也逐渐成为研究热点[6].
经典的机器学习方法认为训练数据和测试数据来自相同分布, 而且只有一个训练集. 为了训练机器学习算法, 我们通常需要搜集充分多的样本, 来得到算法中参数的准确估计. 然而在实际应用中, 为了保护用户的隐私数据, 我们可能无法确保满足上述要求. 首先, 在现实的隐私保护框架下, 数据经常呈现出数据孤岛的现象[7], 并且单个数据源中拥有的数据量可能不足, 这导致我们仅仅在目标域上进行传统的统计分析或大数据挖掘无法训练得到精准的算法参数, 而且也无法简单地通过将分散的数据汇总来增加目标域的样本量[8]. 除此之外, 由于数据拥有者们可能来自不同的地区或者数据产生于不同的时间, 这些来自不同源域的数据可能因此具有不同的分布[9]. 这导致我们无法在目标域上直接使用其他源域中机器学习算法的训练结果. 一个实际例子是本文关注的医学自动诊断领域中基于多数据源域的帕金森疾病得分预测问题[10]. 某非医学的机构需要预测一家医院 (目标医院) 的早期帕金森患者的疾病得分, 该机构已拥有待预测患者关于帕金森疾病的相关生理指标数据, 而未获得疾病得分. 同时, 该机构可以访问其他一些医院 (源医院) 的帕金森病人数据, 包括相关生理指标数据和疾病得分数据. 出于保护隐私以及预防数据被滥用的目的, 每位病人的疾病数据只在其所属医院本地保存, 而不传输到其他机构中. 通常这些源医院和目标医院来自不同的地区, 各医院的病人数据也发生于不同的时间. 由于人种基因、饮食条件、运动习惯、文化环境影响的认知模式和思维方式等的不同, 不同医院的病人在相关生理指标数据上可能会有很大的不同, 而且呈现出区域性的不同. 然而医学上根据相关生理指标数据计算疾病得分的原理对所有人都是相同的.
为了充分利用分散的数据, 联邦学习通过训练不同源域上的算法进行协作而无需共享自身数据来解决多源域数据处理中的隐私问题[8]. 该方法最近在大数据医疗领域中获得了广泛的关注[11]. 近期研究表明, 联邦学习训练的模型可以达到与在中心训练的绩效水平相当的性能水平. Dowlin等人[12]提出加密网以提高数据加密的效率从而实现更好的联邦学习性能. Bonawitz等人[13]引入一种聚合机制以在联邦学习框架下更新机器学习模型. Mohassel等人[14]提出了联邦学习系统中支持多客户端隐私保护合作培训的安全机器学习. Smith等人[15]提出联邦多任务学习, 为每个节点学习一个单独的模型, 其研究成果表明, 多任务学习适合于应对联邦学习中的统计学难题. Liu等人[16]展示了一种能够灵活地应用于各种多方安全机器学习任务的半监督联邦迁移学习框架, 允许知识在网络中通过迁移学习进行传输, 且不必损害用户隐私. Cheng等人[17]提出了对于纵向联邦学习的安全性提升方法, 这是一种新颖的、无性能损失的、保护隐私的提升树系统架构.
联邦学习可以解决数据分散的问题, 使得孤岛形式的多源域数据可以被充分合理地使用[7]. 而在每个源域本地学习的过程中, 如果源域和目标域的分布不同, 传统的机器学习方法不再适用, 迁移学习是一种有效的模型训练方法, 它旨在从可能与目标域不同的源域中提取知识并将知识应用于目标任务[9]. 迁移学习的研究是为了智能地应用以前学到的知识来更快地解决新问题或提供更好的解决方案. 迁移学习的方法可以分为4类: 基于样本的迁移方法[18], 其中主要的技术如样本重新加权和重要性抽样; 基于特征表示的迁移方法[19], 主要想法是通过源域为目标域学习一个特征表示, 其中用于跨域传输的知识被编码到学习的特征表示中; 基于参数的迁移方法[20], 假设源任务和目标任务共享一些参数或者超参数的先验分布, 其中迁移的知识被编码到共享的参数或者先验中; 基于关系的知识迁移[21], 基本假设是源域和目标域中的数据之间的某些关系是相似的, 要传输的知识是数据之间的关系. 通过纠正每个样本数据采样过程中的偏差进行迁移学习的方法, 侧重于数据重要性权重[22]或类重要性权重[23]. 重要性加权方法赋予每个样本一个密度比形式的权重, Sugiyama等人[24]提出在密度比已知情况下的重要性加权交叉验证方法, 将验证风险加权为目标风险的无偏估计. 当密度比未知时, 有一些直接估计密度比的方法, 比如, 核平均匹配方法[25], Kullback-Leiber重要性估计方法[26], 最小二乘重要性拟合方法[27].
目前, 联邦学习以及迁移学习都分别有丰富的研究以及广泛的应用[28]. 然而, 目前在不同源域和目标域具有相同的特征空间但是允许特征分布不同的数据背景和源域拥有隐私保护的要求下对目标数据进行预测的研究还十分有限. 因此本文针对上述数据特点, 提出了联邦重要性加权方法, 该方法结合了联邦学习和迁移学习中基于样本的重要性加权方法. 联邦重要性加权方法首先在每个源域本地学习一个模型而不用汇总或者传输源域数据以在满足源域数据隐私的要求下充分利用所有源域数据. 在每个源域本地学习中, 我们的方法通过重要性加权方法重用源域样本为目标域的风险函数提出一个合理估计, 通过最小化目标风险的估计获得该源域对目标域贡献的一个模型, 从而解决多源域和目标域之间分布不同的问题. 然后, 本文首次提出, 根据各源域和目标域的分布差异为各源域模型构造权重从而将所有源域模型加权整合成一个模型用于目标域的预测任务.
本文的其余部分组织如下. 在第2节中, 我们介绍了本文研究的问题设置. 第3节介绍了联邦重要性加权方法的具体内容和执行该方法的具体算法. 第4节进行数值模拟, 将目前常用的方法与本文提出的方法进行比较. 第5节将联邦重要性加权方法应用于预测帕金森疾病得分. 第6节总结了全文.
2 问题设置考虑上文所述医院的实例, 抽象出研究问题的设置, 本文考虑
第
将第
本文考虑以下条件.
1) 源支撑目标, 且源和目标的特征分布不同, 即对于每个
2) 源和目标的输出变量关于特征变量的条件分布相同, 即:
这两个条件确保源数据可用于目标任务[30]. 对应到上述的实际问题,
除此之外, 在我们的设置中每个源有隐私要求, 数据只保存在本地. 本文的目的是在这样的问题设置下学习一个预测目标输出值的参数模型.
3 联邦重要性加权方法 3.1 超参数选优为了获得一个准确的参数模型, 需要找到目标分布上的最优超参数:
| $ {\theta ^*} = \mathop {\arg \min }\limits_{\theta \in \Theta } {R_t}(\theta ) $ | (1) |
其中,
如果我们已拥有目标输出值, 令
| $ {\hat R^{{\rm{op}}}}(\theta ) = \frac{1}{{n_t^{{\rm{val}}}}}\sum\limits_{(x, y) \in T_{{\rm{val}}}^{{\rm{op}}}} l (h(x;\hat \omega (\theta ), \theta ), y) $ | (2) |
在
| $ \hat \omega (\theta ) = \mathop {\arg \min }\limits_{\omega \in \Omega } \frac{1}{{n_t^{{\rm{tr}}}}}\sum\limits_{(x, y) \in T_{{\rm{tr}}}^{{\rm{op}}}} l (h(x;\omega , \theta ), y) $ |
然后, 把
然而, 在第2节描述的问题设置中, 目标域的数据的输出值无法获得, 上述过程不再适用. 因此我们需要利用输出值可获得的源数据, 但是源域和目标域的分布不同, 无法直接训练机器学习方法. 迁移学习可以很好地解决分布不同的问题, 将源域数据充分合理地用于目标任务. 由于每个源域的数据只保存在本地, 我们根据联邦学习的思想让每个源域在本地学习一个参数模型. 在每个源域本地学习的过程中, 本文使用基于样本的迁移学习方法, 将分布不同的源域样本通过重要性加权重用于目标域的预测任务, 以解决分布不同的问题.
3.2 各源本地的重要性加权估计每个源在本地学习中使用重要性加权方法[27], 这个过程涉及密度函数的比值, 为此我们对
| $ {r_j}(x) = \frac{{{p_t}(x, y)}}{{{p_j}(x, y)}} = \frac{{{p_t}(x)}}{{{p_j}(x)}} $ |
其中, 第2个等式可由第2节中的条件2)推导得到.
由于在我们的超参数优化过程中涉及密度比估计、训练模型参数、估计最优超参数3部分, 我们把
| $ S_j^{{\rm{de}}} \cup S_j^{{\rm{tr}}} \cup S_j^{{\rm{val}}} $ |
其中,
| $ S_j^{{\rm{de}}} = \{ (x_{ji}^{{\rm{de}}}, y_{ji}^{{\rm{de}}})\} _{i = 1}^{n_j^{{\rm{de}}}} $ |
| $ S_j^{{\rm{tr}}} = \{ (x_{ji}^{{\rm{tr}}}, y_{ji}^{{\rm{tr}}})\} _{i = 1}^{n_j^{{\rm{tr}}}} $ |
| $ S_j^{{\rm{val}}} = \{ (x_{ji}^{{\rm{val}}}, y_{ji}^{{\rm{val}}})\} _{i = 1}^{n_j^{{\rm{val}}}} $ |
令:
| $ {n_j} = n_j^{{\rm{de}}} + n_j^{{\rm{tr}}} + n_j^{{\rm{val}}} $ |
| $ {n^{{\rm{tr}}}} = n_1^{{\rm{tr}}} + n_2^{{\rm{tr}}} + \cdots + n_m^{{\rm{tr}}} $ |
| $ {n^{{\rm{val}}}} = n_1^{{\rm{val}}} + n_2^{{\rm{val}}} + \cdots + n_m^{{\rm{val}}} $ |
对于给定的超参数
| $ {\hat R^j}_{IW}(\theta ) = \frac{1}{{n_j^{{\rm{val}}}}}\sum\limits_{i = 1}^{n_j^{{\rm{val}}}} {{{\hat r}_j}} (x_{ji}^{{\rm{val}}})l(h(x_{ji}^{{\rm{val}}};\hat \omega (\theta ), \theta ), y_{ji}^{{\rm{val}}}) $ | (3) |
其中, 密度比估计
| $ \hat \omega (\theta ) = \mathop {\arg \min }\limits_{\omega \in \Omega } \frac{1}{{n_j^{{\rm{tr}}}}}\sum\limits_{i = 1}^{n_j^{{\rm{tr}}}} l (h(x_{ji}^{{\rm{tr}}};\omega , \theta ), y_{ji}^{{\rm{tr}}}) $ | (4) |
第
| $ {\hat \theta ^j} = \mathop {\arg \min }\limits_{\theta \in \Theta } {\hat R^j}_{IW}(\theta ) $ | (5) |
于是, 相应的第
| $ h( \cdot ;\hat \omega ({\hat \theta ^j}), {\hat \theta ^j}) $ |
在获得各源在本地学习到的参数模型之后, 我们需要将这
我们构造如式(6)所示加权模型:
| $ {\hat h_t}( \cdot ) = \sum\limits_{j = 1}^m {\hat \beta ({{\hat \theta }^j})} h( \cdot ;\hat \omega ({\hat \theta ^j});{\hat \theta ^j}) $ | (6) |
其中,
| $ \hat \beta ({\hat \theta ^j}) = \frac{{{n_j}}}{{\widehat d({{\hat \theta }^j})}}/\left(\sum\limits_{k = 1}^m {\frac{{{n_k}}}{{\widehat d({{\hat \theta }^k})}}} \right) $ | (7) |
其中,
| $ \begin{split} \widehat d({{\hat \theta }^j}) =& \frac{1}{{n_j^{{\rm{val}}}}}\sum\limits_{i = 1}^{n_j^{{\rm{val}}}} [ {{\hat r}_j}(x_{ji}^{{\rm{val}}})l(h(x_{ji}^{{\rm{val}}};\hat \omega ({{\hat \theta }^j}), {{\hat \theta }^j}), y_{ji}^{{\rm{val}}}){]^2} \\ & - {\left[\frac{1}{{n_j^{{\rm{val}}}}}\sum\limits_{i = 1}^{n_j^{{\rm{val}}}} {{{\hat r}_j}(x_{ji}^{{\rm{val}}})l(h(x_{ji}^{{\rm{val}}};\hat \omega ({{\hat \theta }^j}), {{\hat \theta }^j}), y_{ji}^{{\rm{val}}})} \right]^2} \\ \end{split} $ |
根据式(7)可以验证
为了描述我们提出的联邦重要性加权方法在具体执行时的流程, 我们设计联邦重要性加权算法如算法1.
算法1. 联邦重要性加权算法
输入: 无输出值的目标数据集
输出: 目标任务的预测模型,
1) 目标数据的拥有者将
2) for
第
a) 把
b) 在
c) 在
d) 在
e) 把
3) 目标数据的拥有者:
根据式(6)加权各源模型.
4) 返回
算法1首先让目标将数据分别传输给每个源, 让每个源在本地利用自己的数据和目标的数据学习一个模型, 将学习得到的参数传输给目标. 因此算法1可以很好地保证源域的数据隐私. 为了解决源域和目标域之间分布不同的问题, 算法1在每个源域本地学习的过程中使用了基于样本的迁移学习方法, 并且根据每个源域和目标域的分布差异为源域构造了模型权重, 由各源域计算模型权重并传输给目标域. 最终, 目标域获得一个加权模型, 作为自己的预测模型.
4 数值分析本节我们先通过模拟实验测试我们的方法, 然后在实际的帕金森疾病数据集[10]上做预测. 后面FedIW表示本文提出的方法, 并且每次实验中都与以下4个方法对比:
1) Naive: 在每个源本地学习时, 不考虑源和目标之间的协变量移位, 通过最小化源域的损失函数获得各源的超参数.
2) Refer: 假设目标数据的输出值可获得, 并只在目标数据上训练模型, 这在我们的设置中是不可行的, 报告其结果作为参考.
3) LI[33]: 通过最小化元损失函数来找到有希望的超参数. 元损失函数定义为每个源域上的损失函数 (式(3)) 的总和. 直观地说, 通过最小化元损失函数, LI估计最优超参数.
4) MS-CS[32]: 根据每个源域和目标域的分布差异为目标风险构造一个估计, 将每个源域上的估计加起来作为目标函数, 通过最小化目标函数获得超参数.
4.1 模拟数据为了验证我们提出的方法的有效性, 我们用10维向量
在训练过程中, 我们使用岭回归模型, 超参数是正则化参数
| $ l(\hat y, y) = {(\hat y - y)^2} $ |
我们用平均绝对误差报告预测误差:
| $ \frac{1}{n}\sum\limits_{i = 1}^n | {\hat y_i} - {y_i}| $ |
我们进行以下几组模拟实验.
1) 源和目标的样本量都为100, 第
| $ {c_j}\sim U( - 5, 5),\; x\sim N({c_j} \times {1_{10}}, {I_{10}}) $ |
其中,
2) 两个源, 特征分布分别为:
| $ N({0_{10}}, {I_{10}}),\; N(2 \times {1_{10}}, {I_{10}}) $ |
样本量分别记为
3) 目标样本量为50, 两个源, 特征分布分别为:
| $ N({0_{10}}, {I_{10}}),\; N(c \times {1_{10}}, {I_{10}}) $ |
对应的样本量分别为100和200, 对于
我们将模拟实验1)–3)的100次实验结果的平均值和标准差分别提供在表1–表3中. 将模拟实验2)的实验结果的平均值和标准差关于不同样本量组合的变化情况分别绘制成图1和图2. 将模拟实验3)的实验结果的平均值关于
|
表 1 模拟实验1)中各方法的表现(平均表现
|
|
表 2 模拟实验2)中各方法的表现(平均表现
|
|
表 3 模拟实验3)中各方法的表现(平均表现
|
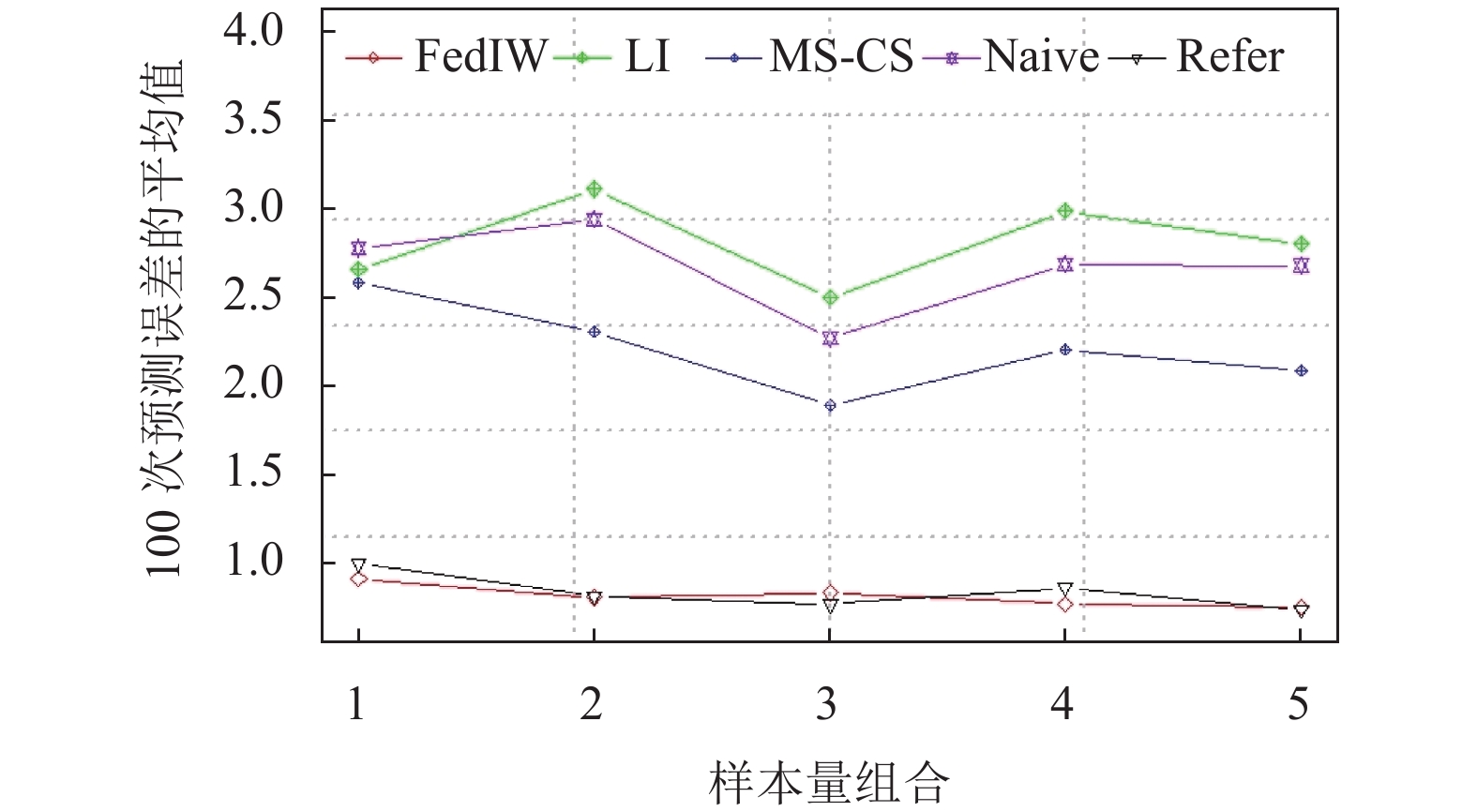
|
图 1 Case 2中各方法在不同样本量组合的平均表现 |

|
图 2 Case 2中各方法在不同样本量组合的标准误差 |

|
图 3 Case 3中各方法在
|
4.3 结果分析
表1的结果显示在源的个数取不同值时, FedIW的平均表现优于Naive, LI和MS-CS, 比Refer略差一点. 表2的结果显示在几组不同的样本量组合下, FedIW不仅平均表现优于另外3种, 而且由图1可看出FedIW的平均表现和Refer很接近. 由图2可看出FedIW的实验结果的标准差是最小的, 且随着样本量逐渐增大, 各方法的标准差都逐渐减小. 表3的结果显示在
FedIW明显优于Naive, 因为我们提出的联邦重要性加权估计可以很好地适应源和目标之间的分布迁移, 而Naive则不能. FedIW表现优于LI和MS-CS, 说明了我们让每个源域本地学习而不必考虑其他源域的做法以及构造的模型权重有助于提升目标域的预测精度. 有时候, FedIW的表现很接近Refer的表现, 甚至略优于Refer, 说明我们提出的方法很有效.
5 帕金森疾病得分预测我们使用帕金森远程监控数据集[10], 该数据集收录了42名早期帕金森患者的一系列生物医学语音测量数据, 这些患者被招募参加为期6个月的远程监测症状进展测试. 这些记录是在患者家中自动记录的. 在这里, 我们将每个患者的家视为一家小医院, 患者的所有记录都是这家医院拥有的数据. 数据集的列包括受试者编号、受试者年龄、受试者性别、从基线招募日期开始的时间间隔、UPDRS (帕金森病评分量表) 总评分和16个生物医学语音测量值. 每行对应于这些人5875条语音记录中的一条. 该数据集的主要目的是预测16次语音测量的UPDRS总分.
我们选择一个医院作为目标, 把其他的医院都作为源. 各源医院的患者数据不离开本地不允许泄露, 不同的源医院的病人疾病数据不可以混合. 我们依然用岭回归模型训练数据, 超参数为正则化参数. 损失函数是平方损失.
实验过程: 使用不包含输出值的目标数据和包含输出值的源数据; 将目标数据按7:3划分为训练集和测试集; 用目标数据的测试集和源数据训练模型; 预测目标数据的测试集的输出值; 计算预测的平均绝对误差; 用不同的随机种子重复100次以上步骤.
我们将这100次实验结果的平均表现、标准差和最坏情况表现展示在表4中, 结果表明FedIW在平均和最坏情形下都拥有比其他方法更好的表现, 并且拥有较小的标准差. 特别地, FedIW的表现比Refer更好, 因为在帕金森数据集上的实验中, 源的样本量总和远大于目标样本量, 而FedIW可以充分有效地将源样本信息迁移到目标任务.
| 表 4 各方法在实际数据集上的实验结果 |
6 结论与展望
本文首次在疾病得分预测上提出了一种新的基于联邦学习和迁移学习的联邦重要性加权方法, 为了保证用户隐私保护, 联邦重要性加权方法在各源域中分别训练模型, 基于重要性加权将多个源域中的样本重用于目标域的预测任务, 以适应源和目标分布不同的情形并且有效地利用了各源域提供的信息, 提升了在目标域上的预测精度. 为了将分散的多源域的模型用于目标域的预测任务, 联邦重要性加权方法为每个源域根据它和目标域的分布差异构造了一个模型权重, 若源域的分布与目标域的差异较大, 则会赋予较小的模型权重, 反之赋予较大的模型权重, 从而获得一个加权模型用于目标域的预测任务, 因而联邦重要性加权方法具有突出的预测效果.
在实际数据中, 本文研究了帕金森疾病的得分预测问题. 研究结果显示, 本文的联邦重要性加权方法相比于没有考虑源域和目标域之间存在分布差异的方法、将各源域的模型用于目标域的预测任务时不考虑根据分布差异区别化采用源域模型的方法, 表现出了更加突出且稳定的预测效果.
在我国大数据医疗飞速发展的背景下, 本文的研究结果为某些疾病的自动化诊断提供了一个有效的参考方法, 更对我国医疗的发展有着深远意义.
首先, 联邦重要性加权方法得出的疾病得分预测为相关部门决定有关疾病的保险预算以及相关政策的制定提供了可靠的依据. 其次, 医院可以依据联邦重要性加权方法的预测结果提前对潜在患者进行医疗干预, 进而延缓或阻止疾病的到来, 从而提高患者的长期生活质量. 总的来说, 我们的实证研究清楚地验证了联邦重要性方法在预测疾病得分时的优异性能, 对于医院的治疗手段、治疗流程以及疾病形式研判等方面具有重要的参考意义.
| [1] |
Sagiroglu S, Sinanc D. Big data: A review. 2013 International Conference on Collaboration Technologies and Systems (CTS). San Diego: IEEE, 2013. 42–47.
|
| [2] |
Malin BA. An evaluation of the current state of genomic data privacy protection technology and a roadmap for the future. Journal of the American Medical Informatics Association, 2005, 12(1): 28-34. |
| [3] |
Madden M, Gilman M, Levy K, et al. Privacy, poverty, and big data: A matrix of vulnerabilities for poor Americans. Washington University Law Review, 2017, 95(1): 53-125. |
| [4] |
Martin KD, Murphy PE. The role of data privacy in marketing. Journal of the Academy of Marketing Science, 2017, 45(2): 135-155. DOI:10.1007/s11747-016-0495-4 |
| [5] |
Shokri R, Shmatikov V. Privacy-preserving deep learning. Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. Denver: Association for Computing Machinery, 2015. 1310–1321.
|
| [6] |
Jain P, Gyanchandani M, Khare N. Big data privacy: A technological perspective and review. Journal of Big Data, 2016, 3(1): 25. DOI:10.1186/s40537-016-0059-y |
| [7] |
Yang Q, Liu Y, Cheng Y, et al. Federated learning. Synthesis Lectures on Artificial Intelligence and Machine Learning, 2019, 13(3): 1-207. DOI:10.2200/S00960ED2V01Y201910AIM043 |
| [8] |
Yang Q, Liu Y, Chen TJ, et al. Federated machine learning: Concept and applications. ACM Transactions on Intelligent Systems and Technology, 2019, 10(2): 12. |
| [9] |
Pan SJ, Yang Q. A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359. DOI:10.1109/TKDE.2009.191 |
| [10] |
Tsanas A, Little MA, McSharry PE, et al. Accurate telemonitoring of Parkinson’s disease progression by noninvasive speech tests. IEEE Transactions on Biomedical Engineering, 2010, 57(4): 884-893. DOI:10.1109/TBME.2009.2036000 |
| [11] |
Lee J, Sun JM, Wang F, et al. Privacy-preserving patient similarity learning in a federated environment: Development and analysis. JMIR Medical Informatics, 2018, 6(2): e20. DOI:10.2196/medinform.7744 |
| [12] |
Dowlin N, Gilad-Bachrach R, Laine K, et al. CryptoNets: Applying neural networks to encrypted data with high throughput and accuracy. Proceedings of the 33rd International Conference on Machine Learning. New York: ACM, 2016. 201–210.
|
| [13] |
Bonawitz K, Ivanov V, Kreuter B, et al. Practical secure aggregation for privacy-preserving machine learning. Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security. Dallas: Association for Computing Machinery, 2017. 1175–1191.
|
| [14] |
Mohassel P, Zhang YP. SecureML: A system for scalable privacy-preserving machine learning. 2017 IEEE Symposium on Security and Privacy (SP). San Jose: IEEE, 2017. 19–38.
|
| [15] |
Smith V, Chiang CK, Sanjabi M, et al. Federated multi-task learning. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: ACM, 2017. 4427–4437.
|
| [16] |
Liu Y, Kang Y, Xing CP, et al. A secure federated transfer learning framework. IEEE Intelligent Systems, 2020, 35(4): 70-82. DOI:10.1109/MIS.2020.2988525 |
| [17] |
Cheng KW, Fan T, Jin YL, et al. SecureBoost: A lossless federated learning framework. IEEE Intelligent Systems, 2021, 36(6): 87-98. DOI:10.1109/MIS.2021.3082561 |
| [18] |
Yao Y, Doretto G. Boosting for transfer learning with multiple sources. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 1855–1862.
|
| [19] |
Raina R, Battle A, Lee H, et al. Self-taught learning: Transfer learning from unlabeled data. Proceedings of the 24th International Conference on Machine Learning. Corvalis: Association for Computing Machinery, 2007. 759–766.
|
| [20] |
Lawrence ND, Platt JC. Learning to learn with the informative vector machine. Proceedings of the 21st International Conference on Machine Learning. Banff: Association for Computing Machinery, 2004. 65.
|
| [21] |
Mihalkova L, Huynh T, Mooney RJ. Mapping and revising markov logic networks for transfer learning. Proceedings of the 22nd National Conference on Artificial Intelligence. Vancouver: AAAI Press, 2007. 608–614.
|
| [22] |
Zadrozny B. Learning and evaluating classifiers under sample selection bias. Proceedings of the 21st International Conference on Machine Learning. Banff: Association for Computing Machinery, 2004. 114.
|
| [23] |
Lipton Z, Wang YX, Smola A. Detecting and correcting for label shift with black box predictors. Proceedings of the 35th International Conference on Machine Learning. Stockholm: Proceedings of Machine Learning Research, 2018. 3122–3130.
|
| [24] |
Sugiyama M, Krauledat M, Müller KR. Covariate shift adaptation by importance weighted cross validation. The Journal of Machine Learning Research, 2007, 8: 985-1005. |
| [25] |
Huang JY, Smola AJ, Gretton A, et al. Correcting sample selection bias by unlabeled data. Proceedings of the 19th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2006. 601–608.
|
| [26] |
Sugiyama M, Suzuki T, Nakajima S, et al. Direct importance estimation for covariate shift adaptation. Annals of the Institute of Statistical Mathematics, 2008, 60(4): 699-746. DOI:10.1007/s10463-008-0197-x |
| [27] |
Kanamori T, Hido S, Sugiyama M. A least-squares approach to direct importance estimation. The Journal of Machine Learning Research, 2009, 10: 1391-1445. |
| [28] |
Nguyen XL, Wainwright MJ, Jordan MI. Estimating divergence functionals and the likelihood ratio by convex risk minimization. IEEE Transactions on Information Theory, 2010, 56(11): 5847-5861. DOI:10.1109/TIT.2010.2068870 |
| [29] |
Kouw WM, Loog M. A review of domain adaptation without target labels. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(3): 766-785. DOI:10.1109/TPAMI.2019.2945942 |
| [30] |
Shimodaira H. Improving predictive inference under covariate shift by weighting the log-likelihood function. Journal of Statistical Planning and Inference, 2000, 90(2): 227-244. DOI:10.1016/S0378-3758(00)00115-4 |
| [31] |
Bergstra J, Bardenet R, Bengio Y, et al. Algorithms for hyper-parameter optimization. Proceedings of the 24th International Conference on Neural Information Processing Systems. Red Hook: Curran Associates Inc., 2011. 2546–2554.
|
| [32] |
Nomura M, Saito Y. Efficient hyperparameter optimization under multi-source covariate shift. Proceedings of the 30th ACM International Conference on Information & Knowledge Management. New York: Association for Computing Machinery, 2021. 1376–1385.
|
| [33] |
Wistuba M, Schilling N, Schmidt-Thieme L. Learning hyperparameter optimization initializations. 2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA). Paris: IEEE, 2015. 1–10.
|
 2022, Vol. 31
2022, Vol. 31


