2. 上海海事大学 物流工程学院, 上海 201306
2. Logistics Engineering College, Shanghai Maritime University, Shanghai 201306, China
由于复杂结构建筑物的数量越来越多, 故当有突发事件发生时, 如何使人员安全高效逃离危险区域是公共安全领域亟需解决的一个核心问题. 对于建筑内的人群疏散而言, 环境因素(如出口和障碍物)将直接对其效率和安全产生重要影响. 因此, 出口处障碍物对人群疏散效率和安全的影响是一个重要研究内容.
在早期的安全管理中, 出口障碍物一般被认为会降低人群疏散效率, 但近来诸多研究表明出口障碍物在某些情况下, 反而会缩短总的人群疏散时间. Helbing等人[1]通过社会力模型模拟出人群在恐慌状态下瓶颈(出口)处的疏散行为, 结果发现在特殊位置设置一些交通设施(障碍物)可以防止出口处压力的积聚, 提高疏散效率. Zuriguel等人[2]为了研究障碍物对疏散人流的影响, 实验通过在恐慌人群流出口附近设置障碍物, 实验结果表明障碍物虽然会减慢个体速度, 但能够增加流出量. Yue等人[3]通过在房间的出口前设置障碍物, 并引入延迟系数来描述障碍物减缓行人移动的效果来研究障碍物对疏散时间的影响, 结果表明疏散时间取决于最窄的通道. 翟龙真等人[4]通过建立能够再现行人流自组织现象的模型, 反映行人不同的移动方式以及疏散的具体过程; 发现障碍物会影响行人距离安全出口的“静态危险度”, 并与出口处人群密度的“动态危险度”耦合, 使得行人自发地向“总危险度”更低的方向移动. Chen等人[5]研究发现疏散效率在一定程度上取决于障碍物的布置. 即对于带有障碍物的人群疏散, 总会存在障碍物最优位置使得疏散效率最高, 但不是所有位置都对疏散有正向影响. Li等人[6]发现当行人具有最合适的期望速度时, 疏散效率随障碍物长度的变长而降低. 当期望速度与最合适的速度相差很大时, 情况则正好相反. 同时, 研究表明当感知范围足够大时, 限制疏散时间的主要因素是行人与出口之间的距离. Garcimartín等人[7]在竞争性疏散的研究中发现障碍物会减弱集体横向冲刺的发展, 放置障碍物可以降低危险事故的发生率. Li等人[8]提出一个基于土力学来计算对称放置障碍物之间的适当间距形成的拱形结构, 得出结论: 对称放置的障碍物之间的适当间距可以缓解拥堵, 提高疏散效率; 为了研究障碍物对疏散效率的影响, Zhao等人[9]采用基于行人轨迹和Voronoi方法对行人密度的分布进行了分析, 研究发现障碍物对疏散效率的影响实际上是通过有效的空间分离显著降低拥挤区域的密度水平; Zuriguel等人[10]推测, 在没有任何障碍时空间系统会被压缩, 竞争行为会导致人群中出现高压, 此时单个出口将无法缓解整个人群承受的压力. 通过设置障碍物, 门上的压力将得到缓解, 当行人离开房间时, 障碍物会阻止快速更换产生的空位, 门上的压力会降低; 为了研究障碍物尺寸和障碍物距出口的距离对疏散的影响, Shi等[11]基于真人实验探究发现不同尺寸和位置处的障碍物有不同表现, 选择恰当的尺寸和位置可增加行人流量, 选择不当则会减少行人流量; 为了研究障碍物位置对疏散效率的影响规律, 吕惠等人[12]通过构造不同条件的疏散场景, 发现在其他条件不变的情况下, 障碍物距离出口由近到远变化, 疏散效率呈现先降低后升高再降低的趋势.
虽然已有对障碍物和人群疏散的研究, 但大都未同时分析障碍物对人群疏散效率和安全的影响. 因此, 本文建立带有障碍物的人群疏散模型, 并考虑障碍物的长度、与出口的距离和与出口中心偏离距离3个因素. 通过控制变量的方法研究其对人群疏散效率和安全的影响规律, 并分析探讨其中的物理机制. 此外, 本研究使用多目标进化算法对以上3个变量进行优化, 给出一组解集来辅助决策人员进行障碍物布局, 对建筑物中行人安全疏散、最大限度保证人员的生命财产安全具有重要的现实和理论意义.
1 模型框架 1.1 行人运动模型 1.1.1 社会力模型本研究通过使用社会力模型来建立人群疏散仿真模型. 社会力模型中假定行人会受到驱动力、吸引力和排斥力的共同作用, 基于牛顿第二定律, 将行人受到的合力转换成加速度和速度, 这个力使得行人的位置发生改变. 社会力模型的基本形式为[13]:
| {midvi(t)dt=f0i+∑j(≠i)fij+∑Wfiwf0i = miv0i(t)e0i(t)−vi(t)τifij = Aierij−dijBinij + kg(rij−dij)nij + κg(rij−dij)Δvtjitijfiw=Aieri−diwBiniw + kg(ri−diw)niw + κg(ri−diw)(−vitiw)tiwg(x)={x,x>00,x⩽0 | (1) |
其中,
排斥力
由于本研究存在障碍物, 故采用基于碰撞预测的社会力模型[14]. 该模型通过行人移动位置的变化来进行碰撞预测, 具体规则如下:
1)障碍物视为刚性介质, 行人无法穿过障碍物.
2)行人接触到障碍物时不会发生反弹, 而是沿着障碍物边界移动.
3)行人能在障碍物的一定范围内就可感知并做出反应.
在障碍物作用范围下, 社会力模型变更为如下:
| {midvi(t)dt=f0i+∑j(≠i)fij+∑Wfiw + ∑WFiwFiw = 2mi(Dib−Diw−viwΔt)(Δt)2 | (2) |
其中,
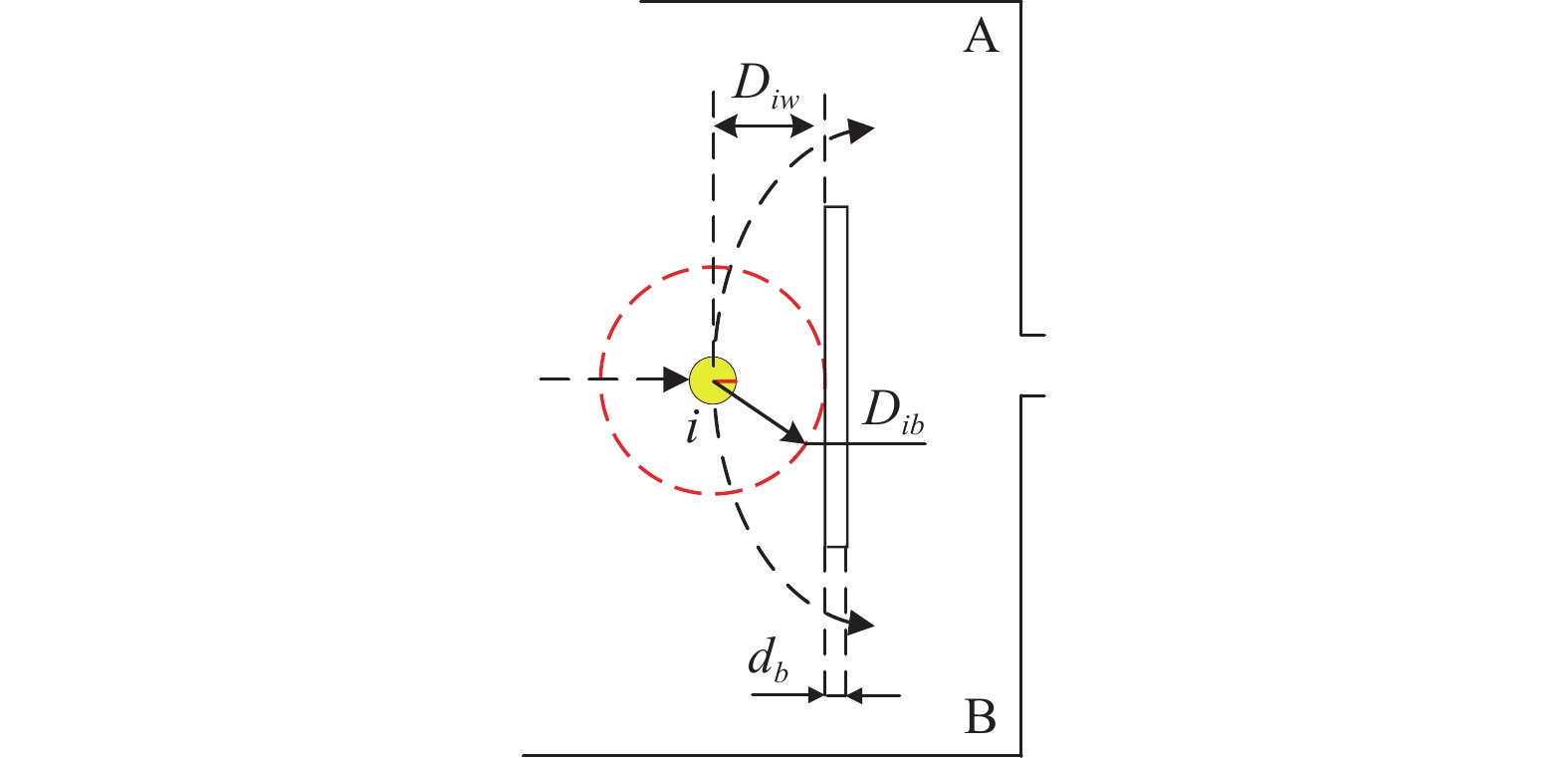
|
图 1 障碍物的作用范围 |
1.2 设有障碍物的人群疏散多目标仿真优化模型 1.2.1 优化目标
根据第1.1节行人运动模型, 本文首先建立一个带有障碍物的室内人群疏散模型. 需要说明的是, 第1.1节的社会力模型被用来模拟室内人群疏散的动力学过程. 考虑到对于设有障碍物的室内人群疏散, 以往研究大都只考虑疏散时间, 而没有同时考虑疏散效率和疏散安全[15, 16]. 因此, 本文将疏散时间
| {SA=max | (3) |
其中,
| 表 1 拥挤状态等级设置 |
部分研究表明, 在设有障碍物的建筑体内, 人群疏散效率和疏散安全是一个多目标优化问题. 因此, 本文的目标函数设置如下:
| \min F\left( x \right) = \left( {{S_T}\left( x \right), {S_A}\left( x \right)} \right) | (4) |
其中,
为求解以上人群疏散多目标优化问题, 本文采用一种知名的多目标进化算法(non-dominated sorting genetic algorithm, the third version, NSGA-III)[17]来对室内障碍物的布局进行优化. 相比于另外一个知名多目标进化算法NSGA-II, 它主要引入参考点机制, 从而可以对于那些非支配解并且接近参考点的种群个体进行保留. 因此, 对于求解3个及其以上目标的优化问题, NSGA-III具有更好的收敛性和多样性.
根据第1.2.1节的优化目标(即疏散时间和疏散安全)和由第1.1.2节的社会力模型构建的室内人群疏散模型(优化变量为障碍物长度、与出口距离、偏离出口中心距离), 使用NSGA-III来对其进行优化. 具体操作步骤如下:
1)初始化: 设置算法参数和随机生成种群规模为
2)通过使用变异和交叉算子生成大小为
3)利用快速非支配排序法将
4)基于参考点法选择优先级高的非支配子集保留到下一代.
5)判断算法是否满足停止准则, 若满足则输出结果; 否则返回第2)步.
基于以上步骤, 其优化流程见图2. 从图2可知, 首先是设置NSGA-III算法的参数和生成初始种群, 然后对种群进行交叉和变异操作, 并将它们(即障碍物长度、障碍物与出口距离、障碍物偏离出口中心距离)输入到人群疏散模型中; 接着, 将人群疏散模型得到的目标(即疏散时间和疏散安全)快速非支配排序, 并通过参考点法进行选择; 最后, 判断算法是否满足终止准则. 如果是, 那么算法停止; 否则, 继续重复以上交叉、变异、选择等操作.
2 实验结果与分析 2.1 实验场景与参数设置出口是发生紧急情况时人员进行疏散的重要通道, 但在紧急情况下人员可能会在出口形成聚集, 造成出口堵塞, 从而影响疏散效率和疏散安全. 因此, 大型建筑和设施内会在出口附近放置障碍物, 起到分流和缓冲行人速度的作用, 达到疏散过程综合最优的目的. 在本实验中, 将从单因素的角度来对障碍物布局进行分析, 即分别对障碍物的长度、障碍物与出口距离和障碍物与出口中心的偏移距离对人群疏散效率和安全的影响进行分析.
本文实验场景设置为18 m×12 m的房间, 出口宽度设置为1.5 m[18]. 实验人员的基本参数设置如下: 直径为0.6 m, 质量为80 kg, 期望速度为1.5 m/s, 反应时间τ=0.5 s; 人群数量N=100且均匀分布在空间左侧12 m×12 m的区域, 具体如图3所示. 社会力模型的参数中, 排斥力A=2000 N; 发生排斥的距离B=0.08 m; 滑动摩擦系数
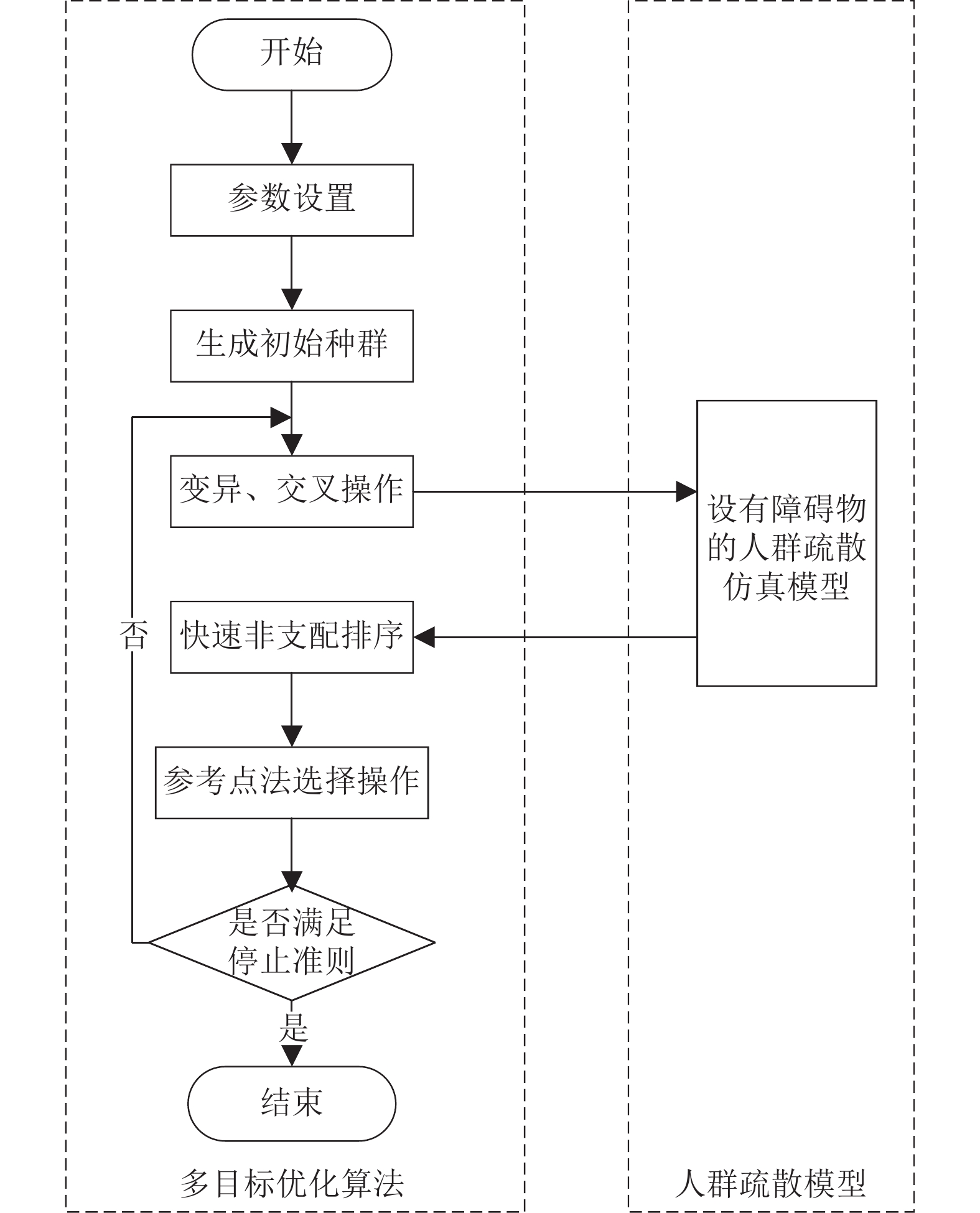
|
图 2 带有障碍物的人群疏散多目标优化流程图 |
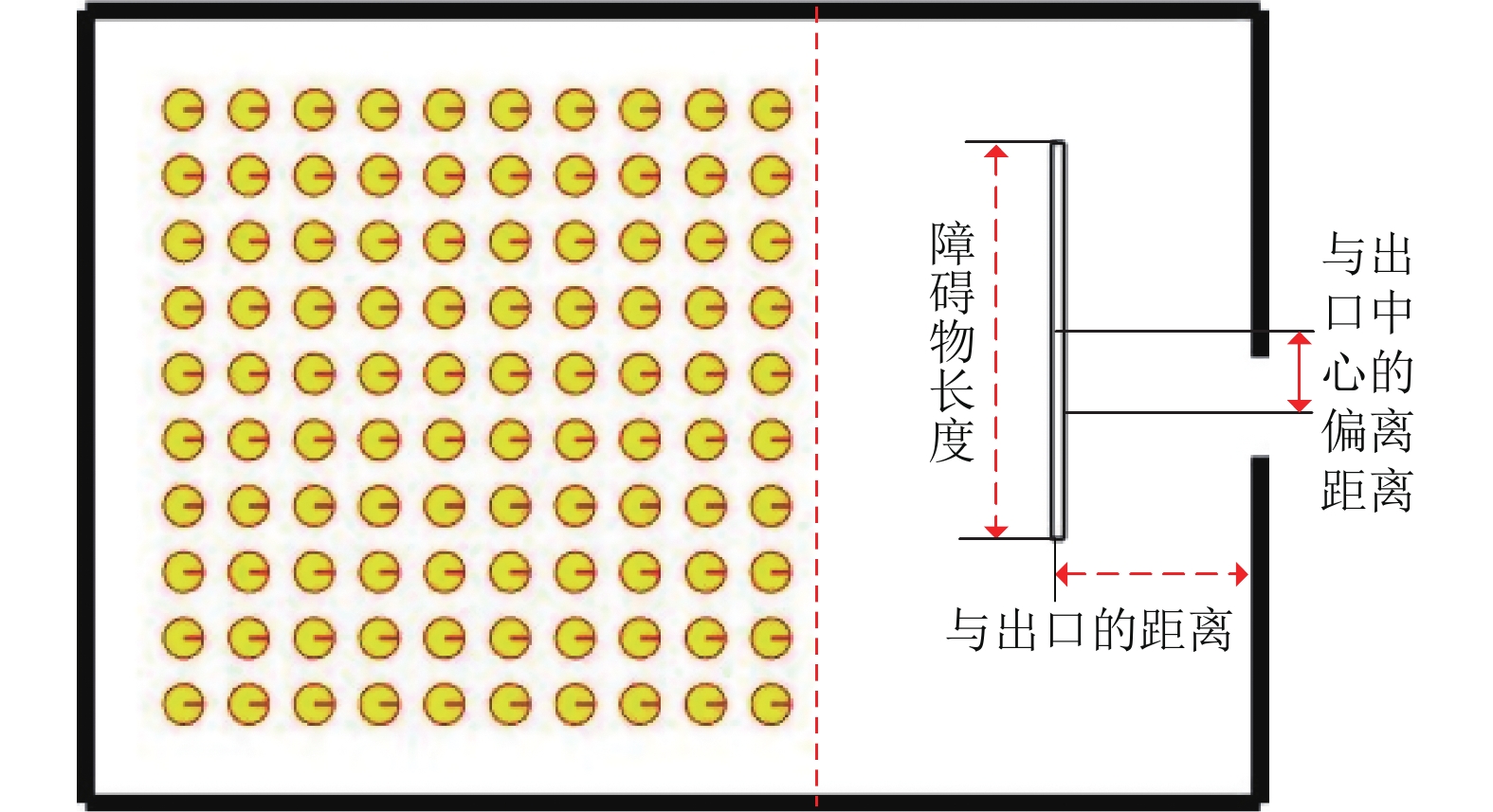
|
图 3 初始参数与障碍物设置 |
2.2 障碍物长度对疏散效率和安全的影响
根据建立的人群疏散模型, 本节实验将对障碍物长度对疏散效率和安全的影响进行分析. 在实验中, 除了障碍物长度发生改变外, 其他模型参数均保持不变. 障碍物长度取值范围为[1, 6], 间隔为0.5 m. 在固定障碍物长度下, 每次实验独立运行20次, 并取疏散效率和安全的平均值作为目标值. 障碍物长度与疏散安全和效率的关系分别见图4(a)和图4(b). 从图4(a)中可以看出, 人群疏散风险会随着障碍物的长度增加而降低. 其主要原因是障碍物可以起到人群分流和减缓人群疏散速度, 进而减少人群集聚. 图4(b)显示人群疏散时间会随着障碍物长度增加而变高. 这是因为随着障碍物长度的增加, 人群疏散速度会被减缓, 故疏散时间会被延长. 此外, 从图4可以看出, 在疏散效率和安全方面, 它们是两个不可调和的目标, 即随着障碍物长度增加, 人群疏散效率会被降低, 而疏散安全会提高. 因此, 障碍物长度需依据实际情况进行设置.

|
图 4 障碍物长度的变化对疏散安全和效率的影响 |
2.3 障碍物与出口距离对疏散效率和安全的影响
本节实验主要研究障碍物与门的距离对疏散效率和安全的影响. 在实验中, 除了障碍物与门的距离发生改变外, 其他模型参数均保持不变. 障碍物与门的距离取值范围为[1, 4.5], 间隔为0.5 m. 在固定障碍物与门的距离下, 每次实验独立运行20次, 并以疏散效率和安全的平均值作为目标值. 随着障碍物与门距离的变化, 人群疏散效率和安全的变化趋势如图5(a)和图5(b)所示. 从图5(a)中可以看出, 障碍物与门的距离从1 m向3 m增加的过程中人群疏散风险下降明显, 之后呈波动趋势. 其主要原因是障碍物将整个疏散流程的压力分散到了整个空间内, 使得出口门前的压力降低, 减轻出口堵塞. 图5(b)显示人群疏散时间会随着障碍物与门的距离增加而降低. 在障碍物与门的距离从1 m向3 m增加的过程中, 疏散时间变化幅度巨大, 从3 min降到了1.83 min, 之后疏散时间逐渐稳定在1.83 min, 说明障碍物与门的距离在1−3 m之间变化时, 对疏散时间的影响比较敏感. 这是因为障碍物与门之间的区域会影响人与人之间的安全距离, 当安全距离增加时, 人群可以受到较少的压力迅速离开房间, 故疏散时间会减少.

|
图 5 障碍物与门距离的变化对疏散安全和效率的影响 |
2.4 障碍物与出口偏离距离对疏散效率和安全的影响
本实验分析了障碍物与出口中心的偏移距离对疏散效率和疏散风险的影响. 在实验中除了障碍物与出口中心的偏移距离发生改变外, 其他模型参数均保持不变. 障碍物偏移范围取值为[0, 2.5], 本文取正向偏移研究, 间隔为0.5 m, 即偏移值为0时, 障碍物中心正对出口. 在固定障碍物与出口中心的便宜距离下, 每次实验独立运行20次, 并以疏散效率和疏散安全的平均值作为目标值. 障碍物与中心偏离的距离与疏散效率和安全的关系分别见图6(a)和图6(b). 随着障碍物与中心的偏离程度增加, 人群风险变化如图6(a)所示. 可以看出, 障碍物从正对着出口向上或下降逐渐偏移的过程中, 人群疏散风险呈二次曲线上升或下降. 这是因为障碍物与门偏离距离越来越大, 障碍物与墙之间形成的空间会发生改变, 导致在人群数量不变的情况下, 空间变小的一侧周围环境对人群的压力增加, 使得疏散风险提高. 从图6(b)中可以看出, 人群疏散时间随着障碍物与中心的偏移变化不大. 说明力在合适的长度和与门的距离固定的条件下, 改变障碍物与出口中心偏离距离主要影响了人群疏散的风险.

|
图 6 障碍物与门中心偏离程度对疏散安全和效率的影响 |
3 基于多目标进化算法的障碍物布局优化 3.1 多目标优化参数设置
在本实验中, 以疏散效率和安全为目标(见式(4)), 使用多目标进化算法NSGA-III对障碍物布局进行研究. 疏散模型参数设置同第2.1节. 多目标优化算法采用实数编码方式, 染色体长度等于决策变量的个数, 根据障碍物布局的不同, 取障碍物位置的坐标作为染色体的组成部分. NSGA-III参数设置如表2所示.
| 表 2 参数设置 |
3.2 实验结果分析
在一定实验条件下, 障碍物的布局会使得疏散效率和疏散安全这两个目标相互冲突. 实验所得帕累托前沿(Pareto front, PF)如图7所示. 从图7中可以看出, 疏散效率和疏散安全有反向关系. 因此, 针对障碍物布局, 决策者无法使得疏散效率和疏散安全同时达到最佳, 而是需要在这两个目标中进行平衡.

|
图 7 疏散时间与疏散风险关系图 |
根据建立的多目标进化算法的障碍物布局优化模型, 本节实验选取图7中人群疏散效率最高且安全最低时与疏散效率最小且安全最高时障碍物的位置进行研究, 障碍物布局如图8(a)、图8(b)所示.
在图8(a)中, 障碍物长度为1.8 m, 障碍物与出口的距离为2.3 m, 障碍物正对门中心. 此时, 人群疏散效率最高、安全最低. 这是因为障碍物减缓出口处的成拱现象, 从而减轻人群聚集对出口造成的压力, 使得疏散效率提高. 但由于障碍物长度较短, 对人群疏散的作用有限, 所以该障碍物布局没有减少人群聚集现象来降低人群疏散风险.

|
图 8 选择的两个障碍物位置 |
在图8(b)中, 障碍物长度为4.7 m, 障碍物与出口的距离为2.8 m, 障碍物正对门中心. 此时, 人群疏散效率最低、安全最高. 对于安全性好的原因在于: 较长的障碍物长度可以起到人群分流和避免人群拥挤, 但是由于障碍物长度较长, 使得人群疏散距离变长, 故使得疏散效率变低.
从以上实验结果可以看出, 在一定条件下, 疏散效率和安全是两个冲突的目标. 因此, 决策者需根据实际情况来选择障碍物的长度和位置, 从而使得人群疏散和安全之间达到平衡.
4 结束语为研究障碍物对人群疏散效率和安全的影响, 建立基于社会力的行人疏散仿真模型. 通过单因素(即障碍物长度、障碍物与出口距离、障碍物与出口中心偏离距离)对疏散效率和疏散安全的影响进行分析. 同时, 以疏散时间与疏散风险最小化为目标, 使用多目标进化算法对障碍物长度和位置进行优化. 实验结论如下:
(1)在一定条件下, 障碍物长度与疏散效率呈正向关系; 而与疏散安全呈反向关系. 障碍物与门的距离与疏散安全与疏散效率均呈负向关系. 障碍物与门的偏离程度与疏散效率与疏散安全均呈正向关系. (2)在一定实验条件下, 疏散效率和疏散安全可能是两个不可调和(即冲突)的目标. 因此, 障碍物的长度和位置需依据实际情况来进行设定, 从而可以兼顾疏散效率和安全.
| [1] |
Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic. Nature, 2000, 407(6803): 487-490. DOI:10.1038/35035023 |
| [2] |
Zuriguel I, Janda A, Garcimartín A, et al. Silo clogging reduction by the presence of an obstacle. Physical Review Letters, 2011, 107(27): 278001. DOI:10.1103/PhysRevLett.107.278001 |
| [3] |
Yue H, Zhang JY, Chen WX, et al. Simulation of the influence of spatial obstacles on evacuation pedestrian flow in walking facilities. Physica A: Statistical Mechanics and its Applications, 2021, 571: 125844. DOI:10.1016/j.physa.2021.125844 |
| [4] |
翟龙真, 冯绍红, 文哲, 等. 基于模糊规则和BFS算法的行人疏散模型研究. 中国安全生产科学技术, 2021, 17(3): 5-11. DOI:10.11731/j.issn.1673-193x.2021.03.001 |
| [5] |
Chen L, Zheng Q, Li K, et al. Emergency evacuation from multi-exits rooms in the presence of obstacles. Physica Scripta, 2021, 96(11): 115208. DOI:10.1088/1402-4896/ac119a |
| [6] |
Li Q, Gao Y, Chen L, et al. Emergency evacuation with incomplete information in the presence of obstacles. Physica A: Statistical Mechanics and its Applications, 2019, 533: 122068. DOI:10.1016/j.physa.2019.122068 |
| [7] |
Garcimartín A, Maza D, Pastor JM, et al. Redefining the role of obstacles in pedestrian evacuation. New Journal of Physics, 2018, 20: 123025. DOI:10.1088/1367-2630/aaf4ca |
| [8] |
Li L, Liu H, Han YB. Arch formation-based congestion alleviation for crowd evacuation. Transportation Research Part C: Emerging Technologies, 2019, 100: 88-106. DOI:10.1016/j.trc.2019.01.015 |
| [9] |
Zhao YX, Lu TT, Fu LB, et al. Experimental verification of escape efficiency enhancement by the presence of obstacles. Safety Science, 2020, 122: 104517. DOI:10.1016/j.ssci.2019.104517 |
| [10] |
Zuriguel I, Echeverría I, Maza D, et al. Contact forces and dynamics of pedestrians evacuating a room: The column effect. Safety Science, 2020, 121: 394-402. DOI:10.1016/j.ssci.2019.09.014 |
| [11] |
Shi XM, Ye ZR, Shiwakoti N, et al. Examining effect of architectural adjustment on pedestrian crowd flow at bottleneck. Physica A: Statistical Mechanics and its Applications, 2019, 522: 350-364. DOI:10.1016/j.physa.2019.01.086 |
| [12] |
吕惠, 刘向元, 王英龙, 等. 人群疏散出口障碍物对疏散效率的影响规律研究. 中国安全生产科学技术, 2020, 16(1): 141-145. DOI:10.11731/j.issn.1673-193x.2020.01.023 |
| [13] |
Helbing D, Molnár P. Social force model for pedestrian dynamics. Physical Review E, 1995, 51(5): 4282-4286. DOI:10.1103/PhysRevE.51.4282 |
| [14] |
陈天德, 黄炎焱, 王振华. 基于碰撞预测的无碰撞航路规划. 系统工程理论与实践, 2020, 40(4): 1057-1068. DOI:10.12011/1000-6788-2018-1790-12 |
| [15] |
孙金龙, 王爽, 陈文瑛. 基于人群恐慌的地铁应急疏散仿真研究. 安全, 2017, 38(3): 8-11. DOI:10.3969/j.issn.1002-3631.2017.03.003 |
| [16] |
丁男哲, 刘婷婷, 刘箴, 等. 社会力模型中恐慌度概念的分析和改进. 计算机应用, 2021, 41(8): 2460-2465. DOI:10.11772/j.issn.1001-9081.2020101550 |
| [17] |
Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535 |
| [18] |
韩雨烔, 王维莉, 范勤勤, 等. 遗传算法与行人疏散模型结合的建筑出口优化. 计算机工程与应用, 2020, 56(13): 254-261. DOI:10.3778/j.issn.1002-8331.1903-0261 |
 2022, Vol. 31
2022, Vol. 31



