1 引言

白内障 (cataract) 是一种常见的致盲性和导致视觉损害的眼病, 其发病与多种因素有关, 如年龄、遗传和局部营养障碍. 根据世界卫生组织 (World Health Organization, WHO) 的统计数据, 到2025年白内障致盲人数将达到4 000万. 根据晶状体结构出现混浊的位置, 白内障通常可分为3种类型: 后囊性白内障 (posterior subcapsular cataract, PSC)、皮质性白内障 (cortical cataract, CC) 和核性白内障 (nuclear cataract, NC). 其中, 皮质性白内障是一种最常见的白内障类型, 其症状为晶状体皮质区域 (皮层) 出现混浊^[1]. 根据实际临床诊断需求和晶状体混浊分类系统 (lens opacities classi-fication system III, LOCS III), 皮质性白内障的发展大致分为3个阶段: 正常、轻度和重度^{[2, 3]}. 正常是指皮质区域没有出现混浊症状; 轻度是指皮质区域出现混浊症状但不明显, 重度是指皮质区域的混浊症状明显且视力下降严重, 其中轻度、重度分别对应LOCS III分级标准下皮质性白内障级别C1–C2、C3–C5^[4]. 在临床上, 轻度皮质性白内障患者可以采用点滴药物来延缓皮质性白内障混浊发展进度; 重度皮质性白内障患者需要接受临床观察或手术治疗.

在临床诊断过程中, 眼科医生通常采用不同模态的眼科图像诊断患者不同类型的白内障严重程度. 这种诊断方法具有较大的主观性, 且主要与医生经验和专业知识有关, 并且容易出错. 如何提高眼科医生白内障诊断的精准性是一个亟需解决的问题和挑战. Xu等人在裂隙灯图像下利用群稀疏回归算法进行核性白内障分类, 并在ACHIKO-NC数据集下准确率达到了85.2%^[5]. 李建强等人基于眼底图像进行白内障筛查并取得了不错的筛查结果^[6]. Zhang等人在后反光照图像 (anterior retro-illumination image) 下提出了一个后囊性白内障筛查框架, 由分水岭算法和马尔科夫随机场算法组成, 筛查结果的敏感度达到了90.1%^[7]. 范文澜在弥散光源图像下提取了纹理特征并用于皮质性白内障自动分类, 在一个临床数据集上取得了86.36%的准确率^[8].

眼前节光学相干断层成像 (anterior segment optical coherence tomography, AS-OCT) 是一种OCT成像, 其具有高分辨率、检查速度快、非接触性、可重复性高、高探测灵敏度等特点^[9]. 相较于其他眼科图像, 它能获取眼睛完整的前节结构信息, 包括晶状体结构. 近年来, 眼科医生已经广泛使用AS-OCT图像诊断眼前节疾病, 如青光眼和角膜疾病^[10]. 在白内障临床研究中, Wong等人采用使用斯皮尔曼相关系数方法 (Spearman’s rank correlation coefficient) 分析在AS-OCT图像下像素均值特征与白内障严重程度之间相关性, 医学统计结果显示两者存在较强的相关性^[11]. Wang等人同样在AS-OCT图像下研究像素特征和软硬核性白内障之间相关性, 并也通过斯皮尔曼相关系数方法分析两者相关性, 得到了类似的统计结果^[12]. 这些临床基础研究为基于AS-OCT图像下自动白内障分类工作提供了临床支撑. Zhang等人采用卷积神经网络模型在AS-OCT图像下实现核性白内障严重程度分类, 但分类的准确率没达到60%^[13]. 章晓庆等人基于晶状体核性区域从AS-OCT图像中提取了18个像素特征, 并利用5个经典的机器学习算法进行分类, 最好的分类准确率达到75.53%^[14].

与弥散光源图像相比, AS-OCT图像可以清楚地观察到皮质区域, 但目前尚未有基于AS-OCT图像进行皮质性白内障自动分类的相关研究. 为此, 本文首次提出了一个在AS-OCT图像下的自动皮质性白内障严重程度分类框架, 由图像预处理、特征提取、特征筛选和皮质性白内障分类4个部分组成. 在预处理部分, 本文采用反光区域去除与对比度增强方法增强不同严重程度皮质性白内障的AS-OCT图像的差异性. 然后是特征提取部分, 本文利用灰度共生矩阵 (grey level co-occurrence matrix, GLCM)、灰度区域大小矩阵 (grey level size zone matrix, GLSZM) 和邻域灰度差矩阵 (neighborhood gray tone difference matrix, NGTDM)方法提取了22个特征. 紧接着是特征筛选部分, 本文采用斯皮尔曼相关系数方法进行特征重要性分析并筛选特征. 最后本文采用了线性支持向量机 (linear support vector machine, linear-SVM) 在筛选的特征上进行皮质性白内障自动分类. 在一个临床AS-OCT数据集上的分类结果表明, 本文提出的分类框架取得了86.04%的准确率和86.18%的召回率, 与先进的深度学习方法的分类性能接近.

2 AS-OCT数据集介绍

本文使用的AS-OCT数据集来自本地某三甲医院, 数据采集设备是日本Tomey公司的CASIA2眼前节OCT仪器. 该数据集包含355个受试者 (平均年龄61.30岁), 来自于195个白内障患者和160个正常人, 其中左眼和右眼图像数量分别为251和228. AS-OCT图像是通过360度环形扫描方式获取到的, 每个受试者从不同角度采集了16张图像, 由于眼睑干扰, 本文在有经验的眼科医生的帮助下删除了不符合要求的图像, 最终得到了3 726张可用的AS-OCT图像.

由于没有基于AS-OCT图像的白内障分类标准. 所有受试者都拍摄了弥散光源图像和AS-OCT图像, AS-OCT图像的皮质性白内障标记是通过弥散光源图像映射得到的, 其中, 3名经验丰富的眼科医生按照皮质性白内障的严重程度对每个受试者的弥散光源图像进行标注, 保证了本文数据的标记质量.

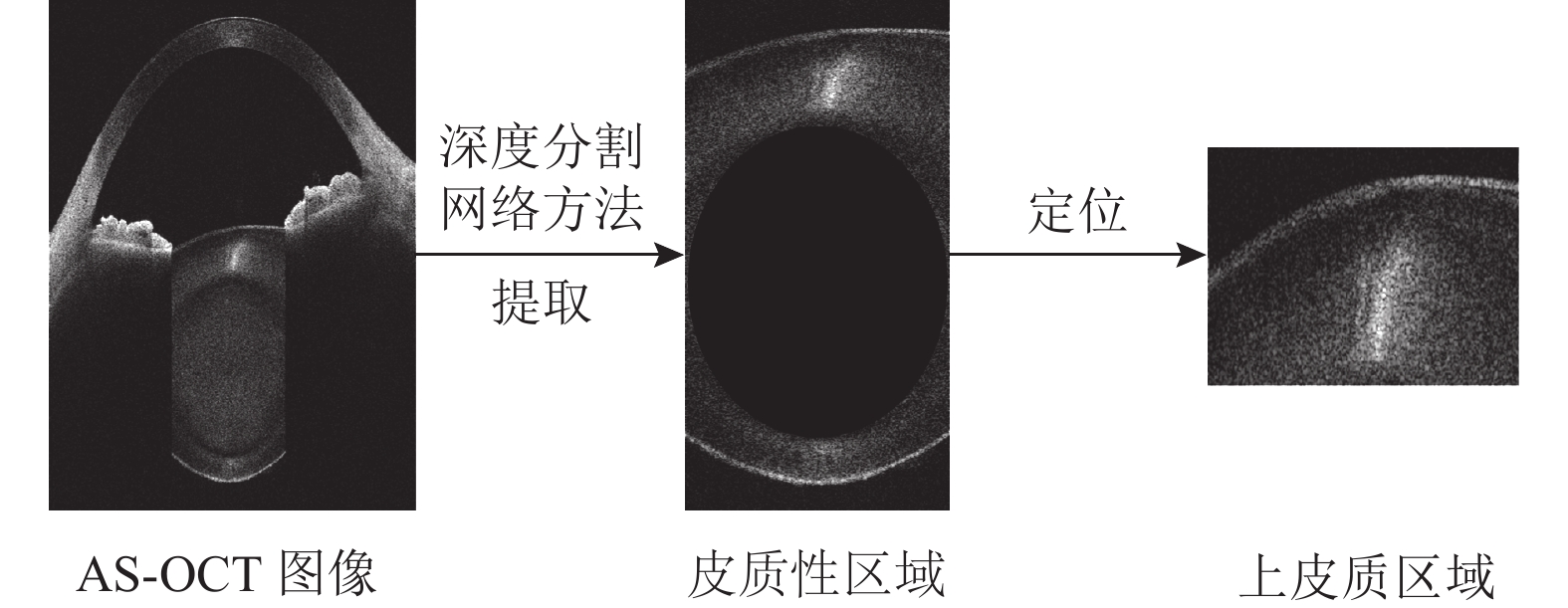
AS-OCT图像能获取整个前节结构, 其中只有皮质区域与皮质性白内障有关. 在临床诊断中, 眼科医生通常基于上皮质区域确定患者的皮质白内障级别^[15]. 因此, 本文只提取上皮质区域并通过两个步骤实现: 皮质区域提取和上皮质区域提取, 如图1所示. 在皮质区域提取步骤中, 本文首先利用深度分割网络U-Net^[16]得到整个皮质区域; 然后本文通过灰度值检测定位核性区域顶端, 得到上皮质区域.

参考文献 [10] 中的数据集划分方法, 本文将AS-OCT图像以眼睛为单位分为训练集和测试集, 保证了同一只眼睛的图像数据不会同时被分到训练集和测试集. 表1所示为训练集和测试集的不同皮质性白内障严重程度的AS-OCT图像分布. 在训练集中, 正常、轻度皮质性白内障和重度皮质性白内障的AS-OCT图像分别有590张、1 219张和964张. 在测试集中, 正常、轻度皮质性白内障和重度皮质性白内障的AS-OCT图像分别有284张、313张和356张.

3 自动皮质白内障分类框架

如图2所示, 本文提出的自动皮质性白内障分类框架可分为4个部分: 图像预处理、特征提取、特征筛选和皮质性白内障分类.

3.1 图像预处理

在拍摄受试者的AS-OCT图像时, 由于受拍摄光线和成像原理影响, 皮质区域的中间部分出现高反光区域, 从而导致不同严重程度的皮质性白内障图像之间的肉眼差异性较小. 为了提高皮质性白内障的分类效果, 本文采用反光区域去除与对比度增强两种方法对皮质区域的AS-OCT图像进行预处理^[17], 具体处理步骤如下: 本文首先将像素大小为196×105的中间高反光区域去除, 将剩下的左上皮质与右上皮质进行拼接; 为了进一步降低反光区域对分类结果的影响, 本文采用式(1)对图像中每个像素值 $pixel[i, j]$ 进行处理, 增强像素对比度:

$ pixel[i, j] \leftarrow pixel[i, j] \times 1.5 + 30 $

(1)

图3为不同严重程度皮质性白内障的AS-OCT图像预处理前后的结果对比分析. 可以看到, 未经过预处理的晶状体皮质区域的病理区域的纹理特征并不明显 (图3左侧), 受反光区域的影响很大. 经过反光区域去除和对比度增强后, 不同严重程度皮质性白内障的混浊度差异性明显增强, 重度皮质性白内障两侧的病理区域尤其明显 (图3右侧). 本文将会在下文具体讨论AS-OCT图像预处理前后的皮质性白内障分类结果, 以验证所提出的图像增强方法的有效性.

3.2 特征提取

随着皮质性白内障严重等级的提升, AS-OCT图像的白色条状病理区域面积增加, 具有更明显的纹理特征. 因此, 参考文献[18-20], 本文采用灰度共生矩阵、灰度区域大小矩阵和邻域灰度差矩阵方法基于AS-OCT图像从皮质区域提取了22个纹理特征.

3.2.1 灰度共生矩阵的特征

灰度共生矩阵通常用于描述灰度的空间相关特性, 也反映了相近亮度像素的位置分布规律, 它可以用一个大小 ${N_g} \times {N_g}$ 的矩阵表示. ${N_g}$ 代表该图像的最大灰度值的级数, 本文选择 ${N_g} = 16$ . 灰度共生矩阵不能直接作为特征, 本文基于它提取了6个常见的纹理特征: 能量、熵、同质性、相关性、相异性和逆差距, 这些特征可采用以下计算公式表达:

(1)能量 (energy): 可用于描述AS-OCT图像的纹理粗细程度以及灰度分布均匀程度:

$ energy = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_g}} {(P(} } i, j){)^2} $

(2)

其中, P(i,j)表示标准化的灰度共生矩阵.

(2)熵 (entropy): 描述纹理的无序程度. 熵值越大, 说明AS-OCT图像的灰度分布越复杂:

$ entropy = - \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_g}} P } (i, j){\log _2}[P(i, j)] $

(3)

(3)同质性 (homogeneity): 描述纹理的规则程度:

$ homogeneity = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_g}} {\frac{{P(i, j)}}{{1 + |i - j|}}} } $

(4)

(4)相关性 (correlation): 描述灰度共生矩阵元素在行或列方向上的相似程度, 可反映图像的局部相关性, 值越大, 相关性越大:

$ correlation = \frac{{\displaystyle\sum\limits_{i = 1}^{{N_g}} {\displaystyle\sum\limits_{j = 1}^{{N_g}} i } jP(i, j) - {\mu _x}{\mu _y}}}{{{\sigma _x}{\sigma _y}}} $

(5)

其中, $\;{\mu _x} = \displaystyle\sum\limits_{i = 1}^{{N_g}} {\displaystyle\sum\limits_{j = 1}^{{N_g}} i } P(i, j), {\text{ }}{\mu _y} = \displaystyle\sum\limits_{i = 1}^{{N_g}} {\displaystyle\sum\limits_{j = 1}^{{N_g}} j } P(i, j), {\text{ }}{\sigma _x} = \displaystyle\sum\limits_{i = 1}^{{N_g}} {\displaystyle\sum\limits_{j = 1}^{{N_g}} }$ $P (i, j){\left( {i - {\mu _x}} \right)^2}, {\text{ }}{\sigma _y} = \displaystyle\sum\limits_{i = 1}^{{N_g}} {\displaystyle\sum\limits_{j = 1}^{{N_g}} P } (i, j){\left( {i - {\mu _y}} \right)^2}.$

(5)相异性 (dissimilarity): 描述纹理的清晰程度:

$ dissimilarity = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_g}} } |i - j|P(i, j) $

(6)

(6)逆差距 (inverse difference moment, IDM): 描述纹理的规则程度, 度量纹理局部变化:

$ IDM = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_g}} {\frac{{P(i, j)}}{{1 + {{(i - j)}^2}}}} } $

(7)

3.2.2 灰度区域大小矩阵的特征

灰度区域大小矩阵反映了图像具有相同灰度等级像素的分布特性, 如大小和个数. 本文考虑了八连通性, 即每一个像素都有8个相邻像素, 并使用 $p(i, j)$ 代表图像灰度值为 $i$ 、连通区域面积为 $j$ 的面积数量. 本文基于灰度区域大小矩阵总共提取了11个特征.

(1)小区域偏好性 (small zone emphasis, SZE): 描述了纹理的精细程度, 数值越大则说明小区域越多, 图像纹理更精细:

$ {\textit{SZE}} = \sum\limits_{j = 1}^{{N_{\textit{z}}}} {\frac{{{p_{\textit{z}}}}}{{{j^2}}}} $

(8)

其中, $ {N_{\textit{z}}} $ 代表最大连通区域的面积大小, $ {p_{\textit{z}}} $ 代表连通区域面积为 $ j $ 的面积数量, 计算公式为 $ {p_{\textit{z}}} =\displaystyle \sum\limits_{i = 1}^{{N_g}} p (i, j) $ .

(2)大区域偏好性 (large zone emphasis, LZE): 描述了纹理的粗糙程度, 数值越大则说明大区域越多, 图像纹理更粗糙:

$ LZE = \sum\limits_{j = 1}^{{N_{\textit{z}}}} {{j^2}} {p_{\textit{z}}} $

(9)

(3)区域百分比 (zone percentage, ZP): 连通区域像素数量占图像总像素数量的比例:

$ ZP = \frac{{{N_s}}}{{{N_p}}} $

(10)

其中, $ {N_s} $ 为连通区域数量 $\displaystyle\sum\limits_{i = 1}^{{N_g}} {\displaystyle\sum\limits_{j = 1}^{{N_{\textit{z}}}} p } (i, j) $ ; $ {N_p} $ 为图像中的像素数量.

(4)低灰度区域偏好性 (low grey level zone emphasis, LGZE): 描述了图像的低灰度区域在图像中占的比例, 其值越高说明低灰度区域在图像中的比例更小:

$ LGZE = \sum\limits_{i = 1}^{{N_g}} {\frac{{{p_g}}}{{{i^2}}}} $

(11)

其中, $ {p_g} $ 为联通区域灰度值为 $ i $ 的面积数量: $ {p_g} = \displaystyle\sum\limits_{i = 1}^{{N_{\textit{z}}}} p (i, j) $ .

(5)高灰度区域偏好性 (high grey level zone emphasis, HGZE): 描述了图像的高灰度区域在图像中占的比例, 值越高说明高灰度区域在图像中的比例更大:

$ HGZE = \sum\limits_{i = 1}^{{N_g}} {{i^2}} {p_g} $

(12)

(6)小面积低灰度级偏好性 (small zone low grey level emphasis,SZLGE): 描述了低灰度值的小面积区域在图像中所占的比例:

$ {\textit{SZLGE}} = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_{\textit{z}}}} {\frac{{p(i, j)}}{{{i^2}{j^2}}}} } $

(13)

(7)小面积高灰度级偏好性 (small zone high grey level emphasis,SZHGE): 描述了高灰度值的小面积区域在GLSZM图像中所占的比例:

$ {\textit{SZHGE}} = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_{\textit{z}}}} {\frac{{p(i, j){i^2}}}{{{j^2}}}} } $

(14)

(8)大面积低灰度级偏好性(large zone low grey level emphasis, LZLGE): 描述了低灰度值的大面积区域在图像中所占的比例:

$ LZLGE = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_{\textit{z}}}} {\frac{{p(i, j){j^2}}}{{{i^2}}}} } $

(15)

(9)大面积高灰度级偏好性(large zone high grey level emphasis, LZHGE): 描述了高灰度值的大面积区域在图像中所占的比例:

$ LZHGE = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_{\textit{z}}}} p (i, j){j^2}{i^2}} $

(16)

(10)灰度方差 (grey level variance, GLV): 描述了灰度等级计算的区域方差:

$ GLV = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_{\textit{z}}}} {{{\left( {i - {\mu _g}} \right)}^2}} } p(i, j) $

(17)

其中, $ \;{\mu _g} $ 为区域灰度值均值 $ \displaystyle\sum\limits_{i = 1}^{{N_g}} {\displaystyle\sum\limits_{j = 1}^{{N_{\textit{z}}}} i } p(i, j) $ .

(11)区域大小方差 (zone-size variance, ZSV): 描述了面积大小不同区域的灰度方差:

$ {\textit{ZSV}} = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_{\textit{z}}}} {{{\left( {j - {\mu _{\textit{z}}}} \right)}^2}} } p(i, j) $

(18)

其中, $\; {\mu _{\textit{z}}} $ 为面积大小不同区域的灰度均值 $\;{\mu _{\textit{z}}} = \displaystyle\sum\limits_{i = 1}^{{N_g}} {\displaystyle\sum\limits_{j = 1}^{{N_{\textit{z}}}} j } p(i, j)$ .

3.2.3 邻域灰度差矩阵的特征

邻域灰度差矩阵用于描述像素灰度值与邻域灰度均值间的相关性. 本文用 $ s(i) $ 表示图像灰度等级为 $ i $ 的像素与它距离为 $ d $ 的像素灰度均值的总和并设置 $ d $ 为1, 其中 $ s(i) $ 可通过式(19)表达:

$ s(i) = \left\{ {\begin{array}{*{20}{l}} {\displaystyle\sum\limits_{{n_i}} {\left| {i - {A_i}} \right|} ,\; {{n_i} > 0} } \\ {0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; {{n_i} \leqslant 0} } \end{array} } \right. $

(19)

其中, $ {A_i} $ 表示该像素相邻像素的灰度值.

本文提取了5个NGTDM的统计纹理特征:

(1)粗糙度 (coarseness): 描述中间像素与邻域间的平均差异:

$ coarseness = {\left[ {\varepsilon + \sum\limits_{{{n}} = 1}^{{{{N}}_{{g}}}} {{p}} ({{i}}){{s}}({{i}})} \right]^{ - 1}} $

(20)

其中, $ {N_g} $ 代表图像中最高的灰度等级, $ \varepsilon $ 是防止coarseness无穷大的一个极小值.

(2)对比度 (contrast, ct): 表示图像强度变化和整体灰度级的动态范围:

$ \left. {ct = \left( {\frac{1}{{{N_p}(1 - {N_p})}}} \right)\sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_g}} p } (i)p(j){{(i - j)}^2}} \right)\left( {\frac{1}{N}\sum\limits_{i = 1}^{{N_g}} s (i)} \right) $

(21)

其中, $ {N_p} $ 代表图像中灰度等级的数量; $ p(i) $ 代表灰度等级为 $ i $ 的概率 $ p(i) = \dfrac{{{n_i}}}{N} $ ; $ {n_i} $ 代表灰度值为i的像素; $ N $ 为像素总数 $ N = \displaystyle\sum {{n_i}} $ .

(3)繁杂度 (busyness): 表示一个像素到周围像素的变化率( $ p(i) \ne 0, {\text{ }}p(j) \ne 0 $ ):

$ busyness = \frac{{\displaystyle\sum\limits_{i = 1}^{{N_g}} p (i)s(i)}}{{\displaystyle\sum\limits_{i = 1}^{{N_g}} {\displaystyle\sum\limits_{j = 1}^{{N_g}} | } ip(i) - jp(j)|}} $

(22)

(4)复杂度 (complexity, cp): 表示NGTDM矩阵中像素均匀度的强度变化 ( $ p(i) \ne 0, {\text{ }}p(j) \ne 0 $ ):

$ cp = \sum\limits_{i = 1}^{{N_g}} {\sum\limits_{j = 1}^{{N_g}} | } i - j|\frac{{p(i)s(i) + p(j)s(j)}}{{N(p(i) + p(j))}} $

(23)

(5)强度 (strength): 用于描述图像灰度强度的变化速度和粗糙度( $ p(i) \ne 0, {\text{ }}p(j) \ne 0 $ ):

$ strength = \frac{{\displaystyle\sum\limits_{i = 1}^{_{\mathop N\nolimits_g }}\displaystyle\sum\limits_{j = 1}^{_{\mathop N\nolimits_g }} {[p(i) + p(j)]{{(i - j)}^2}} }}{{\varepsilon + \displaystyle\sum\limits_{n = 1}^{_{\mathop N\nolimits_g }} {s(i)} }} $

(24)

3.3 特征筛选

本文采用斯皮尔曼相关系数方法^[21]来分析特征与皮质白内障级别之间相关性进行特征筛选, 同时分析特征之间的相似性过滤冗余特征. 斯皮尔曼相关系数方法可通过式(25)得到:

$ \rho = 1 - \frac{{6\displaystyle\sum\limits_{i = 1}^n {d_i^2} }}{{n\left( {{n^2} - 1} \right)}} $

(25)

其中, d_i表示第i个样本点两个相比较的特征的等级之差, n为训练样本总数.

3.4 皮质性白内障分类

支持向量机 (support vector machine, SVM)是一种经典的机器学习方法, 它已经被广泛地应用到医学图像处理领域. 与其他机器学习的分类算法相比, SVM具有训练速度快、可解释行强和鲁棒性强等特点. 本文采用线性支持向量机 (linear-SVM) 自动预测皮质性白内障严重程度, 其表达式如下:

$ \hat y({{x}}) = \sum\limits_{i = 1}^m {{w_i}} {x_i} + {w_0} $

(26)

其中, ${{x}} = \left( {{x_1}, {x_2}, \cdots, {x_m}} \right)$ 为训练特征, ${{w}} = \left( {{w_1}, {w_2}, \cdots, {w_m}} \right)$ 为决定超平面方向的法向量, w₀为决定了超平面与原点间距离的位移项.

4 实验结果与分析 4.1 评价标准

本文采用准确率 (accuracy, ACC) 、宏召回率 (macro recall,Re)、宏精确率 (macro precision,PR) 和宏F1 指标 (macro F1 measure, F1) 4个评价指标来评估方法的总体性能. 准确率是用来衡量算法预测正确的样本数目占总样本数的比例; 召回率是算法预测正确的正例样本的比例; 精确率是算法预测为正例的样本中实际为正例的比例; F1 指标是精确率和召回率的调和均值. 这4个评价指标的计算公式分别为:

$ ACC = \frac{{\displaystyle\sum\limits_{i = 1}^l {\frac{{T{P_i} + T{N_i}}}{{T{P_i} + F{P_i} + T{N_i} + F{N_i}}}} }}{l} $

(27)

$ PR = \frac{{\displaystyle\sum\limits_{i = 1}^l {\frac{{T{P_i}}}{{T{P_i} + {FP_i}}}} }}{l} $

(28)

$ Re = \frac{{\displaystyle\sum\limits_{i = 1}^l {\frac{{T{P_i}}}{{T{P_i} + F{N_i}}}} }}{l} $

(29)

$ F{1} = \frac{{2PR\times Re}}{{PR + Re}} $

(30)

其中, $ T{P_i} $ 、 $ T{N_i} $ 、 $ F{P_i} $ 、 $ F{N_i} $ 分别代表类别 $i\;(i = 1, 2, \cdots, l)$ 的真阳性 (true positive)、真阴性 (true negative), 假阳性 (false positive)和假阴性 (false negative).

4.2 实验环境设置

本文采用OpenCV图像处理包和scikit-learn机器学习分别实现特征提取和机器学习方法. 为了验证本文所提出方法的有效性, 本文也采用先进的卷积神经网络模型 (convolutional neural network, CNN) 作为对比方法: GraNet^[13]、ResNet^[22]、SENet^[23]和EfficientNet^[24]. 所有CNN模型是基于PyTorch框架实现的, 输入的预处理后的AS-OCT图像大小为224×224; 优化器是随机梯度下降优化器 (stochastic gradient descent, SGD) 并采用默认设置. 本文将训练周期 (epochs) 和批量大小 (batch size) 分别设置为100和16; 初始化学习率 (learning rate) 为0.02并采用余弦退火调整学习率策略. 所有CNN模型都采用默认方法初始化后进行训练. 实验的软件环境和硬件环境分别为Ubuntu操作系统和1张Nvidia Titan GPU (10 GB).

4.3 实验结果与分析 4.3.1 不同图像预处理方法的结果对比

图4为AS-OCT图像在不同预处理下的分类准确率对比, 其中使用的特征为上文所提取的22个特征. 为了验证所提的预处理方法的鲁棒性, 本文比较了5个常见的机器学习算法: 线性支持向量机, AdaBoost (AB), 最邻近结点算法 (K-nearest neighbors, KNN), 决策树算法 (decision tree classifier, DT) 和随机森林算法 (random forest, RF). 其中, 蓝色、橙色、灰色和黄色分别代表未经过任何预处理、仅去除反光区域、仅进行对比度增强以及去除反光区域和对比度增强两种方法结合的分类结果.

图4实验可结果分析可见, 基于反光区域去除+对比度增强混合方法在AS-OCT图像取得了最好分类结果, 其比未处理的AS-OCT图像提高了37.13%; 与单独的反光区域去除和对比度增强方法相比, 混合方法分别提高了19.43%和28.01%. 实验结果也验证了所采用的图像增强方法能有效地提高皮质性白内障分类结果和鲁棒性. 在未来的研究工作中, 本文还会进一步改进现有的图像增强方法. 根据图4的结果对比, 在5个机器学习算法中, linear-SVM的分类效果总体上优于其它4种机器学习算法. 因此, 本文选用linear-SVM作为分类算法来识别皮质性白内障严重程度.

4.3.2 特征筛选分析

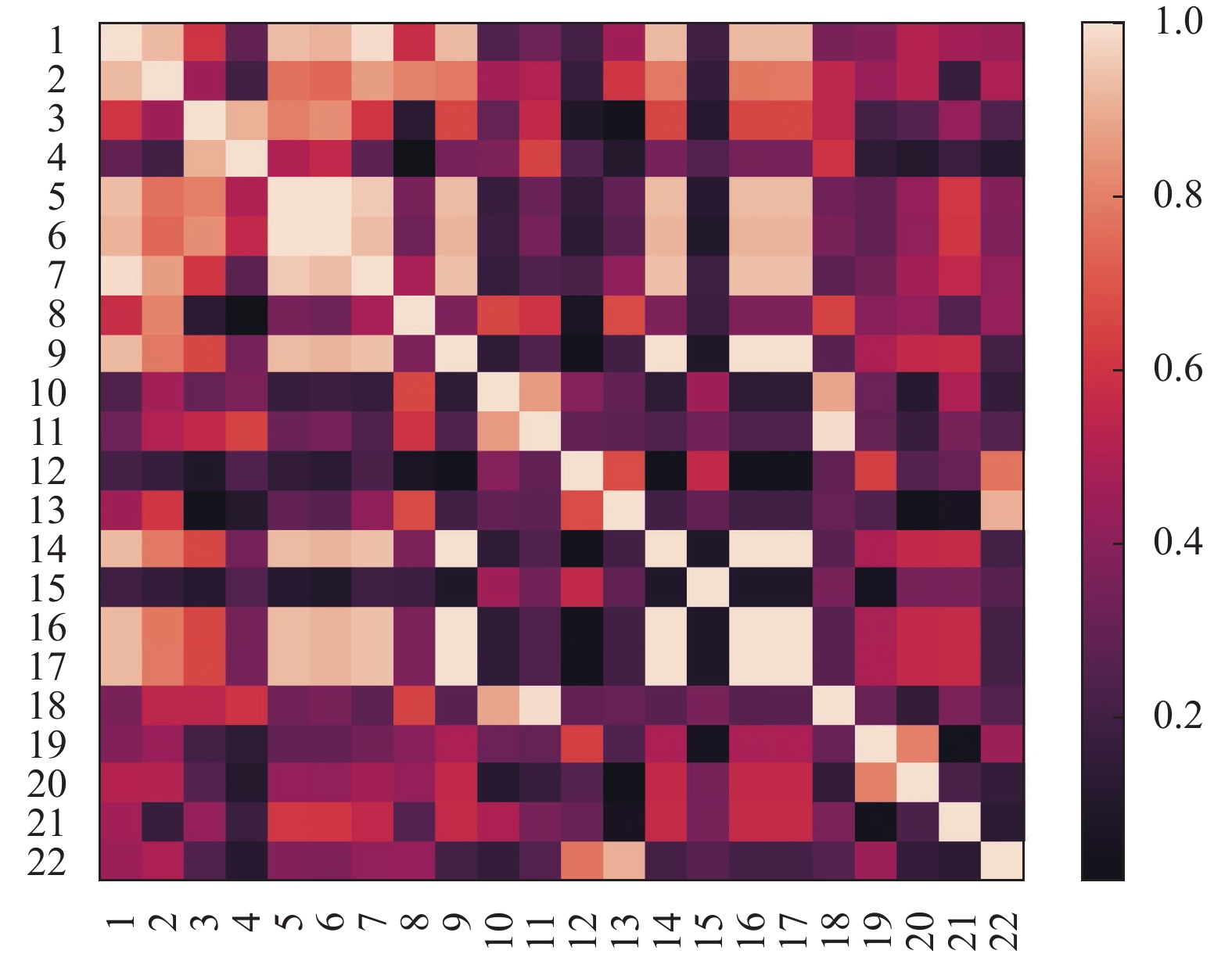
表2为22个特征与白内障级别之间的斯皮尔曼相关系数. 其中, 斯皮尔曼相关系数越大, 表明特征与皮质性白内障严重程度相关性越大, 也说明特征越重要, 反之亦然. 从表2结果可知, 斯皮尔曼相关系数大小排名前8的特征分别是熵、小区域偏好性、区域大小方差、相关性、能量、强度、小面积高灰度级偏好性和大区域偏好性. 图5为提取特征之间的斯皮尔曼系数相关矩阵, 图中序号与第3.2节特征出现顺序一一对应. 图中色块颜色越浅则代表该色块对应特征间的相关性越强, 颜色越深则相关性越弱.

两个特征具有高相关性代表它们具有相似的功能, 会导致特征冗余, 从而影响分类性能. 为了剔除这些冗余特征, 本文设置了以下规则: 若两个特征的斯皮尔曼系数大于0.95, 则认为两个特征间存在很强的线性相关性. 其中, 本文将重要性较小的特征设置为冗余特征并剔除. 基于以上规则, 本文共剔除了8个冗余特征: 逆差距, 大区域偏好性, 大面积高灰度级偏好性, 大面积低灰度级偏好性, 小面积低灰度级偏好性, 复杂度, 相异性和相关性.

表3为基于linear-SVM的不同特征组合的分类结果对比, 本文选择了GLCM的特征, GLSZM的特征、NGDTM的特征、GLCM+GLSZM的特征组合、GLCM+NGDTM的特征组合、GLSZM+NGTDM的特征组合、所有22个特征以及基于斯皮尔曼系数特征筛选后最大的前8, 前5, 前14个特征.

表3实验结果分析可见, 使用单一特征提取方法能达到83.42%的准确率; 使用两个特征提取方法组合最高可以达到84.92%的准确率, 使用3种特征提取方法的组合可以达到85.10%的准确率, 从而表明了基于3种特征提取组合方法能提高分类的准确性. 使用前14个特征的linear-SVM分类结果最好, 较22个特征在准确率提升了0.94%. 不同特征组合的分类结果说明提取的特征越多并不意味着分类结果越好, 因为冗余特征会影响分类器的性能.

基于表3的分类结果, 本文选择了14个特征用于下文实验的分类结果对比.

4.3.3 不同图像预处理方法的结果对比

表4为机器学习与深度学习方法的皮质性白内障分类结果对比. 除了第4.2节提到的4种深度学习方法和第4.3.1节提到的5种机器学习方法, 本文还选择了高斯径向基核支持向量机算法 (radial basis function-SVM, rbf-SVM)^[25]和多项式核支持向量机算法 (poly-SVM)^[26]与linear-SVM作对比. 表4的分析结果可知, linear-SVM的分类结果优于rbf-SVM和poly-SVM, 在准确率上分别提高了0.94%和5.45%. 与其它分类算法对比, linear-SVM取得了最好的皮质性白内障分类结果, 它的准确率、精确率、召回率和F1分别达到了86.04%, 88.27%, 86.18%和86.04%. 例如它比AB和DT在准确率上分别提高了10.28%和10.57%以上. 与4个先进的CNN模型相比, 本文所提出的方法性能总体优于它们, 也证明了本文方法的有效性.

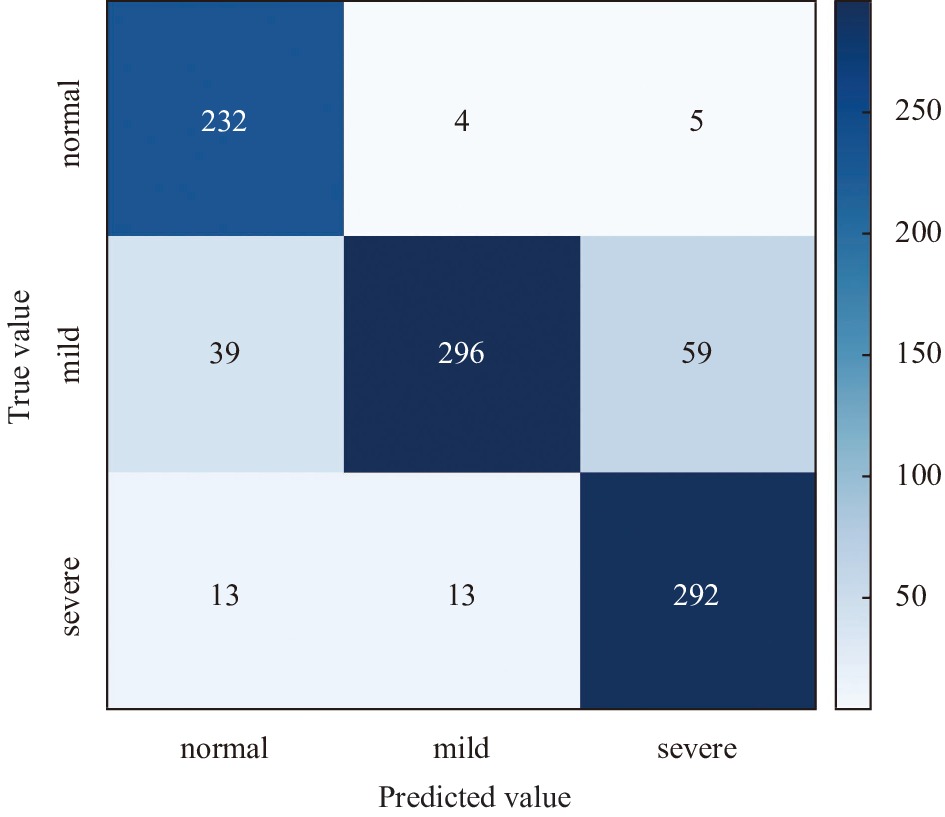
图6为linear-SVM的皮质性白内障分类结果的混淆矩阵. 其中, 正常、轻度和重度白内障的召回率分别为82.04%、96.17%和80.34%. 轻度白内障样本的召回率明显高于重度和正常样本, 其中, 正常和重度白内障样本容易被误分为轻度白内障.

为了增强本文方法的可解释性, 本文分析了14个特征的linear-SVM方法的权重并进行排序, 并与上文利用斯皮尔曼相关系数得到的特征重要性排序进行对比验证. 表5为按照特征权重从大到小排序后的前8个特征. 可以看到, 熵在特征权重排序和表2中的特征重要性排序都位于首位. 在特征权重排序的前8个特征中, 有5个特征在特征重要性排序中位于前8位, 说明使用斯皮尔曼相关系数进行特征重要性排序并筛选特征有助于提升分类结果.

4.3.4 讨论

本文提出了一个准确率达到了86.04%的自动皮质性白内障分类框架, 其具有以下优点: 1) 本文所采用的图像预处理方法简单有效. 2) 本文提取的纹理特征反映了皮质性白内障病理位置, 且多个特征照顾了医学影像的模糊性和不确定性. 3) 本文基于斯皮尔曼相关系数的特征分析和特征筛选剔除了冗余特征并获得了更高准确率. 4) 本文使用的linear-SVM方法进行特征分类并获得特征权重, 与深度学习相比具有较好的可解释性和较少的参数量.

同时, 本文仍有很大的提升空间并存在以下不足: 1) 本文所使用的数据集的图像数量有限, 较难有效地验证本文方法和深度学习的优越性, 但文献[27]已经证明了深度学习算法在大数据集上的分类结果不一定都优于机器学习的分类结果. 2) 本文预处理中裁剪图像去除反光区域的操作无法避免病理区域在裁剪区域的可能性, 存在很大改进空间. 3) 本文仅采用灰度共生矩阵及变异灰度矩阵方法提取了纹理特征. 4) AS-OCT图像是基于环形扫描方式获取得到的, 单个角度的图像不能有效地获取整个皮质区域的混浊度, 可能导致皮质白内障分类结果偏低.

在未来, 本文将计划采集更多的AS-OCT图像数据以验证本文方法的有效性和鲁棒性; 本文将改进现有图像增强和特征提取方法、并利用其它特征提取方法如小波变换^[28]来提取其它类型特征来提高分类效果. 近年来深度学习在医学影像处理领域取得不错的成果, 本文打算将提取的特征作为临床先验知识与神经网络模型融合, 提高皮质白内障的分类性能并增强深度学习模型的可解释性.

5 结论与展望

针对目前尚未有基于AS-OCT图像的皮质性白内障自动分类工作, 本文提出了一个由图像预处理、特征提取、特征筛选、特征重要性分析和分类构成的自动算法分类框架. 在一个临床的AS-OCT数据集上, 本文所提出的算法框架取得了86.04%的准确率和86.18%的召回率, 与先进的神经网络模型性能接近; 且相较于深度学习模型, 本文所提出的框架具有较好的可解释性和较少的参数量, 因此它具有部署在实际的眼科设备上辅助医生诊断皮质性白内障的潜力.