随着工业的快速发展, 大量的工业制造废弃物不仅污染环境, 占用土地面积, 而且浪费资源. 因此, 为解决上述问题需要对工业废旧产品进行高效回收、再制造以及再利用, 这对环境保护以及资源的有效利用具有重要实际意义[1]. 而拆解是实现废旧产品回收再利用的前提, 拆解序列规划的意义在于找到设备最佳的拆卸顺序, 以提高效率, 降低拆解成本[2]. 本研究结合智能算法, 设计了一个高效拆解序列规划模型, 为产品回收作业提供指导.
设备的拆解是一个很复杂的过程, 在对设备拆解过程进行建模时需要考虑不可忽视的实际因素, 将实际的物理模型转化为数学模型, 并且还要建立目标函数以及借助智能算法才能做出可行且较优的决策[3]. 在过去的研究中, 设备组件的表达通常会用到图论中的有向图模型、无向图模型、与或图模型和Petri网模型[4].
图像模型无法被计算机识别并加以计算, 因此需要将建立好的图像模型用数学的形式表达出来. 在拆解序列规划问题中, 常用数学矩阵来进一步描述设备零部件之间的关系, 例如干扰矩阵、接触矩阵和连接矩阵等[5]. 连接矩阵表示零部件之间的连接类型, 干扰矩阵和接触矩阵分别表示零部件之间的空间干扰和接触关系, 常用来从设备中获取拆解信息.
在对设备进行数字化表示后, 需要建立目标函数并结合算法来求解最佳拆解序列. 大量研究表明, 拆解序列规划问题属于复杂的完全非确定性多项式问题[6], 像这类问题可以使用穷举法对结果进行逐个检验, 可以得出最终答案. 但是, 穷举法的计算时间随问题的复杂程度会呈指数增长因而变得不可适用. 随后, 基于种群的智能算法被广泛地被应用于废弃(EOL)产品[7]或设备维修的拆解序列规划中.
杨书仪等[8]将遗传算法与模拟退火算法进行结合, 平衡了算法的全局搜索和局部搜索能力, 为混凝土泵车分动箱的拆解提供了一个更加高效的途径. 张雷等[9]提出了一种并行拆解的规划模型, 其并行拆解相对于串行拆解更加适应工厂的生产模式, 最后利用传统的人工蜂群算法来制定优秀的拆解序列. 郭洪飞等[10]考虑了多种拆解因素, 并利用综合评价方法对拆解序列进行了更加科学的评价.
Kongar等[11]提出将群智能优化算法遗传算法应用到产品的拆解回收利用中, 为后续的拆解序列规划研究提供了新思路. Xu等[12]使用了改进的人工蜂群算法求解了人机协作拆解的工业产品再制造问题, 最大限度地减少了拆解成本和难度. Tseng等[13]通过扁虫的再生特性提出了一种扁虫算法, 基于再生机制的扁虫算法在进行算法求解时不容易陷入局部最优. Zhu等[14]提出了一种基于零部件约束矩阵的方法来构建产品拆解的信息模型, 并使用了混合蛙跳算法来求解拆解序列规划问题.
以上算法都属于经典的元启发式算法, 这些算法通过模拟生物行为或者物理现象来解决问题, 凭借其概念简单且易于实现的优点, 元启发式算法在工程应用领域越来越受欢迎. 除以上算法之外, 近些年才提出的鲸鱼算法[15]具有收敛速度快、全局搜索能力强等优点. 在以往的研究中, 设备的拆解序列规划问题不同于一般的连续空间优化问题[16], 而是离散的空间优化问题. 鲸鱼算法最早提出来用于解决连续的优化问题, 因此如何改进鲸鱼算法解决离散优化问题成为了本研究的关键. 因此, 本研究提出了一种新的离散鲸鱼算法并结合改进的遗传算法变异机制以平衡全局和局部搜索能力并将其运用到了设备拆解序列规划问题中, 以求解出最优的拆解零件顺序, 减少拆解成本和提高拆解效率.
1 拆解序列规划模型拆解序列规划的目标是找到拆解代价或拆解时间最小的拆解序列, 本节将给出约束关系模型、目标函数和评价指标为拆解序列规划问题建立数学模型.
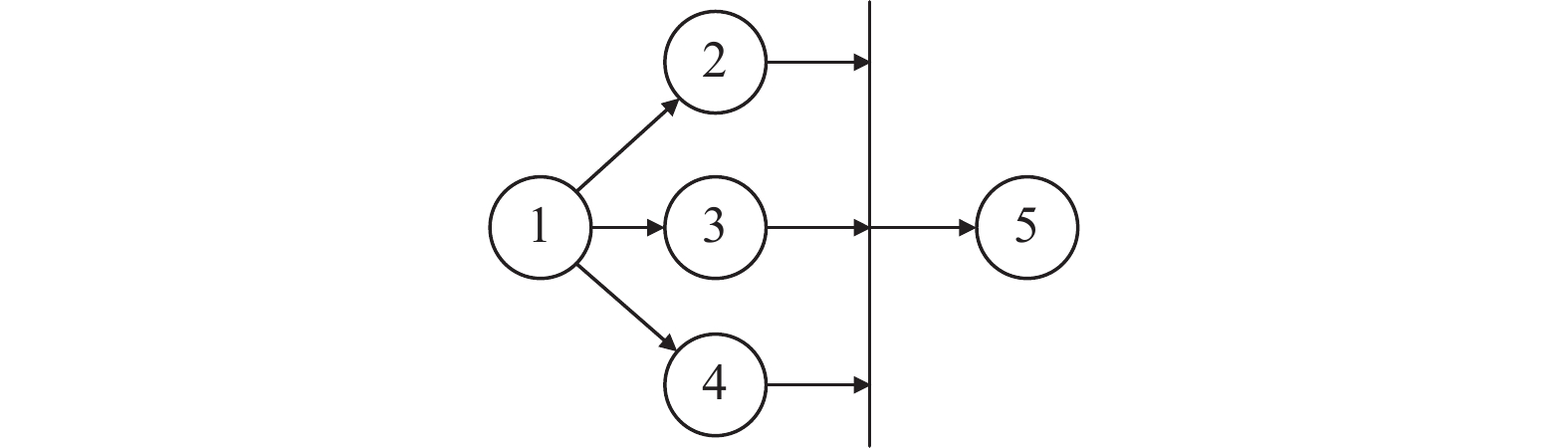
1.1 约束关系图1为某一简单设备零部件的有向图, 图中标号代表各个零部件, 图中箭头表示拆解流向. 箭头前的零件必须比箭头后的零件要先拆, 例如节点3必须要优先于节点5拆解.
|
图 1 简单拆解有向图模型 |
两个拆解节点之间的约束关系转化为数学模型可以由约束矩阵
| $ {c}_{ij}=\left\{ \begin{array}{l}1, \; 如果节点i必须在节点j之前拆除\\ 0, \; 其他 \end{array} \right.$ | (1) |
给出目标函数之前须首先定义一维拆解序列数组ds, 它表示完成设备拆除项目所需要的零件拆解顺序. 在建立目标函数时, 拆卸工作负荷的相同部分已被移除, 例如准备必要的材料, 拆卸操作, 物理消耗等. 由于设备的回收属于完全拆解, 当所有零件都要被拆除时, 单个零件的拆解时间最后相加并被抵消. 因此, 本研究采用惩罚代价的形式对拆解过程中影响最终拆解效率的部分进行考虑. 目标函数由式(2)给出:
| $ \min F = \sum\limits_{k = 0}^{n - 2} {({T_{ds(k), ds(k + 1)}} + {P_{ds(k), ds(k + 1)}} + {D_{ds(k), ds(k + 1)}})} $ | (2) |
其中, k为拆解序列中的零件位置, ds(k)表示第k个零件的编号,
设备零部件的拆解离不开工具. 由于需要拆解的零件类型很多, 拆解工作人员难以避免地需要频繁更换手中的工具来拆卸设备上的零件, 这将十分耗时耗力. 因此将工具的改变作为拆解序列的评价指标很有必要. 一般来讲, 设备上的某一个零件对应着一种拆解工具, 拆解不同零件时, 工具会随之更换. 在此用矩阵
| $ {t}_{ij}=\left\{\begin{array}{l}1, \; 两节点拆解所需工具不同、且节点j拆解工具\\为小型工具\\ 2, \; 两节点拆解工具不同、且节点j拆解工具为大\\型工具\\ 0, \; 两节点拆解工具相同\end{array} \right. $ | (3) |
其中, 节点i是在节点j前拆解的, 所以当下一步拆解的零件j需要大型工具时比较耗时. 比如吊机, 它的启动和调用都很费时. 而小型工具如梅花扳手, 六角扳手, 由于这些工具易于获取, 工具改变代价自然会小一些. 而当前后两个拆解零件节点一样时, 就没必要更换工具了, 代价自然为0.
1.3.2 位置改变在拆解大型设备时, 零件之间的距离较远, 工作人员来回地走动也是一种低效率的表现, 因此需要将零件之间的距离作为拆解序列的评价指标. 然而, 在施工现场很难精确测量设备各个零件的空间位置距离, 此时可以借助三维软件Unity 3D. 成功导入到Unity 3D的设备模型会自动添加一个Transform组件, 在该组件中有一个三元变量position, 它表征模型零件在三维空间的位置, 例如零件i的position为
| $ {p_{ij}} = \sqrt {{{({x_i} - {x_j})}^2} + {{({y_i} - {y_j})}^2} + {{({y_i} - {y_j})}^2}} $ | (4) |
除了零件的位置以外, 在三维直角坐标系中, 零件的拆解方向也起着很关键的作用, 其通常可以用
| $ {d}_{ij}=\left\{\begin{array}{l}0, \; 节点i与j的拆解方向一致\\ 1, \; 拆解方向改变了{90}^{\circ }\\ 2, \; 拆解方向改变了{180}^{\circ }\end{array} \right. $ | (5) |
因此可以用矩阵
标准的鲸鱼算法在早期阶段进行全局搜索, 在后期进行局部搜索. 鲸鱼算法具有收敛速度快, 全局搜索能力强的优点, 然而传统的鲸鱼算法不能有效地跳出局部最优并且容易陷入其中. 与此同时, 遗传算法的变异机制可以打破当前的最优解, 跳出局部最优, 提高局部搜索能力. 受此启发, 提出的离散鲸鱼算法并结合可行解生成器、优先保护约束交叉机制、启发式变异以提高算法的搜索性能.
2.1 可行解快速生成方法在生成初始种群时, 需要得到一组满足约束关系的拆解序列可行解. 然而随着设备节点数量的增多, 如果采用随机排列组合的方式, 会产生很多不满足约束关系的非可行解以及少许可行解. 此时采用排除非可行解并留下可行解的方式会很费时且效率不高. 为此本研究采用了如图2所示的分层组合的方式对图1中的简单设备进行完全搜索, 来完成可行解即初始群体个体的生成.

|
图 2 分层组合法 |
可行解快速生成的具体操作步骤如下.
1) 选定要拆解的节点为5, 第5列检索到1的节点有2, 3, 4, 意味着2, 3, 4节点必须优先于5拆解, 于是先把5放在最后一层C中.
2) 紧接着检索2, 3, 4列, 发现它们都指向1, 于是将2, 3, 4放在B层.
3) 检索第1列, 发现没有约束, 将节点1放在A层停止检索.
4) 为了得到不同的初始种群个体序列, 将这3层内的节点随机排序, 最终将A、B、C三组数据依次放置到拆解序列数组ds中. 对于复杂设备, 如此重复操作选择其他要拆解的节点, 就可以快速的得到满足约束关系的拆解序列初始种群.
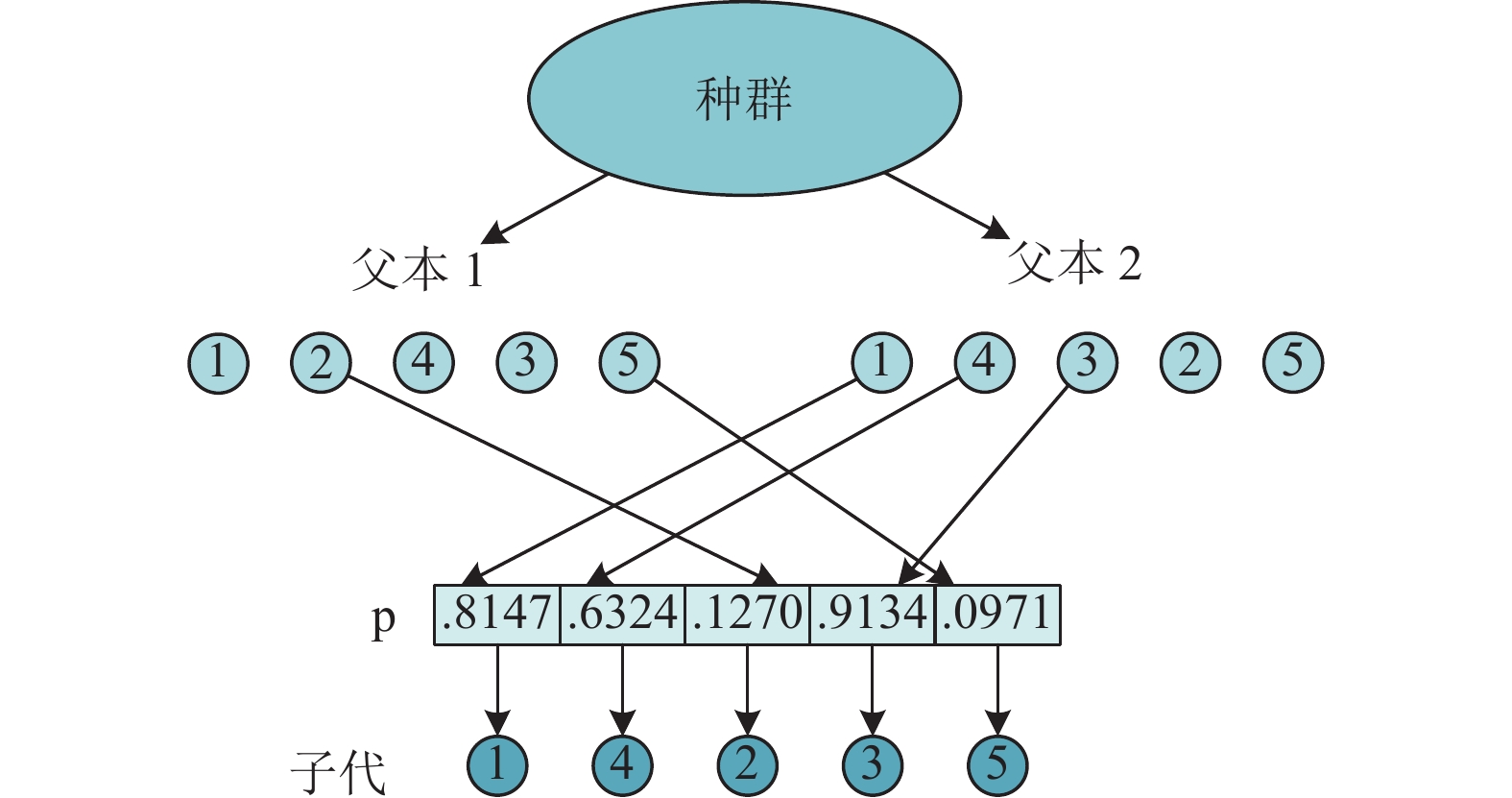
2.2 优先保护约束交叉机制在过去的研究中, 遗传算法里的交叉步骤指选取两个优秀的父本进行交叉运算, 有几率生成更加优秀的子代. 然而遗传算法中的部分匹配交叉是从父代随机选择两个个体P1, P2和两个点并将两点之间部分提取出来, 分别放在子代相同的位置. 这样子确实可以生成新子代但无法确定子代个体里面的所有节点是否还满足约束关系, 因此还要再进行筛选判断, 问题会变得很复杂. 于是, 一种优先保护约束交叉机制被提出来解决这个问题, 如图3所示.
|
图 3 优先保护约束交叉 |
从生成的初始种群中抽出两个父本, 分别为父本1=[1, 2, 4, 3, 5], 父本2=[1, 4, 3, 2, 5]. 它们当中的节点都满足节点间的约束关系, 给出0到1间的随机变量p, 如果p大于0.5, 则从父本2选择节点; 如果p小于0.5, 则从父本1选择节点. 优先保护约束交叉机制子代生成的操作步骤如下.
1) 当p=0.8147>0.5和p=0.623>0.5时, 从父本2中选择最开始的节点1、4存入子代中;
2) 当p=0.1270<0.5时, 从父本1中开始选择, 删除已经存在的1、4节点. 父本1中只剩下2, 3, 5节点, 因此按顺序选择节点2并存入子代.
3) p=0.9134>0.5时, 删去父本2中的1, 4, 2后剩下3, 5, 于是将3存入子代; 当p=0.0971<0.5, 选择父本1中的5存入子代, 最后得出满足约束关系的子代=[1, 4, 2, 3, 5].
2.3 离散鲸鱼更新机制在优先保护约束交叉机制中, 生成子代的两个以上才的父本后才有交叉的意义. 而在离散鲸鱼算法中, 需要确定3个父代个体. 它们分别是当前迭代中种群适应度值最好, 既拆解代价最小的拆解序列个体
| $ X(t+1)=\left\{\begin{array}{l}f[{X}^{*}(t)]\text{, }{\rm{if}}\text{ }\left|A\right| < 1\text{, }p < 0.5\\ f[{X}_{{\rm{rand}}}(t)]\text{, }{\rm{if}}\text{ }\left|A\right|\geqslant 1\text{, }p < 0.5\\ f[G(t))]\text{, }{\rm{if}}\text{ }p\geqslant 0.5\end{array}\right. $ | (6) |
其中,
| $ B = \left[\left(\dfrac{{{N_p}}}{2} - 1\right) \times \left(1 - \dfrac{t}{{{t_{\max }}}}\right) + 1\right] $ | (7) |
其中,
通过交叉可以产生新的优秀个体, 但是交叉随机性太强, 可能迭代很久才会出现一个更加优秀的个体. 因此, 为了增强算法局部搜索能力, 通常采用遗传算法中的变异机制, 但是传统的遗传变异会改变拆解序列中节点的值, 这将使得拆解序列不符合约束关系而被舍去.
因此针对设备拆解的拆解序列优化的变异不应产生新节点, 只能是对拆解节点的位置变异. 一般来讲, 改变位置的方法可以是随机选择两个节点并判断交换后是否满足约束条件再进行交换, 也可以是选出一个节点再在满足约束关系的情况下插入序列中的其他位置. 以上两种方法都可以在不破化拆解序列可行性的情况下产生新的变异可行解, 但由于这两种方法随机性太强, 产生的新序列其适应度可能更好也可能更差, 因此提出一个启发式变异方法, 寻找最优的插入位置可以加强算法的局部收敛能力.
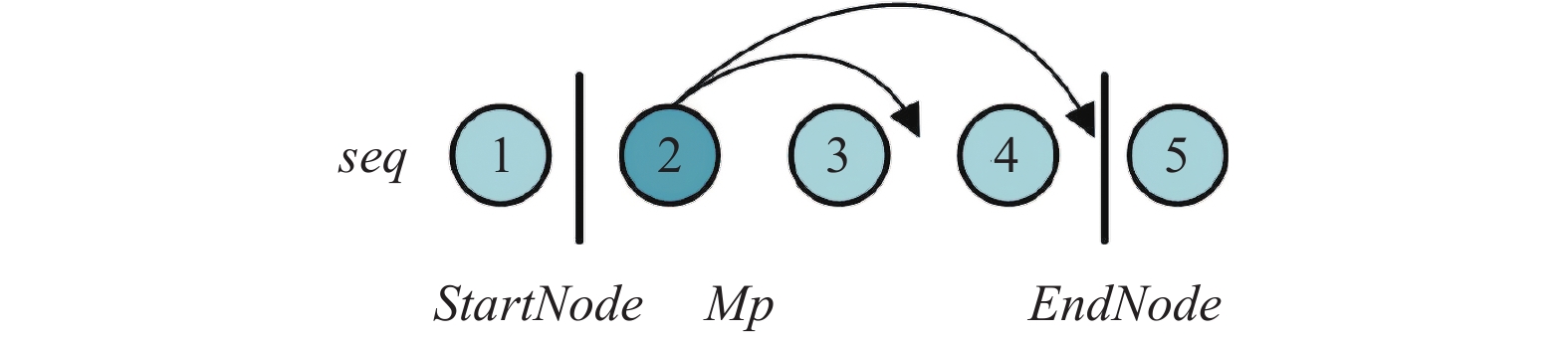
如图4所示, 以简单设备为例. 如果选择节点2作为变异节点, 则检索2的行和列, 并且将约束节点2的节点1和5找到分别作为要插入的起点与终点. 然后将节点2插入如图4所示的箭头指示的位置, 并计算每个位置更改的拆卸代价. 如果拆卸代价较短, 则保存节点2的新位置以获得优异的后代. 启发式变异旨在增强算法局部搜索能力, 对于不同的拆解序列, 优先保护约束交叉机制子代生成的步骤如下.
1) 设定变异次数Nm为种群数量的一半.
2) 从相对工作量较小的拆解序列集合中随机选择一个拆解序列seq作为变异个体.
3) 从选择的变异个体seq中随机选择第Mp个节点作为变异节点, 然后查找该节点可以重新插入的位置范围, 为了减少判断次数, 首先, 检查约束矩阵中第seq(Mp)列, 记录数据等于1所对应列的节点编号作为起始节点集合StartNode, 检查约束矩阵第seq(Mp)行, 记录数据等于1所对应行的节点编号作为终止节点集合EndNode; 然后检查拆解序列seq, 则可插入的位置即在StartNode集合中节点后和EndNode集合中节点前都为可插入位置.
4) 计算所有可插入位置对应的工作量的值, 并保留工作量最小的个体用于更新种群.
|
图 4 启发式变异 |
2.5 离散鲸鱼算法模型
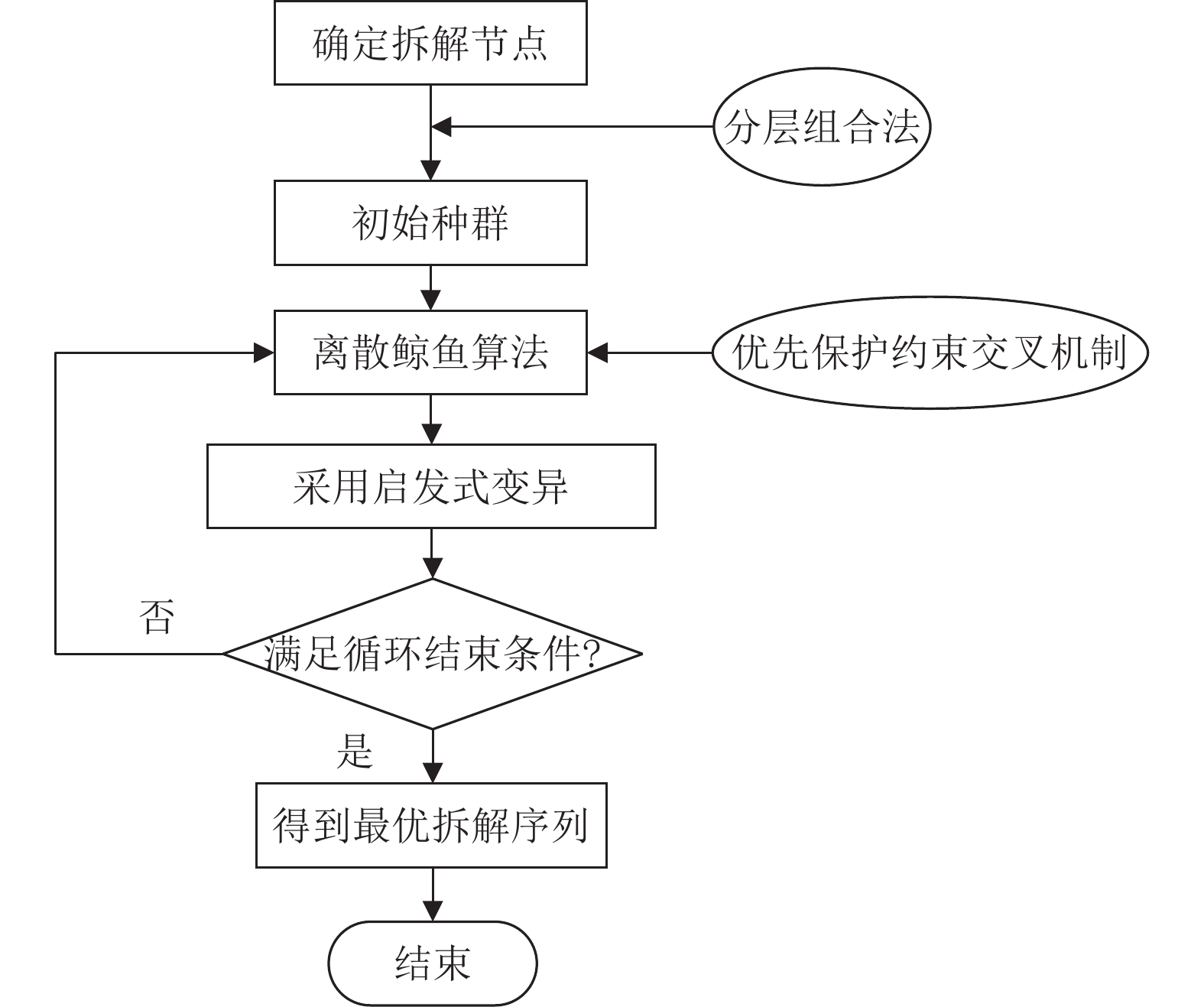
综上所述, 结合启发式变异的离散鲸鱼算法整体的流程如图5所示.
3 实验分析 3.1 实验数据集本实验使用文献[17]中的水轮机主轴密封的零部件信息、约束矩阵以及各设备的拆解代价数据. 针对回收上橡皮板和空气围带两个项目设计实验. 紧接着就是利用这个两个项目来测试各个算法的性能, 在测试实验中, 每个算法都执行100次, 实验结果中记录种群大小 Np, 迭代次数t, 规划得到的拆解序列结果中代价最小值 MIN, 标准差 STD, 平均运行时间T, 以及代价最小拆解序列所占比例 ROM. 运行环境为: 测试软件: Matlab 2016; 编码语言: C语言; 处理器: 英特尔酷睿i5, 6300hq×4, 主频2.3 GHz; 内存: 16 GB.
|
图 5 离散鲸鱼算法模型 |
3.2 实验结果
实验采用Konger等[11]提出的遗传算法GA, Yeh[18]提出的SSO算法和Xia等[19]提出的STLBO算法与DWOA算法进行比对, 根据结果观察DWOA的表现. 其实验对比结果如表1 所示.
| 表 1 实验结果 |
表1中“—”代表算法没有找到拆解代价最小的拆解序列. 根据实验可知, 将每个算法运行100次后, 在项目1与项目2中, DWOA相对于其他算法搜索到了最小拆解代价42.1和66.5, 标准差STD分别为0.431和0.501, 说明鲸鱼算法的稳定性要比GA, SSO, STLBO要强. 但是项目1中DWOA算法的运行时间7.9786 s要大于其他算法, 说明算法性能得到提升的同时也增加了计算量.
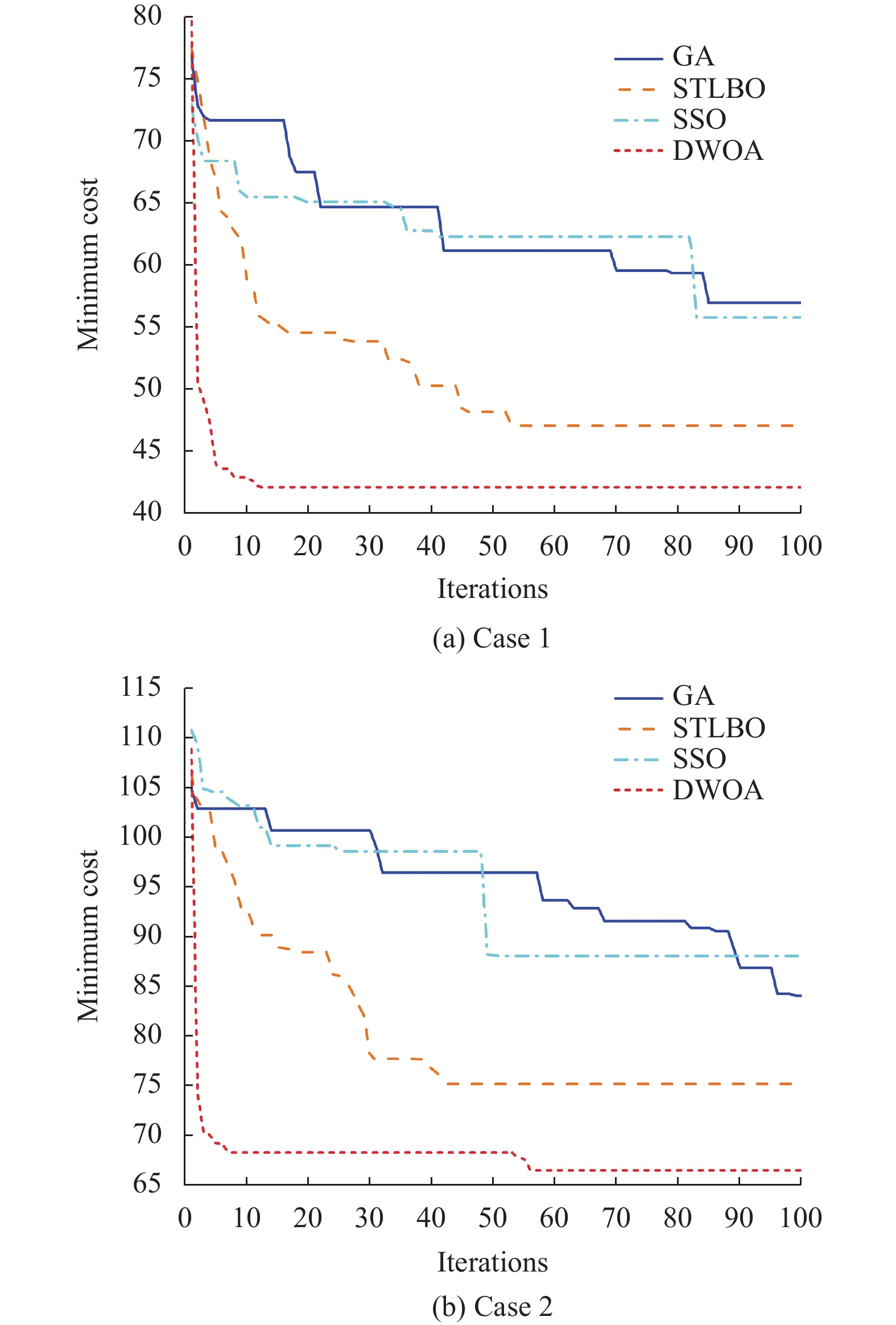
由4种算法获得的最小拆卸代价图像迭代数据如图6所示, 项目1中, DWOA经历了12次迭代后就取到了最小拆解代价42.1, 这表明DWOA可以比其他算法更早地找到最优值. 两个项目中只有DWOA搜索到了最小的拆解代价, 而其他算法则没有, 证明所提DWOA具有更强的稳定性和更快的收敛速度. 项目1最终得到最小拆解代价对应的拆解序列为: 密封水箱上盖板螺栓→密封水箱上盖板→上压板螺栓→上环板密封环连接螺栓→上环板→上压板→上密封橡皮板. 项目2最终得到最小拆解代价对应的拆解序列为: 上密封橡皮板→下压板螺栓→下压板→下密封橡皮板→底座瓣螺栓→水箱底座→空气围带.
|
图 6 不同算法的寻优曲线对比 |
4 结论与展望
本文提出了一种新的离散鲸鱼算法(DWOA)来解决设备回收拆解序列规划问题. 该算法的改进之处在于利用了分层组合的方法快速生成种群初始群体以及结合了启发式变异以及优先保护约束交叉机制. 最后以上橡皮板和空气围带为对象进行对比实验, 验证了它的稳定性、寻优能力、收敛速度要比其他算法强. 接下来的研究工作是借助Unity3D软件并结合算法制作一款软件以增强拆解过程可视化表达也是一个有价值的研究方向.
| [1] |
任亚平. 废旧产品拆解序列规划问题建模与优化研究[博士学位论文]. 武汉: 华中科技大学, 2019.
|
| [2] |
Guo XW, Zhou MC, Abusorrah A, et al. Disassembly sequence planning: A survey. IEEE/CAA Journal of Automatica Sinica, 2021, 8(7): 1308-1324. DOI:10.1109/JAS.2020.1003515 |
| [3] |
Zhou ZD, Liu JY, Pham DT, et al. Disassembly sequence planning: Recent developments and future trends. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2019, 233(5): 1450-1471. DOI:10.1177/0954405418789975 |
| [4] |
Ong SK, Chang MML, Nee AYC. Product disassembly sequence planning: State-of-the-art, challenges, opportunities and future directions. International Journal of Production Research, 2021, 59(11): 3493-3508. DOI:10.1080/00207543.2020.1868598 |
| [5] |
Zhang WL, Ma MX, Li HY, et al. Generating interference matrices for automatic assembly sequence planning. The International Journal of Advanced Manufacturing Technology, 2017, 90(1–4): 1187-1201. DOI:10.1007/s00170-016-9410-x |
| [6] |
李佰霖. 面向水电站设备检修的虚拟仿真及自动规划方法研究与实践[博士学位论文]. 武汉: 华中科技大学, 2020.
|
| [7] |
Favi C, Marconi M, Germani M, et al. A design for disassembly tool oriented to mechatronic product de-manufacturing and recycling. Advanced Engineering Informatics, 2019, 39: 62-79. DOI:10.1016/j.aei.2018.11.008 |
| [8] |
杨书仪, 李京京, 文泽军, 等. 混凝土泵车分动箱拆解序列规划. 机械设计与研究, 2014, 30(5): 106-109, 124. DOI:10.13952/j.cnki.jofmdr.2014.0151 |
| [9] |
张雷, 彭宏伟, 卞本阳, 等. 复杂产品并行拆解建模及规划方法研究. 中国机械工程, 2014, 25(7): 937-943. DOI:10.3969/j.issn.1004-132X.2014.07.016 |
| [10] |
郭洪飞, 陈志彬, 任亚平, 等. 基于零件回收综合评价的废旧产品拆解序列与拆解深度集成决策研究. 机械工程学报, 2022, 58(4): 258-268. |
| [11] |
Kongar E, Gupta SM. Disassembly sequencing using genetic algorithm. The International Journal of Advanced Manufacturing Technology, 2006, 30(5): 497-506. |
| [12] |
Xu WJ, Tang Q, Liu JY, et al. Disassembly sequence planning using discrete bees algorithm for human-robot collaboration in remanufacturing. Robotics and Computer-Integrated Manufacturing, 2020, 62: 101860. DOI:10.1016/j.rcim.2019.101860 |
| [13] |
Tseng HE, Huang YM, Chang CC, et al. Disassembly sequence planning using a flatworm algorithm. Journal of Manufacturing Systems, 2020, 57: 416-428. DOI:10.1016/j.jmsy.2020.10.014 |
| [14] |
Zhu JF, Xu ZG, Su KY, et al. Asynchronous parallel disassembly sequence planning for multi-manipulator based on improved shuffled frog leaping algorithm. SN Applied Sciences, 2020, 2(5): 906. DOI:10.1007/s42452-020-2680-9 |
| [15] |
Mirjalili S, Lewis A. The whale optimization algorithm. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 |
| [16] |
Rana N, Latiff MSA, Abdulhamid SM, et al. Whale optimization algorithm: A systematic review of contemporary applications, modifications and developments. Neural Computing and Applications, 2020, 32(20): 16245-16277. DOI:10.1007/s00521-020-04849-z |
| [17] |
Li BL, Li CS, Cui XL, et al. A disassembly sequence planning method with team-based genetic algorithm for equipment maintenance in hydropower station. IEEE Access, 2020, 8: 47538-47555. DOI:10.1109/ACCESS.2020.2979247 |
| [18] |
Yeh WC. Simplified swarm optimization in disassembly sequencing problems with learning effects. Computers & Operations Research, 2012, 39(9): 2168-2177. |
| [19] |
Xia K, Gao L, Li WD, et al. Disassembly sequence planning using a simplified teaching-learning-based optimization algorithm. Advanced Engineering Informatics, 2014, 28(4): 518-527. DOI:10.1016/j.aei.2014.07.006 |
 2022, Vol. 31
2022, Vol. 31


