车辆轨迹数据包含GPS采样时间和经纬度坐标以及车载状态等信息. 由于GPS传感器在噪声的影响下会存在定位误差, 因此, GPS轨迹数据与真实的移动轨迹之间会有一定的偏移. 若对轨迹数据不进行地图匹配, 那么由于噪声引起的偏移量将会导致移动物体出现在错误的路段上. 对轨迹数据进行地图匹配时, 其中为GPS轨迹点检索候选路段是首要环节.

文献[1]在检索轨迹点的候选路段时, 以轨迹点为中心, 50 m为半径作圆, 将圆内的所有路段作为轨迹点的候选路段. 此外该方法由于未对城市路网进行划分, 因此, 在检索候选路段时, 针对每个轨迹点都得遍历城市路网中的所有路段, 很大程度上降低了候选路段的检索速度. 文献[2]使用网格索引法来计算轨迹点的候选路段, 该方法通过索引的方式将路网划分为矩形网格, 然后将矩形网格内的路段作为轨迹点的候选路段. 文献[3]中首先确定以轨迹点为中心的九宫格区域作为第一次候选路段的筛选区域, 其次在第一次筛选区域的基础上, 以轨迹点的行驶方向为长轴作椭圆形, 最终将该椭圆形区域确定为候选路段检索区域. 上述3个文献中的方法在一定程度上可以减少轨迹点的候选路段数量, 但是当轨迹点噪声较大时, 会出现正确的匹配路段不在候选路段当中或候选路段数量为空的情况, 使得没办法保证地图匹配准确率.

文献[4]采用字符串长度为7的GeoHash网格编码的方式来计算轨迹点的候选路段, 该方法首先将城市路网按照GeoHash编码原则来进行划分, 其次, 将 GPS轨迹点对应的GeoHash网格和其相邻的8个GeoHash网格都作为候选路段的选取范围. 最后, 将该范围内包含的所有路段作为轨迹点的候选路段. 文献[5]计算轨迹点的候选路段的方法与文献[4]相同, 其采用字符串长度为5的GeoHash网格编码, 误差范围为2.4 km, 使得候选路段的选取范围更大. 上述两个文献的方法, 虽然保证了正确的匹配路段在候选路段中, 但是增加了候选路段中的不相关路段, 从而会导致地图匹配效率降低.

文献[6]首先通过历史轨迹点计算各个路段之间的转移矩阵, 然后通过转移矩阵计算相邻两个轨迹点所对应的两个路段之间的转移概率, 其次得到基于隐马尔可夫模型的概率路径预测模型, 最后使用概率路径预测模型确定轨迹点的候选路段集合. 该方法依赖于历史轨迹数据, 因此对历史轨迹数据的有效性和可用性具有一定的要求.

针对地图匹配算法, Newson等人^[7]基于隐马尔可夫模型, 将测量噪声和道路网络的连通路径考虑在内, 使用高斯模型来计算观测概率. Jagadeesh等人^[8]在隐马尔可夫模型的基础上, 在计算转移概率时结合了驾驶员的路径选择习惯.

综上所述, 现有的轨迹点候选路段的检索方法中存在的问题为当轨迹点的候选路段选取区域小时, 会导致正确的匹配路段不会出现在选取区域中, 降低地图匹配准确率. 当选取区域大时, 又会增大候选路段集合中的不相关路段数量, 降低候选路段检索效率. 针对上述问题, 本文旨在提出一种能解决上述问题的新的轨迹点的候选路段检索方法, 然后通过隐马尔可夫模型, 采用增量的方式, 利用维特比算法得到一条最佳匹配路径. 我们在30 s采样时间间隔下, 使用真实西安市出租车数据集对上述所提方法进行了评估.

1 问题陈述

基于浮动网格的路段检索方法的定义如下:

定义1. 物体的移动轨迹是按照移动物体的采样时间先后顺序, 由一系列GPS轨迹点 $ {g_i} $ 构成的时间序列, 其中 $ {g_i} = (tid, t, lon, lat) $ , $ {g_i}.tid $ 为 $ {g_i} $ 的编号, $ {g_i}.t $ 为 $ {g_i} $ 的采样时间, $ {g_i}.lon, {g_i}.lat $ 分别表示 $ {g_i} $ 的经度和纬度.

定义2. 路段 $ e $ 包括路段编号 $ e.eid $ , 路段长度 $ e.l $ , 路段经纬度点集合 $ e.W $ . $ \forall {w_i} \in W $ , $ {w_i} = (e.{w_i}.lon, e.{w_i}.lat) $ , 其中 $ e.{w_i}.lon $ 表示点 $ {w_i} $ 的经度, $ e.{w_i}.lat $ 表示点 $ {w_i} $ 的纬度.

定义3. 路网用有向图 $G(V, E)$ 呈现, 其中E为路网中的路段集合,V为路段之间的交点集合.

定义4. 在一个路网 $ G $ 中给定两个顶点 $ {V_i} $ 和 $ {V_j} $ , 路径 $ P $ 是从起点 $ {V_i} $ 到终点 $ {V_j} $ 的一组连接的线段. 即 $P:{e_1} \to {e_2} \to \cdots \to {e_n}$ , 其中 $ {e_1}.start = {V_i} $ , $ {e_n}.end = {V_j} $ , ${e_K}.end = {e_{K + 1}}.start,\; 1 \leqslant K \lt n$ .

现在, 浮动网格的路段检索方法定义如下: 给定城市路网 $G(V, E)$ 环境, 使用轨迹点 $ \{ {g_i}|1 \leqslant i \leqslant n\} $ 找到移动物体在每个采样时刻 $ t $ 对应的固定范围内的候选路段集合 $C{\text{ = }}\left\{ {{e_k}\left| {\forall {e_k} \in E, k = 1, 2, \cdots, n} \right.} \right\}$ .

2 浮动网格的路段检索方法 2.1 GeoHash网格编码划分路网

在进行地图匹配时, 首先需要为GPS轨迹点检索候选路段, 若不添加任何条件约束的情况下, 路网中的所有路段均可作为轨迹点的候选路段. 然而, 该候选路段检索方法会使得地图匹配效率大幅度降低. 因此, 在实际中需要一种更高效的候选路段检索方法. 本文使用GeoHash网格编码对城市路网进行划分, 其中GeoHash网格编码可以将二维的经纬度坐标转换成二进制编码, 因此通过上述编码方式, 可以计算出组成路段的各个经纬度坐标的GeoHash编码, 进而来完成对城市路网的划分.

本文选择35个比特位的GeoHash网格编码对西安市的城市路网进行网格划分, 最终将西安市城市路网划分为字符长度为7的23 580个GeoHash网格. GeoHash网格编码划分路网步骤为: (1)提取路段中的各个经纬度坐标点. (2)将经纬度坐标转化为二进制码. (3)通过二进制码计算出经纬度点所对应的GeoHash编码.

GeoHash网格编码划分路网示意图如图1所示. $ e.id = $ 51483710593的路段由 $ {w_i}:i = 1, 2, 3, 4, 5 $ 组成. 经过GeoHash网格编码计算得出 $ {w_1} $ , $ {w_2} $ , $ {w_3} $ 位于GeoHash编码为 ${\rm{wqj6ywc}}$ 的网格中, $ {w_4} $ , $ {w_5} $ 位于GeoHash编码为 ${\rm{wqj6yw9}}$ 的网格中.

2.2 浮动GeoHash网格候选路段的检索

本文采用字符串长度为7的GeoHash网格编码, 通过浮动GeoHash网格的方式来实现对轨迹点候选路段的检索. 随着移动对象位置的变化, 采集到的GPS轨迹点也会随之变化, 由于不同的GPS轨迹点会确定不同的GeoHash网格, 因此当GPS轨迹点在地图上以漂浮移动的方式呈现的时候, GPS轨迹点相对应的GeoHash网格也以漂浮移动的方式呈现出来. 因此将轨迹点候选路段的检索也称为浮动GeoHash网格候选路段检索. 字符长度不同的GeoHash网格具有不同的编码精度^[4], 当字符串长度为7时, GeoHash网格编码的经度和纬度误差都为±0.000 68.

浮动GeoHash网格候选路段的检索的过程如下:

① 将GeoHash网格编码的经纬度误差叠加到轨迹点 $ {g_i} $ 的经度 $ {g_i}.lon $ 和纬度 $ {g_i}.lat $ 上.

② 得到4个经纬度点坐标即 ${w_j} = ({g_i}.lon \pm 0.00068, {g_i}.lat \pm 0.00068), j = 1, 2, 3, 4$ .

③ 通过 $ {w_j} $ 计算出对应的GeoHash网格.

④ 将4个GeoHash网格内的所有路段均作为轨迹点 $ {g_i} $ 的候选路段.

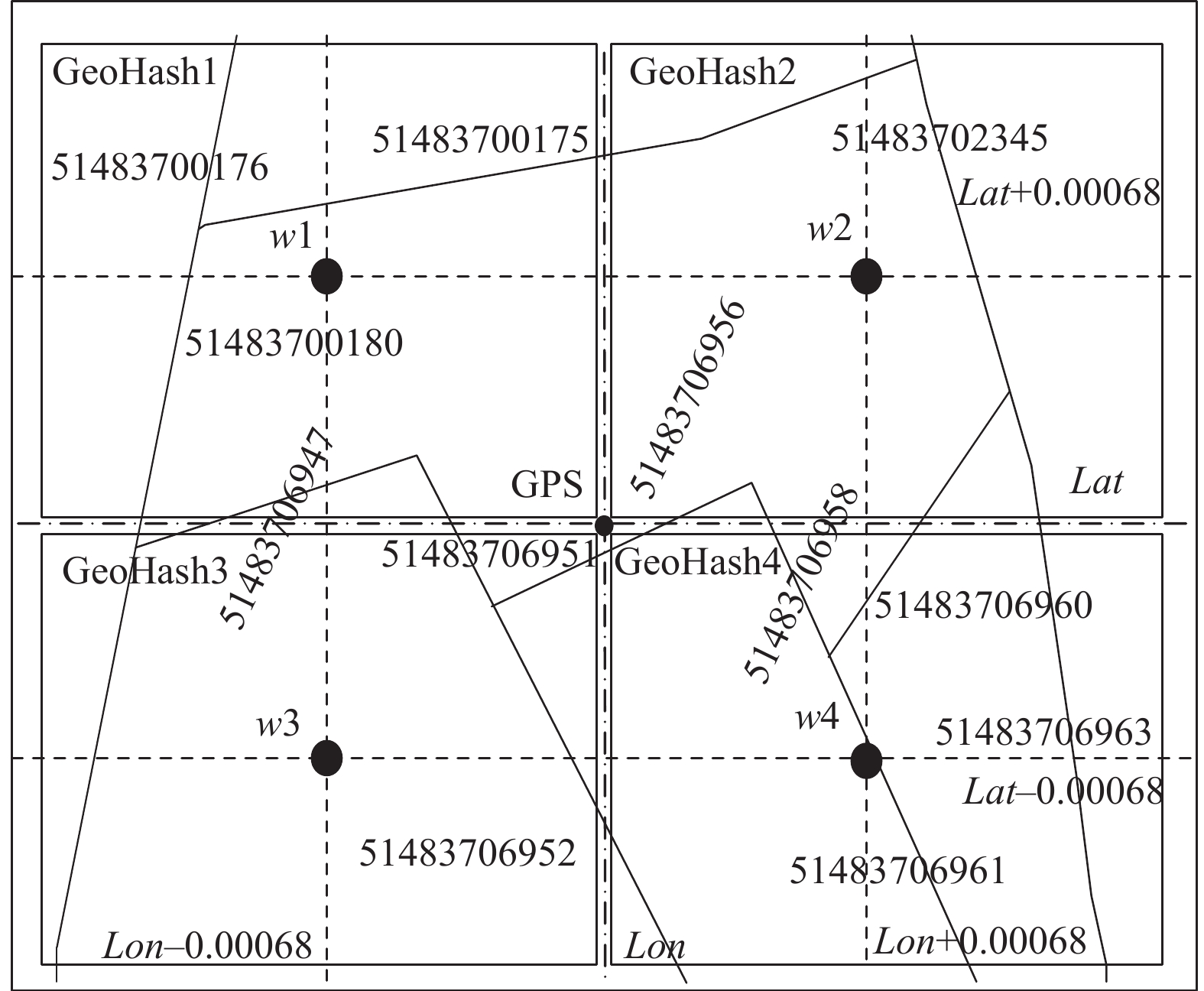
其中浮动GeoHash网格候选路段的检索示意图如图2所示.

综上所述, 浮动网格的路段检索方法由GeoHash网格编码划分路网和浮动GeoHash网格候选路段的检索两部分构成, 其中浮动网格的路段检索方法的伪代码如伪代码1所示.

伪代码1. 浮动网格的路段检索方法的伪代码

输入: 路网 $\scriptstyle G(V, E)$ , 轨迹点 $\scriptstyle {g_i} $

输出: $\scriptstyle {g_i} $ 对应的候选路段集C

1.　/*初始化*/

2.　 $\scriptstyle C \leftarrow \emptyset , Map \leftarrow \emptyset , List \leftarrow \emptyset$

3.　 $\scriptstyle E \leftarrow \left\{ {e\left| {\forall e \in E, e = \left( { {e_i}.lon, {e_i}.lat} \right), i = 1, 2, \cdots, n} \right.} \right\}$

4.　/*GeoHash网格编码划分路网*/

5.　 $\scriptstyle {\rm For}\;{\rm all}\;{ { e} } \in { {E\; {\rm do} } }$

6.　 $\scriptstyle {\rm For}\;j = { { 0\; {\rm to}\; e} }{ {.si{\textit{z}}e} }$

7.　　 $\scriptstyle {{GeoHash } } \leftarrow {\text{ } }\emptyset$

8.　　 $\scriptstyle {{GeoHash } } \leftarrow \left( { {e_j}.lon, {e_j}.lat} \right)$

9.　　 $\scriptstyle {{Map} } \leftarrow \left( {GeoHash, \left( { {e_j}.lon, {e_j}.lat} \right)} \right)$

10.　 $\scriptstyle {\rm End{{ For} }}$

11. $\scriptstyle {\rm End{{ For} } }$

12. /*浮动GeoHash网格候选路段的检索*/

13. $\scriptstyle {{newlon} } \leftarrow \emptyset {{, newlat} } \leftarrow \emptyset$

14. $\scriptstyle newlon \leftarrow {g_i}.lon \pm 0.00068 $

15. $\scriptstyle newlat \leftarrow {g_i}.lat \pm 0.00068 $

16. $\scriptstyle List.append(newlon, newlat) $

17. $\scriptstyle {\rm For}\;m = 0{\text{ to} } \;List { {.si{\textit{z}}e} }$

18.　 $\scriptstyle GeoHash \leftarrow \left( {List(m)} \right) $

19.　 $\scriptstyle C \leftarrow Map(GeoHash) $

20. $\scriptstyle {\rm End{{ For} }}$

21. $\scriptstyle {\text{return} }\; C$

3 隐马尔可夫模型

隐马尔可夫模型(HMM)是一种可以平滑的集成噪声数据和路径约束的算法. 位置观测受到测量噪声的影响, 因此与之对应的真实道路位置是未知的. 这些真实的道路位置被认为是用于地图匹配的HMM中的隐含状态. 理论上, HMM的状态空间将包含道路网络中所有可能的道路位置. 然而, 在实际中, 给定位置观测的状态空间局限于被测位置周围固定范围内的路段. 本文将采样时刻 $ t $ 的第 $ i $ 个状态记为 $ {e_{t, i}} $ .

对于地图匹配, 给定GPS轨迹点 $ {g_t} $ , 每一个候选路段 $ {e_{t, i}} $ 都有观测概率 $ p({g_t}\left| {{e_{t, i}}} \right.) $ , 车辆在采样时刻 $ t - 1 $ 的候选路段 $ {e_{t - 1, j}} $ 到采样时刻 $ t $ 的候选路段 $ {e_{t, i}} $ 存在转移概率 $ p({e_{t, i}}\left| {{e_{t - 1, j}}} \right.) $ . 图3显示了地图匹配的HMM的模型表达, 在采样时刻 $ t $ 时, GPS轨迹点 $ {g_t} $ 的候选路段 $ {e_{t, i}} $ 具有不同的观测概率. 箭头示意各个候选路段之间的转移, 其中不同的候选路段之间的转移具有不同的转移概率.

在HMM中, 可能存在与可观测状态序列一致的多个状态序列. 利用Viterbi算法^[9]可以有效地计算HMM中最可能的状态序列. 在线维特比算法的确定细节如下.

3.1 在线维特比推理

利用维特比算法^[9]可以确定最有可能产生观测状态序列的隐含状态序列. 对拥有 $ k $ 个状态和可观测状态为 $ {g_1}, \cdots, {g_t} $ 的HMM, 状态 $ i $ 的观测概率为 $ p({g_t}\left| {{e_{t, i}}} \right.) $ , 从状态 $ i $ 到状态 $ j $ 的转移概率为 $ p({e_{t, i}}\left| {{e_{t - 1, j}}} \right.) $ , 其中最有可能的状态序列通过以下公式计算得到:

$ {R_{1, K}} = P({g_1}\left| {{e_{1, k}}} \right.) $

$ {R_{t, k}} = P({g_t}\left| {{e_{t, k}}} \right.){\max _j}({R_{t - 1, j}}p({e_{t, k}}\left| {{e_{t - 1, j}}} \right.)) $

其中, $ {R_{t, k}} $ 是前 $ t $ 个最终状态为 $ k $ 的观测结果最有可能对应的状态序列的概率.

3.2 维特比算法的收敛点

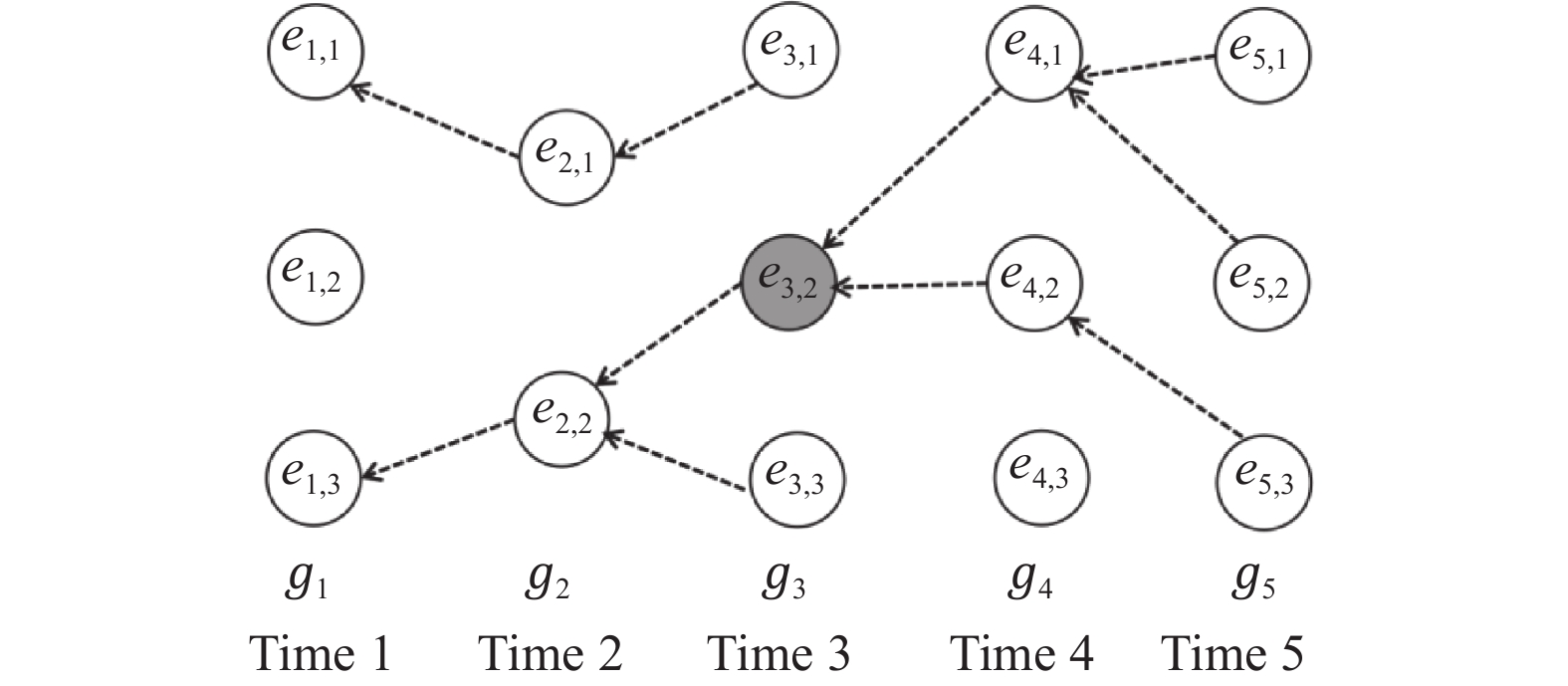
本文针对实时数据流, 无需等待所有观测结果被接收, 不时的生成最可能状态序列的局部最优序列. 本文使用传递闭包^[10]的概念来生成部分最优状态序列, 传递闭包定义了有向图中的可达性关系. 其中传递闭包概念已用于文献[8]中的在线地图匹配. 传递闭包通过检查收敛条件来确定收敛点, 收敛条件为, 若在一个时间步骤中存在一个状态, 该状态可通过来自后续时间步骤的每个状态的一系列反向指针到达, 则将该状态确定为收敛状态. 对于地图匹配, 针对 $ t + j $ 时刻的每个状态 $ {e_{t + j, i}} $ , 经维特比算法计算都会得到一条与 $ t $ 时刻状态 $ {e_{t, i}} $ 相关联的概率最大的连通路径. 将所有的连通路径向前回溯, 若所有的连通路径在某一时刻重合于某一个状态, 即该状态可通过后续时间步骤的每个状态反向指针到达, 则将该时刻对应的轨迹点 $ {g_i} $ 确定为收敛点. 图4显示了收敛点的确定过程.

在Time 5中从任何状态都可以向前回溯到Time 3的状态 $ {e_{3, 2}} $ . 因此将 $ {e_{3, 2}} $ 确定为收敛状态, $ {g_3} $ 确定为收敛点. 到收敛状态 $ {e_{3, 2}} $ 之前的部分序列 $ (即{e}_{1, 3}, {e}_{2, 2}, {e}_{3, 2}) $ , 因为不能被Time 5之后收到的未来观察状态所改变, 所以可以作为部分最优状态序列输出. 在在线模式下, 维特比算法每次发现收敛状态时都可以输出部分最优状态序列. 确定收敛点的伪代码如伪代码2所示.

伪代码2. 确定收敛点的伪代码

输入: 经Viterbi算法计算得到的各个 $\scriptstyle {e_1}, \cdots,e{}_t$ 对应的最大概率矩阵MaxP; 各个 $\scriptstyle {g_1}, \cdots, {g_t}$ 对应的候选路段矩阵R; 最大概率矩阵对应的前置节点矩阵PreR

输出: 收敛点位于 $\scriptstyle {g_1}, \cdots, {g_t}$ 的索引值Index

1./*初始化*/

2. $\scriptstyle index \leftarrow \emptyset $ , $\scriptstyle PathList \leftarrow \emptyset $ , $\scriptstyle Value \leftarrow \emptyset $

3. // $\scriptstyle PathList $ : 从 $\scriptstyle {g_t} $ 的所有的 $\scriptstyle {e_{t, i}} $ 向前回溯得到的路径矩阵

4. /*创建 $\scriptstyle PathList $ 过程*/

5. For $\scriptstyle \;i = { { 0\; {\rm to}\; MaxP} }{ {.si{\textit{z}}e} }$ do

6.　// $\scriptstyle List $ 为存储路径的序列

7.　 $\scriptstyle {{last} } \leftarrow \emptyset$ , $\scriptstyle List \leftarrow \emptyset $

8.　 $\scriptstyle {{last} } \leftarrow {{ MaxP(MaxP} }{{.si{\textit{z}}e - 1)} }$

9.　 $\scriptstyle Value \leftarrow {{ last} }{{.indexOf(last(i))} }$

10.　 $\scriptstyle List \leftarrow append(R(MaxP.si{\textit{z}}e - 1)(Value)) $

11.　For $\scriptstyle \;{j = PreR }{{.si{\textit{z}}e \;{\rm downto}\; 1} }$ do

12.　　　 $\scriptstyle {{List} } \leftarrow { append(PreR(j)(Value)) }$

13.　　　 $\scriptstyle {{Value} } \leftarrow {{ R(j - 1)} }{{.indexOf(PreR(j)(Value))} }$

14.　End for

15.　　 $\scriptstyle {{PathList} } \leftarrow {{ PathList} }{{.append(List)} }$

16. End for

17. /*确定收敛点过程*/

18. For $\scriptstyle \;{ {k = 0\; {\rm to}\; R} }{ {.si{\textit{z} }e} }$ do

19. //temp用来存储 $\scriptstyle PathList $ 矩阵中的每一列数据

20.　　 $\scriptstyle {{temp} } \leftarrow \emptyset$

21.　　For $\scriptstyle \;m = 0{\;{ {\rm to}\; PathList} }{ {.si{\textit{z}}e} }\;$ do

22.　　　 $\scriptstyle temp \leftarrow {{ append(PathList(m)(k))} }$

23.　　End for

24.　　If $\scriptstyle \;temp.distinct.si{\textit{z}}e{ { = 1} }\;$ then

25.　　　 $\scriptstyle index \leftarrow R.si{\textit{z}}e - k - 1$

26.　　　 $\scriptstyle {\rm Output}{\;{ index} }$

27.　End If

28. End for

4 实验与分析

本文使用的实验数据集为陕西省西安市的出租车轨迹数据. 该轨迹数据共包含1辆出租车在一天内的1 052条轨迹数据. 其中轨迹数据特征如表1所示. 实验条件为一台配备intel Core I5-7300HQ @2.50 GHz处理器以及16 GB内存的PC.

4.1 预处理

在低频采样环境下, 无法使用更多的信息来推断物体的精确位置. 为了应对上述情况, 我们提供了3个关键措施.

(1)道路的拓扑结构: 正确的路径是在各个路段之间具有连通性. 通过道路网路的拓扑结构, 可以确定各个路段之间的连接情况, 然后计算出在连续两个轨迹点之间的最短路径.

(2)轨迹数据清洗: 对原始的轨迹数据实行以下操作: 去除重复数据、去除位置和速度异常的数据、对乱序的数据进行排序.

(3)时空约束条件: 在实践中, 真正的路径往往遵循道路的空间和时间限制. 1)连续的轨迹点 $ {g_1} $ 和 $ {g_2} $ , 在采样间隔 $ {g_2}t - {g_1}t = {T_s} $ 内, 按照交通规则, 不同的道路等级有其对应的最大限速 $ {V_{\max }} $ , 在最大限速 $ {V_{\max }} $ 的约束下, 轨迹点 $ {g_1} $ 和 $ {g_2} $ 之间的路径距离应满足 ${l_{{g_1}{g_2}}} \leqslant {T_S}\times{V_{\max }}$ . 2)我们假定车辆在每个交叉路口延时5 s, 则在固定的采样间隔 $ {g_2}t - {g_1}t = {T_s} $ 内, 两个轨迹点的连通路径之间最多经过的路口数量为 $ {T_s}/5 $ . 通过时空约束条件, 可以过滤掉不符合条件的候选路段.

4.2 隐马尔可夫概率模型估计

本文为了验证方法的可行性, 利用HMM 通过Viterbi算法来进行地图匹配. 在计算HMM中的观测概率和转移概率时延用Newson等人^[7]的结论, 最终将观测概率建模为零均值高斯分布, 将转移概率建模为指数分布. 其中概率模型的参数设置也与Newson等人^[7]保持一致.

4.3 实验结果

下面将本文所提出的候选路段检索方法与文献[4]和文献[1]所提出的候选路段检索方法, 在30 s的采样时间间隔下, 进行了分析对比. 为方便起见, 本文将对比文献[4]所提出的候选路段检索方法称为对比方法1, 将对比文献[1]所提出的候选路段检索方法称为对比方法2.

4.3.1 轨迹点的候选路段数量和收敛点分析

针对30 s采样时间间隔的实验数据集, 本文首先分析了各个轨迹点对应的候选路段数量的数理特征, 将本文所提出的方法与对比方法1和对比方法2进行了分析比较, 分析结果如图5所示. 其结果表明, 对于各个轨迹点对应的候选路段数量的数理特征, 本文所提出的方法在平均值、中位数、众数和方差都低于对比方法1. 因此相比于对比方法1, 本文方法可以有效的降低候选路段的数量. 此外对比方法2在选取轨迹点的候选路段时, 是以半径为50 m的圆作为候选区域, 该方法的优势为降低了轨迹点的候选路段数量, 但是当轨迹点噪声较大时, 由于候选区域过小使得正确的匹配路段不在候选区域中, 从而导致地图匹配准确率下降, 这一点将在第4.3.3节中说明.

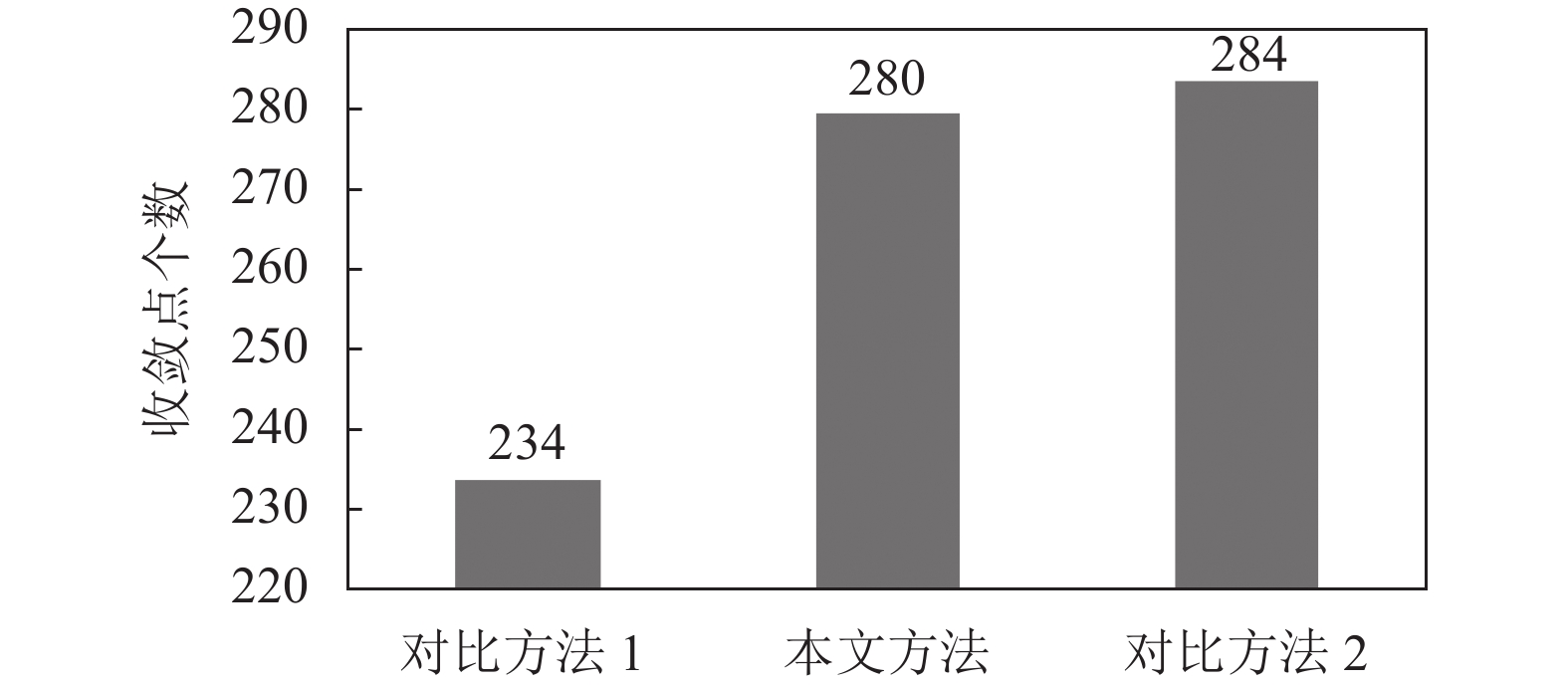
其次我们在实验中发现, 轨迹点候选路段的数量会直接影响维特比算法的收敛点个数. 本文针对全部实验数据集, 从维特比算法的收敛点个数出发, 对本文所提出的方法与对比方法1和对比方法2做了比较, 其结果如图6所示. 结合图5, 从图6显示的结果发现, 随着轨迹点候选路段数量的增加, 其维特比算法收敛点的个数会随之降低.

4.3.2 地图匹配算法的执行时间分析

对于隐马尔可夫模型, 在计算车辆从采样时刻 $ t - 1 $ 的状态 $ {e_{t - 1, j}} $ 到采样时刻 $ t $ 的状态 $ {e_{t, i}} $ 之间的转移概率时, 需要依赖于两个轨迹点之间的最短路径长度. 本文采用Dijkstar算法^[11]来完成两个轨迹点之间的最短路径搜索, 并将搜索结果离线保存. 因此本文的地图匹配算法的执行时间不包含最短路径的搜索时间.

本文针对地图匹配算法的执行时间, 在30 s采样时间间隔的实验数据集下, 首先以固定的轨迹点个数200为步长, 将实验数据集划分为5个子数据集. 其次从5个子数据集出发, 将本文所提出的候选路段检索方法与对比方法1和对比方法2进行了实验分析. 分析结果如图7所示.

图7的结果表明, 本文所提出的候选路段检索方法, 在不同的轨迹点个数下, 均有效提高了地图匹配效率. 由图5的结果表明, 对比方法2中轨迹点的候选路段数量最少, 但是由于对比方法2未对城市路网进行划分, 所以在检索候选路段时, 需要针对每个轨迹点遍历城市路网中的所有路段, 因此很大程度上降低了候选路段的检索速度, 这也正是对比方法2的地图匹配算法执行时间最长的原因.

4.3.3 地图匹配算法的准确率分析

本文将地图匹配的准确率定义为正确的匹配路段个数 ${N_{\rm correct}}$ 与所有轨迹点的对应的匹配路段个数 ${N_{\rm all}}$ 的比值即:

$ Accuracy = {N_{\rm correct}}/{N_{\rm all}} $

下面将本文所提出的候选路段检索方法与对比方法1和对比方法2, 从地图匹配算法的准确率出发, 在30 s的采样时间间隔的全部实验数据集下, 进行了实验对比. 对比结果如表2所示.

由图5和图6表明, 维特比算法的收敛点个数依赖于候选路段的数量, 这意味着, 当候选路段数量增加时, 满足收敛条件需要的轨迹点个数, 即两个相邻的收敛点之间的轨迹点数量也会随之增加. 这就会导致当一些轨迹点出现在如平行路段或十字交叉路口等匹配错误率高的路段时, 在维特比算法计算得到的局部最优解条件下, 一旦其中一个路段出现匹配错误, 就会导致一系列的路段匹配错误, 这也正是表2中对比方法1相比本文方法地图匹配算法准确率较低的原因. 此外对比方法2由于轨迹点的候选路段检索区域过小, 因此在轨迹点噪声较大的情况下, 会导致其正确的匹配路段不在候选路段集合中, 这也正是对比方法2的地图匹配算法准确率相较本文方法低的原因.

5 结论

本文提出了一种基于浮动网格的路段检索方法. 该方法采用浮动GeoHash网格来计算轨迹点的候选路段, 使得轨迹点的候选路段选取变得更具有灵活性. 同时该方法有效地解决了当轨迹点的候选路段选取区域小时, 会导致正确的匹配路段不会出现在选取区域中, 降低地图匹配准确率的问题; 当选取区域大时, 又会增大候选路段集合中的不相关路段数量, 降低候选路段检索效率的问题. 经上述实验结果表明, 该方法并不会因为轨迹点噪声或轨迹点偏离正确匹配路段较远而导致正确的匹配路段被遗漏, 同时因为减少了不必要的候选路段, 因此有效提高了地图匹配的效率.