随着科学技术的飞速发展, 图像匹配技术^[1,2]在不同领域被广泛应用, 其不仅是一项重要的技术, 也是图像处理的一门关键技术. 图像匹配被大量应用于交通监控、医学影像和图像拼接等领域^[3-5], 所以图像匹配技术成为研究的重点和热点. 图像匹配算法主要有两类, 分别是基于灰度和基于特征点的图像匹配^[6], 而后者发展较成熟, 也是目前的研究中的重点^[7], 并且其算法主要有SIFT、SURF和ORB等算法, Lowe提出的SIFT算法^[8]具有很好鲁棒性, 但是特征描述符向量维数高、算法运行时间长且匹配正确率低; Bay等人在优化SIFT算法的基础上, 提出了SURF算法^[9], 该算法将特征描述符维数降低为SIFT算法的一半, 且具有较好的尺度不变性和抗干扰性, 但还是存在匹配正确率低, 计算量大等问题; ORB算法^[10,11]虽然大大提高了运行速率, 但是鲁棒性差, 匹配效果不稳定. 因此, 黄春凤等人提出了改进的SURF算法^[12], 先采用BBF结合Kd-Tree算法快速找出特征点, 并利用双向唯一性匹配实现图像匹配, 再对特征点初始匹配对利用视差梯度剔除掉误差较大的匹配对, 最后使用RANSAC算法进一步提纯匹配对, 达到匹配精度提高的效果. 赵谦等人提出了改进的SURF-RANSAC图像匹配算法^[13], 通过自适应阈值方法来初步匹配特征点, 再用特征向量构建余弦约束对RANSAC算法进行改进, 实现初匹配对提纯, 最终完成图像匹配, 算法速度和精度得到了有效提高.

基于上述分析, 提出了一种改进SURF的图像匹配算法. 通过降低SURF特征描述符维度来减少特征点提取和匹配运行时间, 并用KNN算法对图像特征点进行双向初匹配, 再用RANSAC算法双向剔除初匹配对中的错误匹配对, 来提高特征的匹配正确率. 实验结果表明, 该算法减少了特征点检测时间, 提高了匹配正确率, 还有较好的鲁棒性.

1 传统SURF特征点提取基本原理

SURF算法是对SIFT算法进行优化操作, 利用了积分图像去减少一定的计算量, 提高运行速度^[14]. 该算法首先创建Hessian矩阵, 生成兴趣点, 之后再构建尺度空间, 根据非极大值抑制和插值操作, 精确找到特征点的位置; 构造以特征点为圆心的圆形方形邻域, 统计邻域内的Haar小波响应值, 为特征点指定主方向; 最后, 生成描述符向量. 算法主要有以下几个步骤.

1.1 生成积分图

假设 $ l\left( {x, y} \right) $ 为图像中任意位置像素点, 即其积分图像 $ {l_{\sum {} }}(x, y) $ 为该像素点到原点整个矩形区域内(如图1所示)所有像素值之和, 公式如式(1):

$ {l_{\sum {} }}(x, y) = \sum\nolimits_{i = 0}^{i \leqslant x} {\sum\nolimits_{j = 0}^{j \leqslant y} {l(x, y)} } $

(1)

对图1中的方形ABCD的面积中每个像素点的灰度值求和, 公式如式(2):

$ \sum {} = {l_{\sum {} }}(A) - {l_{\sum {} }}(B) + {l_{\sum {} }}(C) - {l_{\sum {} }}(D) $

(2)

1.2 定位特征点

SURF算法中, 特征点的提取时, 主要利用积分图像计算图像中的每个像素点的 Hessian 矩阵进行操作, 具体流程如下.

(1) 给定一幅图像I中某点 $ l = (x, y) $ , 在该点l处且尺度为 $\sigma $ 的Hessian矩阵 $ H = (l, \sigma ) $ 为:

$ H(l, \sigma ) = \left[ {\begin{array}{*{20}{c}} {{L_{xx}}(l, \sigma )}&{{L_{xy}}(l, \sigma )} \\ {{L_{xy}}(l, \sigma )}&{{L_{yy}}(l, \sigma )} \end{array}} \right] $

(3)

其中, 参数 $ {L}_{xx}(l, \sigma )、{L}_{xy}(l, \sigma ) $ 和 $ {L_{yy}}(l, \sigma ) $ 分别是高斯二阶微分 $ \dfrac{{\partial }^{2}g(\sigma )}{\partial {x}^{2}}、\dfrac{{\partial }^{2}g(\sigma )}{\partial x\partial y}、\dfrac{{\partial }^{2}g(\sigma )}{\partial {y}^{2}} $ 在点 $ l = (x, y) $ 处与图像I做卷积.

(2) 要求在不同尺度空间的同一图像上检测特征点, 来实现特征点的一个重要性质, 即它的尺度不变性. 首先, 如图2所示, 利用盒子滤波器 $ ({D}_{xx}、{D}_{yy}、{D}_{xy}) $ 类似地去替换高斯滤波器 $ ({L}_{xx}、{L}_{yy}、{L}_{xy}) $ , 图像的尺度空间可以通过不同尺寸大小的盒状滤波器和不同方向的积分图像做卷积运算来构造.

(3) 根据Hessian矩阵的和行列式来提取极值点, 由于盒子滤波器的类似替换, 此时的行列式需要加上权值, 即:

$ det (H) = {D_{xx}}{D_{yy}} - {(w{D_{xy}})^2} $

(4)

其中, w为权值, 它的取值一般为0.9.

(4) 在极值点的上下层的 $ 3 \times 3 \times 3 $ 立体邻域进行极大值抑制, 初步确立特征点, 再通过插值操作, 最后确定特征点精确位置和尺度.

1.3 确定特征点主方向

以精确的特征点作为将要构造的圆形区域的原点, 在它的周围建立一个大小为6尺度的半径的圆形区域, 然后计算它的区域内所有像素点所对应的Haar小波的响应值, 再用一个60°扇形区域在圆形区域转动一样大小的度数, 累加该区域内所有的响应值, 得到最大的值设定为主方向. 方法见图3.

1.4 生成特征点描述符

检测到的特征点的信息需要用特征向量来描述. 首先, 构造一个边长大小为20尺度的正方形邻域, 并且特征点在其中心位置, 然后使它的方向转动到特征点的主方向上, 对其划分为16个子区域, 然后用Harr计算出每个小区域的所有像素点在x和y方向上的响应, 并且统计小区域的总响应, 得到一个如下的4维特征向量:

$ v = \left[ {\sum {dx, \sum {dy, } \sum {\left| {dx} \right|, } \sum {\left| {dy} \right|} } } \right] $

(5)

最后把所有子区域的4维特征向量放在一起, 就形成了SURF特征点的64维度的特征描述符.

2 本文算法

在传统的SURF算法里面, 关于特征点的描述符是指一个64维度的向量, 存在维数高, 时效性差等问题, 因此需对其进行改进. 本文提出的图像匹配算法, 主要包括SURF特征点检测、SURF特征描述符降维、双向初匹配、匹配点对双向提纯. 图像匹配的流程图如图4所示.

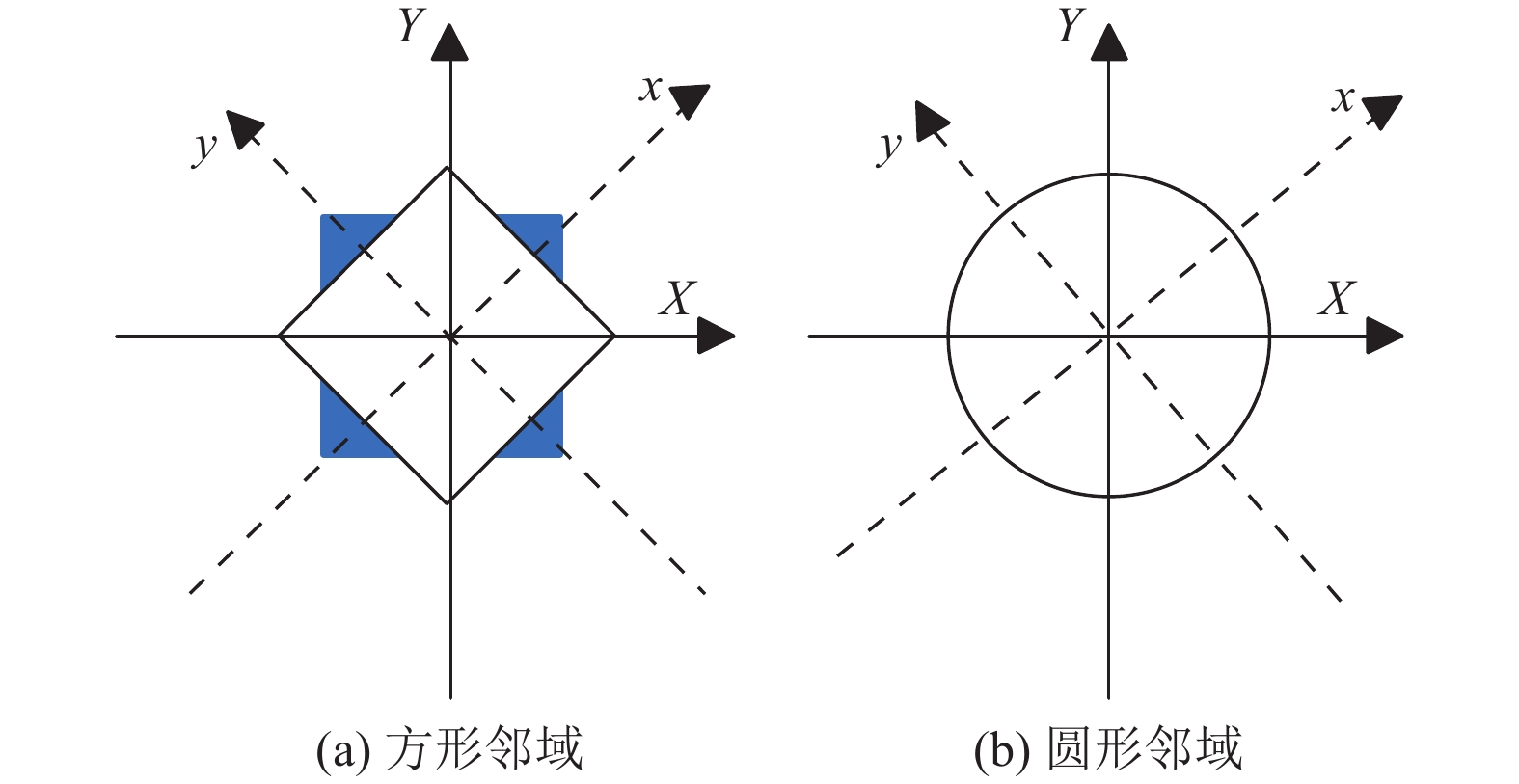
2.1 SURF特征描述符降维

针对传统的SURF特征点检测算法数据复杂, 导致特征点提取以及匹配运行时间长, 本文算法先将改进其描述符的构建过程, 对其实现一个维度的降低处理. 传统SURF算法对描述符计算统计响应的区域采用的是方形邻域, 如图5(a)所示, 这样在确定特征点主方向出现偏差时, 响应的区域也会出现不一样, 从而会产生误差.

因此, 为了解决这类问, 本文算法采用圆形邻域代替方形邻域来计算特征描述符, 圆形邻域旋转前后的区域都不会产生变化, 如图5(b) 所示, 不会引起误差, 也具有较好的旋转不变性.

本文针对SURF描述符构建过程的改进及降维处理具体步骤如下:

(1) 以特征点作为将要构建的圆形领域的圆心, 分别建立外圆直径为10尺度、15尺度、20尺度的圆形邻域. 由于尺度越大, 算法运算速度就随之变慢, 所以圆形邻域的直径选取10尺度. 为了确保旋转不变性, 必须使构建的邻域转动到与特征点主方向一致的方向上.

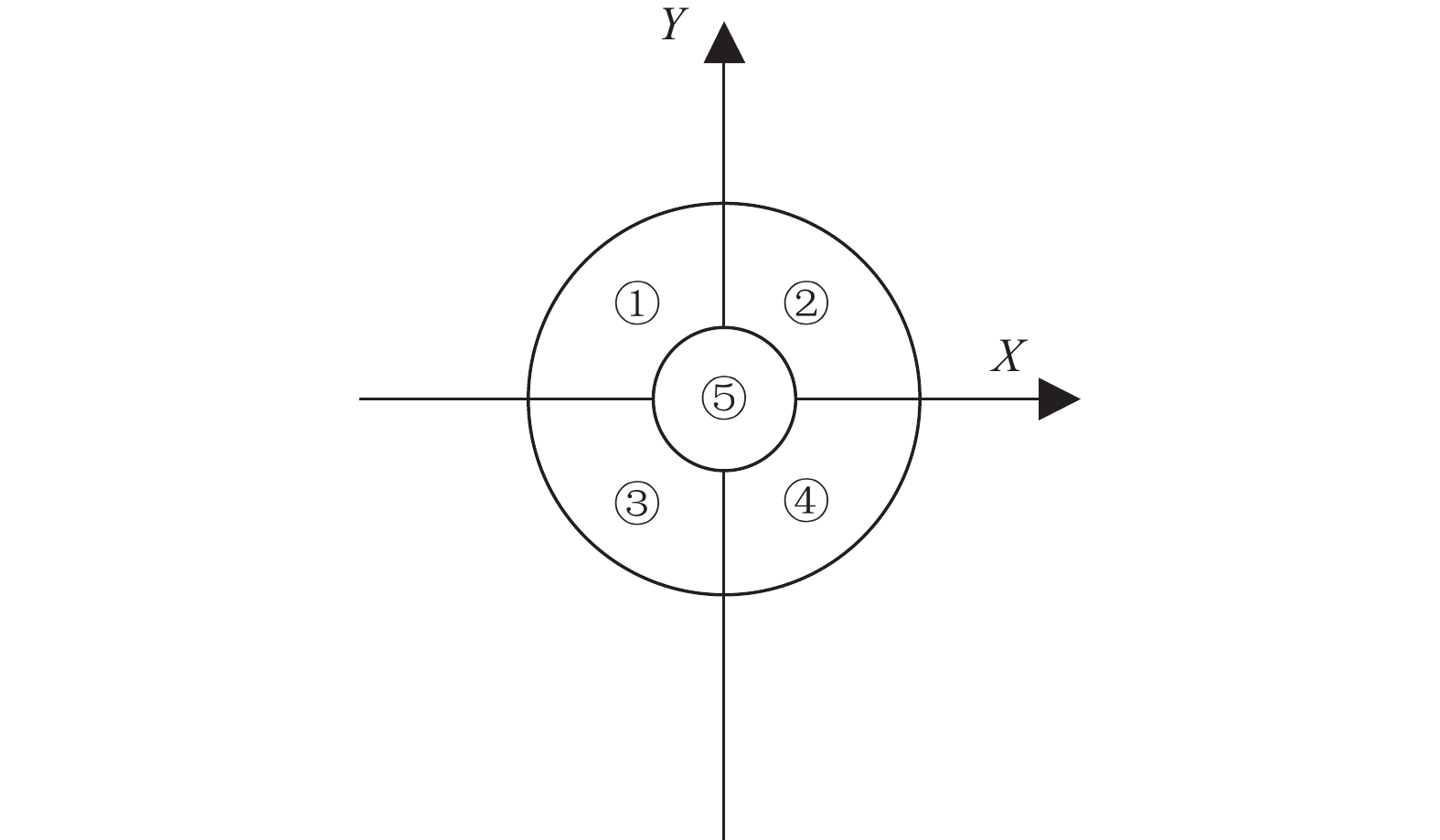
(2) 将圆形邻域划分为5个子区域模块, 编号分别为①–⑤, 其中内圆直径为 $ 2\sqrt {10} $ 尺度为一个子区域, 如图6所示.

(3) 用Haar小波来计算①–⑤区域内的所有采样像素点x方向和y方向的响应值, 定义为dx和dy, 并且进行高斯加权. 最后将相应子区域内所有像素的dx、dy、|dx|和|dy|进行累加, 即可得到一个特征向量, 维度为4维. 5个子区域就可以形成20维的特征点描述符, 表示如式(6):

$ P = [{p_1}, {p_2}, \cdots, {p_{20}}] $

(6)

最后将20维的特征矢量做归一化操作, 公式如式(7):

$ \overline P = \frac{P}{{\sqrt {\displaystyle \sum\nolimits_{i = 1}^{20} {p_i^2} } }} = (\overline {{p_1}} , \overline {{p_2}} , \cdots, \overline {{p_{20}}} ) $

(7)

2.2 KNN双向初匹配

传统的SURF算法依据欧氏距离作为参考度量进行特征点匹配, 公式如式(8):

$ d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $

(8)

本文采用KNN算法^[15], 该算法主要是将待匹配图像中其中某张图像的特征点来匹配另一张图像的特征点, 由于缺少双向唯一匹配性原则的考虑, 在实际操作过程中, 可能会出现图像的反向匹配, 从而出现图像特征点的匹配对不一致, 所以该算法存在许多误匹配, 所以本文算法对需匹配图像特征点进行一个双向的初匹配, 得到初始双向匹配对集合. 设参照图像I₁和被参照图像I₂的特征点集合分别为 $ P = ({P_1}, {P_2},\cdots, {P_N}) $ 和 $ Q = ({Q_1}, {Q_2}, \cdots, {Q_N}) $ , 本文采用KNN双向初始匹配具体流程如下:

(1) 对图像I₁中某一个特征点a, 通过2-最近邻法, 得到与待图像I₂中所有特征点的最近点m距离值d_m与次近点n距离值d_n, 设置阈值T. 如果 $ ({{{d_m}} \mathord{\left/ {\vphantom {{{d_m}} {{d_n}}}} \right. } {{d_n}}}) < T $ , 则将m作为a的匹配点; 否则, 进行图像I₁的下一个匹配, 并且剔除点a. 得到图像I₁到图像I₂的初始匹配点对集A.

(2) 对图像I₂中所有特征点作步骤(1)同样的处理, 得到图像I₂到图像I₁的初始匹配集B. 由此可以获取到两个初始匹配点对集合A和B.

由图7和图8可见, 2NN初步匹配存在大量误差, 所以需要使用RANSAC算法对初匹配对集合进行提纯, 删除不正确的匹配对, 最终得到更加准确的匹配对.

2.3 RANSAC双向提纯

RANSAC算法是一种随机抽样一致性算法, 具有精确度高的特点, 且常用于图像匹配中消除误匹配^[16]. 利用RANSAC算法提纯匹配对, 要计算出一个单应性矩阵, 记作H, 且大小为 $ 3 \times 3 $ . 为了求出一个适用数据点个数最多的最优参数矩阵, 一般设 $ {h_{22}} = 1 $ 对矩阵进行归一化, 即参数方程如下:

$ s\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{y_1}} \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{h_{00}}}&{{h_{01}}}&{{h_{02}}} \\ {{h_{10}}}&{{h_{11}}}&{{h_{12}}} \\ {{h_{20}}}&{{h_{21}}}&1 \end{array}} \right] $

(9)

其中, s为尺度参数, (x₁, y₁)为目标图像的某一角点坐标, (x₂, y₂)为场景图像的某一角点坐标. 由于初始双向匹配对集合中存在大量错误匹配对, 因此需要采用RANSAC算法完成一个错误匹配对筛选的处理, 得到一对初始优化的匹配对集合. 此时, 初始优化的匹配对集合中的对数并不相同, 仍都存在少量不正确的匹配对, 需要双向提纯来二次优化匹配对, 来提高匹配正确率.

本文采用的是RANSAC进行双向筛选匹配, 主要流程如下:

(1) 从初匹配点对集合A中随机选取4个样本匹配点对, 根据样本算出单应性矩阵H, 记为模型M.

(2) 利用这个模型去测试初匹配点对集合A中匹配点对, 计算集合A中的数值与模型M的偏差e, 设立阈值m, 如e小于m, 则视之内点, 加入内点集合C.

(3) 如果最佳内点集合元素小于当前内点集合C总元素个数, 则将内点集C更新为最佳内点集, 并使迭代次数k加1.

(4) 如果迭代的次数多于k, 则终止操作; 否则k加1, 用当前内点集合去重新估计模型, 重复上述(2)–(4)过程, 直至迭代终止, 其中k计算公式如式(10):

$ k = \frac{{\log (1 - p)}}{{\log (1 - {w^m})}} $

(10)

(5) 获取初匹配点对集合A的内点集, 记为初提纯匹配点对集 ${A{'}}$ ; 再将初匹配点对集合B进行步骤(1)–(4), 获取集合B的内点集, 同时记为初提纯匹配点对集 ${B{'}}$ .

(6) 假设集合 ${A{'}}$ 中某一匹配点对为keypoint1和keypoint2, 分别为图像I₁和图像I₂的特征点; 假设集合 ${B{'}}$ 中某一匹配点对为keypoint3和keypoint4, 分别为图像I₂和图像I₁的特征点; 若keypoint1=keypoint4且keypoint2=keypoint3, 该对匹配点匹配成功; 否则, 剔除该对匹配点. 这样总匹配对数会减少, 但匹配的准确率会得到提高.

3 实验结果与分析 3.1 实验环境

本算法实验环境为AMD Ryzen 55600 with Radeon Graphics, 内存16 GB, 显卡为 AMD Radeon^TM Graphics 2 GB, 系统为64位Windows 11, 仿真平台为Visual Studio 2017.

3.2 性能分析

为了验证本文算法的鲁棒性, 从用来测试图匹配算法的性能的Mikolajczyk图像集合中任意选取4组图像. 图9本文算法对尺度和旋转发生变换、光照发生变换、模糊变化的图像和仿射变换的图像进行匹配结果图.

从以上实验的匹配效果图9显示, 能够得出本文算法对缩放、旋转、光照、模糊、仿射、视角变化等情况都具有很好的匹配效果, 匹配正确率均在以上, 因此本文算法在不同的干扰下具有较强的鲁棒性.

从表1 显示, 本文算法与传统的SURF算法相比, 特征点检测和算法运行时间都有所提高. 这是本文算法将传统算法中方形邻域更改为圆形邻域去构建描述符, 增强了算法的旋转不变性. 将特征描述符降至20维度, 减少了数据复杂度, 从而减少算法运算时间.

由以下不同算法的匹配效果图10对比可以看出, SURF匹配算法和文献[7]匹配算法的都存在明显的错误匹配点对. 本文算法的匹配效果图为图10(c)所示, 几乎不存在错误匹配点对. 表2是SURF算法、文献[7]算法和本文算法实验的匹配正确率对比表, 从表中可以看出本文算法由于采用KNN双向初始匹配, 并且结合RANSAC双向剔除误匹配, 减少了伪匹配点对, 提高了匹配正确率.

4 结论与展望

本文研究了一种改进SURF的图像匹配算法, 能有效改善传统SURF算法的描述符纬度高、存在计算量大, 匹配正确率低等问题. 首先, 采用传统的SURF检测图像的特征点, 在构建特征描述符阶段, 用圆形区域代替矩形区域, 将SURF的64维度描述符降到20维度, 增强了算法的旋转不变性, 减少了数据复杂度和算法运算时间; 然后, 通过KNN算法对图像进行双向匹配, 得到双向初匹配点对; 最后, 通过RANSAC算法对初匹配点对进行双向删除错误匹配对, 从而来提高算法的匹配正确率. 实验结果表明, 该算法降低了特征点的检测时间, 具有较好的鲁棒性, 同时还增加了匹配的正确率. 下一步工作, 将对算法的匹配效率和自适应方面进行进一步优化, 并将其应用于自动图像匹配中.