随着互联网技术的发展, 数字图像作品可轻易获取且传播便捷. 然而, 互联网在给人们带来便利的同时, 也带来了盗版、泄露等安全问题. 数字水印技术凭借其版权保护和内容认证功能得到了广泛关注. 从是否修改载体图像角度, 数字图像水印大致分为两类: 一类是传统的通过修改载体图像部分内容实现数字图像水印技术, 该类水印算法在鲁棒性与透明性上存在着不可避免的矛盾. 另一类是在不修改载体图像的情况下来构造水印, 即利用图像的重要特征来构造水印信息.
早在2003年, 零水印的概念被提出[1], 其主要思想是利用图像的特征构造可以唯一识别的水印, 在水印的嵌入过程中不改变原始图像的任何信息, 同时具有更好的透明性. 因此使用零水印算法可以较好地解决水印的鲁棒性和透明性之间的矛盾, 这已成为水印技术的一个研究热点.
1 相关工作零水印算法的关键在于特征提取, 目前零水印图像特征提取方法大致分为以下3类. 第1类是基于使用极谐变换计算图像的不变矩特征, 如极谐运算(polar harmonic transform, PHT)[2]、四元数极谐傅里叶矩(quaternion polar harmonic Fourier moment, QPHFM)[3]、四元数径向分数Charlier矩(quaternion radial fractional Charlier moment, QRFrCM)[4]、小数阶极谐变换(decimal-order polar harmonic transform, DoPHT)[5]等, 该类方法直接由空域中提取到的图像特征, 由图像的整体的均值与子块的均值的稳定关系来构造图像特征. 第2类是基于变换域特征, 如傅里叶变换(Fourier transform, FT)[6]、Gabor变换、平移不变剪切变换(SIFT)[7]、元胞自动机变换(cellular automata transform, CAT)[8]、尺度不变特征变换(shift invariant shearlet transform, SIST)[9]、非亚采样轮廓波变换、轮廓波变换(contourlet transform, CT)[10]、双树复小波变换等(dual-tree complex wavelet transform, DTCWT)[11]等. 第3类是在对图像进行一定的处理之后得到一部分稳定的系数, 即可将之直接构造为图像和的具体特征, 如将这些系数进行奇异值分解(singular value decomposition, SVD)、离散余弦变换(discrete cosine transform, DCT)等处理方法之后提取出其稳定的能量做为图像的特征.
He等人[12]利用DWT的高频和低频特点提出了抗压缩水印算法, 该算法具有较好的鲁棒性. Wei等人[13]提出了基于DCT和DFT的水印算法, 该算法具有较好的嵌入能力. Sun等人[14]提出了一种基于NSST和DCT的鲁棒零水印算法, 该算法将二值水印与彩色图像特征矩阵进行异或操作来构造零水印, 该算法鲁棒性较强. Amiri等人[15]提出了一种基于NSCT-SVD的智能零水印算法, 该算法利用PSO-GA-AI来提取特征构造零水印, 该算法具有较高图像质量. Wu等人[16]提出了一种基于区块链和NSCT-SVD的视频零水印算法, 该算法具有较好的鲁棒性.
上述零水印算法所提取特征具有一定的稳定性, 但是在特殊的情况下, 如所保护图像的数目比较多或者图像的相似度比较高时, 可能会出现图像的虚警问题, 即受攻击图像的零水印与虚警图像的零水印的区分性比较低, 存在将未受保护的图像误识为已受保护的图像的概率.
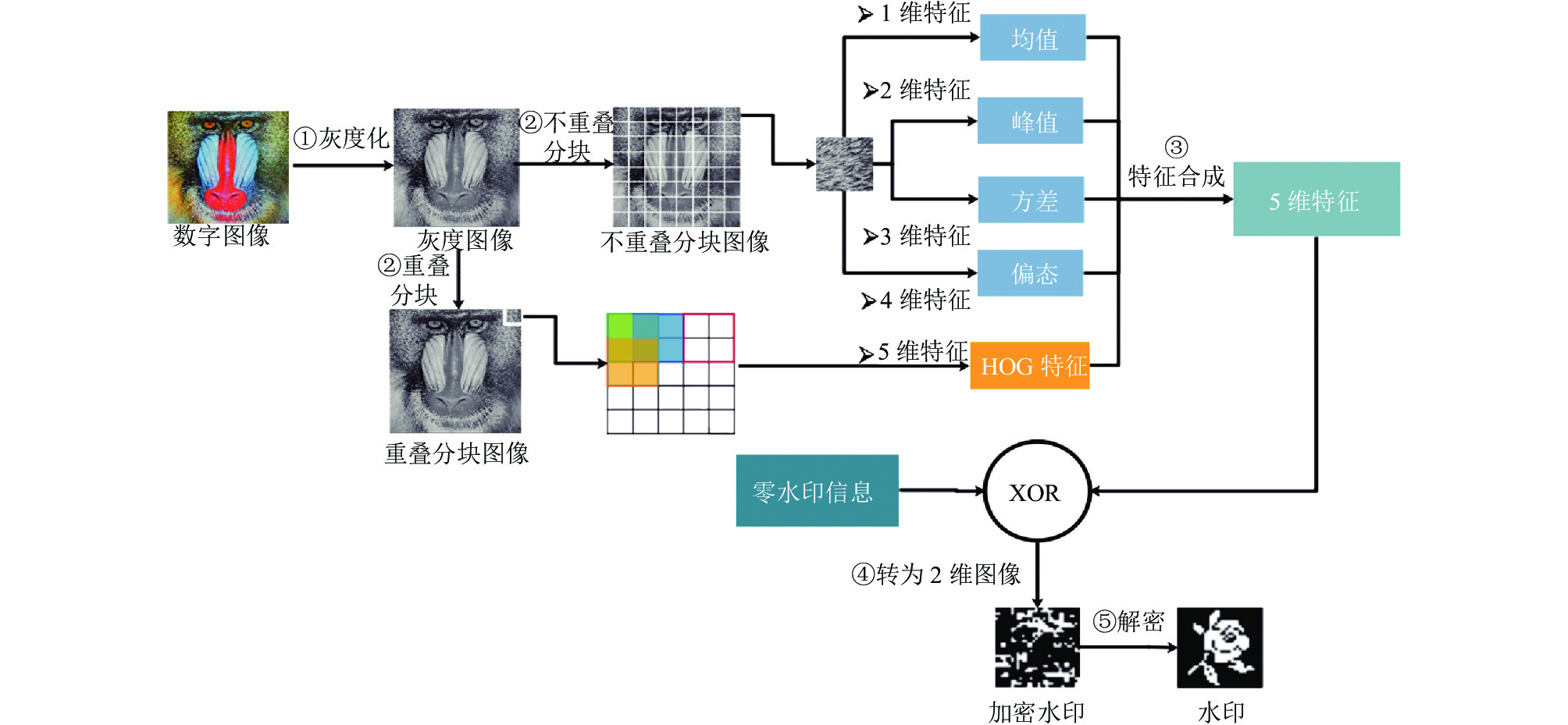
为提升不同图像零水印的可区分性. 本文提出了一种区分性较高的特征提取策略, 具体流程如下: 首先对彩色数字图像灰度化, 然后按照整体特征提取思想, 将灰度图像不重叠分块, 分别提取图像的1维均值特征、2维峰值特征、3维方差特征、4维偏态特征, 按照局部特征提取的思想, 将灰度图像重叠分块, 提取5维HOG特征, 结合基于混沌映射的块置乱加密算法, 最终构造零水印信息, 即可进行版权认证, 如图1所示. 试验结果表明, 该算法在抵抗常规攻击和滤波攻击中取得了很好的效果.
2 多特征提取为更全面得到图像的特征向量, 从不同角度对图像进行特征向量提取. 从整体的角度提取图像的均值特征、方差特征、偏态特征、峰度特征, 从局部角度HOG特征, 从而合成5维特征, 以此构造零水印信息.
2.1 图像不重叠分块假设载体图像I尺寸为m×n, 水印图像
每个分块的均值
| ˉxk=1NkNk∑i=1Ck(i) | (1) |
其中,
统计数据均值的残差
| Dˉx(k)=ˉxk−1−ˉxk | (2) |
整个图像
| ˉX=1m×nm×n∑i=1I(i) | (3) |
其中,
每个分块的均值特征向量
| Bˉx(k)={1,0,Dˉx(k)>ˉXDˉx(k)⩽ | (4) |

|
图 1 基于多特征和块置乱的零水印算法流程图 |

|
图 2 不重叠分块 |
2.3 2维特征——方差
每个分块的方差
| {\delta _k} = \frac{1}{{{N_k} - 1}}\sum\limits_{i = 1}^{{N_k}} {{{({C_k}(i) - \bar X)}^2}} | (5) |
统计数据方差的残差
| \begin{split} \\ {D_\delta }(k) = {\delta _{k - 1}} - {\delta _k} \end{split} | (6) |
整个图像
| \delta = \frac{1}{{m \times n - 1}}\sum\limits_{i = 1}^{m \times n} {{{(I(i) - \bar X)}^2}} | (7) |
每个分块的方差特征向量
| {B_\delta }(k) = \left\{ {\begin{array}{*{20}{c}} \begin{gathered} 1, \\ 0, \\ \end{gathered} &\begin{gathered} {D_\delta }(k) > \delta \\ {D_\delta }(k) \leqslant \delta \\ \end{gathered} \end{array}} \right. | (8) |
每个分块的偏态
| {s_k} = \frac{{\dfrac{1}{{{N_k}}}\displaystyle\sum\limits_{i = 1}^{{N_k}} {{{({C_k}(i) - \bar X)}^3}} }}{{{{\left( {\sqrt {\dfrac{1}{{{N_k}}}\displaystyle\sum\limits_{i = 1}^{{N_k}} {{{({C_k}(i) - \bar X)}^2}} } } \right)}^3}}} | (9) |
统计数据偏态的残差
| {D_s}(k) = {s_{k - 1}} - {s_k} | (10) |
整个图像
| s = \frac{{\dfrac{1}{{m \times n}}\displaystyle\sum\limits_{i = 1}^{m \times n} {{{(I(i) - \bar X)}^3}} }}{{{{\left( {\sqrt {\dfrac{1}{{m \times n}}\displaystyle\sum\limits_{i = 1}^{m \times n} {{{(I(i) - \bar X)}^2}} } } \right)}^3}}} | (11) |
每个分块的偏态特征向量
| {B_s}(k) = \left\{ {\begin{array}{*{20}{c}} \begin{gathered} 1, \\ 0, \\ \end{gathered} &\begin{gathered} {D_s}(k) > s \\ {D_s}(k) \leqslant s \\ \end{gathered} \end{array}} \right. | (12) |
每个分块的峰度
| {\omega _k} = \frac{{\dfrac{1}{{{N_k}}}\displaystyle\sum\limits_{i = 1}^{{N_k}} {{{({C_k}(i) - \bar X)}^4}} }}{{{{\left( { {\dfrac{1}{{{N_k}}}\displaystyle\sum\limits_{i = 1}^{{N_k}} {{{({C_k}(i) - \bar X)}^2}} } } \right)}^2}}} | (13) |
统计数据峰度的残差
| {D_\omega }(k) = {\omega _{k - 1}} - {\omega _k} | (14) |
整个图像
| \omega = \frac{{\dfrac{1}{{m \times n}}\displaystyle\sum\limits_{i = 1}^{m \times n} {{{(I(i) - \bar X)}^4}} }}{{{{\left( { {\dfrac{1}{{m \times n}}\displaystyle\sum\limits_{i = 1}^{m \times n} {{{(I(i) - \bar X)}^2}} } } \right)}^2}}} | (15) |
每个分块的峰值特征向量
| {B_\omega }(k) = \left\{ {\begin{array}{*{20}{c}} \begin{gathered} 1, \\ 0, \\ \end{gathered} &\begin{gathered} {D_\omega }(k) > \omega \\ {D_\omega }(k) \leqslant \omega \\ \end{gathered} \end{array}} \right. | (16) |
HOG特征提取算法通过统计图像局部区域的梯度方向直方图得到图像特征, 该算法步骤可归纳为: 首先计算图像中每个像素点的梯度值; 其次将图像划分成大小为
采用
| G(i, j) = I{(i, j)^{\rm Gamma}} | (17) |
其中,
根据水平方向和竖直方向的掩膜, 可得水平梯度的分量
| gradx = \left[ {\begin{array}{*{20}{c}} {{G_{11}}}& \ldots &{{G_{1n}}} \\ \vdots & \ddots & \vdots \\ {{G_{n1}}}& \cdots &{{G_{nn}}} \end{array}} \right] * \left[ {\begin{array}{*{20}{c}} { - 1}&0&1 \end{array}} \right] | (18) |
| grady = \left[ {\begin{array}{*{20}{c}} {{G_{11}}}& \ldots &{{G_{1n}}} \\ \vdots & \ddots & \vdots \\ {{G_{n1}}}& \cdots &{{G_{nn}}} \end{array}} \right] * \left[ {\begin{array}{*{20}{c}} { - 1} \\ 0 \\ 1 \end{array}} \right] | (19) |
其中,
图像像素点水平方向的梯度值
| {\mu _x}(i, j) = gradx(i + 1, j) - gradx(i - 1, j) | (20) |
| {\mu _y}(i, j) = grady(i, j + 1) - grady(i, j - 1) | (21) |
其中,
根据式(21)、式(22)可得像素点的梯度值
| \mu (i, j) = \sqrt {{\mu _x}{{(i, j)}^2} + {\mu _y}{{(i, j)}^2}} | (22) |
| \theta (i, j) = {\tan ^{ - 1}}\left(\frac{{{\mu _x}(i, j)}}{{{\mu _y}(i, j)}}\right) | (23) |
其中,
将图像分成若干个大小为
为了压缩光照、阴影和边缘的像素点, 缩小梯度范围的变化, 将每4个
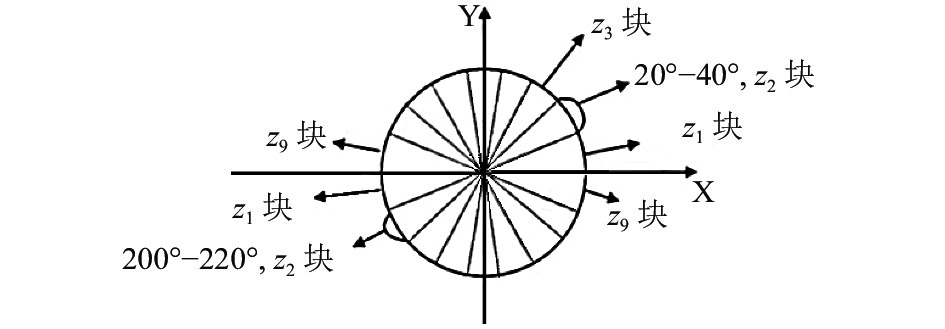
|
图 3 cell单元格梯度分布图 |
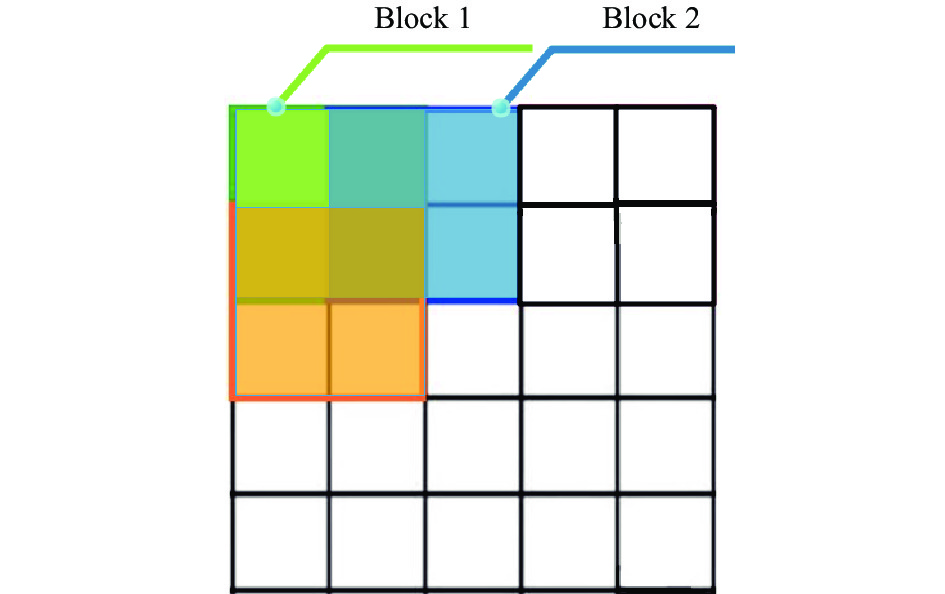
|
图 4 Block分块示意图 |
对每个

|
图 5 HOG特征的2维特征向量 |
对运用
| \begin{split} {B_{\rm HOG}}^\prime (i, j) =& \max \{ {B_{\rm HOG}}(8i - 7, 8j - 7) , \cdots, \\ & {B_{\rm HOG}}(8i + 56, 8j + 56)\} \end{split} | (24) |
其中,
得到局部特征向量
| {B_{{\rm HOG}{\textit{z}}}} = \left\{ \begin{gathered} \begin{array}{*{20}{c}} 1,&{{B_{{\rm HOG}x}} > 128} \end{array} \\ \begin{array}{*{20}{c}} 0,&{{B_{{\rm HOG}{\textit{z}}}} \leqslant 128} \end{array} \\ \end{gathered} \right. | (25) |
将得到的所有特征向量按照由整体到局部的顺序进行组合, 生成图像总体特征向量B为:
| B(o) = \left\{ {\begin{array}{*{20}{c}} \begin{gathered} {B_{\bar x}}(k), \\ {B_\delta }(k), \\ {B_s}(k), \\ {B_\omega }(k), \\ {B_{{\rm HOG}x}}, \\ \end{gathered} &\begin{gathered} 1 \leqslant o \leqslant n/8 \\ n/8 < o \leqslant n/4 \\ n/4 < o \leqslant 3n/8 \\ 3n/8 < o \leqslant n/2 \\ o > n/2 \\ \end{gathered} \end{array}} \right. | (26) |
本文提出了一种基于混沌映射的块置乱方法. 首先, 将水印图像分成不重叠子块, 再基于混沌映射生成秘钥序列, 最后依据秘钥完成图像块位置置乱.
3.1 生成混沌伪随机数混沌系统[11]是指在一种复杂的非线性的动力系统, 即在确定性的系统中, 存在着随机的不规则运动. 其中Logisic映射应用最为广泛, 定义式为:
| {x_{k + {\text{1}}}} = \mu {x_k}{\text{(1}} - {x_k}{\text{)}} | (27) |
其中,
依据式(29)生成块置乱秘钥:
| {R_k} = \left\{ {\begin{array}{*{20}{c}} {1, }&{{x_k} > 0.5} \\ {0, }&{{x_k} \leqslant 0.5} \end{array}} \right. | (28) |
Step 1. 水印图像分块.
将m×n的水印图像分为不重叠的16个大块, 每个大块尺寸大小为m/4×n/4. 再将每一大块进一步分成不重叠的16个小块, 小块尺寸为m/16×n/16.
Step 2. 对每个大块内16个小块实施位置置乱.
首先将大块内每一个小块进行顺序编号1, 2, 3,…,16, 再依据生成的秘钥
以此类推, 按从左至右, 从上到下的顺序, 将每个大块中的16个小块按照上述的方法, 依据秘钥
图6以一组密钥为例, 给出了具体置乱过程. 图7是以Baboon图像为例, 给出了分块置乱的结果.
Step 3. 大块位置置乱.
对每大块按照密钥
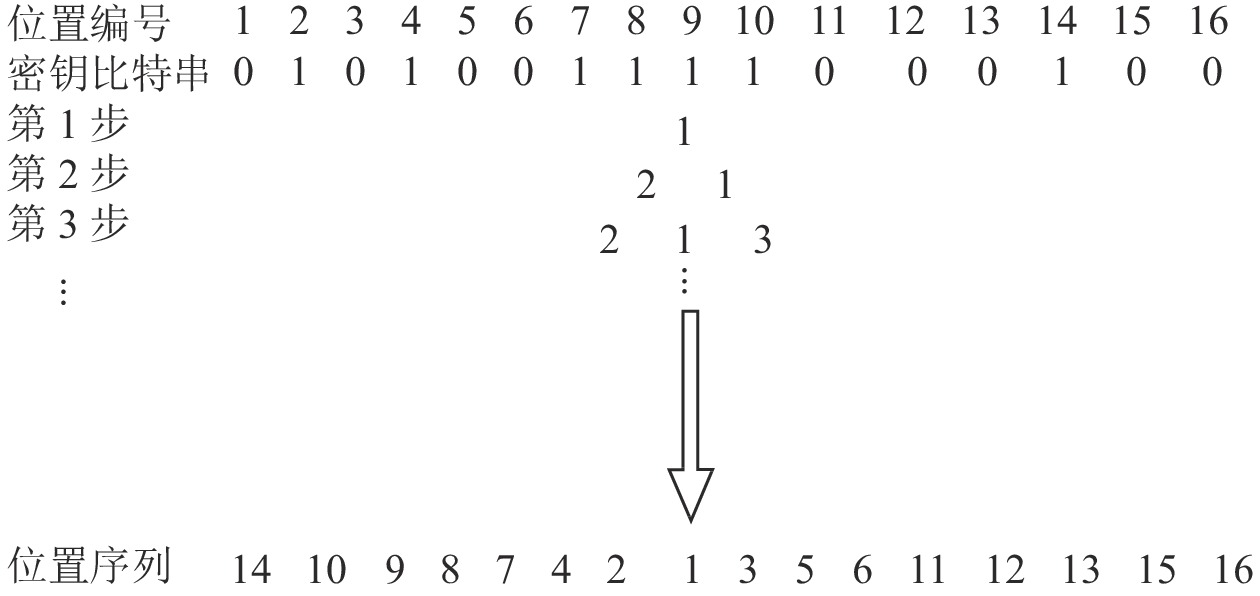
|
图 6 图像位置置乱 |

|
图 7 分块置乱结果 |

|
图 8 整体置乱结果 |
4 零水印构造与检测 4.1 零水印信息的构造
Step 1. 将第3节中得到的加密后2维水印信息转换为1维二进制序列
Step 2. 将第2节得到图像整体特征向量B与
| Z{\text{ = }}B \oplus S | (29) |
在版权认证过程中, 首先提取多特征, 再结合零水印信息, 得到加密后水印; 最后对其进行解密; 即可实现版权认证. 版权认证的过程是零水印构造的逆过程, 如图9所示, 具体如下.
|
图 9 基于多特征和块置乱的零水印算法水印检测流程图 |
Step 1. 将待版权认证的数字图像灰度化.
Step 2. 按照第2.1节中的步骤对图像进行重叠分块与不重叠分块, 并根据第2.2–2.6节中的步骤提取图像的多维特征向量.
Step 3. 将得到的多维特征按照由整体到局部的顺序进行组合, 得到图像的特征向量B.
Step 4. 运用特征向量B与零水印信息Z进行异或得到的加密后水印图像为1维二进制序列
| S{\text{ = }}B \oplus Z | (30) |
Step 5. 将1维二进制序列
Step 6. 若拥有密钥
本算法基于SIPI基准数据集[17], 在Windows 10和Python 3.7平台进行仿真实验, 将实验结果与现有算法进行性能比较和分析, 进一步证明本文算法鲁棒性好, 安全性高、抗攻击能力强, 在版权保护方面具有明性优势.
SIPI数据集中主要使用纹理、天线、杂项、序列4卷, 共306张图像. 每个卷中的图像具有不同大小, 例如 256×256、512×512或 1024×1024.
本文以原始载体图像大小为256×256的标准灰度图像进行说明, 如图10所示(因篇幅受限, 在此只展示6幅图像). 为了衡量水印算法的性能, 利用提取出的水印图像与原始水印图像之间归一化相关系数NC值作为评测的指标.

|
图 10 实验载体图像 |
| \begin{split} &NC(W,W') = \\ &\frac{{\displaystyle\sum\nolimits_{i = 1}^P {\displaystyle\sum\nolimits_{j = 1}^Q {\left[ {W\left( {i,j} \right) \times W'\left( {i,j} \right)} \right]} } }}{{\sqrt {\displaystyle\sum\nolimits_{i = 1}^P {{{\displaystyle\sum\nolimits_{j = 1}^Q {\left[ {W\left( {i,j} \right)} \right]} }^2}} } \sqrt {\displaystyle\sum\nolimits_{i = 1}^P {{{\displaystyle\sum\nolimits_{j = 1}^Q {\left[ {W'\left( {i,j} \right)} \right]} }^2}} } }} \end{split} | (31) |
在零水印构建过程中, 特征提取是关键, 本文利用分块图像与整体图像的均值、方差、偏态、峰度的关系来构造前4维特征, 而第5维HOG特征则直接使用了图像的整体特征. 图11–图14分别给出了Lena图像的均值、方差、偏态、峰度的部分特征与整体特征图, 其中横坐标为部分特征的编号, 纵坐标为特征值的大小, 黄线代表图像整体特征的平均值. 由此可知, 图像的整体特征与分块特征具有较好的区分度, 有助于抵抗均衡化攻击.
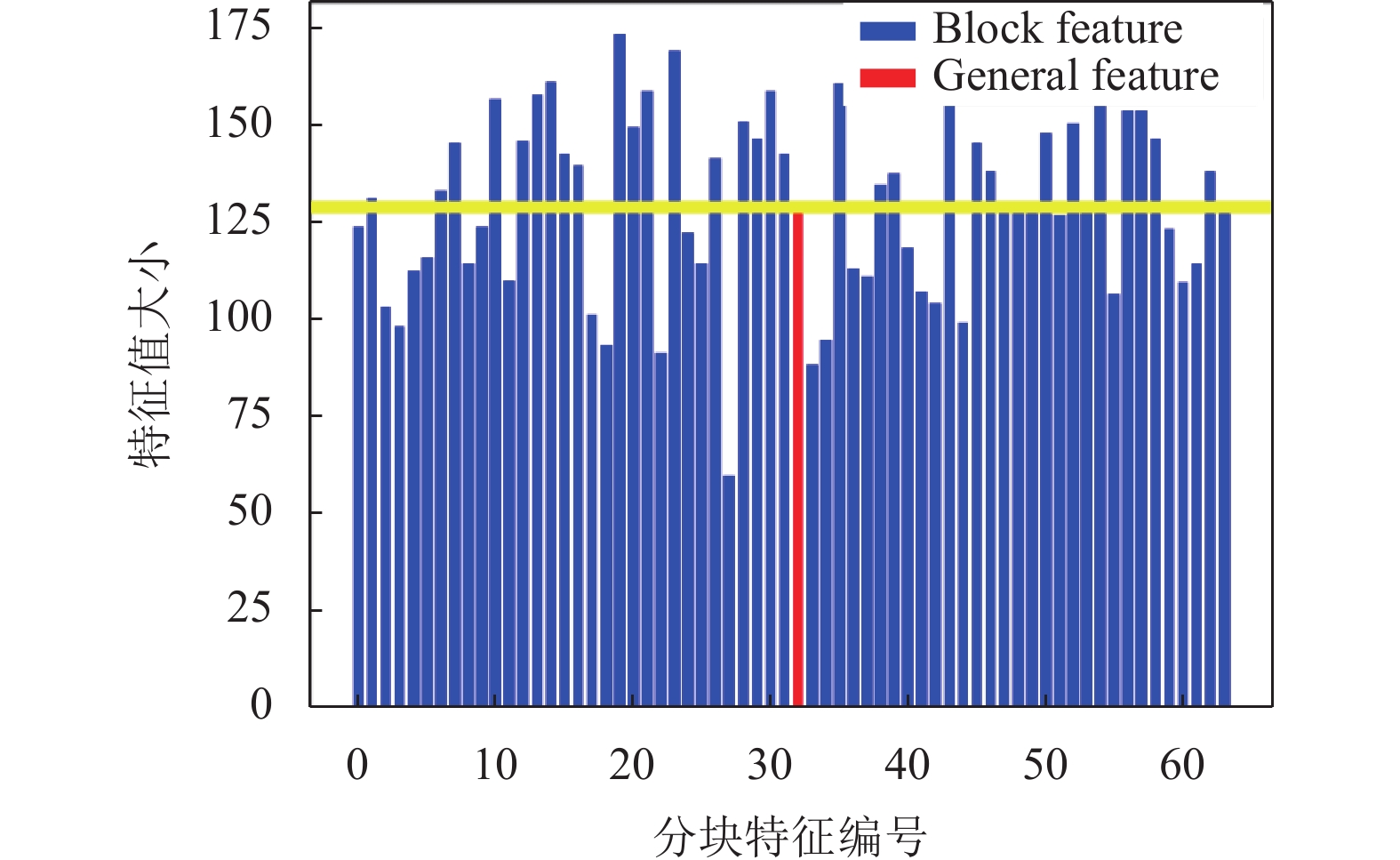
|
图 11 块特征与整体特征图——均值 |
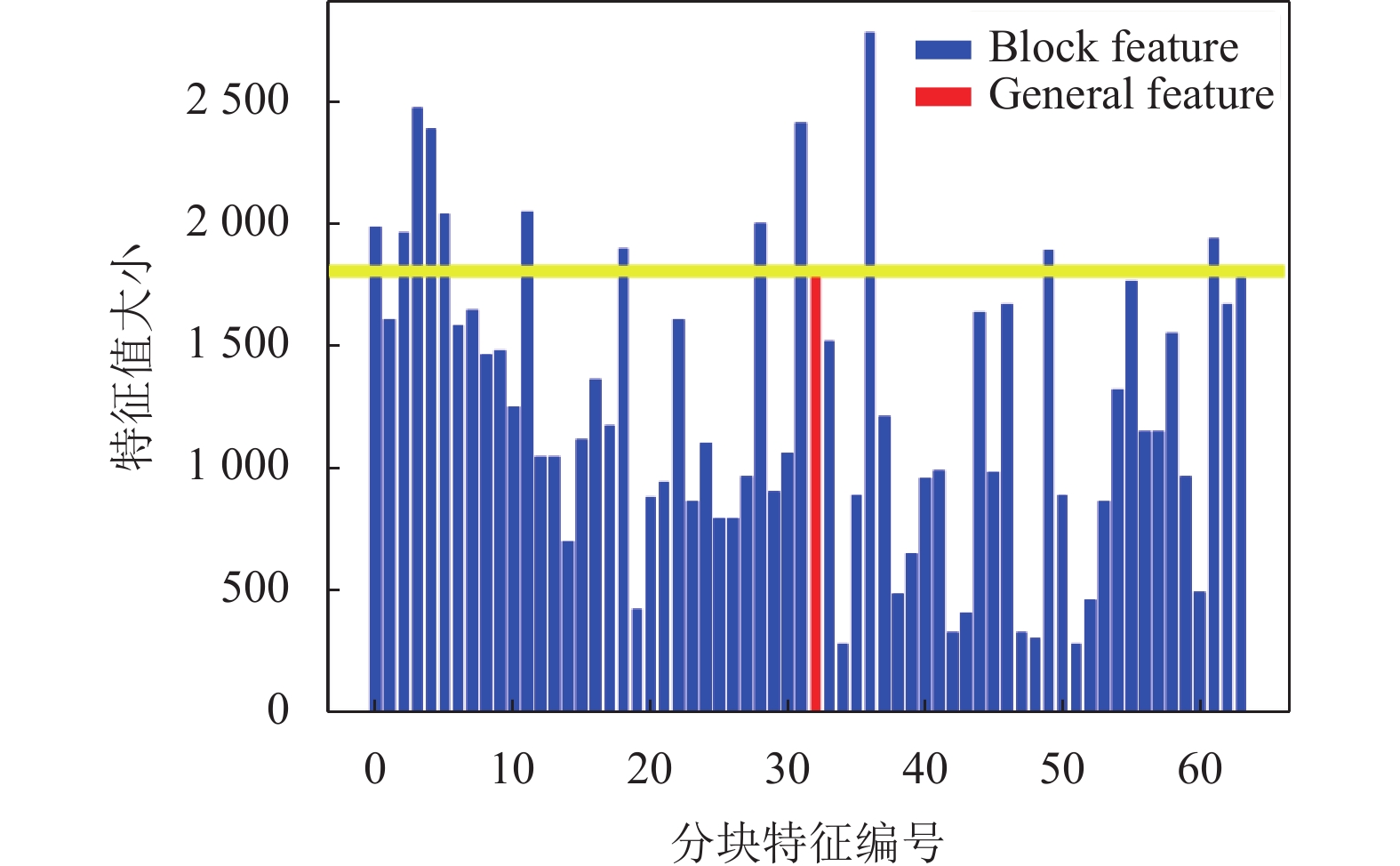
|
图 12 块特征与整体特征图——方差 |
5.3 特征稳定性分析
图像受到攻击后提取的特征可否保持稳定是判断零水印算法优劣的关键, 为了直观地展示图像在受到攻击前后所提取的特征, 以JPEG攻击为例, 图15–图18分别给出了Lena图像在攻击前和采用不同压缩因子攻击后的特征散点图, 其中横坐标代表了特征点的编号, 纵坐标代表着特征值的大小. 由此可见, 攻击前后特征点基本不变, 因此, 本文所提出的特征提取算法具有较好的稳定性.
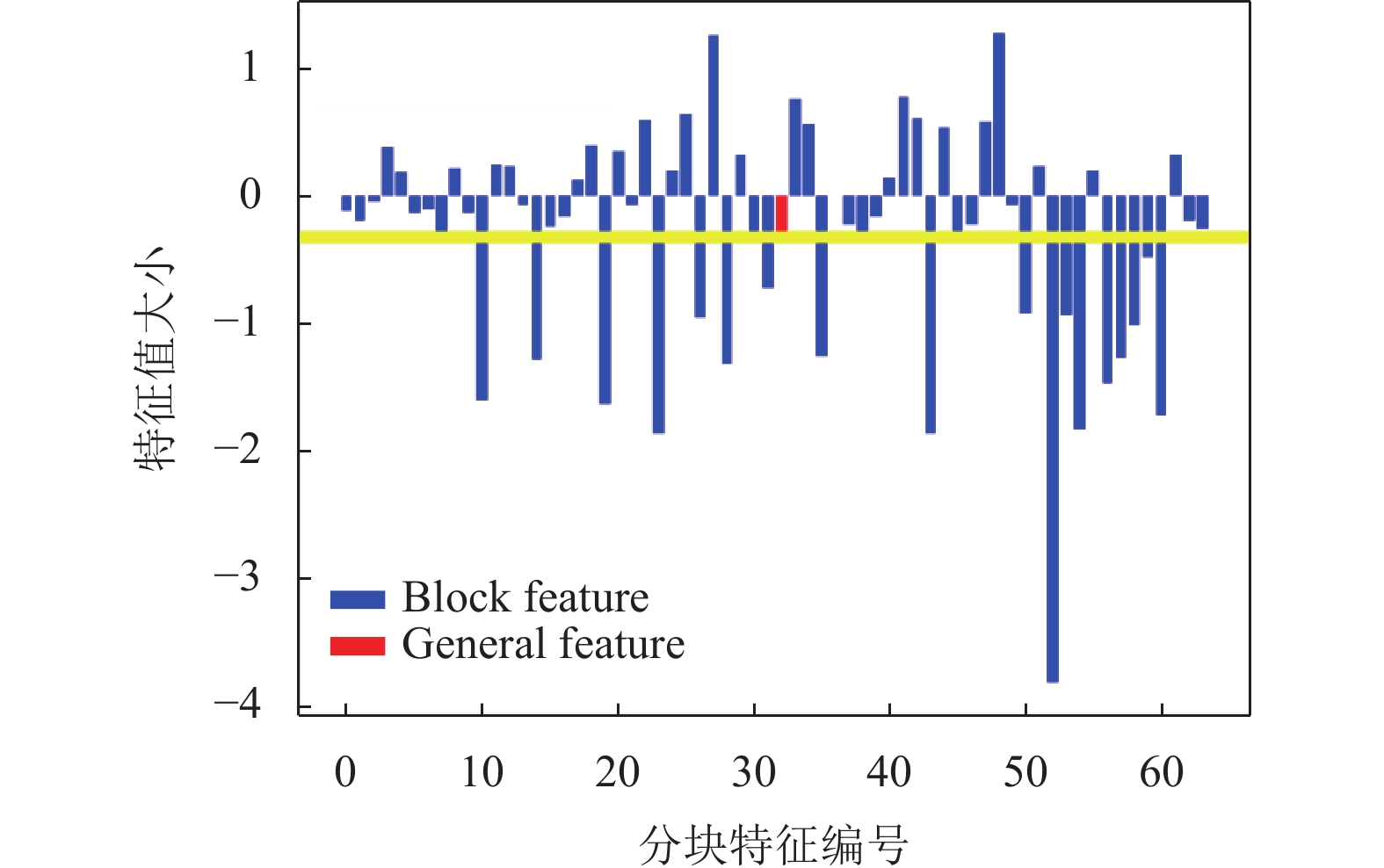
|
图 13 块特征与整体特征图——偏态 |
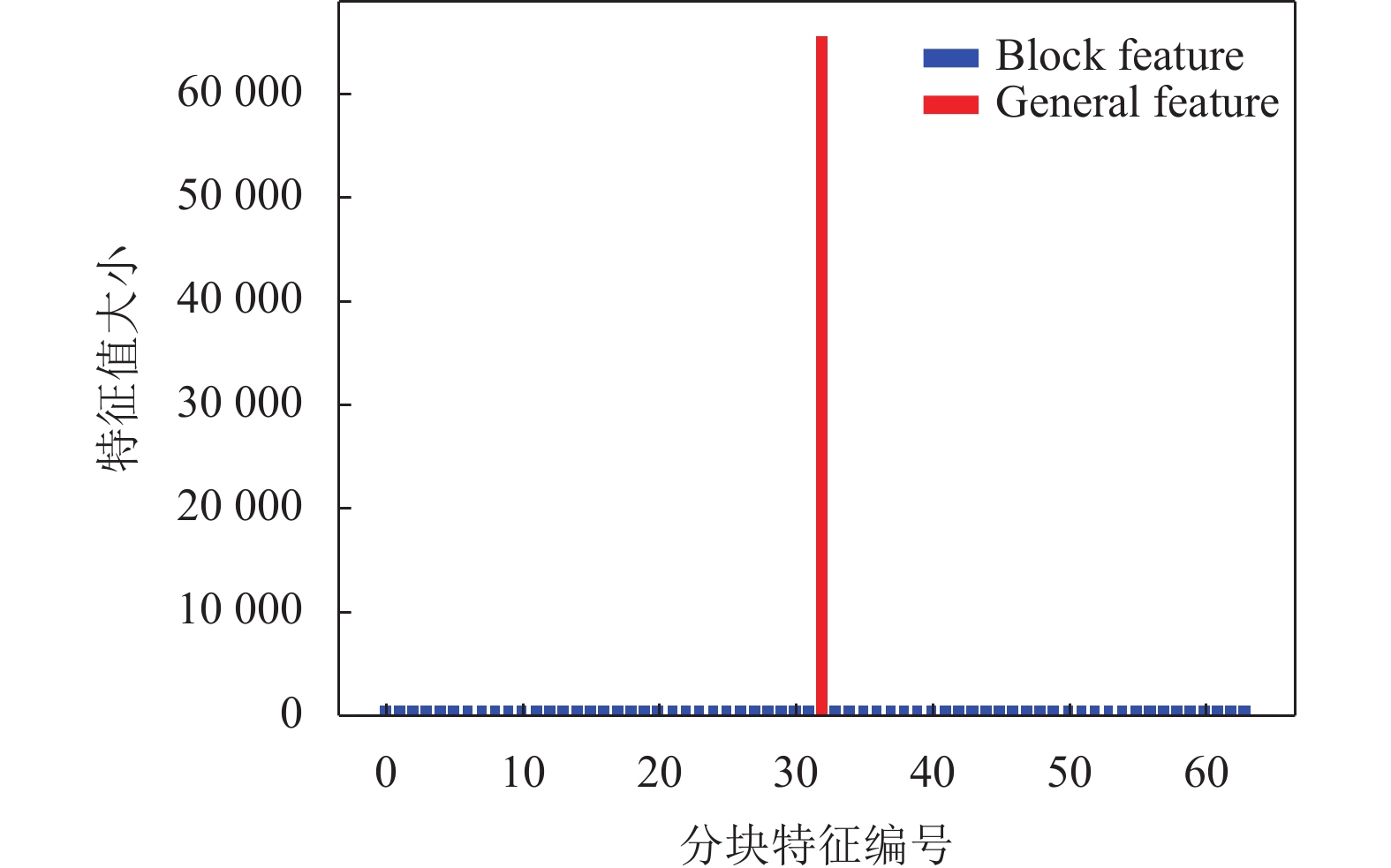
|
图 14 块特征与整体特征图——峰度 |
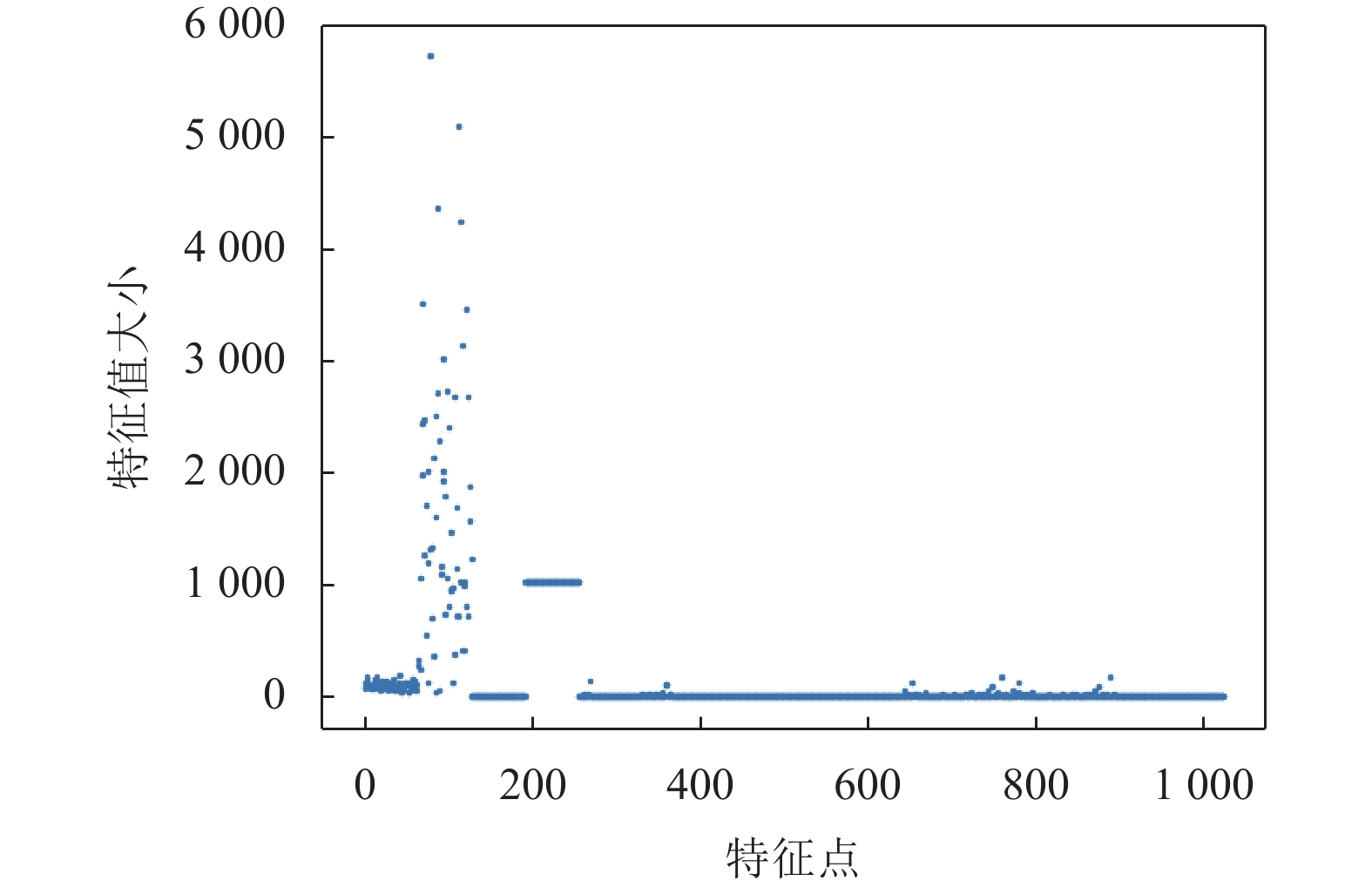
|
图 15 Lena图像特征散点图 |
5.4 均衡性分析
零水印的生成依赖于原始图像的内容特征, 与原始图像的内容高度相关. 从不同的原始图像生成的零水印信号应该是有差异的. 表1给出了6张不同的原始图像生成的零水印信号之间的相关系数NC值, 由表1可知, 6张不同的原始图像生成的零水印信号差异较大, 其NC最大值和最小值分别为0.678 8和0.090 7. 因此, 不同图像之间的零水印信息之间的可区分性是比较高的.
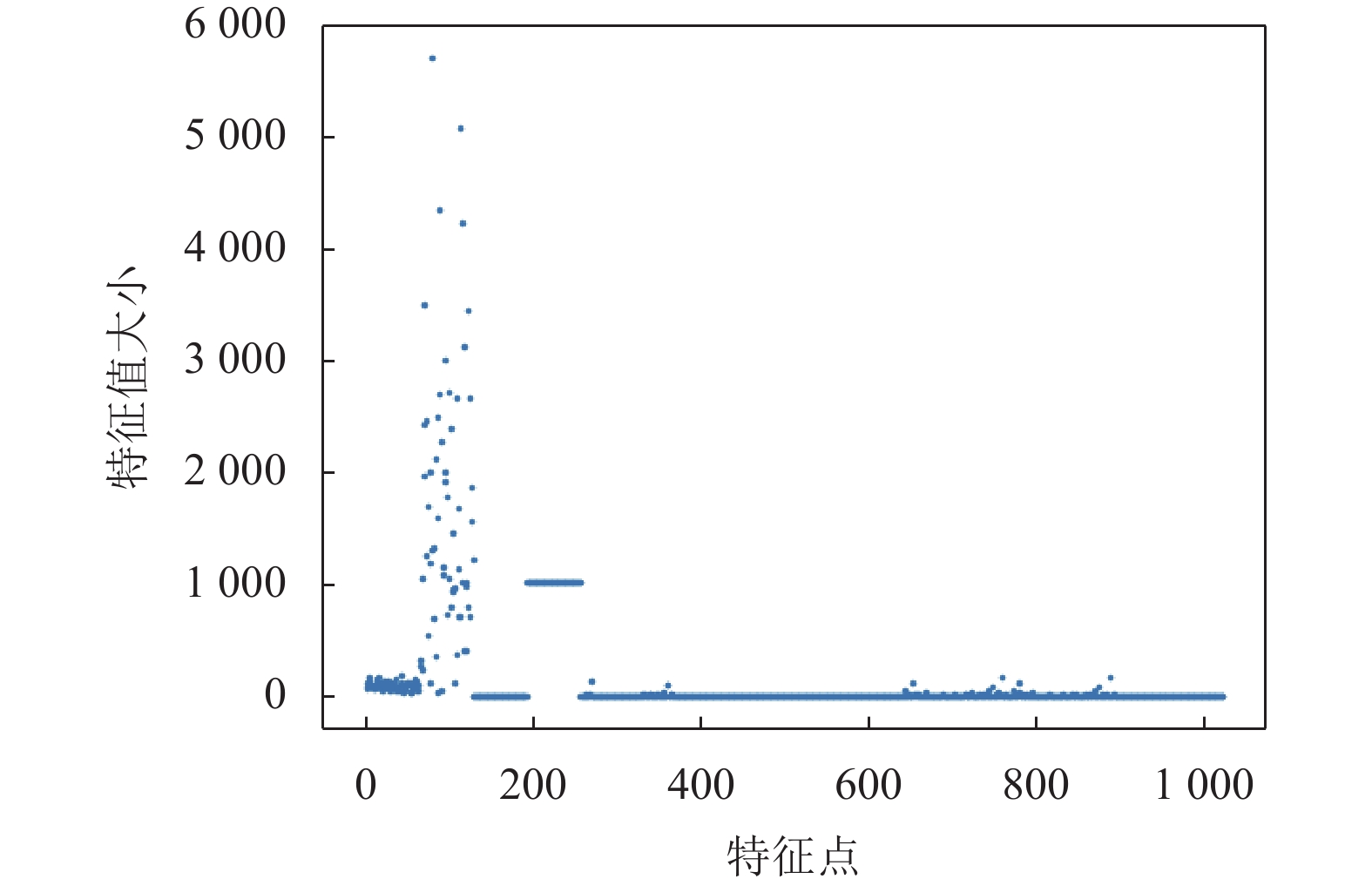
|
图 16 JPEG (压缩因子80)特征散点图 |
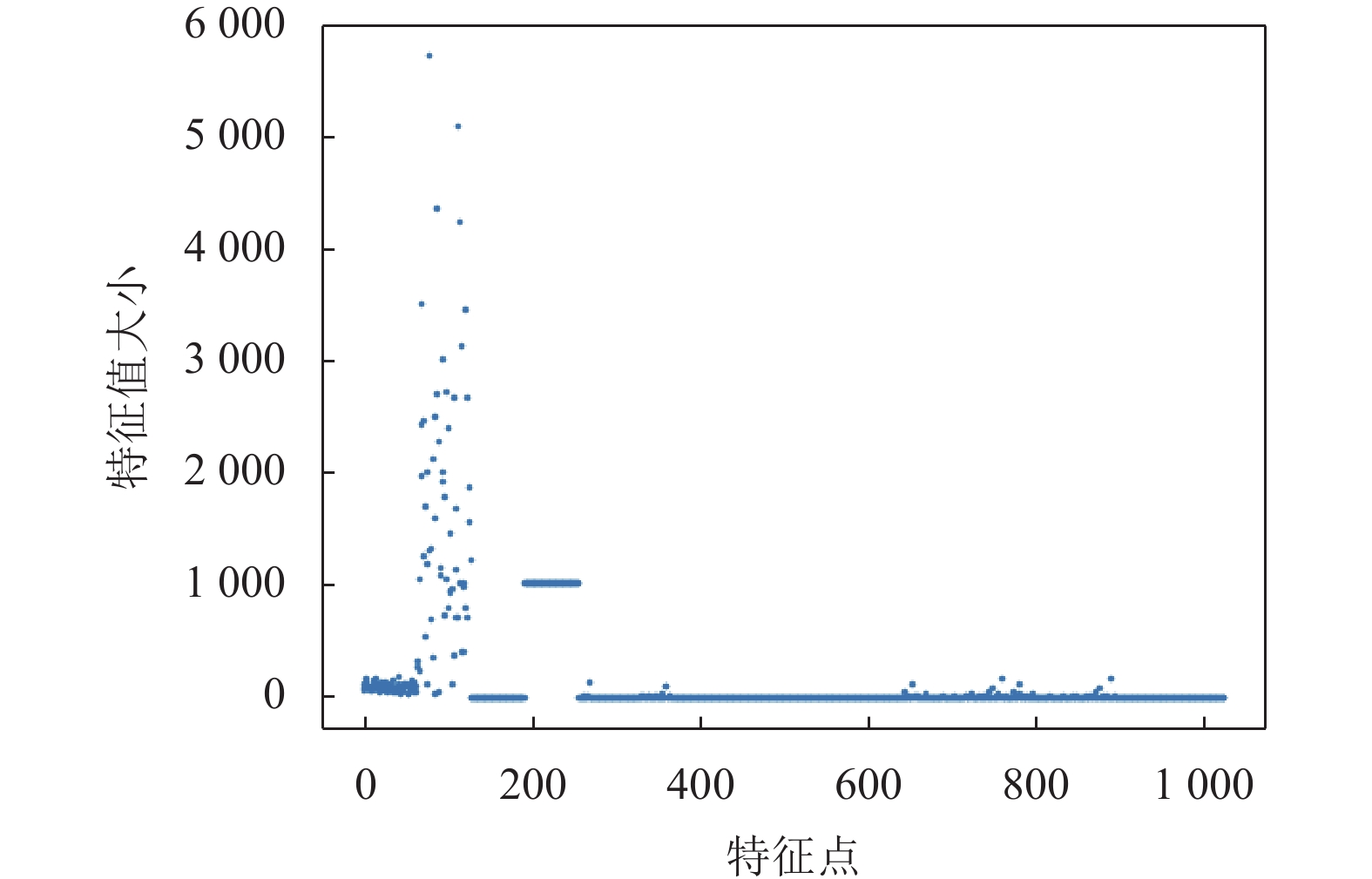
|
图 17 JPEG (压缩因子70)特征散点图 |
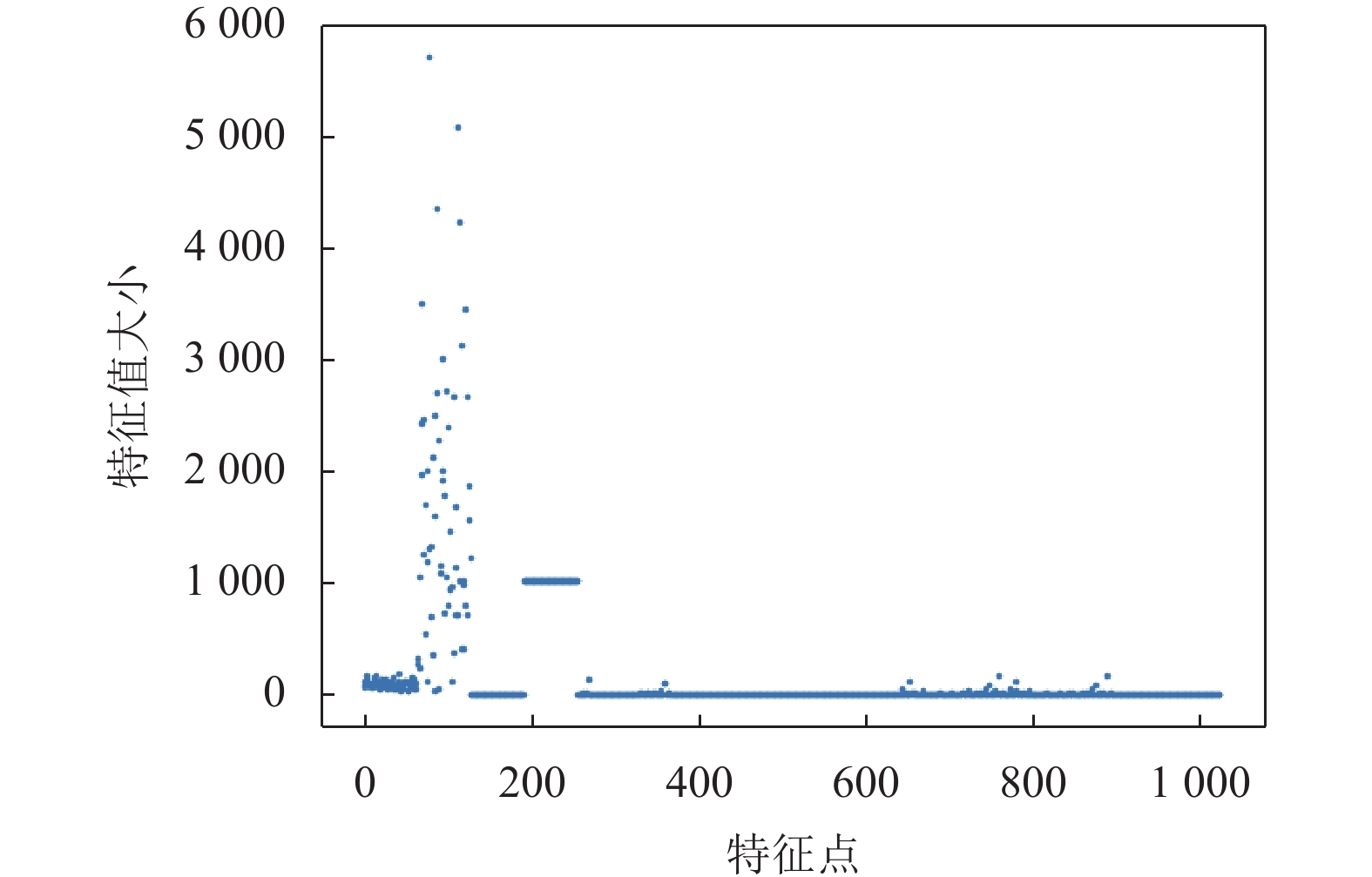
|
图 18 JPEG (压缩因子60)特征散点图 |
| 表 1 不同图像构造水印的NC对比 |
5.5 鲁棒性分析
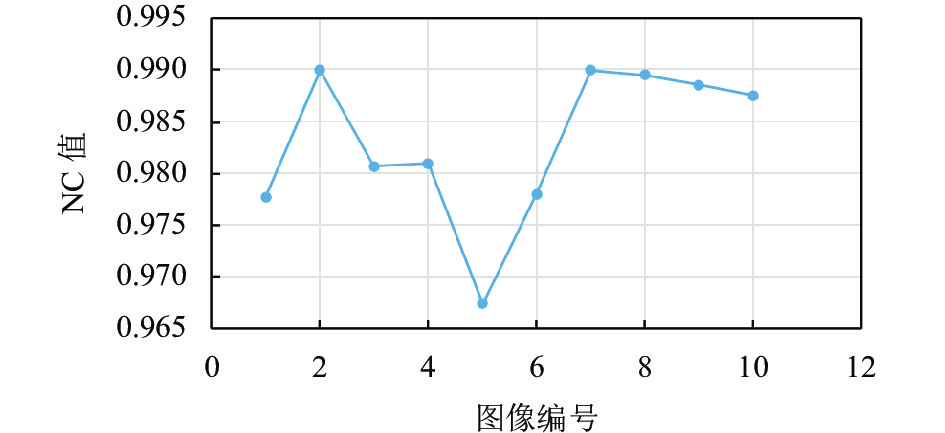
为了保证实验的普遍性, 实验的攻击内容包括滤波攻击、加性噪声攻击、JPEG压缩攻击等. 图19–图25分别给出了不同攻击性不同图像提取水印与原始水印之间的NC值, 其中横轴代表了图像编号, 纵轴代表NC值的大小.
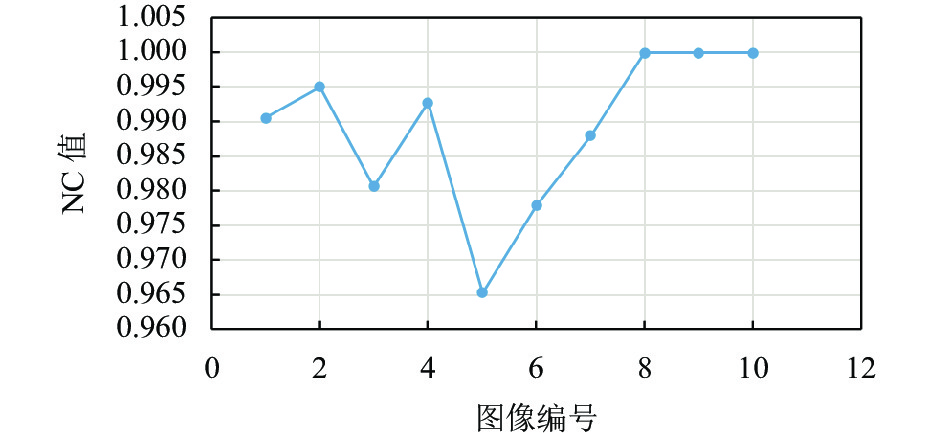
|
图 19 不同图像维纳滤波(9×9)攻击下NC值分布 |
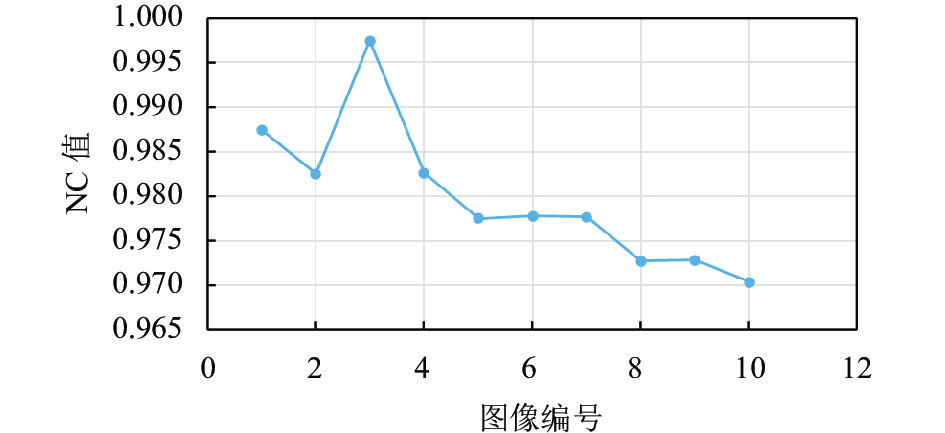
|
图 20 不同图像(9×9)中值滤波攻击下NC值分布 |
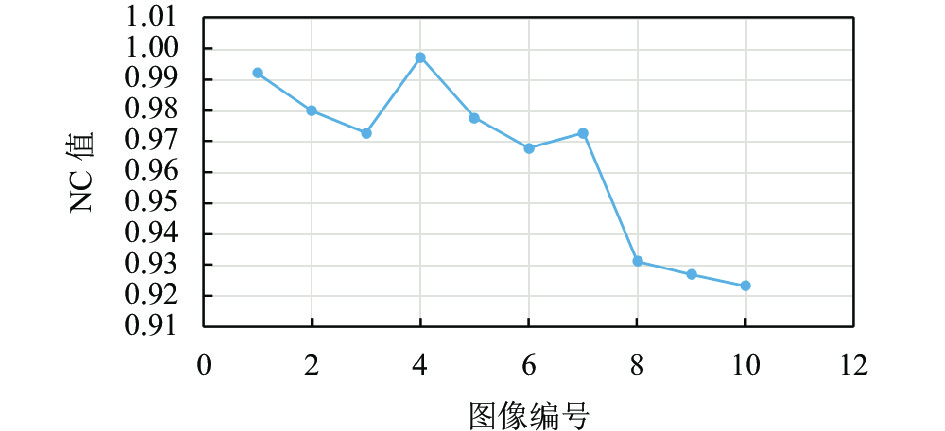
|
图 21 不同图像均值滤波(5×5)攻击下NC值分布 |
表2 给出了本算法与其他相关算法在不同攻击下提取水印图像与原始水印图像NC值的比较结果, 由表2可知, 本算法在维纳滤波、中值滤波、高斯噪声和旋转攻击下的平均NC值分别高达0.997 4、0.984 2、0.987 5和0.997 4, 远高于其他文献; 高斯滤波攻击下, 本算法的平均NC值为0.984 7, 远高于文献[13, 18–20], 但略低于文献[21]; JPEG压缩攻击下, 本算法的平均NC值分别为0.9630, 略低于文献[13, 19,20], 但远高于文献[18,21]; 椒盐噪声攻击下, 本算法的平均NC值为0.9704, 略低于文献[20]的0.9784, 但远高于文献[13,18, 19,21]. 综上, 本算法在不同的攻击之下其NC与相关文献相比, 表明本算法在抗攻击性上有优势之处.
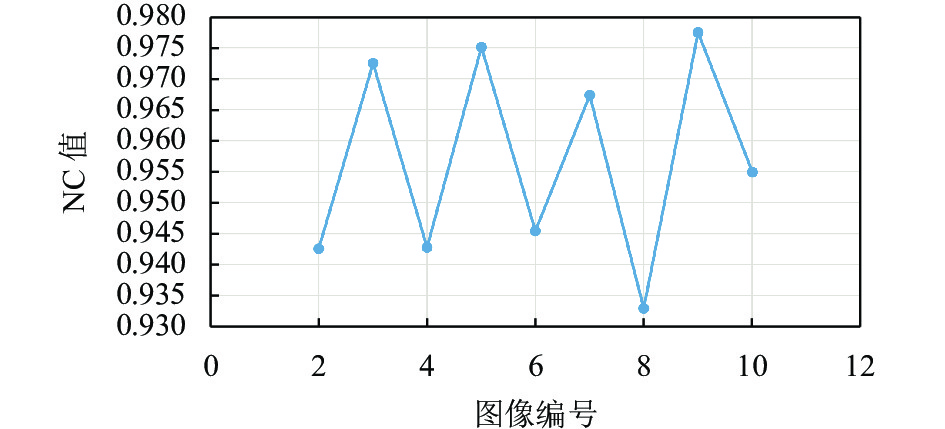
|
图 22 不同图像JPEG (因子10)攻击下NC值分布 |
|
图 23 不同图像高斯噪声(0.1)攻击下NC值分布 |
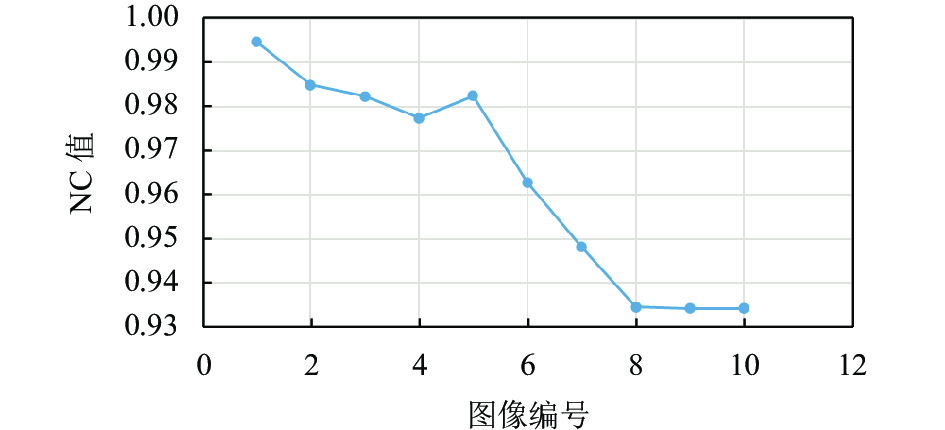
|
图 24 不同图像椒盐噪声(0.1)攻击下NC值分布 |
为了更加全面的衡量零水印的鲁棒性, 引入误码率(bit error ratio,BER)对鲁棒性进一步测试比较. BER是指从水印中提取的错误比特数与原始水印中总比特数的比值, 介于0和1之间. BER越接近0, 水印的鲁棒性越好, 其定义如下:
| {{BER = }}\frac{{\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {Wr(i, j) \oplus W(i, j)} } }}{{m \times n}} | (32) |
其中,
表3给出了本算法与其他算法在不同攻击下提取水印与原图像水印的平均误码率之间的比较. 由表3可知, 高斯噪声攻击下, 本文的误码率仅为0.025 1, 远低于其他文献[7,8,21-23], 表明本文抗高斯噪声攻击能力强; 在高斯滤波攻击下, 本文的BER为0.0082, 仅略高于文献[21], 远低于文献[7, 8,22,23]; 在进行缩放攻击和旋转攻击下, 本文提取水印与原水印之间的误码率分别为0.0203和0.0574, 远低于文献[7, 21–23], 仅略高于文献[8]; 在进行JPEG压缩攻击时, 本文提取水印与原水印之间的误码率为0.0264, 远低于文献[7, 8,22, 23], 仅略高于文献[21]; 在进行中值滤波(采样窗口为3×3)攻击时, 本文提取水印与原水印之间的误码率为0.0174, 远低于文献[7, 21,23] , 略高于文献[8,22]; 在进行中值滤波(采样窗口为9×9)攻击时, 本文提取水印与原水印之间的误码率为0.0223, 远低于文献[7, 8,22,23], 仅略高于文献[21]; 在进行均值滤波攻击时, 本文提取水印与原水印之间的误码率为0.0302, 远低于文献[7,8,21], 只略高于文献[22, 23]. 综上, 与相关文献中的相比, 本算法在不同的攻击之下其误码率较低, 表明本算法在鲁棒性上有优势之处.
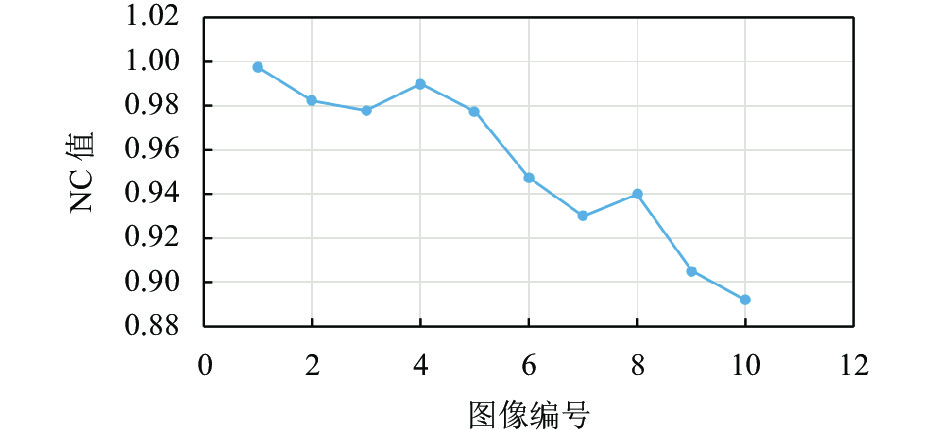
|
图 25 不同图像缩放(0.5)攻击下NC值分布 |
| 表 2 本算法与其他零水印算法NC值比较 |
5.6 时间复杂度分析
随着大数据技术的飞速发展, 水印算法的处理能力越来越重要. 算法的时间复杂度是零水印算法在实际应用中的一项重要指标. 本文分析了水印嵌入(零水印生成)和提取(零水印检测)所需的处理时间. 本实验在8核16线程的3.40 GHz的CPU上进行, 32 GB内存. 表4给出了本算法与其他零水印算法的时间复杂度. 由表4可知, 本文中所提出的零水印算法比文献[20] 略慢, 但明显快于文献[4, 19,21,22,24–26], 这表明了本算法在执行时间方面更有优势.
| 表 3 本算法与其他零水印算法平均误码率的比较 |
| 表 4 本算法与其他零水印算法时间复杂度对比 |
6 结论与展望
本文提出了一种基于多特征和块置乱的零水印算法. 为提升不同图像零水印的可区分性, 本文以图像的均值特征、方差特征、偏态特征、峰度特征、
| [1] |
温泉, 孙锬锋, 王树勋. 零水印的概念与应用. 电子学报, 2003, 31(2): 214-216. DOI:10.3321/j.issn:0372-2112.2003.02.015 |
| [2] |
Wang BW, Wang WS, Zhao P. Multiple color medical images zero-watermark scheme based on quaternion generalized Fourier descriptor and QR code. Proceedings of ACM Turing Award Celebration Conference-China (ACM TURC 2021). Hefei: ACM, 2021. 248–253.
|
| [3] |
Xia ZQ, Wang XY, Zhou WJ, et al. Color medical image lossless watermarking using chaotic system and accurate quaternion polar harmonic transforms. Signal Processing, 2019, 157: 108-118. DOI:10.1016/j.sigpro.2018.11.011 |
| [4] |
Xia ZQ, Wang XY, Han B, et al. Color image triple zero-watermarking using decimal-order polar harmonic transforms and chaotic system. Signal Processing, 2021, 180: 107864. DOI:10.1016/j.sigpro.2020.107864 |
| [5] |
Xia ZQ, Wang XY, Wang CP, et al. Local quaternion polar harmonic Fourier moments-based multiple zero-watermarking scheme for color medical images. Knowledge-based Systems, 2021, 216: 106568. DOI:10.1016/j.knosys.2020.106568 |
| [6] |
Yamni M, Karmouni H, Sayyouri M, et al. Robust zero-watermarking scheme based on novel quaternion radial fractional Charlier moments. Multimedia Tools and Applications, 2021, 80(14): 21679-21708. DOI:10.1007/s11042-021-10717-2 |
| [7] |
Liu JL, Li JB, Chen YW, et al. A robust zero-watermarking based on SIFT-DCT for medical images in the encrypted domain. Computers, Materials & Continua, 2019, 61(1): 363-378. DOI:10.32604/cmc.2019.06037 |
| [8] |
Xia ZQ, Wang XY, Li XX, et al. Efficient copyright protection for three CT images based on quaternion polar harmonic Fourier moments. Signal Processing, 2019, 164: 368-379. DOI:10.1016/j.sigpro.2019.06.025 |
| [9] |
Devi BP, Singh KM, Roy S. New copyright protection scheme for digital images based on visual cryptography. IETE Journal of Research, 2017, 63(6): 870-880. DOI:10.1080/03772063.2017.1324328 |
| [10] |
Sharkas M, ElShafie D, Hamdy N. A dual digital-image watermarking technique. Proceedings of the 3rd World Enformatika Conference. Istanbul: WEC, 2005. 136–139.
|
| [11] |
宋伟, 侯建军, 李赵红, 等. 一种基于Logistic混沌系统和奇异值分解的零水印算法. 物理学报, 2009, 58(7): 4449-4456. DOI:10.3321/j.issn:1000-3290.2009.07.013 |
| [12] |
He ZW, Lu W, Sun W, et al. Digital image splicing detection based on Markov features in DCT and DWT domain. Pattern Recognition, 2012, 45(12): 4292-4299. DOI:10.1016/j.patcog.2012.05.014 |
| [13] |
Wei DY, Li YM. Novel tridiagonal commuting matrices for types I, IV, V, VIII DCT and DST matrices. IEEE Signal Processing Letters, 2014, 4(21): 483-487. DOI:10.1007/s00371-022-02406-4 |
| [14] |
Sun YC, Li D. Robust cartoon zero-watermark algorithm based on NSST. Proceedings of Advances in Computer Science and Ubiquitous Computing. Kuala Lumpur: Springer, 2017. 53–59.
|
| [15] |
Amiri A, Mirzakuchaki S. A digital watermarking method based on NSCT transform and hybrid evolutionary algorithms with neural networks. SN Applied Sciences, 2020, 2(10): 1669. DOI:10.1007/s42452-020-03452-0 |
| [16] |
Wu XQ, Ma P, Jin ZH, et al. A novel zero-watermarking scheme based on NSCT-SVD and Blockchain for video copyright. EURASIP Journal on Wireless Communications and Networking, 2022, 2022: 20. DOI:10.1186/s13638-022-02090-x |
| [17] |
USCViterbi. The USC-SIPI image database. http://sipi.usc.edu/database/. (2018-02-01)[2022-02-01].
|
| [18] |
Zhou WJ, Jiang GY, Yu M, et al. Reduced-reference stereoscopic image quality assessment based on view and disparity zero-watermarks. Signal Processing: Image Communication, 2014, 29(1): 167-176. DOI:10.1016/j.image.2013.10.005 |
| [19] |
Wang CP, Wang XY, Xia ZQ, et al. Ternary radial harmonic Fourier moments based robust stereo image zero-watermarking algorithm. Information Sciences, 2019, 470: 109-120. DOI:10.1016/j.ins.2018.08.028 |
| [20] |
Kang XB, Lin GF, Chen YH, et al. Robust and secure zero-watermarking algorithm for color images based on majority voting pattern and hyper-chaotic encryption. Multimedia Tools and Applications, 2020, 79(1–2): 1169-1202. DOI:10.1007/s11042-019-08191-y |
| [21] |
Ma B, Chang LL, Wang CP, et al. Double medical images zero-watermarking algorithm based on the chaotic system and ternary accurate polar complex exponential transform. Journal of Mathematical Imaging and Vision, 2021, 63(9): 1160-1178. DOI:10.1007/s10851-021-01048-w |
| [22] |
Zou BJ, Du JY, Liu XY, et al. Distinguishable zero-watermarking scheme with similarity-based retrieval for digital rights management of fundus image. Multimedia Tools and Applications, 2018, 77(21): 28685-28708. DOI:10.1007/s11042-018-5995-4 |
| [23] |
Kang XB, Zhao F, Chen YJ, et al. Combining polar harmonic transforms and 2D compound chaotic map for distinguishable and robust color image zero-watermarking algorithm. Journal of Visual Communication and Image Representation, 2020, 70: 102804. DOI:10.1016/j.jvcir.2020.102804 |
| [24] |
Xia ZQ, Wang XY, Wang CP, et al. Novel quaternion polar complex exponential transform and its application in color image zero-watermarking. Digital Signal Processing, 2021, 116: 103130. DOI:10.1016/j.dsp.2021.103130 |
| [25] |
Hosny KM, Darwish MM, Fouda MM. New color image zero-watermarking using orthogonal multi-channel fractional-order legendre-fourier moments. IEEE Access, 2021, 9: 91209-91219. |
| [26] |
Hosny KM, Darwish MM. New geometrically invariant multiple zero-watermarking algorithm for color medical images. Biomedical Signal Processing and Control, 2021, 70: 103007. DOI:10.1016/j.bspc.2021.103007 |
 2022, Vol. 31
2022, Vol. 31










