2. 信息系统需求重点实验室, 南京 210007;
3. 中国电子科技集团公司第五十四研究所, 石家庄 050081
2. Key Lab of Information System Requirement, Nanjing 210007, China;
3. The 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang 050081, China
为实现联合全域作战能力, 2014年我军提出“网络信息体系”[1]作战概念, 其本质是作战体系[2], 通过将全网的感知节点、情报分析节点、决策节点、火力打击节点等组合集成为一个有机整体, 以具备遂行作战的能力. 为应对动态任务和环境, 网络信息体系构建要求资源要素解耦合、入网即用. 为实现作战任务, 大量的作战资源需要动态调用, 因此高效选择哪些作战资源入网成为指挥员面临的问题, 指挥员希望网络信息体系能自动给出面向任务的作战资源集成方案优选, 以供选择.
战场环境变化频繁复杂是网络信息体系资源优选面临的重大挑战. 未来战场中作战要素互相交错, 智能化、无人化、集群化资源要素的占比逐渐增大[3]. 随着精确打击技术的成熟, 物理节点损毁成为未来战场环境变化的重要因素之一. 2021年12月24日, 伊朗革命卫队在代号为“伟大先知-17”的大规模军演最后一天, 连续发射了16枚包括远程、中程、短程等多种射程的弹道导弹, 全部精准命中并摧毁了数十个军事目标, 精准打击技术的发展使得物理节点损毁这一变化频繁出现. 网络信息体系进入未来战场, 环境将更加复杂严峻, 如果不能及时应对战场环境变化做出反应, 及时在存活节点中优选集成恢复能力, 将会带来不可估量的损失.
网络信息体系的特性是资源优选面临的又一难题. 相比我军当前使用的指挥信息系统, 网络信息体系规模庞大, 各类节点资源分布广、数量多且趋于智能化. 目前, 我军作战资源的选取主要依靠预案, 选择想定与当前战场态势相近的预案, 再根据预案选取节点资源完成任务. 随着人工智能技术的发展, AI技术越来越多的应用于战场, 依靠预案的方式进行资源集成有明显不足. 一方面随着智能、无人设备的大量使用, 其能力通过自学习发生变化与预案设计基础不符; 另一方面当前作战是一种快速决策、动态干扰的作战样式, 预案难以覆盖复杂的未来战场态势, 使得资源集成不精确、动态调整资源组合效率低. 因此在高动态环境未来战场, 如何根据战场态势精确给出资源集成方案是网络信息体系建设中亟待解决的难题.
为使作战体系能够应对高变化的战场环境, 王维平等[4]在智能化多无人集群作战体系背景下, 从任务流程适变、组织指控柔性和装备功能抗毁3个方面设置动态适变机制; 赵鑫等[5]针对现有指挥信息系统, 建立了基于“环境认知环–决策执行环”的“双环”自主适变机制; 张维明等[6]结合马尔科夫链, 研究了网络信息体系在敌我动态博弈中的策略选取, 设计了基于理论解析与数据仿真的适变分析框架. 上述文献在宏观角度上, 研究应对高变化战场环境的作战体系架构设计与机制设置, 为网络信息体系应对战场环境变化的资源集成方案调整给出了基本框架.
本文在文献[4-6]给出的框架基础上, 关注资源优选的具体实现, 从典型场景下的现实问题出发, 以防空反导作战体系为网络信息体系示例, 提出一种基于演化博弈优化的资源优选方法, 解决部分物理节点损毁后, 如何精确给出资源集成方案以尽量恢复体系核心能力的问题, 为提升网络信息体系的抗毁性提供有效的方法和实验验证.
首先, 提出一种基于演化博弈优化的资源集成方案求解模型; 接着, 对模型与问题适用性进行了论证, 通过增加扰动过程限制的改进, 提出了资源优选算法; 最后, 通过仿真实验验证了算法的可行性, 并分析了算法效果. 第2节对系统集成方案求解问题进行分析与形式化描述; 第3节介绍了演化博弈优化的基本思想; 第4节提出了问题求解模型并基于此设计了资源优选方法; 第5节构建数据集、设计实验验证算法效果; 第6节总结和展望.
2 相关研究针对资源集成方案求解问题, 胡瑞淇等[7]提出了一种表达式树结构的描述方法, 并通过遗传算法对车间柔性调度问题进行求解; 周康等[8]用网络计划图形式化描述问题, 通过遗传算法进行资源优选; 王有远等[9]将任务按照有无依赖关系描述为两个集合, 设备资源描述为一个集合, 在此基础上建立设备资源双层优化模型, 通过搜索最恰当映射关系解决资源最优分配问题; Xiao等[10]用演化博弈解决虚拟资源重新分配的问题, 不仅考虑新的分配方案的资源消耗, 还考虑到新旧方案迁移的消耗, 建立了综合的能耗模型作为评价函数, 但以上研究主要针对同构资源分配, 在处理网络信息体系背景下的异构节点资源上并不适宜. Arthanari[11]以系统稳定性为关注点, 分别将设计和目标作为博弈双方, 分析影响性能的“噪声因素”和“信噪比”, 通过二元零和博弈公式选定组合方案. Ghotbi等[12]将影响目标的变量作为博弈主体, 利用Stacklberg博弈方法对优化问题进行求解. 以上方法研究系统的构成较为简单, 但网络信息体系是一种复杂军事系统, 构成要素众多、集成度高, 直接通过博弈结构描述问题及建模会导致模型过度复杂而难以求解.
为实现较大规模异构资源优选, 有学者将资源集成方案求解问题看作组合优化问题[13-17], 在此基础上, Yuan等[14]通过粒子群算法求解云资源优选问题, Ergu等[15]通过对资源和用户进行偏好排序给出了云资源优选方法, Warneke等[17]提出了一个动态资源优选框架, 将问题形式化为组合优化问题的描述方法在解决大规模云计算异构资源上取得了较好的效果. Crawley等提出了down-selection模式[13]用于复杂系统架构设计, 将资源集成方案求解问题看作组合优化问题, 根据目标函数设定, 从可用资源集合中选取资源组合价值最高的资源子集或从需求列表中选择能完成任务更好的需求满足资源子集, 将资源集成方案选择求解问题转换成集合同构子集构造问题, 与0/1整数背包这一经典组合优化问题相似. 在此基础上建立的问题求解模型相对简单, 避免了建模过度复杂的问题, 同时可以处理异构资源.
虽然down-selection模式将问题描述得尽量简化, 易建模求解, 但组合优化问题仍然是NP-Hard问题, 需要启发性的优化算法求解. 文献[7, 8]通过遗传算法进行了资源优选, 文献[9, 14]采用了粒子群算法, 遗传算法和粒子群算法作为非梯度优化随机搜索算法在求解组合优化问题上有着广泛的应用, 文献[18]在前期研究成果上提出的网络信息体系演化分析方法也采用了遗传算法, 但遗传算法和粒子群算法都存在容易限于局部最优[19-21]的问题. 文献[11, 12]通过博弈论对资源集成方案问题进行求解, 但经典博弈论基于完全理性的假设, 并在完全信息条件下进行博弈[22], 网络信息体系构成复杂且运行环境多变未知难以达到这样的条件. 叶俊[23]将演化博弈用于组合优化问题求解, 提出了演化博弈优化算法, 并针对背包问题这一典型组合优化问题对算法进行了论证与仿真. 该算法在解决一维背包问题和多维背包问题中解的质量相对遗传算法有明显的优势, 在相同的问题中演化博弈优化取得了价值更高的解, 有效避免了限于局部最优的问题, 且获得了更高的计算效率.
基于上述研究, 本文将借鉴down-selection模式对问题进行形式化描述, 并采用演化博弈优化方法来设计资源优选算法. 但作为复杂的组合优化问题, 以down-selection模式描述的集成方案求解问题与背包问题还有区别, 集成方案的目标函数需要考虑节点之间的冗余、协同等现象, 与决策空间非线性相关, 且计算过程更为复杂. 因此算法设计中要根据问题对用到的定理重新论证, 另外文献[23]中的初始策略组合在当前最优策略组合基础上经过扰动获得, 有概率扰动出重复策略组合, 从而获得同样的演化结果, 降低计算效率, 对于目标函数更复杂的集成方案求解, 计算效率会受到更大影响.
3 问题分析与描述当物理节点损毁时需要作战体系快速准确的给出作战源组合方案[5], 如何优选存活资源入网以恢复体系核心能力是一个关键难题. 本文借鉴down-selection模式, 首先针对网络信息体系领域资源集成方案求解问题进行描述, 描述为给定约束条件下, 从存活节点集合中求解子集, 使得子集能够满足任务需求. 本文从决策空间、约束函数、目标函数3个方面描述问题. 比如, 网络信息体系中的物理节点可能发生损毁、或因通信中断无法入网, 供电系统发生故障, 部分节点资源需依靠不间断电源或其他临时供电设备运行, 因而此时资源优选方法的决策空间为存活节点集, 受到的约束主要为电能消耗约束, 目标为作战效能最大并用核心任务的完成度衡量.
3.1 决策空间——节点资源以防空反导作战体系为例, 本文根据“OODA环”作战模型[24]进行资源集构建, 基于任务将资源节点分为感知节点、情报分析节点、决策节点、火力打击节点(通信节点作为各类节点入网的手段不单独分析) 4类: 感知节点主要有警戒雷达, 远方雷达, 近方雷达, 火控雷达, 制导雷达等, 情报处理节点主要有雷达情报指挥系统, 雷达情报传递处理系统, 全源分析系统(ASAS), 情报电子战系统(IEW)等, 决策节点主要有防空导弹火力分配决策支持系统(DSS), 综合防空与导弹防御作战指挥系统(IBCS), 机动控制系统(MCS)等, 火力节点主要有红旗-9, 红旗-12, S300, S400等. 各类节点与任务完成、电能消耗的相关属性如表1所示.
在此基础上给出存活节点定义, 如定义1.
定义1. 存活节点. 给定存活节点集合
| 表 1 节点资源属性 |
对于
对于
对于
对于
根据特定场景中尽量完成核心的目标, 将任务完成度为目标函数. 防空反导作战体系的核心任务是识别打击空域威胁对象, 根据系统科学和“OODA”环作战理论, 任务可分解可以简单分解为目标感知、情报处理、决策控制、火力打击几个基础功能, 基础功能形成闭合回路并反复迭代以完成防空反导任务, 节点资源集成需要满足4个基础功能的需求, 且因为基础功能需要反复迭代, 每一轮迭代中基础功能的需求可能不同, 借鉴基于贝叶斯网络能力生成模型[25], 用若干条任务需求来描述任务, 再用每个需求的满足度之和来描述任务完成度. 给出任务定义、任务需求属性:
定义2. 任务. 给定任务的需求集合R, 对于每一条需求
| 表 2 需求类别属性 |
以高精度感知范围
通过表2中的属性计算出每一条需求的完成度, 根据定义2累计求和进一步计算出任务完成度给出具体计算方式如下:
为便于描述, 定义如下函数表示范围的相交与相减计算:
| $ \begin{split} & Ins({f_1}(x, y), {f_2}(x, y)) = \{ (x, y)| \\ & (x, y) \in {f_1}(x, y) \wedge (x, y) \in {f_2}(x, y)\} \end{split} $ | (1) |
| $ \begin{split} & Minus({f_1}(x, y), {f_2}(x, y)) = \{ (x, y)| \\ & (x, y) \in {f_1}(x, y) \wedge (x, y) \notin {f_2}(x, y)\} \end{split} $ | (2) |
其中,
对于集成方案
| $ \left\{ {\begin{split} & AoH = \{ (x, y)|\exists ({s_i} \in S' \wedge {s_i}.cl = {O_b} \wedge {s_i}.Do = H) \\ & {\rm{s.t.}}\;{(x - {s_i}.O{o_x})^2} + {(y - {s_i}.O{o_y})^2} \leqslant {s_i}.r{o^2}\} \end{split}} \right. $ | (3) |
若
| $ {c_i}(S') = \frac{{\displaystyle\iint\limits_{x, y} {Minus(Ins(AoH{u_i}, AoH), AoH{l_i})}}}{{\displaystyle\iint\limits_{x, y} {Minus(AoH{u_i}, AoH{l_i})}}} $ | (4) |
否则为0;
当前情报分析力
| $ Co = \sum\limits_{{s_i} \in S' \wedge {s_i}.cl = Or} {{s_i}.Po} $ | (5) |
| $ {c_i}(S') = \left\{ {\begin{array}{*{20}{l}} 1,&{Co > Co{u_i}}&{} \\ {\dfrac{{Co - Co{l_i}}}{{Co{u_i} - Co{l_i}}}},&{Co{l_i} \leqslant Co \leqslant Co{u_i}}&{} \\ 0,&{Co < Co{l_i}}&{} \end{array}} \right. $ | (6) |
每条需求的完成度计算结束后, 当前任务完成度
| $ C(S') = \sum\limits_{{r_i} \in R} {{\omega _i}{c_i}(S')} $ | (7) |
设定故障供电线路为能耗约束, 其形式化定义如下:
定义3. 故障供电线路. 给定故障供电线路集合
则问题约束函数为:
| $ \bigcap\limits_{{r_i}' \in R'} {(\sum\limits_{{s_j} \in ({r_i}'.Rs \cap S')} {{s_j}.En} \leqslant {r_i}'.REn} ) $ | (8) |
综上, 网络信息体系资源集成方案求解问题, 给出如下形式化描述:
| $\left\{ { \begin{gathered} \mathop {\max }\limits_{S' \subseteq S} C(s') \\ {\rm{s.t.}}\bigcap\limits_{{r_i}' \in R'} {(\sum\limits_{{s_j} \in {r_i}'.Rs \cap S'} {{s_j}.En} \leqslant {r_i}'.REn} ) \\ \end{gathered} } \right.$ | (9) |
构造符合约束条件的同构子集, 使得目标函数取得最大值.
4 基于演化博弈的资源优选方法 4.1 资源集成方案求解模型基于叶俊[23]提出的演化博弈优化算法, 提出一种资源集成方案求解模型.
4.1.1 博弈结构为描述收益函数, 首先对问题(9)定义消耗溢出:
定义4. 消耗溢出.
对每一条约束, 若
| $ eove{r_{{r_i}'}} = r{'_i}.REn - \sum\limits_{{s_j} \in r{'_i}.R{s_k} \cap S'} {{s_j}.En} $ | (10) |
| $ Eove{r_{S'}} = \sum\limits_{r{'_{i \in }}R'} {eove{r_{r{'_i}}}} $ | (11) |
| $ {U}_{i}(T{'})=\left\{ {\begin{array}{l} C(T{'}),\qquad T{'}可行\\ {E}_{\rm over},\qquad\;\; T{'}不可行\end{array}} \right. $ | (12) |
对于策略组合
为描述演化模型, 给出如下两个定义:
定义5. 扰动过程[23]记为
定义6. 演化回合[23]记为
在上述定义与论证基础上构建演化模型, 模型的输入为博弈结构
Step 0.
Step 1. 进行一个演化回合
Step 2. 判断是否到达纳什均衡, 如果到达进入Step 3, 否则回到Step 1;
Step 3. 对当前策略组合
Step 4. 判断是否满足终止条件
此时
本文在第3节中将资源集成方案选择求解问题转换成了集合同构子集构造问题, 背包问题同样可看作对给定集合求子集的问题, 文献[23]通过演化博弈优化对背包问题进行了求解, 并给出了如下定理及证明:
定理1. 问题全局最优解对应策略组合为博弈结构纳什均衡;
定理2. 演化模型以概率1收敛到全局最优解对应的策略组合;
定理3. 任何局势可在1个演化回合内达到策略组合对应的子集可行;
定理4. 任何局势可在2个演化回合内达到纳什均衡状态;
本文借鉴文献[23]的演化博弈优化思路提出上述模型, 要基于模型提出算法, 必须在资源优选问题背景下对上述定理进行论证.
定理1. 问题全局最优解对应策略组合为博弈结构纳什均衡.
证明: 对于任意
定理2. 演化模型以概率1收敛到全局最优解对应的策略组合.
证明该定理所用到问题的特性背包问题与资源优选问题相同, 证明过程详见文献[23].
定理3. 任何局势可在1个演化回合内达到策略组合对应的子集可行.
证明: 假设一个演化过程后的策略组合不可行, 那么任意主体此时收益为负值且必然有至少一组约束条件不满足, 该约束条件中必然有主体已选1, 对于任选其中排序最靠后的个体, 在演化回合到该个体时, 策略有1到0必然可以通过提高 提高收益, 这与演化回合的定义相悖, 假设不成立, 得证.
定理4. 任何局势可在2个演化回合内达到纳什均衡状态.
但定理4的证明基于背包问题的如下特性:
假设两个子集
该特性对背包问题成立, 但问题(9)在如下情形不成立: 元素
根据第2节中提出的扰动过程可能会产生重复策略组合从而降低计算效率的问题, 对扰动过程进行限制, 验证扰动过程生成的策略组合是否被计算过, 如果被计算过则重新进行扰动过程.
为保证计算效率, 算法对每一代演化仍然只设计中仍两个演化回合. 算法的目的在于搜索得到使目标函数最大的子集, 根据第4.1.3节中分析的定理4不成立的情形, 某个局势在2个回合内未达到的纳什均衡所对应策略组合, 可以由其他初始策略演化得到.
鉴于基于式(1)–式(4)的
算法 1. 基于演化博弈优化的资源优选(EGA-RO)算法
输入: 集合
输出: 集成方案中的节点集合
1. for
2. 创建
3. end for
4. 所有个体形成列表
5.
6.
7. while (
8. while (
9. for
10. if
11. end for
12. end while
13. while (未达到纳什均衡)
14. for
15.
16.
17.
18. if
19. end for
20. end while
21.
22. if
23. end while
24.
本文选择在Netlogo平台上进行仿真实验. Netlogo是一个可以对自然和社会现象进行仿真的可编程环境, 可以对多智能体进行建模, 平台支持向上千个同时独立运行的智能体发送指令, 通过智能体之间的交互, 探索他们在各种条件下的不同行为, 探索个体微观行为对宏观现象的影响, 本文将Netlogo平台部署在如下硬件环境: 处理器为AMD Ryzen 7 5800H with Radeon Graphics (3.20 GHz); 显卡配置为NVIDIA GeForce RTX 3060 Laptop GPU. 本文仿真实验均在此平台上进行.
构建了80条雷达、情报分析系统、决策系统、导弹4类装备相关信息的数据集, 从数据集中筛选出表1中属性值形成节点资源列表.
按照定义2构建需求列表描述任务, 按照定义3构建线路列表描述约束条件, 构建任务时, 使得任务完全完成需要节点数量为25个左右, 即设置节点资源有68.75%冗余.
5.2 实验设计与结果实验通过以下两个操作模拟物理节点损毁事件: ① 对于当前节点资源列表中每个元素以概率
为了验证算法的有效性, 设计几种情况进行验证.
5.2.1 对比基于遗传算法的资源优选方法基于基本遗传算法[26], 同样使用目标函数式(12), 将一个策略组合看作一个染色体, 设计基于遗传算法的资源优选方法(GA), 首先实验将EGA-RO算法与GA算法对比, 实验参数设置为
实验结果可以明显看出EGA-RO算法所求集成方案任务完成度明显高于GA算法为更可靠地验证资源优选算法效果, 在不同损毁概率、扰动概率、交叉概率与变异概率下, 进行36组对比试验, 得到数据如表3.
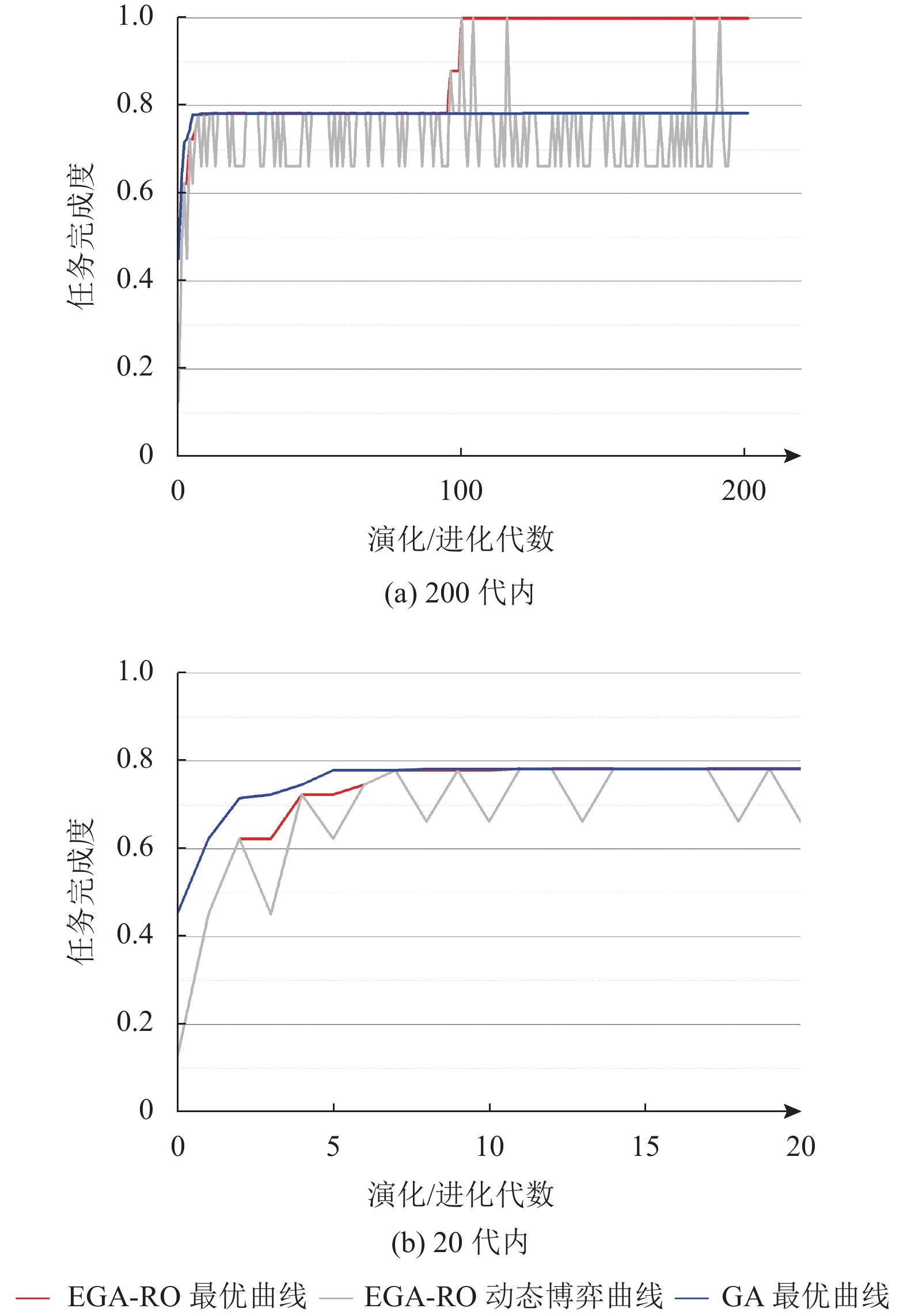
|
图 1 基于演化博弈和遗传算法的资源优选效果对比 |
| 表 3 不同参数下EGA-RO算法与GA算法对比 |
算法结束时获得的方案对应的任务完成度
对表3数据进行分析, 36组对比实验中, GA算法
分析36组对比实验中, 不同损毁概率下两种算法获得方案在各
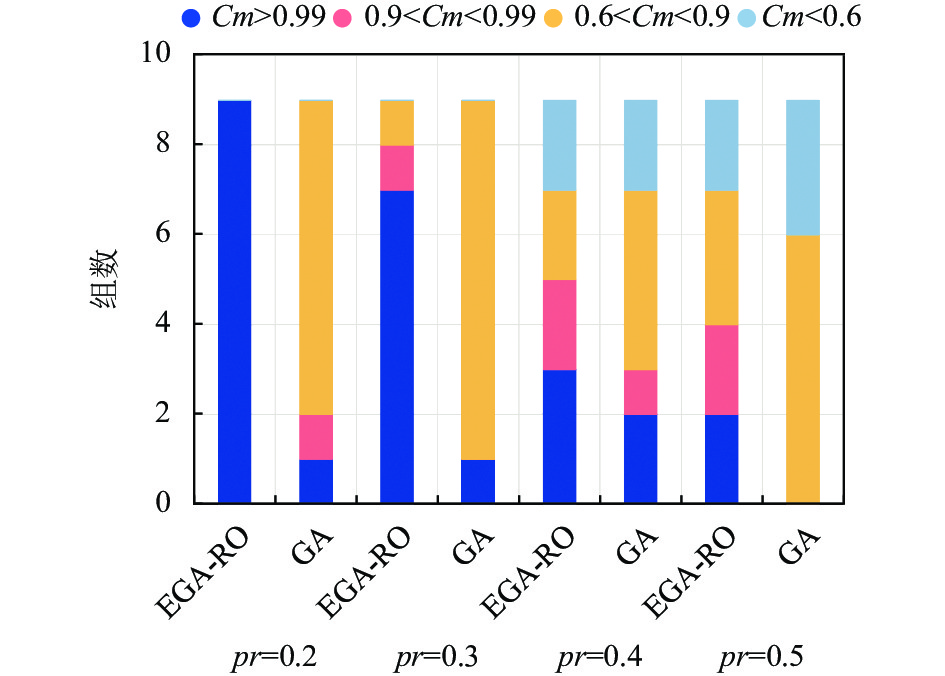
|
图 2 EGA-RO算法与GA算法
|
图2分别描述了损毁率在0.2、0.3、0.4、0.5时两种算法的Cm值, 每个损毁率对应图中两条柱, 分别描述EGA-RO算法和GA算法的情况. 可以看出, 在不同的损毁概率下, EGA-RO算法获得的方案质量都优于GA, 而在物理节点损毁率
36组实验中共有10组两个算法获得了同样的
图3中可以看出, 当两种算法获得任务完成度相同的方案时, EGA-RO
实验结果表明, 本文提出的EGA-RO算法可以有效完成节点资源优选, 且相对GA算法有优势: 相同仿真案例中, 获得优秀方案比例高于GA算法, 解的质量平均提高了6.4%, 获得同样质量解时, EGA-RO算法求解效率高于GA算法60%.
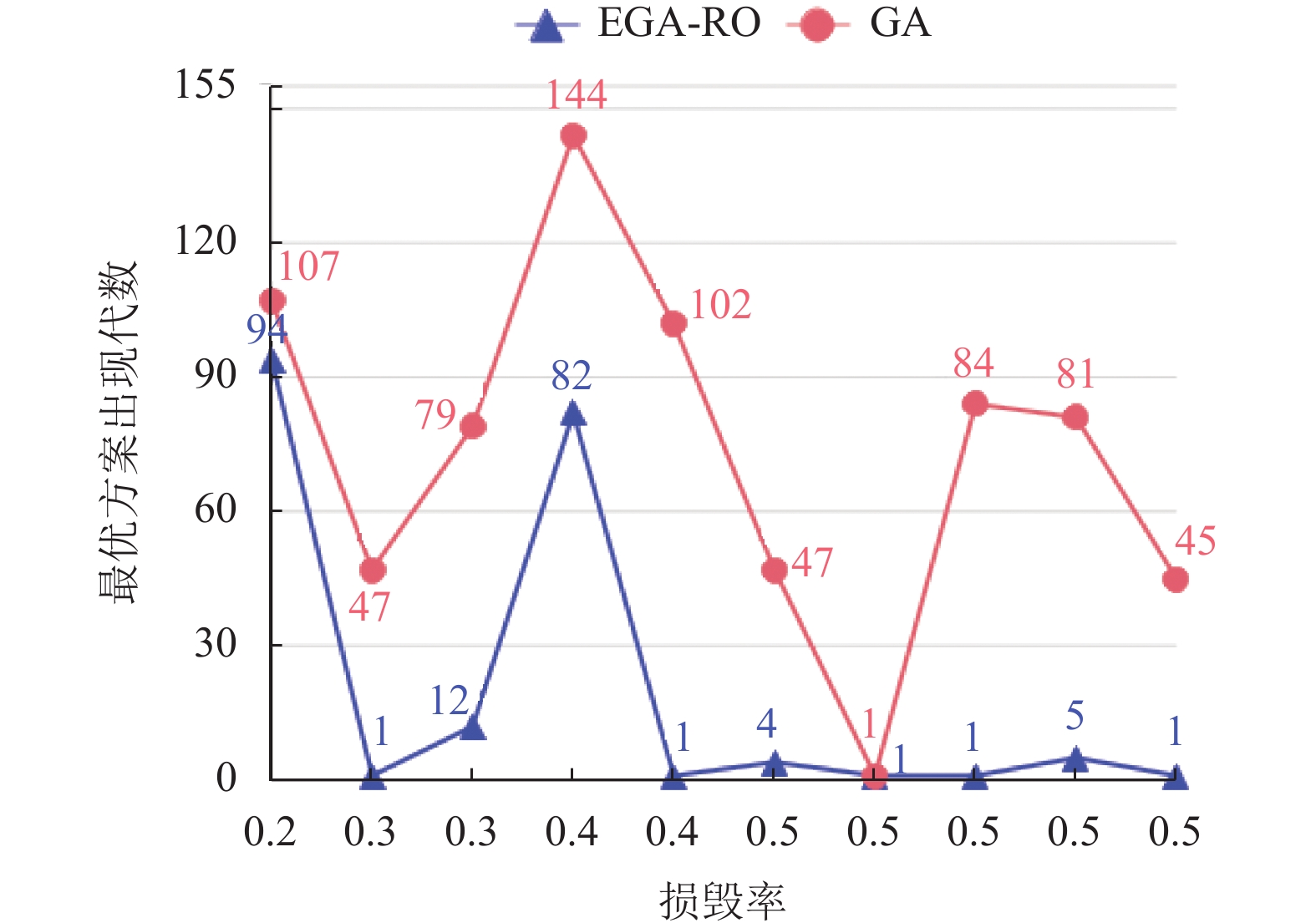
|
图 3 EGA-RO算法与GA算法最优方案出现代数对比 |
5.2.2 对比无扰动限制的资源优选方法
根据算法添加扰动过程限制这一改进, 实验将算法与无扰动过程限制的算法进行对比. 实验分别以损毁概率
通过分析不同损毁概率下两种算法求出集成方案效果(以任务完成度衡量), 发现两种算法最终求得的方案任务完成度相同. 对两种算法

|
图 4 算法有无扰动限制最优方案出现代数对比 |
从图4中可以看出当损毁概率为
本文在物理节点损毁场景下, 以防空反导作战体系为例研究了网络信息体系资源优选问题. 基于演化博弈优化, 提出了集成方案求解模型, 设计了资源优选算法, 在Netlogo上的仿真实验验证了该算法的有效性, 结果表明: 对比基于基本遗传算法的方法, 同样仿真案例中, 获得优秀方案比例更高, 求出方案任务完成度平均提高6.4%, 获得同样任务完成度方案时求解效率提高60%; 对比无扰动限制的资源优选算法, EGA-RO最优方案平均代数提前了38.6%. 本文研究的资源优选方法可为网络信息体系动态架构设计提供方法参考. 本文仅研究了单任务下网络信息体系资源集成优化, 多任务集成方案形成必然存在节点资源互斥的问题, 下一步将针对这个问题展开进一步的研究.
| [1] |
王世忠, 郝政疆, 魏凡. 对网络信息体系本质特征与体系构成的基本认识. 自动化指挥与计算机, 2014, 111(3): 8-11. |
| [2] |
中国电子科技集团公司发展战略研究中心. 网络信息体系构建方法和探索实践. 北京: 电子工业出版社, 2020, 4. |
| [3] |
汪李峰, 杨学军. 战术场景互联网——未来智能化战场的神经系统. 指挥与控制学报, 2021, 7(4): 359-364. DOI:10.3969/j.issn.2096-0204.2021.04.0359 |
| [4] |
王维平, 李小波, 杨松, 等. 智能化多无人集群作战体系动态适变机制设计方法. 系统工程理论与实践, 2021, 41(5): 1096-1106. DOI:10.12011/SETP2020-1800 |
| [5] |
赵鑫, 郭成昊, 黄强, 等. 指挥控制系统自主适变解决方案研究. 中国科学: 信息科学, 2020, 50(11): 1665-1679. |
| [6] |
张维明, 杨国利, 朱承, 等. 网络信息体系建模、博弈与演化研究. 指挥与控制学报, 2016, 2(4): 265-271. |
| [7] |
胡瑞淇, 程辉, 张执南. 基于表达式树的顺序柔性车间调度问题求解. 计算机集成制造系统. http://kns.cnki.net/kcms/detail/11.5946.tp.20220317.1506.002.html. (2022-03-02).
|
| [8] |
周康, 同小军, 许进. 资源优化模型及遗传算法. 华中科技大学学报(自然科学版), 2005, 33(10): 59-62. DOI:10.13245/j.hust.2005.10.019 |
| [9] |
王有远, 钱伟伟, 刘瑞. 基于任务分层策略和属性相对变权决策的设备资源优化. 计算机集成制造系统, 2021, 27(10): 2970-2980. DOI:10.13196/j.cims.2021.07.021 |
| [10] |
Xiao ZJ, Jiang JM, Zhu YY, et al. A solution of dynamic VMs placement problem for energy consumption optimization based on evolutionary game theory. Journal of Systems and Software, 2015, 101: 260-272. DOI:10.1016/j.jss.2014.12.030 |
| [11] |
Arthanari TS. A game theory application in robust design. Quality Engineering, 2005, 17(2): 291-300. DOI:10.1081/QEN-200056498 |
| [12] |
Ghotbi E, Dhingra AK. A bilevel game theoretic approach to optimum design of flywheels. Engineering Optimization, 2012, 44(11): 1337-1350. DOI:10.1080/0305215X.2011.637557 |
| [13] |
Crawley E, Cameron B, Selva D. System Architecture: Strategy and Product Development for Complex Systems. Hoboken: Pearson Higher Education, Inc., 2016. 11.
|
| [14] |
Yuan H, Li CB, Du MK. Optimal virtual machine resources scheduling based on improved particle swarm optimization in cloud computing. Journal of Software, 2014, 9(3): 705-708. |
| [15] |
Ergu D, Kou G, Peng Y, et al. The analytic hierarchy process: Task scheduling and resource allocation in cloud computing environment. The Journal of Supercomputing, 2013, 64(3): 835-848. DOI:10.1007/s11227-011-0625-1 |
| [16] |
Makwe A, Kanungo P. Scheduling in cloud computing environment using analytic hierarchy process model. Proceedings of 2015 International Conference on Computer, Communication and Control. Indore: IEEE, 2015. 1–4.
|
| [17] |
Warneke D, Kao O. Exploiting dynamic resource allocation for efficient parallel data processing in the cloud. IEEE Transactions on Parallel and Distributed Systems, 2011, 22(6): 985-997. DOI:10.1109/TPDS.2011.65 |
| [18] |
张婷婷. 网络信息体系能力演化分析方法研究. 北京: 科学出版社, 2018.
|
| [19] |
徐宁, 李春光, 张健, 等. 几种现代优化算法的比较研究. 系统工程与电子技术, 2002, 24(12): 100-103. DOI:10.3321/j.issn:1001-506X.2002.12.030 |
| [20] |
沈斌, 江维, 胡中功. 三种现代优化算法的比较研究. 自动化与仪器仪表, 2009(3): 111-113. DOI:10.3969/j.issn.1001-9227.2009.03.042 |
| [21] |
朱凤龙. 遗传算法“早熟”现象的探究及改进策略[硕士学位论文]. 重庆: 西南大学, 2010.
|
| [22] |
哈罗德·W·库恩. 博弈论经典. 韩松, 译. 北京: 中国人民大学出版社, 2004.
|
| [23] |
叶俊. 演化博弈优化[博士学位论文]. 武汉: 华中科技大学, 2004.
|
| [24] |
朱江, 蔡蔚, 闻传花, 等. 基于OODA指挥控制环的作战仿真实验. 指挥控制与仿真, 2015, 37(3): 112–115.
|
| [25] |
DeLaurentis DA, Marais K. Assessing the impact of development disruptions and dependencies in analysis of alternatives of system-of-systems. Technical Report, Hoboken: Stevens Institute of Technology, 2013.
|
| [26] |
李刚, 童頫. 自然遗传算法及其性能分析. 应用科学学报, 1999, 17(3): 337-342. |
 2022, Vol. 31
2022, Vol. 31


