1 概述

神经网络是机器学习中的重要技术手段, 在图像处理、语音识别、时间序列预测等领域有着广泛的应用^[1]. 在过去20年中, 随着计算机技术的发展, 神经网络的结构、规模以及训练方法都得到了飞速的发展. 诸如卷积神经网络、循环神经网络等一系列技术的引入使得神经网络的准确率取得了快速的提升. 但是由于引入了大量非线性的结构, 神经网络的训练过程存在非常强的非凸性, 这使得对神经网络准确性的评估也变得更加复杂, 尤其是当神经网络的准确率越来越高时, 其评分也都越来越接近极限^[2].

对神经网络的评估主要是通过对比神经网络在训练集以外的测试集上的表现. 通常会用损失(loss)、准确率(accuracy)等函数作为神经网络的表现分数. 为此在很多问题上, 大量学者和机构提供了很多公开的训练集、验证集以及测试集(如对于手写字体分类的mnist^[3], 对于自然分割问题的Oxford-IIIT^[4]). 由于神经网络的训练是一个非凸问题, 不同的神经网络初始参数可能最终得到的网络模型并不相同, 因此在评估神经网络时, 通常会选择不同次训练中表现最好的模型的表现分数来与其他网络对比. 但这个过程通常具有较大的偶然性和不可复制性, Reimers等^{[5, 6]}指出通过分析同一网络不同随机种子训练得到模型的表现分数的分布能更稳定地比较分数接近的不同网络之间的优劣. 在此基础之上, Dror等^[7]引入了随机占优(stochastic dominance)和几乎随机占优(almost stochastic dominance)来分析两个分数相近的网络分数分布的优劣. 随机占优是一种基于不同随机变量的分布函数间关系得到排序的检验. 最早明确地提出随机占优概念的是Quirk等^[8], 直到上世纪60年代末70年代初, Hadar等^[9]、Hanoch等^[10]一系列随机占优的经典论文发表后, 这一理论的相关发展和应用逐步推广到金融、医学、工程等不同领域中^[11]. 随机占优理论弥补了均值-方差模型判断随机变量分布的局限性. 通常评价两个神经网络时, 我们希望其中一个神经网络分数的期望优于另一网络, 同时其标准差也比另一网络小. 但实际上可能存在期望较优, 但是标准差更大的情况, 随机占优可以很好地应对这种情况.

除了不同初始模型训练得到不同模型的分布值得关注, 我们认为不同模型对于测试集中不同样本的表现的分布也值得关注. 尤其是在对于神经网络预测精度的稳定性有要求的领域(如图像分割、股票预测)^{[12, 13]}, 我们要求训练出的模型在对测试集进行预测时具有较高的准确率且较小的标准差. 因此本文中进一步将随机占优引入到图像分割问题中不同网络模型在测试集中不同样本表现分布的比较中. 以图像分割中常用的卷积编码器-解码器网络(convolutional encoder decoder, 以下简称CED)^[14]和U-Net网络^[15]为例, 本文先对比了两个网络在500个不同初始模型训练之后表现的分布, 再进一步地对比了这些训练出的模型在测试集中不同样本表现的分布. 结果显示尽管不同初始模型训练得到的结果U-Net占优于CED网络, 但是CED网络在测试集不同样本中表现的标准差要小于U-Net网络, 这使得在本文的抽样测试对比中, 半数以上的CED网络模型在不同样本表现中的分布占优于U-Net网络模型. 因此本文认为, 不同模型在测试集中表现的标准差应该引起网络对比中的重视, 通过随机占优方法可以更合理地对比不同的模型, 并给出合适的选择.

2 随机占优和几乎随机占优理论 2.1 随机占优的定义

令随机变量X、Y, 累积分布函数分别为F、G, 且F、G都是定义在 ${\mathbb{R}}$ 上的连续函数. 当且仅当对所有的 $ a \in \mathbb{R} $ , 都有 $ F(a) \leqslant G(a) $ (不等号在某些a处严格成立)时, 称X随机占优于Y (记作 $ Y \succ X $ ). 即对所有a, X中有更高比例大于a的样本. 完全随机占优成立的条件非常严格, 见图1(a), 针对a的每一个值, 不等式 $ F(a) \leqslant G(a) $ 都要成立, 这在应用中几乎难以实现. 因此, 随机占优的条件的放宽引起了更多关注^[16].

Leshno等^[17]提出了几乎随机占优的概念, 允许G在一些a处位于F的下方, 见图1(b). del Barrio等^[18]则采用L₂-Wasserstein距离来定义和检验几乎随机占优. 接下来从分位数的概念开始介绍.

令 $ {F^{ - 1}}(t) = \inf \{ x:t \leqslant F(x)\} , t \in (0, 1) $ 为概率密度函数F对应的分位数函数, 随机占优可表示为: $ X \succ $ $Y \Leftrightarrow {F^{ - 1}}(t) \geqslant {G^{ - 1}}(t), \forall t \in (0, 1) $ . 可以看出当 $ {F^{ - 1}}(t) < {G^{ - 1}}(t) $ 时, X和Y间随机占优不成立. 用分位数函数定义 $ {A_X} $ 和 $ {A_Y} $ :

$\left\{ { \begin{split} &{A_X} = \{ t \in (0, 1):{F^{ - 1}}(t) < {G^{ - 1}}(t)\}\\ &{A_Y} = \{ t \in (0, 1):{F^{ - 1}}(t) > {G^{ - 1}}(t)\} \end{split}} \right.$

del Barrio等^[18]基于这些概念提出占优指数 ${\varepsilon _{{w_2}}}$ 来定义一个随机变量占优于另一个随机变量的程度:

$ {\varepsilon _{{w_2}}}\left( {F, G} \right): = \dfrac{{\int_{{A_X}} {{{({F^{ - 1}}(t) - {G^{ - 1}}(t))}^2}dt} }}{{{{({w_2}(F, G))}^2}}} $

其中, ${w_2}(F, G) = \sqrt {\int_0^1 {{{({F^{ - 1}}(t) - {G^{ - 1}}(t))}^2}dt} } $ 是分布间的单变量L₂-Wasserstein距离. 这个指数满足 $0 \leqslant {\varepsilon _{{w_2}}} \left( {F, }\right. \left. {G} \right) \leqslant 1$ , 其中0表示X完全占优于Y, 1表示Y完全占优于X. 同时有 ${\varepsilon _{{w_2}}}\left( {F, G} \right) = 1 - {\varepsilon _{{w_2}}}\left( {G, F} \right)$ 成立. 较小的指数值(一般定义在0到0.5之间)表示越接近完全随机占优.

同时, 随机占优具有传递性, 这意味着若分布F占优于G, G占优于H, 那么F占优于H. 这样在比较多个分布时, 可以大大减少比较次数^[19].

2.2 几乎随机占优的统计检验

使用占优指数 ${\varepsilon _{{w_2}}}$ , 可以制定以下假设检验问题, 来检验几乎随机占优:

$\left\{ { \begin{split} &{H}_{0}:{\varepsilon }_{w}{}_{{}_{2}}(F, G)\geqslant \epsilon\\ & H_{1}: \varepsilon_{w_{2}}(F, G)> \epsilon \end{split}} \right.$

对于提前给定的 $ {\epsilon} > 0 $ , 若占优指数 $ {\varepsilon _{{w_2}}}(F, G) $ 比 $ {\epsilon} $ 小, 则拒绝原假设, 这意味着分布F以一定的偏差几乎随机占优于G.

累积分布函数F、G可由经验分布函数估计得到: $ {F_n}(t) = \dfrac{1}{n}\Sigma _{i = 1}^n\mathbb{I}({x_i} \leqslant t) $ ; $ {G_m}(t) = \dfrac{1}{m}\Sigma _{i = 1}^m\mathbb{I}({y_i} \leqslant t) $ , 其中 $ \mathbb{I}( \cdot ) $ 为示性函数.

del Barrio等^[18]证明了占优指数 $ {\varepsilon _{{w_2}}}(F, G) $ 的渐近正态性, 并指出在没有更多假设的前提下, 若有:

$ \sqrt{\dfrac{nm}{n+m}}({\varepsilon }_{{w}_{2}}({F}_{n}, {G}_{m})-{\epsilon}) < {\hat{\sigma }}_{n, m}{\Phi }^{-1}(\alpha ) $

则在显著性水平 $ \alpha $ 下拒绝 $ {H_0} $ (本文中 $ \alpha $ 取0.05). 其中, $ {\epsilon} $ 为违规水平, $\Phi $ 是标准正态分布函数, ${\hat \sigma _{n, m}}$ 是式 $\sqrt {\dfrac{{nm}}{{n + m}}} ({\varepsilon _{{w_2}}}(F_n^*, G_m^*) - {\varepsilon _{{w_2}}}({F_n}, {G_m}))$ 的方差估计值, 其中 $F_n^*$ 、 $G_m^*$ 是由原始样本 ${X_n}$ 、 ${Y_m}$ 混合后抽取得到的样本 $X_n^*$ 、 $Y_m^*$ 计算而来.

此外, 在置信水平为 $1 - \alpha $ 下F几乎随机占优于G的最小 ${\epsilon}$ 为:

$ {{\epsilon}}^{{\rm{min}}}({F}_{n}, {G}_{m}, \alpha )={\varepsilon }_{{w}_{2}}({F}_{n}, {G}_{m})-{\hat{\sigma }}_{n, m}{\Phi }^{-1}(\alpha ) $

若 ${{\epsilon}}^{{{\rm min}}}({F}_{n}, {G}_{m}, \alpha ) < 0.5$ , 可以称F优于G, ${{\epsilon}}^{{\rm {min}}}\left({F}_{n}, {G}_{m}, \right. \left. \alpha \right)$ 的值则表明分布间的最大差距, 当 ${{\epsilon}}^{{\rm{min}}}\left({F}_{n}, {G}_{m}, \alpha \right)= 0$ 时, F完全随机占优于G. 然而, 若 ${{\epsilon}}^{{\rm{min}}}({F}_{n}, {G}_{m}, \alpha ) \geqslant 0.5$ , F几乎随机占优于G不成立, 接受原假设.

在 ${\hat \sigma _{n, m}}$ 估计准确的前提下, ${{\epsilon}^{{\rm{min}}}\left({F}_{n}, {G}_{m}, \alpha \right) = 1- } {{\epsilon}^{{\rm{min}}}} {({G}_{m}, {F}_{n}, \alpha )}$ 成立. 因此, 对于给定的 $\alpha $ 值, 除非 ${{\epsilon}}^{{\rm{min}}}\left({F}_{n}, \right. {G}_{m}, \alpha )={{\epsilon}}^{{\rm{min}}}({G}_{m}, {F}_{n}, \alpha )=0.5$ , 我们都能得到一个算法更优的结论.

2.3 几乎随机占优的算法流程

现有来自两个神经网络模型A、B的评分集合: $A = \{ {x_1}, {x_2}, \cdots, {x_n}\} $ , $B = \{ {y_1}, {y_2}, \cdots, {y_m}\} $ , 几乎随机占优模拟算法的伪代码如下:

(1) 将两个集合中分值从小到大排列得到: $A = \left[{x_{(1)}}, \cdots, {x_{(n)}} \right]$ 、 $B = [{y_{(1)}}, \cdots, {y_{(m)}} ], \;$ 其中 $ {x_{(i)}}$ 表示第i小的值.

(2) 计算评分的经验分布函数 ${F_n}$ 、 ${G_m}$ : $ {F_n}(t) = \dfrac{1}{n}\Sigma _{i = 1}^n\mathbb{I}({x_i} \leqslant t) $ .

(3) 用式 $ {F^{ - 1}}(t) = \inf \{ x:t \leqslant F(x)\} , t \in (0, 1) $ 构造得分的经验分布逆函数 $F_n^{ - 1}(t)$ 、 $G_m^{ - 1}(t)$ .

(4) 计算随机占优指数 $ {\varepsilon _{{w_2}}}(F, G) $ , 实践中, 我们用黎曼积分计算积分, 也就是将积分区间(0, 1)分为长度为 $\Delta $ 的小区间, 每个区间的积分乘以 $\Delta $ 再求和.

(5) 估计 $\sigma $ : 从经验分布 ${F_n}$ 、 ${G_m}$ 中抽取足够的样本 $X_n^*$ , $Y_m^*$ , 对每一对样本计算表达式 $\sqrt {\dfrac{{nm}}{{n + m}}} \left({\varepsilon _{{w_2}}}\left(F_n^*, G_m^*) - \right. \left. {\varepsilon _{{w_2}}}({F_n}, {G_m}\right) \right)$ 的值, 将这些值的方差作为 ${\sigma ^2}$ 的估计, 样本越多, 精度越高.

(6) 在置信水平 $1 - \alpha $ 下模型A几乎随机占优于B的最小 $ {\epsilon} $ 为:

$ {{\epsilon}}^{{\rm{min}}}({F}_{n}, {G}_{m}, \alpha )={\varepsilon }_{{w}_{2}}({F}_{n}, {G}_{m})-{\hat{\sigma }}_{n, m}{\Phi }^{-1}(\alpha ) $

当 ${{\epsilon}}^{{\rm{min}}}({F}_{n}, {G}_{m}, \alpha ) < {\epsilon}$ 时, 模型A几乎随机占优于模型B.

3 图像分割 3.1 图像分割简介

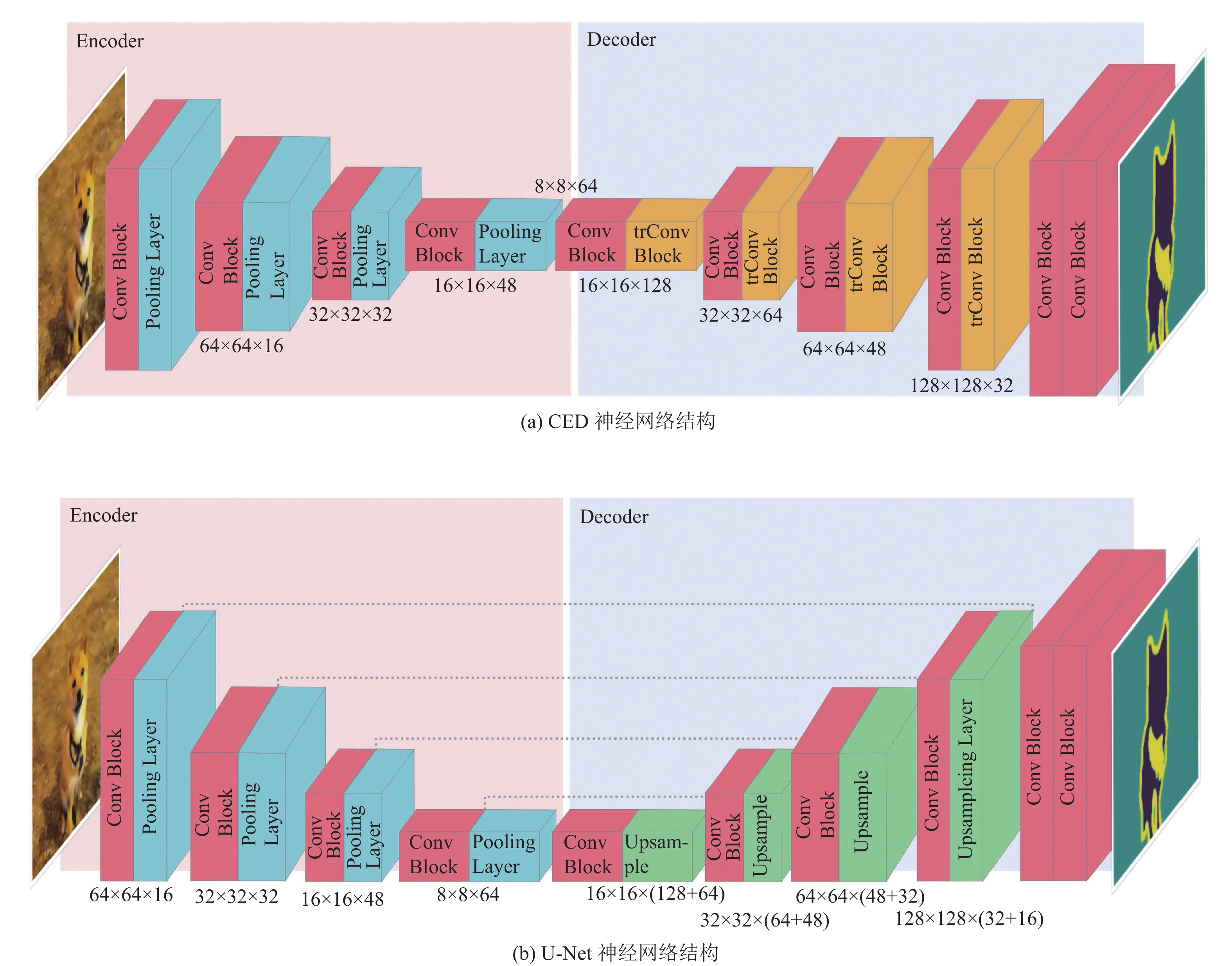
图像分割是神经网络的重要应用, 其主要任务是把图片分割为若干个具有独特特征的区域, 是图像分析以及计算机视觉等领域中的关键步骤^[20]. 高精度的图像分割在工业生产、医学图像处理以及科学研究等诸多领域都具有重要的应用空间. 卷积神经网络(CNN)是图像分割任务中的重要实现手段. 本文以卷积神经网络发展而来的CED和U-Net网络在Oxford-IIIT 3.0.0数据集^[4]中的表现为例, 展示随机占优在神经网络比较中的应用. 两者的网络结构如图2所示, 其中Conv Block表示由两个包含3×3卷积核的卷积层组成卷积块; Pooling Layer为池化层; trConv Block表示由两组转制卷积(transposed convolution)组成的转制卷积块; Upsampling Layer表示上采样层. 需要注意的是, 为通过随机占优直观地对比两组结果相近的神经网络模型, 我们这里仅选用这两种在图像分类任务中经典的神经网络结构, 且无需关注在网络参数和结果精度上的优化.

Oxford-IIIT数据集是一个宠物图像数据集, 包含了37种宠物的图片, 每种宠物约200张图片, 并包含了每张图片的宠物轮廓的标注信息. 我们分别以0, 1, 2标注没有宠物的区域, 宠物的轮廓以及宠物所在的区域. 在训练时, 我们把每一张图片转化为128×128像素的三通道图片, 并定义每一张图片的准确率(accuracy)为和标注完全一致的像素点占总的像素点的比例作为本文对网络评分的主要参数. 如图3所示, 图3(a)为需要进行图像分割的宠物图片, 图3(b)为标注后的轮廓图片, 图3(c)、图3(d)则分别是两个模型预测的结果.

3.2 应用随机占优对比网络模型预测结果的流程

传统的网络对比方法通常只关注网络预测结果与正确标签的误差. Dror等^[7]将随机占优引入到网络对比中, 其主要流程为: 对于两个不同的网络结构A和B, 分别由n个和m个随机初始模型训练得到n个和m个模型 $\{ {A_1}, {A_2}, \cdots, {A_n}\} $ 和 $\{ {B_1}, {B_2}, \cdots, {B_m}\} $ ; 分别计算模型 $\{ {A_1}, {A_2}, \cdots, {A_n}\} $ 和 $\{ {B_1}, {B_2}, \cdots, {B_m}\} $ 在测试集中的评分(对应本文中的评分函数为测试集中每一图片预测准确率的均值)为 $\{ {x_1}, {x_2}, \cdots, {x_n}\} $ 和 $\{ {y_1}, {y_2}, \cdots, {y_m}\} $ ; 通过第2.3节中几乎随机占优算法评估两者间的占优关系即为A网络和B网络的占优关系.

在实际应用中, 比较训练好的每个模型的表现同样值得关注, 因此本文提出随机占优应用于比较两个训练好的图像分割网络模型A和B, 流程如下: 分别计算A和B在测试集中每张图片中的准确率 $\left\{ {x_1}, {x_2}, \cdots, {x_n}\right\}$ 和 $\{ {y_1}, {y_2}, \cdots, {y_m}\} $ ; 再通过几乎随机占优评估两个准确率集合间的占优关系即为A模型和B模型的占优关系.

4 实验与分析 4.1 多次训练U-Net和CED网络之间的比较

我们首先重复Reimers等^[5,6]以及Dror等^[7]的方法对这两个网络进行评估. 我们分别使用500组不同的随机种子生成500组不同的初始模型对U-Net和CED网络各进行了500次训练. 每次训练使用的优化器均为Adam优化器^[21], 且参数完全相同, 每次训练最大训练次数为50次, 并设置了accuracy稳定之后停止训练, 每次训练最终保留验证集表现最好模型.

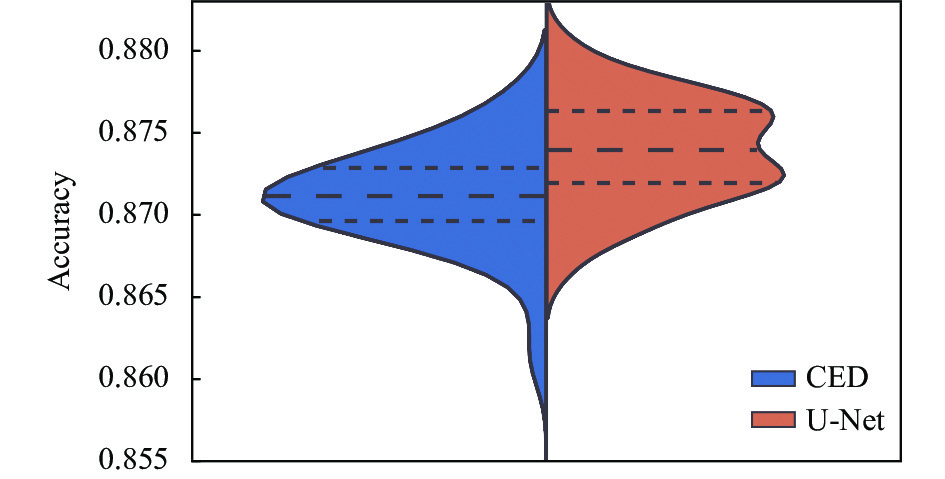
图4展示了通过训练得到的500个U-Net和CED模型在测试集中准确率的分布对比, 表1展示了两个网络得到500个模型准确率的均值、标准差、最大值、最小值. 可以看出U-Net网络表现的均值优于CED网络, 同时其标准差较小. 通过随机占优比较我们计算出U-Net相对于CED的占优指数为0, 这表明U-Net网络得到的模型的表现完全占优于CED网络.

4.2 U-Net和CED不同模型在测试集不同样本表现分布的对比

从不同随机种子的训练结果来看U-Net网络的表现明显是优于CED网络的表现的. 但是我们发现, U-Net网络训练出的模型对于训练集中不同样本的准确率的标准差(0.8附近)要比CED网络训练出的模型对于训练集中不同样本的准确率的标准差(0.7附近)更大. 这意味着U-Net网络训练出的模型尽管表现分数更好, 但是也更加离散. 这里我们从U-Net网络和CED网络中分别选出一个模型进行对比. 表2展示了这两个模型在测试集不同样本中准确率的均值、标准差、最大值和最小值. 从均值上看, U-Net模型的表现仍然优于CED模型的表现, 但是在标准差上U-Net模型的表现的离散程度要比CED模型的离散程度更大. 通过几乎随机占优, 我们可以得到CED相对于U-Net网络的占优指数为0.081928, 此时CED模型占优于U-Net模型.

为了排除这种占优是一种偶然现象, 我们从训练出的模型中有放回地随机选取了500对模型进行对比. 图5展示了这500对模型中CED网络模型相对于U-Net网络模型的占优指数的分布. 根据几乎随机占优理论占优指数小于0.5时CED网络模型占优于U-Net网络模型, 而当占优指数小于0.1时这种占优关系尤为明显, 相反则U-Net占优于CED网络. 从抽样结果中, 共有267对CED网络占优于U-Net网络, 163对占优指数小于0.1, 而占优指数大于0.9的仅有137对. 这显然与网络之间的对比的结论相反. 因此我们认为不同模型对于测试集中不同样本的表现的离散程度值得在神经网络评估时的重视.

在对神经网络结构和训练的研究中, 网络的占优关系可以有效地减少随机因素对研究的影响. 但在实际解决问题中, 模型的占优与否往往要比网络的占优与否更重要. 尤其是随着神经网络的发展准确率越来越接近100%的今天, 不同模型之间的差距越来越小, 模型在测试集中表现的离散度应引起足够的重视. 但仍然需要值得注意的是, 通常在表现相近的网络或模型(如准确率差距小于3%)中, 占优关系才可能和均值的表现相反, 而在表现差距较大时, 占优关系大概率和均值的表现是一致的.

4.3 通过几乎随机占优筛选出更合适的模型

在上文中我们已经验证了随机占优可以有效地对不同模型进行比较. 更进一步我们可以利用随机占优的传递性筛选出更合适的模型, 对于n个训练好的模型其具体流程如下:

(1) 挑选模型集合中排序前两个模型分别命名为A和B;

(2) 通过随机占优对比A和B模型在测试集中评分的表现, 保留其中占优的模型并命名为A;

(3) 将集合序列中下一个模型命名为B;

(4) 重复步骤(2)和步骤(3)直至所有模型都被比较, 最后保留下的A模型即为n个模型中最优模型.

通过上述流程, 可以得到本文训练得到的500个U-Net模型中最优模型的评分均值为0.880197, 标准差为0.071627; 本文训练得到的500个CED模型中最优模型的评分均值为0.877677, 标准差为0.062972; 这两者中CED模型占优于U-Net模型, 计算得到的占优指数为0.187514.

5 结论与展望

如何精确地评估神经网络的表现是当下神经网络的重要问题. 本文在Reimers等^[5,6]以及Dror等^[7]的工作基础之上进一步将几乎随机占优引入到神经网络模型在测试集中不同样本表现分布的对比中. 随机占优可以有效地解决在评估不同分布的对比时均值和方差结论不统一的问题. 通过图像分割的实验对比, 本文关注到不同神经网络模型在测试集中不同样本表现的离散性对于评估不同神经网络的重要性. 对于一些网络, 尽管不同次训练出来的模型总体的表现可能更好, 但是其每个模型对于测试集不同样本表现的方差仍然可能较大. 本文希望通过对随机占优方法的研究进一步提高神经网络对比的有效性.