区块链技术是结合了密码学、数学、分布式计算等一系列学科的跨学科技术, 被广泛应用于农业、金融业、工业等现实场景中, 对现代经济社会的发展作出了重要贡献^[1]. 在区块链技术被提出之前, 数据往往被存储于少量的中心化机构中, 一旦这些数据集中存储的节点被攻击, 就会造成数据泄漏, 带来相当大的安全隐患. 区块链技术的核心在于去中心化, 数据被分布式地存储于链上的各个节点当中, 这在一定程度上解决了数据过于集中, 安全隐患大的问题.

虽然去中心化的区块链技术解决了数据过于集中易被攻击的安全问题, 但也引发了一个新的问题, 即如何在一个去中心化、弱信任的分布式系统中让各个节点对系统的某一行为产生共识, 让系统节点产生共识的机制也被称为共识机制^[2-4]. 共识机制是区块链技术的核心, 它在保证区块链上的数据安全可靠的同时也要兼顾效率. 随着区块链技术的发展, 诸如工作量证明(proof of work, POW)、股权证明(proof of stake, POS)、委任权益证明(delegated proof of stake, DPOS)、实用拜占庭容错算法(practical Byzantine fault tolerance, PBFT)、授权拜占庭容错算法(delegated BFT, dBFT)等共识机制被相继提出^{[3, 4]}.

联盟链是在区块链技术基础上衍生的一种新的实用型分布式处理数据技术, 而Hyperledger Fabric正是在联盟链技术的基础上发展起来的. 它由 IBM、DAH等企业提交到Linux基金会^[5], 现在已经发展成了一个成熟的商业级区块链平台. Hyperledger Fabric将系统中的节点分为客户节点、对等节点以及背书节点. 客户节点负责提交相关交易给背书节点, 背书节点接收到交易之后进行检查, 检查无误之后对交易进行背书签名, 对等节点则检查交易的一致性问题并将交易打包成块提交到区块链中. 不同于传统的区块链共识机制, Hyperledger Fabric对系统节点的功能进行了划分, 从而通过“背书-排序-验证”的方式使得系统节点形成共识^[5].

背书提高了交易的效率, 排序保证了交易的一致性, 验证保证了交易的合法性, 这种将系统各个部分解耦的方式为Hyperledger Fabric提供了灵活的、可插拔式的功能选项, 使其广泛适用于各个场景. Hyperledger Fabric中的背书节点^{[6, 7]}承担了所有客户提交交易的背书工作, 中心化处理交易背书提高了交易的处理效率, 但同时也会引发安全问题. 因为背书节点身份的公开性, 当敌手想要攻击整个Hyperledger Fabric系统时, 只需要攻击相应的背书节点即可达到控制整个链上交易的目的. 为了增强背书节点安全性, Mazumdar等人^[8]设计了利用环签名的方式来选取背书节点; 孟吴同等人^[4]引入了可验证随机函数, 通过随机化选取背书节点的方式来增强背书节点的安全性; 张龙静等人^[9]提出了根据当前物理资源动态调整背书节点的机制.

以上方案虽然都通过动态选取背书节点的方式将背书节点匿名化, 但没有考虑存在硬件加速计算的情况, 敌手可以通过增加算力的方式来达到伪造背书节点身份的目的. 可验证延迟函数是一类能够产生随机数且运算过程不能通过增加算力的方式加快的函数, 为了解决Hyperledger Fabric使用固定背书节点容易引发安全问题以及抵御并行加速计算, 本文在“背书-排序-验证”共识机制的基础上, 引入可验证延迟函数, 提出了Hyperledger Fabric共识机制的优化方案, 具体方案如下.

(1)将原先固定的背书节点改为候选背书节点集合, 引入可验证延迟函数, 利用可验证延迟函数输出随机数的特性, 通过设置阈值的方式从候选的背书节点集中动态选择背书节点对交易进行背书.

(2)因为可验证延迟函数不可并行加速计算的特性, 敌手在事先不知道密钥的情况下无法通过并行计算的方式伪造成被选择的背书节点.

(3)当背书节点对现有交易进行背书之后, 其背书节点的身份被释放, 该节点重新回到候选背书集合中, 可对接下来的交易进行背书, 提高交易的处理效率.

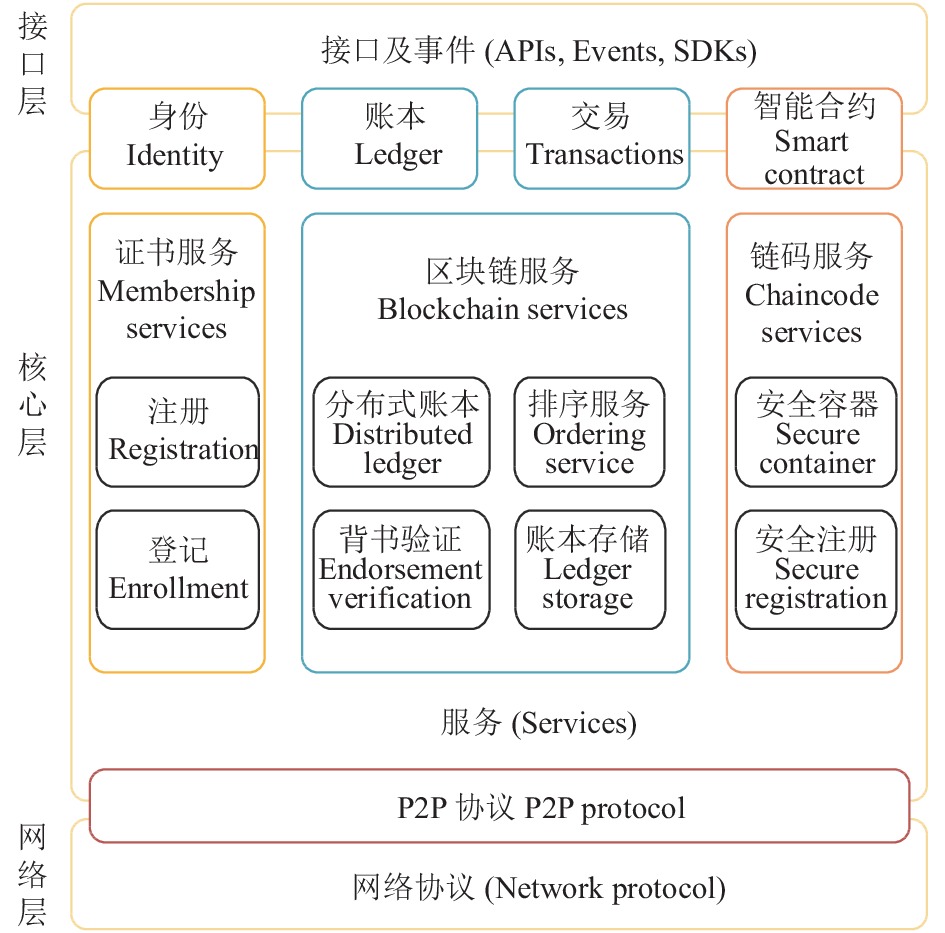
1 相关知识 1.1 Hyperledger Fabric

Hyperledger Fabric是由IBM、DAH等企业^[5]提交到Linux开源基金会的联盟链实体应用, 不同于公有链的完全去中心化, 它需要相应的中心化节点对提交到链上的交易进行认证处理. Hyperledger Fabric由多个功能模块组成^[7], 各个模块之间彼此独立并通过协同工作的方式实现交易的打包成块、上链. Hyperledger Fabric的系统架构如图1所示.

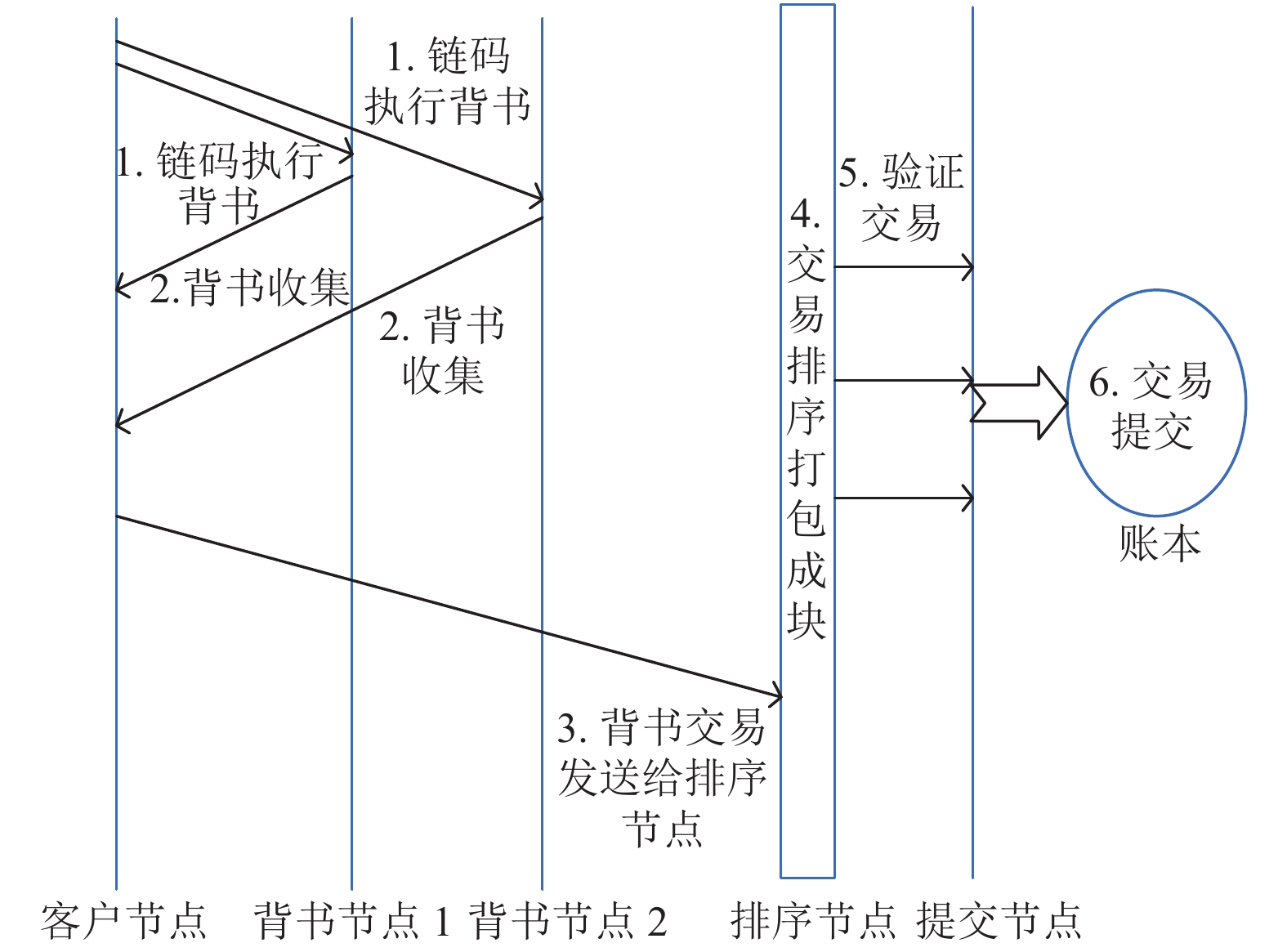
共识机制是保证交易能被正确执行并且提交到链上的关键. 区别于传统的公有链共识机制, Hyperledger Fabric采用“背书-排序-验证”的方式对链上的交易达成共识. Hyperledger Fabric的原始交易流程如图2所示, 具体细节如下:

(1)交易提案 $tx\_pros < ch, p, endo{r_{{\rm{policy}}}} >$ : 当用户想要进行交易时, 通过客户节点发起交易提案 $tx\_pros$ , 交易提案包括一系列链码ch、相关的参数p以及背书策略 $endo{r_{{\rm{policy}}}}$ . 交易提案被创建之后, 客户节点检查相关的背书策略, 并依据背书策略将交易提案发送给需要对该交易进行背书的背书节点.

(2)交易背书 $endor\_tx < tx\_pros, sig, pa > $ : 当交易提案 $tx\_pros$ 被提交到符合背书策略^[10]的背书节点之后, 背书节点检查相应的交易签名 $sig$ 以及其他参数 $pa$ . 检查无误之后背书节点执行交易逻辑, 产生读写集 $set < write, read > $ , 并将结果签名 $sig < tx\_pros, set > $ , 之后发送给客户节点.

(3)交易排序 $order < t{x_1}, t{x_2}, \cdots ,t{x_n} >$ : 客户节点检查交易背书的签名 $sig < tx\_pros, set > $ , 如果检查结果出现错误, 则终止交易, 如果检查结果正确则将交易发送给排序节点. 排序节点接收来自客户节点的交易之后, 检查交易的时间顺序是否符合逻辑, 即检查交易的一致性. 排序节点将符合一致性的交易排序 $order < t{x_1}, t{x_2} ,\cdots , t{x_n} >$ 并打包成块 $block < t{x_1}, t{x_2} , \cdots , t{x_n} >$ , 进行全网广播之后发送给提交节点;

(4)交易提交 $submit < b1, b2, \cdots, bn >$ : 打包成块的交易 $block < t{x_1}, t{x_2} , \cdots , t{x_n} >$ 被发送给提交节点之后, 提交节点对交易进行验证 $verify < {b_1}, {b_2} , \cdots , b_n^{} >$ . 提交节点首先验证交易背书是否符合背书策略, 之后检查执行交易生成的读写集的有效性. 通过验证的交易被提交节点提交到账本中, 进行交易的存储.

1.2 可验证延迟函数

可验证延迟函数(verifiable delay function, VDF)是由Boneh 等人^[11]最早提出来的, 它是一类数学函数, 当输入相应的数值之后, 需要消耗一定的时间来计算出结果. 计算所需的时间不能通过简单的增加算力的方式来缩短, 即不可并行加速运算. 该类函数还必须保证计算结果的可验证性. 为了达到不可并行加速以及可验证的目的, 可验证延迟函数由如下算法组成:

(1) ${\textit{Setup}} (\lambda , t) \to (ek, vk)$ ; 由于可验证延迟函数初始化算法, 以安全参数 ${{λ }}$ 以及时间参数 $t$ 为输入, 输出一个用于计算的参数 $ek$ 以及用于验证的参数 $vk$ , 输出的参数都是公开透明的, 所以也被称为公共参数.

(2) ${{\textit{Eval}}} (ek, x) \to (y, \pi )$ : 计算算法, 接受输入参数 $ek$ 以及具体值 $x$ 作为输入, 得到结果输出 $y$ 以及证明 ${\text{π }}$ .

(3) ${\textit{Verify}} (vk, x, y, \pi ) \to ({\textit{accept}}, {\textit{reject}})$ : 验证算法, 接收一系列的输入, 输出结果验证通过(accept)或者验证失败(reject).

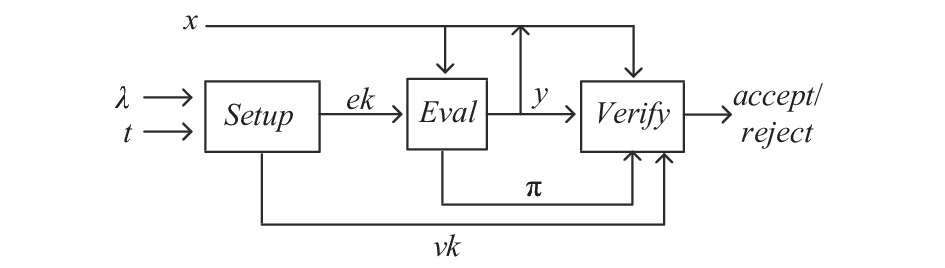
可验证延迟函数的运行流程如图3所示.

可验证延迟函数的概念被提出之后, 许多有效的构造也被相继提出. Wesolowski^[12]基于未知阶的群构造了陷门可验证延迟函数, 该方案构造了可以加速计算的陷门计算方法; Pietrzak等人^[13]基于Rivest-Shamir-Wagner的Time-lock难题构造了一个简单的可验证延迟函数; Ephraim等人^[14]提出了连续可验证延迟函数, 通过迭代可验证延迟函数子过程的每一个输出来进行过程验证, 提高了的输出验证效率; Döttling等人^[15]基于自举定理构造了结构紧凑的可验证延迟函数, 该类函数具有更高的时间效率; Rotem^[16]提出了批量处理可验证延迟函数中幂运算的技术, 降低了函数的通信复杂度.

可验证延迟函数不可并行加速以及验证高效的特性可以用来增强公共可验证随机数的安全性, 是一个十分强大的工具, 研究人员也将其功能与区块链技术结合起来. 可验证延迟函数在Chia区块链的架构中扮演了重要的角色, 以太坊基金会和Protocol Labs也将其列为下一代区块链平台的核心角色.

2 方案设计

本文在Hyperledger Fabric的原始架构基础上引入了可验证延迟函数, 将原始方案中固定的背书节点改为从背书节点候选集中随机抽取背书节点.

2.1 可验证延迟函数的设计

可验证延迟函数的设计关键是要保证匿名的攻击者在未持有背书节点私钥的情况下, 要想得出正确的运算结果以及身份证明, 需要进行大量的连续计算, 这种计算是不能并行加速的, 即不能靠增加计算资源来缩短求解结果的时间. 持有私钥的背书节点可以高效地实现计算求解, 得出正确的计算结果和证明. 本文基于Wesolowski^[12]的工作来实现可验证延迟函数的设计. 可验证延迟函数总体包含4个部分: 用于生成密钥对的密钥生成算法 $keygen()\xrightarrow{{}}(sk, pk)$ ; 陷门计算算法 $trapdoo{r_{sk}}(x, t)\xrightarrow{{}}(y, \pi )$ ; 未持有私钥情况下要想求解结果的不可并行性计算算法 ${\textit{verify}}(x, t)\xrightarrow{{}}(y, \pi )$ 及客户端用于验证背书节点身份的验证算法 ${{\textit{verify}}_{pk}}(x, y, \pi , t)\xrightarrow {{}} ({\rm{true}}, {\rm{false}})$ .

2.1.1 密钥生成算法 $keygen()$

本文的可验证延迟函数基于未知阶的RSA群, 密钥生成算法由式(1)、式(2)得出:

$ pk = N = pq $

(1)

$ sk = (p - 1)(q - 1) $

(2)

其中, $p, q$ 是大素数.

2.1.2 陷门计算算法 $trapdoo{r_{sk}}()$

拥有私钥 $sk$ 的用户可以通过陷门计算算法 $trapdoo{r_{sk}}()$ 快速得到结果 $y$ 以及用于证明自己身份的证明 $\pi $ . 具体的计算过程如下.

(1)计算相关参数 $g, e$ , 具体计算如算法1中①和②所示. 其中 $G$ 表示未知阶的群, ${H_G}$ 表示输出结果是群 $G$ 中元素的哈希函数, $x$ 是输入, $sk$ 是私钥, $t$ 是时间参数.

(2)计算返回给验证者的结果 $y$ , 具体计算如算法1的③所示. 因为用户持有私钥 $sk$ , 可以进行快速运算, 详细计算过程如式(3):

$ \begin{split} y={g}^{{2}^{t}}&={g}^{sk \cdot {n}+{2}^{t}\;{\rm{ mod }}\;sk}={g}^{sk \cdot n} \cdot {g}^{{2}^{t}\; \mathrm{mod} \; sk}\\&={e}_{G} \cdot{g}^{{2}^{t}\;\mathrm{mod}\;sk}={g}^{{2}^{t}\;\mathrm{mod}\;sk}={g}^{e} \end{split} $

(3)

其中, $n$ 是一个正整数, ${e_G}$ 是群 $G$ 中的生成元.

(3)生成证明 $\pi $ , 具体计算如算法1的④–⑦所示, 其中, ${H_{{\rm{prime}}}}$ 是输出结果为素数的哈希函数.

算法1. 陷门计算算法 $trapdoo{r_{sk}}()$

输入: $\scriptstyle sk, \; x, \; t$

输出: $\scriptstyle y, \; \pi$

Begin:

Compute parameters g and e:

① $\scriptstyle g\xleftarrow{{}}{H_G}(x) \in G$

② $\scriptstyle e\xleftarrow{{}}{2^t}\bmod sk$

Compute result y:

③ $\scriptstyle y\xleftarrow{{}}{g^e}$

Compute prove π:

④ $\scriptstyle l\xleftarrow{{}}{H_{{\rm{prime}}}}(g, y)$

⑤ $\scriptstyle r\xleftarrow{{}}{2^{{t}}}\bmod l$

⑥ $\scriptstyle q\xleftarrow{{}}({2^{\text{t}}} - r){l^{ - 1}}\bmod sk$

⑦ $\scriptstyle \pi \xleftarrow{{}}{g^q}$

$\scriptstyle {\rm{return}}(y, \; \pi )$

End

2.1.3 计算算法 $eval()$

没有私钥 $sk$ 的情况下, 恶意用户要想生成有效的结果 $y$ 以及证明 $\pi $ , 需要以下计算过程.

(1)计算参数 $g$ , 具体计算如算法2的①所示, 其中 $G$ 代表未知阶的群, $x$ 表示输入, ${H_G}$ 是输出结果为群 $G$ 中元素的哈希函数.

(2)计算返回给验证者的结果 $y$ , 计算算法如算法2的②所示, 其中 $t$ 代表时间参数.

(3)生成证明 $\pi $ , 具体计算如算法2的③, ④所示. 其中 ${H_{{\rm{prime}}}}$ 表示输出结果为素数的哈希函数.

算法2. 计算算法 $\scriptstyle eval()$

输入: $\scriptstyle x, \; t$

输出: $\scriptstyle y, \; \pi$

Begin:

Compute parameter g:

① $\scriptstyle g\xleftarrow{{}}{H_G}(x) \in G$

Compute result y:

② $\scriptstyle y\xleftarrow{{}}{g^{{2^t}}}$

Compute prove π:

③ $\scriptstyle l\xleftarrow{{}}{H_{{\rm{prime}}}}(g, y)$

④ $\scriptstyle \pi \xleftarrow{{}}{g^{\left\lfloor {{2^t}/l} \right\rfloor }}$

$\scriptstyle {\rm{return}}(y, \; \pi )$

End

在算法2中, 计算结果由等式 $y = {g^{{2^t}}}$ 给出, 在没有私钥 $sk$ 的情况下, 时间复杂度为 ${\rm O}(t)$ . 随着 $t$ 的增大, 计算给出结果的困难性也随之增加. 这在一定程度上增加了没有私钥的攻击者伪造计算结果以及证明的困难度, 提高了安全性.

2.1.4 身份验证算法 ${\textit{verify}}()$

身份验证算法通过验证结果 $y$ 以及证明 $\pi $ 是否匹配来判断背书节点是否为恶意用户, 具体的步骤如下.

(1) 计算参数 $g, \; l, \; r$ , 具体计算如算法3的①–③所示, 其中 $G$ 代表未知阶的群, $x$ 表示输入, ${H_G}$ 是输出结果为群 $G$ 中元素的哈希函数, ${H_{{\rm{prime}}}}$ 代表输出结果为素数的哈希函数, 时间参数 $t$ .

(2)验证结果: 如果 ${\pi ^l}{g^r} = y$ 则验证通过, 返回 ${\rm{true}}$ . 否则返回 ${\rm{false}}$ . 在身份验证的过程中, 有式(4):

$ \begin{split} {\pi }^{{l}}{g}^{r}={({g}^{\lfloor {2}^{t}/l\rfloor })}^{l} \cdot {g}^{{2}^{t} \; \mathrm{mod} \; l}= {g^{\left\lfloor {{2^t}/l} \right\rfloor l + ({2^t} \bmod l)}} = {g^{{2^t}}} = y \end{split}$

(4)

只有在计算结果 $y$ 以及证明 $\pi $ 都正确的情况下, 等式才会成立.

算法3. 身份验证算法 $\scriptstyle verify()$

输入: $\scriptstyle y, \; x, \; t, \; \pi$

输出: $\scriptstyle {\rm{true}}$ $\scriptstyle \rm or$ $\scriptstyle \rm false$

Begin:

Compute parameters g, l, r:

① $\scriptstyle g\xleftarrow{{}}{H_G}(x) \in G$

② $\scriptstyle l\xleftarrow{{}}{H_{{\rm{prime}}}}(g, y)$

③ $\scriptstyle r\xleftarrow{{}}{2^t}\bmod l$

if $\scriptstyle {\pi ^l}{g^r} = y$

return true

else

return false

End

2.2 优化交易流程

改进方案基于可验证延迟函数, 主要是从下列两个方面优化了交易流程.

(1)原始方案中的背书节点是固定且公开的, 客户端需要根据背书策略将交易提交给特定的背书节点进行背书确认. 由于背书是交易能否顺利进行的关键, 外部攻击者为了达到破坏或者安插不法交易的目的, 势必会攻击相应的背书节点, 而背书节点身份的透明又加剧了其遭受攻击的可能性. 本方案匿名化了背书节点, 候选背书节点集只有经过可验证延迟函数的计算后才能对交易进行背书. 由于背书节点的选取是随机的, 攻击者要想控制交易, 必须攻击候选背书节点集, 这增加了攻击者的攻击成本, 提高了背书节点的安全性.

(2)在原始方案中, 被背书策略指定的背书节点才能对交易进行背书. 在同一时间内, 如果被指定的背书节点都有交易要处理, 那么当有新交易被客户端提交给背书节点后, 只能处于等待阶段. 与此同时, 未被背书策略指定的背书节点处于空闲状态, 这造成了资源的浪费. 优化方案采取随机的方式抽取背书节点, 且候选背书集中的每个背书节点被抽取的概率都是相同的. 在同一时间下, 不同的交易可以被提交给不同的背书节点进行背书. 随着交易数量的增加, 繁忙的节点将不再被抽取为背书节点, 而空闲的背书节点被指定为交易背书, 这种随机方式提高了候选背书节点的利用率.

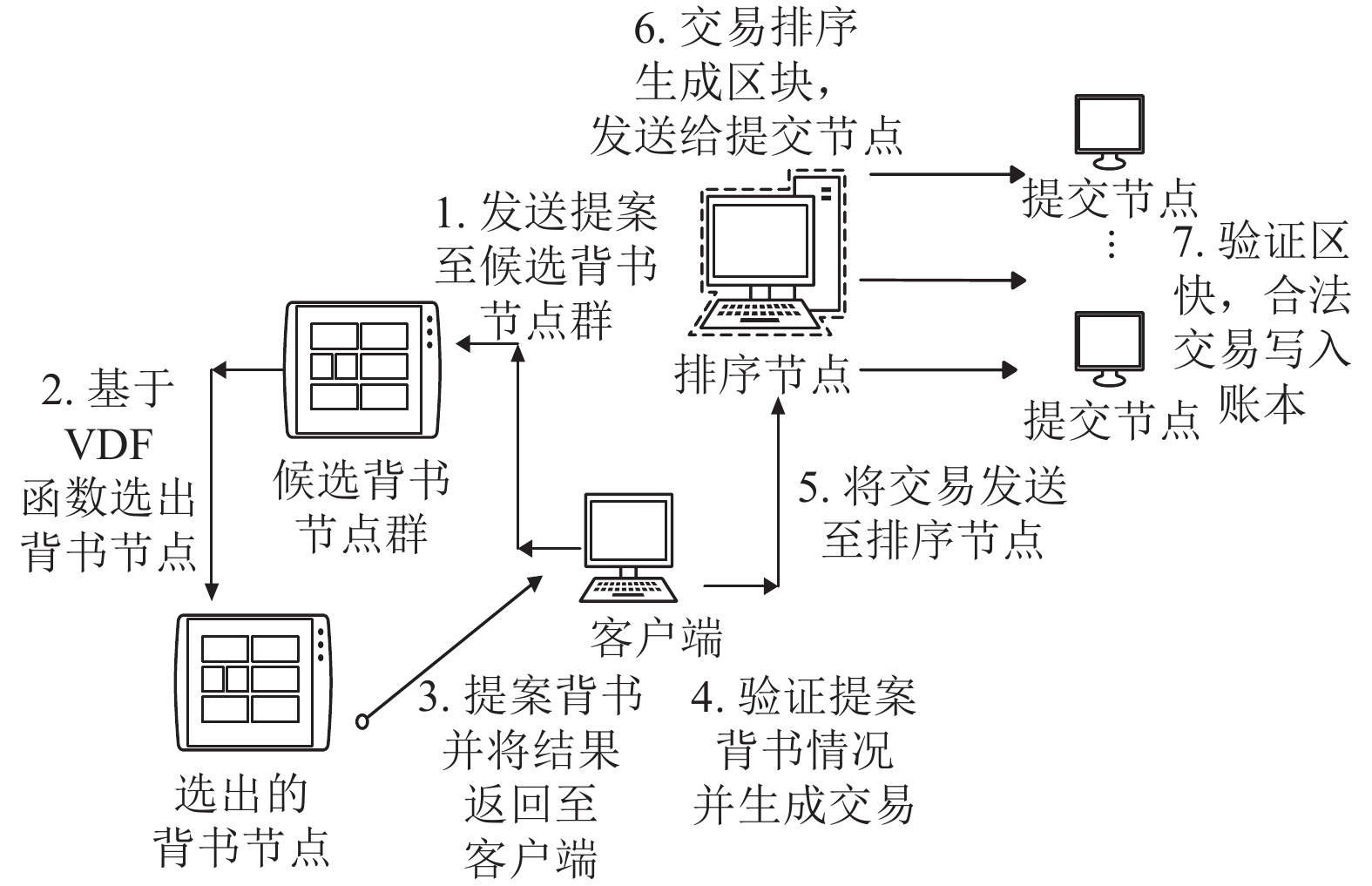
优化后的Hyperledger Fabric交易流程如图4所示.

(1)客户端发起提案 $tx\_pros < ch, p, x, t, sig > $ , 提案包括要调用的交易业务逻辑代码链码 $ch$ 、相关参数 $p$ 、候选背书节点抽取算法的输入 $x$ 以及背书时间参数 $t$ . 客户端对要背书的交易签名后将其发送给候选背书节点集.

(2)候选背书节点集收到来自客户端的需要背书的交易之后, 首先验证其签名 $sig$ 的合法性. 验证签名过后, 候选背书节点运算抽取算法:

$ trapdoo{r_{sk}}(x, t, sk)\xrightarrow{{}}(y, \pi ) $

(5)

其中, $y$ 是运算得出的计算结果, $\pi $ 是生成的身份证明. 由于时间参数 $t$ 的限制, 只有拥有私钥 $sk$ 的背书节点才能快速计算得出结果以及相关证明, 而攻击者因为没有私钥 $sk$ , 在时间的限制下, 即使运算得出了正确结果也不能及时返回背书的交易给客户端.

(3)随机选取的背书节点运算完抽取算法之后, 对相关交易进行背书, 得到读写结果集合 $read\_write$ 及以及背书提案 $tx\_pro{s_{endor}}$ . 将计算结果 $y$ , 证明 $\pi $ , 读写集 $read\_write$ 以及背书提案 $tx\_pro{s_{endor}}$ 打包发送给客户端进行验证.

(4)客户端收到背书节点发来的结果集 $ < y, \pi , read\_write, tx\_pro{s_{endor}} > $ 之后, 进行背书结果的验证, 验证算法如式(6):

$ {{\textit{verify}}_{pk}}(x, y, \pi , t) $

(6)

如果验证结果为 ${\rm{true}}$ , 说明背书节点的身份合法, 该背书节点背书的交易有效; 如果验证结果为 ${\rm{ false}}$ , 说明该背书节点是恶意的, 那么需要抛弃该背书交易, 将交易重新提交给候选背书节点集进行背书.

(5)背书有效的交易被客户端提交给排序节点进行排序, 排序节点接受到交易之后, 将不同的交易排序打包成块并进行签名, 之后将该区块全网广播.

(6)提交节点监听网络上的交易区块, 当有新的交易区块被发送到提交节点时, 提交节点首先验证排序节点的签名合法性, 其次验证读写集的合法性. 通过两项验证之后的交易区块被提交到区块链上并更新账本, 之后提交节点进行全网广播

3 安全性分析

上述改进方案引入了可验证延迟函数(VDF)来处理背书节点的选取问题. 本节将从两个方面来分析方案的安全性: 其一是可验证延迟函数的可靠性; 其二是可验证延迟函数的不可并行加速性.

3.1 可验证延迟函数的可靠性 3.1.1 可靠性的定义

首先给出可靠性的定义: 给定参数 $p$ 、输入 $x$ 、时间参数 $t$ , 通过计算算法 $eval()$ 得到输出 $y$ 以及证明 $\pi $ , 如式(7)所示:

$ eval(x, p, t)\xrightarrow{{}}(y, \pi ) $

(7)

若A通过正确的计算步骤得到结果 $(y, \pi )$ , B通过伪造得到结果 $(y', \pi ')$ , 且有 $y \ne y', \pi \ne \pi '$ . 如果可验证延迟函数的验证算法给出结果如式(8)、式(9), 则可以判定可验证延迟函数是可靠的.

$ {{\textit{verify}}_{pp}}(x, y, \pi , \Delta )\xrightarrow{{}}{\rm{true}} $

(8)

$ {{\textit{verify}}_{pp}}(x, y', \pi ', \Delta )\xrightarrow{{}}{\rm{false}} $

(9)

3.1.2 生成伪证明

根据第2.1.4节的算法 ${\textit{verify}}()$ 可知在 $y, \; \pi $ 都正确的情况下有 $y = {\pi ^l}{g^r}$ . 式中 $r$ 也可以写为:

$ r = {2^t} - l\left\lfloor {{2^t}/l} \right\rfloor $

(10)

将式(10)两边同乘以 ${g^{ - {2^t}}}$ 可得:

$ y{g^{ - {2^t}}} = {(\pi {g^{ - \left\lfloor {{2^t}/l} \right\rfloor }})^l} $

(11)

攻击者可以伪造证明, 即通过不等于 $y$ 的结果 $y'$ 来构造证明 $\pi '$ , 构造方式如下:

① 计算 $\alpha ' = y'{g^{ - {2^t}}}$

② 素数 $l$ ( $l\xrightarrow{{}}{H_{{\rm{prime}}}}(g, y')$ )是已知的, 计算 $\;\beta '{\text{ = }}\sqrt[l]{{\alpha '}}$

③ 计算 $\pi ' = \beta '{g^{\left\lfloor {{2^t}/l} \right\rfloor }}$

根据式(11)可以计算出 $\pi ' = {(y'{g^{ - {2^t}}})^{1/l}}{g^{\left\lfloor {{2^t}/l} \right\rfloor }}$ .

只要攻击者发送给验证者的证明 $\pi '$ 符合上述等式, 就可以在计算结果 $y' \ne y$ 的情况下, 伪造证明.

3.1.3 RSA-VDF群

$(Z/NZ)*$ 是一个RSA群, 而RSA-VDF群则表示为 $(Z/NZ)*/\{ \pm 1\} $ . 对于任意元素 $g, \; h \in (Z/NZ)*$ , 如果满足 $g \cdot {h^{ - 1}} \in \{ \pm 1\} $ , 则在RSA-VDF群中元素 $g, \; h$ 是相同的. 也就是说在RSA-VDF群中, 对于输入 $x$ , $y$ 和 $ - y$ 都是正确的输出结果.

3.1.4 VDF可靠性证明

VDF的可靠性是建立在RSA的大整数分解困难问题之上的. 一般地, 定义 $N = pq$ 是RSA群的模(p, q是未知的大素数), 如果有 $ u\in (Z/NZ)*/\{\pm 1\} $ , 那么在不知道p, q的情况下计算 $\sqrt[l]{u}$ 是十分困难的 $(l = {H_{{\rm{prime}}}}(g, y) \in (Z/NZ)*)$ .

定义 $u = \pi '/\pi $ , 则有:

$ y/y'\xleftarrow{{}}\sqrt[l]{u} $

(12)

假设可验证延迟函数并不可靠, 即攻击者可以在多项式有界时间内产生一个错误的结果集 $ < y', \pi ' > $ , 且能通过验证者的验证, 这将违背RSA大整数分解困难问题.

如果能够绕过上述困难假设, 那么可以很快计算出 $\sqrt[l]{u}$ 的值, 定义 $\xi = \sqrt[l]{u}$ . 根据VDF函数的定义有:

$ eval(x, t)\xrightarrow{{}}(y, \pi ) $

(13)

则 $y', \; \pi '$ $(y' \ne y)$ 可以作以下变换:

$ y' = uy $

(14)

$ \pi ' = \xi \pi $

(15)

上述不是通过 $eval()$ 函数计算得出的 $y', \; \pi '$ 也将通过验证者的验证, 即:

$ y = {x^{{2^t}}}, r = {2^t}\bmod l $

(16)

$ {(\pi ')^l}{x^r} = {(\xi \pi )^l} = u{\pi ^l}{x^r} = uy = y' $

(17)

通过上述论证可知, 在大整数分解困难问题成立的前提下, VDF函数具有很高的可靠性.

3.2 可验证延迟函数的不可并行加速性

在利用可验证延迟函数选出背书节点的过程中, 拥有私钥 $sk$ 的合法背书节点将很快计算出结果 $y$ 以及证明 $\pi $ , 而不含私钥 $sk$ 的情况下, 计算出正确的结果以及证明将耗费多项式时间 ${\rm{O}}(t)$ . 随着 $t$ 的增大, 攻击者能够伪造结果的难度也将增大. 理想的情况下, 攻击者即使拥有多个计算资源能够并行处理输入 $x$ , 也将耗费单个计算资源所需要的计算时间, 也即不可并行加速.

3.2.1 计算模型

定义 $\varpi $ 为计算模型, 即为了实现一定目的而采取的相关操作以及各自的开销. 对于特定的算法 $\psi $ , 定义 $T(\psi , x)$ 为计算模型 $\varpi $ 下输入为 $x$ 的时间花销; $\theta (\psi , x)$ 为计算模型 $\varpi $ 下所有的成本开销总和. $\theta (\psi , x)$ 不考虑并行性的问题, 而 $T(\psi , x)$ 将考虑并行情况下的时间成本变化. 值得注意的是, $T(\psi , x)$ 只是一种分析时间花销的理论模型而不是真正的物理世界的时间. 对于方案的安全参数 $k$ , 定义 $\delta :N*\xrightarrow[{}]{}R$ 是进行单次模平方计算的时间刻度, 与安全参数 $k$ 相关, 也可以写做 $\delta (k)$ .

3.2.2 Time-lock

给定安全参数 $k$ , $g \in (Z/NZ)*$ 且是均匀随机的取值, $N = pq$ $(p, q$ 是大素数), Time-lock的概念如下:

$\Omega (g)\xrightarrow{{}}h(g) = {g^{{2^t}}}$ 定义算法 $\Omega (g)\xrightarrow{{}}h(g) = {g^{{2^t}}}$

$p, q$ 在素数 $p, q$ 未知的情况下计算开销 $T(\Omega , g) < t\delta (k)$ 的概率是一个可以忽略的值.

由Time-lock可知, 在 $N = pq$ 无法快速因式分解得出 $p, q$ 的情况下, 求解 $y = {g^{{2^t}}}$ 需要经过t次求解 $g$ 的平方且无法并行加速. 由于 $\delta (k)$ 是一个与安全参数 $k$ 相关的多项式表达式, 随着安全参数 $k$ 的不断增大, $T(\Omega , g) < t\delta (k)$ 的概率将逐渐趋于零.

拥有私钥的 $sk$ 的用户可以将 $y = {g^{{2^t}}}$ 转换为求解 $y = {g^{{2^t}}}\bmod sk$ 从而缩短计算时间.

综上所述, Time-lock保证了可验证延迟函数的不可并行加速性.

4 实验分析 4.1 实验设计

本文基于Hyperledger Fabric的架构设计了相关的区块链交易系统, 该系统模拟了Fabric的交易流程. 作为对比, 本文将采取两种实验方案: 采用固定的方式抽取背书节点的原有方案以及采用可验证延迟函数抽取背书节点的优化方案. 两种方案都包含4类节点: 客户端节点、背书节点、排序节点以及提交节点. 值得注意的是, 优化方案在客户端节点刚刚发起交易时的背书节点只是候选背书节点集, 只有被可验证延迟函数抽取到的才能作为该交易流程中的背书节点对交易进行背书. 4类节点的数量为: 200个客户端节点, 30个背书节点, 1个排序节点和150个提交节点.

优化方案除了背书节点需要选取之外, 交易流程与原有方案是一样的: 不同的客户端节点独立提交相关的交易提案给背书节点, 交易经过背书返回客户端, 验证无误之后被提交给排序节点进行交易排序打包成区块, 最后提交节点将区块提交上链. 本文的实验环境为: Ubuntu 16.04操作系统, 8核CPU, 16 GB内存, 512 GB硬盘.

考虑Fabric系统的特性, 我们将给予Golang语言来实现交易的业务逻辑, 可验证延迟函数的实现依赖于相关的crypto库以及外部已经实现的模块. 本文采用Caliper系统对实验结果进行测试, 并从平均交易时间以及交易延迟两个方面来进行性能分析.

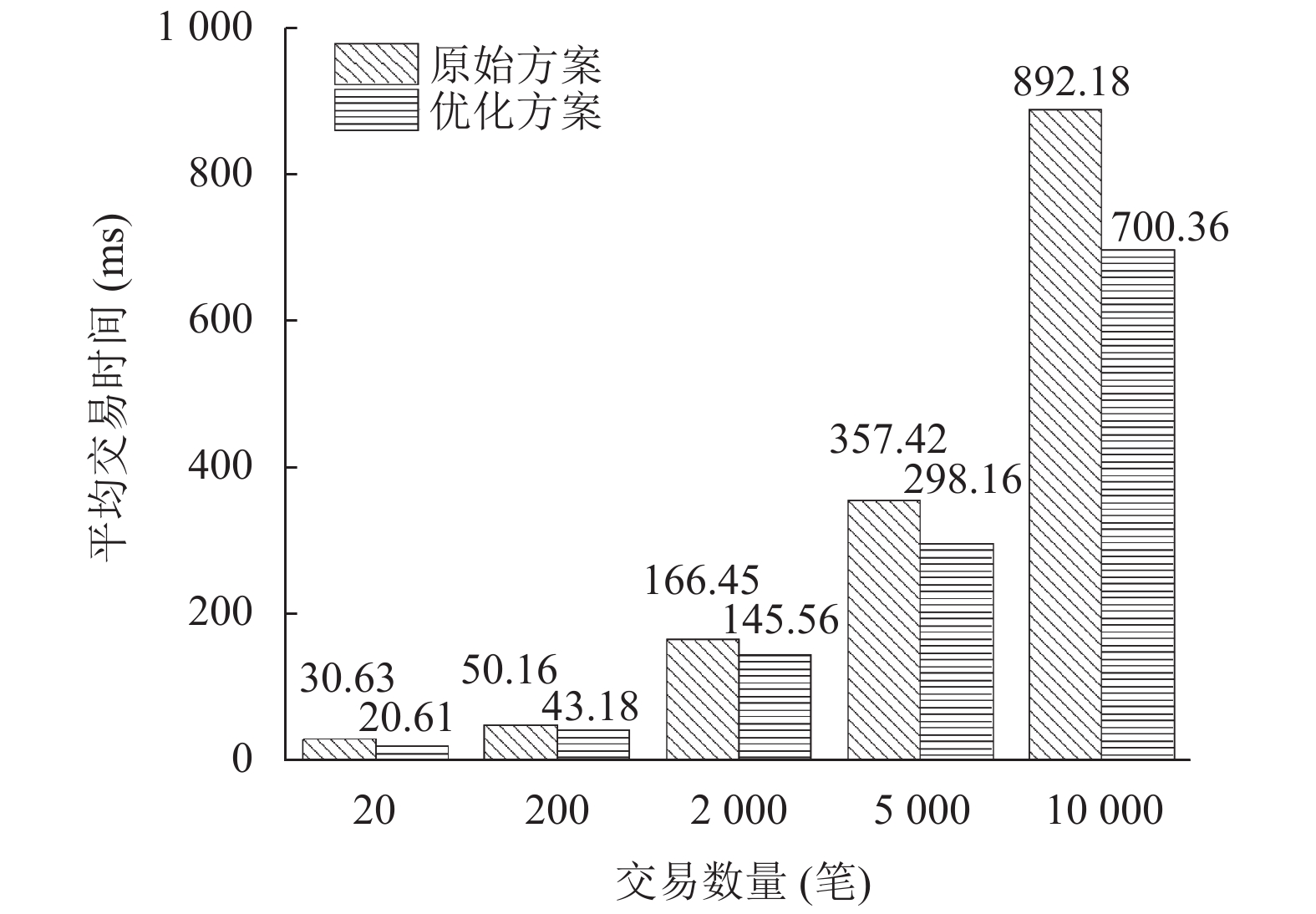
4.2 平均交易时间

对原有方案以及优化方案进行平均交易时间测试, 测试结果如图5所示.

从实验数据可以看出, 随着交易数量的增加, 原始方案和优化方案的平均交易时间也增加, 但优化方案平均交易时间要小于原始方案. 引入可验证延迟函数后, 一方面, 因为非恶意的背书节点拥有私钥SK, 计算求解的速度不会延迟太多, 另一方面, 优化方案随机选取背书节点的方式使得背书节点可以交错为不同的交易背书, 提高了背书节点处理交易的效率; 而原始方案因为背书节点是固定的, 交易只能被背书策略指定的背书节点处理, 其他背书节点不能并行处理不同的交易, 造成资源的浪费.

综上, 优化方案通过引入可验证延迟函数, 既保证了背书节点的安全性, 也减少了背书节点平均交易时间.

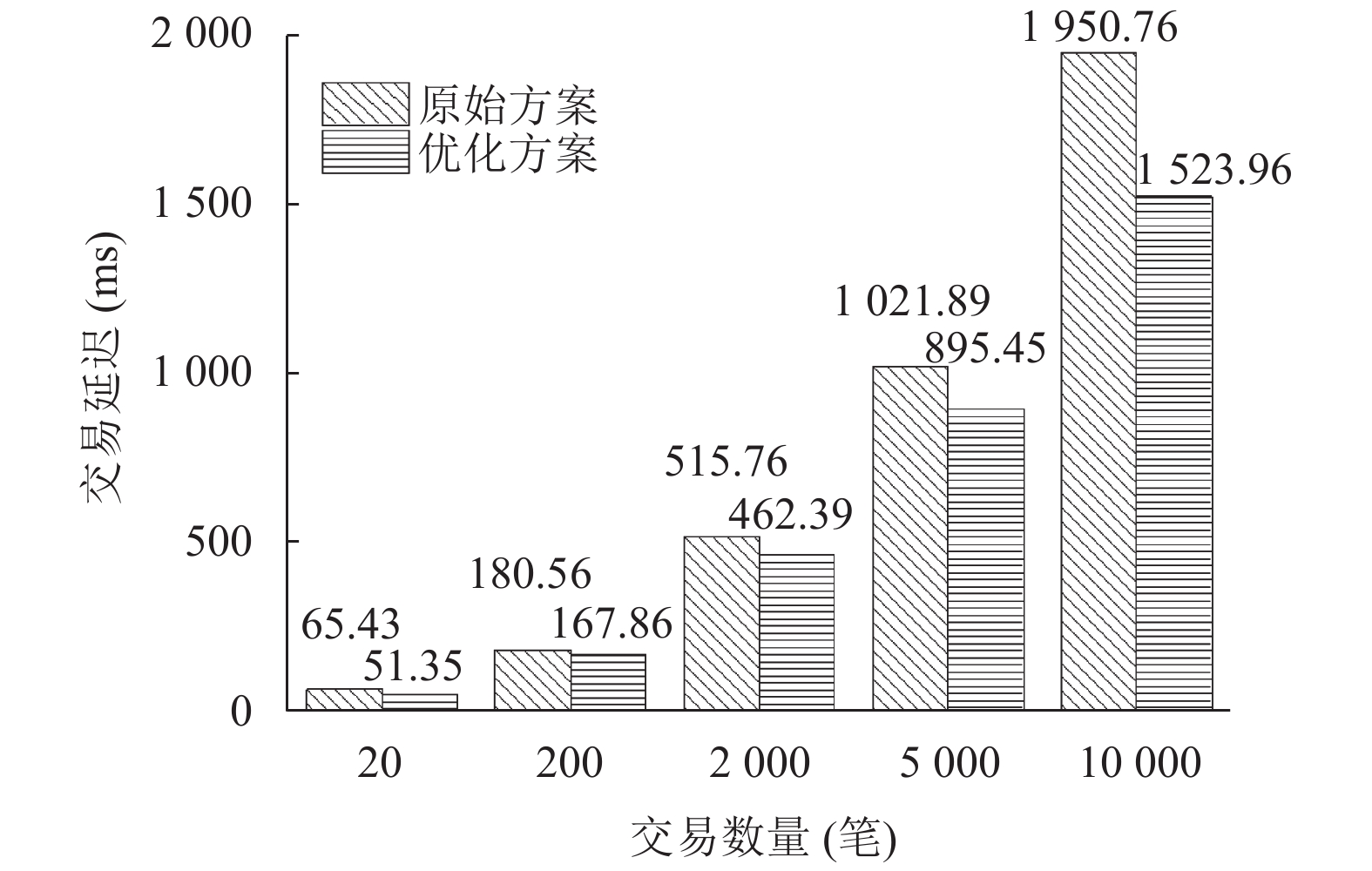
4.3 交易延迟

本文基于Caliper对两种方案的交易延迟进行了测试, 实验结果如图6所示.

交易延迟是一笔交易从提交到能够被处理的时间, 由图6的实验结果可以看出, 两种方案的交易延迟都将随着交易数量的增加为增加且优化方案的交易延迟要小于原始方案. 在原始方案中, 所有的背书节点都是固定的, 当有一笔交易需要背书时, 所有的背书节点都需要等待, 之后根据背书策略对交易进行背书; 优化方案将背书节点划分为不同的群组, 当群组1的背书节点背书交易1时, 群组2的背书节点可以并行背书交易2, 这就在一定程度上提高了背书效率.

5 总结

针对Hyperledger Fabric中背书节点身份暴露易被攻击的安全问题, 本文提出了基于可验证延迟函数的Hyperledger Fabric背书策略优化方案. 本方案将原始方案中固定背书节点划分为候选背书节点集, 通过可验证延迟函数随机抽取背书节点并完成身份验证. 最后, 将优化方案与原始方案作性能对比, 比较了两者的平均交易时间和交易延迟. 结果表明, 优化方案在保证背书节点安全性的同时在效率上也是可行的.