1 引言

近阶段, 量子计算技术发展迅猛. 利用量子固有的并行计算优势, 在因数分解Shor^[1]、大数据搜索Grover^[2]及线性方程组求解HHL^[3]等算法方面, 其计算速度将远超于对应的经典算法. 然而, 尽管量子算法在解决上述问题上独具优势, 其运行却依托于底层的量子芯片.

现今, 较为流行的量子芯片物理实现方式主要包括离子阱、超导、半导体及光学等^[4]. 作为最早的物理实现方式, 离子阱量子芯片控制起来相对容易, 但集成难度高. 基于超导约瑟夫森结方案设计的超导量子芯片易于操作、可规模化, 但环境温度对其影响极大. 受经典计算机硬件材料的影响, 基于半导体研制的量子芯片也备受研究者关注. 半导体量子芯片研制技术成熟, 易于大规模集成, 但是比特间存在电荷噪声. 光量子计算机则在相干时间方面具有优势, 缺点为可扩展能力较弱.

从物理实现方式可以看出, 量子芯片属于极为精密的设备, 易受到内部电路噪声和外部环境噪声的共同影响, 从而导致量子算法结果与理论结果之间存在偏差. 特别是研制更大规模比特数目的量子芯片, 噪声影响尤为明显. 因此, 为了保证量子算法能够在量子芯片上低错误率运行, 需要对量子芯片进行测评. 同时, 相较于传统计算机的芯片而言, 量子芯片的研制仍然处于初级阶段, 不同的量子芯片实现方案层出不穷. 然而, 全方位, 高精度的衡量量子芯片性能指标的测评方法并未统一化. 为了消除人们对不同芯片测评指标及测评方法的误解, 本文对已有的量子芯片测评标准和方法进行综述.

本文第2节介绍量子芯片测评指标. 第3节对测评方法进行论述. 第4节总结目前量子芯片测评技术存在的不足, 同时对量子芯片测评技术进行展望. 第5节为结束语.

2 量子芯片测评指标

为了保证量子芯片能够正确工作的鲁棒性, 要求具有足够高的操作保真度、精密的测量以及足够弱的比特间干扰. 在量子芯片工程实现过程中, 需要对其指标进行全方位, 高精确的测评. 现今较为普遍的量子芯片测评指标包括量子比特布局、相干时间、保真度、量子比特数目、量子体积(quantum volume, QV)^[5-8]及每秒电路层操作数(circuit layer operations per second, CLOPS)^[9]. 以IBM量子云平台免费向用户提供的量子计算机为例, 其指标数值如表1所示(时间: 2022年01月17日)^[10]. 其中, “—”表示无参数.

2.1 量子比特布局

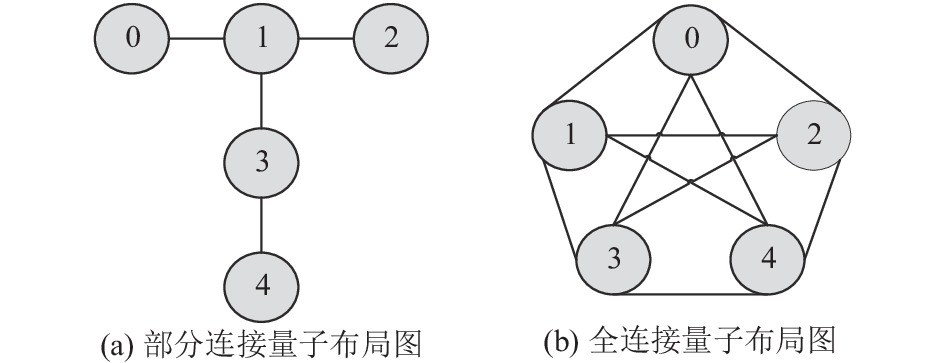
量子芯片中, 量子比特布局是依据电子线路规划而形成的特定组合, 使得一些量子比特不能直接耦合(如图1(a)中的比特1与比特4). 在执行量子算法时, 不能直接耦合的量子比特需要编译器进行调整, 这将导致量子线路深度增加, 从而影响量子芯片的性能.

每个圆圈代表一个量子比特, 两个比特之间的连接线, 代表两个量子比特可以直接耦合, 或双量子比特门可以直接作用在上面. 依据图1(b)可知, 为全连接(all-to-all)量子布局. 该布局表明量子芯片拥有更强的硬件可编程性和可操作性, 应用量子编译器执行门操作更灵活, 且能够减少SWAP门^[11]带来的额外量子线路深度. 然而, all-to-all布局形式的量子芯片会使比特间的串扰增加, 进而增大芯片噪声. 因此, 在衡量量子芯片性能时, 量子比特布局是需要考虑的指标之一.

2.2 退相干时间

量子力学中, 量子态以波函数的形式呈现. 在对量子态编码的信息进行计算时, 为保证量子态系统的相干性, 需要确定波函数的相位关系. 量子退相干则是使量子态失去相干性, 破坏波函数的相位关系, 进而变为经典态的现象. 因此, 退相干时间可定义为量子态到经典态的过渡时间^{[12, 13]}. 退相干时间主要包括两项指标: 能量退相干时间T1和相位退相干时间T2^[14].

2.2.1 能量退相干时间T1

从能量的角度来说, 高能级量子态受到外界环境的影响, 会将能量泄漏到外部环境中. 在量子计算方面, T1描述了量子态从高能级 $ \left | 1 \right\rangle $ 衰变到基态 $ \left | 0 \right\rangle $ 的时间. 当一个量子比特激发到 $ \left | 1 \right\rangle $ 态时起, 经历时间t之后, 该量子比特让处于 $ \left | 1 \right\rangle $ 态的概率为:

$ P\left( {\left| 1 \right\rangle } \right) = {{\rm{e}}^{ - t/{T1}}} $

(1)

通过式(1)可以得出, 量子比特的状态极易消失, 而量子计算本质上就是通过一系列的门操作来改变量子比特的状态. 一旦量子比特状态出现偏差, 或状态消失, 将会导致最终的执行结果不准确. 因此, T1时间对于执行量子算法非常重要.

2.2.2 相位退相干时间T2

指标T2侧重于退相位, 描述比特激发态与比特基态相对相位差随机化所用的时间. 不同于能量退相干, 相位退相干会导致无法分辨叠加态的相位. 相位退相干时间可由T1和T₂^*两项指标进行表征. T₂^*表示系统主体的相位退相干时间, 包括低频噪声引起的退相干. T2、T1及T₂^*满足:

$ \dfrac{1}{{T2}} = \dfrac{1}{{2T1}} + \dfrac{1}{{T_2^ * }} $

(2)

其中, T₂^*表示系统主体的相位退相干时间. 通常情况下, T2 ≤ 2T1^[15].

2.3 保真度

保真度是衡量量子计算机性能的另一重要概念. 保真度可以描述量子计算机真实实验结果与理想结果之间的拟合程度, 其数学表达式^[16]为:

$ F = { \left( tr {\sqrt {\sqrt \rho \sigma \sqrt \rho } } \right)^2} $

(3)

其中, ρ表示为理想σ的实验实现. 本文主要对量子门保真度和读出保真度进行简要介绍.

2.3.1 量子门保真度

量子比特门(量子逻辑门)通过转化量子状态来处理量子信息. 在量子算法执行线路中, 量子门保真度可以理解为实验状态下执行的门操作与理想门操作之间的拟合程度.

2.3.2 读出保真度

完整的量子过程包括: (1)初态制备; (2)操作执行; (3)终态测量3个方面. 在量子操作执行完毕后, 需要仪器对量子态进行测量. 然而, 由于仪器制造误差以及外界环境引起的误差, 量子态读出值并不准确, 此时需要读出保真度这一参数指标. 读出保真度可以衡量量子计算机实际终态测量值与理想测量值之间的拟合程度.

2.4 量子比特数目

经典芯片中, 以比特“0”和“1”呈现及传递信息. 而在量子芯片中, 不仅用比特“0”态和“1”态呈现及传递信息, 还取决于“1”“0”之间的状态, 这种状态能够以一定概率线性表示“0”态, “1”态, 用数学可表示为:

$ \left| \psi \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle , {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| 0 \right\rangle = {\left[ {1, 0} \right]^{\text{T}}}, {\kern 1pt} {\kern 1pt} \left| 1 \right\rangle = {\left[ {0, 1} \right]^{\text{T}}} $

(4)

其中, α, β为复数, |α|²+|β|²= 1. 更为直观的是在Bloch球上表示量子比特状态, 如图2所示. 其中, 箭头与球面接触的点即为量子比特所处状态.

这种叠加态的优势在于m个量子比特描述的信息, 在经典芯片中需要2^m个比特, 即比特数目越多, 所能呈现的信息越大. 例如, 2019年, Google宣称的“量子霸权”就是利用量子比特数目为53比特的“Sycamore”处理器体现的^[17]. 因此, 量子比特数目可直接体现量子芯片能力.

2.5 量子体积

当建造更大规模的量子芯片时, 衡量计算机的能力尤为重要. 虽然, 量子比特数目、量子比特布局、退相干时间及保真度都可以作为衡量量子芯片性能的指标, 但具有片面性. 考虑到这个问题, IBM提出量子体积^[6], 一种衡量量子芯片整体性能的指标. 该指标旨在测量量子处理器可获得的状态空间大小及瞬间捕获处理器上能够产生可靠的随机状态的量子比特数目^[7]. 文献[6]中提供了量子体积的计算公式:

$ {\log _2}{V_Q} = \arg \mathop {\min \max }\limits_m \left( {m, d\left( m \right)} \right) $

(5)

其中, m表示量子比特数量. 理想情况下, d(m)表示量子线路的最大可达深度, 与量子比特数量m相等; 在含有噪声的状态下, d(m)值则小于m, 即噪声产生于d(m)中. 而V_Q表示量子计算机能力的大小——量子体积数值.

量子体积是无关于量子计算机体系结构的测评指标, 与量子比特数目、量子比特布局、退相干时间以及错误率都有联系, 近期已被越来越多的公司认可和接受.

2.6 CLOPS

在2021年10月29日, IBM提出一项量子芯片速度参数——每秒电路层操作数CLOPS^[9]. CLOPS可以定义为使用一组参数化QV电路每秒执行的QV层数, 即衡量芯片可以执行与用于测量量子体积的相同类型的参数化模型线路层的速度, 其计算公式为^[9]:

$ \dfrac{{M \times K \times S \times D}}{{time\_taken}} $

(6)

式(6)利用执行的QV层总数除以总执行时间来呈现CLOPS. 其中, M表示模板数量; K表示参数更新次数; S表示shots次数; D表示QV层数; time_taken表示总执行时间.

从量子芯片的指标中可以看出, 量子比特数目可以作为规模参数, 量子体积可以作为质量参数, CLOPS则可以作为速度参数, IBM声称三者可共同作为衡量量子芯片性能的关键指标.

3 量子芯片测评方法

衡量量子芯片指标的优劣, 需要对其进行全面, 准确的测评. 本节按照电路模型(表2), 将测评方法分为周期电路测评、随机电路测评、应用电路测评及镜像电路测评4个方面.

3.1 周期电路测评

周期电路主要用于呈现量子算法结构, 其电路重复一个子程序O(d)次, “d”表示实现电路所需的物理时钟周期数. 常见的周期电路测评方法涵盖Rabi震荡、Ramsey震荡, 量子层析及周期基准测试.

3.1.1 Rabi震荡

1937年, Isidor Isaac Rabi利用激光脉冲撞击介质, 发现介质上下能级的粒子数发生周期性翻转, 即Rabi震荡^{[18, 19]}. 通过这种现象, 可以用来测量能量退相干时间T1. 测量过程通过施加一个π脉冲, 将比特从 $ \left | 0 \right\rangle $ 态激发到 $ \left | 1 \right\rangle $ 态. 通过等待不同的时间t, 测量 $ \left | 1 \right\rangle $ 态的概率. 其中, Rabi的震荡周期要小于T1, 否则无法观测一个完整Rabi震荡. 依据式(1)可知, 当量子态处于 $ \left | 1 \right\rangle $ 态时, 过得时间t越长, 接近 $ \left | 0 \right\rangle $ 态的概率越大, 而距离 $ \left | 1 \right\rangle $ 态的概率越小. 不难看出, 量子比特的状态极易消失, 而量子计算本质上就是通过一系列的操作来改变量子比特的状态. 一旦量子比特的状态消失或出现误差, 那么将会对量子算法的运行结果造成巨大的影响.

3.1.2 Ramsey震荡

Ramsey震荡^{[20, 21]}实验与Rabi震荡实验都源于核磁共振. 但与Rabi震荡不同, Ramsey震荡用来测量T₂^*. 在量子线路中, 该实验过程(如图3)为: (1)准备一个量子比特, 将其复位成 $ \left | 0 \right\rangle $ 态; (2)添加H门, 使得量子比特从 $ \left | 0 \right\rangle $ 态转变为叠加态; (3)同时改变等待时间; (4)在叠加基础上添加H门, 利用量子门的可逆性操作, 使量子比特从叠加态转变为 $ \left | 0 \right\rangle $ 态; (5)添加测量门, 测量该量子线路.

在完成了一次Hadamard门之后, 量子状态会在Bloch球面的xy平面出现了一个角度偏移. 随着时间的变化, 偏移角度会发生改变, 沿着概率为0.5的轴呈现出周期性的现象.

3.1.3 层析

层析(tomography)是指从许多切片中重建未知目标阴影轮廓的方法, 每个切片都只提供一个有限的视图. 量子层析则是层析技术在量子领域的应用. 本节主要介绍量子态层析(quantum state tomography, QST)^[22-24]、量子过程层析(quantum process tomography, QPT)^[25-27]及门集层析(gate set tomography, GST)^{[28, 29]}(表3).

(1) 量子态层析. 由于量子系统不可能是孤立的系统, 总会受到外界环境的影响, 导致量子芯片存在误差. 因此, 需要一种技术来测评量子态的质量. QST协议旨在利用量子测量提取量子态信息并处理测量结果估计量子态. 密度矩阵(密度算子) ρ为量子态层析测量的首要指标参数. 密度矩阵的数学形式为:

$ \rho = \sum\nolimits_i {{P_i}} \left| {{\psi _i}} \right\rangle \left\langle {{\psi _i}} \right| $

(7)

其中, P_i为产生量子态 $\left| {{\psi _i}} \right\rangle$ 的概率; 密度矩阵必须满足厄米性、归一性及半正定性3个条件. 然而, 在测量过程中, 量子态层析面临着仪器测量精度和随量子比特增多而导致的计算难度大两方面挑战.

(2) 量子过程层析. 量子过程层析(QPT)协议通常以测量理想门与实验门的契合程度为目标, 通过实验确定量子操作中与理想门操作的误差本质, 从而获取量子系统噪声的幅值和类型. 因此, QPT协议在控制量子位与消除退相干方面具有重要作用. 然而, QPT需要测量的次数随着门操作的数量呈指数级增长; 在实际的物理系统中, 单门误差很难精确的计算; 当量子比特数目增多时, 该协议的效率也会呈指数级的下降; 同时, 状态准备和测量(state preparation and measurement, SPAM)^[30]误差也对QPT协议造成一定的影响.

(3) 门集层析. 门集层析(GST)是一种用于详细表征量子芯片上门操作的协议, 旨在描述门操作如何影响其目标量子位. 该协议同时估计所有门操作及SPAM误差, 并且不受到SPAM误差的影响. 即在表征门操作时, GST协议无需校准. 相比于QST协议和QPT协议, GST协议成本更低且精度更高. 在GST协议中, 每个噪声门都由任意传输矩阵详细描述. 然而, GST协议测量的次数随着门操作的数量呈指数级增长; 在量子芯片上, GST并不能捕获与旁观量子比特之间不必要的相互作用引起的误差, 即串扰误差.

3.1.4 周期基准测试

理论上, 使用量子过程层析或门集合层析能够用于描述量子过程. 然而, 描述量子过程的协议都需要大量的实验及繁琐的后期处理并且测试数据随着量子比特数目呈指数增加. 为解决此问题, Erhard等^[31]提出周期基准测试(cycle benchmarking, CB). CB协议是评估影响量子芯片全局噪声过程保真度的一种协议^[31]. 该协议证明单量子比特门和两比特量子门产生的错误率不会随着电路规模的增大而提高. 由于可以用与N量子比特无关的Pauli矩阵来精确评估保真度, 因此CB协议在大规模量子处理器上是非常适用的. 但是, 在没有随机编译的电路中, 会受到相干误差的影响.

3.2 随机电路测评

与周期电路测评不同, 随机电路测评旨在测量特定数据分析的固有出错率, 通过生成一个宽度为W (量子比特数量), 深度为D (电路中子程序的数量)的电路来测试量子芯片的性能. 本节对随机基准测试, 量子体积电路(表4)进行介绍.

3.2.1 随机基准测试

随机基准测试(random benchmarking, RB)是一种用于测评量子芯片门操作“平均性能”的协议, 旨在确定计算环境中每个门操作的错误概率^[32-35]. RB协议的量子线路可以运行在一个真实量子芯片上, 亦能使用量子模拟器进行模拟. 当使用量子模拟器进行模拟时, 在理想的情况下执行完量子线路之后最终的结果应该与初态完全相同. 而在真实量子芯片中, 随着门线路深度的增加, RB测试的平均单门的误差率会提升. 这也就意味着在真正的量子计算机中运行一个较大的程序时, 极有可能难以得到正确的结果.

RB协议是一个较为简单的从整体上来评估量子噪声的协议模型. 与量子过程层析相比, RB在表征的门操作集合所作用的量子比特数量是可扩展的, 并且对状态准备和测量噪声具有鲁棒性. 但是, 随着量子比特数目规模的增大, RB协议对噪声的描述并不完整^[36].

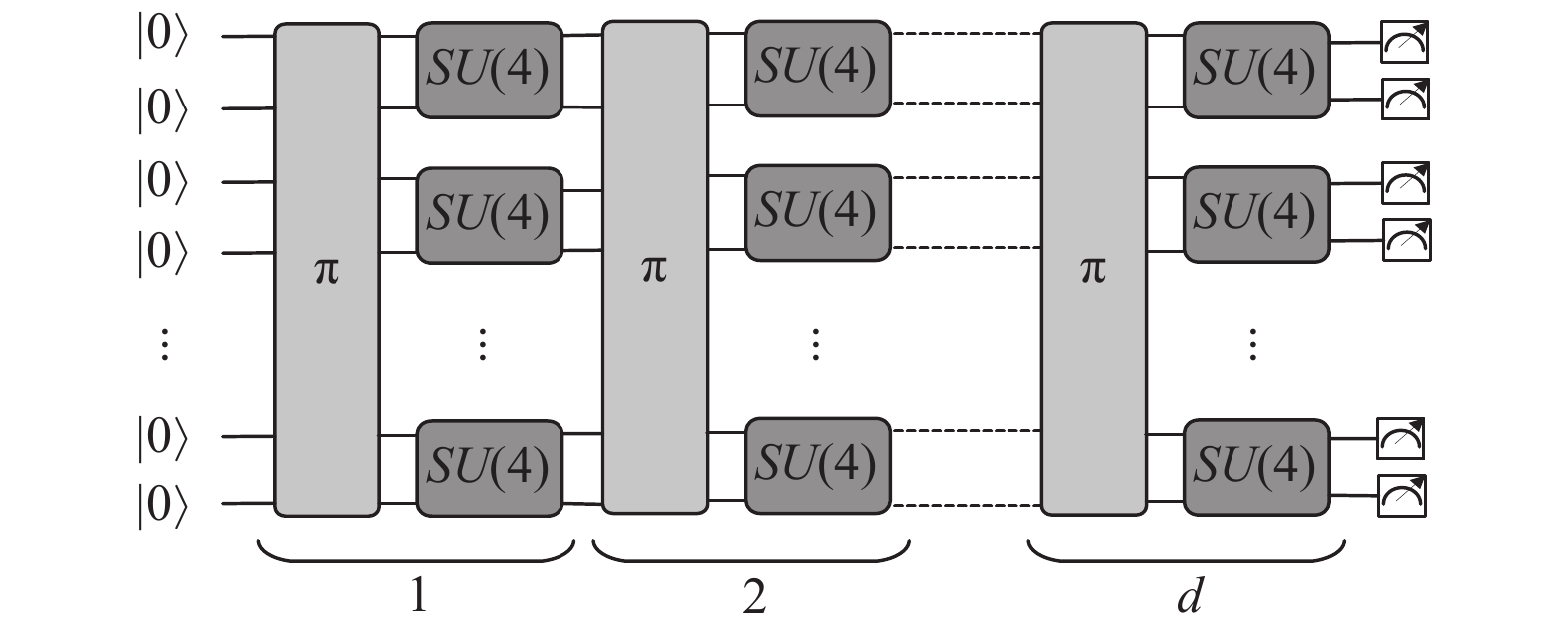
3.2.2 量子体积电路

对于量子体积的测试, 文献[6]提出量子体积模型电路, 如图4所示.

图4中, $\left | 0 \right\rangle$ 态表示量子比特已进行初始化; “π”表示在量子体积电路中, 为每两个量子比特进行均匀随机分配, 也可以称为均匀洗牌; 若量子比特数量为奇数, 则在每次分配时, 使得一个比特处于空闲状态; SU(4)矩阵为4×4的复数矩阵, 通过KAK分解^[37]可以将其分解为3个CNOT门和7个单比特门的交叉形式, 其分解后线路可参考文献[38].

量子体积测量电路为随机电路, 通过输出一组二进制串的重复率(>2/3)来描述错误率. 错误率越低, 所能建造的量子计算机规模越大, 容错率越强. 由此可见, 在研发量子计算机时, 低错误率显得尤为重要. 然而, 虽然量子体积能够在一定程度上衡量量子芯片整体性能指标, 但其测量运行“方形电路”, 并不能衡量“非方形”算法电路的性能.

3.3 应用电路测评

由于某些研制的量子芯片执行特定量子线路, 如“量子霸权”验证, 导致并不是所有的量子芯片指标都需要用周期电路和随机电路进行测试. 因此, 需要提供与现实量子芯片电路相符的测量电路, 即应用电路. 目前, 常见的应用电路有求解质因数问题的Shor算法、大数据搜索的Grover算法、验证量子霸权的Boson采样和随机电路采样以及测试线性代数问题的量子LINPACK.

3.3.1 Shor 算法

1994年, 贝尔实验室的应用数学家Shor提出用于将一个很大的整数分解成质因子的乘积的Shor算法^[1]. 作为第一个能够利用量子计算机在多项式时间内解决质因数分解问题的算法, Shor算法将会威胁到RSA加密体系. 若大规模比特数量的量子芯片研制完成, 且能够高保真度运行Shor算法, 那么RSA加密体系就会瞬间瓦解, 区块链技术所依赖的基础也将不复存在.

在衡量量子芯片性能时, Shor算法可作为一种专用量子芯片的测试方案, 其分解的质因数越大, 错误率越低, 其量子芯片性能越优. 但目前量子芯片还未达到分解一个大数的能力, 所以, Shor算法并不会成为衡量量子芯片能力的首要指标.

3.3.2 Grover算法

计算机科学中, 数据搜索算法极为常见. 对于在乱序中搜索某些特定数据时, 经典搜索算法执行复杂度为O(N), N为数据总量. 而在量子领域, 由同在贝尔实验室的Grover于1996年提出的Grover算法, 可以对一些启发式算法起到二次加速作用, 即将搜索复杂度降为O(sqrt(N))^[2]. 在超大数据搜索中, Grover算法将极大提升搜索效率. 因此, 国内外许多研究团队欲将Grover算法作为衡量量子芯片性能的测试方法.

3.3.3 Boson采样

Boson采样(Boson sampling)^[39]是指通过线性光学网络发送玻色子的概率分布进行采样, 能够解决某些搜索问题. 在经典计算领域, 天河2号超级计算机模拟玻色子采样上限约为100分钟50个光子样本^[40]. 而在量子计算领域, 2020年12月, 76个光子量子芯片“九章”^[41]实现了“高斯玻色采样(Gaussian Boson sampling, GBS)”^[42]的计算, 其计算速度为超级计算机的100万亿倍. 因此, Boson采样可以作为验证量子芯片优越性的一项指标.

3.3.4 随机电路采样

随机电路采样(random circuit sampling, RCS)^[43]是指从随机选择的量子线路的概率分布中采样. 最具里程碑事件的是2019年, Google发布了53位的量子芯片sycamore, 通过执行随机量子线路输出采样电路, 宣称实现“量子霸权”^[17]. 而在2021年, 中国科学技术大学团队研发66位量子比特的“祖冲之号”^[44], 并且利用56个量子比特执行随机电路采样, 其优越性超出sycamore芯片2–3个数量级. 虽然该技术可以用来作为量子芯片测评的一种方法, 但却与Shor算法, Grover算法不同, 研发专用于随机电路采样的量子芯片并不能解决实际问题.

3.3.5 量子LINPACK

LINPACK协议通过求解线性方程组Ax = b, 衡量经典高性能计算机的浮点计算能力^[45]. 类比于LINPACK协议, 文献[46]提出一种测试线性代数任务的协议——量子LINPACK. 该协议采用Hermitian随机电路块编码矩阵(Hermitian random circuit based block-encoding matrix, H-RACBEM)与量子奇异值变换(quantum singular value transformation, QSVT)模型^[47], 适应几乎任何给定的基于门的量子体系结构的耦合映射, 并且能够显著减轻量子算法优化和编译带来的额外开销.

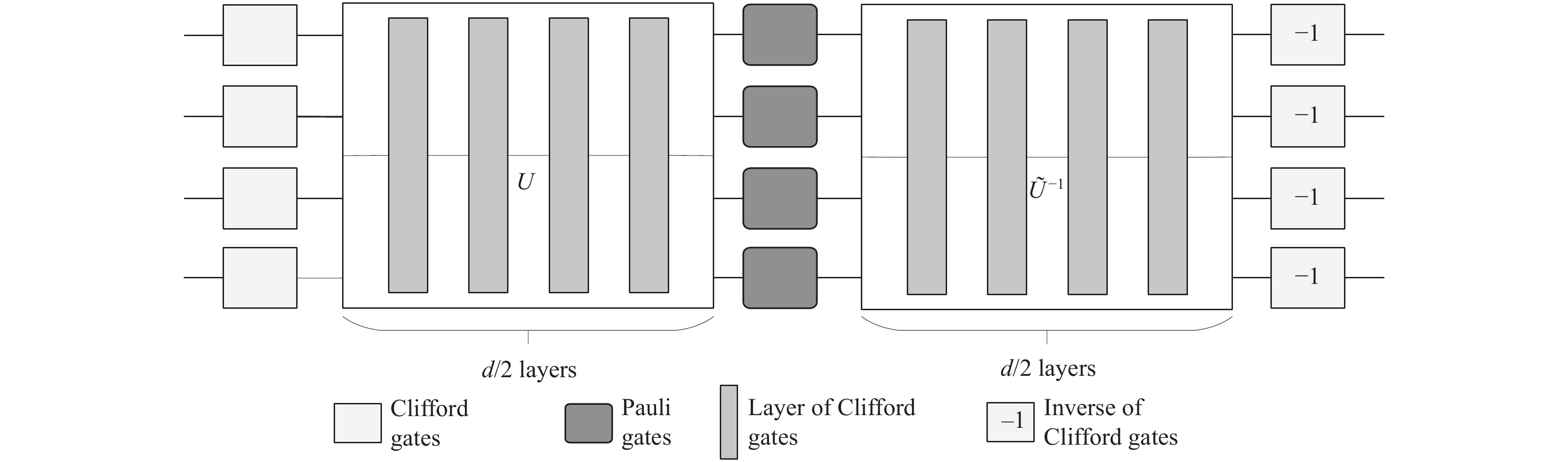
3.4 镜像电路测评

作为精密器件, 量子芯片总是受到串扰, 相干噪声等的混合影响. 周期电路测评具有呈现量子算法结构的功能, 但对相干误差极其敏感. 随机电路测评在测量特定数据分析的固有出错率具有优势, 但对于结构错误的测量时低效的, 并且对噪声的描述并不完整. 应用电路测评可以用作衡量量子芯片运行特定程序的能力, 然而, 单一的应用级电路并不能衡量通用性量子芯片的整体性能. 为了更高效, 更可靠的消除衡量量子芯片性能的不准确预测, 文献[48]提出镜像电路基准测试(mirror circuit benchmark)协议. 镜像电路是一种具有反射结构的电路(如图5).

图5中, Ｕ·Ũ ⁻¹ = Pauli. 镜像电路内部可涵盖周期电路、随机电路及应用算法电路. 因此, 镜像电路协议能够为测试人员提供在处理器上运行特定程序的能力. 目前, 与其他现有测试协议相比, 该测试协议具有一定的优势, 然而, 能否成为衡量量子芯片性能的统一标准仍需拭目以待.

4 量子芯片测评现存问题与展望

对量子芯片进行综合的、全面的测评是量子芯片走向工程化的必经之路. 然而, 目前国内外现存的量子芯片测评方案种类繁多. 本节简述量子芯片测评技术存在的问题, 同时依据存在的问题对测评技术进行展望.

4.1 现存问题 4.1.1 测评指标问题

目前, 较为流行的量子芯片指标涵盖量子比特布局、退相干时间、误差率量子比特数目、量子体积、CLOPS及非作用量子比特对作用量子比特造成的串扰误差等. 从任何一项指标测量量子芯片性能, 都是不完整的.

4.1.2 测评技术问题

第3节中, 尽管涵盖4种测评电路供用户选择, 但每种测评电路侧重的功能不同, 这将导致不能通过一种测评电路来衡量量子芯片总体性能的好坏.

4.2 展望 4.2.1 构建量子芯片测试集

针对量子芯片测评指标及技术的现存问题, 需要构建统一的量子芯片测试集. 该测试集能够保证综合评估量子芯片的性能, 从而达到有效地验证量子芯片的实用化程度.

4.2.2 设立量子芯片QTOPN榜单

从1993年TOP500榜单^[49]诞生时起, 世界上许多国家都投入大量财力来争夺高性能计算TOP500排名. 类比于TOP500, 未来可以设立量子芯片QTOPN榜单. 该榜单依据统一构建的量子测试集, 对每项指标的性能值进行测试; 同时, 按其指标的重要性分配权重值, 将所有指标测试值总和作为量子芯片的总体性能值, 从而对量子芯片进行QTOPN排名.

5 结束语

本文针对量子算法依托的底层硬件——量子芯片, 介绍了现有的芯片测评指标; 随后对指标测评方法进行论述; 最后, 展望未来量子芯片指标测评技术方向.

量子芯片测评技术能够从不同的角度对量子芯片进行全方面测评, 这将对量子计算机的成功研制具有极为重要的作用, 同时对量子算法的高保真度执行也提供了一定的支撑. 此外, 随着时间的推移, 量子芯片内部结构容易损坏, 利用测评方法长时间采集指标数据, 并构建机器学习模型自动化分析数据走势, 来预测芯片使用寿命, 以便及时校准量子芯片参数. 因此, 量子芯片测评技术具有非常重要的现实意义.