随着决策系统的复杂化、非线性化, 使决策过程具有高度的不确定性, 传统的决策方法包括了概率论和模糊数学等. Atanassov^[1]提出的直觉模糊集是在经典模糊集上的扩展, 它同时考虑了元素的隶属度和非隶属度, 从而从不同角度描述决策者评价的不确定性. 然而, 在复杂的决策环境下, 决策者的直觉偏好信息可能会在某个中心值的附近波动. 因此, 在决策过程中模糊性和随机性不应该被随意割裂. 李德毅等^[2]在概率论和模糊数学的基础上提出了云模型理论, 可以实现定性概念和定量数据间的相互转换, 可以很好地将模糊性和随机性结合在一起. 因此, 在直觉模糊集的基础上融入云模型理论可以同时考虑到决策过程中的模糊性和随机性. 本研究针对属性值为区间直觉模糊数的多属性群决策问题, 考虑到直觉模糊集和云模型的结合优势, 对以往的区间直觉模糊数的排序方法进行了改进, 可用云模型理论计算出方案的综合评价值的贴近度和犹豫度来代替.

目前, 国内外学者对于区间直觉模糊数的群决策方法有了卓有成效的研究成果. 李沃源等^[3]针对经济管理决策活动中的模糊双边匹配问题, 以区间直觉模糊数的得分函数为基础, 建立了以双边的满意度最大化的决策模型, 较好地解决了区间直觉模糊环境下双边匹配的决策问题. 汪恒等^[4]针对船舶在港口航行的各种不确定因素, 构建相关指标体系, 最后通过区间直觉模糊数的相似度确定各港口环境的风险等级, 为相关部门制定风险预案提供了依据. Giri等^[5]考虑了一个新的广义非线性直觉模糊数, 提出了一种新的去模糊化方法来解决所建立的多物品库存模型. 龚日朝等^[6]基于传统的得分函数和精确函数的内涵, 运用概率论全概率公式思想提出了一种新的得分函数和精确函数, 并通过对比分析验证了其有效性.

综上所述, 国内外学者在区间直觉模糊信息下的决策问题取得了相应的成果. 较传统直觉模糊数的排序方法中的得分函数和精确函数不同, 本研究提出了一种新的基于云模型的排序方法, 本研究将排序方法转化为利用云模型理论计算其排序优劣, 能够在区间直觉模糊数的基础上, 将随机性和模糊性有机地融合进去.

1 基本理论 1.1 云模型基本理论

设U是一个用精确数值表示的定量论域, C是U上的定性概念, 若定量值 $x \in U$ , 且x是定性概念C的一次随机实现, 若x满足: $x \sim N\left( {Ex, {{\left( {E{n^{'}}} \right)}^2}} \right)$ . 其中, $E{n^{'}} \sim N\left( {En, H{e^2}} \right)$ , 且x对C的确定度满足:

$\mu {\text{ = }}\exp \left[ { - {{\left( {x - Ex} \right)}^2} \div 2{{\left( {E{n^{'}}} \right)}^2}} \right]$

则x在论域U上的分布称为正态云^[7]. 根据正态云模型的“3En规则”^[8]可以将区间数转化为云模型的3个数字特征. 将一维云模型推广至多维云模型^[9], 可以来反映多维定性概念. 设U是一个m维论域 $U = \{ {x_1}, {x_2}, \cdots, {x_m} \}$ , T是U上的定性概念, U中的元素 $\left( {{x_1}, {x_2}, \cdots, {x_m}} \right)$ 对于T的隶属度 $\;\mu$ 是一个具有稳定倾向的随机数, 即: $\mu :U \to \left[ {0, 1} \right], \forall \left( {{x_1}, {x_2}, \cdots , {x_m}} \right) \in U, \left( {x_1}, {x_2}, \cdots, {x_m} \right) \to \mu$ . 设论域各维互不相关, 则m维正态云可由3m个数字特征量来描述: $x \in U$ . 其中, $E{x_1}, E{x_2}, \cdots, E{x_m}$ 为期望, $E{n_1}, E{n_2}, \cdots, E{n_m}$ 为熵, $H{e_1}, H{e_2}, \cdots, H{e_m}$ 为超熵. 多维正态云的数学期望超曲面MEHS方程为:

${MEHS}\left(x_{1}, x_{2}, \cdots, x_{m}\right)=\exp \left[-\frac{1}{2} \sum_{i=1}^{m} \frac{\left(x-E x_{i}\right)^{2}}{E n_{i}^{2}}\right]$

1.2 区间直觉模糊数基本理论

称 $e\left( {\tilde \alpha } \right)$ 为区间直觉模糊数^[10] $\tilde \alpha = \left( \left[ {{\mu ^L}\left( x \right), {\mu ^U}\left( x \right)} \right], \right. \left.\left[ {{v^L}\left( x \right), {v^U}\left( x \right)} \right] \right)$ 的模糊信息熵, 当且仅当满足如下条件:

$e\left(\tilde{\alpha }\right)=0,$ 当 $e\left(\tilde{\alpha }\right)=\left(\left[1, 1\right], \left[0, 0\right]\right)$ 或 $e\left(\tilde{\alpha }\right)=\left(\left[0, 0\right], \left[1, 1\right]\right)$

$e\left(\tilde{\alpha }\right)=1,$ 当 $e\left(\tilde{\alpha }\right)=\left(\left[0.5, 0.5\right], \left[0.5, 0.5\right]\right)$

$e\left(\tilde{\alpha }\right)=e\left({\tilde{\alpha }}^{c}\right)$

对任意两个区间直觉模糊数 $\tilde \alpha$ 和 $\; \tilde \beta$ , 若有:

${d^o}\left( {\tilde \alpha , \left( {\left[ {0.5, 0.5} \right], \left[ {0.5, 0.5} \right]} \right)} \right) \geqslant {d^o}\left( {\tilde \beta , \left( {\left[ {0.5, 0.5} \right], \left[ {0.5, 0.5} \right]} \right)} \right)$

则有 $e\left( {\tilde \alpha } \right) \leqslant e\left( {\tilde \beta } \right)$ . 关于 $e\left( {\tilde \alpha } \right)$ 的计算方法, 本文采用: $e\left( {\tilde \alpha } \right) = 1 - {d^o}\left( {\tilde \alpha , \left( {\left[ {0.5, 0.5} \right], \left[ {0.5, 0.5} \right]} \right)} \right)$ . 表明其包含的犹豫程度越大, 因此熵值越大. 根据以下公式可以将区间直觉模糊数转化为云模型的3个数字特征, 第1个云模型为支持云模型, 第2个云模型为反对云模型.

$\begin{array}{c} \alpha = [\left( {E{x_1}, E{n_1}, H{e_1}} \right), \left( {E{x_2}, E{n_2}, H{e_2}} \right)] \\ E{x_1} = \dfrac{{{\mu ^L}\left( x \right) + {\mu ^U}\left( x \right)}}{2}; \; E{n_1} = \dfrac{{{\mu ^U}\left( x \right) - {\mu ^L}\left( x \right)}}{6} \\ H{e_1} = \dfrac{{E{n_1}}}{{10}}; \; E{x_2} = \dfrac{{{v^L}\left( x \right) + {v^U}\left( x \right)}}{2} \\ E{n_2} = \dfrac{{{v^U}\left( x \right) - {v^L}\left( x \right)}}{6}; \; H{e_2} = \dfrac{{E{n_2}}}{{10}} \\ \end{array}$

区间直觉模糊集能够同时描述不确定信息的隶属度、非隶属度和犹豫度, 考虑到当隶属度区间数和非隶属区间数服从正态分布时, 即不确定性信息在期望中心附近波动, 不仅包含了原有直觉模糊集包含的模糊性, 也考虑到了不确定性信息的随机性. 根据云模型的3En规则可以实现区间数和云模型的3个数字特征的相互转换, 即将隶属度区间和非隶属度区间各自转换为支持云模型和反对云模型. 原有的一个区间直觉模糊数转换为了一个支持云模型和一个反对云模型. 效仿隶属度区间和非隶属度区间的距离可以得到该区间直觉模糊数的犹豫度, 本文将支持云模型和反对云模型的距离即云相似度也作为求出犹豫度的一种方法. 使云模型从只能描述不确定性信息的隶属度, 进而可以求出支持云模型和反对云模型的犹豫度. 支持云模型本身即代表了不确定性信息的隶属度, 反对云模型即代表了不确定性信息的非隶属度, 支持云模型和反对云模型的距离即云相似度则可以求出该区间直觉模糊云的犹豫度.

综上, 根据支持云模型和反对云模型的相似度可以得到各个方案的犹豫度. 其中, 支持云模型和反对云模型越相似, 其方案的犹豫度就越大, 不确定性就越大, 反之, 其犹豫度就越小, 不确定性就越小. 本研究将采用云相似度理论计算出各个方案综合评价值的犹豫度. 对于各方案的综合评价值可以由传统的得分函数和精确函数的排序方式转化为由支持云、反对云模型计算出犹豫度和各方案与正、负理想云模型的云相似度即贴近度来评价各方案, 通过比较各方案的贴近度和犹豫度能够较好地实现方案排序, 云模型也能够最大程度上将决策过程中的模糊性和随机性有机地结合在一起.

2 模型构建

针对属性值为 $\tilde \alpha = \left( {\left[ {{\mu ^L}( x ), {\mu ^U}( x )} \right], \left[ {{v^L}( x ), {v^U}( x )} \right]} \right)$ 的多属性群决策问题, 可以设 $A = \left\{ {{A_1}, {A_2}, \cdots, {A_m}} \right\}$ 为决策问题的决策方案集, $C = \left\{ {{C_1}, {C_2}, \cdots, {C_n}} \right\}$ 为n个评价属性组成的方案属性集, 有 $l$ 个决策者组成的决策群体 $E = \left\{ {{e_1}, {e_2}, \cdots, {e_l}} \right\}$ 对每个方案的每个属性进行评判并给出评价信息, 第k个专家对第i个方案的指标 ${C_j}$ 给出的评价信息用区间直觉模糊数 $\tilde S_{ij}^k$ 表示, 则第k个专家给出的决策矩阵记为 ${S^k} = {\left[ {\tilde S_{ij}^k} \right]_{m \times n}}$ .

2.1 属性权重计算

根据专家给出的区间直觉模糊矩阵 $S = {\left[ {{{\tilde S}_{ij}}} \right]_{m \times n}}$ , 计算属性 ${C_j}$ 的信息熵 ${E_j}$ , 即 ${E_j} = \dfrac{1}{m} \displaystyle \sum\limits_{i = 1}^m {e\left( {{{\tilde S}_{ij}}} \right)}$ 计算属性 ${C_j}$ 的权重 ${\omega _j}$ , 即为:

${\omega _j} = \frac{{1 - {E_j}}}{{ \displaystyle \sum\limits_{j = 1}^n {\left( {1 - {E_j}} \right)} }}$

2.2 基于灰色关联系数的专家权重确定

专家权重由其给出的评价意见与专家群体意见的相似度来确定. 相似度越大, 专家权重越高. 相似度用灰色关联系数^[11]度量. 记第k个专家对第i个方案的评价信息为 $\left( {\tilde S_{i1}^k, \tilde S_{i2}^k,\cdots, \tilde S_{in}^k} \right)$ , 综合评价值为 $\tilde Z_i^k = \displaystyle \sum\limits_{j = 1}^n {\omega _j^k\tilde S_{ij}^k}$ . 专家群体意见用所有专家的评价信息的均值表示, 即 ${\tilde Z_{io}} = \dfrac{1}{l} \displaystyle \sum\limits_{k = 1}^l {\tilde Z_i^k}$ . 则灰色关联系数为:

$\xi \left( {{{\tilde Z}_{io}}, \tilde Z_i^k} \right) = \dfrac{{\mathop {\min }\limits_k \mathop {\min }\limits_i {d^o}\left( {{{\tilde Z}_{io}}, \tilde Z_i^k} \right) + \rho \mathop {\max }\limits_k \mathop {\max }\limits_i {d^o}\left( {{{\tilde Z}_{io}}, \tilde Z_i^k} \right)}}{{{d^o}\left( {{{\tilde Z}_{io}}, \tilde Z_i^k} \right) + \rho \mathop {\max }\limits_k \mathop {\max }\limits_i {d^o}\left( {{{\tilde Z}_{io}}, \tilde Z_i^k} \right)}}$

其中, $\; \rho$ 为分辨系数, $0 < \rho < 1$ . 则关联度为 ${\gamma _{ok}} = \dfrac{1}{m} \displaystyle \sum\limits_{i = 1}^m \xi \geqslant \left( {{{\tilde Z}_{io}}, \tilde Z_i^k} \right)$ .

为最大限度地使专家意见趋于一致, 依据在专家权重约束条件下确保专家意见与群体意见关联度最大原则和极大熵准则建立如下基于二次优化的专家权重计算:

$\begin{gathered} \max \left[ {\mu \sum\limits_{k = 1}^l {{{\left( {{\beta _k}{\gamma _{ok}}} \right)}^2} - \left( {1 - \mu } \right)\sum\limits_{k = 1}^l {{\beta _k}{{\ln k}}} } } \right] \\ {\rm{s.t.}}\left\{ \begin{gathered} \sum\limits_{k = 1}^l {{\beta _k} = 1} \\ {\beta _k} \geqslant \eta , \; k = 1, 2, \cdots, l \\ \end{gathered} \right. \\ \end{gathered}$

其中, $0 < \mu < 1$ , 通常取 $\;\mu = 0.5$ ; $\;{\beta _k} \geqslant \eta$ 可保证专家均参与到决策中; $\eta$ 作为临界值, 取值为:

$\eta = \frac{1}{{2l}}$

2.3 计算方案综合值

采用加权平均方式, 计算各方案的综合评价值. 为保留专家对于属性的属性值的评价信息完整性, 本文将方案的综合评价值先用区间直觉模糊数表示为:

${\tilde x_i} = \sum\limits_{k = 1}^l {{\beta _k}\sum\limits_{j = 1}^n {\omega _j^k\tilde S_{ij}^k} }$

2.4 云相似度排序法

本研究认为各方案的综合评价值即区间直觉模糊数近似服从正态分布, 可将各方案的综合评价值转为 ${C_i} = \left( {{C_{i1}}, {C_{i2}}} \right) = \left( {\left( {E{x_{i1}}, E{n_{i1}}, H{e_{i1}}} \right), \left( {E{x_{i2}}, E{n_{i2}}, H{e_{i2}}} \right)} \right)$ , ${C_{i1}}$ 为第i个方案的支持云模型, ${C_{i2}}$ 为第i个方案的反对云模型. 通过比较各方案与正、负理想云模型的贴近度大小进行排序; 计算 ${C_{i1}}$ 和 ${C_{i2}}$ 的云相似度即为第i个方案的犹豫度 $\; {\mu _i}$ , 当第i个方案的支持云模型和反对云模型越相似, 那么第i个方案的犹豫度 ${\mu _i}$ 就越大. 本文最终用云模型的数字特征来表达区间直觉模糊数, 利用云相似度计算最后实现排序.

比较各方案的支持云模型和反对云模型的形状相似度、距离相似度和综合相似度和各支持云模型和反对云模型与正、负理想云模型的贴近度, 可以得到每一个方案相对于正、负理想云模型的相似度和每一个方案的综合支持云模型和反对云模型的相似度即该方案的犹豫度. 设两朵云为 ${C_{i1}} = \left( {E{x_{i1}}, E{n_{i1}}, H{e_{i1}}} \right)$ 和 ${C_{i2}} = \left( {E{x_{i2}}, E{n_{i2}}, H{e_{i2}}} \right)$ , 综合相似度也即犹豫度具体计算的步骤如下:

步骤1. 基于正态云模型的形状相似度^[12]计算:

${{\textit{Sim}}_{si}}\left( {{C_{i1}}, {C_{i2}}} \right) = \frac{{\min \left( {\sqrt {En_{i1}^2 + He_{i1}^2} , \sqrt {En_{i2}^2 + He_{i2}^2} } \right)}}{{\max \left( {\sqrt {En_{i1}^2 + He_{i1}^2} , \sqrt {En_{i2}^2 + He_{i2}^2} } \right)}}$

步骤2. 基于正态云模型的距离相似度简化计算:

${{\textit{Sim}}_{di}} = \frac{1}{{\sqrt {{{\left( {E{x_{i1}} - E{x_{i2}}} \right)}^2} + {{\left( {E{n_{i1}} - E{n_{i2}}} \right)}^2} + {{\left( {H{e_{i1}} - H{e_{i2}}} \right)}^2}} }}$

步骤3. 计算云模型综合相似度即犹豫度 $\; {\mu _i}$ :

${\mu _i} = {{\textit{Sim}}_{ci}} = {{\textit{Sim}}_{si}} \times {{\textit{Sim}}_{di}}$

由此可以得到每一个方案的支持云和反对云模型的相似度即该方案的犹豫度 $\; {\mu _i}$ . 第一优先排序法则为贴近度, 贴近度越大, 则方案越优, 反之, 越次, 若贴近度相等, 则比较各方案的犹豫度, 犹豫度越低, 则方案越优.

3 算例

假设某企业对于应聘者进行考核面试时, 制定了5项较为核心的属性: X1 (个人思想素质)、X2 (工作态度)、X3 (文化水平和知识结构)、X4 (团队协作能力)、X5 (创新能力). 企业指定3位较为权威的管理者对3位应聘者甲、乙、丙分别进行评估, 评价值均采用区间直觉模糊数.

步骤1. 构造专家对各方案的决策矩阵, 即:

$\left\{ {\begin{array}{l} {S^1} = \left[ {\begin{array}{*{20}{c}} {([0.7, \; 0.8], \; [0.1, \; 0.2])}&{([0.8, \; 0.9], \; [0.1, \; 0.3])}&{([0.5, \; 0.8], \; [0.0, \; 0.1])}&{([0.6, \; 0.8], \; [0.1, \; 0.2])}\\ {([0.6, \; 0.7], \; [0.2, \; 0.3])}&{([0.5, \; 0.7], \; [0.3, \; 0.4])}&{([0.7, \; 0.8], \; [0.1, \; 0.2])}&{([0.5, \; 0.6], \; [0.2, \; 0.3])}\\ {([0.5, \; 0.7], \; [0.3, \; 0.4])}&{([0.7, \; 0.8], \; [0.1, \; 0.2])}&{([0.5, \; 0.6], \; [0.2, \; 0.3])}&{([0.5, \; 0.7], \; [0.1, \; 0.2])} \end{array}} \right]\\ {S^2} = \left[ {\begin{array}{*{20}{c}} {([0.6, \; 0.8], \; [0.1, \; 0.2])}&{([0.8, \; 0.9], \; [0.2, \; 0.3])}&{([0.6, \; 0.8], \; [0.0, \; 0.1])}&{([0.7, \; 0.8], \; [0.1, \; 0.2])}\\ {([0.6, \; 0.7], \; [0.2, \; 0.3])}&{([0.4, \; 0.6], \; [0.3, \; 0.4])}&{([0.6, \; 0.7], \; [0.1, \; 0.2])}&{([0.6, \; 0.7], \; [0.1, \; 0.2])}\\ {([0.4, \; 0.7], \; [0.0, \; 0.3])}&{([0.7, \; 0.8], \; [0.1, \; 0.2])}&{([0.5, \; 0.6], \; [0.1, \; 0.2])}&{([0.5, \; 0.7], \; [0.5, \; 0.6])} \end{array}} \right]\\ {S^3} = \left[ {\begin{array}{*{20}{c}} {([0.6, \; 0.8], \; [0.1, \; 0.2])}&{([0.7, \; 0.9], \; [0.1, \; 0.2])}&{([0.7, \; 0.8], \; [0.1, \; 0.2])}&{([0.6, \; 0.7], \; [0.1, \; 0.2])}\\ {([0.6, \; 0.7], \; [0.2, \; 0.3])}&{([0.5, \; 0.6], \; [0.2, \; 0.3])}&{([0.6, \; 0.8], \; [0.3, \; 0.4])}&{([0.4, \; 0.6], \; [0.2, \; 0.3])}\\ {([0.5, \; 0.6], \; [0.1, \; 0.3])}&{([0.7, \; 0.8], \; [0.0, \; 0.2])}&{([0.5, \; 0.6], \; [0.1, \; 0.3])}&{([0.5, \; 0.7], \; [0.1, \; 0.3])} \end{array}} \right] \end{array}} \right.$

步骤2. 确定指标权重.

根据式(2), 将区间直觉模糊数的决策矩阵转化为区间直觉模糊数的信息熵矩阵, 转换结果为:

$\left\{ {\begin{split} &{h^1} = \left[ {\begin{array}{*{20}{c}} {0.384}&{0.329}&{0.293}&{0.408}&{0.452} \\ {0.576}&{0.700}&{0.384}&{0.626}&{0.827} \\ {0.700}&{0.384}&{0.626}&{0.461}&{0.510} \end{array}} \right]\\ & {h^2} = \left[ {\begin{array}{*{20}{c}} {0.408}&{0.384}&{0.286}&{0.384}&{0.452} \\ {0.452}&{0.735}&{0.452}&{0.452}&{0.859} \\ {0.417}&{0.384}&{0.490}&{0.776}&{0.542} \end{array}} \right]\\ &{h^3} = \left[ {\begin{array}{*{20}{c}} {0.408}&{0.329}&{0.384}&{0.452}&{0.452} \\ {0.576}&{0.626}&{0.613}&{0.613}&{0.776} \\ {0.542}&{0.314}&{0.542}&{0.510}&{0.520} \end{array}} \right] \end{split}} \right.$

由式(3)可计算得到每位专家的决策矩阵对应的指标权重, 即:

$\left\{ {\begin{split} & {\omega ^1} = \left( {0.183, \; 0.216, \; 0.231, \; 0.205, \; 0.165} \right) \\ & {\omega ^2} = \left( {0.229, \; 0.199, \; 0.235, \; 0.184, \; 0.153} \right) \\ & {\omega ^3} = \left( {0.201, \; 0.236, \; 0.199, \; 0.194, \; 0.170} \right) \\ \end{split}} \right.$

步骤3. 确定专家权重.

根据得到的与每位专家的决策矩阵相对应的指标权重, 对每位专家的决策矩阵进行加权, 可得每名专家对各方案的综合评价和3位专家对方案的综合评价值.

$\left\{ {\begin{split}& {\tilde{Z}}^{1}=\left[\begin{array}{c}\left[0.693, 0.846\right], \left[0.000, 0.209\right]\\ \left[0.573, 0.696\right], \left[0.209, 0.326\right]\\ \left[0.588, 0.755\right], \left[0.172, 0.290\right]\end{array}\right]\\&{\tilde{Z}}^{2}=\left[\begin{array}{c}\left[0.710, 0.846\right], \left[0.000, 0.209\right]\\ \left[0.547, 0.665\right], \left[0.159, 0.270\right]\\ \left[0.575, 0.755\right], \left[0.000, 0.314\right]\end{array}\right]\\& {\tilde{Z}}^{3}=\left[\begin{array}{c}\left[0.686, 0.833\right], \left[0.120, 0.224\right]\\ \left[0.527, 0.677\right], \left[0.235, 0.349\right]\\ \left[0.588, 0.710\right], \left[0.000, 0.288\right]\end{array}\right]\\&{\tilde{Z}}_{o}=\left[\begin{array}{c}\left[0.697, 0.842\right], \left[0.000, 0.214\right]\\ \left[0.549, 0.680\right], \left[0.198, 0.313\right]\\ \left[0.584, 0.741\right], \left[0.000, 0.297\right]\end{array}\right] \end{split} } \right.$

计算得到各专家与群体意见的灰色关联系数, 即:

${\xi ^1} = \left[ {\begin{array}{*{20}{c}} {1.000} \\ {0.785} \\ {0.363} \end{array}} \right]; \;{\xi ^2} = \left[ {\begin{array}{*{20}{c}} {0.925} \\ {0.643} \\ {0.854} \end{array}} \right]; \;{\xi ^3} = \left[ {\begin{array}{*{20}{c}} {0.453} \\ {0.661} \\ {0.793} \end{array}} \right]$

计算各个专家意见与群体意见的关联度, 即:

${\gamma }_{o1}=0.716;\; {\gamma }_{o2}=0.807;\; {\gamma }_{o3}=0.636$

二次优化模型通过LINGO软件可得到专家权重:

${\beta }_{1}=0.323;\; {\beta }_{2}=0.382;\; {\beta }_{3}=0.295$

步骤4. 计算各方案的综合评价值, 即:

$\begin{split}& {\tilde{x}}_{1}=\left(\left[0.698, 0.843\right], \left[0.000, 0.213\right]\right) \\&{\tilde{x}}_{2}=\left(\left[0.550, 0.679\right], \left[0.195, 0.310\right]\right)\\& {\tilde{x}}_{3}=\left(\left[0.583, 0.743\right], \left[0.000, 0.298\right]\right) \end{split}$

并得到正、负理想云模型. 将方案的综合评价值转化为各方案的支持云和反对云模型, 即:

$\begin{split}& {\tilde x_1} = {C_1} = \left( {\left( {0.770, 0.140, 0.014} \right), \left( {0.107, 0.036, 0.004} \right)} \right)\\& {\tilde x_2} = {C_2} = \left( {\left( {0.614, 0.113, 0.011} \right), \left( {0.252, 0.019, 0.002} \right)} \right)\\& {\tilde x_3} = {C_3} = \left( {\left( {0.663, 0.124, 0.012} \right), \left( {0.149, 0.050, 0.005} \right)} \right)\\&{C}^+=\left(0.770, 0.113, 0.011\right) , \; {C}^-=\left(0.252, 0.050, 0.005\right) \end{split}$

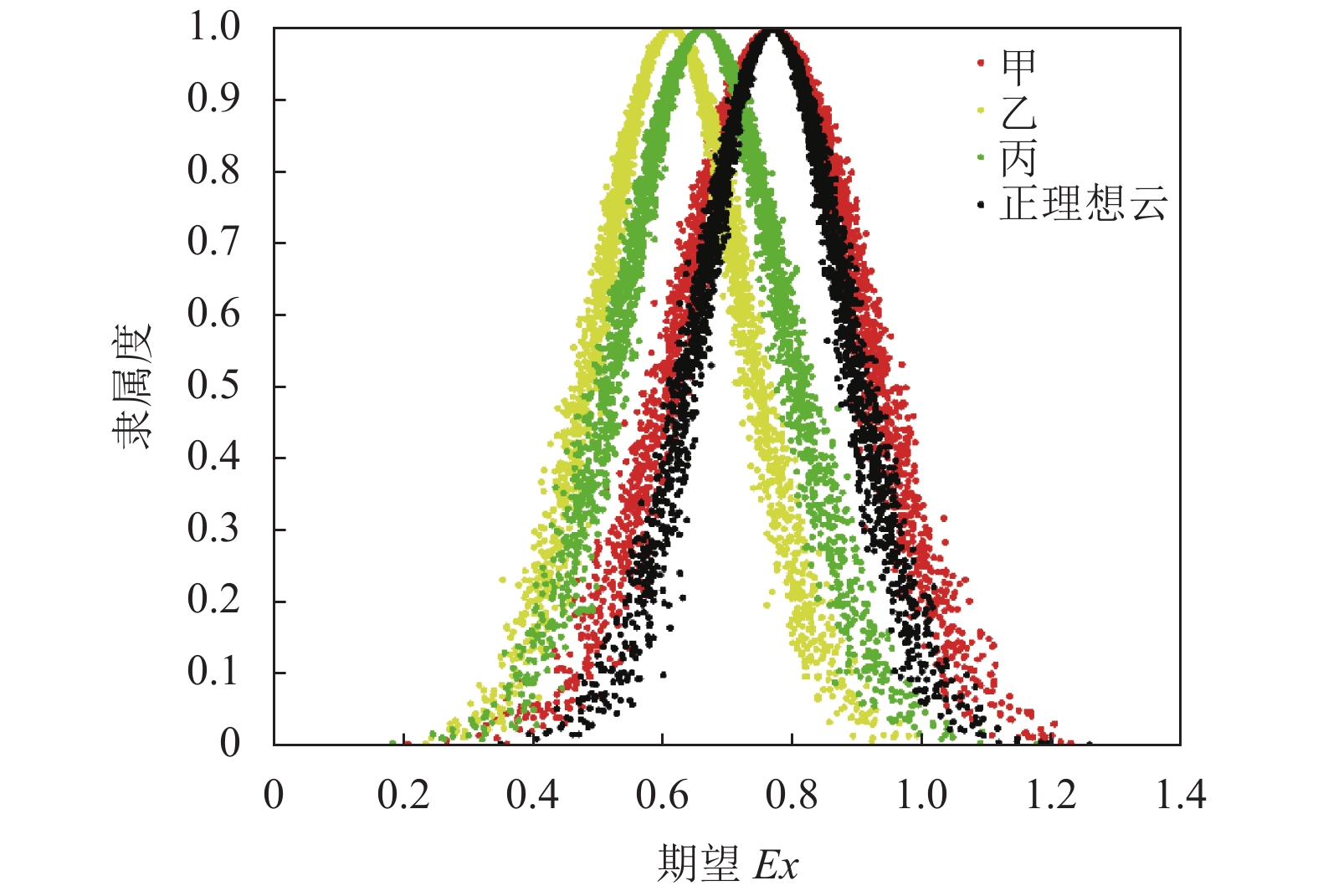
根据支持云模型与正理想云模型的形状和距离相似度, 得到各方案与正理想云模型的正相似度, 同样地可以得到各反对云模型与负理想云模型的负相似度, 从而得出方案相对于正负理想云模型的贴近度(正相似度/(正相似度+负相似度)). 通过各方案的支持云和反对云的相似度可计算出方案的犹豫度, 见表1.

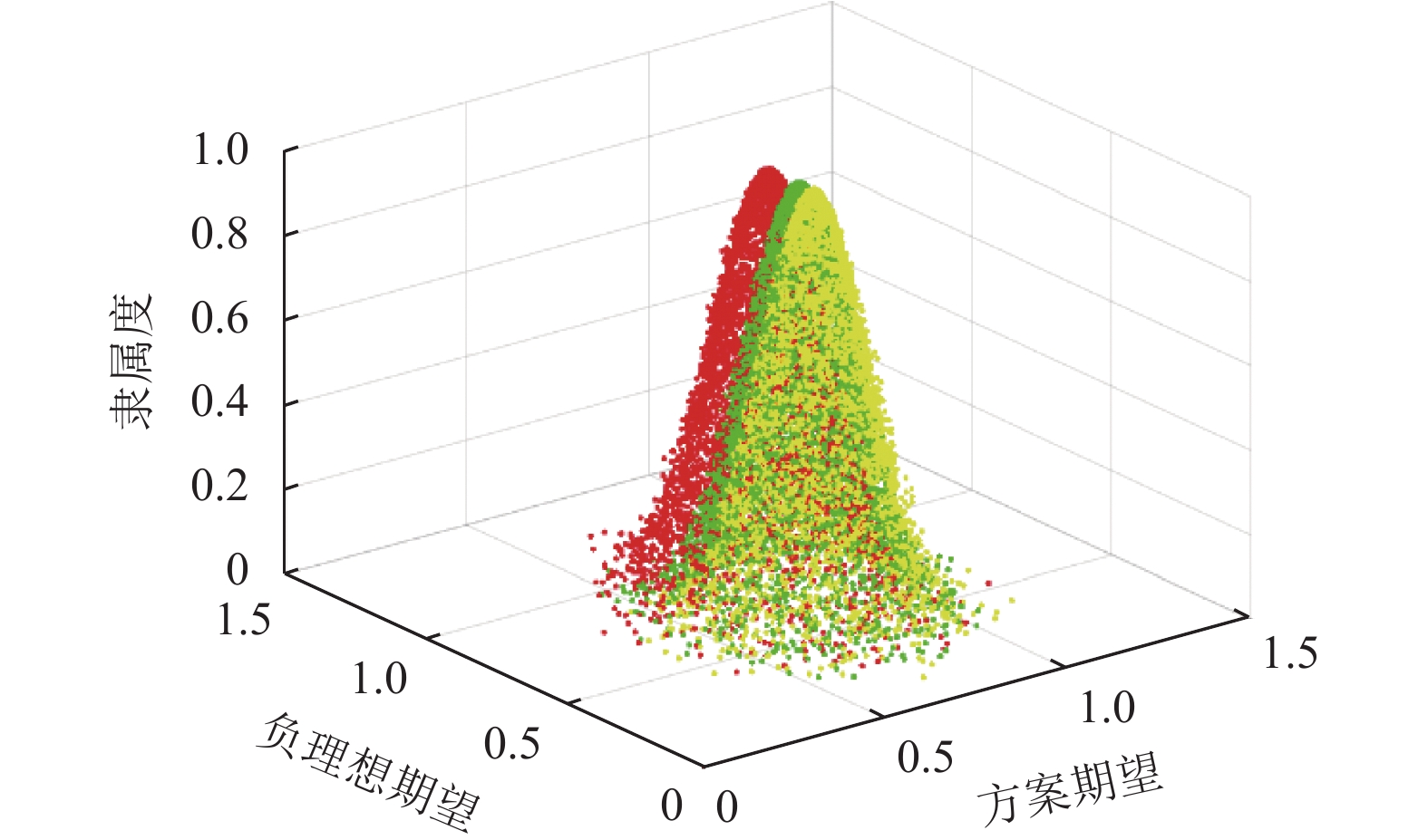
通过将各方案与正、负理想云模型进行对比, 由Matlab绘图可直观反映出正相似度和负相似度,

通过图1和图2的二维云图与图3和图4的三维云图可以直观看出各方案的支持云和反对云模型与正、负理想云的形状、距离相似度和综合相似度, 通过表1与图1–图4的直客观结合可知排序优劣为甲>丙>乙. 再通过比较其他文献中的区间直觉模糊数的排序方式, 发现各方案的排序结果与本文的排序结果一致, 见表2, 即甲>丙>乙. 表示本文的方法具有较强的有效性和可行性.

文献[13-15]对于区间直觉模糊数的排序方法各有不同, 通过对3个相同的区间直觉模糊数进行排序, 所得到的结果都是甲>丙>乙, 可见本文所提出的决策方法具有较强的有效性和可行性. 本文所提出的新的排序方法, 相较于以上传统的通过得分函数和精确函数的数值来进行排序的方法, 考虑到了区间直觉模糊数其在某个中心波动的随机性, 当隶属度区间数和非隶属度区间数都服从正态分布时, 将利用云模型的3En规则将区间直觉模糊数转化为一个支持云模型和一个反对云模型, 这样一来不仅考虑到了决策信息的模糊性还考虑到了随机性, 而云模型正是在模糊数学和概率论的基础上建立的, 可以很好地将模糊性和随机性结合在一起. 在区间直觉模糊数的排序方法选择上, 本文通过比较各支持云模型和反对云模型与正、负理想云模型的相似度获得综合评价值的贴进度, 通过比较一个方案中的支持云模型和反对云模型的相似度则可以得到该方案的犹豫度, 使得云模型从描述不确定信息的隶属度, 进而可以使支持云模型和反对云模型两者同时描述不确定信息的隶属度、非隶属度和犹豫度.

4 结论与展望

本文基于区间直觉模糊理论在决策过程中的优点, 将犹豫度和随机性融入其中, 利用云相似度计算方案的贴近度和犹豫度, 通过比较各个方案的相较于正理想云模型和负理想云模型的相似度得出整个方案的贴近度, 随后比较各个方案的支持云模型和反对云模型得出各个方案的犹豫度, 并得到最终的决策结果. 选择的最优方案是该方案贴近度大且犹豫度小, 即综合评价值高且不确定性小的方案, 研究结果仅是对于排序结果的理性排序, 着眼于现有的结果. 通过与其他区间直觉模糊数的排序方法进行对比, 可知通过云相似度方法对其进行排序同样具有有效性和科学性, 云模型在解决决策过程中的模糊性和随机性更胜一筹.

对于犹豫度大的方案, 可能会出现支持的隶属度和非隶属度一样大或差不多大, 即该方案的争议度较大, 支持和反对意见各执一方, 这可能会出现在对于新兴事物的发展的决策过程中, 对于新兴事物的抉择和判断是具有较大的争议性, 专家们对新兴事物的看法具有较大的不确定性, 但在实际过程中, 对于未来具有前瞻性的观点或方案还需另外考虑, 因此对于该决策问题的研究还需考虑到决策者的偏好和具体的现实环境等. 除此, 对于多种混合评价信息的结合与转化还亟待研究, 本文只针对评价信息为区间直觉模糊数的群决策问题提出了一种新的基于云相似度的排序方法, 未来对于其他属性信息的融合还需深度探索.