铁路是国家的重大战略工程, 是国家综合交通运输体系的主体. 铁路运输的发展为人们的出行以及工业运输带来了巨大的便利. 相比公路、水路和民航运输, 铁路运输具有明显的低能耗、大运量、安全性高等优势. 随着经济社会的发展, 旅客出行需求的不断增加, 工业上对于物料转移的需求不断增大, 我国铁路运输呈现列车开行密度大、运行路线长、运营环境复杂等特征, 铁路运行秩序的稳定以及运营效率面临着巨大的挑战. 以经验为主的人工调度难以满足广域高密度条件下列车“按图行车”的要求. 列车运行图是铁路综合计划和行车调度工作的基础, 需要协调车辆、乘务等各方面资源. 科学合理地编制列车运行图对保证行车安全与秩序, 合理配置运输资源, 提高运行效率和服务品质具有重要意义.
同时, 基于常态化列车调度方案无法适应突发事件条件下因运力资源骤变而引起的运力下降. 面对不可预知的突发事件, 以及其造成的不同程度的影响, 列车运行计划应如何进行调整, 才能尽快恢复秩序并保证铁路系统安全高效运行, 已成为目前迫切需要解决的问题. 研究突发事件条件下的应急处置方案以及安排列车重调度计划, 对降低突发事件影响、提高运输效率具有理论价值和现实意义.
为求解列车调度问题, 此前的研究者提出了很多算法. Sato等[1]建立了列车运行调度的混合整数规划模型求解. Almodóvar等[2]运用离散事件仿真法进行研究, 以旅客最小出行时间为优化目标建立模型设计贪婪算法求解. Haramina等[3]利用计算机仿真设计了以牵引能源消耗最少为目标的仿真优化模型. Espinosa-Aranda等[4]建立二进制整数规划线性模型, 提出启发式算法(AMDAA)解决列车调整问题. 王瑞峰等[5]设计了改进粒子群算法对两目标优化的调度模型求解, 并实证了算法高效性. 徐小明[6]建立均衡列车运行图优化模型, 结合遗传算法求解, 优化了总延迟率. 林博等[7]引入调整策略控制粒子群算法参数, 以总晚点时间最小和列车总晚点数量最少为目标求解. 刘辉等[8]通过调整行车顺序和到发时间, 提出改进蚁群算法使用信息启发式因子和期望启发式因子的权重组合及挥发因子动态调整方法提高收敛速度. 徐虎[9]设计改进的萤火虫算法使列车上行时间和下行时间误差的总和最小. 韩忻辰等[10]建立列车延误时间总和最小为目标的高铁动态调度模型, 采用强化学习中的Q-Learning算法进行求解. 汪臻等[11]以遗传算法为基础, 结合模拟退火算法优化了列车晚点时间. Nitisiri等[12]提出基于混合采样策略和学习的变异并行多目标进化算法来解决列车调度问题. Jeremić等[13]提出一种检测和管理单线列车路径冲突的高级Petri网仿真模型并在斯洛文尼亚西南部某单线上进行测试, 取得不错的效果.
本文在列车运行调度理论的基础上, 建立了单线铁路列车调度的数学模型, 设计了一种两阶段列车调度算法, 第1阶段使用一种自适应更新规则结合几种优秀算子寻找最优列车速度组合, 第2阶段调整与速度组合相应的停站时间, 并考虑了突发事件下的处理方式以及重调度方法. 将所提算法与其他研究者的算法在相同实验条件下进行测试对比, 并进行突发事件测试, 验证了所提算法的有效性.
1 问题描述双向单线铁路上开行的列车之间不可避免地会出现对同一运行区间或同一车站的占用冲突, 本文所研究的单线铁路列车调度问题是在列车安全稳定运行的前提下, 通过调整列车运行速度、停站时间等操作, 解决上述列车冲突, 并在某一评价函数上达到最优, 求得一个合理且高效的列车调度方案.
列车实际运行过程中可能会发生无法预知的突发事件, 根据突发事件造成影响的程度, 可分为普通级、严重级等. 一般情况下, 普通突发事件可通过微调使列车逐渐恢复到原始运行计划上. 本文研究区间铁路损坏类型突发事件下的应急处置方案, 该类型事件影响较为严重, 原始运行计划无法在预期时间内恢复, 无法继续运行, 需对列车进行重新调度, 编制新的列车运行图. 该类型突发事件发生时, 被损坏铁路段所在的运行区间将被封锁, 此时列车共存在4种状态(第2.5节中所提), 本文将对4种状态下的列车进行分析, 研究此状态下列车的处理和调整策略.
1.1 符号定义单线铁路列车调度模型中所使用的模型参数符号定义如表1所示.
| 表 1 模型参数与变量定义 |
1.2 数学模型
根据单线铁路列车运行调度的特点以及上述问题描述, 建立如下数学模型.
目标函数为最小化列车的延迟率, 即列车总延迟时间与所有列车无其他列车共享铁路时离开系统时间之和的比率. 其中, 列车延迟时间为列车实际到达终点站时间与列车无其他列车共享铁路条件下到达终点站时间的差值. 目标函数的数学表达式如式(1)所示:
| $ Delay {\text{-}} ratio = \dfrac{{\displaystyle\sum\nolimits_{i = 1}^N {(T_i^{{\rm{real}}} - T_i^{{\rm{ideal}}})} }}{{\displaystyle\sum\nolimits_{i = 1}^N {T_i^{{\rm{ideal}}}} }} $ | (1) |
约束条件:
1) 停站时间约束
列车
| $ {D_{ij}} - {A_{ij}} \geqslant T_{ij}^{\min } $ | (2) |
2) 发车间隔约束
相邻列车
| $ {D_{i, j}} - {D_{i - 1, j}} \geqslant T_d^{\min } $ | (3) |
3) 到站间隔约束
相邻列车
| $ {A_{i, j}} - {A_{i - 1, j}} \geqslant T_a^{\min } $ | (4) |
4) 行车速度约束
列车
| $ v_i^{\min } \leqslant {v_{ij}} \leqslant v_i^{\max } $ | (5) |
5) 车站股道约束
车站
| $ \left\{ \begin{gathered} {S_{{l_j}}} \in \{ 0, 1\} \\ \sum\nolimits_{{l_j} = 1}^{{L_j}} {{S_{{l_j}}} \leqslant {L_j}} \\ \end{gathered} \right. $ | (6) |
本文设计了的两阶段列车调度算法, 第1阶段使用粒子群优化算法作为基本框架, 在其基础上进行改进, 用于搜索列车区间运行速度最优组合, 第2阶段设计了一种启发式调整规则, 用于调整列车的停站时间, 解决列车运行冲突, 使得到的解可行. 该算法还具备突发事件应急处理能力, 设计了应对铁路部分路段损坏所导致的运行计划中断的处理方案.
2.1 编码方式列车实际运行时, 往往不会全程以恒定速度运行, 且一些区段内可能存在限速. 本文采用列车区间平均速度进行编码, 不仅贴近实际运行, 对区间平均速度的组合优化调整, 还可能减少运行期间潜在的冲突.
本文优化的目标在于寻找列车的最优区间平均速度组合和与之对应的最优停站时间组合, 如该单线铁路存在
| $ V = \left( {\begin{array}{*{20}{c}} {{v_{1, 1}}}&{{v_{1, 2}}}& \cdots &{{v_{1, M - 1}}} \\ {{v_{2, 1}}}&{{v_{2, 2}}}& \cdots &{{v_{2, M - 1}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{v_{N, 1}}}&{{v_{N, 2}}}& \cdots &{{v_{N, M - 1}}} \end{array}} \right) $ | (7) |
列车在每站的停站时间构成式(8)所示的
| $ ST = \left( {\begin{array}{*{20}{c}} {s{t_{1, 1}}}&{s{t_{1, 2}}}& \cdots &{s{t_{1, M}}} \\ {s{t_{2, 1}}}&{s{t_{2, 2}}}& \cdots &{s{t_{2, M}}} \\ \vdots & \vdots & \ddots & \vdots \\ {s{t_{N, 1}}}&{s{t_{N, 2}}}& \cdots &{s{t_{N, M}}} \end{array}} \right) $ | (8) |
列车区间平均速度矩阵
粒子群优化算法(particle swarm optimization, PSO)[14]是源于鸟群捕食行为提出的, 因其易于实现, 参数少, 收敛速度快等优点, 在连续优化问题上表现良好, 适合应用于该列车速度优化组合问题. 但该问题的解是范围庞大的二维矩阵, PSO算法易产生早熟收敛, 陷入局部最优, 搜索空间多样性丢失, 搜索效率下降. 为更好地利用PSO算法的优势去寻找调度最优解, 本文将交叉、扰动算子以及反向学习算子与PSO算法结合, 通过一种自适应选择机制, 发挥各算子的优点, 在保留PSO优点的基础上, 提高全局寻优能力.
第1阶段是使用改进的PSO算法对列车的区间速度组合进行调整, 并进行初步列车时刻表的构建. 在算法一开始对列车速度在限速范围内随机赋值, 随后通过以下方式进行更新.
2.2.1 粒子更新公式粒子更新公式采用包括PSO标准公式在内的适用于处理实数解的以下4种, 进行列车区间速度的更新:
1) PSO标准更新公式:
| $ \begin{split} v_{ij}^* = &\omega \times {v_{ij}} + {c_1} \times {r_1} \times (pbes{t_{ij}} - {x_{ij}}) \\ &+ {c_2} \times {r_2} \times (gbes{t_{ij}} - {x_{ij}}) \end{split} $ | (9) |
| $ x_{ij}^* = {x_{ij}} + {v_{ij}} $ | (10) |
其中,
2) 反向学习算子:
| $ x_{ij}^* = {x_{{{\rm low}}}} + {x_{{\rm {up}}}} - {x_{ij}} $ | (11) |
其中,
3) 随机扰动算子:
| $ x_{ij}^* = {x_{ij}} + {x_{ij}} \times r \times R $ | (12) |
其中,
4) SBX交叉算子:
| $ \left\{ \begin{gathered} x_{ij}^{1*} = 0.5 \times \left[(1 + \beta ) \cdot x_{ij}^1 + (1 - \beta ) \cdot x_{ij}^2\right] \\ x_{ij}^{2*} = 0.5 \times \left[(1 - \beta ) \cdot x_{ij}^1 + (1 + \beta ) \cdot x_{ij}^2\right] \\ \end{gathered} \right. $ | (13) |
| $ \beta = \left\{ \begin{gathered} {(2 \times r)^{1/(1 + \mu )}}, r \leqslant 0.5 \\ {\left[{\text{1/(2}} - 2 \times r)\right]^{1/(1 + \mu )}}, r > 0.5 \\ \end{gathered} \right. $ | (14) |
其中,
在算法搜索的不同阶段, 每种算子所起到的作用有所变化, 例如在搜索初期, PSO标准公式收敛快, 而在搜索中后期, PSO标准公式可能陷入停滞, 其他算子能扩大搜索空间, 此时起到的作用更大. 使用自适应方式动态调整各搜索算子比重, 可让其在不同阶段发挥出自身优点.
采用分组方式, 假设种群大小为
| $ {P_i} = \dfrac{{\alpha + \left(u{p_i}/Up\right)}}{{\displaystyle\sum\nolimits_{i = 1}^k {\left[\alpha + \left(u{p_i}/Up\right)\right]} }} $ | (15) |
| $ {N_i} = N \times {P_i} $ | (16) |
其中,
在对列车区间速度进行更新后, 根据列车的区间运行平均速度矩阵
| $ RT = \left( {\begin{array}{*{20}{c}} {r{t_{1, 1}}}&{r{t_{1, 2}}}& \cdots &{r{t_{1, M - 1}}} \\ {r{t_{2, 1}}}&{r{t_{2, 2}}}& \cdots &{r{t_{2, M - 1}}} \\ \vdots & \vdots & \ddots & \vdots \\ {r{t_{N, 1}}}&{r{t_{N, 2}}}& \cdots &{r{t_{N, M - 1}}} \end{array}} \right) $ | (17) |
| $ r{t_{i,j}} = di{s_{j, j + 1}}/{v_{i, j}} $ | (18) |
其中,
已知列车每个区间的运行时间和每站的停站时间, 按照列车序号和运行方向逻辑进行累加记录即可快速得到初步的可能带有冲突的列车时刻表, 然后进入第2阶段进行调整.
2.3 第2阶段第1阶段得到的初步列车时刻表可能带有冲突, 在该阶段中进行检查和调整, 将使之成为一个可行解.
对于问题描述中所提到的列车冲突, 具体情况如图1所示, 并通过如下方式进行调整.
区间冲突为区间内列车出现运行线交叉, 如图1(a)、图1(b)所示, 冲突解决方式可以是向后平移列车

|
图 1 列车冲突解决方式 |
对于相邻列车, 若出入站间隔时间较短, 会出现到发线冲突, 严重时可能出现追尾. 列车出入站一般遵循先入先出原则, 即在车站内后入(出)站列车若未满足与相邻先入(出)站列车的最小时间间隔, 应增加停站时间直至满足最小到(离)站时间间隔. 图1(c)中列车
以列车区间速度和停站时间编码, 基于带有多种算子及自适应更新规则的PSO, 结合冲突调整策略, 构成两阶段列车调度算法(TE-TSA), 流程如图2所示.
2.5 突发事件处理突发区间铁路损坏会导致原运行计划中断, 且无法短时间恢复. 原运行计划不再受用, 需对列车进行重调度, 更新列车时刻表, 应对该事件带来的影响.
突发事件发生时, 要先确定事件类型以及其影响的范围, 要对受直接影响的铁路区间进行封锁, 避免其他列车驶入导致影响范围扩大.
在对列车进行重新调度时, 需要知道突发事件发生时, 所有列车所处的状态. 突发事件发生时, 列车共存在以下4种状态以及相应处理方式.
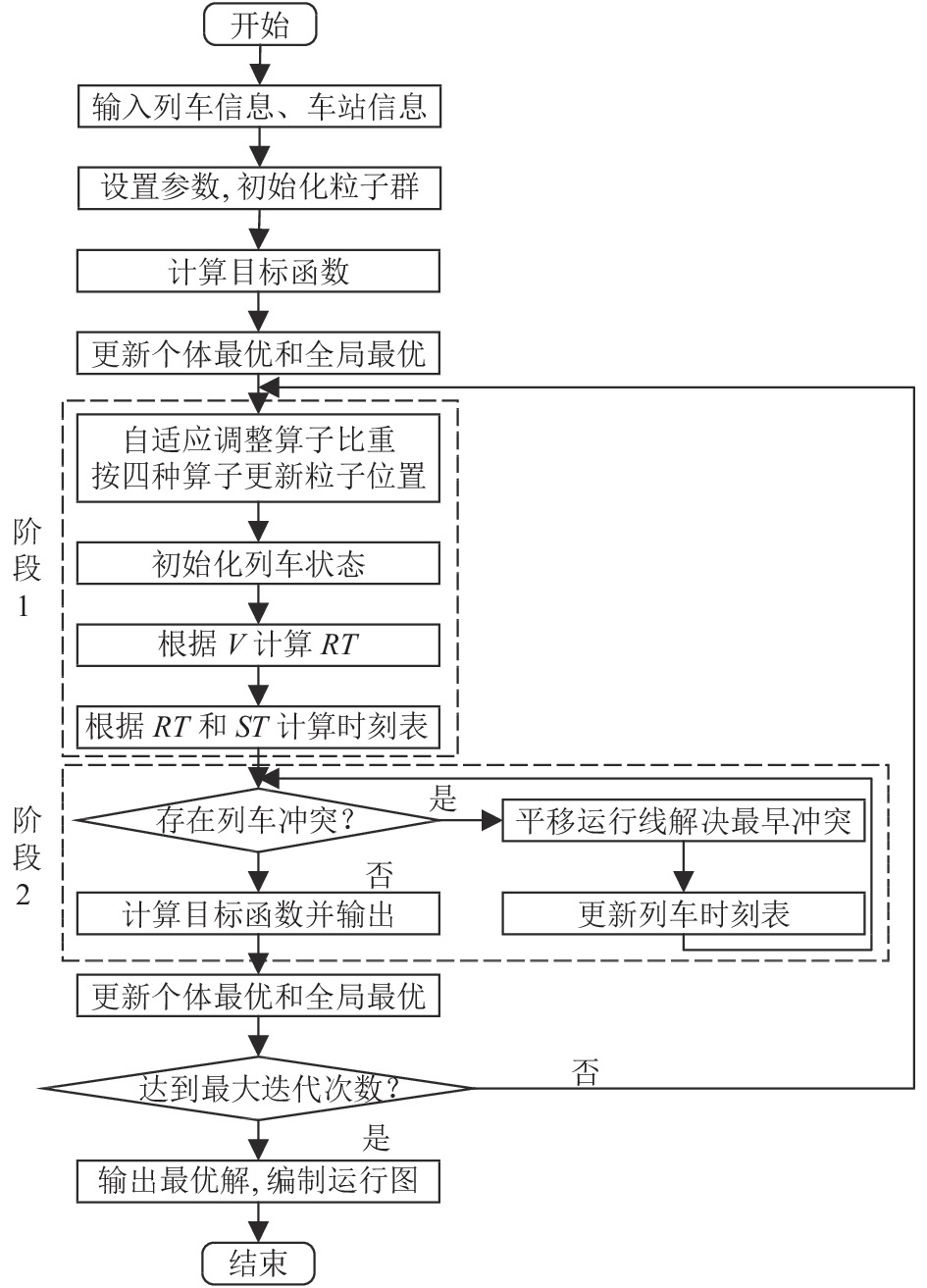
|
图 2 TE-TSA算法流程图 |
1) 列车正在区间内运行且正处于事件发生路段
列车正受突发事件直接影响, 应在当前位置停车, 并对突发事件所涉及的运行区间进行封锁, 待突发事件解决后该列车才可继续运行.
2) 列车正在区间内运行且前方非封锁路段
列车前方剩余运行区间未受突发事件直接影响, 可继续运行到下一车站.
3) 列车在车站内且前方运行区间为封锁路段
列车处于站内, 前方运行区间被封锁, 列车应在此站停车等待, 待突发事件解决后才可继续运行.
4) 列车在车站内且前方运行区间非封锁路段
列车处于站内, 前方区间可通行, 但需考虑前方车站是否因突发事件被迫停车, 若前方车站容纳列车数量已达上限, 则在当前车站等候, 待事件解决后才可继续运行. 若未达车站容量上限, 则可继续运行.
综上所述, 在突发事件发生时, 列车应在满足约束条件的基础上, 尽可能保证最大作业完成率. 待铁路恢复后, 列车从当前状态开始继续运行, 以当前位置为起点编制后续运行图. 该算法处理流程如图3所示.

|
图 3 突发事件处理流程图 |
3 实验分析
为证明本文所提算法的有效性, 本文进行了对比实验和事件测试. TE-TSA算法以Visual Studio 2019 为开发工具C++编程实现. 实验环境和配置为Intel(R) Core(TM) i5-7300HQ CPU@2.50、8.00 GB RAM、Windows 10 64位操作系统.
本次实验给出了TE-TSA算法与Xu等[15]提出的GA-ITAS算法在相同实验条件下的测试结果以及TE-TSA算法在某个突发事件下的表现.
3.1 对比实验本次对比实验数据来源于Xu等[15]在其研究中进行实验所使用的数据集. 图4给出了用作对比测试的单线铁路结构, 该铁路由17个站点和16个可双向行驶的单线轨道组成, 全长275 km. 车站A和B分别为下行和上行的终点站, 进行到发车操作. 其他车站为中间站, 用于列车停靠作业或避让其他列车. 算例共18辆同等级列车, 其中9辆上行、9辆下行, 同方向发车间隔为1 h. 列车平均速度变化范围在18 m/s到22 m/s之间.

|
图 4 单线铁路算例 |
GA-ITAS算法未对列车间距进行约束, 同时只考虑避让列车的停站时间, 未考虑列车的停站作业时间. 为了与GA-ITAS算法保证实验条件相同, 本次测试也暂不考虑列车车站作业时间与列车间距. 种群规模和迭代次数同样设置为20和150. PSO惯性权重上限为0.9, 下限为0.4, 学习因子
为评估TE-TSA算法的有效性, 采用Xu等[15]测试所使用的4个指标进行对比: 线路清空时间
| $ {J_1} = T_{{\rm{Last}}}^{{\rm{real}}} - {t_0} $ | (19) |
| $ {J_{\text{2}}}{\text{ = }}\displaystyle\sum\limits_{{\text{i = 1}}}^N \left({T_i^{{\rm{real}}} - } T_i^{{\rm{ideal}}}\right) $ | (20) |
| $ {J_{\text{3}}}{\text{ = }}\mathop {\max }\limits_i \left\{ T_i^{{\rm{real}}} - T_i^{{\rm{ideal}}}\right\} $ | (21) |
| $ \eta {\text{ = }}\dfrac{{T_{{\rm{Last}}}^{{\rm{ideal}}} - {t_0}}}{{T_{{\rm{Last}}}^{{\rm{real}}} - {t_0}}} $ | (22) |
其中, 线路清空时间为实际运行中最后一辆列车到达终点站离开铁路线路的时间.
两种对比算法的相对差距如式(23)计算:
| $ GAP{\text{ = }}\left({{\text{Z}}_{{\rm {TE {{-}} TSA}}}} - {Z_{{\rm{GA {{-}} ITAS}}}}\right)/{Z_{{\rm{GA {{ -}} ITAS}}}} $ | (23) |
其中,
算例运行10次, 取平均值对比. 图5为GA-ITAS算法结果对应运行图, 图6为TE-TSA算法对应运行图. 表2列出了TE-TSA与GA-ITAS算法得到的列车运行图的各项指标结果, 不同指标的相对差距GAP在表底给出. 对比发现, TE-TSA的测试结果在各项指标及目标函数上都优于GA-ITAS算法, 证明本文算法设计有效. 通过图6也可观察到列车运行图在均衡性上有所提升. 以上对比充分证明了TE-TSA算法的有效性, 适合处理单线铁路列车调度问题.

|
图 5 GA-ITAS运行图 |
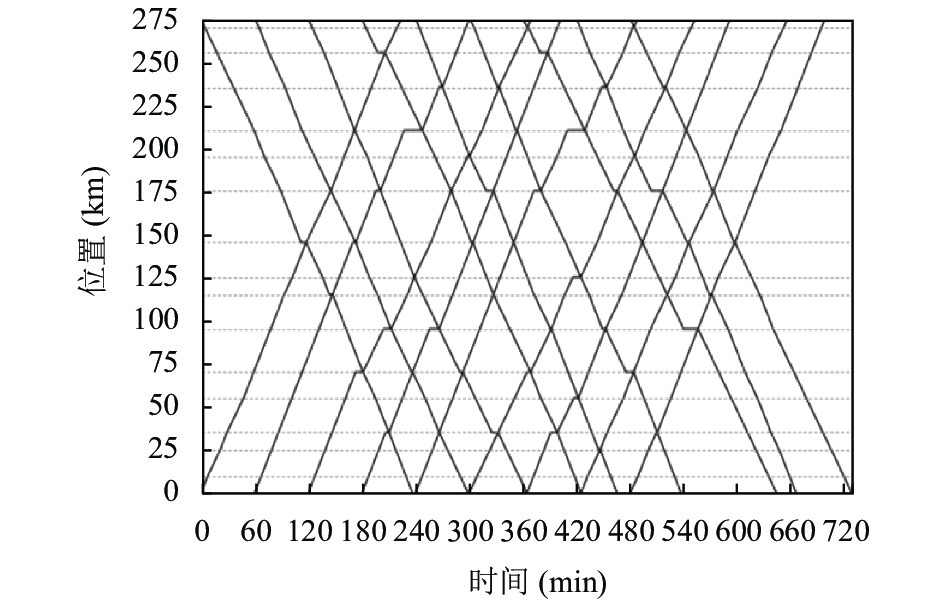
|
图 6 TE-TSA运行图 |
| 表 2 算例测试结果 |
3.2 突发事件实验
为验证TS-TSA算法对突发事件的处理效果, 使用与第3.1节不同的算例对算法进行测试. 该算例包含10辆列车, 20个车站, 列车发车时间和停站时间随机设置. 本算例重点考察对突发事件的处理, 故具体算例不必给出. 突发事件发生位置设在S09−S10区间内, 事件类型为铁路损坏, 发生时间为13:30, 铁路恢复时间为16:00. 本次测试考虑了对比测试中未考虑的到发间隔时间约束以及列车的车站作业时间.
图7为列车出发前所设定的计划运行图, 图8为经历突发事件并等待恢复继续运行至结束的完整实际运行图. 由图8可知, 列车在13:30前均按照计划运行图行驶, 在突发事件发生时, 处于事件发生区域的列车紧急停靠在铁路无法继续行驶, 其他未受事件直接影响的列车继续运行直至离事件发生区域最近的车站等候, 保证了列车作业的最大完成率. 在铁路恢复前, 列车始终保持当前状态不变. 在16:00时, 铁路恢复运行, 因事件导致列车严重脱离计划运行图, 对列车进行重新调度, 通过该算法得到新的延迟率最低的计划运行图, 保证后续运行的高效性. 该算法同时考虑了到发间隔时间约束与作业时间, 符合列车实际运行规律, 图中相邻列车之间始终保持一定安全距离. 16:00之后列车陆续恢复运行直至终点站. 本次实验证明了TE-TDSA在具备高效的列车无障碍调度能力的基础上, 同时具备处理突发事件的能力.
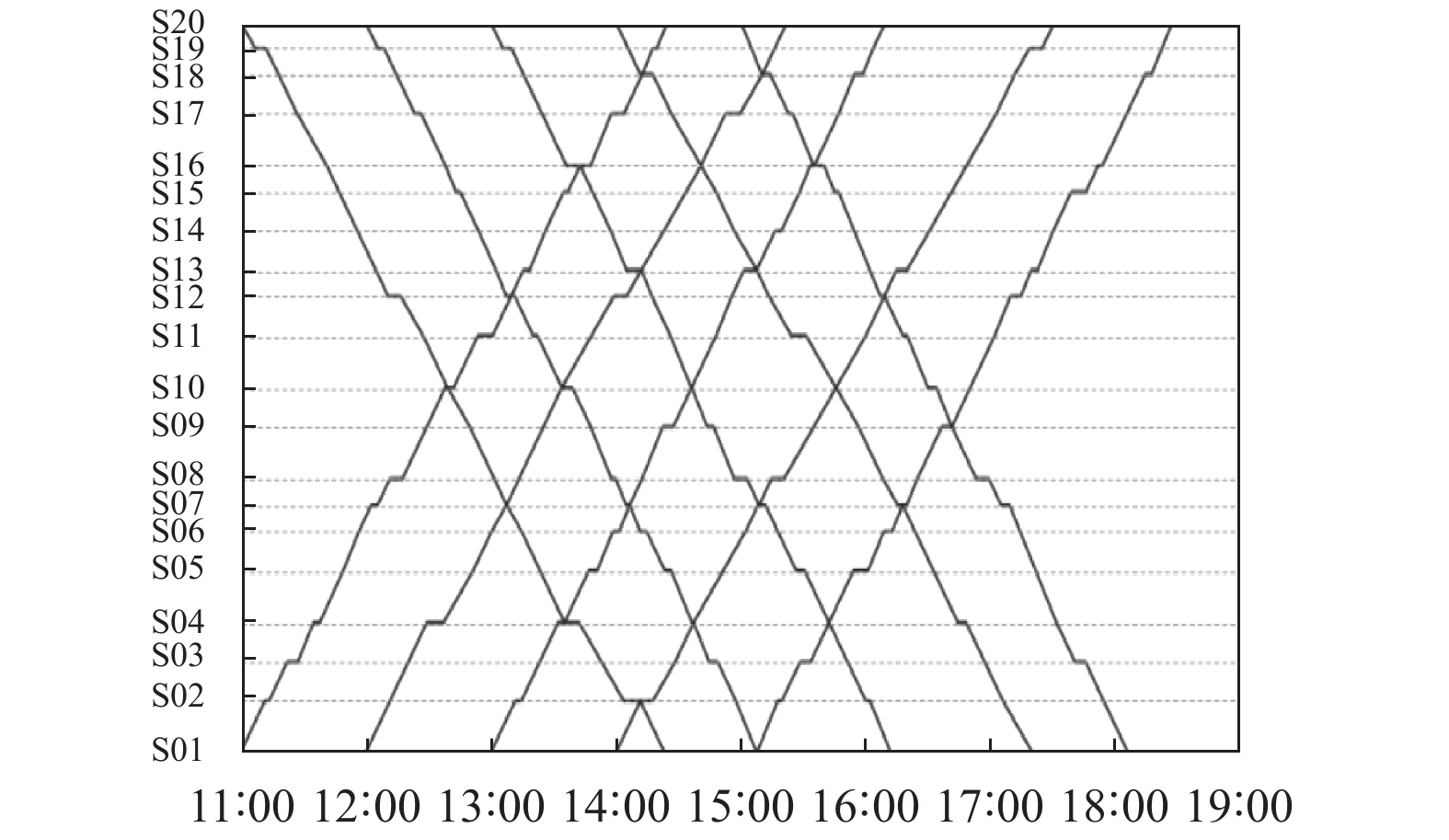
|
图 7 计划运行图 |
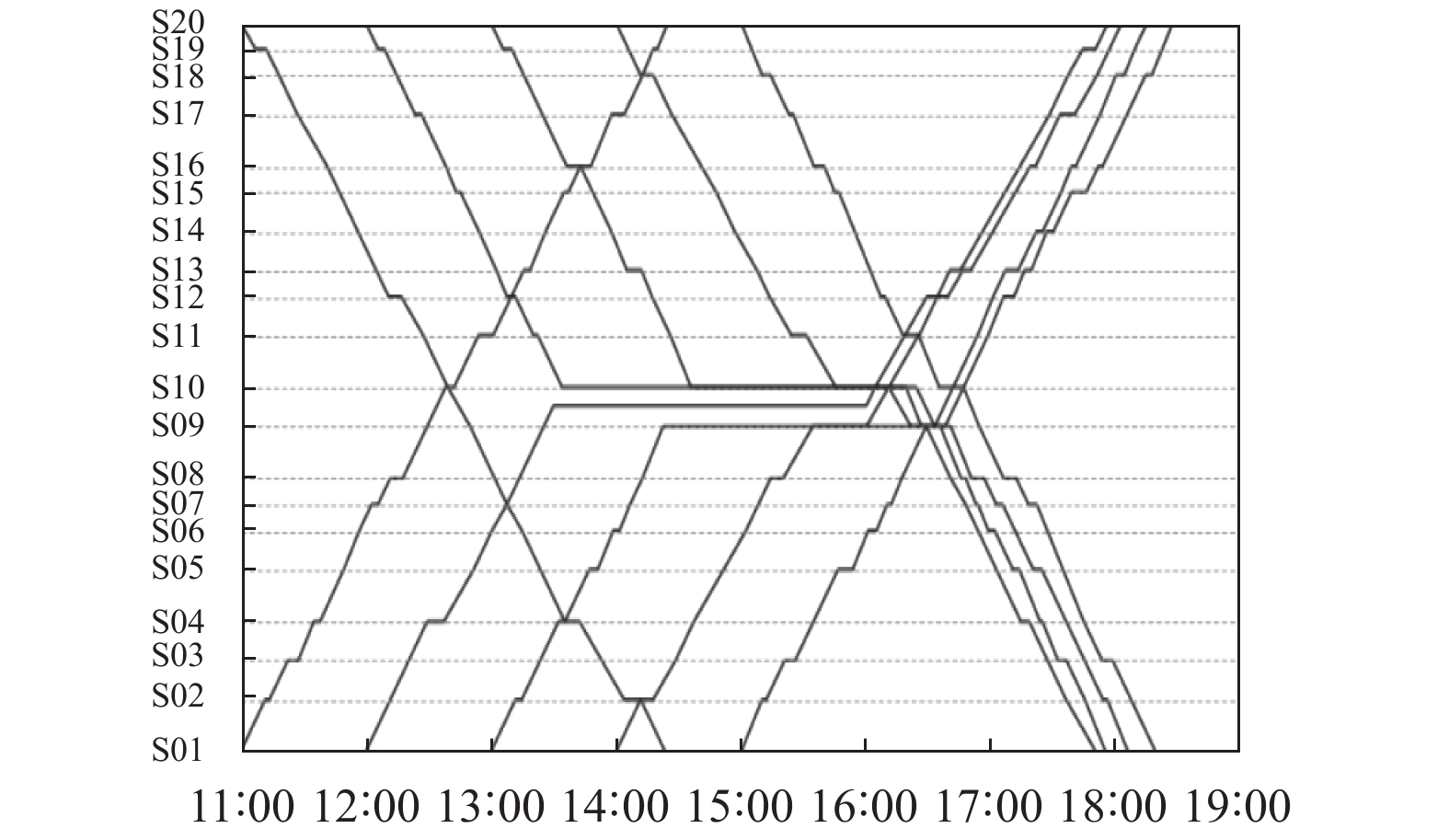
|
图 8 实际运行图 |
4 结论与展望
本文研究单线铁路列车调度问题, 设计了一种两阶段列车调度算法, 将交叉、扰动算子以及反向学习算子与PSO算法结合, 设计了自适应动态调整搜索算子比重的规则, 在保留PSO优势的基础上适当提高其全局搜索能力, 使算法更容易不遗漏地搜索到最优调度解, 优化了列车延迟率. 同时该算法还具备处理突发事件的能力, 当铁路损坏发生时, 算法能够及时安排列车有序停靠, 减少突发事件影响范围, 并能够在突发事件恢复后尽快恢复列车继续高效稳定运行. 通过实验证明TE-TSA算法有效.
列车调度问题的规模、约束条件及求解难度还在不断增大, 本研究具有重要的意义, 下一步将致力于多目标优化方向, 以满足多方面资源的协调, 并研究扰动条件下以降低列车晚点程度的动态调度问题.
| [1] |
Sato K, Tamura K, Tomii N. A MIP-based timetable rescheduling formulation and algorithm minimizing further inconvenience to passengers. Journal of Rail Transport Planning & Management, 2013, 3(3): 38-53. |
| [2] |
Almodóvar M, García-Ródenas R. Online reschedule optimization for passenger railways in case of emergencies. Computers & Operations Research, 2013, 40(3): 725-736. |
| [3] |
Haramina H, Mandić M, Nikšić M. New method for energy-efficient train operation on commuter rail networks. Tehnicki Vjesnik, 2012, 19(4): 801-806. |
| [4] |
Espinosa-Aranda JL, García-Ródenas R. A demand-based weighted train delay approach for rescheduling railway networks in real time. Journal of Rail Transport Planning & Management, 2013, 3(1–2): 1-13. |
| [5] |
王瑞峰, 孔维珍, 詹生正. 杂交粒子群算法在列车运行调整中的应用研究. 计算机应用研究, 2013, 30(6): 1721-1723. DOI:10.3969/j.issn.1001-3695.2013.06.031 |
| [6] |
徐小明. 基于离散事件的列车调度问题模型与算法研究[博士学位论文]. 北京: 北京交通大学, 2016.
|
| [7] |
林博, 俞胜平, 刘子源, 等. 基于改进粒子群算法的高铁列车动态调度. 控制工程, 2021, 28(7): 1334-1341. DOI:10.14107/j.cnki.kzgc.20190615 |
| [8] |
刘辉, 代学武, 崔东亮, 等. 基于参数自适应蚁群算法的高速列车行车调度优化. 控制与决策, 2021, 36(7): 1581-1591. DOI:10.13195/j.kzyjc.2020.0992 |
| [9] |
徐虎. 基于改进萤火虫算法的铁路运行调度算法研究. 微型电脑应用, 2019, 35(11): 102-105. DOI:10.3969/j.issn.1007-757X.2019.11.032 |
| [10] |
韩忻辰, 俞胜平, 袁志明, 等. 基于Q-Learning的高速铁路列车动态调度方法. 控制理论与应用, 2021, 38(10): 1511-1521. DOI:10.7641/CTA.2021.00612 |
| [11] |
汪臻. 基于遗传模拟退火算法的高速列车运行调整问题研究[硕士学位论文]. 北京: 北京交通大学, 2019.
|
| [12] |
Nitisiri K, Gen M, Ohwada H. A parallel multi-objective genetic algorithm with learning based mutation for railway scheduling. Computers & Industrial Engineering, 2019, 130: 381-394. |
| [13] |
Jeremić D, Milinković S, Kasalica S. Simulating train dispatching logic with high-level Petri nets. Tehnički Vjesnik, 2021, 28(2): 639-648. |
| [14] |
Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of International Conference on Neural Networks (ICNN’95). Perth: IEEE, 1995. 1942–1948.
|
| [15] |
Xu XM, Li KP, Yang LX, et al. Balanced train timetabling on a single-line railway with optimized velocity. Applied Mathematical Modelling, 2014, 38(3): 894-909. DOI:10.1016/j.apm.2013.07.023 |
 2022, Vol. 31
2022, Vol. 31


