2. 福建师范大学 福建省网络安全与密码技术重点实验室, 福州 350007;
3. 福建省无线通讯重点实验室, 福州 350002
2. Fujian Provincial Key Lab of Network Security & Cryptology, Fujian Normal University, Fuzhou 350007, China;
3. Key Laboratory of Wireless Communication in Fujian Province, Fuzhou 350002, China
社会网络(social networks, SNs)是一种人与人之间的关系与互动的结合[1]. 社会网络把网络中的每个节点看作参与这个网络中人的抽象, 每个人之间的关系则抽象成节点之间的连边, 网络中每个人的行为不同且具有不同的属性特征. 随着网络与计算机技术的快速发展, 人们的日常生活与互联网正在不断的相互融合, 人们通过微信、QQ、新浪微博等各种软件以及平台来发布自己的兴趣爱好、位置等信息. 随着用户发布的信息越来越多, 其网络形象就被进一步的丰富, 服务提供商可以对这些数据进行分析与筛选, 获得有用的数据来为用户带来更好的服务体验. 而攻击者可以通过数据分析获得用户的身份信息以及关系信息等隐私数据, 造成用户隐私的泄露, 对用户的个人信息及财产安全带来严重的威胁的同时也严重地影响了数据发布者的信誉. 在社交网络[2]、医疗大数据[3]与金融机构[4]中都存在着隐私泄露的风险, 因此隐私保护是一个不容忽视的问题. 民法典中明确规定了数据的流动和处理应建立在个人信息保护的基础之上. 因此, 如何在保证发布数据具有可用性的同时保护用户数据的隐私, 成为服务提供商以及消费者共同关注的一个问题.
图数据集中可能包含敏感、可辨别个人身份信息. 因此, 必须对公开发布的数据采取一定的隐私保护方法, 防止攻击者通过背景知识或链接攻击等手段获取到用户的隐私信息[5]. 在数据发布时, 通过去掉用户的身份标识来对原始图进行处理并不能很好的保护用户的隐私, 对手可以根据背景知识, 从发布图中识别出用户的身份[2, 6]. 为了缓解社会网络中的隐私泄露问题, 产生了基于匿名化的技术[7]、加密技术[8, 9]和差分隐私技术[10, 11]等诸多隐私保护技术. 例如近期Ding等人[12]提出了一种新的k-分解方法对大型图数据集进行隐私保护, 在隐私、数据可用性和效率之间取得了较好的平衡. 许佳钰等人[13]提出了一种基于节点平均度的k-度匿名隐私保护方案, 利用基于平均度的贪心算法对社会网络节点进行划分, 然后利用优先保留重要边的图结构修改方法对图进行修改, 从而实现图的k-度匿名化. 黄海平等人[14]提出了一种基于边介数模型的差分隐私保护方案, 根据介数排序的dk序列将重要性相近的边归为一类进行分组加噪, 保留了更多结构特征的同时也具有较好的数据可用性. Huang等人[15]结合聚类和随机化算法提出了一种隐私保护算法PBCN, 在数据可用性和隐私保护水平之间实现折中. Zhu等人[16]将网络物理系统中的数据发布问题转移到机器学习问题中, 减少了查询集之间的相关性, 同时对新的输入查询进行预测.
k-匿名与差分隐私是两种常用的轻量级匿名术. 在k-匿名中, 节点被重新识别的概率最多为1/k, 数据发布者可以通过调整k值的大小来调整匿名数据集的信息损失以及所能达到匿名程度. 数据所有者可以利用k-匿名技术修改图结构, 然后发布匿名后的图用于图数据挖掘以及分析[17-20]. 使用差分隐私对图数据进行扰动, 可以最大限度地提高对统计值的查询精度, 同时, 通过添加特定的噪音, 可以最大限度地降低识别出个体的概率[21-23]. 与k匿名技术不同, 差分隐私技术具有数学证明来保证其安全性. 然而, 当在图数据上使用差分隐私时, 因为差分隐私只支持有限的统计值, 这就限制了其在高级数据挖掘中的操作. 相比之下, k匿名的安全性很容易证明, 通过要求共享数据中存在一定数量(
最近的研究表明, 如果攻击者拥有目标节点的度、邻居或子图等背景知识信息, 则可以通过实施1-邻居攻击以较大的概率在匿名图中重新识别出目标节点. Zhou等人[25]利用k-邻居匿名技术, 使得每个节点的1-邻居图与其他k–1个节点的1-邻居图同构, 能够较好地抵御1-邻居攻击. Liu等人[26]为了抵抗1-邻居攻击, 同时保持发布图的高可用性, 提出了一种启发式不可区分群体匿名化方案, 在真实和合成数据集上取得了较好的效果.
但是, 在多数k-邻居匿名方案中, 未充分利用待修改图中节点1-邻居图之中的相似性. 导致匿名后的图可用性较低, 或者在针对度分布比较特殊的图进行修改时, 鲁棒性较差. 针对以上问题, 本文提出了一种基于KL散度的社会网络数据匿名案. 与传统方案相比, 本方案通过在粗划分过程中考虑同类节点之间的度差异, 初步将同一类中大多数节点匿名前后的度改变量控制在一个较小的范围内; 使用类的平均度与平均聚类系数来定义类距离, 可以反映出类中节点的平均度以及1-邻居图的聚集程度, 在合并过程中考虑待合并类与其上下类的类距离, 使得同一类中的节点具有相似的度以及1-邻居结构; 在类拆分时使用节点的1-邻居特征分布来代表节点的1-邻居结构特征, 使用概率分布来对节点的1-邻居特征进行建模, 通过KL散度反映类中任意两节点的1-邻居特征分布相互拟合所产生的信息损耗, 将1-邻居分布最相似的节点拆分为同一类, 来充分利用节点1-邻居结构的相似性, 使得本方案修改后的图可用性较高.
1 相关定义定义1 (1-邻居图). 给定图的节点集
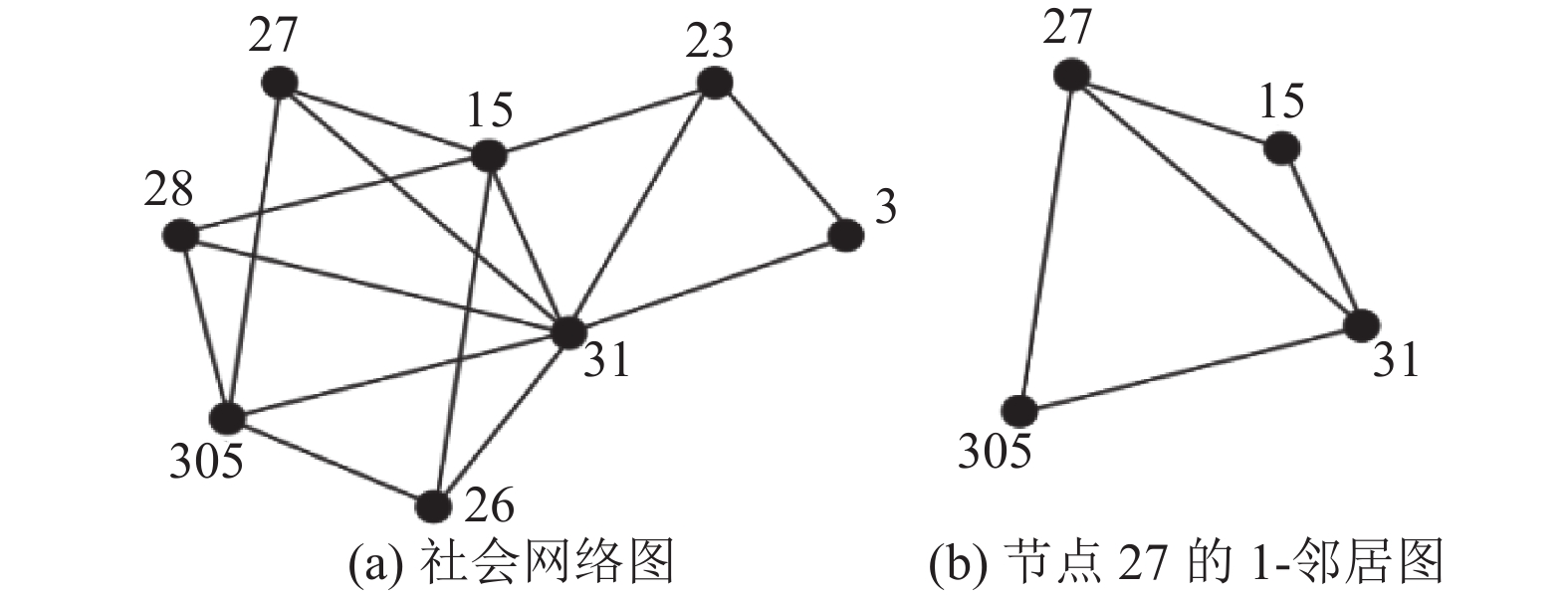
|
图 1 1-邻居示意图 |
定义2 (1-邻居攻击). 给定图
定义3 (聚类系数). 给定图
| $ {C_u} = \frac{{2E(u)}}{{k(u)(k(u) - 1)}} $ | (1) |
本文从提高数据可用性, 降低信息损失量等方面出发, 提出了一种基于KL散度的社会网络数据匿名方案. 该方案主要分为4步: (1)粗划分. 将度差值小于
本方案通过k匿名来进行隐私保护, 首先对原始节点集进行粗划分, 将节点按度值从大到小排序, 从度最大的节点开始, 将度差值小于
定义4 (类距离Dist(C1, C2, W1, W2)). 类与类之间的度与聚类系数加权距离. 为了衡量两个类之间的相似程度, 使得待合并的小数量类能够加入最相近的类中, 本方案使用类与类之间平均聚类系数与平均度加权求和之后的差来衡量类之间的距离, 其值可用式(2)计算出:
| $ \begin{split} Dist =& {W_1} \times \frac{{|AVGD({C_1}) - AVGD({C_2})|}}{{AVGD({C_1})}} \\ &+ {W_2} \times \frac{{|AVGC({C_1}) - AVGC({C_2})|}}{{AVGC({C_1})}} \end{split} $ | (2) |
其中,
定义5 (类指针
完成粗划分后, 同一类中节点之间的度差值小于一个预设值
算法1. 类合并
输入: 待修改图G, k匿名值k, 度差值在合并时所占权重W1, 聚类系数在合并时所占权重W2, 粗划分得到的类集合M
输出: 若干个节点数量大于k的集合P
1) for each class in M
2) BC←Before(M,C);
3) AC←After(M, C);
//获得当前类C的上一类BC和下一类AC
4) if len(C) < k
5) TOP←Dist(C, BC
6) SUB←Dist(C,AC,W1, W2);
//获得当前类C与上下类BC和AC的度与聚类系数的加权距离
7) if TOP < SUB
8) Add(BC,C);
9) else
10) Add(AC,C);
11) end for
12) return P
2.3 类拆分定义6
| $ KL({L_i}, {L_j}) = \frac{1}{2}\left(\sum\limits_{t = 1}^n {{P_{it}} \times \log \frac{{{P_{it}}}}{{{P_{jt}}}}}+ \sum\limits_{t = 1}^n {{P_{jt}} \times \log \frac{{{P_{jt}}}}{{{P_{it}}}}} \right) $ | (3) |
其中, Li和Lj是同一类中两个节点的1-邻居度特征分布, n为Li和Lj中节点个数的最大值,
完成类合并后, 类集合P中每一个类中节点的数量都大于k. 其中节点个数在k到2k–1之间的类, 由于本文使用类距离作为合并标准, 使用平均度保证了在同一类中的节点邻居数量相似, 同时, 采用平均聚类系数保证了同一类中节点的1-邻居图具有相似的聚集程度, 因此, 在同一类中的节点具有相似的1-邻居结构, 满足k匿名需求. 为了使处理后的图满足k匿名, 使得每个类中的节点数量满足
下面给出类拆分的具体流程: (1)寻找节点数量大于2k–1的类. (2)使用节点1-邻居图的3种度分布(节点在整个网络中的度、节点在1-邻居图中的度、整个网络中的度与1-邻居图中的度的差值)的组合来表示节点的1-邻居度分布特征. (3)对于同一类中的节点, 使用KL散度计算节点1-邻居分布之间差异程度, 得到差异化矩阵S, 使用1–S得到同类节点之间的相似度矩阵M. 矩阵中i行j列的值M[i][j]代表了同类节点i与j之间的相似程度. (4)在相似度矩阵中寻找最大值. 最大值在矩阵中的行列值即为当前类中最相似的节点对. 将最相近的节点对放入新的类New[num]中. 将矩阵中的最大值对应的行与列赋值为最小值, 重复步骤(4), 直到新类New[num]中节点数量大于k, 或相似度矩阵中最大值与最小值相等. (5)若新类New[num]中节点的数量大于k, 令num加一, 创建新的类New[num], 重复步骤(4). (6)若相似矩阵中的最大值与最小值相等, 则说明拆分已经完成. 类拆分和相似度矩阵生成的具体算法如算法2.
算法2. 类拆分
输入: 合并完后类的集合
输出: 划分好的类的集合
1) for each Class in P
2) num = 0;
3) if len(Class) > 2 k – 1
4) L←Generate(Class);
//生成同一类节点的1-邻居图度分布列表L
5) Matrix←Sim(L,len(Class));
//使用算法3生成相似度矩阵
6) Min←min(Matrix);
7) Max←max(Matrix);
8) while(Min!=Max)
9) (i,j)←Index(Matrix,Max);
//找出最大值所对应的行列值
10) if len(C[num]) < k
11) Add(C[num]
12) Setcr(Matrix,Min);
//将矩阵第i行和第j列设为最小值
13) else
14) num = num + 1;
//在类集合中选择下一个空的新类
15) Add(C[num], Class[i], Class[j]);
16) Setcr(Matrix, Min);
17) end for
18) return C
算法3. 相似度矩阵生成
输入: 同一类节点的1-邻居图特征分布列表L, 类中的节点个数length
输出: 相似度矩阵Matrix
1) for i in range(length)
2) for j in range(i+1, length)
3) Matrix[i][j]←KL(Li,Lj);
4) End for
5) Min←min(Matrix);
6) Matrix←Setlowertriangle(Min);
//将矩阵下三角全部设置为最小值
7) Matrix←(1–Matrix);
//使用一个上三角除对角线部分元素全为1的矩阵减去矩阵Matrix, 得到相似度矩阵Matrix
8) return Matrix
如算法2所示, 类拆分的过程包括4个部分: 1)相似度矩阵生成; 2)相似度矩阵最大值与最小值的查找; 3)寻找最大值所对应的节点对, 将其加入长度小于k的新类中; 4)将矩阵中最大值所对应的行与列设置为最小值. 下面详细介绍这4个部分的处理过程.
步骤1. 相似度矩阵生成
对于合并完的类集合P, 有
| $\left\{ { \begin{split} &{L_1} = \{ d|d = {d_G}(y), y \in V({G_N})\}\\ &{L_2} = \{ d|d = {d_{{G_N}}}(y), y \in V({G_N})\}\\ & {L_3} = \{ d|d = {d_G}(y) - {d_{{G_N}}}(y), y \in V({G_N})\} \end{split}} \right.$ |
其中,
| $ \begin{split} {sim}=&\left(\begin{array}{cccc} 0 & 1 & \cdots & 1 \\ \vdots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & 1\\ 0 & \cdots & \cdots & 0 \end{array}\right)\\ -& I[i]\left(\begin{array}{cccc} 0 & K L_{i}\left(L_{0}, L_{1}\right) & \ldots & K L_{i}\left(L_{0}, L_{n}\right) \\ \vdots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & K L_{i}\left(L_{n-1}, L_{n}\right) \\ 0 & \cdots & \cdots & 0 \end{array}\right) \end{split}$ | (4) |
其中,
步骤2. 矩阵最大值与最小值的查找
在本步操作中, 由相似矩阵的计算过程可知, 相似矩阵的最大值对应的行列值, 是同类中最相似的节点对的坐标.
步骤3. 寻找最大值所对应的节点对, 将其加入长度小于k的新类中
在本步操作中, 获得最大值所对应的节点对, 需要将其加入同一个类中, 这时在新类的构造时, 为了使匿名后的图满足k匿名, 需要类中的节点数量在k到2k–1的范围之内, 所以当上一个类中的节点数量大于k时, 需要创建新的类来加入当前的节点对.
步骤4. 将矩阵中最大值所对应的行与列设置为最小值
上面的操作已经将矩阵最大值所对应的节点对加入新的类中, 所以在下面进行循环的过程中, 最大值所对应的行与列已经不存在于待拆分的类中. 如图2所示, 将相似度矩阵最大值所对应的行与列设置为矩阵的最小值, 在后面的循环中就不再考虑这些元素, 当矩阵所有的元素都为最小值时, 说明当前类已经拆分完成, 退出循环.

|
图 2 相似矩阵变化 |
2.4 图修改
完成类拆分后, 每一个类中都有(k, 2k–1)个节点, 要实现k匿名, 同时实现同一类中节点的1-邻居图之间具有概率不可区分性, 需要对在同一类中的每个节点的1-邻居图进行图修改, 使得同类中每个节点的1-邻居图同构, 从而抵御1-邻居攻击. 以下是图修改的流程: (1)对于类集合中的每一个待修改类, 寻找类中度最大的节点Max. (2)对于当前待修改类中的每一个节点, 调用最优图编辑距离算法, 获得当前节点所对应的1-邻居图与Max节点所对应的1-邻居图同构的节点与边修改序列. (3)根据修改序列, 将当前节点所对应的1-邻居图中的节点与边进行增删操作, 完成子图重构. (4)当类集合中所有类的节点所对应的1-邻居图完成重构操作后, 返回修改后的图G*. 图修改的算法如算法4.
算法4. 图修改
输入: 待修改的图G, 划分好的类的集合
输出: 修改后的图G*
1) for each Class in C
2) Max←max(Class);
//寻找同一类中度最大的节点
3) for each node in Class
4) Edit_list←OEP(G, node, Max);
//使用optimize_edit_path算法计算使节点node的1-邻居图与节点Max的1-邻居图同构的修改序列
5) G_mo(G, Edit_list, node);
//根据修改序列对节点node进行图修改
6) end for
7) end for
8) return G*
在本步操作中, 使用每个节点所对应的修改序列, 对原图中节点的1-邻居图进行相应的修改, 使得节点所在的1-邻居图与最大度节点所在的1-邻居图同构. 如图3所示为节点232修改前后的拓扑图, 修改后节点232的1-邻居图与Max节点1-邻居图同构.
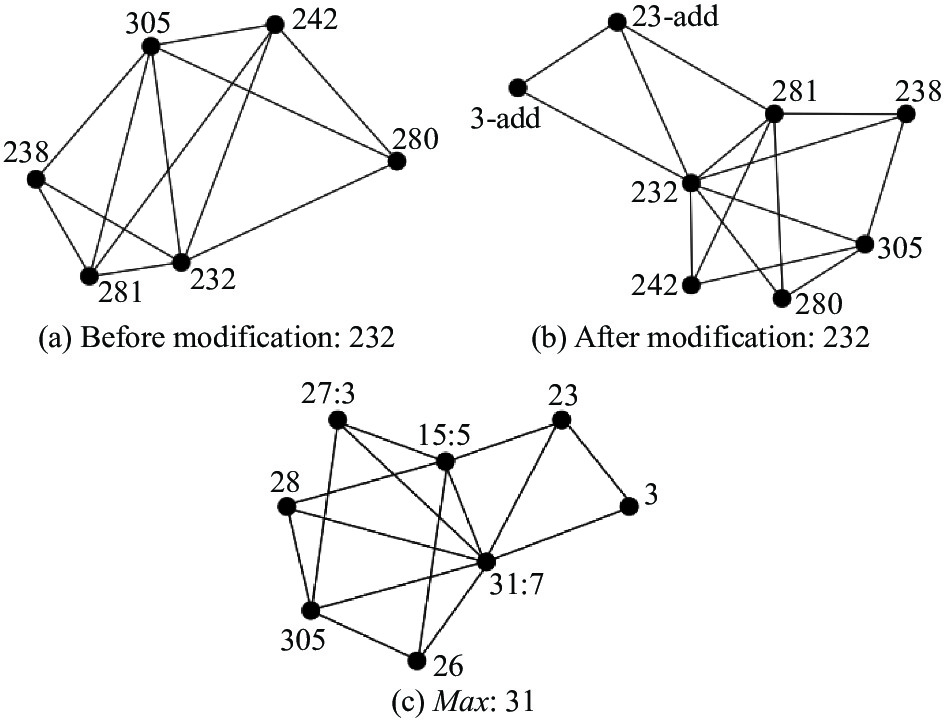
|
图 3 1-邻居图修改 |
3 实验分析
实验采用真实数据集email-Enron、ca-CondMat、ca-HepTh和ego-Facebook. 这4个真实数据集来自于斯坦福大学大型网络数据集(
本节分析了可能的隐私攻击手段以及本方案对此类攻击的抵挡能力.
(1)攻击者已知目标节点的邻居节点数.
在子图同构的过程中, 本方案会使同一类中每个节点的1-邻居图与度最大节点的1-邻居图同构, 所以在每一类处理完成后, 同一类中每个节点的度值与当前类中度最大节点的度值相同, 因此也满足k度匿名, 使得攻击者从匿名图G*中重新识别出目标节点的概率不超过1/k.
(2)攻击者拥有原图中目标节点的1-邻居图结构信息.
攻击者使用原始图中节点t的1-邻居图结构G(t)(攻击者的背景知识), 尝试从发布的匿名图G*中重新识别出目标图G*(t), 可以知道G*(t)一定属于一个概率不可区分的组合g, 其中
由此可知, 本方案对于度攻击以及1-邻居攻击具有较好的抵抗性. 能够在攻击者拥有目标节点度以及1-邻居结构的背景知识之下, 保护目标节点的隐私.
3.2 数据可用性分析本文通过衡量平均度(AVE)改变量、平均聚类系数(ACC)改变量、平均最短路径(APL)改变量来衡量匿名前后图结构数据的变化程度, 其变化越小, 说明数据可用性越好. 如表1所示, 本文分析了随着k值(每一个概率不可区分的组合中节点数量的大小)从5变化到25 (隐私要求越来越高), 本方案在不同数据集上关于结构可用性保持情况方面的表现. 第1行为图的名称; 第2行分别为: (1)平均度(AVE); (2)平均聚类系数(ACC); (3)平均最短路径(APL). 下一行为原始图中的各项指标大小, 下面各行为k取不同值的情况下, 匿名图各项指标的大小. 此表分析了匿名程度不同情况下, 匿名前后图可用性的变化. 可以看出, 随着k的增加, 匿名图的可用性会呈降低趋势, 本方案通过在类划分过程中对同类节点之间的相似度进行控制, 使得修改前后图的结构可用性得到了较好的保证.
| 表 1 匿名图的可用性测试 |
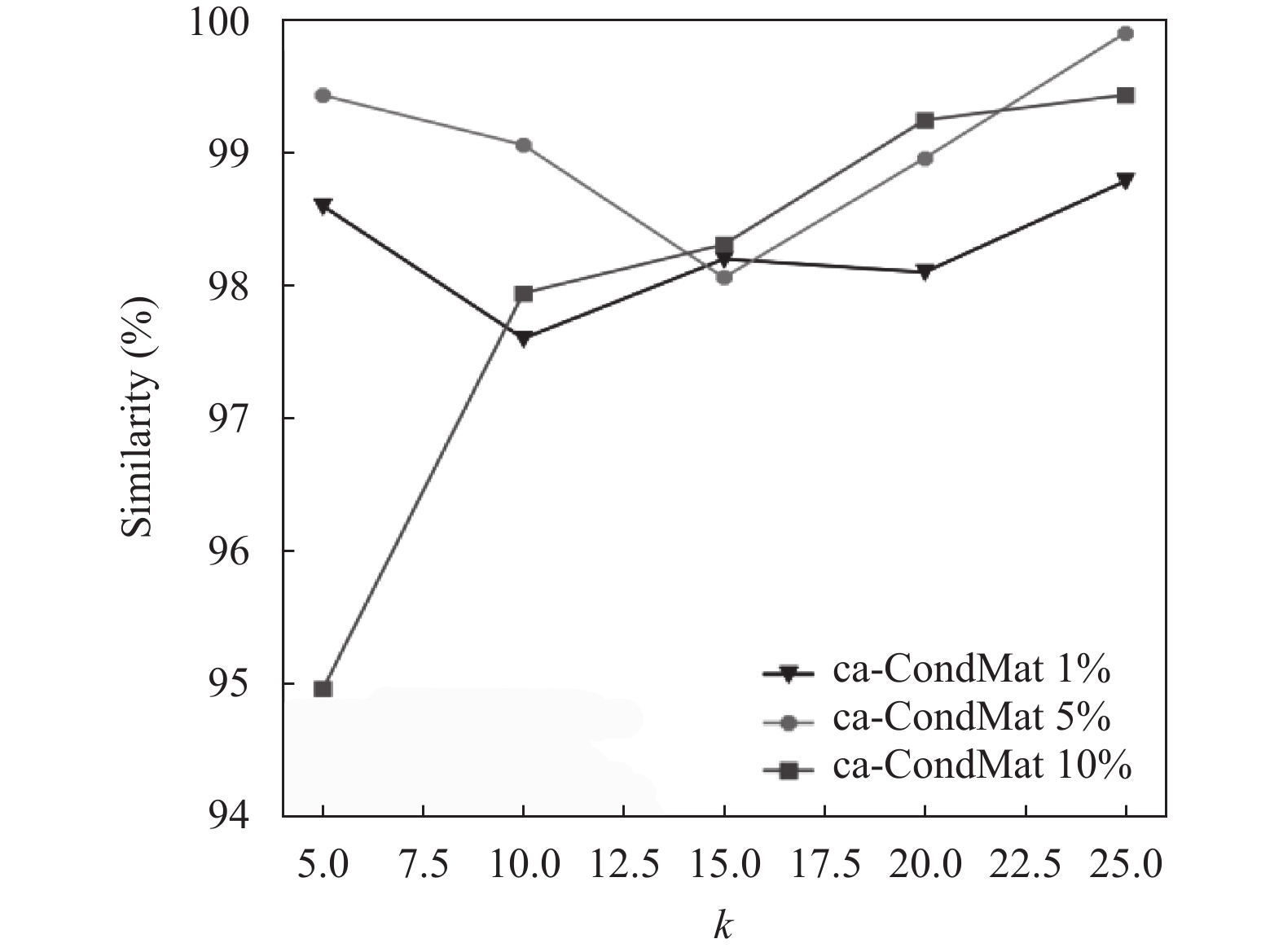
图4–图7表示在修改后的图中度值排在前1%、5%、10%的节点集与原图中度值在前1%、5%、10%的节点集的重合度, 可以看出随着k值的增加, 重合度不会发生很大的变化, 大多保持在95%以上. 因此可知, 使用本方案进行匿名能够以很大的概率保留在原图中比较重要的节点.
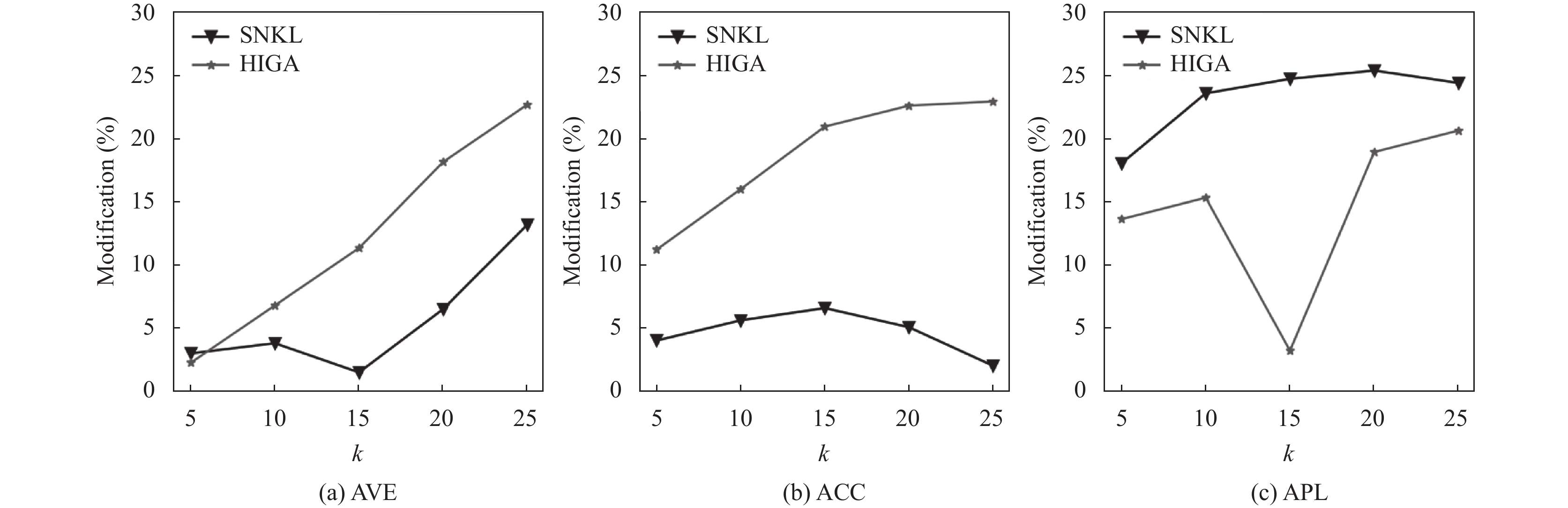
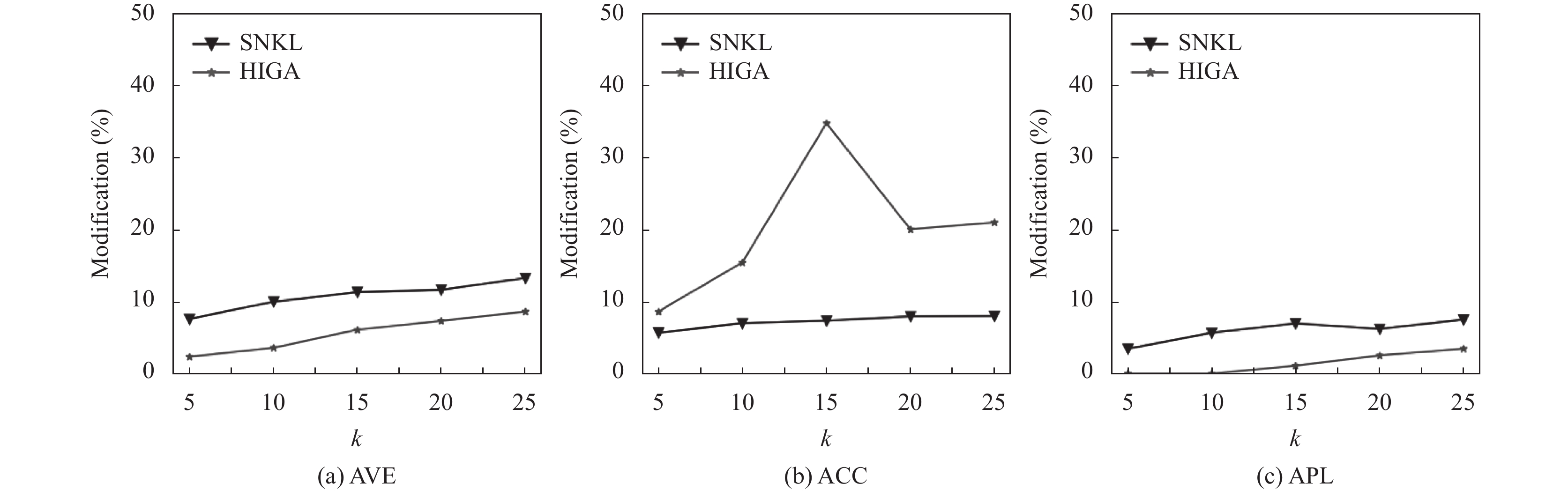
图8和图9分析了本方案与Liu等人[26]的HIGA匿名方案关于匿名后图可用性的对比. 可以发现, 两种方案随着k值的增加, 对原始图各项指标改变的百分比都是呈现出上升趋势, 在Facebook数据集上, HIGA模型生成的匿名图可用性随着k的增大迅速下降, 不能够保证匿名图的可用性, 这是因为Facebook数据集的度分布十分不平衡, 存在着少量且度数相差较大的大度节点, 同时存在着大量的十分密集的小度节点, 这就使得HIGA模型在对这种度分布差异较大的图进行修改时, 需要大量的修改才能保证匿名程度. 本方案在对节点进行分类时, 考虑了1-邻居节点的分布特征, 保证了在同一类中的节点拥有相同的结构特征, 同时在进行修改时, 将同一节点的1-邻居图修改成同构, 在一定程度上保留了节点本身的结构特征, 因此对原图的结构破坏较小, 保留了较高的可用性, 对于类似Facebook这种度分布十分不均匀的图, 也具有很好的鲁棒性. 对于平均聚类系数指标, 与HIGA方法相比, SNKL方法在聚类系数上的改变量平均降低了17.3%, 对于平均度与平均最短路径指标, SNKL方法与HIGA方法相差较小, 因此使用SNKL方法进行数据匿名, 可以在保证隐私的前提下, 使得匿名后图的结构特征得到更好的保留.

|
图 4 Facebook保持百分比 |
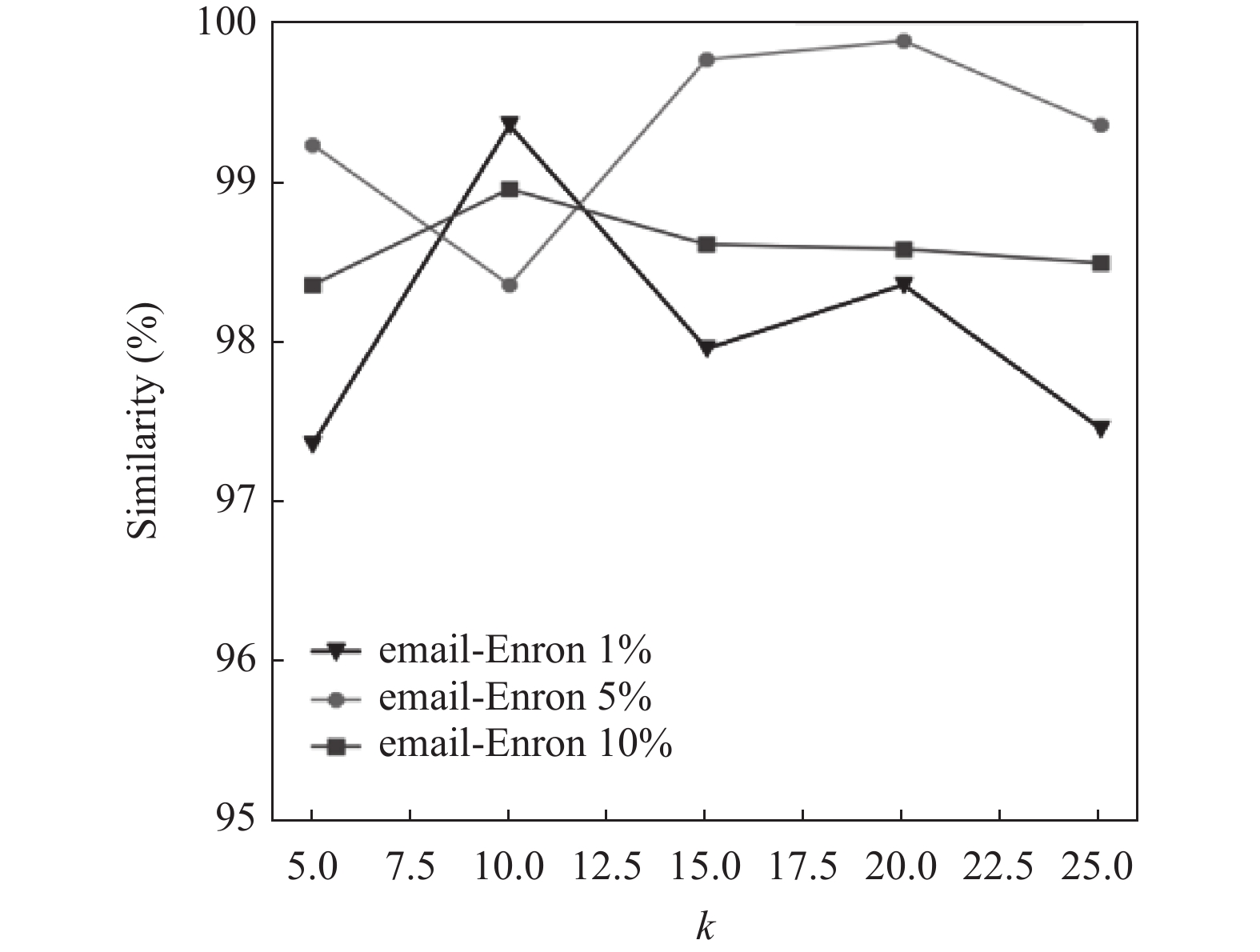
|
图 5 email-Enron保持百分比 |
4 结语
本文研究了社会网络中用户的匿名问题, 并提出了一种基于节点1-邻居图相似性的社会网络数据匿名方案. 该方案通过对1-邻居结构相似的节点集进行修改, 实现同类中的节点之间近似同构, 使得拥有在原图中目标节点1-邻居结构这种背景知识的攻击者在匿名后的图中成功识别出目标节点的概率不会超过1/k, 从而实现群体化匿名. 同时该算法在进行类合并和类划分时, 考虑了同类节点间的结构特征, 使得修改后的图也会保留主要的特征结构, 减少了信息损失. 实验结果表明, 该算法在实现群体化匿名的同时, 还保留了较高的可用性. 下一步可以考虑对类似于Facebook这种度分布十分不均匀的图, 分析其独特的分布趋势, 将数量较少的大度节点单独处理, 在实现匿名的同时减少修改量, 进一步提高匿名图的可用性.
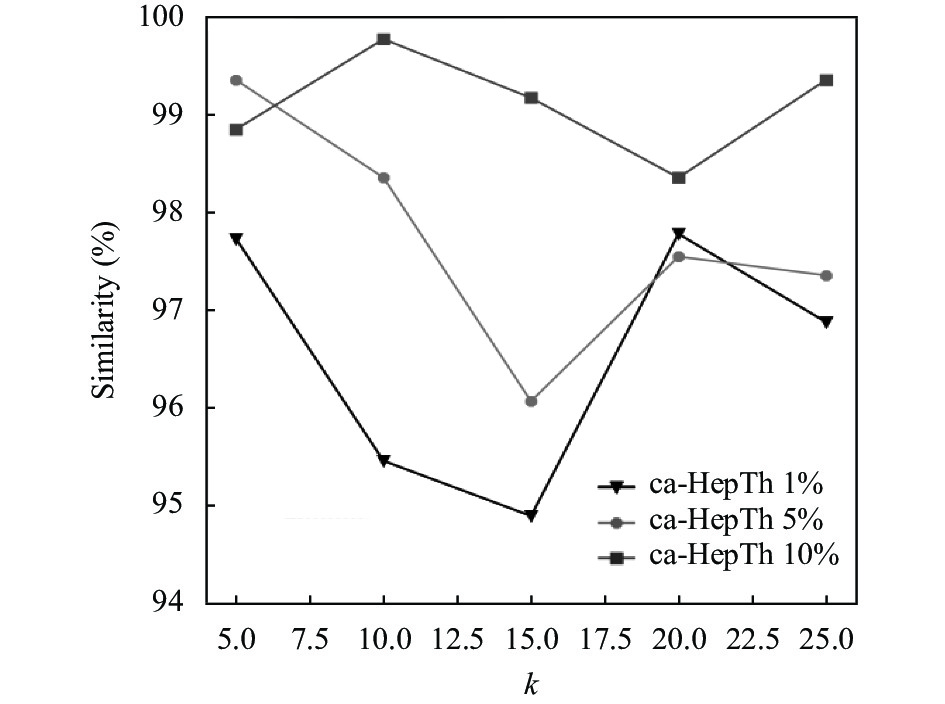
|
图 6 ca-HepTh保持百分比 |
|
图 7 ca-CondMat保持百分比 |
|
图 8 Facebook可用性对比 |
|
图 9 ca-CondMat可用性对比 |
| [1] |
Banerjee S, Jenamani M, Pratihar DK. A survey on influence maximization in a social network. Knowledge and Information Systems, 2020, 62(9): 3417-3455. DOI:10.1007/s10115-020-01461-4 |
| [2] |
Ji SL, Li WQ, Srivatsa M, et al. General graph data de-anonymization: From mobility traces to social networks. ACM Transactions on Information and System Security, 2016, 18(4): 12. |
| [3] |
Liu Y, Ma Z, Liu XM, et al. Privacy-preserving object detection for medical images with faster R-CNN. IEEE Transactions on Information Forensics and Security, 2022, 17: 69-84. DOI:10.1109/TIFS.2019.2946476 |
| [4] |
Chen C, Wu BZ, Wang L, et al. Nebula: A scalable privacy-preserving machine learning system in ant financial. Proceedings of the 29th ACM International Conference on Information & Knowledge Management. ACM, 2020. 3369–3372.
|
| [5] |
Ye AY, Jin JL, Yang ZJ, et al. Evolutionary game analysis on competition strategy choice of application providers. Concurrency and Computation Practice and Experience, 2021, 33(8): e5446. |
| [6] |
Ozalp I, Gursoy ME, Nergiz ME, et al. Privacy-preserving publishing of hierarchical data. ACM Transactions on Privacy and Security, 2016, 19(3): 7. |
| [7] |
Sweeney L. k-Anonymity: A model for protecting privacy
. International Journal of Uncertainty, Fuzziness and Knowledge-based Systems, 2002, 10(5): 557-570. DOI:10.1142/S0218488502001648 |
| [8] |
Meng XR, Kamara S, Nissim K, et al. GRECS: Graph encryption for approximate shortest distance queries. Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. Denver: ACM, 2015. 504–517.
|
| [9] |
Ding XF, Liu P, Jin H. Privacy-preserving multi-keyword top-k similarity search over encrypted data
. IEEE Transactions on Dependable and Secure Computing, 2019, 16(2): 344-357. DOI:10.1109/TDSC.2017.2693969 |
| [10] |
马苏杭, 龙士工, 刘海, 等. 面向高维数据发布的个性化差分隐私算法. 计算机系统应用, 2021, 30(4): 131-138. DOI:10.15888/j.cnki.csa.007870 |
| [11] |
Dwork C. Differential privacy. Proceedings of the 33rd International Colloquium on Automata, Languages and Programming. Venice: Springer, 2006. 1–12.
|
| [12] |
Ding XF, Wang C, Choo KKR, et al. A novel privacy preserving framework for large scale graph data publishing. IEEE Transactions on Knowledge and Data Engineering, 2021, 33(2): 331-343. |
| [13] |
许佳钰, 章红艳, 许力, 等. 社会网络中基于节点平均度的k-度匿名隐私保护方案
. 计算机系统应用, 2021, 30(12): 308-316. DOI:10.15888/j.cnki.csa.008230 |
| [14] |
黄海平, 王凯, 汤雄, 等. 基于边介数模型的差分隐私保护方案. 通信学报, 2019, 40(5): 2019095. |
| [15] |
Huang HP, Zhang DJ, Xiao F, et al. Privacy-preserving approach PBCN in social network with differential privacy. IEEE Transactions on Network and Service Management, 2020, 17(2): 931-945. DOI:10.1109/TNSM.2020.2982555 |
| [16] |
Zhu TQ, Xiong P, Li G, et al. Differentially private model publishing in cyber physical systems. Future Generation Computer Systems, 2020, 108: 1297-1306. DOI:10.1016/j.future.2018.04.016 |
| [17] |
Casas-Roma J, Herrera-Joancomartí J, Torra V. A survey of graph-modification techniques for privacy-preserving on networks. Artificial Intelligence Review, 2017, 47(3): 341-366. DOI:10.1007/s10462-016-9484-8 |
| [18] |
Huang XZ, Liu JQ, Han Z, et al. Privacy beyond sensitive values. Science China Information Sciences, 2015, 58(7): 1-15. |
| [19] |
Mahanan W, Chaovalitwongse WA, Natwichai J. Data privacy preservation algorithm with k-anonymity
. World Wide Web, 2021, 24(5): 1551-1561. DOI:10.1007/s11280-021-00922-2 |
| [20] |
Singh A, Singh M, Bansal D, et al. Optimised K-anonymisation technique to deal with mutual friends and degree attacks. International Journal of Information and Computer Security, 2021, 14(3–4): 281-299. |
| [21] |
Liu F. Generalized Gaussian mechanism for differential privacy. IEEE Transactions on Knowledge and Data Engineering, 2019, 31(4): 747-756. DOI:10.1109/TKDE.2018.2845388 |
| [22] |
Wang Q, Zhang Y, Lu X, et al. Real-time and spatio-temporal crowd-sourced social network data publishing with differential privacy. IEEE Transactions on Dependable and Secure Computing, 2018, 15(4): 591-606. |
| [23] |
Backes M, Berrang P, Humbert M, et al. Membership privacy in microrna-based studies. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. Vienna: ACM, 2016. 319–330.
|
| [24] |
张强, 叶阿勇, 叶帼华, 等. 最优聚类的k-匿名数据隐私保护机制. 计算机研究与发展, 2022, 59(7): 1625–1635.
|
| [25] |
Zhou B, Pei J. The k-anonymity and l-diversity approaches for privacy preservation in social networks against neighborhood attacks
. Knowledge and Information Systems, 2011, 28(1): 47-77. DOI:10.1007/s10115-010-0311-2 |
| [26] |
Liu Q, Wang GJ, Li F, et al. Preserving privacy with probabilistic indistinguishability in weighted social networks. IEEE Transactions on Parallel and Distributed Systems, 2017, 28(5): 1417-1429. DOI:10.1109/TPDS.2016.2615020 |
 2022, Vol. 31
2022, Vol. 31


