2. 南京信息工程大学 江苏省大气环境与装备技术协同创新中心, 南京 210044
2. Jiangsu Provincial Collaborative Innovation Center of Atmosphere Environment and Equipment Technology, Nanjing University of Information Science and Technology, Nanjing 210044, China
在我国, 鸟类资源十分丰富, 鸟类又是对栖息地和周围环境变化十分敏感的一种生物[1]. 对一个地方特定鸟类的检测, 记录其初鸣, 终鸣可以来反应当地的气候变化. 随着未来几年气候变化和土地利用的影响, 栖息地内鸟类的分布预计会在数量和密度上发生变化[2]. 以往通过人工对鸟类检测通常采用的环志站的方式, 但是进行连续不间断的检测往往很困难而且这种入侵式检测往往会破坏生态影响鸟类而且在高山, 荒漠, 沼泽这类危险地区, 人工检测又十分困难. 考虑到鸟鸣声与鸟类的形态特征都是重要的生物学特征, 而且鸟声信号不会受到视野影响, 不同种类的鸟之间的声音特征也各不相同, 通过低成本的嵌入式系统[3-12]记录鸟鸣声, 对它做信号分析可以捕捉到丰富信息能够作为鸟声识别的重要依据. 近年来, 国内的语音识别研究方向主要为人的语音识别, 在鸟类声音识别方面比较少. 对于鸟声识别, 提取合适的语音特征是难点. 根据目前语音识别研究, 语音的倒谱参数包含的信息较多[13], 是目前采用最多的语音特征参数, 其中梅尔倒谱系数(MFCC)[14-18]和线性预测倒谱系数(LPCC)[15]这两种应用广泛. MFCC与LPCC不同的是, MFCC是模拟人耳的听觉系统, 这不仅充分考虑了人类的听觉特能力, MFCC参数具有较好的鲁棒性[19-25], 在研究鸟类叫声与蛙类叫声的识别研究中, MFCC特征参数也表现出良好的性能. 文献[16]提出一种改进的 MFCC 算法, 是通过对鸟鸣声进行经验模态分解得到固有的模态函数后再进行快速傅里叶变换, 得到改进后到的MFCC参数结合高斯混合模型就行分类识别. 未改进的算法相比识别率提高了3.42%. 文献[17] 综合基于音节长度、梅尔频率倒谱系数, 基于线性预测编码(LPCC)系数等多种特种, 在分类算法上集成多种算法, 最终对11类的鸟鸣声样本识别能实现92%的准确率.
认知科学领域的最新研究成果表明, 多个不同频带的信息对于鸟鸣的感知识别尤为重要[18]. MFCC描述的是语音在频率上的能量分布, 通过使用连串的三角滤波器组来获得声音在频域的特征. 但是由于MFCC特性是的滤波器组在低频范围内分布数量多, 交叉密集而在高频范围内分布稀疏造成MFCC特征对语音高频部分信息表征不足, 影响后续分类算法的准确度. 针对这一不足, 本文采用基于Fisher值的MFCC和翻转梅尔倒谱系数(IMFCC)[15]特征融合弥补MFCC特征在高频表征信息不足的缺陷, 更好的表征鸟声信息. 并使用遗传算法优化支持向量机对特征训练. 实验表明, 特征融合后的参数提高了鸟声识别正确率.
1 特征提取 1.1 MFCC提取梅尔倒谱系数是根据人耳的听觉特性, 相较于高频的语音信号, 人耳对于低频语音信号有更强的感知力. 梅尔值是一种新的量度, 相较于常用的频率机制, 它更加趋近于人耳的听觉系统, 当声音频率范围在1 000 Hz以下, 人耳对声音的感知接近于线性关系, 而当频率高于1 000 Hz, 人耳对声音的感知近似于对数关系. 当来到Mel域, 人耳与声音 Mel域的感知近似于线性关系. 如图1所示将频域转化为梅尔域可以看到, 低频范围内的梅尔值增长很快, 而到了高频范围内其增长速度变得很慢. 两种坐标转换关系如式(1):
| $ 1127\cdot \mathrm{ln}(1+{f}_{\rm Hz}/700) $ | (1) |

|
图 1 MFCC尺度变化曲线 |
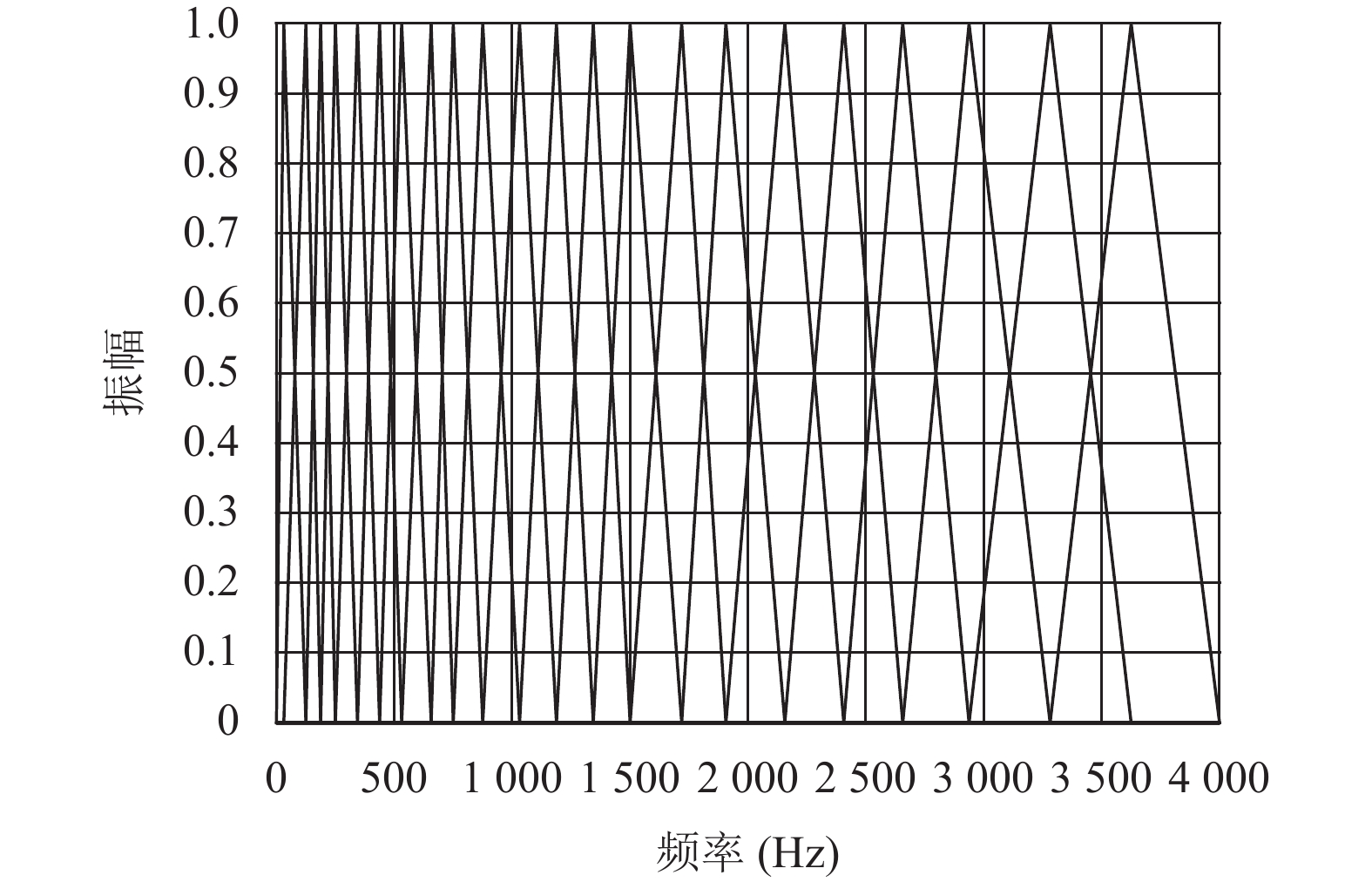
MFCC是通过在Mel域分布均匀的三角带通滤波器组计算出来的, 如图2所示. 由于从频域来看Mel值在低频增长速度快, 而在高频增长缓慢, 导致在1 000 Hz以下的频率范围内, 滤波器组的分布比较密集而到了高频后, 滤波器组分布比较稀疏.
|
图 2 MFCC滤波器组分布情况 |
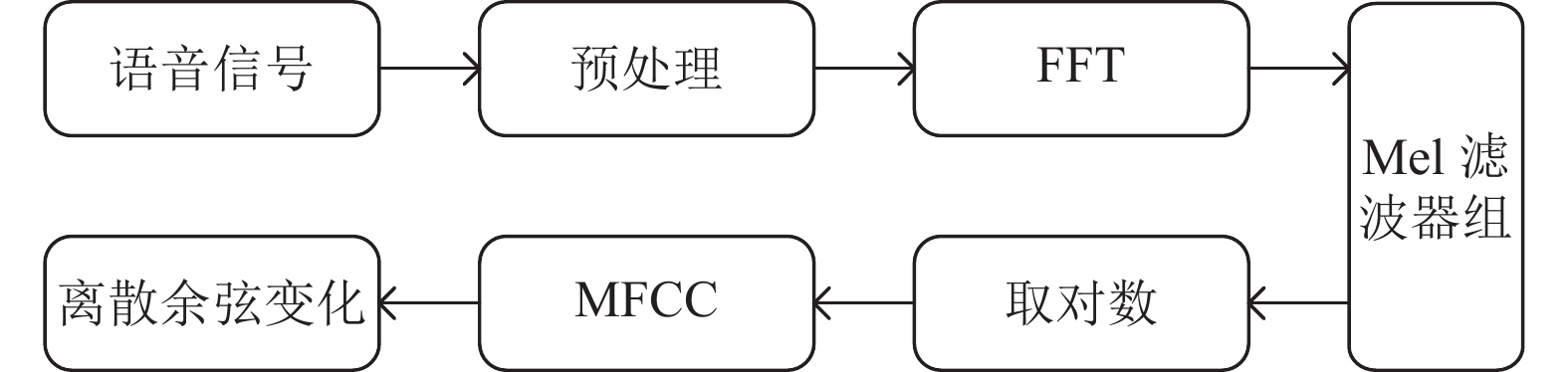
MFCC参数提取流程如下.
① 对语音信号经过分帧, 加窗等预处理, 将一段语音信号分成一系列的语音帧, 然后对这些语音帧做快速傅里叶变换, 如式(2):
| $ Y(k) = \sum\limits_{n = 1}^N {y(n){{\rm e}^{(\frac{{ - j2\pi nk}}{N})}}} $ | (2) |
其中,
对变换后的值取其模的平方得到离散功率谱
② 将步骤①得到的离散功率谱通过三角滤波器组进行滤波, 得到一组滤波系数. 将这组系数作对数运算后进行离散余弦变换如式(3):
| $ {C_n} = \sum\limits_{m = 0}^{M - 1} {S(m)} \cos \left(\frac{{\pi n(m - 0.5)}}{M}\right) $ | (3) |
其中,
|
图 3 MFCC提取过程 |
1.2 IMFCC的提取
上文对于MFCC参数提取过程中, 可以清楚看到由于滤波器组多分布于低频部分, 注重声音信号的低频部分, 而在声音高频部分分布稀疏, 对于声音高频部分信息表征不足. 这就导致了最终提取的MFCC特征参数无法最大程度地表征鸟声. 为了能够充分的表征鸟声的语音信息, 引入了翻转梅尔倒谱系数, 如图4所示将频域转化为Mel域可以看到, 低频范围内的梅尔值增长很慢, 而到了高频范围内增长速度变得很快. IMFCC在Mel刻度与频率的关系如式(4):
| $ {F}_{\rm IMel}=2146.1-1127\cdot \mathrm{ln}\left(1+\frac{4000-{f}_{\rm Hz}}{700}\right) $ | (4) |

|
图 4 IMFCC尺度变化曲线 |
在IMFCC特征参数提取过程中, 频率与Mel转换主要体现在滤波器上面. 如图5所示, IMFCC低频部分滤波器分布稀疏而在高频部分分布密集能够表征高频范围的频谱特征. 除此之外IMFCC提取过程与上文MFCC提取保持一致.

|
图 5 IMFCC滤波器组分布情况 |
2 Fisher比准则特征融合
上文求取的MFCC和IMFCC包含了鸟声的各个频段信息特点, 可以结合到一起来对鸟鸣信号进行描述. 由于对MFCC和IMFCC各取12维, 如果对其简单的叠加就会得到24维语音特征, 在充分表征语音信息的同时, 也会导致信息冗余, 增加后续分类识别算法的计算量. 同时, 不同特征对信号表征的贡献程度各不相同, 所以可以根据特征贡献度的不同, 进行特征选择. 特征选择就是去除贡献度较低的特征, 保留其他的原始特征. 通过计算Fisher score过滤冗余特征.
Fisher score是特征选择有效方法之一. 其主要思想是鉴别性能较强的特征表现为类内距离尽可能小, 类间距离尽可能大. 通过计算各个特征参数的Fisher score来区分他们对语音信息的贡献程度. Fisher score求取如式(5):
| $ {F_{\rm Fisher}} = \frac{{{\sigma _{\rm between}}}}{{{\sigma _{\rm within}}}} $ | (5) |
其中,
| $ {\sigma _{\rm between}} = \sum\limits_{i = 1}^N {{{(m_k^i - {m_k})}^2}} $ | (6) |
| $ {\sigma _{\rm within}} = \sum\limits_{i = 1}^N {\frac{1}{{{n_i}}}} \sum\limits_{c \in {\omega _i}} {{{(c_k^i - m_k^i)}^2}} $ | (7) |
其中,
类间方差
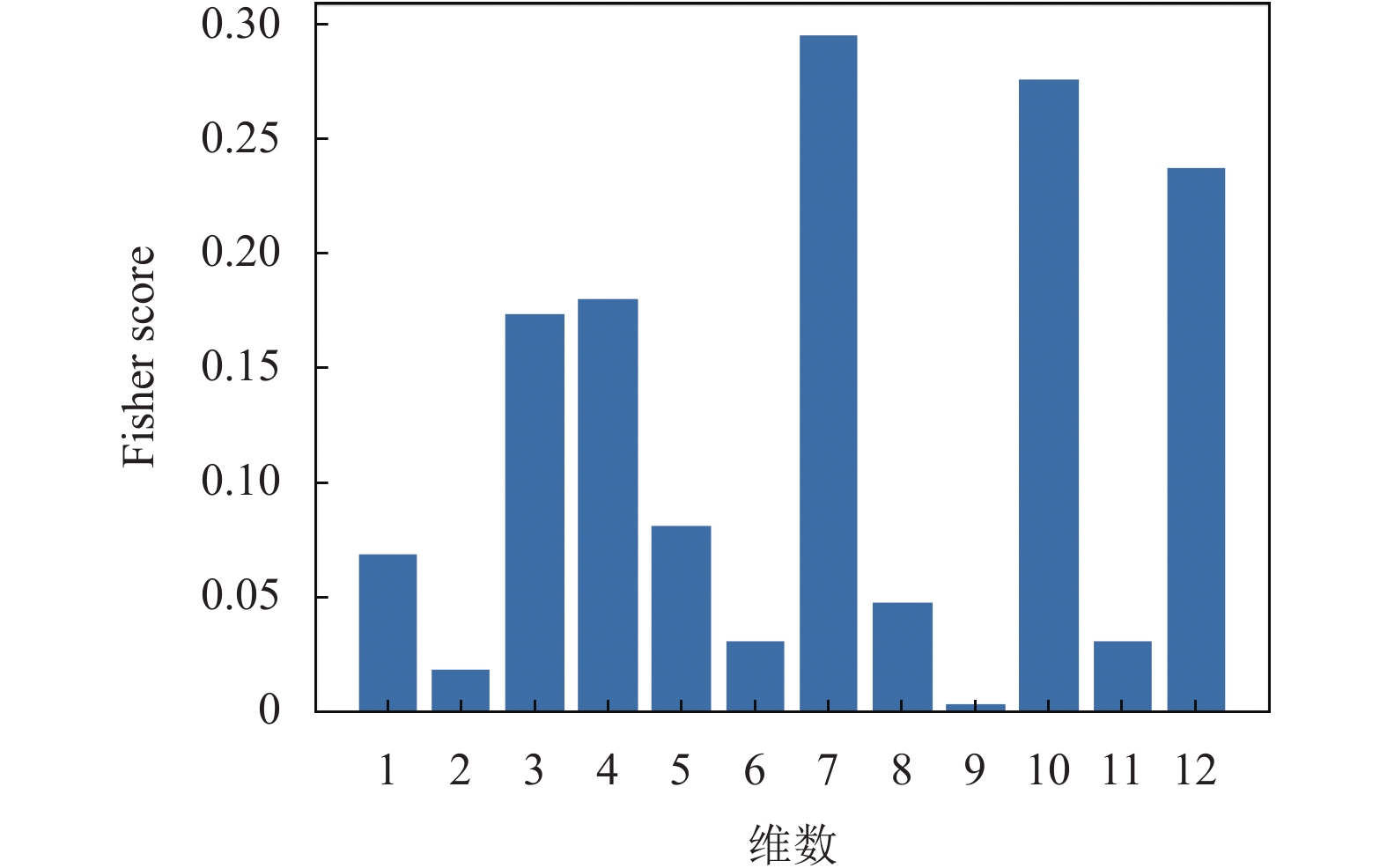
|
图 6 MFCC各维参数的Fisher score |
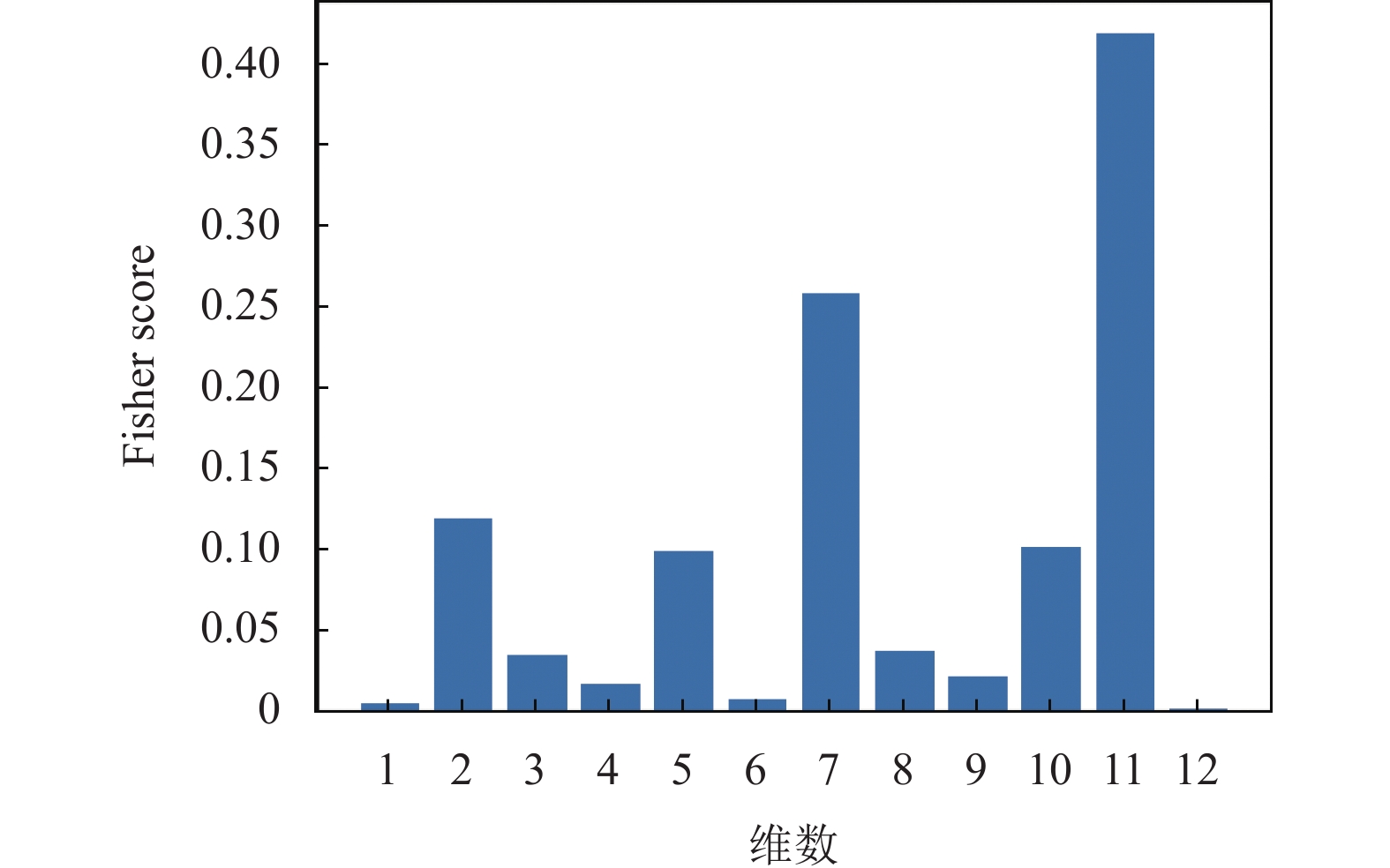
|
图 7 IMFCC各维参数的Fisher score |
3 算法模型优化 3.1 SVM分类模型
智能算法等先进算法[26-43]在信号分离识别中广泛使用. 支持向量机(SVM)是于1995年提出的机器学习算法. SVM是基于统计学理论的, 应用于分类和回归分析, 在语音识别, 图像分类等领域应、应用广泛. SVM分类思想是在将低维, 线性不可分训练样本数据映射到高维空间找到一个超平面, 将样本中不同类别的数据分开, 且使样本数据尽可能远离超平面.
对于训练集
| $ {\omega ^{\rm T}}{x_i} - b = 0,\; i = 1, 2,\cdots, n $ | (8) |
在实际应用中由于使用的数据集不可能很完美, 会出现求得的超平面不能完美地将样本数据精准分类. 我们通常引入松弛因子
| $ \frac{1}{2}||\omega |{|^2} + C\sum\limits_{i = 1}^n {{\zeta _i}} $ | (9) |
为了处理线性不可分的训练样本, 需要使用核函数将样本数据映射到高维空间使其线性可分. 常见的处理样本数据的核函数有线性核函数, 多项式核函数, RBF核函数和Sigmoid核函数. 其中RBF核函数与线性核函数相比能够处理样本标注和属性的非线性关系, 与多项式核函数相比又具有更少参数的优点, 同时和Sigmoid核函数一样具有易使用的优点. 所以RBF核函数应用更广泛. RBF核函数公式为:
| $ K(x, {x_i}) = \exp ( - g||{(x - {x_i})^2}||) $ | (10) |
其中,
| $ g = \frac{1}{{2{\sigma ^2}}} $ | (11) |
使用SVM设计分类器时设计到两个重要的参数惩罚因子
遗传算法是受生物学启发, 用计算机模拟生物界进化方式的一种全局搜索和优化算法. 遗传算法借鉴生物学中的遗传, 变异, 杂交来求取一种最优解法. 其本质是一种高效, 并行的全局搜索方法, 能够在探寻的过程中不断积累相关搜索空间知识, 并且能够自适应的控制搜索过程以求得最优解. 遗传算法搜索效率高, 是以群体为单位对其中的所有个体进行并行搜索, 它不受目标函数影响可以进行全局寻优, 避免了局部最优, 优化步骤如图8.
① 对惩罚因子
② 计算初代种群个体的适应度后对种群进行进化操作: 选择, 充足, 变异, 选择出最优个体保留产生种群知道满足寻优的终止条件.
③ 利用最优

|
图 8 遗传算法流程图 |
将提取好的特征作为训练样本, 使用SVM进行分类训练, 并在此过程中对惩罚因子

|
图 9 参数寻优适应度曲线 |
4 实验与分析
本文实验用的鸟声数据均来自Xeno-canto网站、该网站对于鸟声信号录制均在野外复杂的声学环境下, 时长从数十秒到几分钟不等. 使用Cool Edit对下载下来的鸟声作统一处理, 把每条鸟声记录都转化为采样率为44.1 kHz, 采样精度设置为16 bit, 单声道wav格式, 并且时长统一为2 s. 实验中用到的训练样本集测试样本如表1所示. 实验用到SVM分类算法和遗传算法均使用Python编写平台为PyCharm 2021.
| 表 1 各物种的训练集与测试集 |
在仿真实验过程中, 分别以传统的MFCC, IMFCC和MFCC-IMFCC三种方法提取鸟声特征, 提取后的特征分别在GA-SVM模型和SVM模型进行训练识别, 根据混淆矩阵所得准确率. 其中遗传算法寻优后得到:
| 表 2 SVM和GA-SVM在不同特征下的识别率(%) |
从表2可知, 相比于传统的MFCC改进后的MFCC-IMFCC对于鸟类识别有更好的分类效果, 所有鸟类的识别率都有提升. 通过遗传算法进行参数优化后的支持向量机训练模型(GA-SVM)相比于SVM在识别效果上也均有改进. 表中的紫水鸡较于其他鸟类识别率低, 是因为在下载的样本声音环境更为复杂, 背景声杂.
5 结论本文针对传统MFCC参数在鸟声识别领域上对鸟声信息在高频上描述不全的问题, 利用Fisher准则对MFCC和IMFCC按照对语音贡献程度进行特征选择, 融合出新的特征参数MFCC-IMFCC, 更加全面的表征鸟声信号. 利用遗传算法对支持向量机中的惩罚因子
| [1] |
Gregory RD, Noble D, Field R, et al. Using birds as indicators of biodiversity. Ornis Hungarica, 2003, 12–13: 11–24.
|
| [2] |
斯幸峰, 丁平. 欧美陆地鸟类监测的历史、现状与我国的对策. 生物多样性, 2011, 19(3): 303-310. |
| [3] |
赵苏徽, 陈晓. 基于树莓派和云平台的智能灌溉系统. 计算机系统应用, 2022, 31(4): 123-129. DOI:10.15888/j.cnki.csa.008456 |
| [4] |
陈晓, 张凯. 嵌入式自动气象站故障检测系统研究. 电子测量技术, 2021, 44(23): 158-164. |
| [5] |
荣百川, 陈晓. 基于蓝牙的智能防摔监测系统设计. 激光杂志, 2019, 40(7): 32-34. |
| [6] |
邢玉品, 陈晓. 基于TDC-GP22的超声波测风仪设计. 现代电子技术, 2018, 41(21): 128-131, 136. |
| [7] |
杨应鹏, 陈晓. 基于蓝牙的可穿戴式脉搏波形采集系统设计. 激光杂志, 2018, 39(6): 74-77. |
| [8] |
陈晓. 基于无线通信的激光超声测量系统. 光学学报, 2009, 29(1): 203-207. |
| [9] |
陈晓. 基于无线通信的脉搏信号采集系统. 通信技术, 2008, 41(12): 268-270, 273. DOI:10.3969/j.issn.1002-0802.2008.12.093 |
| [10] |
陈晓. 基于通用串行总线的高速脉搏信号检测系统. 中国组织工程研究与临床康复, 2008, 12(39): 7653-7656. |
| [11] |
陈晓. 基于压电传感器和个人计算机构成的脉搏信号实时监测系统. 中国组织工程研究与临床康复, 2008, 12(35): 6847-6850. |
| [12] |
陈晓. 便携式电子脉搏计的设计. 中国组织工程研究与临床康复, 2008, 12(17): 3349-3352. |
| [13] |
王家盛, 郭其威, 吴松, 等. 基于特征相对贡献度对加权Mel倒谱的改进. 声学技术, 2021, 40(3): 408-414. |
| [14] |
杨瑶, 陈晓. 基于神经网络的说话人识别实验设计. 实验室研究与探索, 2020, 39(9): 38-41, 50. DOI:10.3969/j.issn.1006-7167.2020.09.008 |
| [15] |
Li Q, Yang YZ, Lan TX, et al. MSP-MFCC: Energy-efficient MFCC feature extraction method with mixed-signal processing architecture for wearable speech recognition applications. IEEE Access, 2020, 8: 48720-48730. DOI:10.1109/ACCESS.2020.2979799 |
| [16] |
程龙, 张华清. 基于改进MFCC的鸟鸣声识别方法研究. 中国传媒大学学报: 自然科学版, 2017, 24(3): 41-46. |
| [17] |
徐淑正, 孙忆南, 皇甫丽英, 等. 基于MFCC和时频图等多种特征的综合鸟声识别分类器设计. 实验室研究与探索, 2018, 37(9): 81-86, 91. DOI:10.3969/j.issn.1006-7167.2018.09.020 |
| [18] |
张赛花, 赵兆, 许志勇, 等. 基于Mel子带参数化特征的自动鸟鸣识别. 计算机应用, 2017, 37(4): 1111-1115. DOI:10.11772/j.issn.1001-9081.2017.04.1111 |
| [19] |
陈莎莎, 李应. 结合时-频纹理特征的随机森林分类器应用于鸟声识别. 计算机应用与软件, 2014, 31(1): 154-157, 161. DOI:10.3969/j.issn.1000-386x.2014.01.040 |
| [20] |
王萌, 王福龙. 基于端点检测和高斯滤波器组的MFCC说话人识别. 计算机系统应用, 2016, 25(10): 218-224. DOI:10.15888/j.cnki.csa.005425 |
| [21] |
朱春媚, 黎萍. 基于子带能量变换改进MFCC的咳嗽识别. 计算机工程与应用, 2016, 52(11): 148-151, 157. DOI:10.3778/j.issn.1002-8331.1511-0062 |
| [22] |
Chen GH, Zeng XP. Multi-modal emotion recognition by fusing correlation features of speech-visual. IEEE Signal Processing Letters, 2021, 28: 533-537. DOI:10.1109/LSP.2021.3055755 |
| [23] |
Shi YY, Bai J, Xue PY, et al. Fusion feature extraction based on auditory and energy for noise-robust speech recognition. IEEE Access, 2019, 7: 81911-81922. DOI:10.1109/ACCESS.2019.2918147 |
| [24] |
Ferras M, Leung CC, Barras C, et al. Comparison of speaker adaptation methods as feature extraction for SVM-based speaker recognition. IEEE Transactions on Audio, Speech, and Language Processing, 2010, 18(6): 1366-1378. DOI:10.1109/TASL.2009.2034187 |
| [25] |
王恩泽, 何东健. 基于MFCC和双重GMM的鸟类识别方法. 计算机工程与设计, 2014, 35(5): 1868-1871. DOI:10.3969/j.issn.1000-7024.2014.05.071 |
| [26] |
陈晓, 杨瑶. 基于长期递归卷积网络的无创血压测量. 电子测量技术, 2022, 45(4): 139-146. |
| [27] |
孙超文, 陈晓. 基于多尺度特征融合反投影网络的图像超分辨率重建. 自动化学报, 2021, 47(7): 1689-1700. |
| [28] |
陈晓, 倪龙. 用分数阶微分实现时频重叠多模式兰姆波的模式分离. 声学学报, 2020, 45(2): 205-214. |
| [29] |
任晓晔, 陈晓, 郭妍. 基于Fluent和LSTM神经网络的超声波测风仪阴影效应补偿研究. 计算机应用与软件, 2019, 36(7): 89-98. DOI:10.3969/j.issn.1000-386x.2019.07.016 |
| [30] |
朱娟, 陈晓. 改进胶囊网络的有序重叠手写数字识别方法. 激光杂志, 2019, 40(7): 43-46. |
| [31] |
任晓晔, 陈晓, 郭妍. 超声波测风换能器对风速的影响研究. 电子测量技术, 2019, 42(7): 118-124. |
| [32] |
郭妍, 陈晓, 任晓晔. 一种优化随机森林模型的室内定位方法. 激光杂志, 2018, 39(10): 70-74. |
| [33] |
倪龙, 陈晓. 基于频散补偿和分数阶微分的多模式兰姆波分离. 物理学报, 2018, 67(20): 204301.34.
|
| [34] |
徐畅, 陈晓, 季仟亿. 基于稀疏编码的Shearlet域图像去噪. 激光杂志, 2017, 38(10): 96–100.
|
| [35] |
邹胜男, 陈晓, 陈霞. 基于改进的UKF算法的室内测距定位. 激光杂志, 2017, 38(4): 61-65. |
| [36] |
陈霞, 陈晓, 邹胜男. 基于正态检验的室内定位算法. 激光杂志, 2017, 38(3): 41-45. |
| [37] |
胡春杰, 陈晓, 陈霞. 基于改进广义Arnold映射的多混沌图像加密算法. 包装工程, 2017, 38(3): 144-149. |
| [38] |
胡春杰, 陈晓, 郭银. 基于多混沌映射的光学图像加密算法. 激光杂志, 2017, 38(1): 110-114. |
| [39] |
沈千里, 陈晓, 支亚京, 等. 一种新的人脸图像去噪算法. 传感器与微系统, 2015, 34(11): 133-136. |
| [40] |
陈晓, 汪陈龙. 基于赛利斯模型和分数阶微分的兰姆波信号消噪. 物理学报, 2014, 63(18): 184301. |
| [41] |
支亚京, 陈晓, 蔡婷婷. 单通道时频重叠高斯调幅通信信号盲分离方法. 科学技术与工程, 2016, 16(1): 204-208. |
| [42] |
陈晓, 徐晓庆. 卫星图像码率控制方法的改进. 光电工程, 2012, 39(9): 7-11. |
| [43] |
卢明乔, 陈晓. 基于ZigBee组网的智能照明系统的研究与设计. 信息技术, 2013(12): 106-109. DOI:10.3969/j.issn.1009-2552.2013.12.028 |
| [44] |
吴祖慷, 朱晓冬, 刘元宁, 等. 基于GA-SVM模型的虹膜质量评估方法. 吉林大学学报(理学版), 2022, 60(1): 89-98. |
 2022, Vol. 31
2022, Vol. 31


