车辆路径规划问题 (vehicle routing problem, VRP) 最早于1959年提出[1], 该问题可以描述为: 对于一组客户点以及一定数量的车辆, 在满足一定的约束条件的情况下, 对处于不同物理位置上的大规模客户进行服务, 并使得总成本最小. 大多数的物流运输问题都可以看成是VRP问题, 该问题根据约束条件的不同, 可分为CVRP、VRPTW、DCVRP、VRPB等不同类型的问题. 其中, CVRP (capacitated vehicle routing problem) 是一种经典的车辆路径问题, 每辆车都有相同的容量限制, 车辆都从同一个配送中心出发并最终返回到配送中心, 且已知各个客户点的位置和需求量; 带时间窗的车辆路径问题 (VRP with time windows, VRPTW) 则是在CVRP问题的基础上增加了时间窗约束, 车辆必须在规定时间窗内到达客户点并提供服务.
车辆路径问题通常使用精确算法或启发式算法进行求解. 其中精确算法包括分支定价法[2-4]、割平面法[5-6]和动态规划法[7]等. 然而, 该类算法通常应用于小规模的车辆路径规划问题, 当客户点的数量较大时, 该类精确算法就会失效. 文献[8]提出了一种标签法, 解决了超过15个此前未得到最优解的Solomon测试例, 但部分测试例的求解时间超过了10个小时. 因此, 精确算法很难用于求解大规模的车辆路径规划问题. 车辆路径问题属于NP难的组合优化问题, 目前对于大规模的车辆路径规划问题一般采用启发式算法求解. 其中元启发式算法是求解VRP问题常用的启发式算法, 这类算法包括遗传算法、蚁群算法、模拟退火算法、禁忌搜索等[9-14]. 改进型启发式算法, 如2-opt、3-opt等[15], 通过在路径内部或路径之间的交换操作改进解的质量. 构造型启发式算法则通过逐步构造路径来形成可行解, 常见的构造型启发式算法有节约算法[16]、最近邻法[17]、扫描法[18]等.
对于复杂的VRP, 采用单一的启发式算法往往很难得到令人满意的结果, 目前, 通常采用混合式的启发式算法来求解该问题. 该类算法首先通过采用合理的启发式算法来构造车辆路径问题的初始解, 然后采用群体智能搜索模式, 如遗传算法、蚁群算法、模拟退火算法、禁忌搜索等, 在初始解的基础上对复杂的车辆路径规划问题进行求解. 由于该类组合优化问题属于多变量多陷阱的最优解的问题, 因此, 初始解的生成质量, 往往也影响着群体搜索算法的搜索效率和最终解的质量. 基于此, 本文对几种启发式算法进行了实验分析和改进, 并将其用于求解现实生活中常见的一类带时间窗的车辆路径问题, 以期望得到更好的初始解, 最后, 在常用的一些关于车辆路径规划问题的数据集上对改进的启发式算法进行了比较, 并对结果进行了分析.
1 问题描述及数学模型VRPTW问题可以表述为: 配送中心给定m辆容量为Q的车辆, 为n个客户提供服务. 其中, 车辆集V = {1, 2, 3, …, m}, 客户集C = {0, 1, 2, …, n}, 客户0表示配送中心, 客户i的货物需求量表示为qi (q0 = 0); 从客户i到客户j的距离为dij, 所耗费的行驶时间为tij, 在客户i上花费的服务时间为si ; 客户i所允许的服务时间窗为 [ai, bi], 则车辆k到达客户i的时间rik应满足rik∈[ai, bi]. 车辆从配送中心出发, 为每个客户提供服务, 最后返回到配送中心, 要求规划运输路径, 使得运输成本最小. 因此, VRPTW数学模型可表示为:
| $ \min Z = \sum\limits_{i \in C} {\sum\limits_{j \in C} {\sum\limits_{k \in V} {{d_{ij}}{x_{ijk}}} } } $ | (1) |
| $ \sum\limits_{j \in C} {\sum\limits_{k \in V} {{x_{ijk}} = 1,\; \forall i \in C - \{ 0\} } } $ | (2) |
| $ \sum\limits_{i \in C} {{x_{ihk}} - \sum\limits_{j \in C} {{x_{hjk}} = 0,\; \forall h \in C,\; \forall k \in V} } $ | (3) |
| $ \sum\limits_{j \in C} {{x_{0jk}} = 1,\; \forall k \in V} $ | (4) |
| $ \sum\limits_{i \in C} {{q_i}\sum\limits_{j \in C} {{x_{ijk}} \leqslant Q,\; \forall k \in V} } $ | (5) |
| $ {r_{ik}} + {t_{ij}} + {s_i} - K(1 - {x_{ijk}}) \leqslant {r_{jk}},\; \forall i, j \in C,\; \forall k \in V $ | (6) |
| $ {a_i} \leqslant {r_{ik}} \leqslant {b_i},\; \forall i \in C,\; \forall k \in V $ | (7) |
| $ {x_{ijk}} \in (0, 1), \;\forall i, j \in C,\; \forall k \in V $ | (8) |
式(1)表示最小化车辆总行驶路程; 式(2)和式(3)表示每个客户均有一辆车提供服务且只能被服务一次; 式(4)约束了车辆从配送中心出发服务客户并且只出发一次; 式(5)是对车辆容量的约束; 式(6)和式(7)是车辆到达各个客户的时间窗约束, 其中K是一个足够大的常数.
2 传统的启发式算法CW (Clarke Wright) 节约算法是解决车辆路径问题最常用的启发式算法, 其核心思想是通过合并路径减少总路程[16]. 在开始时, 由n辆车为n个客户点提供服务, 形成n条初始路径. 如果两条路径 (0, …, i, 0) 和 (0, j, …, 0) 合并成一条路径 (0, …, i, j, …, 0) 后, 不违反车辆的容量约束, 那么合并后的路径将产生节约值: sij = di0 + d0j − dij. 节约值sij表示路径合并后节约的路程. CW算法优先对节约值大的路径进行合并, 直到不存在可进行合并的路径时停止.
最近邻法通过每次选择距上一个客户点最近的客户点来构造路径[17]. 首先, 选择配送中心作为路径起点, 之后每次选择与上一个客户点最近邻的客户点加入路径. 当将客户点加入路径后不满足车辆容量约束时, 开始一条新的路径, 重复过程至所有客户点均被服务.
扫描法是一种“先分组后排线”的启发式算法[18]. 分组时, 首先从配送中心引出一条射线, 按顺时针或逆时针顺序扫描, 将扫描到的客户点依次加入路径. 当客户点加入路径后客户总需求量超出车辆容量时, 开始规划一条新路径, 重复该过程直至所有客户点均被服务. 排线时, 使用精确算法或2-opt等启发式算法对各组客户点重新排线或进一步优化.
插入法在构造路径时, 根据特定的原则选取初始路径的第一个客户点, 而后选择最佳的客户点插入最佳插入位置[19]. 为了减少计算次数, 可以使用启发式算法构造一个包含所有客户点的初始序列, 并初始化一条空路径, 依次从初始序列中取出客户点插入到初始路径的最佳插入位置, 使得总路程增加最少. 当插入客户点后总需求量超过车辆容量时, 开始规划新路径. 最后, 考虑到在构造路径时, 插入法仅在初始路径中寻找客户点的最佳插入位置, 因此对每个客户点, 尝试将之插入到后续构建的路径中以减少总路程.
3 考虑时间窗的启发式算法在上述4种传统启发式算法中引入时间窗约束. 传统的启发式算法在路径末尾添加客户点时由于不需要考虑时间窗, 因此很容易出现车辆到达了下一个客户点而时间窗尚未开始、车辆被迫等待的情况, 这必然会减少当前车辆服务的客户点数量. 为此, 本文的算法会优先将可能使时间窗更紧凑的客户点加入路径, 以减少等待时间. 如果客户点i、j满足bi + si + dij > aj, 则有可能访问客户点i后访问客户点j时, 没有或只要少许的等待时间. 其中, bi、si分别是客户点i时间窗的结束时间和服务时间, dij是从客户点i到客户点j经过的路程, aj是客户点j时间窗开始的时间. 本文以此作为判断考虑是否优先将客户加入路径.
1) CW算法
改进的CW算法优先考虑了可能使时间窗更紧凑的子路径, 重新定义客户点i、j的节约值为: 如果bi + si + dij > aj, 则sij = di0 + d0j − dij+N, 其中N是一个大的正数; 对于其他情况, 仍是sij = di0 + d0j − dij. 算法步骤如下.
Step 1. 计算两两客户点之间的节约量sij, i, j∈C, C = {1, 2, 3, …, n}, 并将节约量按从大到小的顺序排序.
Step 2. 初始化n条路径, 每条路径中只有一个客户点, 起点和终点为配送中心.
Step 3. 依次选取节约量sij, 如果客户点i、j分别位于路径的开始和末尾处, 且二者不在同一条路径上, 进入Step 4; 否则, 依Step 3重新选取节约量. 当所有节约量均被选取时, 算法终止.
Step 4. 如果路径 (0, …, i, 0) 和 (0, j, …, 0) 合并为路径 (0, …, i, j, …, 0) 后不违反车辆的容量约束和时间窗约束, 则将该路径合并, 然后返回Step 3; 否则, 直接返回Step 3, 重新选取节约量.
2) 最近邻法
与CW算法的改进相似, 改进的最近邻法优先将时间窗更紧凑距离更近的客户点加入路径. 具体的, 如果不满足条件bi + si + dij > aj, 则将客户点i、j之间的距离定义为: 真实距离加上一个大的正数N. 改进的算法步骤如下.
Step 1. 初始化一条空路径, 将配送中心作为起点加入路径.
Step 2. 计算客户集C中的客户点到路径最后一个客户点的距离, 如果在客户集C中存在加入路径末尾后不违反车辆容量约束和时间窗约束的客户点, 则进入下一步; 否则, 转至Step 4.
Step 3. 在不违反约束的客户点中选取距离最小的加入到路径末尾, 并在客户集C中移除该客户点. 返回Step 2.
Step 4. 将配送中心加入到路径末尾. 如果客户集C不为空, 则算法返回至Step 1, 开始安排新的路径; 否则, 所有客户均已被服务, 算法终止.
3) 扫描法
在随机选定起始客户点i后, 优先将满足 bi + si + dij > aj的客户点插入路径. 采用此策略时, 单向的扫描将遗漏部分客户点, 因而本文采用的是双向扫描的策略, 即从当前加入路径的客户点开始, 同时进行顺、逆时针的扫描. 同时, 由于车辆到达起始客户点时可能存在较长的等待时间, 因而将扫描到的客户点加入到起始或末尾位置. 改进后的算法步骤如下.
Step 1. 初始化一条空路径, 将配送中心作为起点加入路径. 从客户集C中任选一个客户点加入路径.
Step 2. 以路径中最后一个客户点i与配送中心的连线为始边, 计算配送中心与各客户点连线的角度. 如果客户j不满足bi + si + dij > aj, 则将角度值加上一个大的正数N.
Step 3. 当客户集C不为空时, 选择客户集C中角度最小的客户点, 若加入路径起始或末尾位置后不违反车辆容量约束和时间窗约束, 转至Step 4; 否则, 转至Step 5.
Step 4. 将该客户点加入路径的起始或末尾位置, 并从客户集C中移除该客户点, 返回Step 2.
Step 5. 将配送中心加入路径末尾, 表示车辆返回配送中心. 若客户集C不为空, 则开始规划一条新路径, 返回Step 1; 否则, 所有客户均已被服务, 算法终止.
4) 插入法
插入法会尝试将客户点插入到路径中间, 因而不需要考虑时间窗是否紧凑的问题. 在此, 仅考虑将客户点插入到满足时间窗约束的位置. 假定初始序列为 (c1, c2, …, cn), 算法步骤如下.
Step 1. 令j = 1, k = 2, 并初始化路径routej = (0, c1, 0).
Step 2. 如果客户点ck插入路径routej后总需求量超过车辆容量, 则开始规划一条新的车辆路径routej+1 = (0, ck, 0), 并令j = j + 1, 转至Step 4. 否则, 进入下一步.
Step 3. 对路径routej中所有可以插入客户点ck而不违反时间窗约束的位置, 计算插入代价. 将ck插入路径 (0, …, i, j, …, 0) 中i、j之间的位置时, 其插入代价为 costij = dick + dck j − dij. 若不存在合适的插入位置, 则规划一条新的车辆路径routej+1 = (0, ck, 0), 并令j = j + 1, 转至Step 4. 否则, 选择插入代价最小的位置插入客户点ck, 并转至Step 4.
Step 4. k = k + 1 . 若k ≤ n, 返回Step 2. 否则进入下一步.
Step 5. 设所规划的路径数量为J, 路径routej经过的客户点数量为nj, 且routej = (0, r1, r2, …, rnj, 0), j = 1, 2, …, J; 令j = J.
Step 6. 令i = nj .
Step 7. 对客户点ri , 计算路径 (routej+1, routej+2, …, routeJ), 以及routej的部分路径 (ri+1, ri+2, …, rnj, 0) 中的插入代价. 在满足车辆容量约束和时间窗约束的插入位置中, 选择插入代价最小的位置插入客户点 ri .
Step 8. 令i = i − 1. 若i > 0, 转至Step 7.
Step 9. 令 j = j − 1. 若j > 0, 转至Step 6; 否则算法终止.
4 仿真实验 4.1 实验数据实验采用CMT数据集以及Solomon数据集进行测试. CMT数据集由14个测试例构成, 客户点数量在50到200之间. 其中CMT1, CMT2, CMT3, CMT4, CMT5, CMT11以及CMT12是属于CVRP的测试例, CMT6, CMT7, CMT8, CMT9, CMT10, CMT13以及CMT14则在CVRP的基础上对每个客户点添加了服务时间, 对每辆车限制了最大行驶时长. Solomon数据集带有时间窗, 是VRPTW的一个标准测试集, 由56个测试例构成, 每个测试例有100个客户点, 测试例可分为6大类, 分别是R1类、R2类、C1类、C2类、RC1类和RC2类. 其中, R类的客户点坐标分布均匀, C类问题的客户点呈聚集性分布, RC类的测试例同时包含了均匀分布的客户点和呈聚集性分布的客户点. 此外, C1类、R1类和RC1类具有较窄的时间窗和较小的车辆容量, 而剩余的3类问题则具有较宽的时间窗和更大的车辆容量.
4.2 实验设置实验使用Matlab进行编程实现, 分别将CW算法、最近邻法、扫描法以及插入法对CMT以及Solomon数据集的每个测试用例进行了实验. 其中CMT数据集的部分测试用例属于带行驶时间限制的车辆路径问题(duration constrained CVRP), 对于这部分测试例, 将上述各算法对时间窗的约束改为对行驶时长的约束.
对该问题求解过程中本文设置了以下的一些假设:
(1) 各客户点之间的距离采用欧氏距离, 并以双精度的浮点数表示.
(2) 假定车辆的行驶速率恒定, 并且车辆的行驶时间大小等于行驶距离.
(3) 插入法的初始序列由扫描法给出, 扫描法的初始客户点随机给出.
(4) 为了方便比较, 扫描法不使用3-opt等改进算法.
(5) 确定性算法CW算法以及最近邻法对每个测试例仅测试一次, 随机算法包括扫描法和插入法则对每个测试例都进行150次测试.
4.3 实验结果与分析4种算法在CMT数据集上的测试结果如表1所示. 对于CW算法、最近邻法, 表1给出了运行结果的精确值, 对于扫描法和插入法, 则给出在150次测试中得到的平均结果. 如表1所列, CW算法和插入法的效果明显优于其余两种算法. 在所有测试例上最近邻法明显优于扫描法. 为了进一步验证CW算法在CMT数据集上是否显著优于其他算法, 本文使用配对样本t检验将CW算法同其他算法进行比较, 并在表1底部给出显著性分析结果(Y表示CW算法显著优于该算法)和对应的p值. 可以看到, CW算法在CMT数据集上显著优于其他算法.
| 表 1 4种算法在CMT数据集上的测试结果 |
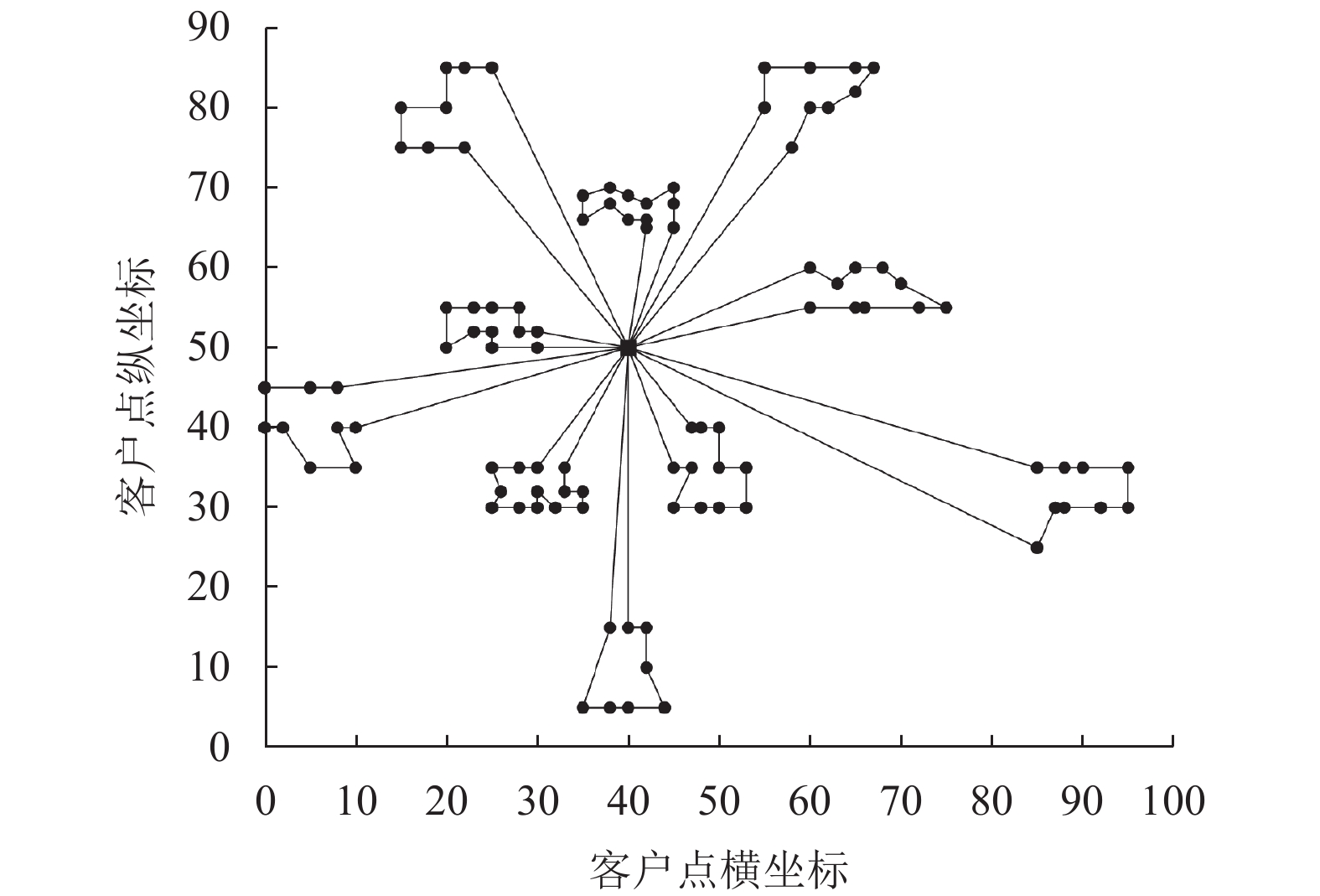
表2给出了4种算法在Solomon数据集上的部分测试结果以及已知的最优结果, 其中扫描法和插入法给出的是在150次测试中得到的最优结果, 已知最优解来自文献[20]. 如表2所列, 节约算法和插入法更接近已知最优解, 但CW算法所需要的车辆数较多, 而插入法除了R1以及RC1之外, 所需的车辆数量更接近已知最优解. 同时, 应注意到CW算法在测试例C101上达到了已知最优解, 插入法在测试例C101, C105, C107以及C201上得到了与已知最优解一样的结果. 在测试例R202, R211, RC201以及RC202上, 插入法所需的车辆数多于已知最优解, 但在路程上得到了优于已知最优解的结果, 这表明插入法更可能得到接近最优解的结果. 图1–图6给出了插入法在部分测试例上得到的路径.
| 表 2 4种算法在Solomon数据集部分测试例上的运行结果 |
|
图 1 插入法得到的C107测试例路径 |
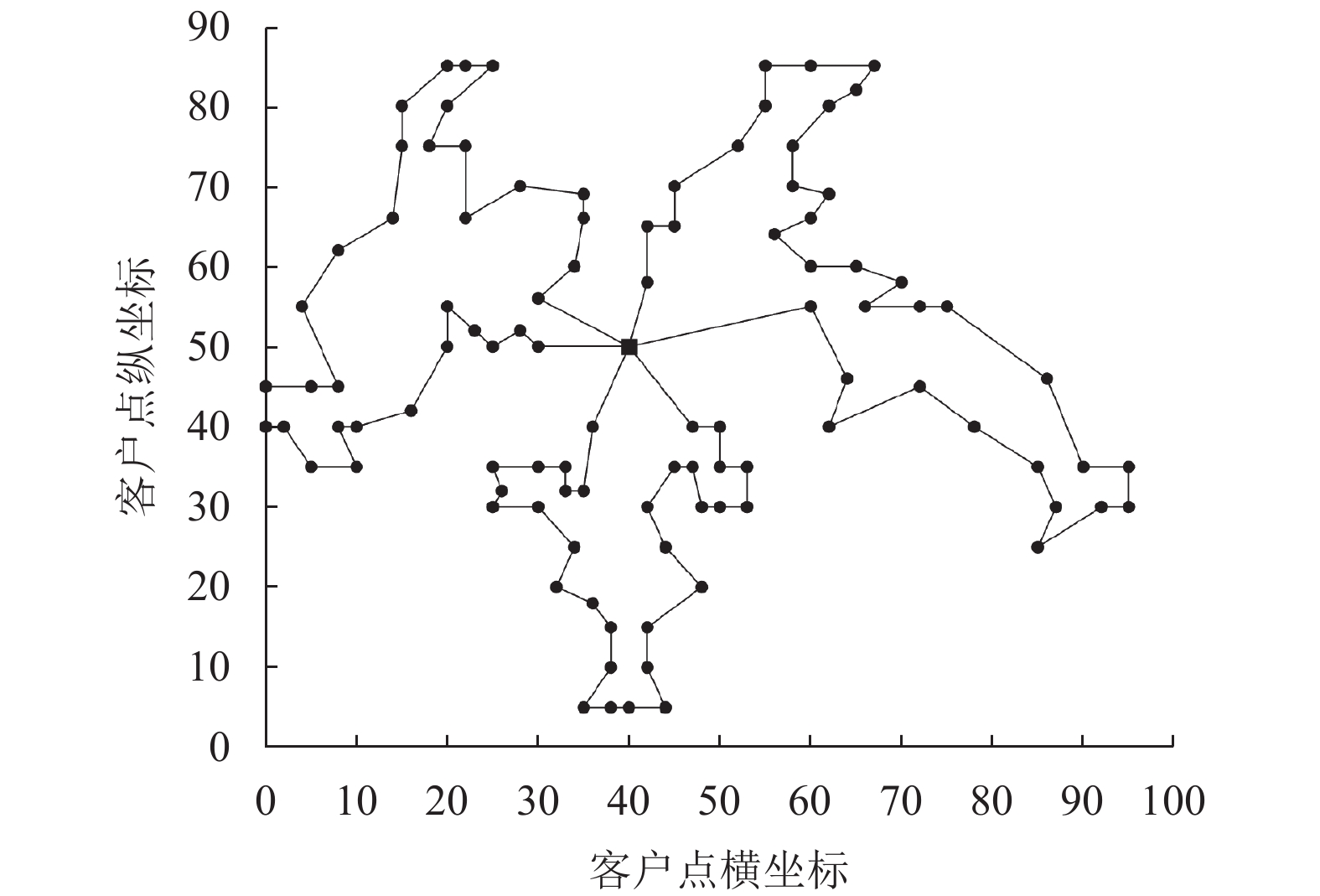
|
图 2 插入法得到的C201测试例路径 |
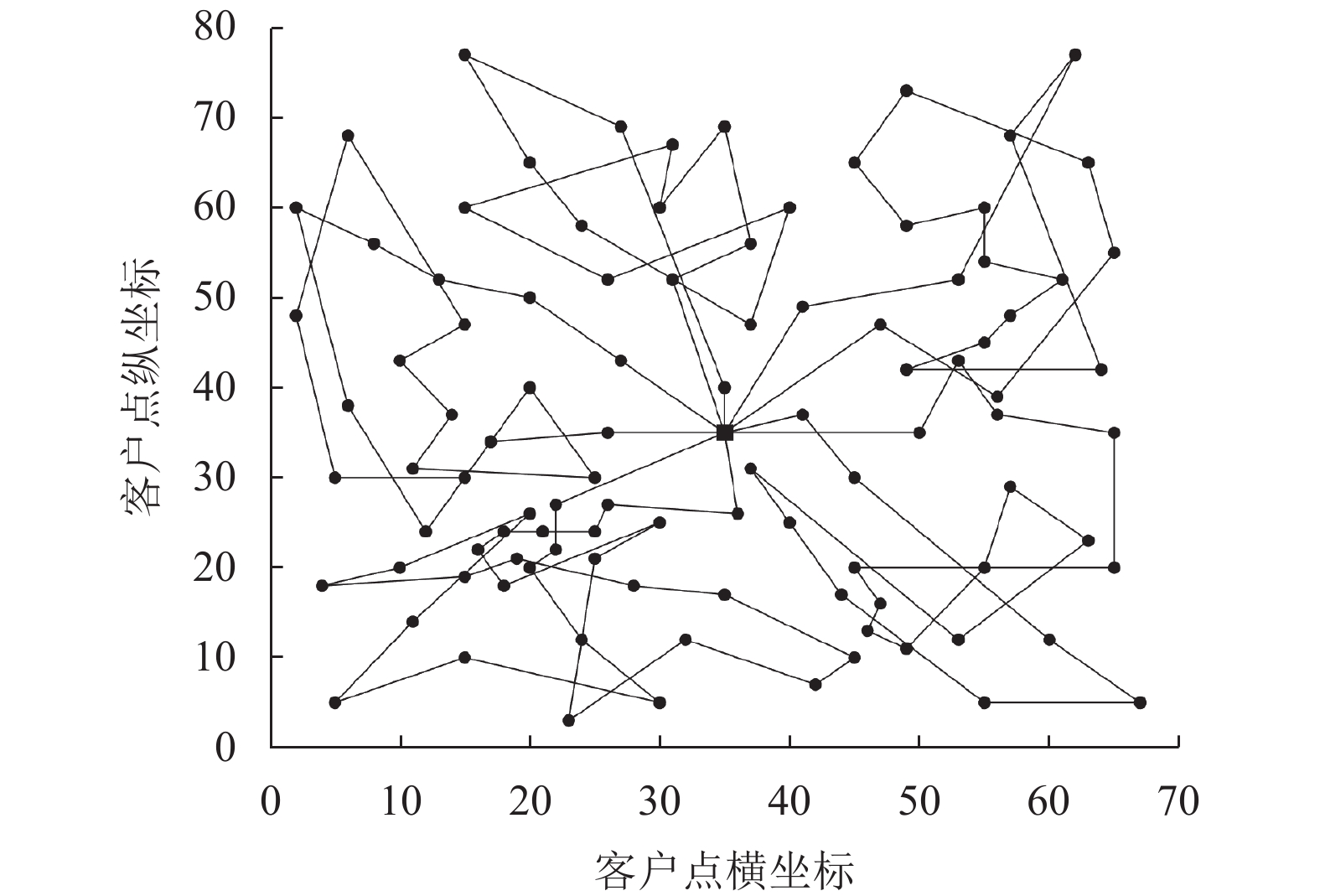
|
图 3 插入法得到的R202测试例路径 |
表3列出了4种算法在6种类型的测试用例上的平均结果. 结果显示, 节约算法和插入法明显优于其他算法, 扫描法表现最差. 但不同于在CMT数据集上的测试结果的是, 插入法在含有均匀分布客户点的R类及RC类测试例上得到了比节约算法更好的结果. 但对于客户点呈聚集性分布的C类测试用例, 改进的节约算法则明显优于改进的插入法.
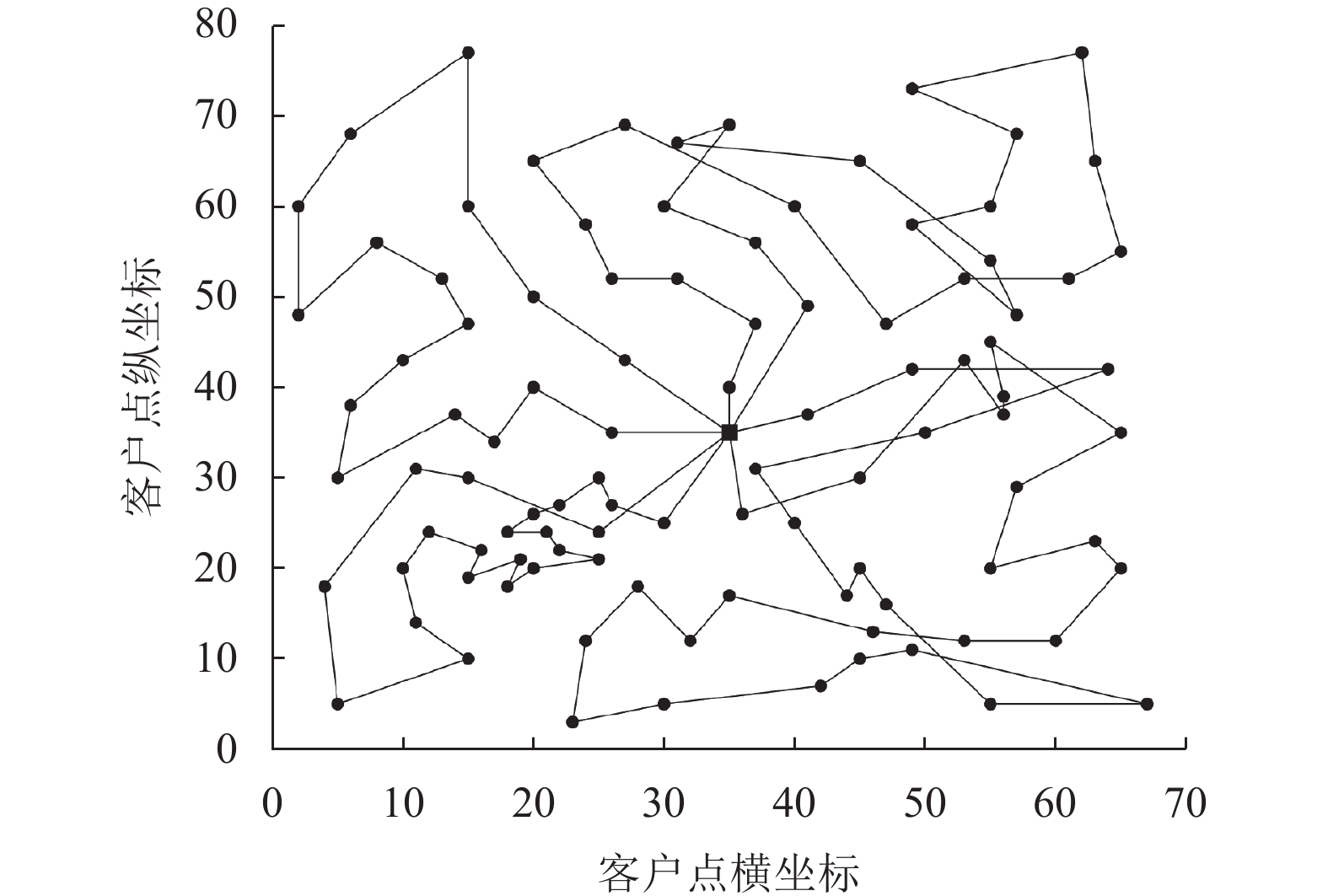
|
图 4 插入法得到的R211测试例路径 |
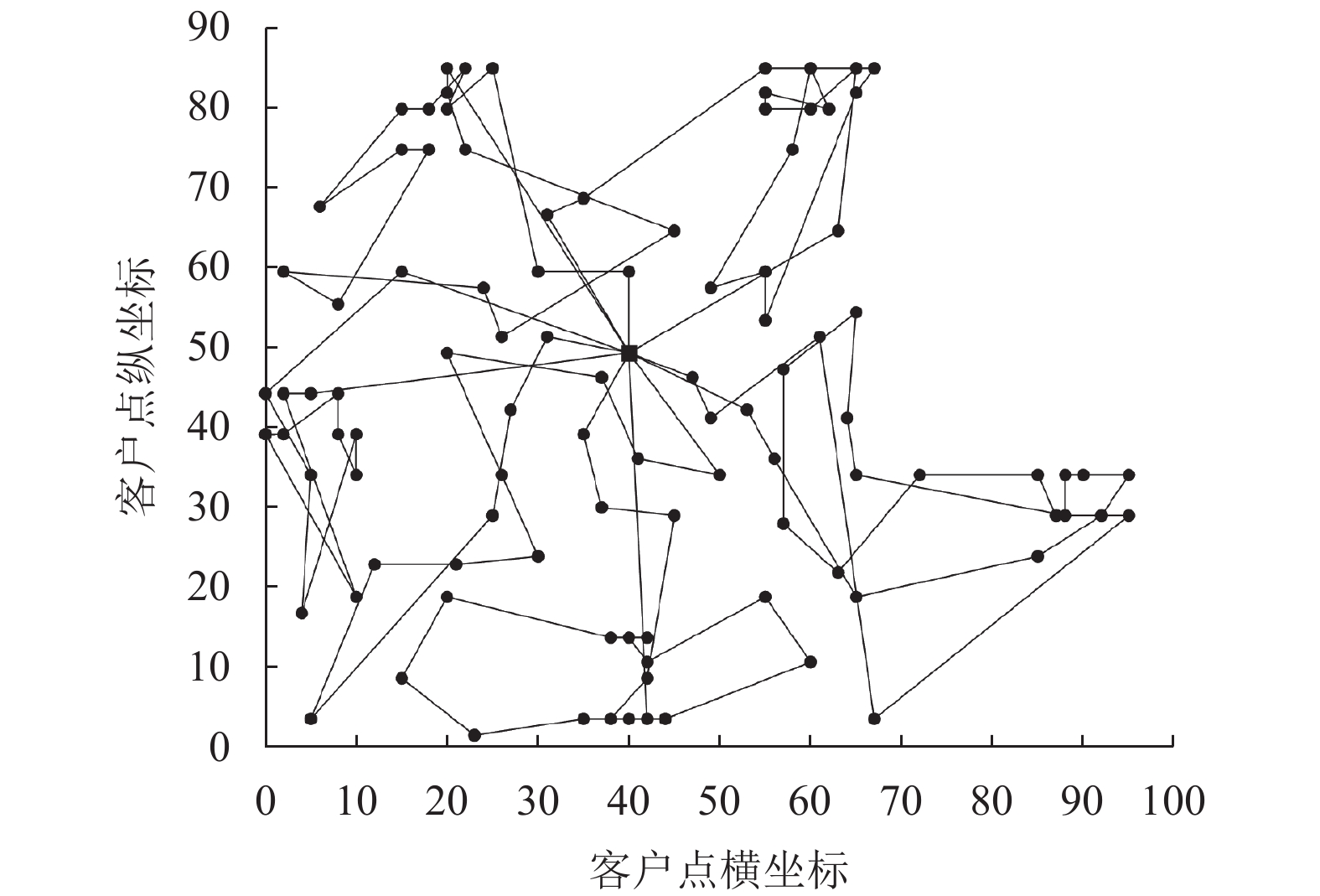
|
图 5 插入法得到的RC201测试例路径 |
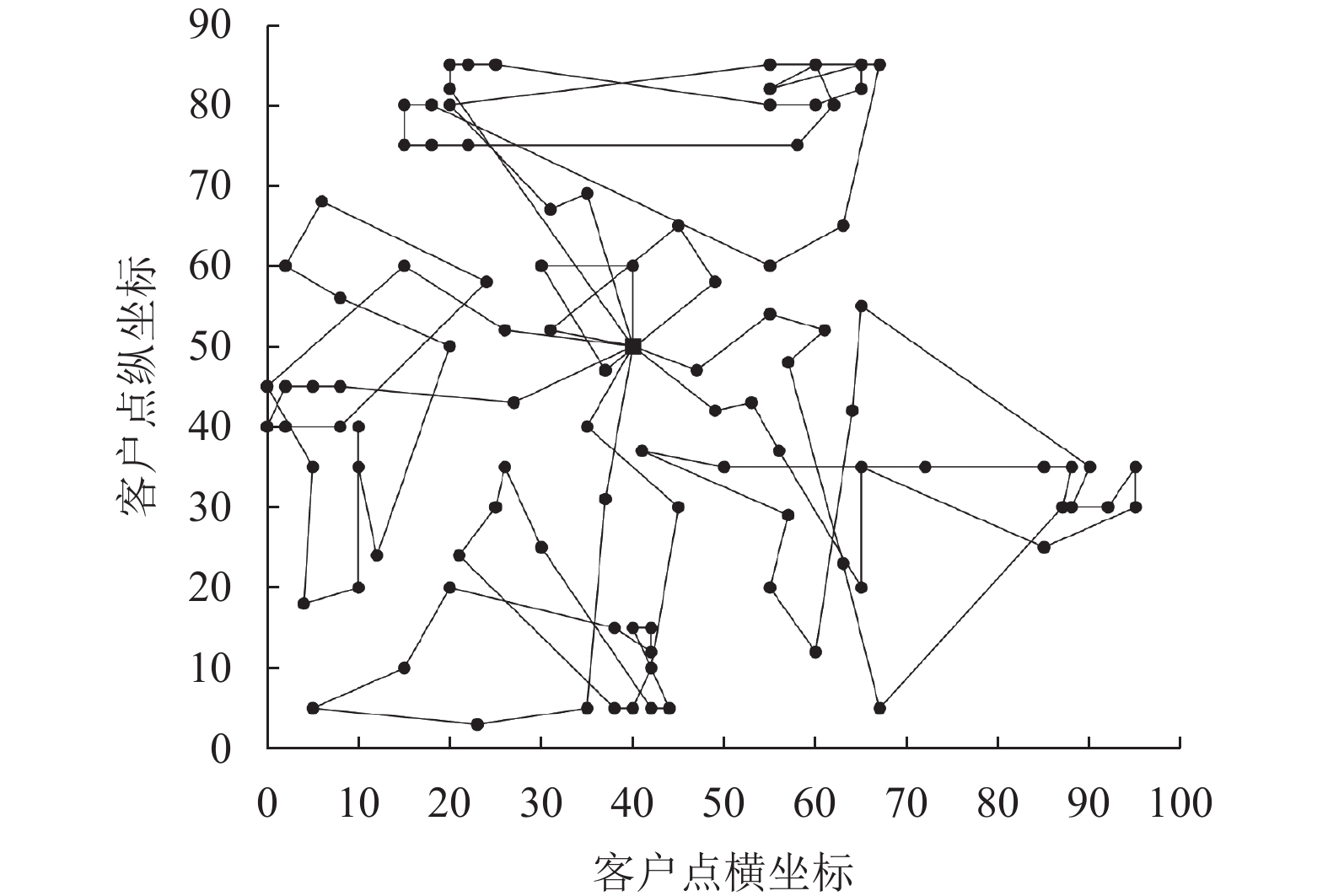
|
图 6 插入法得到的RC202测试例路径 |
5 结论
本文针对带时间窗的车辆路径规划问题, 基于时间窗来调整客户插入优先级, 以此改进了传统的启发式算法, 并分别在CVRP以及VRPTW的相关数据集上测试. 结果表明, 改进的CW算法和插入法均能获得较好的结果. 并且, 在CVRP的相关数据集上, CW算法优于其他算法; 而在VRPTW的相关数据集上, 改进的插入法对含有均匀分布客户点的测试例效果最好, 改进的CW算法则在客户点均匀分布的测试例上有更好的表现.
| 表 3 4种算法在Solomon数据集上的平均测试结果 |
| [1] |
Dantzig GB, Ramser JH. The truck dispatching problem. Management Science, 1959, 6(1): 80-91. DOI:10.1287/mnsc.6.1.80 |
| [2] |
Taş D, Gendreau M, Dellaert N, et al. Vehicle routing with soft time windows and stochastic travel times: A column generation and branch-and-price solution approach. European Journal of Operational Research, 2014, 236(3): 789-799. DOI:10.1016/j.ejor.2013.05.024 |
| [3] |
Dabia S, Ropke S, van Woensel T, et al. Branch and price for the time-dependent vehicle routing problem with time windows. Transportation Science, 2013, 47(3): 380-396. DOI:10.1287/trsc.1120.0445 |
| [4] |
Hernandez F, Feillet D, Giroudeau R, et al. Branch-and-price algorithms for the solution of the multi-trip vehicle routing problem with time windows. European Journal of Operational Research, 2016, 249(2): 551-559. DOI:10.1016/j.ejor.2015.08.040 |
| [5] |
Mak V, Ernst AT. New cutting-planes for the time-and/or precedence-constrained ATSP and directed VRP. Mathematical Methods of Operations Research, 2007, 66(1): 69-98. DOI:10.1007/s00186-006-0141-x |
| [6] |
Kallehauge B, Larsen J, Madsen OBG. Lagrangian duality applied to the vehicle routing problem with time windows. Computers & Operations Research, 2006, 33(5): 1464-1487. |
| [7] |
Mahmoudi M, Zhou XS. Finding optimal solutions for vehicle routing problem with pickup and delivery services with time windows: A dynamic programming approach based on state-space-time network representations. Transportation Research Part B: Methodological, 2016, 89: 19-42. DOI:10.1016/j.trb.2016.03.009 |
| [8] |
Irnich S, Villeneuve D. The shortest-path problem with resource constraints and k-cycle elimination for k ≥ 3
. Informs Journal on Computing, 2006, 18(3): 391-406. DOI:10.1287/ijoc.1040.0117 |
| [9] |
范厚明, 刘鹏程, 吴嘉鑫, 等. 集货需求随机的同时配集货VRP及混合变邻域搜索算法. 系统工程理论与实践, 2019, 39(10): 2646-2659. DOI:10.12011/1000-6788-2018-0957-14 |
| [10] |
王丹. 基于改进遗传算法的物流配送车辆路径问题研究[硕士学位论文]. 长春: 长春工业大学, 2016.
|
| [11] |
王雪红. 基于遗传算法的车辆路径优化问题的应用研究[硕士学位论文]. 天津: 天津科技大学, 2016.
|
| [12] |
孙小军, 介科伟. 求解带时间窗动态车辆路径问题的改进蚁群算法. 大连理工大学学报, 2018, 58(5): 539-546. DOI:10.7511/dllgxb201805015 |
| [13] |
宋燕子. 基于模拟退火算法的启发式算法在VRP中的应用[硕士学位论文]. 武汉: 华中师范大学, 2013.
|
| [14] |
苏欣欣, 秦虎, 王恺. 禁忌搜索算法求解带时间窗和多配送人员的车辆路径问题. 重庆师范大学学报(自然科学版), 2020, 37(1): 22-30. |
| [15] |
Lin S. Computer solutions of the traveling salesman problem. The Bell System Technical Journal, 1965, 44(10): 2245-2269. DOI:10.1002/j.1538-7305.1965.tb04146.x |
| [16] |
Clarke G, Wright JW. Scheduling of vehicles from a central depot to a number of delivery points. Operations Research, 1964, 12(4): 568-581. DOI:10.1287/opre.12.4.568 |
| [17] |
Solomon MM. Algorithms for the vehicle routing and scheduling problems with time window constraints. Operations Research, 1987, 35(2): 254-265. DOI:10.1287/opre.35.2.254 |
| [18] |
Gillett BE, Miller LR. A heuristic algorithm for the vehicle-dispatch problem. Operations Research, 1974, 22(2): 340-349. DOI:10.1287/opre.22.2.340 |
| [19] |
Mole RH, Jameson SR. A sequential route-building algorithm employing a generalised savings criterion. Journal of the Operational Research Society, 1976, 27(2): 503-511. DOI:10.1057/jors.1976.95 |
| [20] |
Woch M, Łebkowski P. Sequential simulated annealing for the vehicle routing problem with time windows. Decision Making in Manufacturing and Services, 2009, 3(1–2): 87-100. |
 2022, Vol. 31
2022, Vol. 31


