2. 正元地理信息集团股份有限公司, 北京 101300
2. Zhengyuan Geographic Information Group Co. Ltd., Beijing 101300, China
随着智慧城市进程的快速发展, 新增城市建筑物不断出现, 在城市类高层建筑物遥感图像中, 由于光照的倾斜照射和自身的遮挡会在高分辨率遥感影像上呈现暗色调阴影, 尤其是进入米级分辨率以后, 阴影引起的低照度区域在遥感图像上的占比率增加, 这对城市高层建筑物信息的解译工作和要素的定量提取带来了麻烦[1]. 一方面, 高层建筑阴影会使得原有图像视觉可视化效果减弱, 造成一定程度的影像完整性信息量缺失, 不利于地理空间数据更新、遥感图像档案建立等高级应用的需求; 另一方面, 阴影的出现对提取高层建筑遥感图像的轮廓信息产生干扰, 不利于遥感图像的基础应用潜力. 因此, 如何有效地对遥感高层建筑物影像阴影进行检测, 对于城市建筑物的识别和分类、大比例尺度遥感图像制图、遥感图像档案建立、地理空间数据的更新、智慧城市群的有效检测等都具有重要的实际意义.
Makarau等提出了一种基于直射光和反射光的辐射模型[2], 利用直射光和反射光的不同进行阴影区域的提取, 但是这种方法需要太阳照射时的高度和角度属性, 局限性明显, 成本高, 不利于实现. 卢建华提出了一种能利用直方图阈值的阴影分割算法, 但是这种方法存在阈值分割效果较差的问题[3]. 赵显富等提出了一种利用HIS变化的阴影检测模型[4], 其利用阴影指数区分阴影区域与非阴影区域, 但是此方法存在误判率较高的问题.
针对上述算法存在的问题, 本文提出了一种改进阈值分割和注意力残差网络结合的高层建筑物遥感影像阴影检测方法. 图1所示为本文设计的遥感影像高层建筑物阴影检测框架流程图, 主要包括两个部分, 第1部分为轮廓分割模型, 首先对遥感影像数据进行灰度化处理, 然后利用改进的最大类间和最小类内阈值分割算法进行阈值分割, 接着利用八邻域线性约束关系进行端点检测, 最后利用欧式距离度量方式进行断点修复得到分割的阴影轮廓, 此时得到的阴影轮廓会有误判现象; 第2部分为基于卷积神经网络CNN的遥感影像分类模型, 利用生成对抗模型GAN和随机旋转、裁剪等几何变换法对误判数据进行扩充增强处理, 然后利用改进的基于注意力机制残差网络卷积算子建立误判分类模型, 并利用扩充误判数据对误判模型卷积算子参数进行优化, 最后对第1部分的阴影轮廓结果进行误判数据去除, 得到最终的阴影识别结果.

|
图 1 阴影识别流程图 |
1 改进阈值阴影分割 1.1 灰度预处理
在对阴影检与识别问题中, 为了更为方便地对阴影进行识别, 首先将RGB图像的3个通道进行分离得到R、G、B单通道信息, 然后采用式(1)线性加权算法进行通道间信息融合处理[5, 6], 设遥感影像3个通道分别为R, G, B, 则加权后的灰度值Igray为:
| $ {I_{\rm gray}}(x, y) = 0.3R(x, y) + 0.59G(x, y) + 0.11B(x, y) $ | (1) |
经过灰度线性处理后阴影部分具有的像素强度要低于非阴影区域, 以0–255像素灰度级强度为横坐标, 以各灰度级像素强度出现的次数为纵坐标, 建立遥感图像中灰度级强度频数与灰度级强度之间的函数统计映射关系.
图2(c)灰度分布图中, 灰度等级低的区域为阴影区域, 灰度等级高的区域为非阴影区域, 灰度分布图中存在两个波峰, 阴影区域的灰度值变化较为集中, 非阴影区域的分布范围相比于阴影区域要更加广泛, 将两个波峰之间的波谷作为阈值进行分割, 虽然能够对阴影区域进行识别, 但是分割识别效果较差[7, 8]. 目前较为普遍的方法是利用最大类间方差法建立基于像素强度的阈值分割模型, 利用阈值分割模型自适应确定一个阈值T[9-11]. 但是基于最大类间方差确定阴影与非阴影区域分界阈值的方式, 仅是刻画了阴影和非阴影两个类别之间的方差距离, 并没有考虑到各个类内部之间的差异, 本文在最大类别方差的基础上加入了一个最小类内方差约束项, 首先计算需要区分两个类别之间的最大方差距离, 距离越大, 表示对阴影与非阴影两个类别的分类效果越好, 然后计算各个类内元素之间的最小方差距离, 最小方差距离越小, 类内元素越密集, 表示个灰度像素属于同一类别的概率越大, 具体步骤如下.

|
图 2 改进算法寻优过程示意图 |
第1步. 设遥感图像中阴影区域与非阴影区域的灰度值区间为[0, m], 则所有像素灰度值数量如式(2)所示, 每一个灰度等级的概率如式(3)所示, 总体灰度平均值μall如式(4)所示:
| $ N = \sum\limits_{i = 0}^m {{{h}}(i)} $ | (2) |
| $ {{{p}}_i} = {{{{h(i)}}} \mathord{\left/ {\vphantom {{{{h(i)}}} N}} \right. } N} $ | (3) |
| $ {\mu _{{\text{all}}}} = {{\sum\limits_{i = 0}^m {\left( {h(i) \times i} \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 0}^m {\left( {h(i) \times i} \right)} } {\sum\limits_{i = 0}^m {h(i)} }}} \right. } {\sum\limits_{i = 0}^m {h(i)} }} $ | (4) |
其中, i为灰度分布图的灰度级数, h(i)为灰度级数i对应的频数, m为灰度分布图最大灰度级数(本文为255), μall为全局平均灰度级数.
第2步. 设T为区间[0, m]的任意一个灰度值, 用T作为分割阈值, 将阴影区域与非阴影区域的图像分割为灰度区间为[0, T]以及[T+1, m]两部分, 分别记为C1, C2, 利用式(5)和式(6)分别计算两部分的平均灰度级数μC1和μC2:
| $ {\mu _{{{C}}1}} = {{\sum\limits_{i = 0}^T {\left( {h(i) \times i} \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 0}^T {\left( {h(i) \times i} \right)} } {\sum\limits_{i = 0}^T {h(i)} }}} \right. } {\sum\limits_{i = 0}^T {h(i)} }} $ | (5) |
其中, i为灰度分布图中阴影区域暗部像素灰度级数, h(i)为阴影区域暗部像素灰度级数i对应频数, T为阴影区域与非阴影区域分界阈值, μC1为C1区域的平均灰度等级.
| $ {\mu _{{{C}}2}} = {{\sum\limits_{i = {{T}} + 1}^m {\left( {h(i) \times i} \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{i = {{T}} + 1}^m {\left( {h(i) \times i} \right)} } {\sum\limits_{i = T + 1}^m {h(i)} }}} \right. } {\sum\limits_{i = T + 1}^m {h(i)} }} $ | (6) |
其中, i为灰度分布图非阴影区域亮部像素灰度级数, h(i)为非阴影区域亮部像素灰度级数i的对应频数, T为阴影区域与非阴影区域分界阈值, μC2为C2区域的平均灰度等级.
第3步. 利用式(7)–式(10)分别计算暗部阴影区域内C1和亮部非阴影区域内C2的方差:
| $ {w_{C1}} = \sum\limits_{i = 0}^T {p(i)} $ | (7) |
| $ {w_{C2}} = \sum\limits_{i = T + 1}^m {p(i)} $ | (8) |
| $ {\sigma _{C1}} = \sum\limits_{i = 0}^T {{{(i - {\mu _{C1}})}^2}} \times {{h(i)} \mathord{\left/ {\vphantom {{h(i)} {\sum\limits_{i = 0}^T {{{h}}(i)} }}} \right. } {\sum\limits_{i = 0}^T {{{h}}(i)} }} $ | (9) |
| $ {\sigma _{C2}} = \sum\limits_{i = T + 1}^m {{{(i - {\mu _{C2}})}^2}} \times {{h(i)} \mathord{\left/ {\vphantom {{h(i)} {\sum\limits_{i = T + 1}^{{m}} {{{h}}(i)} }}} \right. } {\sum\limits_{i = T + 1}^{{m}} {{{h}}(i)} }} $ | (10) |
第4步. 利用式(11)计算最大类内方差、最大类间方差和最优化评估函数. 阈值T处的最大类内方差σw为:
| $ {\sigma _{{w}}} = {w_{C1}}{\sigma _{C1}} + {w_{C2}}{\sigma _{C2}} $ | (11) |
阈值T处的最大类间方差σb为:
| $ {\sigma _{{b}}} = {{{w}}_{C1}}{({\mu _{C1}} - {\mu _{{\text{all}}}})^2} + {{{w}}_{C2}}{({\mu _{C2}} - {\mu _{{\text{all}}}})^2} $ | (12) |
要确保得到最佳分割阈值需要两个条件: 一是阴影部分与非阴影部分类之间的方差最大, 二是阴影区域内部方差、非阴影区域内部方差最小, 为了描述这一现象, 定义了分割优化函数:
| $ \zeta (T)\text=\mathrm{max}({\sigma }_{b}(T)/{\sigma }_{w}(T)) $ | (13) |
其中, ζ为T时的优化因子, 利用迭代法遍历所有的灰度等级, 则最大的优化因子对应的阈值T即为最佳分割阈值, 即为在灰度空间中, 阴影与非阴影区域的最大类阈值T为阈值分割线. 图2为本文改进算法最佳分割阈值寻优过程示意图, 图例中bin代表灰度强度分布情况, var代表利用最大类间方差和最小类内方差结合算法寻找最优因子ζ的过程, thres为寻找到的最优分割阈值.
第5步. 设定上述阈值T, 利用式(14)对图像进行分割:
| $ dst(x, y) = \left\{ \begin{gathered} 255, \;\;src(x, y) > T \\ 0, \;\;\;\;\;\;src(x, y) \leqslant T \\ \end{gathered} \right. $ | (14) |
假设P1点为需要判断的像素点, 其八邻域分别记为P2–P9, 则邻域端点类型如图3所示, 总共有8种类型可以判断为端点, 利用8种情况分别进行判别会影响检测效率, 针对这一问题进行了优化处理, 建立待判别像素点八邻域的约束关系[12, 13], 如果上述约束关系成立, 则此点即为轮廓一个端点, 否则, 为非端点并将此判别点舍弃.
| $ P2 + P3 + \cdots + P9 = 1 $ | (15) |
同一高层建筑遥感影像图会有多个阴影, 如果检测端点与断裂轮廓匹配错误, 不仅无法达到断点修复的目的, 还会破坏原有的轮廓区域. 针对如何对多个端点进行匹配的问题, 通过实验发现, 属于同一轮廓的断裂端点距离较近, 属于不同轮廓的断裂端点距离较远, 因此利用最小端点距离可以将同一个轮廓的断裂端点进行匹配. 常见的距离度量公式有曼哈顿距离、欧氏距离、马氏距离等, 由于本文处理对象是二维数据, 因此选用欧式距离进行不同断裂轮廓间的端点匹配, 依次判断端点之间的距离, 并将距离最小的两个端点进行连接. 图4为检测到的同一图像中两个不同轮廓断裂情况, 图4(a), 图4(b)和图4(e), 图4(f)分别为轮廓1和轮廓2断裂情况, 图4(c), 图4(d)和图4(g), 图4(h)分别为轮廓1和轮廓2利用八邻域约束关系及最小欧式度量距离修复后的结果, 从两个断裂轮廓连接修补后结果可知, 基于最小欧式距离八邻域约束关系能够对断裂的轮廓进行检测和连接修复.

|
图 3 邻域端点类型 |
2 阴影负例检测模型
经过上述改进阈值分割算法处理后获取的轮廓边界范围能够更加准确, 通过对遥感影像数据分析可知, 遥感影像中存在较多的地物信息, 如湖泊、树木偏绿色地物会引起较多误检现象, 这些误检地物对于本文检测高层建筑物阴影的目标起干扰作用, 因此需要去除这些阴影负例干扰, 本文设计了一个阴影负例(湖泊、树木等偏绿色地物)卷积网络模型对负例进行检测, 以便去除误判地物阴影.
2.1 数据处理针对遥感影像负例检测样本短缺问题, 利用生成式对抗网络模型GAN生成负例数据扩充数据[14], 优化函数如下所示:
| $\begin{split} & \mathop {\min }\limits_G \;\mathop {\max }\limits_D V(D, G) = \\ &{E_{{{x}} \sim {p_{\rm data}}(x)}}\left[ {\log D({{x}})} \right] + {E_{{\textit{z}} \sim {p_{\textit{z}}}({\textit{z}})}}\left[ {\log (1 - D(G({\textit{z})}))} \right] \end{split} $ | (16) |
其中, x表示真实样本, z表示噪声样本, G(z)表示生成样本, D(x)表示把真实样本分类为真的概率, D(G(z))表示把生成样本分类为真的概率, max表示最大化判别器, min表示最小化生成器.
图5所示为本文利用GAN进行扩充数据流程图, GAN生成数据包括生成和判别两个模型结构, 在训练过程中, 两个模型在每个批次中是分开进行训练的. 在生成器模型中, 噪声数据经过生成器生成数据后经过判别器优化, 使其结果接近正例(湖泊、树木等偏绿色地物); 在判别器模型中, 真实样本经过判别器优化, 使其结果接近正例; 噪声数据经过生成器生成数据后 经过判别器优化, 使其结果接近负例. 利用GAN优化函数对两个模型进行优化从而得到最优参数.

|
图 4 不同轮廓断裂连接 |
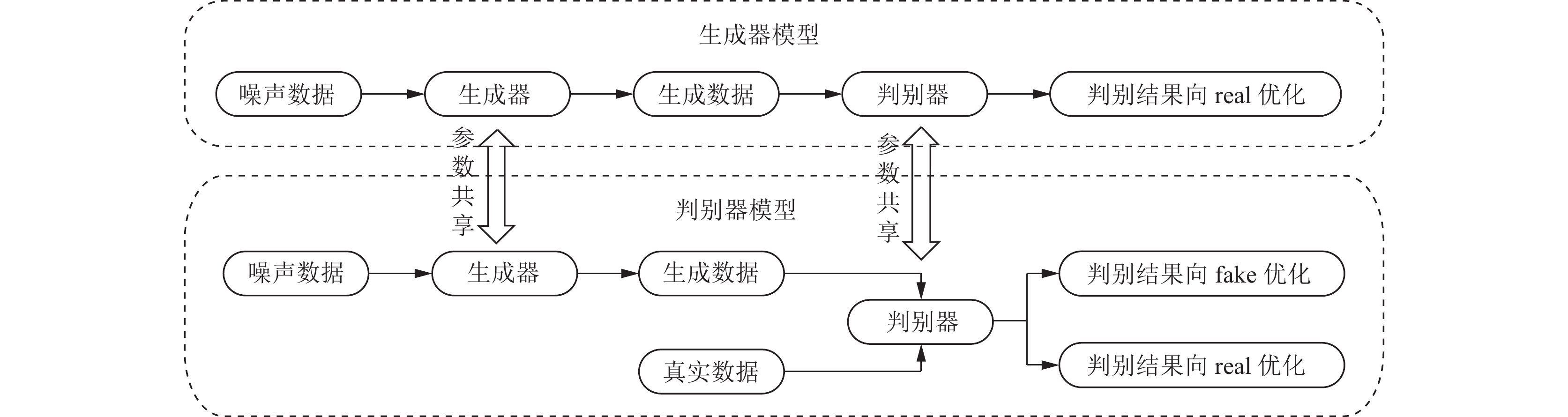
|
图 5 GAN生成阴影负例数据流程图 |
本文所用数据集由GAN网络生成、谷歌卫星收集和RSOD Dataset公开数据集3部分组成. RSOD Dataset是武汉大学2015年公开的用于遥感图像中物体检测的数据集, 其包含4 993 架飞机、191 个操场、180 座立交桥和1 586 个油桶4类目标. 根据本文研究的实际需求, 从RSOD Dataset中挑选出操场数据集, 从谷歌卫星遥感图截图河流、湖泊、树木数据集, 并利用随机翻转、裁剪等图像增强方法对上述数据进行处理, 获取2 200张数据影像; 利用GAN网络结构生成负例数据(湖泊、树木等偏绿色地物) 1 100张, 正常阴影1 100张. 共计4 400张数据影像, 并将数据按照8:1:1的比例划分为训练集(3 520张)、验证集(440张)和测试集(440张) 3个部分.
2.2 改进注意力残差网络ResNet18虽然利用短路链接方式能够有效防止过拟合现象, 但是无法有效提取全局特征, 本文在残差模型基础上对其进行了改进, 加入了注意力机制模块, 通过全局池化把ResNet提取的每个特征图空间维度压缩处理, 将每个中间层特征图变成一个实数, 使靠近输入层的地方由于这个实数在存在使其能够响应全局分布的感受野[15, 16], 图6所示为改进前后模块对比.
图6(a)为原始残差模块, 图6(b)为增加全局注意力机制的残差模块, 注意力权重用式(17)计算:
| $ {{\textit{z}}_c} = {1 \mathord{\left/ {\vphantom {1 {(H{ \times }W)}}} \right. } {(H{ \times }W)}}\sum\limits_{i = 1}^H {\sum\limits_{j = 1}^W {{u_c}(i, j)} } $ | (17) |
其中, zc为每个通道的注意力权重, H和W分别为每个通道的特征图尺寸, uc为每个通道特征图的均值. 加入注意力权重能够更好地拟合遥感特征图通道之间的全局特征, 通过Sigmoid门限获得0–1归一化权重, 最后通过scale操作把归一化后的注意力权重与每个遥感特征通道进行加权融合.

|
图 6 改进网络模型对比 |
2.3 CNN网络模型
本文所用的分类网络模型是以残差网络ResNet18模型为基础骨架, 并利用第2.2节所述改进注意力残差网络模块对ResNet18中的残差模块进行改进来对高层建筑物阴影与非阴影分类处理. CNN网络模型由1个输入层、4个改进注意力残差模块和1个输出层组成. 首先, 将输入数据集进行预处理, 统一尺寸为224×224, 然后, 输入到输入层; 输入层包括一个卷积层和一个最大池化层, 卷积层是由7×7×64大小卷积核构成, 最大池化层尺寸为4×4×64, 经过卷积和池化层处理后输出大小为56×56×64, 然后输入4个注意力残差模块; 4个注意力残差模块分别由第2.2节改进的两个残差单元组成, 经过4个注意力残差模块处理后, 输出特征图尺寸为7×7×512; 最后的输出层由全局池化层和全连接层构成, 最终输出尺寸为1×2, 代表阴影和非阴影两类.
2.4 损失函数针对梯度消失和梯度弥漫问题, 残差网络提出了恒等变化的思想[17], 通过恒等变化, 使浅层特征能够直接传递给高层特征, 并使目标函数不断逼近一个恒等映射来进行参数优化学习, 式(18)、式(19)为残差网络通过链式求导进行参数更新的过程:
| $ \frac{{\partial L{{oss}}}}{{\partial {X_1}}}{\text{ = }}\frac{{\partial {F_N}({X_{{L_N}}}, {W_{{L_N}}}, {b_{{L_N}}})}}{{\partial {X_L}}} \times \cdots \times \frac{{{F_2}({X_{{L_2}}}, {W_{{L_2}}}, {b_{{L_2}}})}}{{\partial {X_1}}} $ | (18) |
| $ \frac{{\partial {X_L}}}{{\partial {X_1}}}{\text{ = }}\frac{{\partial {X_l} + F({X_l}, {W_l}, {b_l})}}{{\partial {X_l}}} = 1 + \frac{{\partial F({X_L}, {W_L}, {b_L})}}{{\partial {X_L}}} $ | (19) |
式(18)为原始参数更新过程, 当层数较深时, 其损失变化非常小, 式(19)为增加残差块后的参数偏导优化, 更能敏感的感知参数的变化, 在浅层学习时参数是线性叠加, 在深层学习时, 参数扰动变量会趋于零, 使残差模块处于恒等映射, 从而更好进行参数更新.
本文利用改进注意力机制残差网络对遥感图像进行二分类, 正例为真实的遥感图像阴影, 负例为湖泊、数目等偏绿色干扰地物, 采用交叉熵损失函数, 并利用Softmax函数将模型输出结果转化为0–1范围内.
| $ {{{y}}_j} = {{{{\rm e}^{{x_j}}}} \mathord{\left/ {\vphantom {{{e^{{x_j}}}} {\sum\nolimits_{i = 1}^{{N_{\rm class}}} {{{e}^{{x_i}}}} }}} \right. } {\sum\nolimits_{i = 1}^{{N_{\rm class}}} {{{\rm{e}}^{{x_i}}}} }} $ | (20) |
| $ L{{oss}} = - \sum\nolimits_{j = 1}^{{N_{\rm class}}} {{t_j}\log ({y_j})} $ | (21) |
其中, x、y为输入输出层的特征, i、j是输出层的索引值, Nclass是类别的总数目, tj为第j类的真实类别, yj为模型输出预测概率的结果.
3 实验分析经过对实验过程及数据进行分析, 在检测过程中精度指标主要是漏检和误检现象引起的, 因此本文选用漏检率和误检率作为高层建筑物阴影检测效果评价指标:
| $\left\{ { \begin{split} & 漏检率 = 漏检数/(真实数目+漏检数)\\ & 误检率 = 误检数/(真实数目+误检数) \end{split}} \right.$ |
为了验证本文改进最大类间方差和最小类内方法的阈值分割和基于八邻域约束端点检测断点修复轮廓检测方法的性能, 与文献[2–4]所述方法在不同场景下的高层建筑物阴影集群进行了对比实验, 实验结果如图7所示.
图7为4个场景下文献[2–4]和本文分割算法的阴影检测效果示意图, 其中图7(a1)–图7(e1)、图7(a2)–图7(e2), 图7(a3)–图7(e3), 图7(a4)–图7(e4)分别各个场景下对比效果. 表1为不同检测算法误检率和漏检率的对比情况. 在场景1和场景2下文本算法比其他算法误检率分别降低16.8%和11.1%; 在场景3有绿色操场的场景下, 本文算法误检率和漏检率都为0, 优于其它算法; 在场景4有河流的场景下, 本文改进阈值分割算法与文献[3]和文献[4]相比虽然误检率和漏检率结果相同, 但是由图7(e4)、图7(c4)和图7(d4)可以看出, 本文改进阈值分割算法分割效果边缘细粒度更加平滑.

|
图 7 不同场景下各种阴影检测算法对比效果图 |
由上述实验可知, 本文改进阈值阴影分割方法在漏检率和误判率两方面都优于文献[2]、文献[3]、文献[4]所述方法, 但是仍存在误检率过高的情况如场景4误检率为40%, 分析原因这些误检主要是湖泊、树木等偏绿色地物引起的, 为了验证本文改进注意力残差检测网络模型对误检地物的分类性能, 在操作系统Ubuntu 20.04、显卡RTX3060、本文第2.1节440张测试数据集上, 分别与SVM、VGG、Inception、ResNet18算法进行了对比实验. 表2为不同阴影分类算法在440张测试集上的测试结果, 从表中可以看出, 本文加入全局注意力机制的残差算法能够更好地区分正例阴影和负例阴影. 将本文改进阈值分割算法和注意力残差网络融合进行误判去除实验, 结果如表3所示, 从实验结果可知, 单使用改进阈值分割算法平均误检率为18.75%, 使用改进阈值分割和加入注意力机制残差算法后平均误检率为2.08%, 平均误检率降低了16.67%. 为了验证数据集样本多少对本文算法精度的影响, 分别采用不同数量的数据集进行训练并测试, 结果表明, 增加数据量大小能够提升算法的精度.
| 表 1 不同阴影检测算法结果对比 |
| 表 2 不同阴影分类算法对比 |
| 表 3 融合算法实验结果对比 |
4 结论与展望
针对高层建筑物遥感影像阴影提取困难、误检率大的问题. 本文提出了一种改进阈值分割和注意力残差网络结合的方法对建筑物遥感进行检测. 利用改进最大类间和最小类内方差模型来解决阈值选择困难的问题, 利用灰度变化的梯度特征进行轮廓提取, 利用边缘方向与梯度垂直特性进行边缘非极大值抑制解决边缘冗余的问题, 结合邻域联通特性建立邻域约束方程解决端点检测问题, 利用生成对抗网络模型进行数据扩充解决数据不足的问题, 对残差网络的每个特征图中加入注意力权重提取通道间的全局特性. 虽然本文阴影检测算法在上述数据集下检测结果良好, 但是仍然存在误判和漏检现象, 后期考虑收集更多的数据集进行实验, 根据实验结果, 对模型做进一步的优化.
| [1] |
葛乐. 遥感影像高大建筑物阴影检测与去除算法研究[硕士学位论文]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2018.
|
| [2] |
Makarau A, Richter R, Muller R, et al. Adaptive shadow detection using a blackbody radiator model. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2049-2059. DOI:10.1109/TGRS.2010.2096515 |
| [3] |
卢建华. 基于直方图阈值法的遥感图像分割算法研究[硕士学位论文]. 福州: 福建农林大学, 2013.
|
| [4] |
赵显富, 胡晓雯, 赵轩. 一种基于彩色模型的遥感影像阴影检测方法. 测绘通报, 2014, (5): 20–22, 59.
|
| [5] |
李晓芳. 基于自适应线性加权的彩色图像灰度化算法研究[硕士学位论文]. 兰州: 兰州大学, 2019.
|
| [6] |
崔靖茹, 李晨, 潘宁, 等. 基于线性加权的自适应图像去雾算法. 计算机应用与软件, 2017, 34(3): 148-153. |
| [7] |
王晓明, 徐涛, 冉彪. 最小类内方差支持向量引导的字典学习. 计算机工程, 2020, 46(4): 60-69. |
| [8] |
易三莉, 张桂芳, 陈菊. 基于信息熵的OTSU二次分割算法. 昆明理工大学学报(自然科学版), 2019, 44(2): 56-62. |
| [9] |
肖熙, 周路. 基于k均值和基于归一化类内方差的语音识别自适应聚类特征提取算法
. 清华大学学报(自然科学版), 2017, 57(8): 857-861. |
| [10] |
廖斌, 付忠旺. 基于边缘敏感递归滤波的彩色航拍图像云检测. 系统工程与电子技术, 2015, 37(12): 2879-2886. |
| [11] |
Raghuwanshi BS, Shukla S. Minimum class variance class-specific extreme learning machine for imbalanced classification. Expert Systems with Applications, 2021, 178: 114994. DOI:10.1016/j.eswa.2021.114994 |
| [12] |
王凡, 周国清, 张荣庭, 等. 面向FPGA的连通域快速标记方法. 计算机工程与应用, 2020, 56(22): 230-235. DOI:10.3778/j.issn.1002-8331.1909-0222 |
| [13] |
戴斌宇, 吴静静. 基于机器视觉的定子表面缺陷检测系统研究. 传感技术学报, 2019, 32(10): 1589–1594.
|
| [14] |
王正龙, 张保稳. 生成对抗网络研究综述. 网络与信息安全学报, 2021, 7(4): 68-85. |
| [15] |
马咏莉, 徐金东, 孙潇, 等. 基于注意力机制生成对抗网络的图像去雾. 中国科技论文, 2021, 16(11): 1215-1219. |
| [16] |
徐金东, 孙潇, 马咏莉, 等. 注意机制生成对抗网络单通道盲图像分离. 中国科技论文, 2021, 16(3): 266-270. |
| [17] |
韩彦岭, 崔鹏霞, 杨树瑚, 等. 基于残差网络特征融合的高光谱图像分类. 国土资源遥感, 2021, 33(2): 11-19. |
 2022, Vol. 31
2022, Vol. 31


