许多真实世界的数据集都是用图来表示的, 如社交网络^{[1, 2]}, 物理系统^{[3, 4]}, 交通网络^{[5, 6]}, 引用网络^[1,7,8], 推荐系统^{[9, 10]}和知识图谱^{[11, 12]}等. 由于图数据的每个节点的邻域大小都是不一致的, 而绝大多数深度学习模型, 如CNN, RNN等都先假设输入的数据为有序、大小固定的欧几里得数据, 这使得我们无法直接使用现有的深度学习模型来处理图数据. 因此, 研究者们提出了图嵌入模型将图数据转化为欧几里德数据并应用于实际任务中, 如社群分割、交通流量预测、蛋白质结构预测等.

图嵌入模型是一种将图数据映射到低维向量空间的算法. 早期的图嵌入模型, 如LINE^[13]通过计算节点之间的一阶和二阶邻域的相似度来生成节点嵌入. DeepWalk^[14]、Node2Vec^[15]和TADW^[16]等方法, 利用随机游走算法, 生成图的节点序列, 并利用跳字模型(skip-gram^[17])来计算节点的嵌入. 随着深度学习的快速发展, 图神经网络(GNNs)被提出, 它使用专门设计的神经层来学习图的表示. 基于谱域的图神经网络, 包括ChebNet^[18]和GCN^[19]等, 先对图数据进行图傅立叶变换, 将空域信号转化为谱域信号. 在此基础上使用卷积算子来进行特征扩散, 最后使用逆傅立叶变换将谱信号转化为空域信号. 基于空间的图神经网络, 包括GraphSAGE^[1], GAT^[20]和许多其他变体^[6,10,21], 通过直接在空域中进行信息传播, 解决了基于谱的模型的可扩展性低、泛化能力不好和计算量大的问题.

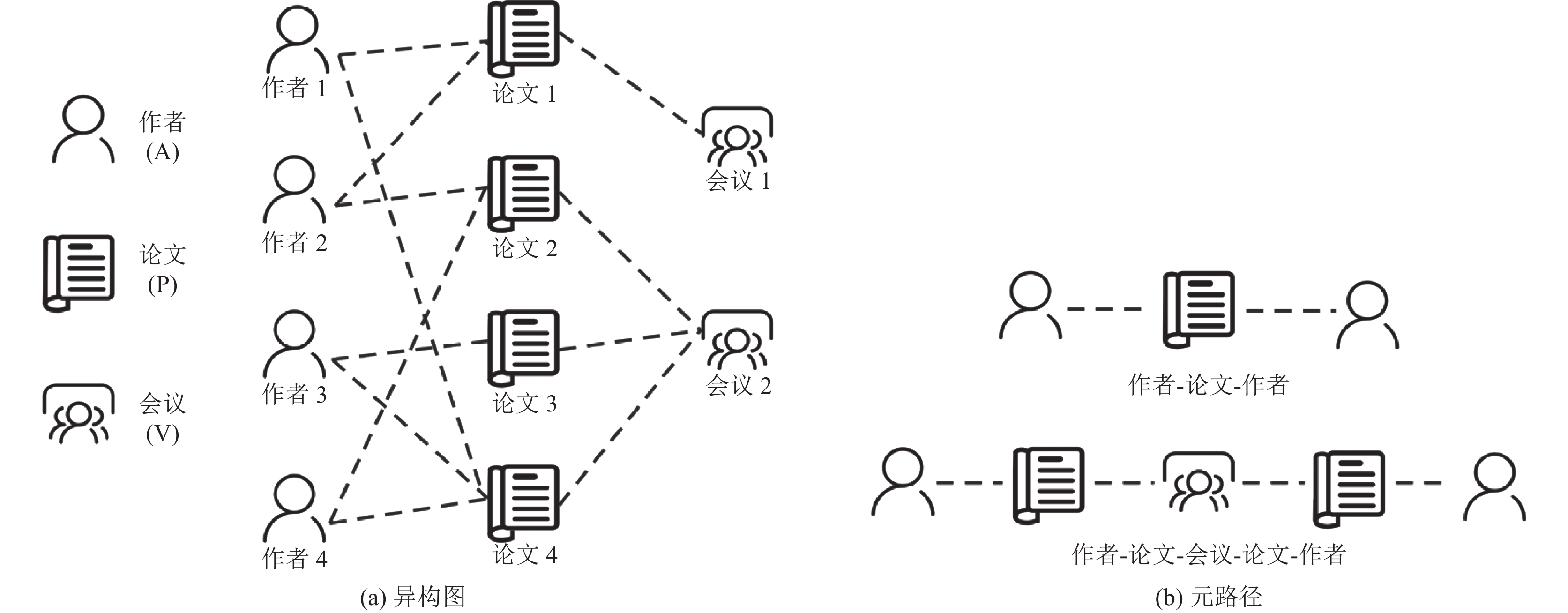
尽管图神经网络在许多任务上都取得了很好的结果, 但是他们都在异构图上表现不佳. 其主要原因是这些方法没有考虑异构图的异构信息, 如: 节点/边的属性/类型等、图的时间信息等. 现有多数异构图模型都基于元路径的思想. 元路径是一条抽象节点与具体边交替而成的序列. 比如在包含作者 (authors)、论文(papers)、会议 (venue) 3种节点类型的学者网络中, 作者-论文-作者 (APA)和作者-论文-会议-论文-作者 (APVPA) 是两条可以描述作者节点之间不同关系的元路径. 元路径APA表示为两个作者为共同作者; APVPA则可以表示为两个作者都在同一个会议里面发表过论文. 我们发现相比于传统的图嵌入模型和图神经网络方法, 元路径包含了异构图中的异构信息、语义信息和高阶结构信息. 目前基于元路径的异构图嵌入方法主要有如下问题: 1) 模型通常只考虑首尾的节点, 忽略了元路径中间节点和关系(如HERec^[22]和HAN^[23]). 2) 模型只考虑单一元路径(ESim^[24]、HIN2vec^[25])信息, 这会导致节点丢失掉来自其他元路径的邻居信息, 从而导致次优的性能.

为了解决这些局限性, 我们提出了一种新的基于元路径聚合与Transformer模型^[26]的异构图神经网络(MaGTNN). MaGTNN通过修改过的Transformer模型, 来捕获当前节点下所有的元路径邻居和元路径的语义信息. 具体来说, MaGTNN首先利用特定的线性变换矩阵来将不同属性的节点映射到相同的向量空间中. 接下来, MaGTNN会预先计算当前节点与其元邻居之间的位置编码. 随后, MaGTNN利用节点自身的特征、位置编码和边编码来计算当前节点和目标节点之间的注意力, 并在特征聚合操作中利用计算出来的注意力将元邻居的特征聚合到当前节点. 在元路径注意力计算步骤中, MaGTNN可以从相邻节点和中间的元路径上下文中捕获异构图的结构和语义信息; 在元邻居节点聚合的步骤中, MaGTNN可以捕获多条元路径的特征.

总之, 本文的主要工作有以下几个方面的贡献:

(1) 本文提出了一种新的基于元路径聚合与Transformer模型的异构图神经网络(MaGTNN).

(2) 本文设计了一个全新元路径注意力计算方法, 该方法可以考虑到了元路径中所有的节点特征和边信息, 具有更好的特征捕获能力.

(3) 本文在DBLP、ACM 和IMDB数据集上进行了节点分类和节点聚类的实验, 以评估本文提出的模型的性能. 在所有这些数据集和任务上的实验表明, MaGTNN学习的节点嵌入在分类、聚类两个下游任务上均优于其他基准模型生成的节点嵌入.

1 相关工作

现有的异构图嵌入方法主要目的是尽可能地保留图的异构结构信息. PME^[27]、EOE^[28]和HeGAN^[29]等方法只考虑节点一阶信息, 即节点的链接. 这类方法将每个链接类型视为一个关系, 并使用特定的关系矩阵将节点转换到不同的度量空间. 这样, 通过不同类型的链路连接的节点可以在不同的度量空间中彼此接近, 从而捕获图的异构性. 由于基于链接的方法只能获得异构图的局部结构, 因此研究者们试图引入复杂的高阶结构信息来获得一个更好的图嵌入. 比较常用的异构图高阶结构信息有路径和子图. Metapath2Vec^[30]及其衍生Metapath2Vec++, Spacey^[31], JUST^[32], BHIN2vec^[33], HHNE^[34]主要利用元路径引导的随机游走生成语义丰富的异构节点序列; 然后利用跳字模型(skip-gram)来保持节点 $v$ 与其上下文节点之间的邻近性, 即随机游走序列中的邻居; Metagraph2Vec^[35], DHNE^[36], HEBE^[37]等方法则是考虑了子图信息. Metagraph2Vec利用元图引导的随机游走生成异构节点序列. 然后采用跳字模型来学习节点嵌入. 基于此策略, Metagraph2Vec可以捕获丰富的结构信息和节点间的高阶相似性. DHNE和HEBE则是基于超边的图嵌入方法. DHNE使用了3层神经网络和非线性的元组相似度以学习超边的高阶结构信息. HEBE则是把与一个事件相关的所有节点都关联到一个超边中, 并且在训练中使节点与其所属超边之间的近邻度最大化. 在最大化近邻度后, HEBE可以保持同一超边内的节点相似度, 同时降低属于不同超边的节点相似度.

2 预备知识 2.1 异构图

异构图(heterogeneous graph)可表示为 $\mathcal{G} = (\mathcal{V}, \mathcal{E})$ , 其中 $\mathcal{V}$ 表示节点的集合, $\mathcal{E}$ 表示边的集合. 对于每一个节点存在一种映射关系 $\phi (v):\mathcal{V} \to \mathcal{A}$ , 对于每一条边存在一种映射关系 $\varphi (e):\mathcal{E} \to \mathcal{R}$ , $\mathcal{A}$ 和 $\mathcal{R}$ 分别代表节点类型和边类型, 且 $|\mathcal{A}| + |\mathcal{R}| \gt 2$ . 图1(a)即为一个异构图, 该异构图包含3个类型的节点, 分别为作者节点、论文节点和会议节点; 一个类型的边, 即代表两个节点之间存在某种关联.

2.2 异构图嵌入

对于给定的一个异构图 $\mathcal{G} = (\mathcal{V}, \mathcal{E})$ , 对图节点类型 ${A_i} \in \mathcal{A}$ , 图节点属性矩阵为 $ {X_{{A_i}}} \in {\mathbb{R}^{{\mathcal{V}_{{A_i}}} \times {d_A}_i}} $ . 异构图嵌入的任务是学习一个映射函数 $\mathcal{F}:\mathcal{V} \to {\mathbb{R}^d}$ , 其中 $d \lt \lt |\mathcal{V}|$ , 使得图中的节点能表示为隐空间 ${\mathbb{R}^d}$ 中的向量, 并且保留图中丰富的结构信息和语义信息.

2.3 元路径

对于给定的一个异构图, 元路径 $P$ 可定义为一组连接多种类型节点的复合关系, 具体形式为 $ {A_1}\mathop \to \limits^{{R_1}} {A_2}\mathop \to \limits^{{R_2}} \cdots \mathop \to \limits^{{R_l}} {A_{l + 1}} $ , 其中 ${R_i}$ 表示节点间的关系. 节点类型 ${A_1}, {A_{l + 1}}$ 之间的复合关系记为 $R = {R_1} \circ {R_2} \circ \cdots \circ {R_l}$ . 图1(b)即为预先定义的两条元路径, 其分别代表共同作者关系和共同在某个会议发表过论文关系.

2.4 Transformer架构

Transformer架构是由一系列Transformer层组成, 每一个Transformer层都含有如下两个模块: 自注意力模块和前馈神经网络模块. 令 ${{H}} = {[{{h}}_1^{\rm{T}}, {{h}}_2^{\rm{T}}, \cdots , {{h}}_n^{\rm{T}}]^{\rm{T}}} \in {\mathbb{R}^{n \times d}}$ 为自注意力模块的输入, 其中, ${{d}}$ 为隐藏层维度. 输入 ${{H}}$ 由3个向量 $Q, K, V$ 来计算其注意力:

$ Q = {{H}}{W_Q}, \; K = {{H}}{W_K}, \; V = {{H}}{W_V} $

(1)

$ E = \frac{{Q{K^{\rm{T}}}}}{{\sqrt {{{{d}}_K}} }}, \; Att({{H}}) = {\textit{Softmax}}(E)V $

(2)

其中, ${W_Q} \in {\mathbb{R}^{d \times {d_K}}}, {W_K} \in {\mathbb{R}^{d \times {d_K}}}, {W_V} \in {\mathbb{R}^{d \times {d_K}}}$ 分别为 $Q, K, V$ 的映射矩阵.

3 基于元路径的图Transformer网络

本文提出了一种基于元路径的图Transformer神经网络(MaGTNN) 来同时捕获元路径自身的语义信息与多条元路径间的全局相关性. 在第3.2节和第3.3节, 我们介绍了MaGTNN几个关键的特征计算方法. 在第3.4节, 我们则展示了每一个MaGTNN层的具体实现细节. 下面将对 MGTNN中的各个组件进行详细介绍.

3.1 模型输入

首先, 对于一个输入的异构图 $\mathcal{G}$ 及其节点特征 ${{{h}}_i} \in {\mathbb{R}^{{d_n}}}$ , 节点 $ij$ 之间的边特征 ${e_{ij}} \in {\mathbb{R}^{{d_e}}}$ . 由于节点的类型不同, 他们的自身特征属性也有可能不一样, 比如在IMDB中, 电影节点和演员节点的属性特征是不一样的, 电影节点可能包含电影类型、电影时长等特征, 而演员节点可能包含演员的姓名、性别等特征. 因此, 我们首先对节点特征进行一个线性变换:

$ h_i^\prime = {M_{{A_i}}} \cdot {{{h}}_i} $

(3)

其中, ${M_{{A_i}}}$ 为转换矩阵, ${A_i}$ 为节点 $i$ 所对应类型. 将变换之后的节点特征作为初始输入.

3.2 位置编码

在自然语言处理中, 基于Transformer架构的模型通常对每一个单词的词嵌入上加入单词的位置编码. 这一步的目的在于确保句子中每一个单词的编码都是独一无二的. 并且, 由于注意力机制通常会丢失单词之间的顺序信息, 因此加上单词的位置编码也可以保留词之间的顺序关系^[37]. 然而对于图结构来说, 节点并没有组织成序列. 因此, 早期的图神经网络在单层网络中只考虑了直接连接节点, 并使用堆叠(stack)的方法来获得图的高阶结构信息. 这些网络通常只能获得局部的结构信息, 缺少图的全局结构信息. 最近的一些研究RPGNN^[38], CGNNs^[39], DEGNN^[40]和文献[41]都在尝试在训练时同时融入节点的位置信息和图的结构信息. 本文的位置编码参考了文献[41, 42], 使用了拉普拉斯特征向量作为位置编码. 拉普拉斯向量定义如下:

$ \Delta = I - {D^{ - 1/2}}A{D^{ - 1/2}} = {U^{\rm{T}}}\Lambda U $

(4)

其中, $A$ 为 $n \times n$ 的邻接矩阵, $D$ 为度矩阵, $\Lambda $ , $U$ 分别代表特征值和特征向量. 对于节点 $i$ , 我们选择了 $k$ 个最小的非平凡特征向量作为其位置编码并记为 ${\lambda _i}$ . 值得注意的是, 直接将节点位置编码与节点特征相加会显著提高显存消耗. 因此本文将位置编码使用一个线性变换将其作为注意力系数的偏置量, 这个做法与和节点特征相加是等效的.

3.3 边编码

在异构图中, 边通常也包含结构信息, 如IMDB中, 演员-电影和电影-导演之间的边都包含不同的语义信息. 这种语义信息对于整个图的特征表示和节点的特征聚合是非常重要的. 在之前的基于元路径的图神经网络中, 研究者们通常只关注元路径中的节点特征, 忽略掉了元路径中的边的特征. 因此, 为了获得一个更加合理的, 我们在注意力计算步骤中加入了节点编码, 并将其作为一个偏置量, 来区分在不同元路径下节点的注意力.

记 ${P_r}(i, j) = ({R_1}, {R_2}, \cdots , {R_N})$ 为节点 $i, j$ 中一条元路径中的边序列, 则元路径中边编码计算为:

$ {\delta _{ij}} = \frac{1}{N}\mathop \sum \limits_{n = 1}^N {{{x}}_{{R_n}}}{(w_n^R)^{\rm{T}}} $

(5)

其中, ${{{x}}_{{R_n}}}$ 为边序列 ${P_r}(i, j)$ 中的第 $n$ 条边的特征, $w_n^E \in {\mathbb{R}^{{d_E}}}$ 为对应的权重向量, ${\mathbb{R}^{{d_E}}}$ 为边特征的维度.

3.4 基于元路径的图Transformer层

基于元路径的图Transformer层是在原始Transformer架构上的改进. 下面我们来介绍如何在节点特征在层 $\ell $ 处是如何进行更新.

对于给定的元路径集 $\mathcal{P}$ , 我们首先利用路径集 $\mathcal{P}$ 来构建基于元路径的邻接矩阵 $Met{a_{adj}}$ , 并利用式(4)来计算节点 $i$ 与其元路径邻居 $j$ 之间的距离编码 ${\lambda _{ij}}$ .

对于 $Met{a_{adj}}$ 中的一条元路径 $P$ , 记 $P(i, j)$ 为一条元路径实例, $i$ 为当前聚合节点, $j \in \mathcal{N}_i^P$ 为元路径邻居. 为了学习到元路径 $P(i, j)$ 中的中间节点的特征, 我们首先将其聚合为一个向量. 由于异构图中含有多个关系, 我们在这里参考了MaGNN^[42], RotatE^[12], 将关系向量映射到了复空间. 记 $P(i, j) = ({t_0}, {t_1}, \cdots , {t_n})$ , ${t_i}$ 为异构图的节点, 且 ${t_0} = i, \; {t_1} = j$ , ${R_m}$ 为节点 ${t_{m - 1}}$ 和 ${t_m}$ 之间的关系, ${r_m}$ 为关系向量, 则元路径聚合步骤为:

$ \left\{ {\begin{split} & {o_0} = h^\prime _{{t_0}} = h_u^\prime \\ & {o_m} = h^\prime _{{t_i}} + {o_{i - 1}} \odot {r_i} \end{split} } \right.$

(6)

$ {h_{P(i, j)}} = \frac{{{o_n}}}{{n + 1}} $

(7)

在完成中间节点聚合之后, 我们使用Transformer的注意力计算方式来计算元路径实例 $P(i, j)$ 与目标节点 $j$ 之间的注意力系数, 并利用该注意力系数来更新目标节点 $j$ 的特征. 注意力计算公式及节点更新函数为:

$ e_{ij}^\ell = \frac{{(h_i^{\prime (\ell )}W_Q^{k\ell })(h_j^{\prime (\ell )}W_K^{k\ell })}}{{\sqrt {{d}} }} + {b^\ell } \cdot {\lambda _{ij}} + {\delta _{ij}} $

(8)

$ \alpha _{ij}^\ell = {{}}{{\textit{Softmax}}_j}(e_{ij}^\ell ) $

(9)

$ {h_i}^{\prime \prime (\ell )} = O_h^\ell \mathop {||}\limits_{k = 1}^{{T}} \left(\mathop \sum \limits_{j \in {\mathcal{N}_i}} \alpha _{ij}^{k, \ell }{V^{k, \ell }}h_j^\ell \right) $

(10)

其中, $ W_Q^{k\ell }, W_K^{k\ell } $ 为式(1)在第 $\ell $ 层 $k$ 个注意力头中的映射矩阵, ${b^\ell }$ 为一个可学习矩阵, ${\delta _{ij}}$ 为式(4)中边的编码, $O_h^\ell \in {\mathbb{R}^{d \times d}}$ , $k \in [1, {{T}}]$ 为多头注意力数量, $||$ 为向量拼接操作.

整个基于元路径的Transformer层的最终输出还需要经过一个正则化层 (layer norm)、残差连接 (residual connection)和一个前馈神经网络(FNN):

$ \hat h_i^{(\ell + 1)} = {{Norm}}(h_i^{\prime (\ell )} + h_i^{\prime \prime (\ell + 1)}) $

(11)

$ \hat{\hat{h}}_{i}^{(\ell+1)}=W_{2}^{\ell} {ReLU}\left(W_{1}^{\ell} \hat{h}_{i}^{\ell}\right) $

(12)

$ h_{i}^{(\ell+1)}={Norm}\left(\hat{h}_{i}^{\ell}+\hat{\hat{h}}_{i}^{\ell+1}\right) $

(13)

其中, $ {W_1}^{(l)} \in {\mathbb{R}^{2d \times d}}, W_2^l \in {\mathbb{R}^{d \times 2d}} $ 为可学习映射矩阵.

4 实验 4.1 数据集简介

为了评估 MaGTNN模型, 本文在3个异构图数据集: DBLP ( http://web.cs.ucla.edu/~yzsun/data/)、ACM ( https://github.com/Jhy1993/HAN)和IMDB ( https://www.kaggle.com/datasets/karrrimba/movie-metadatacsv)上进行节点分类与节点聚类实验. 表1中展示了实验使用的异构图数据集的基本统计信息, 各数据集的划分遵循文献[23]的设置.

DBLP是一个计算机科学领域的文献集成网站.在本文中, 我们使用的是从DBLP中抽取的一个子集^{[43, 44]}, 其中包含4057个作者, 14328篇论文, 7723个主题和20 个出版社. 作者被划分为4个研究领域 (数据库, 数据挖掘, 人工智能和信息检索). 每一个作者都由其论文中的关键词所构成的词袋来表示. 在本文中, 作者节点被划分为训练集, 验证集和其测试集, 其中各个划分所包含的节点数目分别为: 400个(9.86%), 400个(9.86%), 和3257个(80.28%).

IMDB是一个互联网电影数据库. 我们从IMDB中抓取了一个子集来构建数据集, 其中包括4278 个电影, 2081个导演, 和5257 个演员. 电影节点被分为3个类型(动作片, 喜剧和戏剧). 每个电影都的特征由其情节的关键词所构成的词袋表示. 在本文中, 电影节点被划分为训练集, 验证集和其测试集, 其中各个划分所包含的节点数目分别为: 400个(9.35%), 400个(9.35%)和3478个(81.30%).

ACM数据集是从发表在KDD, SIGMOD, SIGCOMM, MobiCOMM和VLDB中论文抽取构建来. 我们从其中抽取了3025篇论文, 其中包含5835个作者和56个主题. 论文被大致划分为3类(数据库, 无线通信和数据挖掘). 论文节点的特征由其关键词词袋所表示, 标签为其发表的会议. 同时, 在本文中, 论文节点被划分为训练集, 验证集和其测试集, 其中各个划分所包含的节点数目分别为: 400个(13.22%), 400 个(13.22%)和2225个 (73.56%).

4.2 对比方法及参数设置

本文选取了同构图嵌入模型、同构图神经网络和异构图神经网络作为基准模型与MaGTNN的实验结果进行比较, 各基准模型介绍如下.

Node2Vec^[15]: 基于随机游走算法的同构图嵌入模型. 该模型使用随机游走算法来生成图的节点序列, 并利用跳字模型来学习节点嵌入.

Metapath2Vec^[25]: 基于元路径随机游走算法的异构图嵌入模型. 该模型通过元路径随机游走生成节点序列后使用跳字模型来学习节点嵌入.

HERec^[22]: 该模型在元路径随机游走的基础上删除掉游走节点序列中与起始节点类型不同的节点, 将其原始的异构节点序列转化为同构节点序列, 随后在所获得的同构游走序列上使用Node2Vec来计算节点嵌入. 该模型可以在学习到异构信息的同时降低训练的难度.

GCN^[8]: 基于谱域的卷积图神经网络. 该模型通过对图的拉普拉斯矩阵上的卷积操作, 并堆叠了多个图卷积层, 来捕获图的高阶结构信息.

GAT^[20]: 基于自注意力机制的图神经网络. 该模型通过自注意力机制来对邻居节点进行聚合, 实现了对不同邻居权值的自适应匹配. GAT堆叠多个自注意力层来获得图的高阶结构信息.

HAN^[23]: 基于层次注意力的异构图神经网络. 该模型包含了节点级注意力和语义级注意力. 通过使用节点级注意力来学习元路径的邻居节点权重并将其聚合获得当前语义的节点嵌入, 最后利用语义级别注意力机制评判每个元路径的权重并进行聚合, 获得最终的节点嵌入.

实验中对于基于随机游走算法的模型(Node2Vec、Matapath2Vec、HERec), 我们将游走窗口设置为5, 游走长度设置为100, 每个节点游走次数为40次, 负采样设置为5. 对于同构图模型 (Node2Vec、GCN和GAT), 本文将原始异构图直接输入, 忽略节点和边的异质性. 对于基于注意力的图神经网络模型 (GAT、HAN以及MaGTNN), 多头注意力的注意力头数统一设置为8, 注意力向量维度设置为128. 为了保证公平性, 所有模型生成的节点嵌入维度均设置为128. 由于图神经网络模型 (GCN、GAT、HAN和MaGTNN) 在训练的损失函数计算时使用了训练集和验证集的节点标签, 因此, 为了保证标签不被泄漏, 我们仅使用测试集的节点作为下游任务的实验评估. 对于下游任务的评价指标, 在节点分类任务上, 我们采用micro-F1作为评价指标, 其常用来衡量多分类任务下模型的准确度; 在节点聚类任务上, 我们采用聚类任务常用的评价指标: 标准化互信息 (NMI)和调整兰德里系数 (ARI).

4.3 节点分类任务

在节点分类任务中, 本文将各模型训练出来的节点嵌入直接输入到一个线性支持向量机(support vector machine, SVM) 中, 计算SVM分类结果的micro-F1值作为评估. 我们还测试了各模型在不同训练率 (在训练集中随机选取20%–80%的节点进行训练)下的节点分类结果. 表2记录的是在同样的数据集划分和训练率, 所有模型10次运行结果的平均值.

从表2中可以看出, MaGTNN在不同数据集和训练率下都普遍优于其他的基准模型. 同时在3个数据集中我们可以看到, 忽略掉异构信息的模型Node2Vec反而在ACM和IMDB数据集上都普遍优于只考虑单条元路径异构图模型Metapath2Vec, HERec. 这是由于元路径本来就是一个信息损失的过程, 使用元路径会在一定程度上减少模型可以获得的路径数量, 这很大程度上影响了模型的效果. 图神经网络模型, 尤其是异构图神经模型在所有数据集和训练率都优于传统图嵌入模型. 相比于目前的最优表现模型HAN, MaGTNN在3个数据集上面都有1%–4%的提升. 这表示在注意力计算时, 考虑位置和边信息的注意力计算会有更好的表现.

4.4 节点聚类任务

我们也在所有数据集上对各模型进行了节点聚类实验. 在这一部分中, 我们使用K-均值( K-means) 算法对各模型训练出来的节点嵌入进行聚类运算. 我们将数据集的节点标签数设置为K-means算法的聚类簇数. 与节点分类实验相同, 我们对每个数据集进行了10次实验, 并取所有结果平均值作为最终结果记录于表3中.

从表3中可见, 在ACM和DBLP数据集中, 异构图神经网络模型HAN、MaGTNN效果要优于传统图嵌入模型 (Node2Vec、Metapath2Vec、HERec)和同构图神经网络模型 (GCN、GAT) , 这证明了结合元路径信息和图神经网络能更有效学习图的异构信息. 同时, 相对于HAN, MaGTNN在以上两个数据集上均提升了2%左右, 其中一个原因为MaGTNN在进行结构学习时考虑了边信息对注意力的影响; 此外, Node2Vec模型在聚类任务中表现优异, 这是由于在随机游走过程中, 邻近的节点在有更大的概率在同一条游走序列中, 因此在特征聚合时, 这些节点在欧式空间中的映射也会分布得更加靠近, 在聚类任务中也更容易分为同一簇. 相对于HAN, MaGTNN在输入的特征中加入了位置编码, 这可能是MaGTNN表现优异的另一个原因. 此外, 值得注意的是在聚类任务中, 所有模型在IMDB数据集上表现均不佳, 其原因可能是由该数据集中电影节点的标签导致: 在IMDB中一部电影含有多个类别作为其标签, 而在聚类问题中, 我们只能选择一个类别作为其标签, 这极大的影响到了聚类的准确性.

5 结论与展望

本文针对异构图提出了一种基于元路径的图Transformer神经网络(MaGTNN) 模型来学习节点嵌入. 我们提出的模型首先将异构图使用元路径进行采样, 构建出基于元路径的多关系子图, 通过引入了元路径上的位置编码和节点编码, MaGTNN 相比其他模型能够获得更多的语义信息. 并且, MaGTNN使用了经过改进的图Transformer层来聚合元邻居下的所有节点特征, 可以学习到元路径间的全局相关性. 本文在3个真实数据集上进行了节点聚类和分类实验, 实验表明 MaGTNN 在这两个任务上相较其他基准模型一致取得最好的预测效果.