1 引言

近年来, 日益丰富化、智能化的移动设备应用也不断涌现, 例如虚拟现实、增强现实、在线游戏、4K/8K超高清视频等等. 此类应用通常具有计算数据量大、时延敏感等特点. 尽管新的智能移动设备具备的计算能力越来越强大, 但是受自身硬件条件的限制, 仍然无法在短时间内处理此类计算密集型应用, 影响用户的使用体验^[1]. 同时, 运行此类应用会带来巨大的电量消耗, 从而降低移动设备的续航能力.

为了解决上述问题, 移动边缘计算(mobile edge computing, MEC)技术应运而生^[2]. MEC技术通过在用户附近部署具有强大计算、存储能力的MEC服务器, 使用户可以将移动设备本地无法处理的计算任务卸载到MEC服务器上计算, 借助服务器强大的计算能力在短时间内完成任务计算, 再将计算结果回传给移动设备, 从而有效减少任务处理时延并降低移动设备能耗.

与此同时, 随着无线局域网的快速发展, Wi-Fi成为社会数字化的关键基础网络设备, 承载了60%的移动通信业务流量^[3]. 而Wi-Fi网络中的AP (access point)与移动设备的相比, 可以配备更加强大的计算能力, 包括集成具有更强计算能力或者固化了AI算法的处理器. 同时, 与蜂窝网络相比, Wi-Fi网络具有大带宽、低时延、高速率以及无需考虑运营商资费问题等优势. 因此, 研究将MEC技术应用到Wi-Fi网络中, 以克服移动设备计算、能耗以及存储方面的限制, 是未来通信、计算、存储一体化发展的一个重要趋势.

针对边缘计算中的任务卸载和资源分配, 许多学者做了相关研究. 现有研究中根据研究场景进行分类, 可分为单MEC服务器场景^[4]与多MEC服务器场景. 而多MEC服务器场景又可分为不支持基站 (base station, BS)间协作^[5]与支持BS间协作^[6]两类. 在单MEC服务器场景中, 只存在一个BS, 且在该BS中部署了一个MEC服务器. 在多MEC服务器场景中, 存在多个BS, 且每个BS中部署了一个MEC服务器. 在进行数据传输时, 不同BS间可能复用相同的频谱资源, 从而产生干扰, 影响数据传输速率. 而支不支持BS间协作的区别在于, 若支持BS间协作, 一个BS可通过BS间通信链路将无法处理的任务进一步卸载到有剩余计算资源的BS中进行计算.

根据研究方向进行分类, 大致可分为任务卸载策略算法研究、任务卸载策略与资源分配联合优化算法研究以及MEC网络架构设计^[7] 3类. 文献[8]中, 针对蜂窝网络单MEC服务器场景, 以任务执行时间限制下最小化能耗作为优化目标, 利用非协作博弈算法解决了任务卸载决策的问题, 但并未考虑通信资源分配的问题. 文献[9] 则针对蜂窝网络中MEC任务卸载决策、通信和计算资源分配联合优化问题, 以最小化用户任务处理时延与能耗加权值作为优化目标, 将Q学习和凸优化理论整合到一起, 压缩动作空间的维度, 降低计算复杂度.

根据优化目标进行分类, 大致可分为最小化时延、最小化能耗、权衡时延和能耗3类. 文献[10]以在满足能耗限制的条件下最小化时延作为优化目标, 将SDN网络与MEC结合, 利用Q学习和协作Q学习的强化学习算法联合优化计算任务卸载和资源分配. 文献[11]以在时延限制条件下最小化移动设备能耗作为优化目标, 联合优化蜂窝网络下MEC卸载策略、通信和计算资源分配, 将优化问题建模为混合整数非线性规划问题, 利用变量融合的分支限界算法求解.

综上所述, 尽管当前业界对MEC系统下任务计算卸载策略和资源分配问题已经有了多方面的研究, 但大多针对蜂窝网或车联网, 而Wi-Fi网络下的MEC系统研究几乎没有. 而Wi-Fi网络与蜂窝网、车联网之间在网络资源特征、设备移动性等方面存在较大差异. 例如, 在蜂窝网络中, 基站在为用户分配通信资源时, 以固定大小的RB (resource block)作为单位, 一个用户可分配得到多个RB; 而在Wi-Fi网络中, AP在为用户分配通信资源时, 以RU (resource unit)作为单位, 一个用户只能分配得到一个RU. 所以目前针对蜂窝网以及车联网的MEC方案并不完全适用于Wi-Fi网络. 同时, 现有大多数研究中仅对任务卸载决策以及计算资源分配进行研究, 而并未考虑移动设备在进行任务卸载时所使用的通信资源分配. 但系统中通信资源也是有限的, 如果移动设备分配得到的通信资源较少, 且卸载任务量较大时, 也会产生较大的数据传输时延. 由此可见, 在MEC系统中, 通信资源与计算资源互为瓶颈. 基于此, 本文对Wi-Fi网络中的MEC系统进行研究, 针对多MEC服务器多AP协作场景, 提出了一种任务卸载和资源分配方案, 通过对任务卸载决策、通信资源分配以及计算资源分配的联合优化, 实现在满足任务处理时延限制的前提下, 最小化移动设备端能耗的目标.

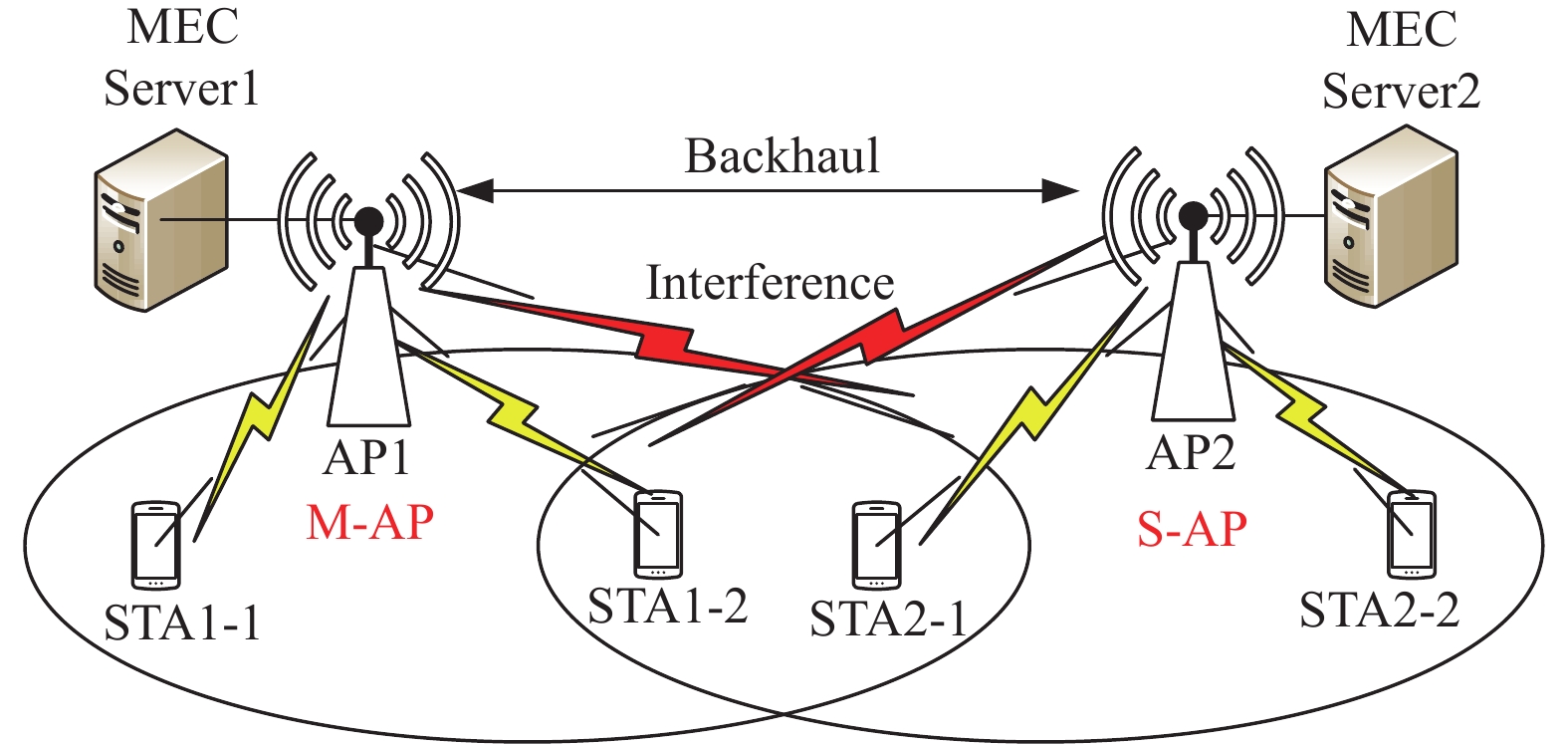
2 系统模型

假设多MEC服务器多AP协作场景中存在的多个AP, 并且网络中的AP通过某种方式形成了相应的多AP协作集, 本文针对一个多AP协作集下的计算卸载与资源分配问题进行研究. 如图1所示, 一个多AP协作集中包含了一个主AP, 其余为从AP. 每个AP关联着多个STA (station), 且每个AP部署了一个MEC服务器. 同时, AP可以通过AP间的高速通信链路与其他AP进行信息的交互^[12]. 因此, 在进行卸载决策时, STA除了可以将任务卸载到关联AP的MEC服务器上计算之外, 还可以通过AP间协作, 将无法处理的任务进一步卸载到有剩余计算资源的邻居服务器上计算.

Wi-Fi网络下的MEC任务卸载流程可分为以下4个阶段.

(1)信息交互及算法决策阶段: 各AP收集关联STA的计算资源、任务量大小与任务时延限制等信息. 随后各从AP将收集到的本基本服务集 (basic service set, BSS)内相关信息上报给主AP. 主AP在收集到各个从AP的BSS信息后, 根据本文所设计的算法, 对所有AP的计算卸载、通信资源分配和计算资源分配进行统一决策. 随后, 主AP将决策结果告知各个从AP.

(2)任务卸载阶段: 根据上一阶段获得的任务卸载决策与通信资源分配结果, STA首先将计算任务卸载到关联AP上, 如果需要执行协作卸载, 则关联AP再通过AP间的高速回传链路将任务卸载到其他AP的MEC服务器上执行.

(3)任务计算阶段: MEC服务器根据第一阶段执行任务卸载及资源分配联合优化算法得到的计算资源分配结果对STA卸载的任务进行计算.

(4)计算结果回传阶段: MEC服务器完成STA卸载任务的计算后, 将卸载任务计算结果回传给STA.

2.1 网络模型

假设网络中存在M个AP, 每个AP下关联了N个STA, STA_m,n表示AP_m下关联的第n个STA, 每个AP部署有一个MEC服务器, MEC服务器可以并行对多个任务进行计算. 假设每个STA都有一个计算密集、时延敏感型任务 $ C{T_{m, n}} = \{ {D_{m, n}}, {X_{m, n}}, {\tau _{m, n}}\} $ 需要计算, 且任务不可分割, 其中, D_m,n表示任务的数据量, X_m,n表示任务的计算量, 即计算该任务所需要的CPU周期, 本文中假设任务在AP和STA上计算单位相同, 通常 ${X_n} = g \times {{{D}}_n}$ , 其中g表示任务的平均计算密度, $ {\tau _{m, n}} $ 表示任务处理能容忍的最大时延, 即时延限制. 定义 $ {a_{m, n}} \in \{ 0, 1, 2, \cdots , M\} $ 为STA_m,n的决策, 其中, $ {a_{m, n}} = 0 $ 表示STA_m,n的计算任务在本地执行, $ {a_{m, n}} = k $ 表示将STA_m,n的计算任务卸载到AP_k的MEC服务器上执行. 定义h_m,n为任务CT_m,n卸载所经过的AP间跳数, 为了避免任务无限制地卸载, 造成网络拥塞等问题, 本文规定, AP间协作卸载只允许卸载到相邻AP, 即 $ {h_{m, n}} \leqslant 1 $ . 所有STA的任务卸载决策向量表示为 ${A_{M \times N}} = \{ {a_{1, 1}}, {a_{1, 2}}, \cdots , {a_{1, N}}; \cdots ;{a_{{{M}}, 1}}, {a_{{{M}}, 2}}, \cdots , {a_{M, N}}\}$ .

2.2 通信传输模型

对于802.11ax设备, 既可以通过CSMA/CA方式独立竞争进行上行传输, 也可以通过上行OFDMA方式, 在AP调度下进行上行传输. 为了避免出现用户向AP上报任务卸载请求, 请求AP为其分配通信资源后, 该用户再通过CSMA/CA竞争信道进行上行任务卸载, 导致通信资源浪费的情况, 本研究中假设, STA如果向AP上报任务卸载请求, 请求AP为其分配通信资源, 则该用户不再通过CSMA/CA的方式竞争信道进行上行任务卸载. 同时本文主要针对STA采用上行OFDMA方式的情况进行研究. 即AP利用剩余的通信资源通过OFDMA的方式为进行任务卸载的STA分配一个RU, 调度STA在对应的RU上进行上行传输, 完成任务卸载. 对于既存在通信任务又存在计算任务的STA, 本文中假设计算任务优先级高于通信任务优先级, 优先调度计算任务, 且通信任务与计算任务不进行混合调度.

在进行任务卸载时, 假设用B_m表示AP_m所使用的信道带宽, 其中包含了S_m个子载波. 同时, 假设AP_m所关联的STA中有O_m个STA需要进行任务卸载, 则在通信资源充足的情况下, AP_m需要将带宽B_m划分O_m个RU, 并分配给需要进行任务卸载的STA用于数据传输. 定义r_m,n表示AP_m为STA_m,n分配的子载波个数, 即RU的大小. 在IEEE 802.11ax协议中规定, RU的取值包括: (26, 52, 106, 242, 484, 996)个子载波. 因此 $ {r_{m, n}} \in \{ 0, 26, 52, 106, 242, 484, 996\} $ , 其中 $ {r_{m, n}} = 0 $ 表示STA_m,n的计算任务在本地执行, 不为其分配通信资源. 则包含所有STA的通信资源分配向量表示为: ${R_{M \times N}} = \{ {r_{1, 1}}, {r_{1, 2}}, \cdots , {r_{1, N}}; \cdots ;{r_{{{M}}, 1}}, {r_{{{M}}, 2}}, \cdots , {r_{M, N}}\}$ .

根据香农公式, 任务CT_m,n进行任务卸载时的最大数据传输速率为:

$ {{{v}}_{m, n}} = {B_m} \times \frac{{{r_{m, n}}}}{{{S_m}}} \times {\log _2}(1 + {\textit{SINR}}_{m, n}) $

(1)

其中, SINR_m,n表示STA_m,n在RU_m,n上的信干噪比.

由此, 可计算出STA_m,n将任务卸载到MEC服务器的传输时延和传输能耗分别为:

$ T_{m, n}^{\rm trans} = \frac{{{D_{m, n}}}}{{{v_{m, n}}}} $

(2)

$ E_{m, n}^{\rm trans} = {p_{m, n}} \times T_{m, n}^{\rm trans} $

(3)

其中, p_m,n表示STA_m,n的发送功率.

本文中假设AP间通过高速回传链路进行通信, 因此, 在进行AP间协作卸载时, 任务在AP间的传输时延可忽略不计. 同时, 根据文献[13,14], 无线网络中下行传输速率一般远高于STA上传速率, 且MEC服务器计算完成后的回传数据大小通常远小于原始计算任务的数据大小, 因此, 在本文中, 任务计算结果回传所产生时延开销也忽略不计.

2.3 计算模型

当任务在STA_m,n本地进行计算, 所产生的计算时延表示为:

$ T_{m, n}^{\rm local} = \frac{{{X_{m, n}}}}{{f_{m, n}^{\rm local}}} $

(4)

其中, $f_{m, n}^{\rm local}$ 表示STA_m,n的计算频率.

本地计算能耗为:

$ E_{m, n}^{\rm local} = \kappa {(f_{m, n}^{\rm local})^2}{X_{m, n}} $

(5)

其中, $ \kappa $ 为功耗系数^[15].

假设 ${C_{M \times N}} = \{ {c_{1, 1}}, \;{c_{1, 2}},\; \cdots ,\; {c_{1, N}}; \cdots ;{c_{M, 1}},\; {c_{M, 2}}, \;\cdots , {c_{M, N}}\}$ 表示MEC服务器分配给STA的计算资源的比例, ${c_{m, {{n}}}} \in [0, 1]$ . 当 ${c_{m, {{n}}}} = 0$ 表示STA_m,n的计算任务在本地执行, 则STA_m,n将任务卸载到MEC服务器上计算所需计算时延为:

$ T_{m, n}^{\rm server} = \frac{{{X_{m, n}}}}{{{c_{m, n}} \times f_m^{\rm server}}} $

(6)

其中, $f_m^{\rm server}$ 表示AP_m 上MEC服务器的计算频率.

2.4 优化问题模型

定义STA_m,n完成任务CT_m,n处理的能耗开销为:

$ {E_{m, n}} = \left\{ \begin{gathered} E_{m, n}^{\rm local}, {\text{ }}{\rm if}{\text{ }}{a_{m, n}} = 0 \\ E_{m, n}^{\rm trans}, {\text{ }}{\rm if}{\text{ }}{a_{m, n}} \ne 0 \\ \end{gathered} \right. $

(7)

同时, 定义完成任务CT_m,n处理的时延开销为:

$ {T_{m, n}} = \left\{ \begin{gathered} T_{m, n}^{\rm local}{\text{ }}, {\text{ }}{\rm if}{\text{ }}{a_{m, n}} = 0 \\ T_{m, n}^{\rm trans} + T_{m, n}^{\rm server}, {\text{ }}{\rm if}{\text{ }}{a_{m, n}} \ne 0 \\ \end{gathered} \right. $

(8)

本文主要研究问题是在多MEC服务器AP协作场景中, 在AP通信资源和MEC服务器剩余计算资源有限的条件下, 联合优化任务卸载决策、通信资源分配以及计算资源分配, 实现在满足任务处理时延限制的前提下, 最小化STA端能耗的目的. 问题可归纳为下列表达式:

$ P:\mathop {\min }\limits_{A, R, C} \sum\nolimits_{m = 1}^M {\sum\nolimits_{n = 1}^N {{E_{m, n}}} } $

(9)

s.t.

$ C1:{\text{ }}{h_{m, n}} \leqslant 1, {\text{ }}\forall m, \forall n $

(10)

$ C2:{\text{ }}\sum\nolimits_{n = 1}^N {{r_{m, n}}} \leqslant {S_m}, {\text{ }}\forall m $

(11)

$ C3:{{ C}}_m^{sum} \leqslant 1, {\text{ }}\forall m $

(12)

$ C4:{{ }}{{\text{T}}_{m, n}} \leqslant {\tau _{m, n}}, {\text{ }}\forall m, \forall n $

(13)

其中, C1表示AP间协作卸载决策中只允许在相邻AP间进行; C2表示各AP分配给关联STA的子载波总数不能超过该AP竞争到的子载波总数; C3表示各AP分配给STA的计算资源不能超过MEC服务器的总资源; C4表示任务需要在时延限制内完成计算.

3 边缘计算卸载和资源分配方案

为了解决第2节中提出的问题, 本节设计了一种基于遗传算法与匈牙利算法任务卸载及资源分配联合优化方案, 方案总体流程如图2所示.

3.1 任务卸载决策

当场景中MEC服务器数量为M, STA总数量为N时, 任务卸载决策存在(M+1)^N种组合, 当MEC服务器数量或STA总数较多时, 卸载决策组合数也会指数级增长, 因此采用遍历的方式获得最优任务卸载决策是不现实的. 而遗传算法, 将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程, 按照优胜劣汰的原理, 在每一代, 根据问题域中个体的适应度大小选择“优质”的个体, 并模拟遗传学中的交叉、变异过程, 产生出代表新的解集的种群, 逐代演化产生出越来越好的近似解. 在求解较为复杂的优化问题时, 遗传算法相对一些常规的优化算法, 通常能够较快地获得较好的优化结果. 因此, 本文选择了遗传算法对卸载决策进行求解. 首先, 介绍遗传算法中较为重要的几个概念.

个体: 优化问题中所需优化的变量, 在本文中即为卸载决策A_M×N, 而多个个体组成一个种群.

适应度: 每个个体都有其对应的适应度, 用于衡量个体是否“优质”, 适应度越大, 个体越“优质”. 适应度函数通常利用优化问题的目标函数进行构建, 本文的优化目标是在满足任务处理时延的限制下, 最小化STA总能耗, 因此将适应度函数表示为:

$ fitvalue = \left\{ \begin{gathered} \frac{1}{{{e_{\rm sum}}}}{\text{ }}, {\text{ }}{\rm if}{\text{ }}{N_{OD}} = 0 \\ \frac{1}{{pf \times {e_{\rm sum}}}}{\text{ }}, {\text{ }}{\rm if}{\text{ }}{N_{OD}} \ne 0 \\ \end{gathered} \right. $

(14)

其中, e_sum表示STA总能耗, N_OD表示超出任务处理时延限制的STA数量, pf表示惩罚因子, 表示为:

$ pf = \alpha \times {N_{OD}} $

(15)

其中, $ \alpha $ 表示惩罚影响因子, $ \alpha $ >1, $ \alpha $ 值越大, 惩罚因子对适应度值的影响越大.

选择: 根据种群中个体的适应度, 选择若一定数量的个体遗传到下一代, 适应度越大, 被选择遗传到下一代的概率越高. 本文采用保留前5个适应度最高的个体, 其余个体采用轮盘赌的方式进行选择.

交叉: 指的是两个父代个体的部分结构以一定的概率进行替换重组而生成新个体的操作, 本文中即对应两个卸载决策向量A_M×N中的部分结构以一定的概率进行替换重组而生成新的卸载决策向量.

变异: 个体中某个位置以很小的概率变异出新的个体. 本文中即对应卸载决策向量A_M×N中的某个STA的卸载决策发生了突变, 生成新的卸载决策向量.

任务卸载决策的算法流程如算法1所示.

算法1. 基于遗传算法的任务卸载决策算法

1. pop = Initial_pop(popsize); %初始化种群

2. While 未达到最大迭代次数且最优个体的适应度未收敛

3. fitvalue = Cal_fitness(pop); %计算种群适应度

4. pop_sel = selection(pop, fitvalue); %执行选择操作

5. pop_cros = crossover(pop_sel); %执行交叉操作

6. pop_mut=mutation(pop_cros); %执行变异操作

7. pop = pop_mutation; %更新种群

8. loop = loop + 1; %更新迭代次数

9. End while

10. fitvalue = Cal_fitness(pop); %计算完成迭代后种群适应度

11. [~, index] = max(fitvalue); %找到种群中适应度最大的个体

12. A = pop(index); %输出任务卸载决策

3.2 通信资源分配

完成任务卸载决策后, 则需为进行任务卸载的STA分配通信资源. 而通信资源分配包括两个步骤: 一是根据执行任务卸载的STA个数, 确定所使用的RU规格组合; 二是根据确定的RU规格组合, 为各个进行任务卸载的STA分配RU.

对于第1步, 在执行任务卸载的STA数量N_o确定后, 由于需要为每个STA分配一个RU, 因此AP需要将带宽划分为N_o个RU分配, 而将一定带宽划分为N_o个RU具有不同的划分方式, 不过由于RU规格种类有限, 且为了减小传输时延, 应尽量将所有子载波用完, 因此将一定带宽划分为一定数量的RU的划分方式也有限的, 所以, 本文中采取遍历的方式, 找寻出使得STA传输能耗最小的RU规格组合.

对于第2步, 则是需要考虑如何将N_o个RU分配给N_o个STA, 且一个RU只能分配给一个STA, 一个STA也只能得到一个RU, 这是一个典型的指派问题, 而匈牙利算法可以通过较低的复杂度, 快速求解出指派问题的最优解. 因此, 本文中采用了匈牙利算法求解RU分配问题.

要利用匈牙利算法求解RU分配问题, 首先需要构造一个效率矩阵Cost,Cost是一个维度为N_o×N_o的方阵, 其中的元素c_ij表示STA_i在RU_j上传输的能耗. 同时, 利用矩阵X表示RU分配方式, X是一个维度为N_o×N_o的方阵, 其中的元素x_ij表示是否将RU_j分配给STA_i, 1表示是, 0表示否.

由于本节的优化目标为: 求解出一种RU分配方式, 使得所有进行任务卸载的STA传输总能耗最小, 因此, 可将问题归纳为下列表达式:

$ P:{\text{ }}\mathop {\min }\limits_x \sum\nolimits_{i = 1}^{{N_o}} {\sum\nolimits_{j = 1}^{{N_o}} {{c_{ij}}{x_{ij}}} } $

(16)

s.t.

$ C1:{\text{ }}\sum\nolimits_{i = 1}^{{N_o}} {{x_{ij}} = 1, {\text{ }}j = 1, 2, \cdots, {N_o}} $

(17)

$ C2:{\text{ }}\sum\nolimits_{j = 1}^{{N_o}} {{x_{ij}} = 1,\; {{ i}} = 1, 2, \cdots, {N_o}} $

(18)

$ C3:{\text{ }}{x_{ij}} = 0{\text{ }}{\rm or}{\text{ }}1, {\text{ }}i, j = 1, 2, \cdots , {N_o} $

(19)

其中, C1表示一个RU只能分配给一个STA. C2表示一个STA只能分配得到一个RU. C3表示RU分配矩阵的取值范围.

在利用匈牙利算法求解上述问题前, 首先需要了解匈牙利算法中关键的一个定义与两个定理.

定义1. 在效率矩阵C中, 若存在一组0元素, 其中任意两个0元素均处在不同行不同列, 则该组0元素称为独立0元素组, 其中每个元素称为独立0元素.

定理1. 将效率矩阵中的某一行或列同时减去一个常数t, 得到新的效率矩阵C', 则以C'为效率矩阵的新指派问题与原指派问题的最优解相同, 只是其最优值比原最优值减少了t.

定理2. 效率矩阵C中独立0元素的最多个数等于能覆盖效率矩阵C中所有0元素的最少直线数.

通过定理1, 可以推导出: 若将指派问题的效率矩阵每行及每列分别减去各行及各列的最小元素, 则得到的新指派问题与原指派的最优解相同. 且生成的新效率矩阵C'必然会出现一些零元素, 元素 $ c_{i, i}^{\prime}=0 $ 表示若将RU_j分配给STA_i, 产生的传输能耗最低. 而利用匈牙利算法求解指派问题的本质是通过变换效率矩阵, 将效率矩阵的部分元素化为0, 如果存在一个独立0元素组中0元素个数等于矩阵的阶数(即等于RU个数), 则该组独立0元素组所对应的分配方式即为最优解. 而具体算法流程分为以下4步:

Step 1. 对效率矩阵进行初等行列变换, 每行减去该行的最小数, 每列减去该列的最小数, 得到新的效率矩阵C', 使各行各列都出现0元素.

Step 2. 执行试指派. 1)找出只有一个0元素的行, 将该0元素标记为T, 同时将该0元素所在列的其他0元素标记为F; 2)找出只有一个0元素的列, 将该0元素标记为T, 同时将该0元素所在行的其他0元素标记为F; 3)若存在还没有被标记的0元素, 则从剩余的0元素最少的行(列)开始, 选0元素标记为T, 将同行同列的其它0元素标记为F, 反复进行, 直到所有0元素均被标记, 被标记为T的0元素即为一组独立0元素组; 4)若被标记为T的0元素个数等于矩阵维度N_o, 则找到最优解, 根据0元素的位置, 确定RU分配结果, 随后结束程序; 否则, 执行Step 3.

Step 3. 找出覆盖所有0元素的最少直线. 1)标记不存在被标记为T的0元素的行; 2)对已被标记行中存在被标记为F的0元素所在的列进行标记; 3)对已被标记列中存在被标记为T的0元素所在的行进行标记; 4)重复2)–3), 直至不存在需要被标记的行或列; 5)对没有被标记的行画横线, 对被标记的列画竖线, 能覆盖效率矩阵C中所有0元素的最少直线数L; 6)如L等于矩阵维度N_o, 则执行Step 2, 重新试指派, 若L小于N_o, 根据定理2可知, 效率矩阵C'中独立0元素的最多个数小于N_o, 这种情况下, 无法求解出问题的最优解, 需要执行Step 4.

Step 4. 增加0元素. 寻找效率矩阵C'中未被直线覆盖部分的最小元素, 对未被划线的行减去最小元素, 并对被划线的列加上最小元素, 随后执行Step 2.

通信资源分配的算法流程如算法2所示.

算法2. 基于匈牙利算法的通信资源分配算法

1. N_off=length(find(A~=0)); %统计执行卸载的STA数量

2. IfN_off > N_RU %如果卸载STA数大于最大可划分的RU数量

3. 将卸载STA按时延限制升序排序

4. 取前N_RU个STA执行任务卸载, 其余STA回退到本地执行

5. 更新卸载决策A与卸载STA数N_off

6. End if

7. RU_group=get_RU_group(B, N_off);%根据卸载STA数量及带宽获取RU规格组合

8. N_group = size(RU_group, 1); % RU规格组合数

9. For i = 1:N_group

10. Cost = Cal_cost(N_group(i, :)); :%计算RU规格组合i的效率矩阵

11. [X{i}, E(i)] = Hungarian(Cost); %利用匈牙利算法得到RU规格组合i的分配结果以及对应的STA传输总能耗

12. End for

13. [~, index] = min(E); % 找出使STA传输总能耗最小的RU规格组合

14. N = RU _group(index, :);%得到RU分配结果

3.3 计算资源分配

假设任务处理时延恰好等于时延限制, 即式(13)左右两边相等时, 可推导出计算资源分配比例:

$ {c_{m, n}} = \dfrac{{{X_{m, n}}}}{{\left({\tau _{m, n}} - \dfrac{{{S_m} \times {D_{m, n}}}}{{{r_{m, n}} \times {B_m} \times {{\log }_2}(1 + S{{I}}N{R_{m, n}}) \times f_m^{\rm server}}}\right)}} $

(20)

计算资源分配的算法流程如算法3所示.

算法3. 计算资源分配算法

1. c_sum=0; %初始化已分配的计算资源比例

2. For i = 1:N %依次为STA分配计算资源

3. If r_i == 0 %如果STA本地计算

4. c_i = 0;

5. else % 如果为STA分配了通信资源

6. 利用式(20)计算c_temp

7. If 1 – c_sum < c_temp%_{如果剩余计算资源不足}

8. r_i = 0; c_i = 0; % STA回退到本地计算

9. else %存在剩余计算资源

10. c_i = c_temp; %分配计算资源

11. c_sum = c_sum +c_i %更新已分配计算资源

12. End if

13. End if

4 仿真结果及分析 4.1 仿真场景与参数设置

为了验证本文所提出的基于遗传算法与匈牙利算法任务卸载及资源分配联合优化算法对能耗、时延性能的影响, 本文利用Matlab对其进行了仿真分析. 同时, 为了对比所提方案的性能提升, 本文还提出了4种基线方案. 具体如下.

基线1: 全部本地执行, 即所有STA均不进行任务卸载, 而是在本地执行.

基线2: 全部卸载到MEC服务器执行, 即所有STA将任务卸载到MEC服务器上执行, 且各个STA均分AP的通信资源与MEC服务器的计算资源.

基线3: 采用了在资源管理领域比较常用的匈牙利算法^[16]进行通信资源分配, 随机选择STA将任务卸载到MEC服务器执行, 且利用匈牙利算法为执行任务卸载的STA分配通信资源, 并为采用均分的方式分配计算资源, 其余STA任务在本地执行.

基线4: 利用在求解MEC卸载决策领域比较常用的遗传算法^[17]设置了基线4, 通过遗传算法决定各STA的卸载决策, 对于卸载到MEC服务器执行的STA, 采用均分的方式分配通信资源与计算资源, 其余STA任务在本地执行.

4种基线方案与本文所设计方案所采用的卸载决策、通信资源分配、计算资源分配方式如表1所示.

仿真与算法参数如表2所示.

4.2 仿真结果分析

本文在同一网络场景下, 分别对4种基线方案与本文所设计方案的性能进行了仿真, 对比了用不同方案情况下, 能耗、时延性能与任务量大小之间的关系, 对于同一任务量大小, 采用了进行200次实验, 然后将200次实验结果取平均值的方式得到最终性能结果.

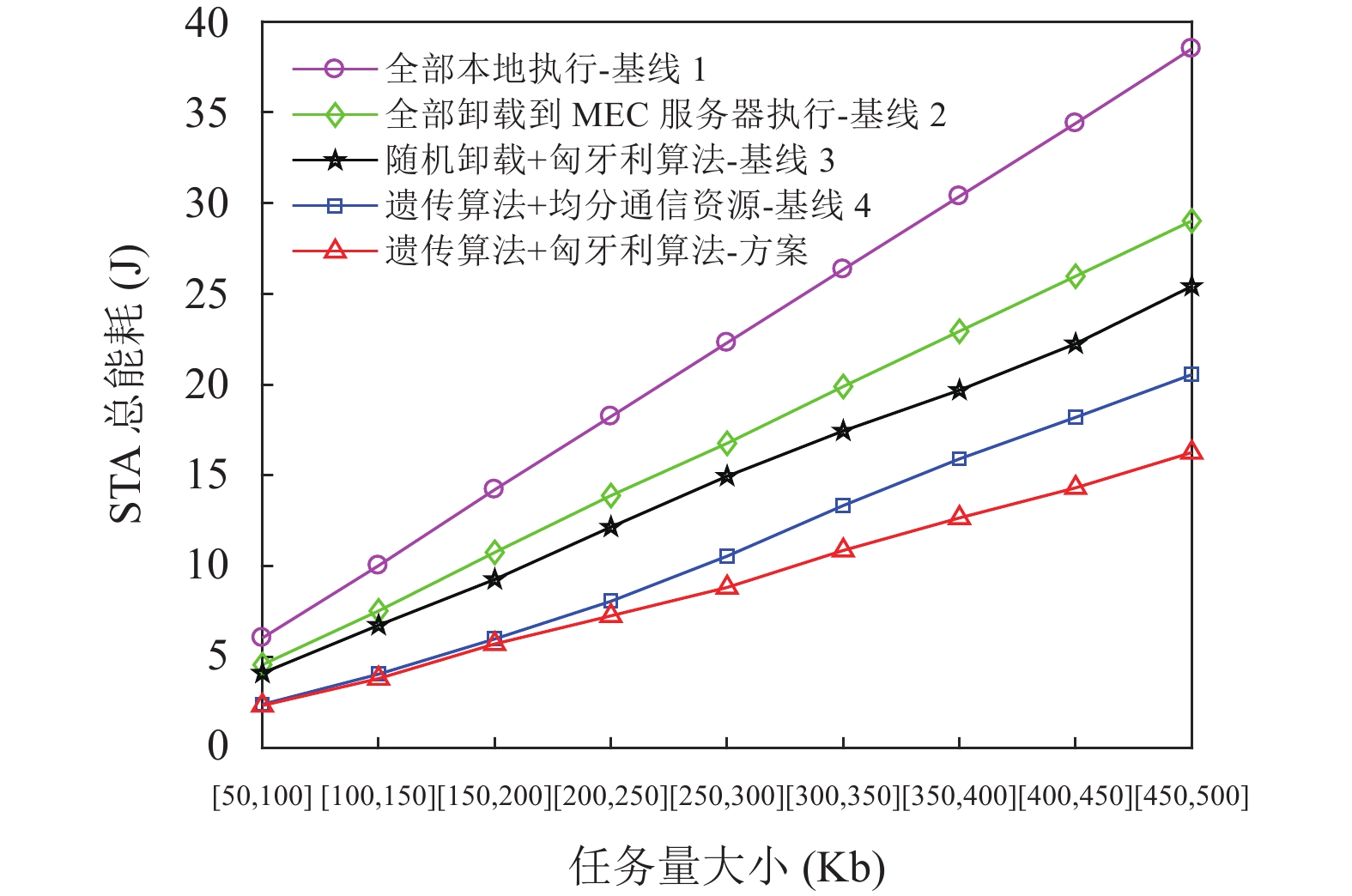
图3比较了采用不同方案情况下, STA总能耗与任务量大小之间的关系(图中横坐标的范围表示各STA从该范围中随机选择一个数作为任务量大小).

可以看出, 随着STA任务量的增加, STA总能耗也随之增加, 但对于同一任务量大小, 相比于4种基线方案, 采用所设计的基于遗传算法与匈牙利算法任务卸载及资源分配联合优化方案所消耗的STA总能耗最小. 其中, 当任务量大小范围为[450, 500] Kb时, 与基线1相比, 方案的STA总能耗下降了58%, 这是因为基线1中所有任务由STA本地执行, 会产生巨大的计算能耗. 与基线2相比, 方案的任务处理总能耗下降了44%, 这是因为系统中通信资源是有限的, 当STA数量较多时, 若全部STA均将任务卸载到MEC服务器上计算, 则每个STA分配得到的通信资源较少, 导致传输时延增大, 从而产生较大的传输能耗. 由此可以看出, 相比于基线1和基线2, 合理地将部分STA的任务卸载MEC服务器上计算能够有效降低STA的任务处理能耗. 与基线3相比, 方案的STA总能耗下降了36%, 这是因为在进行通信资源分配时, 虽然基线3与方案都采用了匈牙利算法, 但在进行卸载决策时, 基线3采用的是随机卸载, 并没有根据STA的任务量与时延限制等因素合理地安排卸载决策, 而本文所设计的方案通过遗传算法对可以满足时延限制前提下最小化能耗的卸载决策进行搜索, 从而实现更低的能耗, 这也验证了方案中采取遗传算法进行卸载决策对降低任务处理能耗的增益. 类似地, 与基线4相比, 方案的STA总能耗下降了21%, 这是因为在进行通卸载决策时, 虽然基线4与方案都采用了遗传算法, 但在进行通信资源时, 基线4采用的是均分通信资源, 并没有根据STA的任务量与信道条件合理地进行通信资源分配, 而本文所设计的方案通过匈牙利算法, 对最小化STA传输能耗的通信资源分配方式进行求解, 从而实现更低的能耗, 这也验证了方案中采取匈牙利算法进行通信资源分配对降低任务处理能耗的增益.

图4比较了采用不同方案情况下, STA在时延限制下完成任务计算的比例与任务量大小之间的关系.

可以看出, 当任务量较小时, 所有方案时延限制下完成任务计算的比例均能保持在一个较高的水平, 但随着任务量的增大, 逐渐超出了STA或MEC服务器的处理能力, 时延限制下完成任务计算的比例会随之下降. 其中基线1下降速度最快, 这是因为STA算力较弱, 当任务量范围达到[150, 200] Kb时, 已经超出了STA的处理能力范围, 导致部分STA无法在时延限制下完成任务计算. 而基线2、基线3、基线4都采用均分的方式分配计算资源, 未考虑到STA的任务量与时延限制等因素, 因此时延限制下完成任务计算的比例均低于本文所设计方案. 而采取本文所设计的方案, 在任务量范围达到[450, 500] Kb, 时延限制下完成任务计算的比例依然能保持在90%以上. 这是因为在利用遗传算法对卸载决策进行搜索时, 将超出任务处理时延的STA数量作为适应度函数的惩罚因子, 因此在搜索卸载决策时, 除了考虑STA总能耗外, 会优先选择超出任务处理时延的STA数量小的卸载决策.

图5比较了支持多AP协作与不支持多AP协作两种情况下, 任务处理能耗与AP1所关联STA任务量大小之间的关系.

可以看出, 当不支持多AP协作时, AP1与AP2独立完成所关联STA任务的处理, 因此, 随着AP1所关联STA任务量的增大, AP1所关联STA的任务处理总能耗不断增大, 而由于仿真场景中假设AP2所关联的STA任务量始终保持在一个较低的水平, 因此, AP2所关联STA的任务处理总能耗并不随AP1所关联STA任务量的变化而变化. 而在支持多AP协作情况下, 随着AP1所关联STA任务量的增大, 逐渐超出了AP1所关联STA或MEC服务器的处理能力, AP1通过协作将部分STA的任务进一步卸载到有剩余计算资源的AP2上进行处理. 因此所产生的能耗要小于不支持多AP协作情况下所产生的能耗. 而由于AP2需要将部分计算资源分配给来自AP1的任务, 因此AP2所关联的部分STA在保证其能在时延限制内完成任务计算的情况下, 选择将任务本地执行, 所以AP2所关联STA的任务处理总能耗会随AP1所关联STA任务量增大而增大. 然而当AP2的计算任务也趋近于饱和, 不存在剩余计算资源时, AP2也就不会再接受来自AP1的任务卸载, 因此AP2所关联STA的任务处理总能耗也就不再随之变化.

图6比较了支持多AP协作与不支持多AP协作两种情况下, STA在时延限制内完成任务计算的比例与AP1所关联STA任务量大小之间的关系.

可以看出, 在不支持多AP协作情况下, 随着AP1所关联STA任务量的增大, 逐渐超出了AP1所关联STA或MEC服务器的处理能力, 因此在时延限制内完成任务计算的比例不断降低. 而由于AP2所关联的STA任务量较小, AP2所关联STA在时延限制内完成任务计算的比例始终保持在100%. 在支持多AP协作情况下, 当任务量超出AP1所关联STA与MEC服务器的处理能力时, AP1通过协作将部分STA的任务进一步卸载到有剩余计算资源的AP2上进行处理, 因此在时延限制内完成任务计算的比例要高于不支持多AP协作的场景. 而AP2虽然将部分计算资源分配给来自AP1的任务, 但分配的前提是AP2拥有剩余计算资源, 因此并不影响AP2所关联STA在时延限制内完成任务计算的比例, 始终保持在100%.

图7展示了采用所设计方案情况下, STA总能耗随迭代次数的变化.

本文优化问题的决策变量包含了卸载决策向量、通信资源分配向量以及计算资源分配向量, 本文将上述3个决策变量转换为3个子问题进行求解. 对于计算资源分配向量, 是根据任务处理时延限制与通信资源分配结果利用公式直接计算获得, 求解复杂度可以忽略不计. 对于通信资源分配向量, 本文将其转换为一个匹配问题, 并利用匈牙利算法进行求解, 将算法时间复杂度从O(n!)降低为O(n³)^[18]. 而对于卸载决策向量的求解, 则是利用遗传算法进行求解, 求解结果的好坏与遗传算法中种群规模与迭代次数等因素有关, 种群规模越大、迭代次数越多, 越接近最优解. 而通过图7可看出, 随着迭代次数的增大, STA总能耗逐渐减小后趋于平稳, 在经过10–15次左右的迭代后即可实现收敛, 且每次收敛时, 所得到的STA总能耗指标均比较稳定, 维持在3.4 J左右. 说明所设计方案能在较少的迭代次数内实现收敛, 通过较低的算法复杂度得到一个较为理想和稳定的性能指标.

5 总结

本文对Wi-Fi网络中MEC卸载决策、通信资源、计算资源分配联合优化问题进行研究. 提出了一种基于遗传算法与匈牙利算法任务卸载及资源分配联合优化方案. 首先, 通过遗传算法确定用户的任务卸载决策. 随后, 利用匈牙利算法为进行任务卸载的用户分配通信资源. 最后, 根据任务处理时延限制, 为进行任务卸载的用户分配MEC服务器计算资源, 使其满足任务处理时延限制要求. 虽然在极端情况下, 可能会出现部分需要执行任务卸载的STA由于通信或计算资源不足, 而回退到本地执行的情况, 但是仿真结果表明, 所提出的方案能够显著提高系统在时延限制下完成任务计算的比例, 并且有效降低系统中STA总能耗. 在后续工作中, 也会进一步考虑网络中计算任务与通信任务联合调度的问题.