深度估计旨在获取输入RGB图像对应的深度图像, 深度图中每个像素点的值可用来表示场景中某一点与相机成像平面的距离, 可用于机器人定位导航、自动驾驶和三维重建等领域[1]. 目前虽有一些硬件能够直接得到深度图, 但都有各自缺陷, 如激光雷达设备较为昂贵; 基于结构光的深度摄像头在室外无法使用, 且得到的深度图噪声较多, 需要进一步处理; 双目摄像头需要利用立体匹配算法, 计算量相对较大, 且对于低纹理场景的深度估计效果不好[2]. 与之相比, 单目摄像头成本最低, 设备也最为普及; 为此, 开展单目深度估计研究具有重要的研究意义.
传统单目图像深度估计是使用目标场景中存在的多种视觉线索来获取深度信息, 主要包括: 从明暗度变化的规律恢复形状(shape from shading, SFS)[3]、从运动中恢复形状(shape from motion, SFM)[4]、从对焦获取深度(depth from focus, DFF)及从离焦获取深度(depth from defocus, DFD)[5]等. 通过这些视觉线索, 可以初步推断出图像中的整体构成和视差等深度相关信息, 进而结合相机参数计算出对应的深度值. 但这些方法都需要额外的辅助设备或对应用场景有着特殊的要求, 且预测结果很容易受到环境因素的影响, 使用条件苛刻, 难以推广. 近年来, 得益于卷积神经网络强大的特征提取能力和硬件设备不断提升的计算性能, 使用深度学习的方法预测图像深度信息逐渐成为主流研究方向[6].
根据训练数据集中是否带有深度标签, 即输入RGB图像对应的真实深度图, 可分为有监督学习的单目深度估计和无监督学习的单目深度估计. 其中, 有监督深度估计算法要求输入RGB图像都有对应的深度标签, 而深度标签的获取成本非常昂贵且得到的深度图存在一定的误差[7]. 无监督深度估计算法在训练时则不需要输入对应的真实深度图, 极大减轻了对大量深度标签的需求, 逐渐受到研究学者们的重视. Garg等人[8]于2016年最先提出了一个无监督单目深度估计网络框架, 通过类似于自动编码器的方式来训练网络, 输入为源图像和目标图像构成的图像对. 首先, 使用编码器预测目标图像的深度图, 并计算此图像对的相对位移. 然后解码器使用上一步预测的深度图和相对位移重构目标图像, 最后计算重构目标图像与原目标图像之间的误差来对网络进行监督. Wong等人[9]针对目标场景中物体边缘梯度不连续等问题, 提出了一种自适应正则化方案和左右视差间的双边一致性约束来降低物体边缘位置的深度误差, 并使得网络能够处理立体图像对中的共同可见区域和遮挡区域, 表现出了较好的泛化性能. Zhou等人[10]基于光场多向对极几何提出了一种无监督单目深度估计网络. 该网络从光场中心位置预测深度, 根据光场内部深度线索和几何约束, 提出了由光度损失、散焦损失和对称损失组成的新损失函数, 并验证了该算法对真实场景光场图像的有效性和通用性. 近期, Zhou等人[11]提出了一种基于光流的网络训练方法, 通过提供更清晰的训练目标和单独处理非纹理区域来降低无监督学习的难度, 并使用密集光流来监督深度和位姿的学习, 在室内场景中取得了较好的预测效果. 相比Zhou等人采用的方法, Yu等人[12]提出的面片匹配与平面正则化网络(patch-match and plane regularization, P2Net)使用基于面片的光度损失来监督网络的训练, 并使用平面一致性损失来调整非纹理区域内的深度值, 进一步降低了预测误差. 但是其深度预测网络DepthNet所采用的上采样方法为计算过程较为简单的最近邻插值算法, 使得预测深度图的生成质量较差、整体效果不理想.
针对上述问题, 本文对P2Net中主要组成模块之一的深度预测网络DepthNet进行改进, 基于多种上采样算法构建出残差上采样结构来替换原网络中的上采样层, 以进一步提高预测深度图中物体结构的完整性, 降低预测误差.
1 融合残差上采样结构的P2Net 1.1 P2Net整体网络结构介绍P2Net整体网络框架如图1所示, 主要包含深度预测网络DepthNet和位姿预测网络PoseNet两个可学习的模块; 其中, DepthNet用来预测目标图像It对应的深度图Dt, PoseNet用来预测目标图像It与源图像Is (即目标图像的相邻帧)之间的相对位姿Tt→s. 之后, 使用相对位姿Tt→s、从目标图像It提取的关键点和深度图Dt来计算基于面片的光度损失; 并使用从目标图像It提取到的超像素来获得对应的分段平面, 再结合深度图Dt计算出平面一致性损失; 这两种损失即为P2Net损失函数的主要组成部分, 用来对网络的训练过程进行监督.
P2Net网络提出基于面片的光度损失和平面一致性损失; 前者通过面片匹配法将一个关键点和以该点为中心的局部窗口相结合以提高其辨识能力, 并结合相对位姿Tt→s和深度图Dt计算该局部窗口的重构误差作为其光度损失, 其中图像关键点通过直接稀疏测距法 (direct sparse odometry, DSO)[13]获得. 后者使用较大的超像素来代替具有相似属性的同质区域, 并计算超像素预测深度与拟合平面深度的绝对误差作为其平面一致性损失, 其中超像素是由一些位置相邻、颜色和纹理相似的像素点组成的小区域, 通过Felzenszwalb法[14]获得.
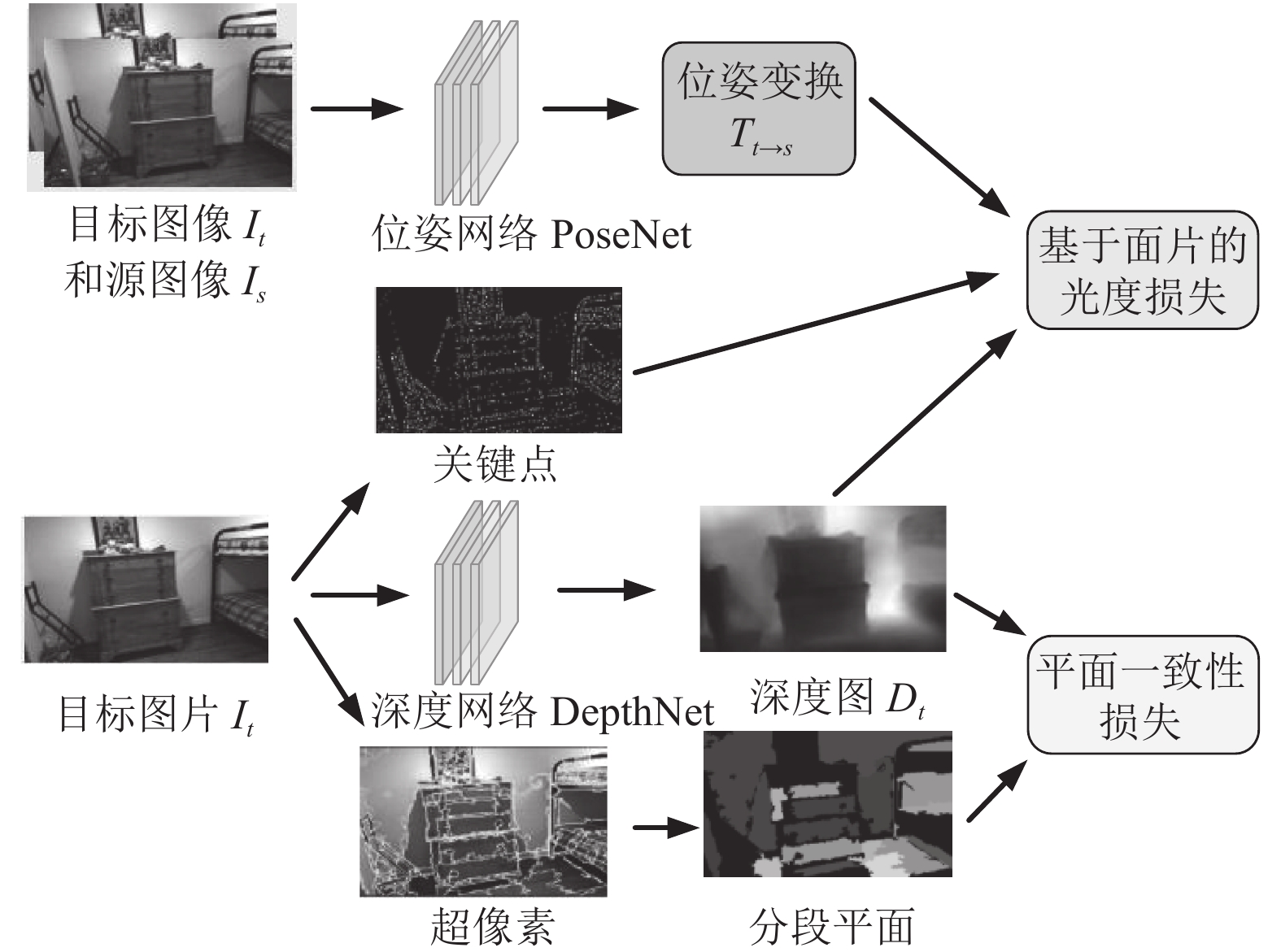
|
图 1 P2Net网络框架 |
1.2 位姿预测网络PoseNet介绍
相机在现实三维场景中的运动为六自由度的刚性运动, 因此相机的位姿变化可以使用6个变量进行表示, 包括沿x、y、z轴的3个平移变量tx、ty、tz和绕x、y、z轴旋转的3个欧拉角rx、ry、rz. PoseNet的输出即为此6个变量, 之后利用这6个变量计算出对应的平移向量T和旋转矩阵R, 最后构造出4×4的位姿变换矩阵Tt→s[15], 如式(1)所示. PoseNet的详细结构如图2所示. 其中, 2×表示输入图像尺寸为当前图像尺寸的2倍, 图像块下方数字表示当前图像通道数.
| Tt→s = [R T0 1] | (1) |
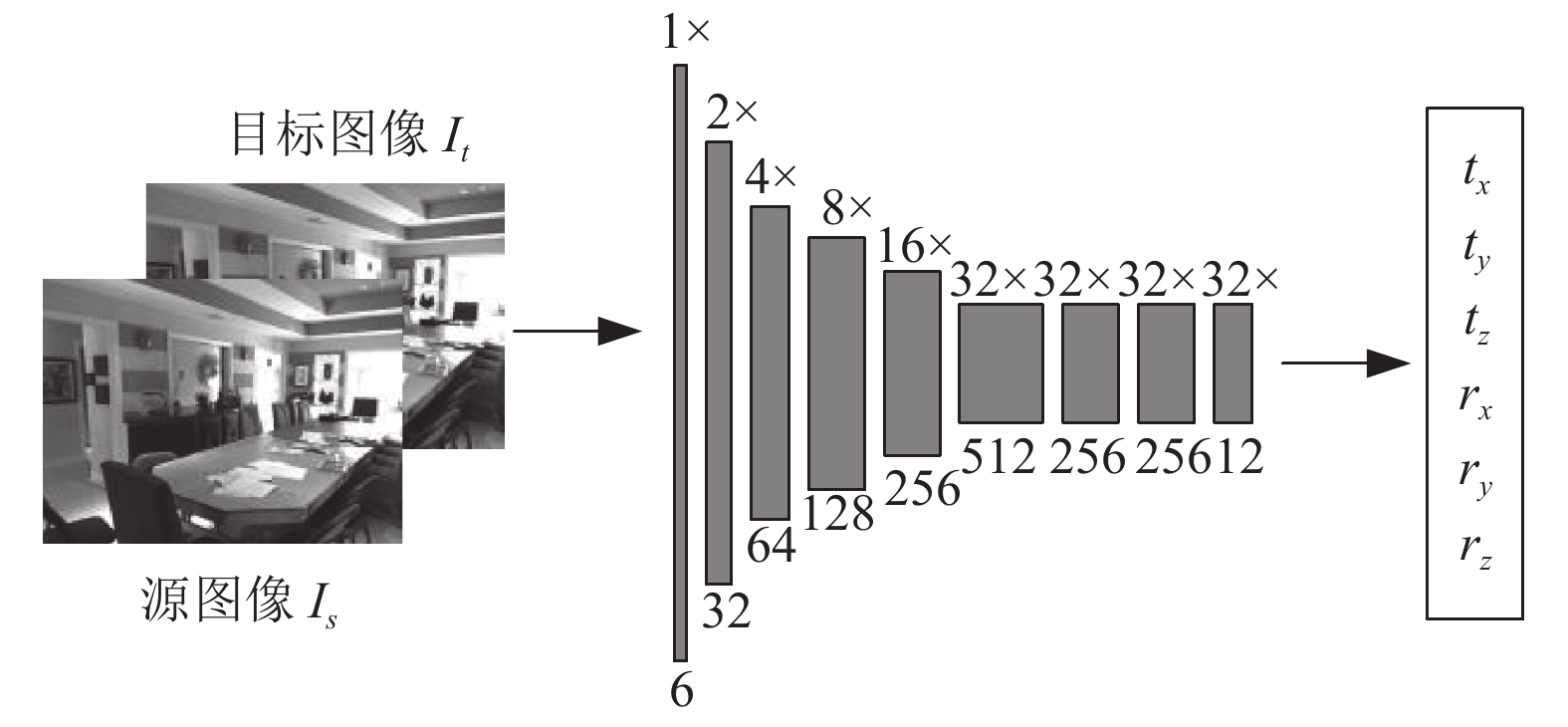
|
图 2 PoseNet网络结构 |
1.3 深度预测网络DepthNet介绍
本文DepthNet为U形结构的网络, 由下采样部分(Conv)、上采样部分(Cat_UpProj和UpProj)和连接这两部分的跳跃连接组成, 如图3所示. 随着下采样操作的进行, 输出图像尺寸不断缩小, 输出通道数不断增大, 网络模型可以提取到更高级别的语义信息. 上采样操作是对输入图像进行放大的过程, 在上采样的同时, 还融入了跳跃连接传递过来的信息, 如图3中虚线箭头所示. 跳跃连接有利于将下采样获得的各种尺度信息在上采样时进行整合, 更好地恢复图像的细节信息. 这样的U形结构有助于整个网络很好地“记住”图像的所有信息, 其中包含跳跃连接的4层上采样操作均使用Cat_UpProj实现, 最后一层不包含跳跃连接的上采样操作使用UpProj实现.

|
图 3 本文DepthNet网络结构 |
(1) DepthNet的残差上采样结构
残差网络通过使用跨层的连接来避免误差梯度的消失, 使得前层的参数能够及时得到更新[16]. 如图4所示, 图中的x代表输入, F(x)代表经过激活函数后的输出. 普通网络中输出对输入的梯度为∂F(x)/∂x, 残差网络的梯度为∂(F(x) +x)/∂x = ∂F(x)/∂x + 1. 随着网络层数的不断增加, ∂F(x)/∂x逐渐减小直至衰减为0, 而残差网络的梯度能够一直维持在1附近, 从而避免了梯度消失现象的产生. 在误差梯度逐层反向传播时, 残差网络不仅可以使用普通网络的非线性层逐步传播, 还可以通过自身跨层的连接直接跨层传播, 显著提升了参数的更新效率.
由于原始DepthNet使用的上采样结构为类似图4 (a)所示的普通结构, 且使用的上采样方法为计算过程较为简单的最近邻插值算法, 使得预测深度图的生成质量较差、整体效果不理想. 而残差结构在加深网络层数提高特征信息获取能力的同时, 能够避免网络退化现象(即网络模型的精度随着层数的增加逐渐饱和甚至降低)的产生, 因此本文基于图4 (b)的基本残差单元构建出图5所示的残差上采样结构, 即Cat_UpProj模块. 该模块中X为上采样层的输入特征图, skip为跳跃连接传递的特征图. UpSample层为上采样方法, 分别使用反卷积算法、双线性插值算法和像素重组算法实现. Conv、BN和ReLU分别为卷积操作、批标准化和激活函数, 这3部分组成一个小的特征提取单元. 批标准化BN层对数据的分布进行修正, 能够在一定程度上缓解过拟合问题. 激活函数ReLU层能够增加网络的非线性, 降低计算量. 图5中右侧的UpProj模块用于图3中最后一层不包含跳跃连接的上采样.
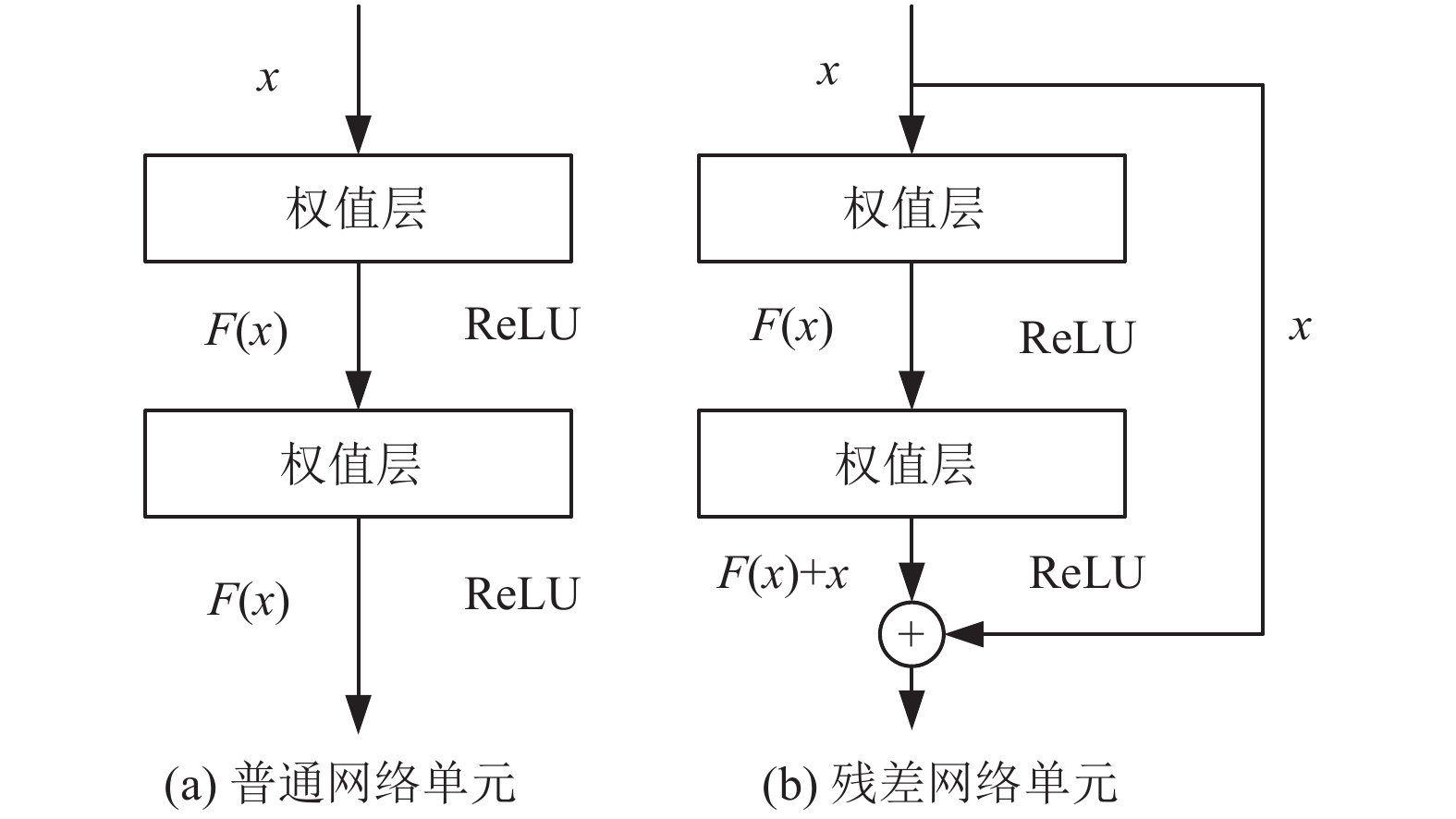
|
图 4 普通网络单元与残差网络单元 |

|
图 5 本文DepthNet中的上采样模块 |
(2) 多种上采样算法
图5中的上采样层UpSample分别采用反卷积算法、双线性插值算法和像素重组算法实现, 并进行实验对比分析.
1) 反卷积算法
输入图像通过标准卷积计算后, 得到的输出图像尺寸会变小, 而有时我们需要将输出图像尺寸增大以顺利进行下一步的操作. 增大图像尺寸, 将小分辨率图像扩展到大分辨率图像的操作, 即为上采样. 反卷积(transpose)[17]为上采样方法中的一种, 也称为转置卷积. 先将卷积核反转, 然后按照设定值对输入图像进行补0以增大图像尺寸, 最后使用反转后的卷积核对补0后的图像进行标准卷积.
① 卷积核反转. 此处的反转并不是线性代数中的转置操作, 而是对4方向的参数进行逆序操作. 反转前后对比如图6所示.
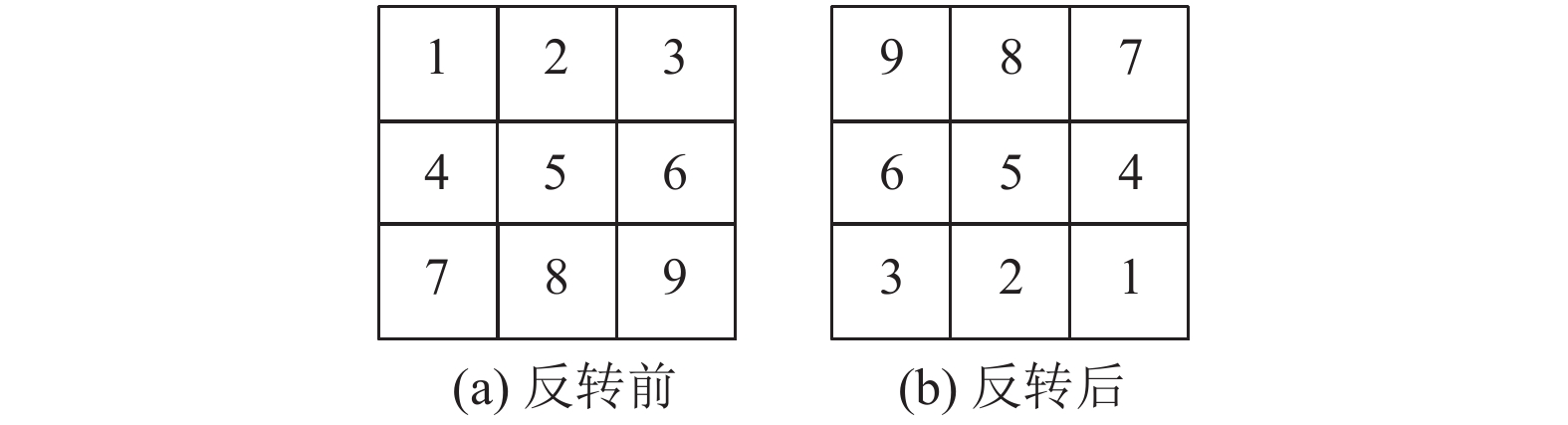
|
图 6 卷积核反转 |
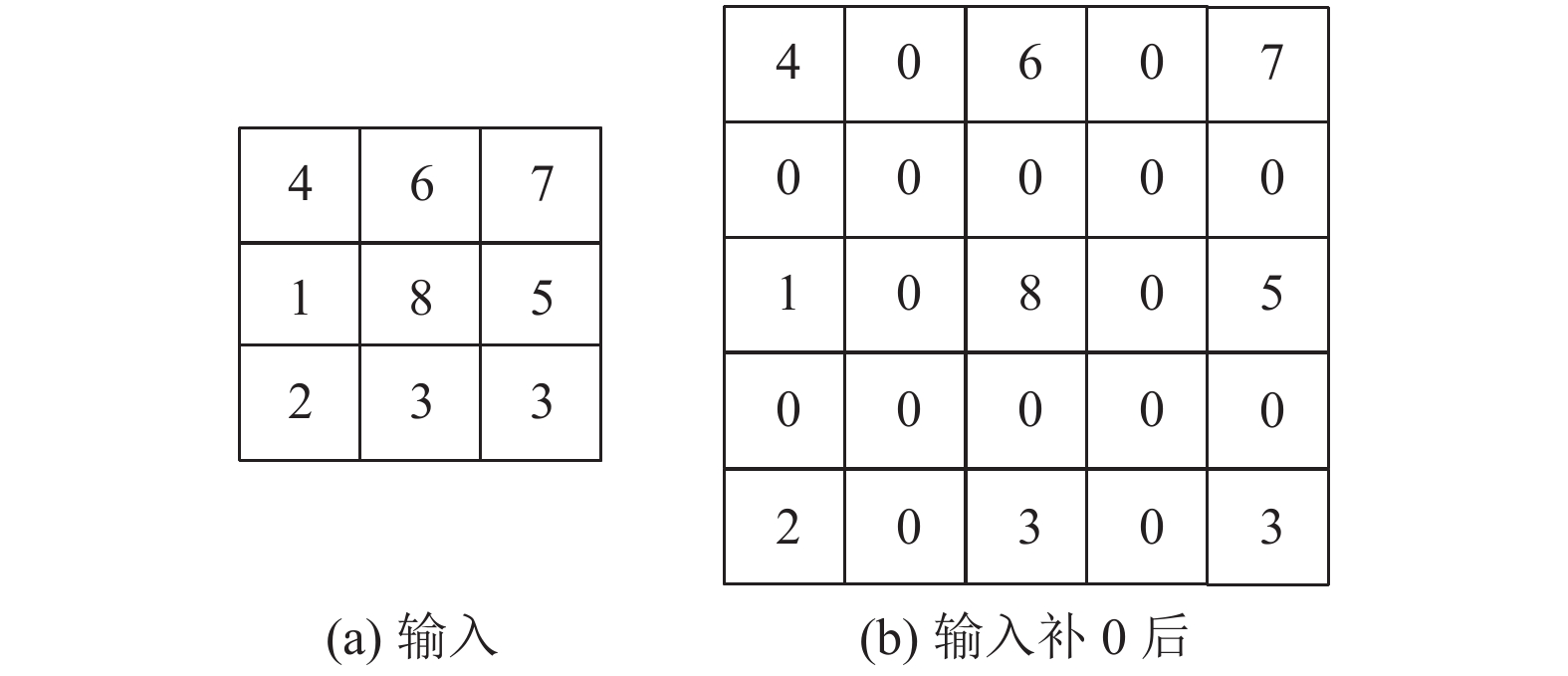
② 对输入进行补0操作, 补0个数为步长减1, 如果步长为1, 则不补0. 如图7所示, 输入尺寸为3×3, 步长为2, 输出为6×6, 补0后的矩阵为5×5.
|
图 7 根据步长补0 |
③ 对补0后的输入矩阵再做整体补0. 以补0后的5×5输入矩阵作为输入, 反转以后的卷积核作为权重, 此时的步长参数变为1. 按照普通卷积的填充方式计算补0参数, 并将计算出的补0参数赋给各自的反方向, 填充后的矩阵如图8所示.
④ 使用反转后的卷积核对整体补0后的矩阵进行步长为1的标准卷积运算, 即可完成反卷积的计算.

|
图 8 整体补0 |
2) 双线性插值算法
双线性插值算法(bilinear)[18]是通过对待求点的邻近4点求两次线性插值, 将所得结果作为待求点像素值的方法, 图9给出了双线性插值的计算示意图.

|
图 9 双线性插值示意图 |
图9中, Q11、Q12、Q22、Q21为待求点P=(x, y)的邻近4点, 首先对Q11、Q21和Q12、Q22分别在x方向上进行插值操作, 得到点R1=(x, y1)和R2=(x, y2)的像素值. 计算公式如下:
| f(R1)≈x2−xx2−x1f(Q11)+x−x1x2−x1f(Q11) | (2) |
| f(R2)≈x2−xx2−x1f(Q12)+x−x1x2−x1f(Q22) | (3) |
然后再对R1和R2在y方向上进行插值, 得到P点的像素值, 计算公式为:
| f(P)≈y2−yy2−y1f(R1)+y−y1y2−y1f(R2) | (4) |
3) 像素重组算法
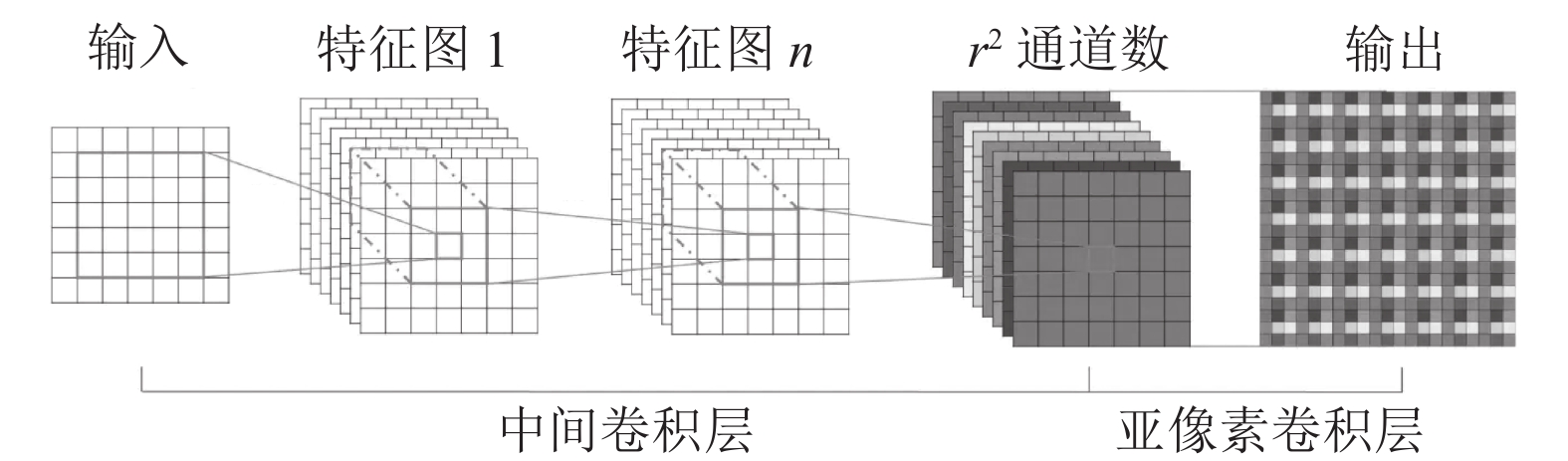
像素重组算法(PixelShuffle)主要是使用尺寸不变卷积和多通道间像素重组来将低分辨率输入图像采样为高分辨率输出图像, 其中多通道间像素重组操作也称为亚像素卷积[19]. 该算法的主要作用是将一个尺寸为H×W的输入图像变为rH×rW的输出图像, r为放大倍数. 首先通过中间卷积层进行多次尺寸不变卷积后得到r2个通道的特征图, 然后通过轮询的方式依次选取每个通道对应位置的像素进行重组以得到高分辨率的输出图像, 如图10所示.
|
图 10 PixelShuffle处理过程 |
1.4 损失函数
P2Net在每个关键点pt的局部窗口上定义了一个支持域
| Lph=αSSIM(It[Ωpt],Is[∧ Ωpt])+(1−α)‖It[Ωpt]−Is[∧ Ωpt]‖1 | (5) |
此外, P2Net假设大多数同质颜色区域都是平面区域, 并采用Felzenszwalb法进行超像素分割. 对于从输入图像提取的某一超像素SPPm和对应的预测深度
| Lspp=∑Mm=1∑Nn=1|D(pn)−D′(pn)| | (6) |
除上述基于面片的光度损失Lph和平面一致性损失Lspp之外, 最终的损失函数还添加了边缘感知的梯度平滑损失Lsm.
| Lsm(dt,It)=∑pt|∂xdt|e−|∂xIt|+|∂ydt|e−|∂yIt| | (7) |
其中,
| L=Lph+λ1Lsm+λ2Lspp | (8) |
本文采用纽约大学公开的室内图像数据集NYU-Depth V2[20]对网络模型进行训练与测试. 该数据集由微软的Kinect摄像机拍摄采集, 包含464个场景, 场景的深度范围为0–10 m. 本文使用P2Net提供的方法对官方数据集进行处理, 得到约238个场景, 共15543个连续帧图像对, 每个连续帧图像对包含9张连续图片. 采用Adam优化器, 总训练批次epochs为41, 批量大小batch_size为12. 前25个epoch的初始学习率设置为10–4, 然后在接下来的每10个epoch, 乘于一次0.1. 在训练过程中采用随机翻转等预处理操作, 所有输入图像的大小调整为288×384. 在测试过程中, 对预测深度图进行上采样, 使其恢复到原始尺寸640×480. 在网络训练之前, 需要先使用Felzenszwalb超像素分割算法对目标图片提取超像素. 之后, 在网络训练过程中会基于提取的超像素重建分段平面, 同时也会使用DSO算法对目标图像提取关键点.
单目深度估计的评价指标主要分为两种[21], 一种为误差指标, 本文主要采用均方根误差(root mean squared error, RMSE)和平均相对误差(absolute relative error, REL); 另一种为准确率, 本文采用阈值内准确度δ, 其中阈值thr = 1.25, 1.252, 1.253, 阈值越小, 说明评价指标越严格. 这3个客观指标表达式如下:
| RMSE=√1n∑ni=1(di−gi)2 | (9) |
| REL=1n∑ni=1|di−gi|gi | (10) |
| δ = max | (11) |
其中, di表示预测值, gi表示真实值, n表示每张图片中像素的数量.
2.2 实验结果分析表1为原P2Net网络和基于本文残差上采样结构得到的3种改进P2Net网络的实验结果, 其中Res-T、Res-B和Res-P分别代表基于反卷积算法、双线性插值算法和像素重组算法构建出的残差上采样结构, Nearest为原网络中最近邻插值上采样结构. 误差指标均方根误差RMSE和平均相对误差REL的值越小表示效果越好, 准确度指标δ1.25、δ1.252和δ1.253的值越大效果越好, 表1中加粗字体为每列最优值. 图11为实验结果可视化图片示例, 图像颜色越深表示距离越近, 反之越远.
| 表 1 实验结果对比 |
由表1可知, 3种改进P2Net网络在所有评价指标上均优于原P2Net网络, 表明本文新的残差上采样结构相比原上采样层有着更强的特征提取能力和更好的预测效果. 与原P2Net网络相比, 改进网络P2Net-1、P2Net-2和P2Net-3在均方根误差RMSE指标上分别降低了2.25%、2.73%和3.05%; 在平均相对误差REL指标上分别降低了1.77%、2.96%和1.78%. 3种改进网络中, 基于Res-B和Res-P得到的P2Net-2和P2Net-3网络均有3项评价指标取得了最优结果, 且整体表现都要优于P2Net-1网络.
由图11中可以看出, 相比于原P2Net网络, 本文3种改进网络的预测深度图整体数值分布更接近于真实深度图. 同时, 从图中虚线框可以看出, 3种改进网络的预测深度图中物体结构更加完整, 细节信息更加丰富, 说明本文的改进网络能够获取更多特征信息, 提高图像的生成质量. 而3种改进网络中, P2Net-2预测的深度图中物体结构更为清晰, 整体预测效果要略优于P2Net-1和P2Net-3网络.
3 结论与展望由于P2Net中深度预测网络DepthNet所采用的上采样方法为计算过程较为简单、图像生成质量较差的最近邻插值算法, 使得预测深度图中物体完整性较差、整体效果不理想. 因此, 本文基于多种上采样算法构建出残差上采样结构来替换原网络中的上采样层, 进一步提高了预测深度图中物体结构的完整性, 降低了预测误差. 本文训练与测试的输入数据均为连续帧图像对, 并未对视频数据进行训练与分析, 下一步将会由图像深度估计扩展到视频深度估计进行研究.

|
图 11 实验结果可视化 |
| [1] |
张敏. 基于多线索信息的深度估计算法研究与实现[硕士学位论文]. 大连: 大连理工大学, 2021.
|
| [2] |
公冶佳楠, 李轲. 基于光场图像序列的自适应权值块匹配深度估计算法. 计算机系统应用, 2020, 29(4): 195-201. DOI:10.15888/j.cnki.csa.007387 |
| [3] |
Tankus A, Sochen N, Yeshurun Y. Reconstruction of medical images by perspective shape-from-shading. Proceedings of the 17th International Conference on Pattern Recognition. Cambridge: IEEE, 2004. 778–781.
|
| [4] |
Skarbek W. Shape from motion revisited. Proceedings of the 10th International Conference on Active Media Technology. Warsaw: Springer, 2014. 383–394.
|
| [5] |
Zhang XD, Liu ZQ, Jiang MS, et al. Fast and accurate auto-focusing algorithm based on the combination of depth from focus and improved depth from defocus. Optics Express, 2014, 22(25): 31237-31247. DOI:10.1364/OE.22.031237 |
| [6] |
张喆韬, 万旺根. 基于LRSDR-Net的实时单目深度估计. 电子测量技术, 2019, 42(19): 158-163. DOI:10.19651/j.cnki.emt.1902912 |
| [7] |
詹雁, 张娟, 金昌基. 联合语义感知与域适应方法的单目深度估计. 传感器与微系统, 2021, 40(5): 60-63. DOI:10.13873/J.1000-9787(2021)05-0060-04 |
| [8] |
Garg R, Kumar BGV, Carneiro G, et al. Unsupervised CNN for single view depth estimation: Geometry to the rescue. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 740–756.
|
| [9] |
Wong A, Soatto S. Bilateral cyclic constraint and adaptive regularization for unsupervised monocular depth prediction. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 5637–5646.
|
| [10] |
Zhou WH, Zhou EC, Liu GM, et al. Unsupervised monocular depth estimation from light field image. IEEE Transactions on Image Processing, 2020, 29: 1606-1617. DOI:10.1109/TIP.2019.2944343 |
| [11] |
Zhou JS, Wang YW, Qin KH, et al. Moving indoor: Unsupervised video depth learning in challenging environments. Proceedings of 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 8617–8626.
|
| [12] |
Yu ZH, Jin L, Gao SH. P2Net: Patch-match and plane- regularization for unsupervised indoor depth estimation. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 206–222.
|
| [13] |
Engel J, Koltun V, Cremers D. Direct sparse odometry. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(3): 611-625. DOI:10.1109/TPAMI.2017.2658577 |
| [14] |
Felzenszwalb PF, Huttenlocher DP. Efficient graph-based image segmentation. International Journal of Computer Vision, 2004, 59(2): 167-181. DOI:10.1023/B:VISI.0000022288.19776.77 |
| [15] |
高昊昇. 基于深度学习的无监督单目图像序列深度估计[硕士学位论文]. 南京: 东南大学, 2020.
|
| [16] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [17] |
Zeiler MD, Krishnan D, Taylor GW, et al. Deconvolutional networks. Proceedings of 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2528–2535.
|
| [18] |
Jaderberg M, Simonyan K, Zisserman A, et al. Spatial transformer networks. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2015. 2017–2025.
|
| [19] |
Shi WZ, Caballero J, Huszár F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 1874–1883.
|
| [20] |
Silberman N, Hoiem D, Kohli P, et al. Indoor segmentation and support inference from RGBD images. Proceedings of the 12th European Conference on Computer Vision. Florence: Springer, 2012. 746–760.
|
| [21] |
Cheng XJ, Wang P, Yang RG. Depth estimation via affinity learned with convolutional spatial propagation network. Proceedings of the 15th European Conference on Computer Vision. Munich: Springer, 2018. 108–125.
|
 2022, Vol. 31
2022, Vol. 31



