深度学习技术^[1]作为人工智能领域最具振奋人心的技术之一, 引发了学术界和生产领域的广泛关注. 以卷积神经网络(convolutional neural network, CNN)、循环神经网络(recurrent neural network, RNN)、生成对抗网络(generative adversarial network, GAN) 等为代表的深度学习网络技术彻底改变了语言处理、图像识别、计算机视觉等众多应用领域. 在金融领域, 金融科技(Fintech)已成为金融业未来的主流趋势, 深度学习(deep learning, DL)更是Fintech的应用前沿^[2]. DL具有自主学习数据中隐藏特征以及学习能力强的优点, 相比于其它模型, 深度学习模型能够获得更精确的预测结果. 杨青等^[3]将长短期记忆(long short-term memory, LSTM)网络用于全球30 个股票指数的3种不同期限的预测研究, 验证了LSTM网络在金融预测中的广泛适用性和预测优越性. Bao等^[4]提出了一种基于小波变换-堆叠式自动编码器-LSTM的框架, 在6个股票指数上回测, 研究结果表明复杂网络模型的预测性能相较单一网络模型性能更优秀. 孙达昌等^[5]分别将ANN、CNN和LSTM用于预测沥青期货主力合约价格的涨跌, 回测结果表明深度学习算法适用于高频率短周期预测任务. 孟徐然等^[6]将GAN模型用于高频交易, 实证结果表明, 基于GAN训练下的LSTM 模型具有显著优势.

相对于经典的时间序列等方法, 深度学习技术在金融预测上具有更加优越的性能, 但在实践的过程中也发现了一些不足之处: 1) DL模型没能考虑数据和模型中广泛存在的不确定性, 限制了DL模型的实际应用; 2) DL模型是确定性的模型, 无法估计预测结果的不确定性, 减弱了对投资决策的指导意义; 3) DL 模型是“黑箱”模型, 不具有可解释性, 也无法进行推理; 4)面对对抗性攻击的脆弱性是在安全关键型应用中采用深度学习的主要障碍之一, DL模型不够稳健, 细微改变权重都可能对深度学习造成影响. 考虑到金融时间序列普遍存在不确定性和高噪声的特性, 研究和开发相应DL 模型来处理金融预测中的不确定性并为决策提供可靠的决策参考是至关重要的.

贝叶斯深度学习(Bayesian deep learning, BDL)^[7], 以贝叶斯推理为框架, 融合了贝叶斯方法和深度神经网络的互补优势, 可以对数据和模型的不确定性进行系统刻画和计算, 提供了不确定性建模的框架^[8], 为应对复杂问题中的不确定性建模与推断提供了强大的工具. 不同于DL模型, BDL是概率模型, 能借助概率论的知识进行概率推理, 使模型更具解释性^[9]. 此外, BDL对于基于梯度的对抗式攻击具有稳健性且可以提高精度^[10]. 因此BDL在众多领域得到广泛的研究和应用, 如计算机视觉^[11–13]、空气质量预测^[14] 、医学成像领域^[15]、风速预测^[16]等. 但BDL在金融预测领域的应用有待于深入研究, 因此针对金融序列的特点, 构建BDL模型, 进而解决金融序列预测中的不确定性难题非常有意义.

BDL模型的关键是确定参数后验分布, 通常采用变分贝叶斯法(variational Bayes, VB)^[17]或蒙特卡洛采样的方法近似得到参数后验分布. 上述文献的研究一般是采用VB方法估计参数的后验分布: 首先假定预测分布服从正态分布, 其次从一个简单分布族(通常为正态分布族)中找到一个与参数后验分布KL散度^[18]最小的分布作为参数后验分布的最优估计, 最后基于此进行贝叶斯推断. 上述的VB法具有运行快速的优点, 然而, VB法在金融预测中存在以下问题: 1)金融数据多具有厚尾分布的特征, 因而正态分布作为预测分布与实际数据分布存在偏差; 2) KL 散度具有不对称的问题, 通过VB法可能得到一个单峰且过于紧凑的后验分布估计^[19], 而真实后验分布大多是多峰且多模态的, 二者之间存在较大偏差; 3)简单分布族并不一定是最优的分布族, 甚至这样的最优分布族可能并不存在.

针对上述问题, 通过对多个分布族和算法的对比分析, 本文提出一种以t 分布为预测分布、用循环随机梯度汉密尔顿蒙特卡洛(circular stochastic gradient Hamiltonian Monte Carlo, CSG-HMC)算法采样估计模型参数后验的BDL 模型框架. 在全球15个典型的股票指数(包含8个国际指数和7个国内指数)上的实证检验显示, 所构建的模型具有显著优越性. 本文的主要贡献有以下几点: 1) 构建以t分布为预测分布、采用CSG-HMC 算法的BDL模型, 优化参数并进行实证检验, 结果显示模型在全球股指预测上具有显著优越性; 2) 分别以ANN、CNN 和RNN 为基础网络构建相应的BDL模型, 验证该框架的普适性; 3) 我们采用的算法通过多次采样减少了参数初始化对深度学习造成的影响, 并设置超参数来实现“探索”和“采样”阶段的权衡, 既充分探索了参数后验空间, 又解决了模型无法跳出局部区域的问题, 提高了采样效率; 4)本文定义了不确定性度量, 并通过实证分析验证所定义的不确定性度量具有识别预测偏差的作用, 表明所定义的不确定性是有效的, 对不确定性建模具有重要意义.

本文结构安排如下: 第1节给出了贝叶斯深度学习模型的构建方法、算法以及不确定性度量, 第2节在全球15个典型的股票指数上从预测精度和稳定性方面验证t分布相比正态分布具有优越性; 第3节验证了第1节定义的不确定性度量的有效性.

1 BDL模型

本节从模型构建、参数后验估计方法和不确定性度量3个方面阐述本文的BDL模型框架.

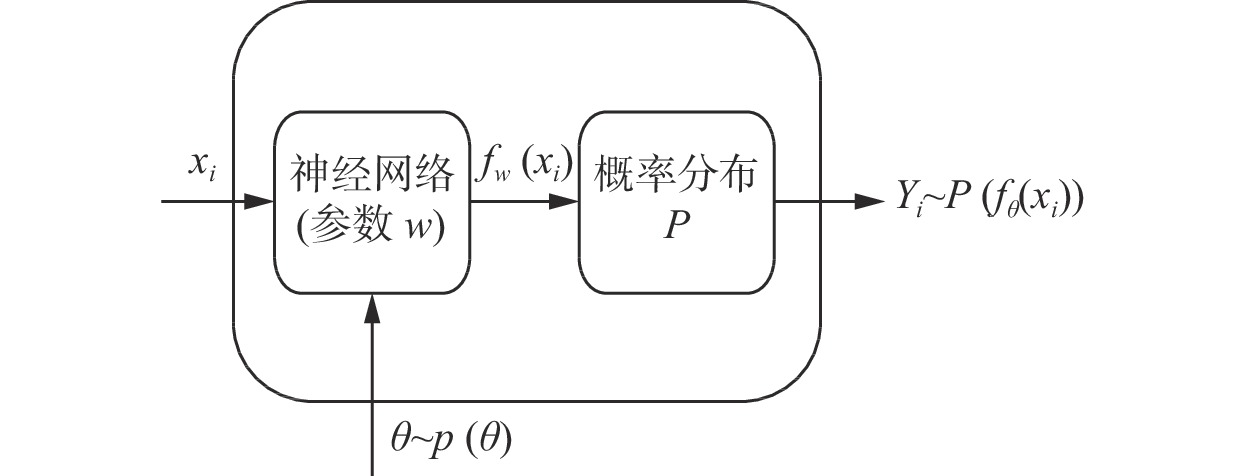
1.1 模型构建

给定训练数据集 $D = \left\{ {\left( {{x_i}, {Y_i}} \right)} \right\}_{i = 1}^N$ , 其中, $N$ 为数据集个数, ${x_i} \in {R^d}$ 为特征数据, ${Y_i}$ 为标签数据. 学习的任务是预测输入数据的标签. 本文的BDL模型框架由两部分构成: 深度神经网络DN和概率分布 $P$ , 如图1所示, 这里 $\theta $ 为模型参数, 其先验分布记为 $p(\theta )$ , DN的输出 $ {f_\theta }({x_i}) $ 为分布 $P$ 参数. 在BDL模型中, 假设标签满足: ${Y_i}{\text{|}}{x_i}\sim P({f_\theta }({x_i}))$ , $D$ 中的 $N$ 个数据以及数据和参数 $\theta $ 相互独立. 令 ${\boldsymbol{Y}} = \left( {{Y_1}, \cdot \cdot \cdot , {Y_N}} \right)^{\rm T}$ , ${\boldsymbol{X}} = \left( {{x_1}, \cdot \cdot \cdot , {x_N}} \right)^{\rm T}$ , 这里T表示转置. 根据上述假设, $\left( {{\boldsymbol{Y}}, \theta } \right)$ 的联合分布对数似然满足:

$ {{ - }}\varphi \left( \theta \right) = \log p({\boldsymbol{Y}}, \theta |{\boldsymbol{X}}) = \sum\limits_{i = 1}^N {\log P({f_\theta }({x_i}))} + \log p(\theta ) $

(1)

由贝叶斯法则, 参数的后验分布满足:

$ p(\theta |D) \propto p({\boldsymbol{Y}}, \theta |{\boldsymbol{X}}) $

(2)

在式(1)中, 模型参数的最优先验分布通常是未知的. 在无法确定最优先验分布的情况下, 采用标准正态分布是最有效的解决方案之一. 故本文假定 $\theta $ 先验分布为 $N({\mathbf{0}},\; {\boldsymbol{I}})$ , 其中 ${\boldsymbol{I}}$ 为单位矩阵. 概率分布 $P$ 属于参数分布族, 常见有正态分布族和t分布族, 一般包含两个参数: 位置参数 $u$ 和刻度参数 $\sigma $ , 前者代表中心趋势, 而后者代表离散程度. 因而在本文中假定 $ {f_\theta }({x_i}) = \left( {{u_\theta }({x_i}), {\sigma _\theta }({x_i})} \right) $ . 文献中通常假设为 $P$ 正态分布, 然而金融实证数据一般服从厚尾分布, 通过分析发现, 以t分布作为预测分布相比于正态分布更符合实际情况.

当 $P({f_\theta }({x_i}))$ 分别为正态分布和t分布时, 可得到其对应的 $ {\varphi _1}\left( \theta \right) $ 和 $ {\varphi _2}\left( \theta \right) $ :

$ \left\{ {\begin{split} {\varphi _1}(\theta ) =& \sum\limits_{i = 1}^N {\frac{1}{2}} \exp ( - s({x_i})){\left( {{Y_i} - {u_\theta }({x_i})} \right)^2} + \frac{1}{2}s({x_i}) - \log p(\theta ) \\ {\varphi _2}(\theta ) =& \sum\limits_{i = 1}^N {\frac{{fd + 1}}{2}} \log \left(1+ {\frac{{\exp ( - s({x_i})){{({Y_i} - {u_\theta }({x_i}))}^2}}}{fd}} \right) \\ & + \frac{1}{2}s({x_i}) - \log p(\theta ) \end{split} } \right.$

(3)

其中, $ s({x_i}) = \log \sigma _{_\theta }^2({x_i}) $ , $ fd $ 为t分布自由度. $N$ 通常较大, 故实际训练过程中常使用小批量(mini-batch)学习, 即从数据集 $D$ 中随机抽取 $n$ 个数据 $\left\{ {\left( {{x_{{k_i}}}, {Y_k}_{_i}} \right)} \right\}_{i = 1}^n$ 作为训练样本, 按式(4)近似 $ {\varphi _1}\left( \theta \right) $ 和 $ {\varphi _2}\left( \theta \right) $ :

$\left\{ { \begin{split} {{\tilde \varphi }_1}(\theta ) =&\frac{N}{n} \sum\limits_{i = 1}^N {\frac{1}{2}} \exp ( - s({x_{{k_i}}})){\left( {{Y_{{k_i}}} - {u_\theta }({x_{{k_i}}})} \right)^2} \\ & + \frac{1}{2}s({x_{{k_i}}}) - \log p(\theta ) + {c_1} \\ {{\tilde \varphi }_2}(\theta ) =& \frac{N}{n}\sum\limits_{i = 1}^N {\frac{{fd + 1}}{2}} \log \left(1+ {\frac{{\exp ( - s({x_{{k_i}}})){{({Y_{{k_i}}} - {u_\theta }({x_{{k_i}}}))}^2}}}{fd}} \right) \\ & + \frac{1}{2}s({x_{{k_i}}}) - \log p(\theta ) + {c_2} \end{split} } \right.$

(4)

其中, c₁和c₂为常数.

ANN、CNN和RNN为DL网络模型最基础的3种网络结构, 也是目前业界开发的最先进的网络模型的基础网络结构. ANN由多个节点层所组成, 每一层节点都与下一层的节点相连接, 而相同层之间的节点没有连接关系. ANN节点层可以分为输入层、输出层和隐藏层, 输入层接收特征数据, 输出层输出预测结果, 在输入层和输出层之间包含一到多个隐藏层, 上一层的输出为下一层的输入, 各层之间存在激活函数. 常用的激活函数有Sigmoid函数、tanh函数和ReLU函数等, 它的作用是引入非线性因素从而解决非线性问题. 相比于其他激活函数, ReLU函数可以有效避免深度学习中出现梯度爆炸和梯度消失的问题, 因而本文采用ReLU函数. CNN引入了卷积层和池化层, 其中, 卷积层中包含若干卷积核, 通过卷积操作提取相关特征, 而池化层相当于降采样, 经过池化操作可以获得最显著特征并降低模型参数数量. RNN是另一种模型范式, 采用循环结构使得网络能“记忆”时间序列数据的趋势, 其中, LSTM和门控循环单元(gate recurrent unit, GRU)通过门控控制单元解决普通RNN的梯度消失和梯度爆炸问题, 因而成为在实际应用中较为普遍的RNN模型技术. 在每个循环单元中, LSTM包含3个门控装置: 输入门、遗忘门和输出门, 而GRU 包含两个门控装置: 重置门和更新门, 相比于LSTM, GRU更新门相当于LSTM中的输入门和遗忘门, 从而使得GRU的内部参数减少, 模型训练时间随之减少. 因而本文采用GRU.

针对图1 中的DN, 本文将分别使用ANN、CNN和RNN进行建模. 这里CNN和RNN结构见图2和图3, 其中, ANN包含4个节点层, 其中两个隐藏层节点个数分别为64和32; CNN中包含两层卷积层、两个Norm层和一个最大池化(MaxPool)层, 卷积层中卷积核大小为1, 16个通道, Norm层的作用是将输入数据标准化(均值为0, 标准差为1), 这有助于提升模型的预测性能; RNN中有两层GRU, 相应的隐藏层维度为64. CNN和RNN提取相关特征后通过Flatten层和Dense层, 最后得到模型输出. CNN和RNN结构见图2和图3.

1.2 模型参数后验采样

式(2)的 $ p(\theta |D) $ 一般无法通过分析方法求解, 我们常用如下两种近似求解的方法: 变分贝叶斯法和采样的方法. 正如引言中所介绍的, 变分贝叶斯法存在一些问题, 故本文使用后者. 随机梯度马尔科夫链蒙特卡洛^[20]是BDL模型常用的基于采样的方法, 它包含很多变体, 如随机梯度朗之万动力学(stochastic gradient Langevin dynamics, SGLD)算法^[21,22]和随机梯度汉密尔顿蒙特卡洛(stochastic gradient Hamiltonian Monte Carlo, SG-HMC)算法^[23] . 基于如下几点原因, 本文采用SG-HMC算法: (1) HMC引入动量, 相比于SGLD 加快了收敛速率; (2) $ p(\theta |D) $ 通常为非凸函数, SG-HMC 在解决随机非凸优化问题上比SGLD具有更好的性能^[24].

SG-HMC算法具体方法如下: 引入辅助变量 $v$ , 在第 $i$ 个迭代过程中参数 $\theta $ 和辅助变量 $v$ 的更新遵循:

$ \left\{ {\begin{split} {\theta _i} =& {\theta _{i - 1}} + {v_i} \\ {v_i} =& (1 - \delta ){v_{i - 1}} - {\alpha _i}\nabla \tilde \varphi ({\theta _{i - 1}}) + \sqrt {2{\alpha _i}\delta {\gamma ^{ - 1}}} {\varepsilon _i} \end{split}} \right. $

(5)

其中, $\alpha $ 为学习率, $1 - \delta $ 为动量项, $\gamma > 0$ 为逆温系数, ${\varepsilon _i}$ 为标准正态分布随机变量. 关于学习率有如下特点: 较小的 $\alpha $ 有利于算法充分探索局部区域, 但无法帮助算法“跳出”局部区域, 导致未采样的区域的存在, 整体采样效率不高; 当 $\alpha $ 较大时, 尽管有利于算法“跳出”局部区域从而更好地探索参数后验分布, 但存在算法无法收敛的问题. 实践中, 学习率通常采用递减的更新模式: 初始化一个较大的学习率, 然后递减到零, 但这样的更新模式下存在采样效率不高的问题. 为了提高采样效率, Zhang等^[25]提出一种新的SG-HMC 算法: CSG-HMC. 该算法采取周期递减的学习率, 在一个周期内以较大的学习率开始, 然后递减到零, 随后在下一个周期继续以较大的学习率开始. 因而, 相比于学习率递减更新SG-HMC算法, CSG-HMC能够更好地“跳出”局部区域, 从而提升了采样效率. 在CSG-HMC下, 学习率的更新过程为:

$ \begin{split} {\alpha _i} =& \frac{{{\alpha _0}}}{2}\left[ {\cos \left( {\frac{{\pi \bmod (i - 1, \left\lceil {I/K} \right\rceil )}}{{\left\lceil {I/K} \right\rceil }}} \right) + 1} \right], \; i = 1, \cdot \cdot \cdot , I \\ \end{split} $

(6)

其中, ${\alpha _0}$ 为初始学习率, $K$ 为循环次数, $I$ 为总的迭代次数, mod表示求余, $ \left\lceil {I/K} \right\rceil $ 为小于等于 $ \left\lceil {I/K} \right\rceil $ 的最大整数. 由式(5) 和式(6), BDL模型的CSG-HMC采样算法如算法1所示, 每个循环周期包含探索阶段(exploration stage, ES)和采样阶段(sampling stage, SS), 前者为后者提供“热启动”, 有助于在训练过程中获得更好的后验样本.

算法1. CSG-HMC采样算法

(1) $\scriptstyle \theta $ 和 $\scriptstyle v$ 初始化

(2) while $\scriptstyle e = 0,\; \cdots ,\; {n_e} - 1$ do;

　 1) while $\scriptstyle i = 0,\; \cdots ,\; m - 1$ do;

　　调整学习率:

　　　 $\scriptstyle \begin{gathered} \scriptstyle \alpha \leftarrow \frac{{{\alpha _0}}}{2}\left[ {\cos \left( {\frac{{\pi \bmod (r, \left\lceil {I/K} \right\rceil )}}{{\left\lceil {I/K} \right\rceil }}} \right) + 1} \right], \\ \scriptstyle r = e \times m + i \\ \end{gathered} $

　　　 If $\scriptstyle \bmod (e, M) + 1 < {\beta _1}$ do:

　　　　 $\scriptstyle \begin{gathered} \scriptstyle v \leftarrow (1 - \delta )v - \alpha \nabla \tilde \varphi (\theta ) \\ \scriptstyle \theta \leftarrow \theta + v \\ \end{gathered} $

　　　 Else

　　　　 $\scriptstyle \begin{gathered}\scriptstyle v \leftarrow (1 - \delta )v - \alpha \nabla \tilde \varphi (\theta ) + \sqrt {2\alpha \delta {\gamma ^{ - 1}}} \varepsilon \\\scriptstyle \theta \leftarrow \theta + v \\ \end{gathered} $

　　　 If $\scriptstyle \bmod (e, M) + 1 > {\beta _2}$ do:

　　　　　　 保存 $\scriptstyle \theta $

　2)end while

(3) end while

1.3 不确定性度量

相比于经典网络模型, 本文构建的BDL模型基于概率论, 可以进行概率推理, 提升了模型可解释性, 与此同时BDL可以估算预测结果的不确定性, 因此更适合于实际应用. 那么这里的不确定性要如何度量. 金融数据中存在噪音和不确定性, 我们称由数据带来的不确定性为任意不确定性(aleatoric uncertainty, AU), 而称由模型参数和模型结构引起的不确定性为模型不确定性(model uncertainty, MU), 也称为认知不确定性(epistemic uncertainty). 本节将给出不确定性度量的相关概念与原理.

对新的输入向量 $x$ , 对应标签 $ Y $ 和参数 $\theta $ 的联合分布满足:

$ p(y, \theta |x, D) = p(y|x, \theta )p(\theta |D) $

因而标签的条件分布满足:

$ Y\sim p(y|x, D) = \int {P({f_\theta }(x))} p(\theta |D)d\theta $

(7)

式(7)可通过蒙特卡洛模拟近似求解. 设CSG-HMC算法采样得到了 $T$ 个参数 $\left( {{\theta ^1}, \cdots , {\theta ^T}} \right)$ , 则有:

$ p(y|x, D) \approx \frac{1}{T}\sum\limits_{t = 1}^T {P({f_{{\theta ^t}}}(x))} $

(8)

式(8)中为t分布, 因而 $ p(y|x, D) $ 近似为 $T$ 个t分布的密度函数的平均. 对标签Y求期望和二阶矩:

$ \begin{split} {{E(}}Y) = &\int {yp(y{\text{|}}x, D)} dy \\ \approx & \frac{1}{T}\sum\nolimits_{t = 1}^T {\int {yp({f_{{\theta ^t}}}(x))} dy} = \frac{1}{T}\sum\limits_{t = 1}^T {{u_{{\theta ^t}}}(x)} \end{split} $

(9)

$ {{E(}}{Y^2}{\text{) = }}\int {{y^2}p(y{\text{|}}x, D)} dy \approx \frac{1}{T}\sum\limits_{t = 1}^T {u_{_{{\theta ^t}}}^2(x) + } \sigma _{_{{\theta ^t}}}^2(x) $

(10)

因而得到方差的近似表达:

$ \begin{split} {{Var}}(Y) =& {{E(}}{Y^2}{{) - (E(}}Y{\text{)}}{{\text{)}}^{\text{2}}} \\ \approx& \frac{1}{T}\sum\limits_{t = 1}^T {\sigma _{_{{\theta ^t}}}^2(x)} + \frac{1}{T}\sum\limits_{t = 1}^T {{{\left( {{u_{{\theta ^t}}}(x) - \hat u} \right)}^2}} \end{split} $

(11)

其中, $ \hat u = \dfrac{1}{T}\displaystyle\sum\limits_{t = 1}^T {{u_{{\theta ^t}}}(x)} $ . 由式(9), $ \hat u $ 为 $Y$ 的渐进无偏估计, 方差可以视为预测的不确定性, 因此本文将基于式(11)定义两种不确定性度量, 它们分别对应式(11)中不等号右边的两部分. 金融数据中普遍存在噪音和不确定性, 本文将数据中的不确定性被称为任意不确定性(aleatoric uncertainty, AU). 模型不确定性(model uncertainty, MU)代表模型参数和模型结构的不确定性, 也称为认知不确定性(epistemic uncertainty). 具体定义为:

$ MU = \frac{1}{T}\sum\limits_{t = 1}^T {{{\left( {{u_{{\theta ^t}}}(x) - \hat u} \right)}^2}} $

(12)

$ AU = \frac{1}{T}\sum\limits_{t = 1}^T {\sigma _{_{{\theta ^t}}}^2(x)} $

(13)

总不确定性 $U$ 定义为:

$ U = MU + AU $

(14)

对比式(3)和式(9)–式(14), 在模型后验对数似然中蕴含数据和模型的不确定性, 可见在BDL建模时充分考虑了不确定性. $U$ 为预测 $ \hat u $ 的置信程度, 在 $U$ 较大的情况下, 意味着预测的不确定性较大, 而在 $U$ 较小时, 意味着预测的准确性较高. 在实际投资分析应用中, 设置阈值 $\tau $ , 当BDL模型估计的不确定性 $U > \tau $ 时, 可以借助专家系统等引入人工分析的方法, 避免仅依靠深度学习模型, 具体如如图4, 这有助于提升风险控制能力, 同时也可以极大减少人工分析所带来的人工成本和时间成本.

2 实证分析

为了充分评估上述所构建的BDL模型的性能和适用性, 本文选取全球具有代表性的股票指数进行实证预测分析.

2.1 数据来源与样本选择

为了验证模型的普适性, 本文选取中国大陆、美国市场、欧洲市场和其他亚太市场中具有代表性的15 个市场指数进行实证分析, 中国7个, 其他亚洲国家2个, 美国3个, 欧洲3个, 具体为: 上证指数, A股指数, B股指数, 深证A 指, 深证B 指, 恒生指数, 富时新加坡海峡指数, 日经225指数, 标普500 指数, 道琼斯工业指数, 纳斯达克指数, 德国DAX指数, 法国CAC40指数, 英国富时100指数. 选取每日股指收盘价作为变量, 选取2017年1月3日到2021年7月30日的每日数据作为样本, 共有1 114个样本. 相关指数数据来自Wind 数据库.

由于DL模型对数据十分敏感, 故为了提高模型的预测性能, 需要对初始数据进行预处理. 首先进行标准化处理. 对每个指数, BDL模型的预测思路为: 用前 $l$ 天的指数收盘价信息预测未来1天的指数收盘价. 取 $l = 5$ (以过去一周的数据为基础, 预测未来数据), 得到数据集 $D$ . 在获得上面数据集的基础上按照下面方法构建训练集、验证集和测试集: 将前1 000组按照8:2的比例分为训练集和验证集, 将后109组数据作为测试集. 训练集用于训练模型参数, 验证集是用于评估模型以获得最优的超参数. 最后, 在测试集上评估各个模型预测性能.

为了验证所构建的基于t分布的BDL模型的优越性, 本节以预测分布为正态分布的BDL模型作为对照模型进行实证分析. 采样过程中使用的超参数范围见表1, 其中不同数据上最优的 ${\alpha _0}$ 和自由度fd通过网格搜索的方法从表1给出的范围中选出.

本节将从预测精度和模型通用性两个维度分析各个模型的预测性能. 预测精度评估采用MSE, MSE越小代表预测精度越高. 表2–表4分别报告了不同模型下7个国内股票指数和8个国际股票指数预测的MSE, 其中, BDL₁、BDL₃、BDL₅表示分别基于ANN、CNN、RNN和正态分布构建的BDL模型, BDL₂、BDL₄、BDL₆表示分别基于ANN、CNN、RNN和t分布构建的BDL模型. 根据表2–表4显示的数据不难发现, 对于 8个国际指数和 7个国内指数, 在预测精度方面, t 分布相比正态分布表现更好. 由表2, 在 8个国际指数中, 道琼斯工业指数、标普 500 指数、德国 DAX 指数性能提升明显, 而在 7个国内指数中, A 股指数、深证综指性能提升明显, 而上证指数性能略有下降; 由表3, 在 8个国际指数中, 标普500、纳斯达克指数、德国 DAX、法国 CAC40 指数性能提升明显, 在国内指数中两者性能相当; 由表4, 在 8个国际指数和 7个国内指数中, 性能提升明显.

表5展示了国内、国际及全部指数下各模型的平均预测效果. BDL₂在国际指数中平均MSE值为0.038, 相比BDL₁模型, 平均MSE降低了0.066, 在国内指数中平均MSE值为0.014, 相比BDL₁模型, 平均MSE降低了0.003; BDL₄在国际指数中平均MSE值为0.020, 相比BDL₃模型, 平均MSE降低了0.016, 在国内指数中平均MSE值为0.013, 相比BDL₃模型, 平均MSE降低了0.001; BDL₆在国际指数组中平均MSE值为0.132, 相比BDL₅模型, 平均MSE降低了1.165, 在国内指数组中平均MSE值为0.015, 相比BDL₅模型, 平均MSE降低了0.266. 总体来看, BDL₂在全部15个股票指数的平均MSE值为0.027, 比BDL₁降低0.036; BDL₄在全部15个股票指数的平均MSE值为0.017, 比BDL₃降低0.008; BDL₆在全部15个股票指数的平均MSE值为0.077, 比BDL₅降低0.746.

为了估计模型在不同数据影响下预测精度的差异, 本文统计了预测MSE的标准差, 一般标准差越小表明受数据影响越小, 模型通用性越好. 表6展示了国内、国际及全部指数下各模型预测的标准差. BDL₂在国际指数中MSE标准差值为0.050, 相比BDL₁模型, 标准差降低了0.124, 在国内指数中MSE标准差值为0.009, 相比BDL₁模型, 标准差降低了0.002; BDL₄在国际指数中MSE标准差值为0.016, 相比BDL₃模型, 平均MSE降低了0.017, 在国内指数中MSE标准差值为0.008, 相比BDL₃模型, 标准差降低了0.001; BDL₆在国际指数组中MSE标准差为0.149, 相比BDL₅模型, 标准差降低了0.843, 在国内指数组中MSE标准差为0.009, 相比BDL₅模型, 标准差降低了0.205. 总体来看, BDL₂在全部15个股票指数的MSE标准差值为0.038, 比BDL₁降低0.093; BDL₄在全部15个股票指数的MSE标准差值为0.013, 比BDL₃降低0.014; BDL₆在全部15个股票指数的MSE标准差值为0.121, 比BDL₅降低0.766.

表7报告了忽略基础网络模型后的BDL模型的预测效果评估结果. 相比于正态分布的模型, 正态分布的模型, 在7个国内指数、8个国际指数和全部15个指数中的MSE均值分别降低了0.090、0.416和0.253, 标准差分别降低了0.205、0.843和0.766. 因此, 就股票指数预测的整体水平而言, 以t分布为预测分布的BDL模型在预测精度和通用性方面优于以正态分布为预测分布的BDL模型.

3 不确定性度量作用验证

相比于传统的DL模型, BDL模型能估计预测结果的不确定性. BDL模型借助不确定性度量, 可以“识别”模型预测结果的偏差, 从而避免使用者盲目地“相信”模型的预测结果, 减少预测风险. 这正是不确定性度量在预测中的作用. 本小节将采用如下简单的方法验证不确定性度量 $U$ 的作用: 在测试集中得到预测 $\left\{ {{{\hat u}_i}} \right\}_{i = 1}^{109}$ 和对应的不确定性度量 $\left\{ {{U_i}} \right\}_{i = 1}^{109}$ , 以误差绝对值的平均值(mean absolute error, MAE)作为度量, 不确定性的阈值 $\tau $ 取值为 $\left\{ {{U_i}} \right\}_{i = 1}^{109}$ 的第90 (或95)个百分位数, 分别计算了在不确定性阈值之下所对应的预测的MAE₁和整体预测的MAE₂, 并计算 $\Delta = ({{MA}}{{{E}}_2} - {{MA}}{{{E}}_1})/ {{MA}}{{{E}}_2}$ , 当 $\Delta > 0$ 时, 表明在不确定性阈值 $\tau $ 之下所对应的预测结果的MAE更小, 表明 $U$ “识别”了模型预测结果中的偏差, 从而提升了预测性能, 具体结果如表8. 在表8中, ${\Delta _1}$ 、 ${\Delta _2}$ 和 ${\Delta _3}$ 分别对应于模型BDL₂、BDL₄和 BDL₆下计算的 $\Delta $ . 在BDL₂模型下, 对于8个国际指数, MAE均得到了提升, 性能平均提升了3.1%, 而在7个国内指数中, 除了深证A指、深证综指有略微下降, 其余指数MAE均得到了提升, 性能平均提升了1.8%. 对于BDL₄和BDL₆模型也有同样结果. 综合来看, MAE可以提升性能约为2.73%. 因而正如图4所示, 将BDL模型应用于实际投资分析中, 使用者依据不确定性 $U$ 识别相应的预测不确定性, 从而在不确定性较大的情形下采取更加谨慎的策略, 避免造成损失. 总之, 从不确定性角度来看, 相比于传统的DL模型, BDL模型在实际应用中更具有优势.

4 结论与展望

科技创新已成为当前众多领域的主流趋势, Fintech更是金融领域研究的热门课题. 基于对实际数据特征和t分布性质的分析研究, 本文构建了一种以t分布为预测分布并采用CSG-HMC采样算法的BDL框架, 而且从预测方差入手定义了不确定性度量. 为了检验模型的性能, 本文分别在ANN、CNN 和RNN 上构建具体的BDL模型, 并应用于全球15个股票指数的预测分析, 同时与基于正态分布的BDL模型对比. 得出以下结论: 1) 本文提出的框架在ANN、CNN和RNN上均有显著提高, 该框架具有普适性; 2) 15个指数的预测效果显示在预测精度和通用性方面, t分布相比正态分布具有显著优越性. 3) 通过设定阈值, 将不确定性在阈值之下的预测值MAE与初始MAE对比发现, 前者相较后者可以提升约为2.73%, 表明不确定性的定义是有效的. 本文提出的BDL框架, 可用于众多自然科学和社会科学领域, 具有广阔的前景.

本文对BDL模型在金融预测方向进行积极探索, 验证了以t分布作为预测分布的优越性和不确定性度量的有效性, 为深度学习在金融预测中的不确定性研究提供了实践经验. 不足之处在于: 1) 市场数据在上涨和下跌的时候可能具有不同的分布特性, 因而需要基于未来涨跌情况构造条件概率分布, 而本文选取的预测分布是对称的, 未考虑非对称的情况, 这一点需要深入探索; 2) 本文主要集中于模型预测精度的研究, 未分析模型的盈利能力; 3) 深度学习模型结构仍是传统结构, 有待于创新以拓展适用性. 后续研究工作将继续围绕这些方面, 探讨深度学习的应用和理论创新.