2. 贵州理工学院 大数据学院, 贵阳 550003
2. School of Big Data, Guizhou Institute of Technology, Guiyang 550003, China
为降低负荷序列的复杂性, 可在训练模型前, 利用常见的信号分解方法将负荷序列分解一组具有不同时间尺度特征的固有模态函数然后再利用该组模态函数训练模型. 如文献[11-13]利用EMD分解方法与神经网络相结合的方法, 通过EMD方法分解负荷序列, 得到了一组规律性更强的固有模态函数, 再送入神经网络训练, 从而降低了模型的预测难度, 提高了模型的预测精度.
基于以上研究, 本文提出了基于EMD-TCN-ELM的短期电力负荷预测方法. 为降低负荷序列的复杂性, 利用EMD分解方法得到不同的分量. 为降低训练时间和减小分量逐个预测所带来的累计误差, 利用分量过零率大小将分量重构为高频分量和低频分量. 由于高频分量规律性更差, 利用TCN模型预测负荷的高频分量. 而低频分量的规律性更强, 考虑到训练时间和预测精度, 本文选用极限学习机ELM预测低频分量. 通过实验将所提模型EMD-TCN-ELM分别与3个单模型TCN、ELM、LSTM和3 个混合模型EMD-TCN、EMD-ELM、EMD-LSTM比较, 其MAPE分别降低0.538%, 1.866%, 1.191%, 0.026%, 1.559%, 0.323%, 所提模型的预测精度最高. 且所提模型在预测精度前3的模型中训练时间最短, 验证了所提模型在负荷预测精度和训练时间方面的优越性.
1 经验模态分解1) 确定序列x(t)的极大值和极小值点, 利用3次样条插值法分别对极大值点和极小值点拟合得到上包络线和下包络线. 在得到上下包络线后, 对上下包络线取平均值得到m1.
2) 将列x(t)减去m1得到c1. 得到二者之差:
| c1=x(t)−m1 | (1) |
3)若
4)在得到
| d1=x(t)−IMF1 | (2) |
5)在得到
| x(t)=n∑i=1IMFi+dn | (3) |
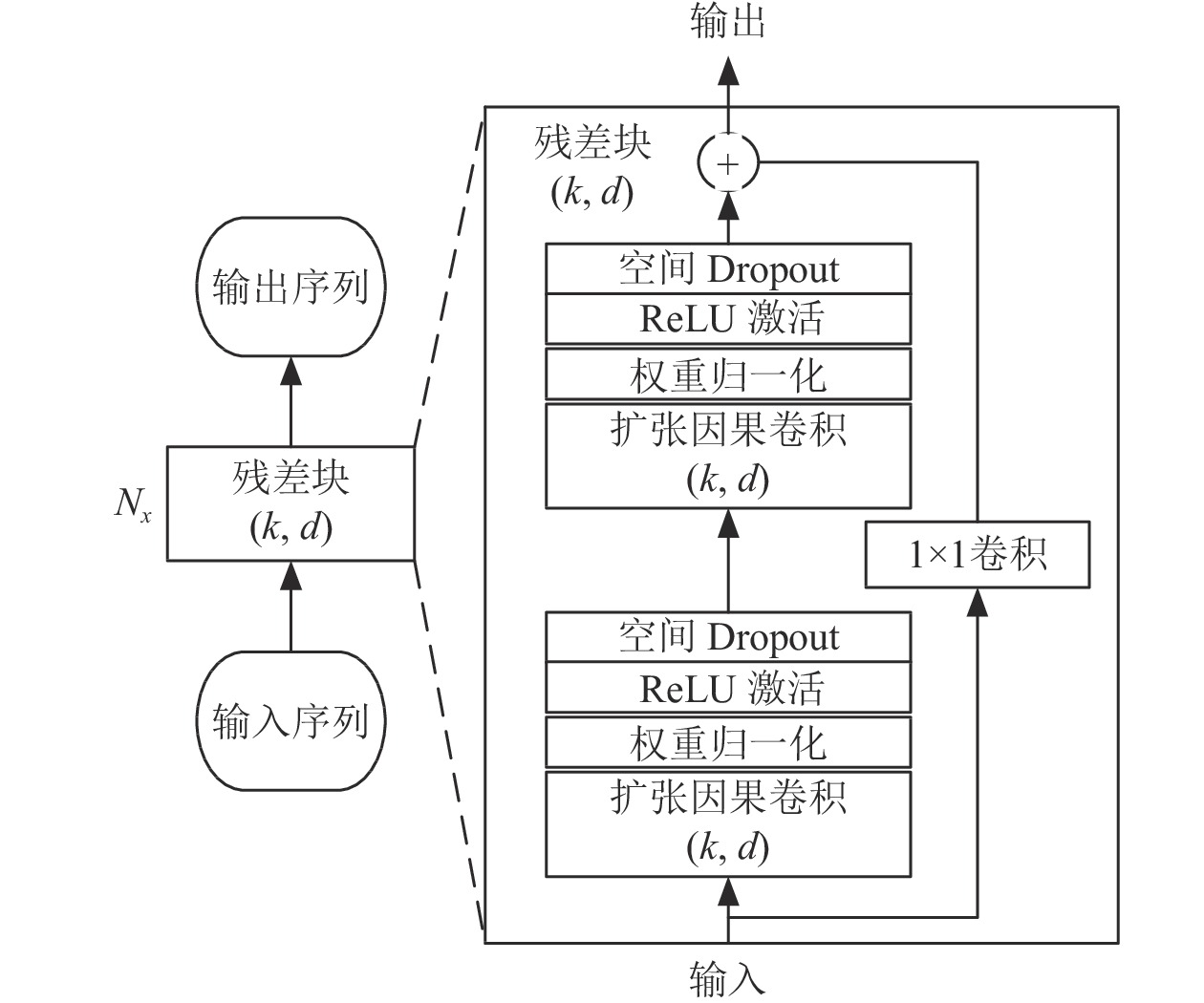
TCN网络由若干个残差块堆叠而成. 残差块的内部构造块包括扩展因果卷积层, 权重归一化操作, ReLU激活函数, 空间Dropout, 残差链接, 以及可选的1×1卷积层. 残差块中卷积层的扩张系数d从输入序列到输出序列成倍数地增加, 增加了网络的感受野, 减少了网络的深度和参数, 更有利于神经网络的训练. 因果卷积的引入使得卷积层第t个时间步的输出仅与前t个时间步的输入相关. 权重归一化是针对卷积核的归一化操作, 能够加速神经网络的收敛. ReLU激活函数引入了非线性映射. 空间Dropout是针对卷积神经网络的正则化技术, 能够降低神经网络过拟合的风险. 残差连接的引入有利于梯度在整个神经网络中传播, 有利于神经网络的学习. 而当残差块的输入与输出通道大小不一致时, 需要引入1×1的卷积核改变输入的通道大小从而与输出相加.
|
图 1 TCN架构 |
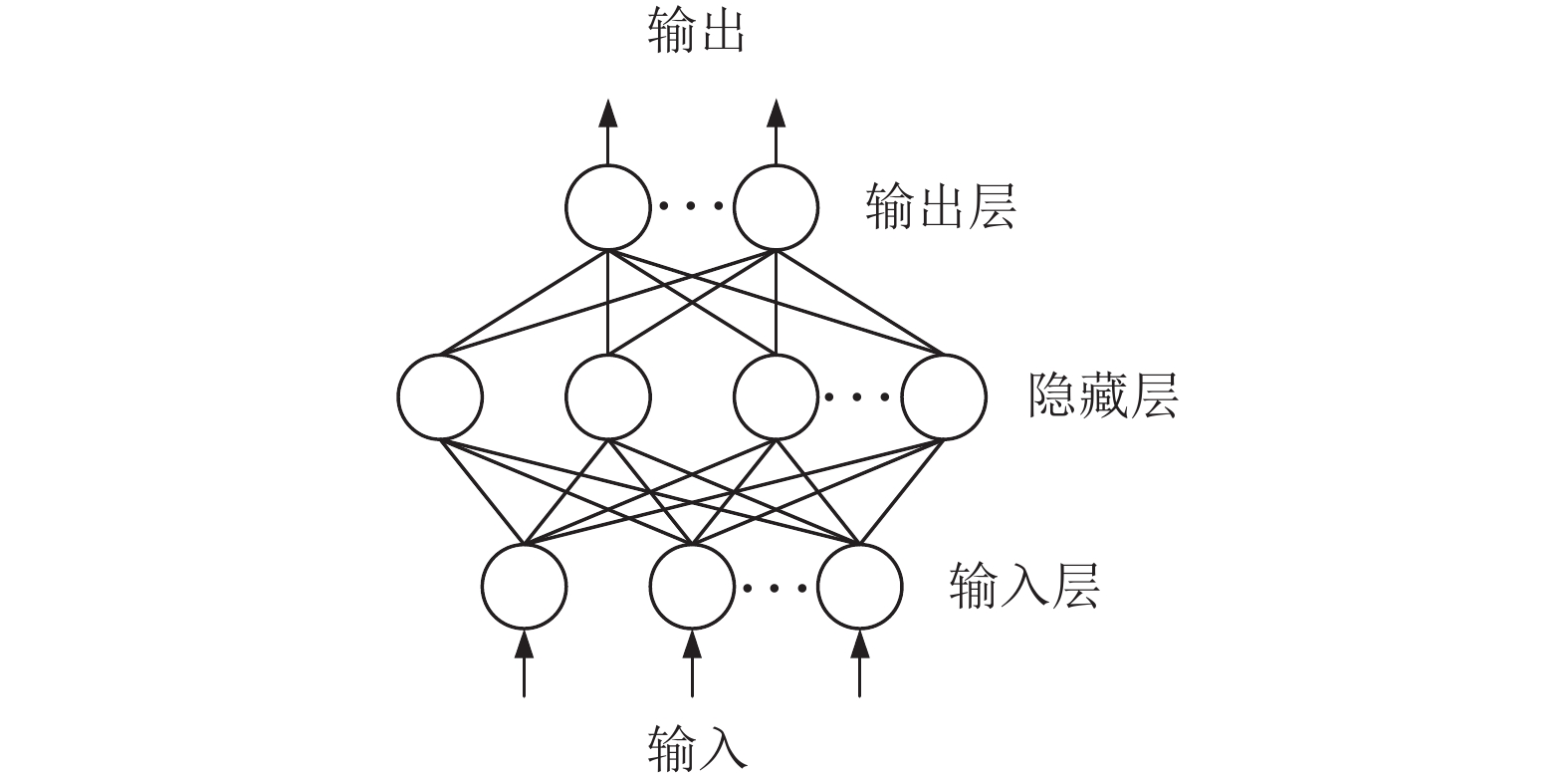
3 极限学习机
|
图 2 ELM架构 |
| ∑Li=1βig(Wi⋅Xj+bi)=oj,j=1,⋯,K | (4) |
其中,
如果模型的所有输出
| ∑Li=1βig(Wi⋅Xj+bi)=tj,j=1,⋯,K | (5) |
式(5)可简述为:
| Hβ=T | (6) |
其中,
| H=[g(W1⋅X1+b1)⋯g(WL⋅X1+bL)⋮⋱⋮g(W1⋅XN+b1)⋯g(WL⋅XN+bL)]N×L | (7) |
最优输出权重为
| ‖Hˆβ−T‖=minβ‖Hβ−T‖ | (8) |
对线性系统
| ˆβ=H+T | (9) |
其中,
相较于一般的神经网络, ELM的训练不需要通过梯度的反向传播来更新权重. 其训练过程只需要通过以下步骤: 1)随机初始化
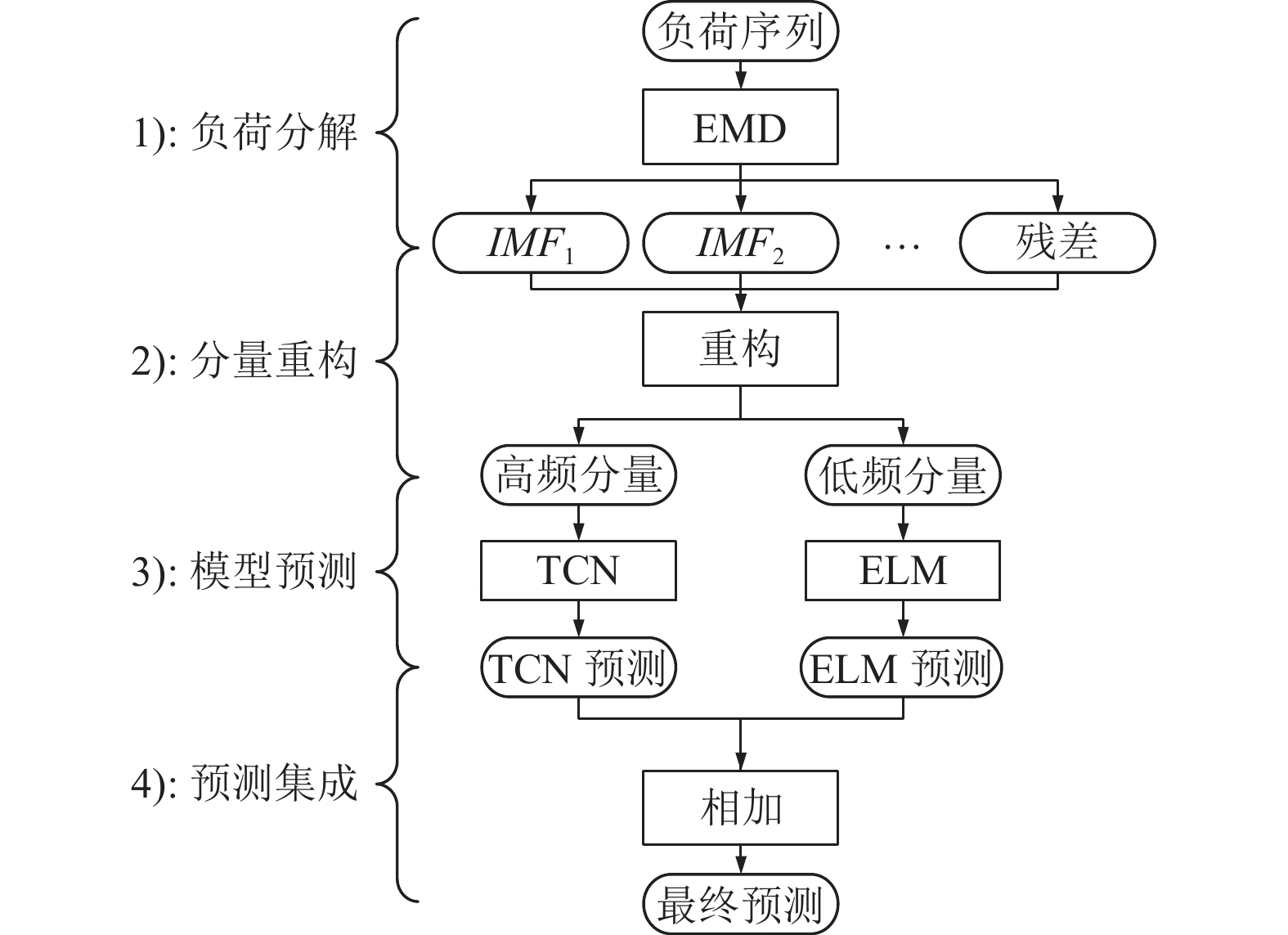
本文所提负荷预测方法由4个阶段构成: 1)负荷分解; 2)分量重构; 3)模型预测; 4)预测集成. 如图3所示.
1)负荷分解: 首先, 利用EMD算法将负荷序列分解为一组不同的固有模态分量和一个残差分量. 相较于原始负荷序列, 通过EMD算法得到的分量更为简单, 规律性更强, 更有利于模型的预测. 若分别对所有的分量进行预测, 存在以下问题: 第一, 由于神经网络模型训练所需时间较长, 对所有的分量预测需要较大的时间成本. 第二, 由于对每个分量的预测会产生误差, 若对所有的分量预测, 则在最终的预测集成阶段可能产生误差积累.
2)分量重构: 基于以上原因, 本文将EMD得到的分量重构为高频分量和低频分量. 重构方法为: 利用所得分量过零率的大小将分量分为高频分量组和低频分量组. 将高频分量组的分量相加的高频分量, 将低频分量组的分量相加得低频分量.
3)模型预测: 由于高频分量随机性较强, 规律较为复杂, TCN模型由于其结构的复杂性, 其对时间序列高频分量的特征提取有更大的优越性, 因此, 利用TCN模型对高频分量进行预测. 而低频分量变化较为平缓, 规律性较为明显, 若将TCN模型用于预测低频分量, 其预测效果相较于其他模型并无明显的优势, 而ELM的训练速度快, 所需时间较少, 且对规律性较强的低频分量的预测精度也较高. 此外, 不同模型的引入还能降低模型的泛化误差, 进而提高模型的预测精度. 在权衡训练时间和预测精度后, 利用ELM模型对低频分量进行预测.
4)预测集成: 在得到分别来自TCN模型和ELM模型的高频分量和低频分量预测后, 由于高频分量和低频分量在负荷序列中的占比为1:1, 因此, 将高频分量预测和低频分量预测直接相加得到负荷的最终预测.
|
图 3 预测方法 |
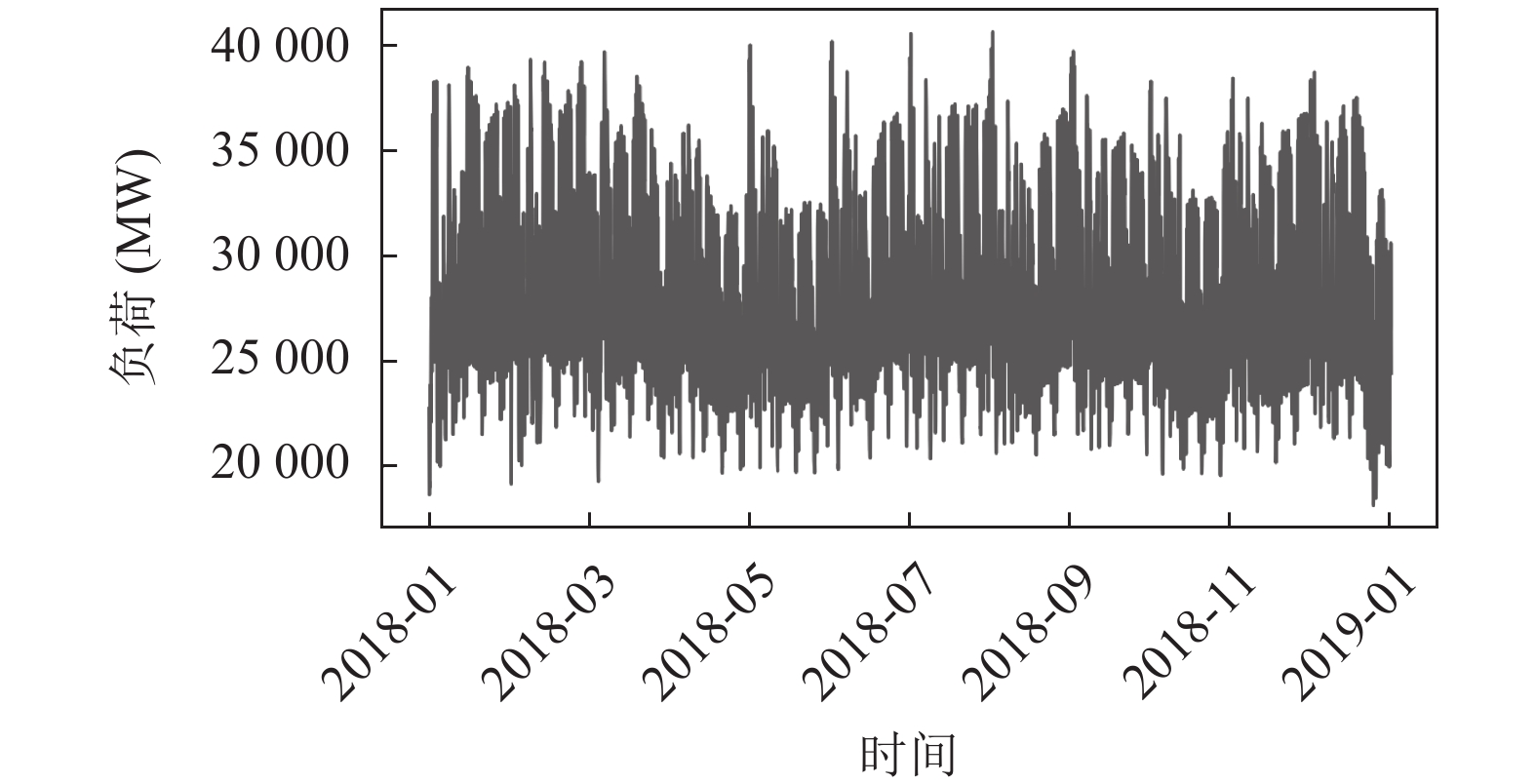
5 实验设计 5.1 数据集
|
图 4 西班牙电力消耗 |
5.2 评估指标
本实验评估指标采用均方根误差(RMSE)和平均绝对百分误差(MAPE). 公式如下:
| MAPE=1n∑ni=1|˜yi−yi|yi×100% | (10) |
| RMSE=√n∑i=1(˜yi−yi)2n | (11) |
其中, n表示预测点个数,
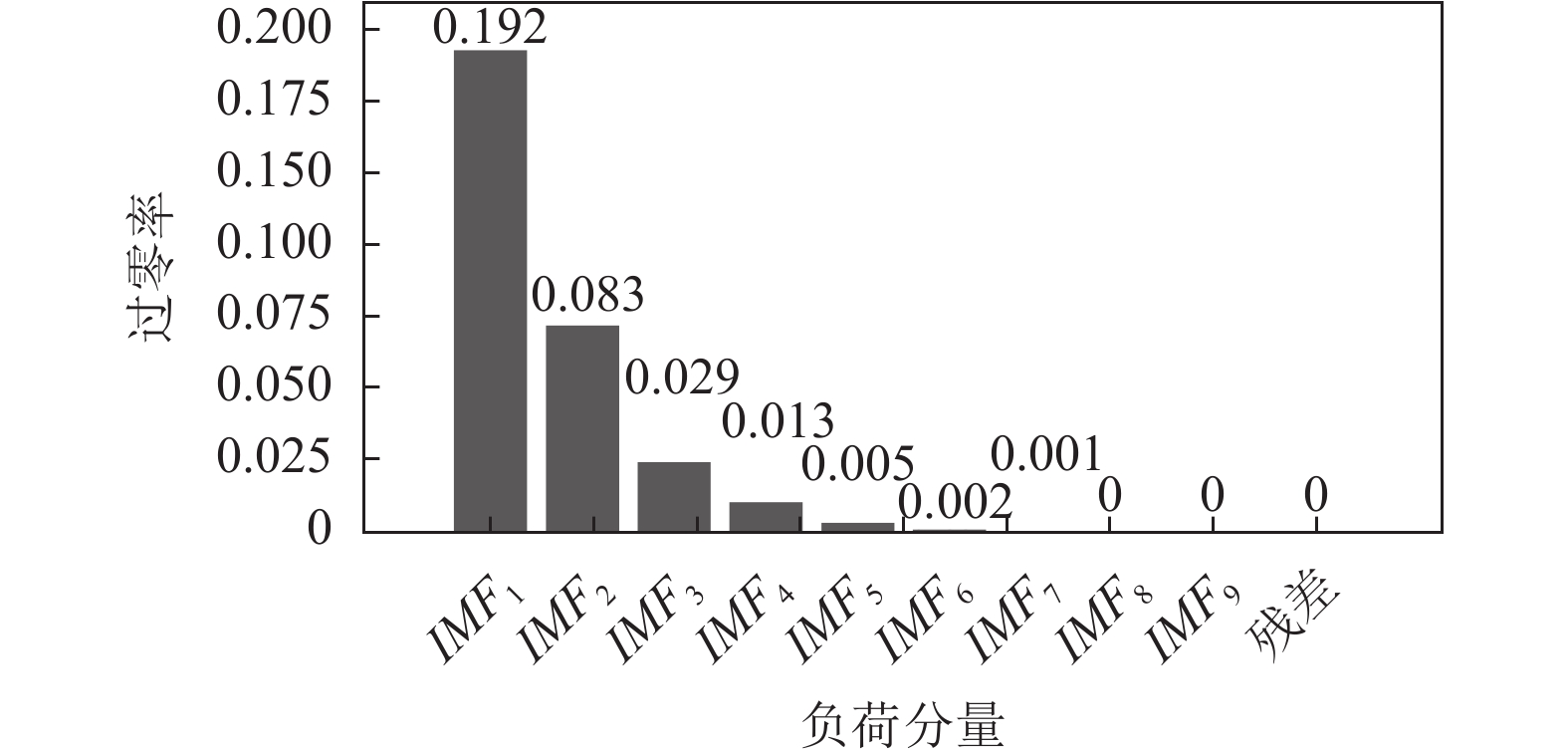
为降低预测模型的训练时间成本和减少逐个分量预测可能带来的累计误差, 利用各个分量过零率大小, 将高于某个过零率的分量划分到高频分量组, 低于该过零率的分量划分到低频分量组. 将高频分量组的分量相加重构得高频分量, 低频分量组的分量相加重构得低频分量, 本实验中过零率的大小选为0.01. 各个分量过零率大小如图6所示.

|
图 5 EMD分解结果 |
|
图 6 各分量过零率 |
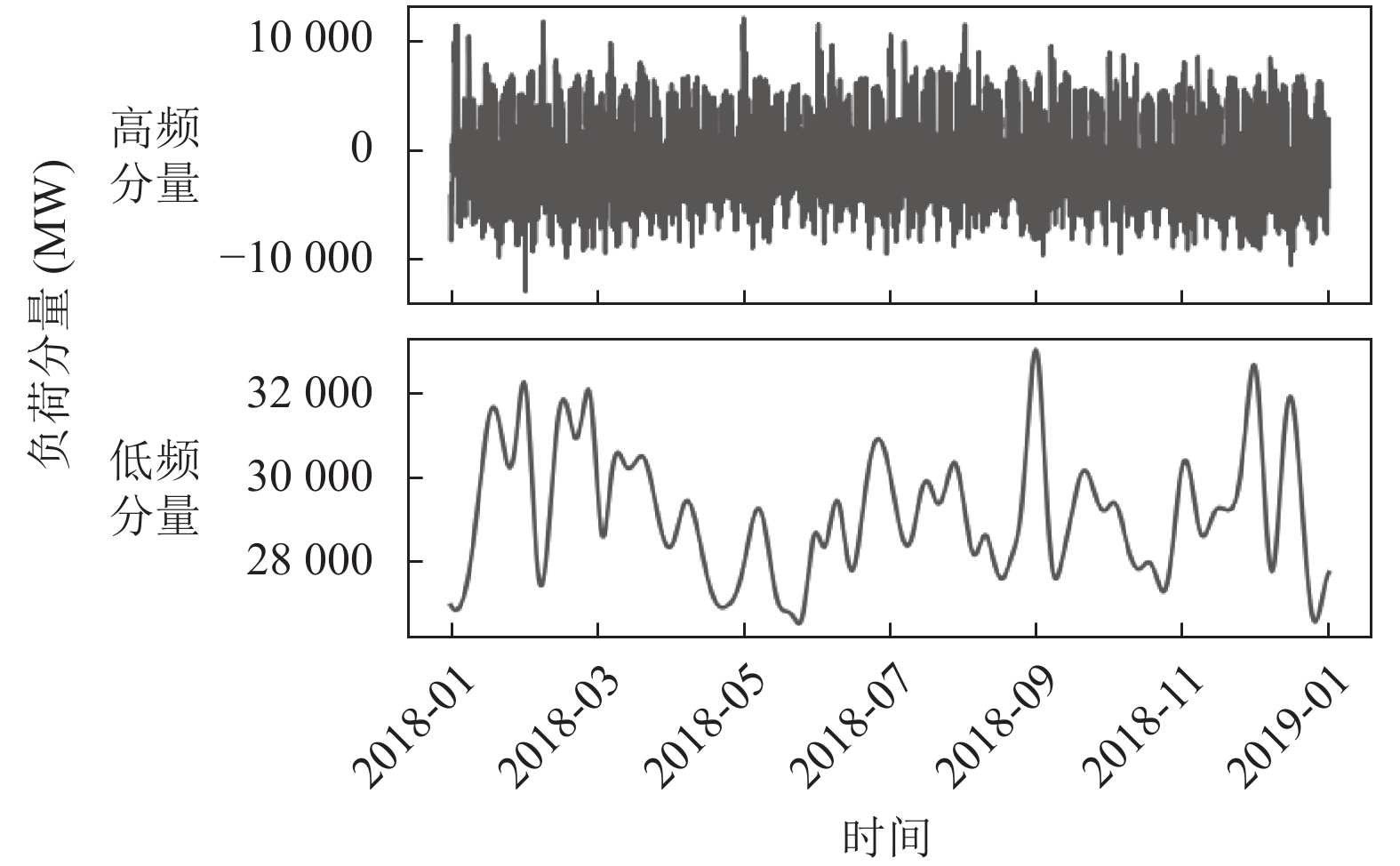
通过计算各分量的过零率, 并且四舍五入到小数点后3位可知: 分量IMF1–IMF4的过零率高于0.01, IMF5–IMF9和残差分量的过零率低于0.01, 因此, 将IMF1–IMF4重构为高频分量, IMF5–IMF9和残差分量重构为低频分量. 各个分量重构结果如图7所示.
5.4 模型构建与训练为验证所提混合模型的优越性, 本文构造并训练了3个单一模型: TCN、ELM、LSTM. 3个混合模型: EMD-TCN、EMD-ELM、EMD-LSTM. 本文所提模型: EMD-TCN-ELM. 各个模型的结构和超参数如下:
1) TCN. 输入层: 输入形状=(7, 24), 即为加快模型的收敛和减少模型参数, 将7×24个历史观测值分布到7个时间步上, 每个时间步共享24个单元. 卷积块1: 卷积核个数=64, 卷积核大小=2, 步长=1, 扩张系数=1, 激活函数=ReLU, 空间Dropout=0.2, 1×1卷积核个数=64; 卷积块2: 卷积块2超参数设置与卷积块1类似. 区别在于扩张系数=2, 1×1卷积核个数=24, 卷积块2的第2个卷积层的单元数为24, 第2个卷积层不设置激活函数. 输出层: 在得到卷积块2残差连接的输出后, 应用Sigmoid函数得到输出层的激活, 即预测值; 损失函数=MSE, 优化器=adam, 批大小=32.
2) ELM. 输入层: 单元数=168; 隐藏层: 单元数=128, 激活函数=ReLU; 输出层: 单元数: 24.
3) LSTM. 输入层: 输入形状=(7, 24). LSTM层1: 单元数=64, 激活函数=tanh; LSTM层2: 单元数=32, 激活函数=tanh. 输出层: 单元数: 24, 激活函数=Sigmoid. 损失函数=MSE, 优化器=adam, 批大小=32.
|
图 7 分量重构结果 |
本实验中模型的训练和预测采用的是Keras和TensorFlow框架.
6 实验结果| 表 1 单模型与所提模型性能比较 |
| 表 2 混合模型与所提模型性能比较 |
将所提预测模型EMD-TCN-ELM与引入EMD后的3个混合模型EMD-TCN、EMD-ELM、EMD-LSTM的预测结果比较可观察到以下结果: 1)对3个单模型引入EMD技术后得到3个混合模型EMD-TCN、EMD-ELM、EMD-LSTM, 相较于原来的3个单一模型TCN、ELM、LSTM. 3个混合模型的MAPE和RMSE均有所降低, 相较于单一模型, 其MAPE分别降低了0.512%、0.307%、0.868%. RMSE分别降低了132.399 MW、85.415 MW、228.385 MW, 验证了EMD在对负荷预测精度提升方面的稳健性. 可见、EMD能降低原始负荷序列的复杂性, 通过训练“EMD分解-重构”的规律性更强的重构子序列, 降低了预测模型的预测难度, 进而提高了模型的预测精度. 2)在所有的预测模型中, EMD-TCN-ELM的预测误差最低, 然后依次是EMD-TCN、EMD-LSTM、EMD-ELM. EMD-TCN-ELM模型相较于其他3种模型EMD-TCN、EMD-ELM、EMD-LSTM. MAPE分别降低了0.026%, 1.559%, 0.323%. RMSE分别降低6.686 MW、446.002 MW、91.456 MW. 可见, 不管是与单模型TCN、ELM、LSTM比较, 还是混合模型EMD-TCN、EMD-ELM、EMD-LSTM比较, EMD-TCN-ELM模型的预测误差仍然最低, 预测精度最高. 验证了所提模型的稳健性. 3)就训练时间而言, EMD-ELM的训练时间最低, 然而, 相较于其他3种模型, 其预测误差较大. 而在余下的3种模型EMD-TCN-ELM、EMD-TCN、EMD-LSTM中, EMD-TCN-ELM的训练时间最短, 且预测精度最高.
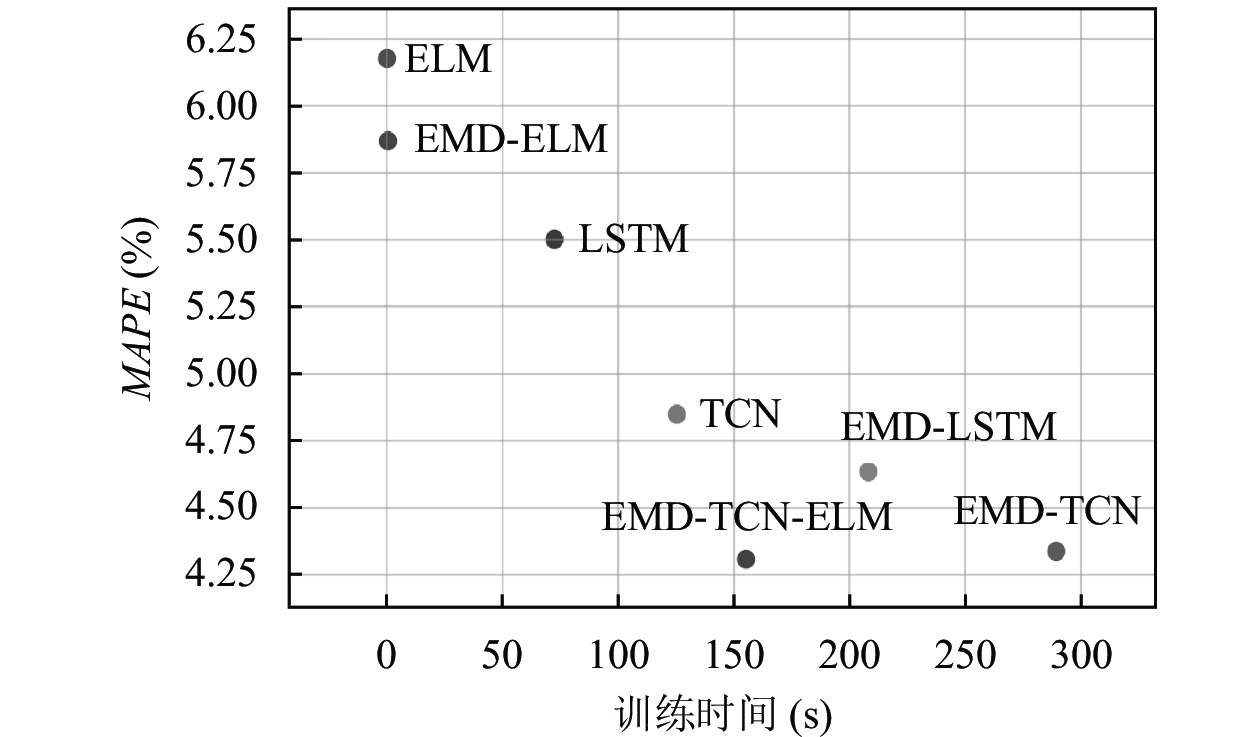
所有模型MAPE与训练时间对比图如图8所示, 由图可知, 在所有预测模型中, 本文所提模型预测精度最高, 在预测精度前面前3的模型EMD-TCN-ELM, EMD-LSTM、EMD-TCN中, 本文同时还具有最短的训练时间. 可见, 本文所提模型在保证最高的预测精度前提下还具有较短的训练时间, 相较于其他预测模型, 本文所提模型EMD-TCN-ELM有较大的优势.
|
图 8 模型训练时间与MAPE对比图 |
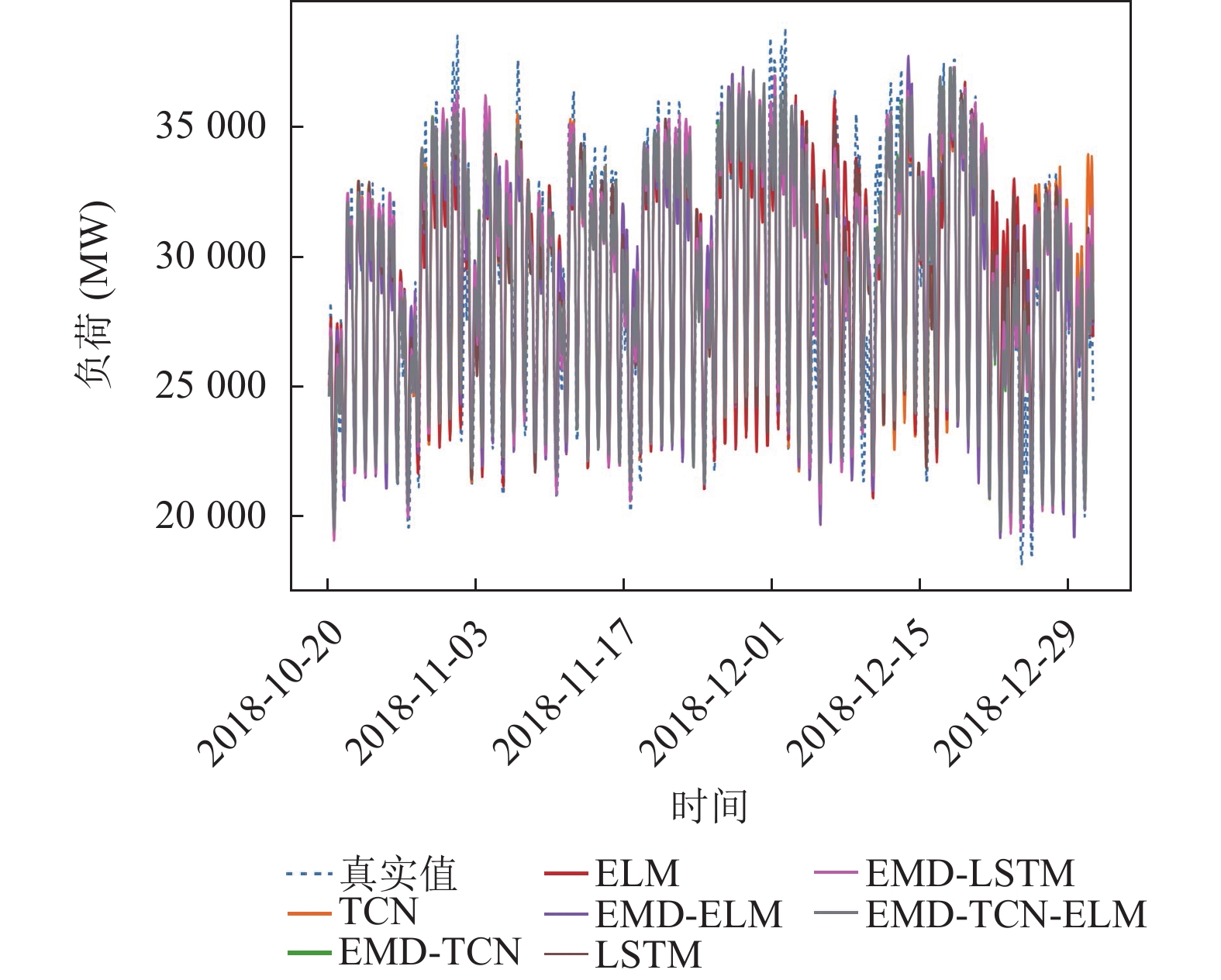
各个预测模型在测试集的预测负荷与真实负荷对比如图9所示.
|
图 9 预测负荷与真实负荷对比图 |
7 结论
1) EMD分解-重构技术的引入能降低原始负荷序列的复杂性, 有利于模型的预测, 从而提高模型的预测精度.
2) TCN模型相较于LSTM、ELM模型, 其预测精度更高, 但训练时间也最长. 而ELM模型的训练时间最短, 但在复杂时间序列问题上, 其预测精度较差.
3) 利用TCN模型捕捉高频分量信息, 利用ELM模型捕捉低频分量信息. 在保证预测精度最高的前提下, 还能较大程度的缩短训练时间. TCN-ELM模型的组合方式有较大的优越性.
EMD-TCN-ELM的组合方式预测精度最高的原因在于EMD-TCN-ELM的组合方式增加了模型的多样性. 从而降低了模型的泛化误差, 提高了模型的预测精度.
| [1] |
周纲, 黄瑞, 刘谋海, 等. 基于变分模态分解和复合变量选取的短期负荷预测. 电测与仪表, 1–9. http://kns.cnki.net/kcms/detail/23.1202.th.20220114.0939.002.html. [2022-01-20].
|
| [2] |
包满. 基于Elman神经网络模型的短期电力负荷预测模型. 电子设计工程, 2022, 30(1): 121-126. DOI:10.14022/j.issn1674-6236.2022.01.026 |
| [3] |
王洪亮, 陈新源, 赵雨梦. 基于集合经验模态分解和ARIMA-GRNN的负荷预测方法. 电子科技, 2021, 34(12): 42-48. DOI:10.16180/j.cnki.issn1007-7820.2021.12.008 |
| [4] |
杨首晖, 陈传彬, 王雪晶, 等. 基于小波变换和季节性Holt-Winters模型的短期负荷预测方法. 电力需求侧管理, 2021, 23(5): 70-75. DOI:10.3969/j.issn.1009-1831.2021.05.014 |
| [5] |
石文清, 吴开宇, 王东旭, 等. 基于时间序列分析和卡尔曼滤波算法的电力系统短期负荷预测. 自动化技术与应用, 2018, 37(9): 9-12, 23. DOI:10.3969/j.issn.1003-7241.2018.09.003 |
| [6] |
亓晓燕, 刘恒杰, 侯秋华, 等. 融合LSTM和SVM的钢铁企业电力负荷短期预测. 山东大学学报(工学版), 2021, 51(4): 91-98. |
| [7] |
冯忠义, 王咏欣, 袁博, 等. 基于随机森林和改进局部预测的短期电力负荷预测. 水利水电技术(中英文), 2021, 52(S2): 300-305. DOI:10.13928/j.cnki.wrahe.2021.S2.067 |
| [8] |
那幸仪, 贾俊铖, 赵晓筠, 等. 基于小波变换和LSTM模型的城市天然气负荷预测. 计算机应用与软件, 2021, 38(12): 61-66. DOI:10.3969/j.issn.1000-386x.2021.12.011 |
| [9] |
郭玲, 徐青山, 郑乐. 基于TCN-GRU模型的短期负荷预测方法. 电力工程技术, 2021, 40(3): 66-71. DOI:10.12158/j.2096-3203.2021.03.010 |
| [10] |
秦勉, 钟建伟, 朱永丹, 等. 基于GA-ELM的短期负荷预测研究. 湖北民族大学学报(自然科学版), 2021, 39(1): 111-114. DOI:10.13501/j.cnki.42-1908/n.2021.03.021 |
| [11] |
方娜, 余俊杰, 李俊晓, 等. 注意力机制下的EMD-GRU短期电力负荷预测. 华侨大学学报(自然科学版), 2021, 42(6): 817-824. |
| [12] |
任成国, 肖儿良, 简献忠, 等. EMD-LSTM算法在短期电力负荷预测中的应用. 电力科学与工程, 2019, 35(8): 12-16. DOI:10.3969/j.ISSN.1672-0792.2019.08.003 |
| [13] |
郭涛, 马林东, 葛智平, 等. 基于EMD和神经网络的短期电力负荷预测. 电子设计工程, 2013, 21(21): 105-106, 109. DOI:10.3969/j.issn.1674-6236.2013.21.034 |
| [14] |
Huang ME, Shen Z, Long SR, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [15] |
庞红旗, 高飞翎, 程国开, 等. 基于经验模态分解和极限学习机的日输电量分时建模预测. 智慧电力, 2021, 49(9): 63-69. DOI:10.3969/j.issn.1673-7598.2021.09.009 |
| [16] |
Bai SJ, Kolter JZ, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv: 1803.01271, 2018.
|
| [17] |
Huang GB, Zhu QY, Siew CK. Extreme learning machine: A new learning scheme of feedforward neural networks. Proceedings of 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541). Budapest: IEEE, 2004. 985–990.
|
 2022, Vol. 31
2022, Vol. 31



