2. 中国科学院大学, 北京 100049;
3. 南京师范大学, 南京 210023
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Nanjing Normal University, Nanjing 210023, China
强相互作用是自然界中4种(强、弱、电磁、引力)基本相互作用之一. 1974年, Wilson建立的格点量子色动力学(Lattice quantum chromodynamics, 格点QCD)规范理论[1]是从第一性原理出发研究强相互作用的基本理论和方法, 尤其是在高能物理的低能区, 格点QCD是当前已知的最为系统最为可靠的非微扰理论方法, 对高能物理实验和理论的研究都有着重要意义.
格点QCD算法与软件的研究是利用该方法开展强子谱学、核子结构、QCD相变、标准模型精确检验和新物理寻等高能物理研究的基础支撑.
在国际上, 格点QCD作为重要的高性能计算应用, 并且形成诸多优秀的模拟计算软件. 例如21世纪初美国USQCD的Chroma[2], 以及2010年发展出的GPU异构加速计算库QUDA[3, 4]; 日本从2009年开始研发适应日本格点计算研究需求的计算软件Bridge++[5, 6], 而后发展出面向日本超级计算机“富岳”的格点QCD的计算库QWS[7, 8]; 近年来英国的Grid[9, 10]在数据处理的矢量化设计上表现突出, 对于不同架构的机器具有较好适应性.
目前, 随着国内高性能计算机的发展, 国内格点QCD研究团队积极开展面向国产超算平台的格点计算软件研发工作. 在申威、天河等不同超算平台上探索式地进行了软件移植和自主开发工作[11-16].
本团队致力于使用HIP框架开发针对国产ROCm异构平台的格点QCD异构计算程序库Openchiral, 首次在HIP框架下自主实现了国产ROCm环境的格点QCD计算所需基本核心功能模块. 格点QCD计算的核心热点模块为有限差分的狄拉克(Dirac)方程求解, 也即QCD传播子的求解过程, 下称求解器, 其热点运算为Dslash运算(参见第2.1节). 本文工作首先实现了格点QCD相关的矩阵向量操作、基本核函数Dslash和共轭梯度(conjugate gradient, CG)求解器出发, 而后逐步进行算法改进和计算优化, 实现了在ROCm国产异构平台上高效稳定的格点QCD传播子求解器.
2 格点QCD求解器及基本流程格点QCD是定义在
本文以基本的格点QCD的Wilson费米子作用量为例, 对应的求解方程形式如下:
| $ \left[ {{\gamma _\mu }{D_\mu } + m} \right]\varphi = M\varphi = {\text{b}} $ | (1) |
其中,
| $ \begin{split} M = & \left( {4 + m} \right){\delta _{\tilde x, \tilde y}} - \frac{1}{2}\sum\limits_{\mu = 0}^3 {\left[ {(1 - {\gamma _\mu }){U_\mu }(\tilde x){\delta _{\tilde x + \mu , \tilde y}}} \right.} \\ & + (1 + {\gamma _\mu })U_\mu ^{\dagger} (\tilde x - \mu )\left. {{\delta _{\tilde x - \mu , \tilde y}}} \right] \end{split} $ | (2) |
其中,
稳定高效的Dslash运算和求解器将会显著提升格点QCD计算的整体性能. 通常使用的共轭梯度等迭代求解算法需调用第2.1节所述的Dslash操作, 现有的稀疏矩阵求解库难以满足需求, 通常需要为其专门实现一套求解器.
格点QCD求解器模块工作流程如下:
1) 初始化费米子数据.
2) 加载组态数据.
3) 开始迭代求解.
4) 对求出的解进行验算.
计算流程图如图1所示, 待求解矩阵
程序中主要包含以下模块:
1) 数据初始化模块: 初始化费米子场、组态数据.
2) 迭代求解模块: 使用费米子场、组态数据构造所求的矩阵方程
3) Dslash模块: 在异构加速卡完成迭代求解过程中的矩阵向量乘运算.
4) 验算模块: 对求解器给出的解进行验算, 确认正确性.

|
图 1 求解流程示意图 |
3 优化方案设计与实现
在基于HIP框架实现面向国产ROCm异构平实现核心运算Dslash基础上, 进一步通过算法改进和异构访存优化, 用以提高收敛速度、降低问题规模. 具体优化方案如下:
1)在实现CG (算法1)求解器的基础之上实现BiCGSTAB (算法2)求解器, 相对于CG求解器迭代次数更少、收敛速度更快.
2)采用奇偶预处理方法降低求解问题的规模, 进一步减少迭代次数并提高每轮迭代的速度.
3)在异构访存优化方面, 通过Dslash合并异构访存与改用锁页内存方式, 减少每轮迭代时CPU与加速卡的通讯开销, 降低每轮迭代耗时.
算法1. CG算法
procedure CG (
end if
算法2. BiCGSTAB算法
procedure BiCGSTAB (M,x,
相对于CG算法(算法1), BiCGSTAB算法(算法2)能够求解非正定矩阵. 更重要的是, BiCGSTAB可以减少迭代次数, 提升计算效率. 在第i轮迭代中, 记
| $ \begin{split} r_i^B &= {\rho _i}\left( M \right)r_i^G = \left( {I - {\omega _i}M} \right){\rho _{i - 1}}\left( M \right)r_i^G \\ &= \left( {I - {\omega _i}M} \right)\left( {I - {\omega _{i - 1}}M} \right){\rho _{i - 2}}\left( M \right)r_i^G \\ &= \cdots = \mathop \prod \limits_{k = 0}^i \left( {I - {\omega _{\text{k}}}M} \right)r_i^G \end{split} $ | (3) |
由式(3)可知当
在迭代求解过程中, 主要的热点是Dslash操作. BiCGSTAB需要计算
根据格点QCD离散化的时空结构网格和费米子矩阵类差分形式, 对费米子矩阵
| $ M = \left[ {\begin{array}{*{20}{c}} {{M_{ee}}}&{{M_{eo}}} \\ {{M_{oe}}}&{{M_{oo}}} \end{array}} \right] $ | (4) |
其中,
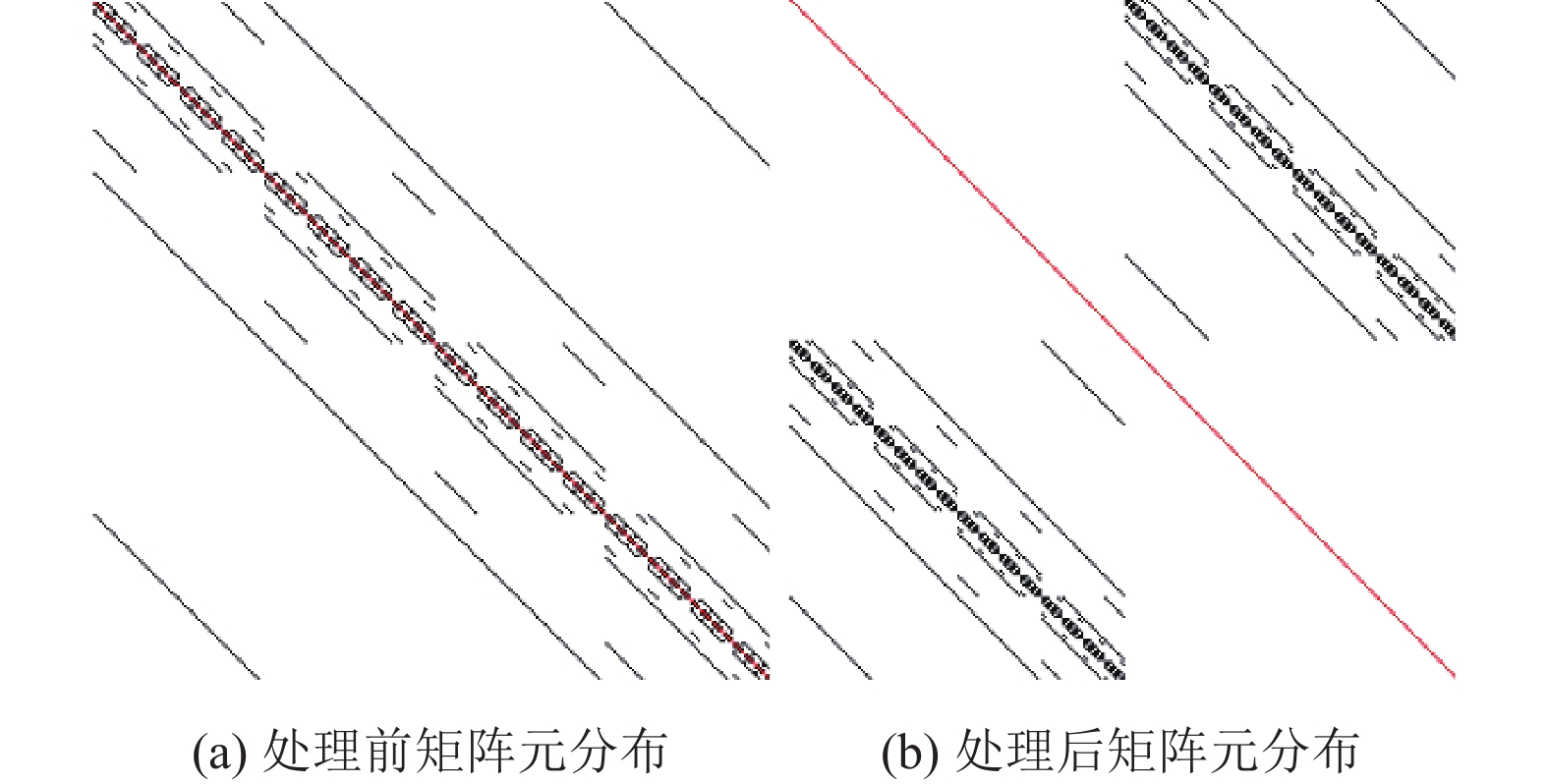
|
图 2 费米子矩阵奇偶预处理示意图 |
经过奇偶预处理后的费米子矩阵M, 可以做如下形式的分解:
| $ M = L\tilde MU $ | (5) |
其中,
| $ \tilde M = \left[ {\begin{array}{*{20}{c}} {{M_{ee}}}&0 \\ 0&{{M_{oo}} - {M_{oe}}M_{ee}^{ - 1}{M_{eo}}} \end{array}} \right] $ | (6) |
因此, 经过奇偶预处理后, 式(1)所示的线性求解问题
| $\left\{ { \begin{gathered} {L}{\tilde MU}{\varphi} ={ b} \\ {\tilde M}{\varphi }' = {b'} \end{gathered}} \right. $ | (7) |
其中,
| $ L = \left[ {\begin{array}{*{20}{c}} {1}&{0} \\ {{M_{oe}}M_{ee}^{ - 1}}&{1} \end{array}} \right], \; U = \left[ {\begin{array}{*{20}{c}} {1}&{M_{ee}^{ - 1}{M_{eo}}} \\ {0}&{1} \end{array}} \right] $ |
其逆矩阵
| $ {L^{ - 1}} = \left[ {\begin{array}{*{20}{c}} I&0 \\ { - {M_{oe}}M_{ee}^{ - 1}}&I \end{array}} \right], \; {U^{ - 1}} = \left[ {\begin{array}{*{20}{c}} I&{ - M_{ee}^{ - 1}{M_{eo}}} \\ 0&I \end{array}} \right] $ |
其中,
| $ M_{oo}^{ - 1} = M_{ee}^{ - 1} = 1/\left( {4 + m} \right) $ |
因此, 经过奇偶预处理后, 需要数值迭代求解仅为式(6)和式(7)下半部分, 仍记为
在迭代求解过程中, Dslash操作是计算热点, 提升这部分的计算效率可以显著提升迭代求解的速度. 我们基于HIP框架实现了Dslash的异构计算加速, 优化了异构计算访存.
经过奇偶预处理后, 迭代求解中的Dslash操作的内容就变为了
由于费米子矩阵元素数量是所依赖数据元素数量的12倍, 所以Dslash操作不直接构建和存储稀疏矩阵
迭代求解时, 每轮迭代进行Dslash操作时都需要通过PCIe接口向加速卡传输组态数据与费米子场数据, 这一操作是由HIP框架提供的API完成的.
默认情况下C、C++中使用new或malloc所分配的内存空间是可分页内存. 在HIP框架中, 从主存向显存传输数据前必须先分配临时页锁定数据, 再传输到显存, 如图4(a)所示.

|
图 3 两次Dslash操作数据传输优化示意图 |

|
图 4 可分页内存与锁页内存通讯示意图 |
HIP框架提供了分配锁页内存的功能, 即hipHostMalloc()函数. 相比可分页内存, 将待传输的数据存入锁页内存省去了锁页与拷贝的步骤, 可以加快数据传输速度, 如图4(b)所示. 在格点QCD计算迭代求解时, 需要传输的数据为费米子场向量与规范场数据. 将费米子与规范场的数据存储在锁页内存, 可以大幅提高加速卡与内存通讯的速度.
4 实验分析本工作完成了以上几种优化手段的代码实现与性能测试. 在中科先导一号计算平台上, 优化后的求解程序相比最初的程序大体达到了30倍的加速比.
为适应不同问题规模, 本论文以下性能测试为弱扩展性测试, 具体测试规模如表1所示: 每节点的负载不变, 总计算量随节点数成比例扩展. 程序测试的规模以格子的
| 表 1 测试规模 |
以
在表2中, 我们给出了不同规模下上述几种优化手段的求解耗时表现, 表格中从左到右优化手段顺次叠加, “锁页内存”即为最终优化后的程序. 可以看出, 充分优化后的程序在不同规模都达到了30倍左右的加速比. 图5直观地展示、对比了几种优化手段之间的耗时表现.

|
图 5 求解耗时优化示意图 |
在表3中, 给出各优化手段与对应减少的耗时, 从各个方法所优化耗时与最终减少的耗时的占比来看, 奇偶预处理降低了所求解问题的规模, 对耗时优化贡献最大, 平均贡献总优化耗时的48%; BiCGSTAB算法减少了迭代次数, 平均贡献了总优化耗时的26%; 合并访存、锁页内存降低了加速卡访存的开销, 降低了每轮迭代的耗时, 对总优化耗时分别贡献了12%与13%.
4.2 迭代次数优化效果本文所采取的几种优化手段中, BiCGSTAB与奇偶预处理有效减少了收敛迭代次数, 接下来将两者与原始程序的迭代收敛表现做对比分析.
在表4中, 我们在不同规模下对比了几种收敛优化手段的迭代收敛表现, 从左到右优化手段顺次叠加, 分别为原始程序(CG)、BiCGSTAB求解器与奇偶预处理的BiCGSTAB求解器. 从中我们可以看出, 原始程序中的CG求解器, BiCGSTAB与奇偶预处理在不同规模下都展现出了大致相同的优化效果. 最终优化后的程序求解收敛所需的迭代次数在不同规模下平均减少为原始程序的33.4%.
在图6中, 我们给出了3种算法在128卡下求解

|
图 6 求解收敛优化示意图 (128卡) |
| 表 2 求解速度对比 |
| 表 3 优化表现对比 |
| 表 4 迭代次数对比 |
5 结论与展望
本文针对格点QCD求解器设计实现, 采取了多项优化措施, 实现了BiCGSTAB求解器, 显著减少迭代次数; 采用了奇偶预处理技术, 降低了求解问题的规模; 针对HIP/ROCM异构计算平台采取了合并、加速访存等优化方式. 本文还开展了多种规模的并行测试, 最大规模为64节点、256块加速卡, 相比原始程序实现了约30倍的加速比.
格点QCD是一种重要的高性能计算应用, 性能优化后的程序可以更好地支撑格点QCD研究, 充分发挥国产异构超算平台的算力.
| [1] |
Wilson KG. Confinement of quarks. Physical Review D, 1974, 10(8): 2445-2459. DOI:10.1103/PhysRevD.10.2445 |
| [2] |
Edwards RG, Joó B. The chroma software system for Lattice QCD. Nuclear Physics B-Proceedings Supplements, 2004, 140: 832-834. |
| [3] |
Clark MA, Babich R, Barros K, et al. Solving Lattice QCD systems of equations using mixed precision solvers on GPUs. Computer Physics Communications, 2010, 181(9): 1517-1528. DOI:10.1016/j.cpc.2010.05.002 |
| [4] |
Babich R, Clark MA, Joó B, et al. Scaling Lattice QCD beyond 100 GPUs. Proceedings of 2011 International Conference for High Performance Computing, Networking, Storage and Analysis. Seattle: ACM, 2011. 70.
|
| [5] |
Akahoshi Y, Aoki S, Aoyama T, et al. General purpose Lattice QCD code set Bridge++ 2.0 for high performance computing. arXiv: 2111.04457, 2021.
|
| [6] |
Ueda S, Aoki S, Aoyama T, et al. Development of an object oriented Lattice QCD code “Bridge++”. Journal of Physics: Conference Series, 2014, 523: 012046. DOI:10.1088/1742-6596/523/1/012046 |
| [7] |
Kanamori I, Ishikawa KI, Matsufuru H. Object-oriented implementation of algebraic multi-grid solver for Lattice QCD on SIMD architectures and GPU clusters. Proceedings of the 21st International Conference on Computational Science and Its Applications. Cagliari: Springer, 2021. 218–233.
|
| [8] |
Ishikawa KI, Kanamori I, Matsufuru H, et al. 102 PFLOPS Lattice QCD quark solver on Fugaku. arXiv: 2109.10687, 2021.
|
| [9] |
Boyle P, Yamaguchi A, Portelli A, et al. Grid: A next generation data parallel C++ QCD library. Proceedings of the 33nd International Symposium on Lattice Field Theory. Kobe: Kobe International Conference Center, 2016.
|
| [10] |
毕玉江, 周超, 吴郁非, 等. 格点量子色动力学Grid数值模拟软件的并行计算特征分析. 计算机系统应用, 2020, 29(7): 199-204. DOI:10.15888/j.cnki.csa.007498 |
| [11] |
张淼, 周宇, 陈建海, 等. LQCD Dslash在神威·太湖之光上的研究分析与MPI实现. 计算机科学与探索, 2019, 13(10): 1664-1676. DOI:10.3778/j.issn.1673-9418.1811029 |
| [12] |
田英齐, 毕玉江, 贺雨晴, 等. 格点量子色动力学组态产生和胶球测量的大规模并行及性能优化. 计算机系统应用, 2019, 28(9): 25-32. DOI:10.15888/j.cnki.csa.007036 |
| [13] |
栾钟治, 张增校, 杨海龙, 等. 基于异构众核处理器的格点量子色动力学并行加速方法: 中国, CN201910750655.3. 2019-08-14.
|
| [14] |
Bi YJ, Xiao Y, Guo WY, et al. Lattice QCD package GWU-code and QUDA with HIP. Proceedings of the 37th International Symposium on Lattice Field Theory. Wuhan: PoS, 2020.
|
| [15] |
Bi YJ, Xiao Y, Guo WY, et al. Lattice QCD GPU Inverters on ROCm Platform. EPJ Web of Conferences, 2020, 245: 09008. DOI:10.1051/epjconf/202024509008 |
| [16] |
宫明, 蒋翔宇, 陈莹, 等. 从格点量子色动力学应用看国产超算环境的基础软件. 大数据, 2021, 7(5): 31-39. |
 2022, Vol. 31
2022, Vol. 31


