2. 中国科学技术大学 国际金融研究院, 合肥 230026
2. International Institute of Finance, University of Science and Technology of China, Hefei 230026, China
推荐系统作为一种有效的过滤手段, 可对体量庞大、类型繁多、结构复杂的数据进行挖掘和建模分析, 帮助用户快速、准确地筛选其感兴趣的信息, 大幅节省检索花费的时间和精力, 从而缓解信息过载问题. 其应用可涵盖诸多领域, 如电子商务领域中的“猜你喜欢”专栏、书籍影音领域中电影评分及推荐功能;社交网络领域中推荐可能认识的好友.
矩阵分解模型因其在Netfilx举办的推荐系统大赛上获得优胜而倍受研究者关注[1]. 该模型针对用户与项目间的评分进行建模, 假定用户的偏好、项目的特征由高维空间中的隐因子向量所决定, 隐因子各分量表示无法被直接观测到的属性特征, 进一步用其内积表示评分.
为更好地利用相似用户间的信息以提高预测性能, 本文采用了基于用户聚类的概率矩阵分解模型(clustering Bayesian probabilistic matrix factorization, CBPMF), 在已知聚类结果的条件下, 通过指数族共轭先验形成概率生成模型, 利用矩阵分解思想进行评分预测.
1 相关工作推荐系统可分为3大类方法: 基于内容、协同过滤和混合式方法[2, 3]. 本文主要关注协同过滤方法, 此方法应用广泛, 预测表现优异, 其核心假设为相似的用户会与相似的商品产生相似的交互, 因此可仅依靠已存在的用户和项目之间的历史交互, 即观测评分, 完成目标用户推荐. 而矩阵分解则隶属协同过滤方法大类, 研究关注于在不同场景中拓展矩阵分解模型, 利用高效的算法估计模型参数, 同时保持预测精度.
传统矩阵分解方法假设观测到的数据来自低维的线性子空间, 重构便可得到矩阵的低秩结构, 可利用特征值分解、非负矩阵分解等方法求解参数[4, 5]. 而Salakhutdinov等人对矩阵分解施加了严格的概率分布, 从而建立概率矩阵分解模型的基本框架, 用于处理体量大、数据稀疏、结构不平衡的电影评分数据集[6]. 进一步地, 为了解决超参数选择困难的问题, Salakhutdinov等人引入共轭先验, 提出贝叶斯概率矩阵分解模型, 对应地使用Gibbs采样算法估计参数[7].
矩阵分解还融合除观测评分外的其他信息, 提出了概率矩阵分解模型的变体, 以缓解数据稀疏问题, 从而提高预测性能. 为了利用用户间关系, Ma等人将用户信任矩阵与评分矩阵结合, 提出了基于社交网络的概率矩阵分解模型, 缓解了只考虑评分信息时的数据稀疏问题[8]. Liu等人融合了社交关系和项目内容信息, 假设用户和项目隐因子各自服从不同的先验分布, 以此提高预测精度[9]. Peng等人考虑现实中具有信任关系的用户偏好其实并不相似的情况, 将用户偏好相似性约束在特定领域, 提出了基于信任和偏好切分的矩阵分解模型[10]. Feng等人同时考虑用户评分和局部关系相似性, 以解决推荐系统场景中数据稀疏的问题[11].
在参数估计方面, 目前求解隐因子的算法主要有MCMC[12]、变分近似推断[13, 14]以及梯度下降. Lim等人提出了基于变分推断的SVD矩阵分解算法[15]. Luo等人利用伽马共轭先验缓解正态假设不稳健及数据缺失的问题, 采用了MCMC方法进行参数估计, 提供了统计意义上的解释[16]. Zhao等人构造了L1范数惩罚, 利用变分近似推断求解低秩矩阵分解模型中的参数, 在计算机视觉领域取得了较好结果[17]. 王娟等人使用随机梯度下降算法进行矩阵分解模型的参数求解[18]. Blei等人指出相比于MCMC方法, 变分推断以损失部分精度为代价获得更快的收敛速度, 因此更适合于体量较大的数据集[19].
目前研究大多考虑将用户集合视作整体, 或认为各用户之间互不相同, 两种建模思路均未采用聚类方法, 无法利用相似用户之间的信息提升预测表现, 且后者还会因待估参数过多而造成过拟合. 本文采用的聚类概率矩阵分解模型可有效解决用户先验分布设置过于粗糙或过于精细而导致评分预测不准确的问题. 具体来说, 此模型有两处创新, 其一, 通过贝叶斯分层使同一水平之间的随机变量共享信息, 对用户聚类并使同类用户服从同一先验, 进而提升用户偏好预测的准确性; 其二, 更换先验形式, 构建贝叶斯框架, 完成对模型参数的正则化, 并且考虑多个模型的平均而非某一特定模型, 防止过拟合现象. 此外, 本文将采用变分推断方法, 对应CBPMF模型, 推导得到各随机变量对应变分分布的显式表达式, 从而建立变分坐标下降算法以估计参数.
2 聚类概率矩阵分解模型本节主要对CBPMF模型的评分生成过程作详细说明. 概率矩阵分解模型主要针对推荐系统中的评分数据进行建模. 假定用户i对项目j的评分
| p(Rij|UTiVj,σ20)=N(Rij|UTiVj,σ20) | (1) |
给定用户聚类结果, CBPMF模型假定同一类别中用户的先验分布相同, 在每一类下利用各自先验参数分别进行矩阵分解, 最后根据隐因子估计预测评分. 具体来说, 假定用户的类别为常数K, 类别向量为
| {p(Ui|μUzi,τUzi)=ND(Ui|μUzi,(τUzi)−1I)p(Vj|μV,τV)=ND(Vj|μV,(τV)−1I) | (2) |
其中,
| {p(μUk|μ0,σ2U)=ND(μUk|μ0,σ2UI)p(τUk|a0,b0)=Γ(τUk|a0,b0) | (3) |
其中,
| {p(μV|μ0,σ2V)=ND(μV|μ0,σ2VI)p(τV|a0,b0)=Γ(τV|a0,b0) | (4) |
此处模型所采用的先验为正态-正态、正态-伽马双重共轭分布, 对应的概率生成过程如图1所示, 其中实心圆

|
图 1 CBPMF模型概率图 |
3 变分近似算法
模型过于复杂而导致参数无法求解是概率生成模型常见的困难之一. 本文将采用变分推断近似估计模型参数, 从而完成评分的预测工作.
3.1 贝叶斯变分推断理论根据贝叶斯推断, 参数估计需根据后验分布进行, 但其因为积分运算过于复杂而无显式表达, 故无法直接通过最大化后验分布估计参数
| q(U,V,ΘU,ΘV)=N∑i=1q(Ui)M∑j=1q(Vj)⋅K∑k=1{q(μUk)q(τUk)}q(μV)q(τV) | (5) |
CBPMF模型似然函数
| {q(Ui)∝exp{E−Ui[logp(U,V,ΘU,ΘV,R|Θ0)]}q(Vj)∝exp{E−Vj[logp(U,V,ΘU,ΘV,R|Θ0)]} | (6) |
其中,
| {μUk∼ND(μU∗k,ΣU∗k),k=1,⋯,KμV∼ND(μV∗,ΣV∗) | (7) |
其中, 均值向量为:
| {μU∗k=ΣU∗−1k⋅(σ−2Uμ0+E[τUk]∑i∈U(k)E[Ui])μV∗=ΣV∗−1⋅(σ−2Vμ0+E[τV]∑j=1ME[Vj]) | (8) |
协方差矩阵为:
| {ΣU∗k=(σ−2U+E[τUk]NUk)−1IΣV∗=(σ−2V+E[τV]M)−1I | (9) |
其中,
同样条件下, 先验参数
| {τUk∼Gamma(aU∗k,bU∗k),k=1,⋯,KτV∼Gamma(aV∗,bV∗) | (10) |
其中, 形状参数为:
| aU∗k=DNUk2+a0,k=1,⋯,K;aV∗=DM2+a0 | (11) |
且
| {bU∗k=b0+12∑i∈U(k)E[(Ui−μUk)T⋅(Ui−μUk)]bV∗=b0+12M∑j=1E[(Vj−μVk)T⋅(Vj−μVk)] | (12) |
在此基础上, 可推导得预测评分所必须的用户、项目隐因子参数服从多元正态分布, 即:
| {Ui∼ND(μ∗Ui,Σ∗Ui),i=1,⋯,NVj∼ND(μ∗Vj,Σ∗Vj),j=1,⋯,M | (13) |
其中, 均值向量为:
| {μ∗Ui=Σ∗Ui⋅(E[τUzi⋅μUzi]+σ−20M∑j=1IijRijE[Vj])μ∗Vj=Σ∗Vj⋅(E[τV⋅μV]+σ−20N∑i=1IijRijE[Ui]) | (14) |
及协方差矩阵为:
| {Σ∗Ui=(E[τUzi]I+σ−20M∑j=1IijE[VjVTj])−1Σ∗Vj=(E[τV]I+σ−20N∑i=1IijE[UiUTi])−1 | (15) |
由于CBPMF模型采用指数族共轭先验, 故导出变分分布形式上与原分布保持一致. 上述期望计算均可根据基本矩阵运算得到, 在此不过多赘述.
3.2 评分预测算法根据上述理论推导, 本节给出CBPMF模型评分预测算法. 具体来说, 该算法可视作坐标下降过程, 首先初始化变分参数集
算法1. CBPMF模型评分预测算法
(1) 清洗数据得到评分矩阵
(2) 初始化变分参数集
(3) while 变分下界未达到收敛 do:
(4)
1) 根据式(7)、式(8), 更新每一类别中用户先验均值向量
2) 根据式(7)、式(8), 更新单一项目先验均值向量
3) 根据式(14)、式(15), 更新每一用户的隐因子向量的多元正态分布参数;
4) 根据式(14)、式(15), 更新每一项目的隐因子向量的多元正态分布参数;
5) 根据当前变分参数
(5) end while
(6) 根据收敛的用户、项目隐因子, 预测未观测的评分, 即
(7) 将目标用户的预测评分进行排序, 推荐排名最靠前的k个项目;
得到变分参数集合
本算法基于变分近似推断的统计原理构建, 运用变分参数近似CBPMF模型中的真实后验分布, 从而根据最大化后验分布估计参数, 其理论复杂度为
为了契合推荐系统应用场景, 本文根据协同过滤思想来产生模拟数据, 同时结合聚类方法, 考虑不同类别中用户表现存在的差异[20], 具体来说, 模拟数据假定存在
基准模型则采用贝叶斯概率矩阵分解模型BPMF以及社交关系矩阵分解模型SRBPMF, 其中BPMF模型对应未考虑用户的相似性, 不进行聚类, 假定所有用户隐因子服从同一先验分布的情况, 因此对模型参数的惩罚较弱; 而SRBPMF模型则对应所有用户各自服从参数不同的先验分布的情况, 即每个用户各为一类, 此方法假设过于强, 存在相当大的过拟合风险. 本文采用的CBPMF模型则可视作通过聚类对上述两种方法作了折中处理.
从表1 MAE、MSE可明显看出本文采用的CBPMF模型在预测上的表现优于BPMF模型和SRBPMF模型, 且三者中SRBPMF模型表现最差; MAE、MSE的标准差于括号中显示, 从中可以看出模拟数据中3类模型预测波动不大. 因SRBPMF模型需要待估参数与用户数量成线性增长, 当用户数量较多时, 过拟合的风险非常高; 而BPMF模型则无法利用同一类别用户之间的相似关系, 两者均无法较好处理模拟数据中的异常值, 因此预测表现均不如CBPMF模型. 另一方面, CBPMF模型具有分层贝叶斯结构, 在对用户进行聚类后, 可共享同一水平的用户信息, 当某用户观测到异常值而导致估计偏差时, 该类别下的参数先验分布通过赋予一个较低的先验概率值而达到正则化的作用, 降低异常值影响, 表现更为鲁棒.
| 表 1 评分预测情况汇总表 |
|
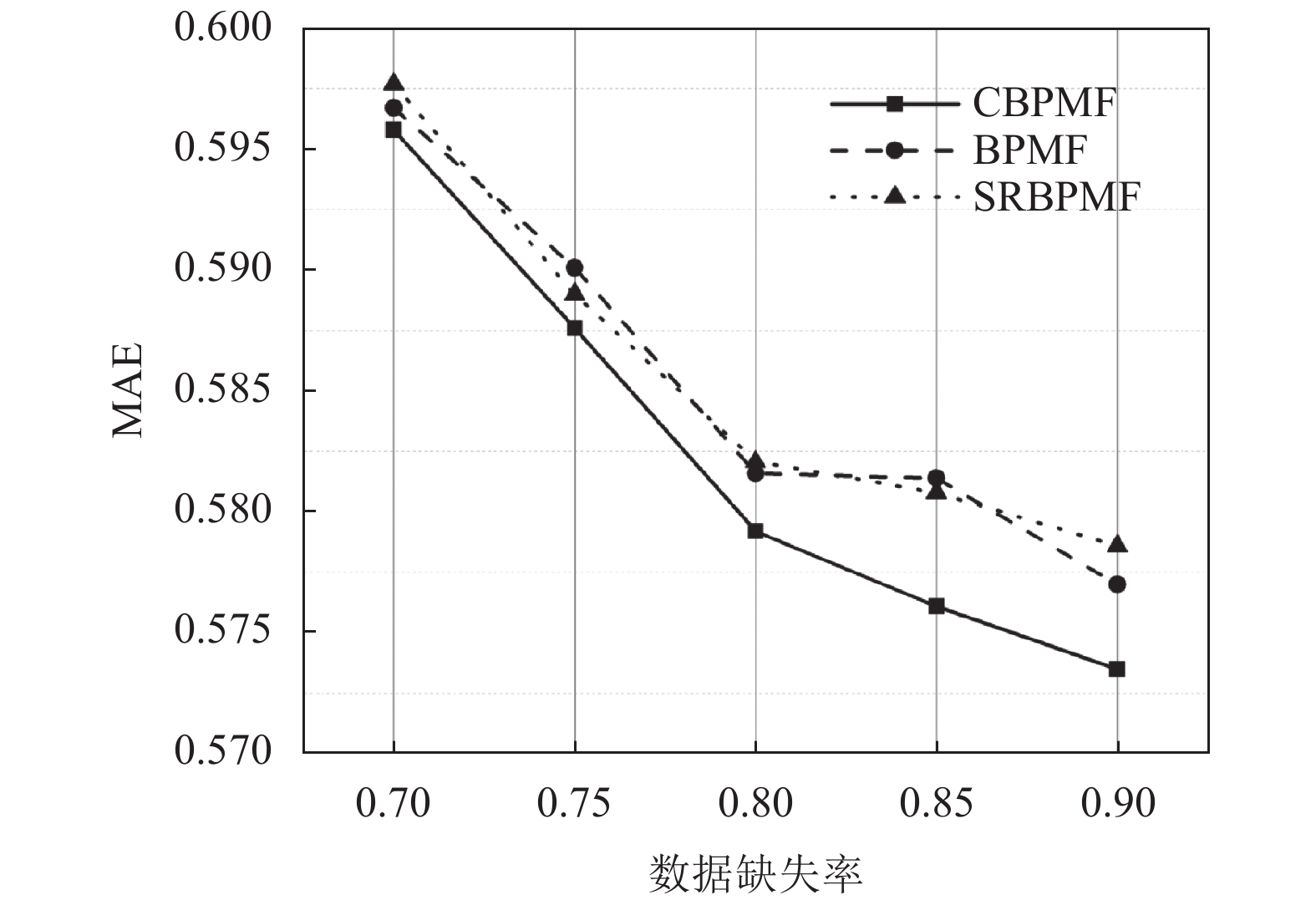
图 2 各模型MAE随数据缺失率变化折线图 |
模拟考虑不同数据缺失率对模型预测准确性的影响, 结果如图2所示, 对于任一数据缺失率而言, CBPMF模型预测表现均优于基准模型. 由于异常值占比恒定为10%, 随着可观测数据的增加, 异常值的数量也随之同步增加, 故在本模拟中数据缺失率和模型预测准确性之间成反比关系. 另外, 随着异常值总数降低, 相比于基准模型, CBPMF模型可以获得更大的提升, 意味着其能够更好地应对异常值对模型的干扰.
4.2 实证分析本小节运用MovieLens电影评分公共数据集进行实证分析. 该数据集包含943名用户和1682部电影, 交互得到评分数据共计10000条, 具体还包括用户的性别与年龄、电影的名称及类型等描述性信息. 为保证评分有效性, 该数据集中每位用户至少对20部以上电影给出过评分. 评分取值于离散有限集合, 即
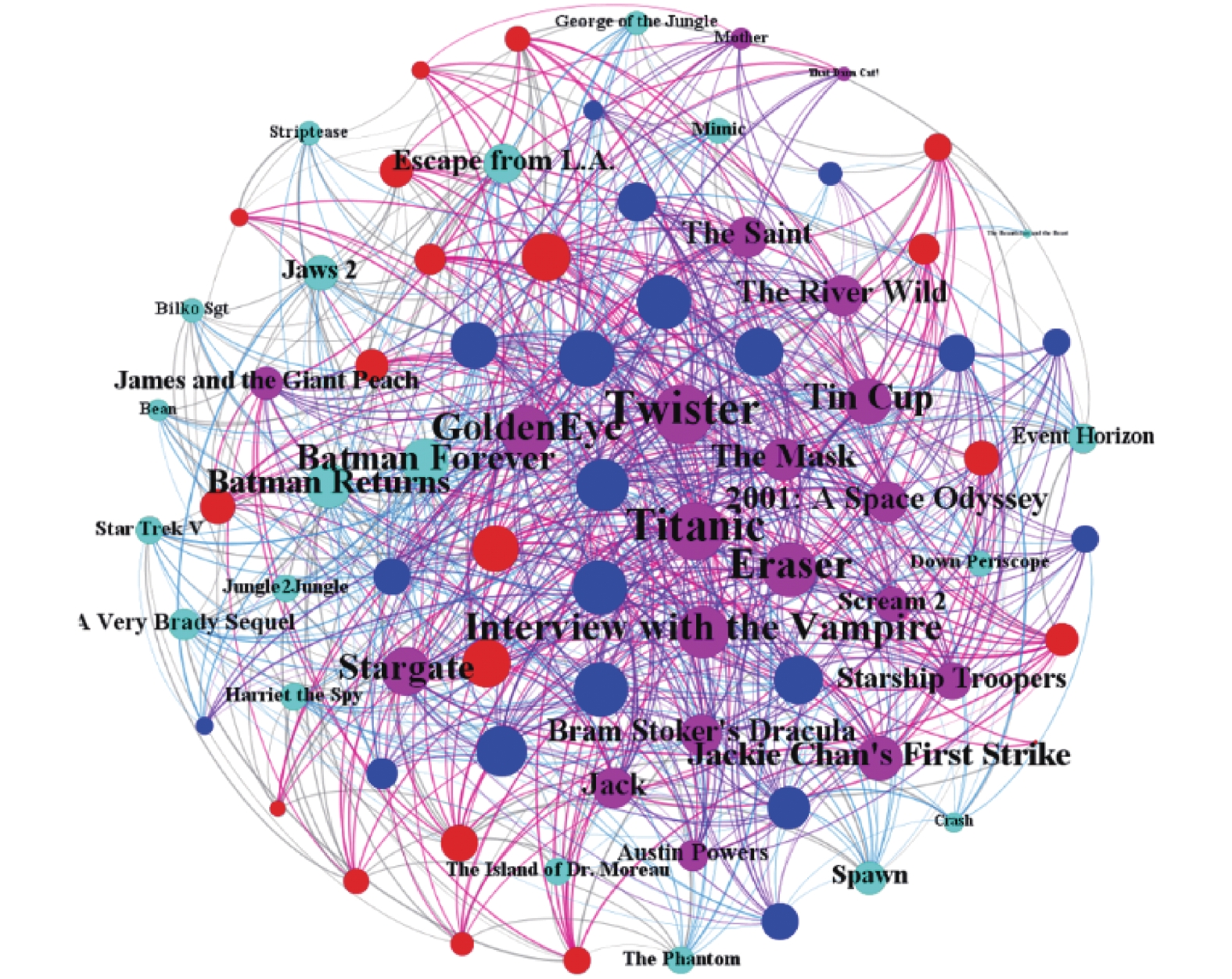
为了更加直观地观测用户对电影评分的倾向, 本小节挑选了平均评分位于正态分布前25%的严格用户(用深蓝色节点表示), 以及位于后25%的宽容用户(用红色节点表示)两类用户群体, 根据评分情况绘制网络结构图, 如图3所示. 若电影节点的度越大, 则表明该电影被观看次数越多, 反之亦然; 若用户节点发出的边为红色, 则说明该用户给出评分为4或5的积极评价, 反之则用蓝色边表示消极评价.
|
图 3 用户电影评分球状网络结构图 |
对球形网络图进行分析可得以下结论: (1) 电影的评分与其自身质量紧密相关. 高质量电影(粉色节点)集中在球形网络中间且边为红色, 标签对应为现实中《007》《泰坦尼克号》等电影; 反之低质量电影(浅蓝色)游离于网络边缘, 边为蓝色, 对应的电影知名度较低; (2) 电影所受关注度与其自身质量紧密相关. 半径较大的节点所多为红色, 表示高质量电影受到关注度高; 反之则半径小的节点颜色多为蓝色, 表示低质量电影较少被人观看; (3) 用户评分表现出明显的倾向性. 对于同一电影而言, 宽容用户更倾向于给出积极评价, 表现为红色节点的边多为红色; 反之严格用户倾向于给出消极评价, 表现为浅蓝色节点的边多为蓝色.
根据用户评分均值, 事先得到类别数量为K=3的聚类结果. 根据不同随机数种子进行5折交叉验证, 进一步得到MovieLens数据集中的评分预测的评价指标MAE和MSE的均值如表2所示. 与模拟表现类似, 在隐空间维度和10和20的情况下, CBPMF模型预测表现均明显优于基准模型BPMF和SRBPMF. 标准差于括号中显示, 从标准差表现上看, CBPMF模型表现更为稳定, 随5折交叉验证抽取数据的变化较小. 另外, 不难发现, 随着隐空间维数的增加, 模型预测性能增强.
| 表 2 MovieLens数据集上模型预测情况汇总表 |
5 结论与展望
本文考虑现实中不同用户之间存在相似性的特点, 通过正态-正态、正态-伽马两种共轭指数先验构建贝叶斯分层结构, 将矩阵分解模型拓展为用户聚类情形下的概率矩阵分解模型. 一方面, 聚类概率矩阵分解模型(CBPMF)将具有相似评分倾向的用户聚为一类, 使其共享同一先验参数, 以此提高模型的预测准确性. 另一方面, 贝叶斯框架可通过对先验参数积分来考虑多个模型的平均, 从而达到防止过拟合的作用, 事实上在模型角度, 先验可视为对参数的一种正则化. 在参数估计上, 本文运用平均场变分推断思想, 使用变分分布近似真实后验分布, 严格推导得到变分参数的显式表达式, 从而对应拓展得到CBPMF模型评分预测算法, 此算法与推荐系统内的用户和项目数量呈线性关系, 可快速得到变分参数的近似估计.
虽然实证表明用户聚类可显著提高预测表现, 但本文未考虑不同的聚类方法所带的影响. 如K-means、层次聚类法等, 从而进一步挖掘评分数据中用户的潜在倾向, 讨论预测工作. 此外, 类别数量
| [1] |
Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer, 2009, 42(8): 30-37. DOI:10.1109/MC.2009.263 |
| [2] |
Bobadilla J, Ortega F, Hernando A, et al. Recommender systems survey. Knowledge-based Systems, 2013, 46: 109-132. DOI:10.1016/j.knosys.2013.03.012 |
| [3] |
Najafabadi MK, Mohamed AH, Mahrin MN. A survey on data mining techniques in recommender systems. Soft Computing, 2019, 23(2): 627-654. DOI:10.1007/s00500-017-2918-7 |
| [4] |
Shi JR, Zheng XY, Yang W. Survey on probabilistic models of low-rank matrix factorizations. Entropy, 2017, 19(8): 424. DOI:10.3390/e19080424 |
| [5] |
Qiao HL. New SVD based initialization strategy for non-negative matrix factorization. Pattern Recognition Letters, 2015, 63: 71-77. DOI:10.1016/j.patrec.2015.05.019 |
| [6] |
Salakhutdinov R, Mnih A. Probabilistic matrix factorization. Proceedings of the 20th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2007. 1257–1264.
|
| [7] |
Salakhutdinov R, Mnih A. Bayesian probabilistic matrix factorization using Markov chain Monte Carlo. Proceedings of the 25th International Conference on Machine Learning. Helsinki: ACM, 2008. 880–887.
|
| [8] |
Ma H, Yang HX, Lyu MR, et al. SoRec: Social recommendation using probabilistic matrix factorization. Proceedings of the 17th ACM Conference on Information and Knowledge Management. Napa Valley: ACM, 2008. 931–940.
|
| [9] |
Liu JT, Wu CH, Liu WY. Bayesian probabilistic matrix factorization with social relations and item contents for recommendation. Decision Support Systems, 2013, 55(3): 838-850. DOI:10.1016/j.dss.2013.04.002 |
| [10] |
Peng W, Xin BG. A social trust and preference segmentation-based matrix factorization recommendation algorithm. EURASIP Journal on Wireless Communications and Networking, 2019, 2019(1): 272. DOI:10.1186/s13638-019-1600-4 |
| [11] |
Feng CJ, Liang JY, Song P, et al. A fusion collaborative filtering method for sparse data in recommender systems. Information Sciences, 2020, 521: 365-379. DOI:10.1016/j.ins.2020.02.052 |
| [12] |
Brooks S. Markov chain Monte Carlo method and its application. Journal of the Royal Statistical Society: Series D, 1998, 47(1): 69-100. DOI:10.1111/1467-9884.00117 |
| [13] |
Beal MJ, Ghahramani Z. The variational Bayesian EM algorithm for incomplete data: With application to scoring graphical model structures. Proceedings of the Bayesian Statistics 7: The 7th Valencia International Meeting. Tenerife, 2002. 453–464.
|
| [14] |
Wainwright MJ, Jordan MI. Graphical models, exponential families, and variational inference. Foundations and Trends® in Machine Learning
, 2008, 1(1–2): 1-305. DOI:10.1561/2200000001 |
| [15] |
Lim Y, Teh Y. Variational Bayesian approach to movie rating prediction. Proceedings of Knowledge Discovery and Data Mining. 2006.
|
| [16] |
Luo C, Zhang B, Xiang Y, et al. Gaussian-Gamma collaborative filtering: A hierarchical Bayesian model for recommender systems. Journal of Computer and System Sciences, 2017, 102: 42-56. DOI:10.1016/j.jcss.2017.03.007 |
| [17] |
Zhao Q, Meng DY, Xu ZB, et al. L1-norm low-rank matrix factorization by variational Bayesian method
. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(4): 825-839. DOI:10.1109/TNNLS.2014.2387376 |
| [18] |
王娟, 熊巍. 基于矩阵分解的最近邻推荐系统及其应用. 统计与决策, 2019, 35(6): 17-20. DOI:10.13546/j.cnki.tjyjc.2019.06.004 |
| [19] |
Blei DM, Kucukelbir A, McAuliffe JD. Variational inference: A review for statisticians. Journal of the American Statistical Association, 2017, 112(518): 859-877. DOI:10.1080/01621459.2017.1285773 |
| [20] |
Godoy-Lorite A, Guimerà R, Moore C, et al. Accurate and scalable social recommendation using mixed-membership stochastic block models. Proceedings of National Academy of Sciences of the United States of America, 2016, 113(50): 14207-14212. DOI:10.1073/pnas.1606316113 |
 2022, Vol. 31
2022, Vol. 31



